Persistence and origin of the lunar core dynamo

Abstract

The lifetime of the ancient lunar core dynamo has implications for its power source and the mechanism of field generation. Here, we report analyses of two 3.56-Gy-old mare basalts demonstrating that they were magnetized in a stable and surprisingly intense dynamo magnetic field of at least ∼13 μT. These data extend the known lifetime of the lunar dynamo by ∼160 My and indicate that the field was likely continuously active until well after the final large basin-forming impact. This likely excludes impact-driven changes in rotation rate as the source of the dynamo at this time in lunar history. Rather, our results require a persistent power source like precession of the lunar mantle or a compositional convection dynamo.

The existence of a global planetary magnetic field provides evidence of an advecting liquid core. Although the Moon does not have a global field today, lunar crustal magnetism and paleomagnetism in returned samples provide evidence of an ancient lunar dynamo (1, 2). Laser ranging experiments (3) and reanalysis of Apollo-era seismic data (4, 5) indicate that the Moon currently has a small (∼330 km) partially molten metallic core. Recent paleomagnetic studies of slowly cooled, unshocked samples demonstrate that the Moon had a core dynamo at 4.2 Ga (6) and 3.7 Ga (7). However, the subsequent history of the lunar dynamo is largely unknown.

Determining the lifetime of the lunar dynamo would constrain the nature of its power source and the mechanism of magnetic field generation. Models of core thermal convection have found that a lunar dynamo can only unambiguously persist for as late as 4.1 Ga, well before the youngest current evidence for the magnetic field at 3.7 Ga (7). Although a compositional convection dynamo driven by the crystallization of the core is also possible, the lifetime of such a dynamo is currently unclear. This has motivated alternative models that use precession (8, 9) and/or basin-forming impacts (10) to power the dynamo mechanically via differential motion between the liquid core and rocky mantle. Precession appears to be capable of powering a dynamo until as late as ∼1.8–2.7 Ga (9). By comparison, a dynamo driven by impact-induced unlocking from synchronous rotation could likely be active only when basin-forming impacts occurred, before or during the Early Imbrian epoch (≥∼3.72 Ga). Therefore, these two mechanisms could potentially be distinguished using measurements of the lunar magnetic field after this time.

Some Apollo-era paleomagnetic studies argued that the termination of the lunar dynamo occurred before the eruption of the Apollo 11 high-K basalts at ∼3.6 Ga (11), whereas others suggested that the dynamo persisted but slowly decayed until at least ∼3.2 Ga (12). Two Apollo 11 samples, mare basalts 10017 and 10049, provided contrasting results that were central to this debate. Analyses of 10017 (13–16) identified one of the most stable natural remanent magnetization (NRM) records identified in any lunar sample. However, the presence of Johnson Space Center (JSC) saw marks on some subsamples and what was perceived to be a wide range of paleointensities (∼40–90 μT) led these investigators to exclude 10017 as a constraint on the lunar dynamo. Instead, these authors relied on their analyses of 10049, whose subsamples were found to carry a unidirectional magnetization (17) with a seemingly weak paleointensity (4–10 μT). However, our reanalysis of their data with modern multicomponent methods yields paleointensities up to ∼30 μT (SI Appendix).

A recent paleomagnetic study found that lunar samples with ages of 3.3 Ga and in the range 3.7–3.94 Ga may have recorded a field of several tens of microteslas (18). In this study, only one sample (12002, which has an age of 3.3 Ga) was younger than Apollo high-K basalts. However, the nature of its paleomagnetic record is currently ambiguous: Its NRM does not trend toward the origin during alternating field (AF) demagnetization, its remanent magnetization derivative (REM') paleointensity (19) varies by nearly an order of magnitude throughout the demagnetization, the sample was measured while encased in a container whose moment was similar to the demagnetized sample, and no mutually oriented subsamples were measured.

Samples

Mare basalts 10017 and 10049 are fine-grained, high-K ilmenite basalts of petrological group A (20, 21). Their major phases are pyroxene (50.6 vol % and 51.3%, respectively), plagioclase (23.6 vol. % and 24.5%, respectively), and ilmenite (15.1 vol % and 14.1%, respectively), and minor mesostasis includes high-K glass (21) (SI Appendix). These basalts erupted at ∼3.56 Ga and form the present surface of most of the southwest portion of Mare Tranquillitatis. The collected rock samples are thought to have been excavated by the impact that formed West Crater ∼100 Ma (21), ∼0.5 km from the Apollo 11 landing site.

We observed similar mineral assemblages and compositions as those previously described for these samples (21). Our electron microprobe analyses of metal in 10017,62 and 10049,40 found that it has a composition of nearly pure metallic iron (Fe_1−xNi_x with x < 0.02) and is typically intergrown with troilite (SI Appendix). Because the high-temperature taenite phase (γ-Fe) with this bulk composition transforms fully to kamacite at 912 °C, which is above Curie temperature of 780 °C (22), the kamacite in these rocks should have acquired a pure thermoremanent magnetization (TRM) during primary cooling rather than the thermochemical remanent magnetization that forms when x > 0.03 (23). Rock magnetic experiments (SI Appendix) indicate that the kamacite grain size is in the multidomain range for both 10017 and 10049.

To constrain the samples’ cooling rates below 1,100 °C, we measured the width of the largest plagioclase lath perpendicular to the (010) faces following the method used by Grove and Beaty (20) (SI Appendix, Section 9). Our measured values of 550 μm and 120 μm indicate cooling rates of ∼0.03 °C⋅h⁻¹ and ∼0.43 °C⋅h⁻¹ for 10017 and 10049, respectively, which correspond to cooling times from the Curie point to ambient lunar surface temperatures of ∼10³ d and ∼10² d, respectively. Because these samples are antiophitic, these are likely minimum estimates of the cooling timescale (20). These time scales are much longer than the expected 1-d maximum lifetime of fields generated by basin-forming impacts (24). Therefore, any primary magnetization in these samples is likely a record of a temporally stable field like that expected for a core dynamo. Furthermore, we observed no petrographic evidence for shock (peak pressure <5 GPa), such as plagioclase fracturing, mechanical twinning, or alteration to maskelynite (SI Appendix). Mare basalts 10017 and 10049 are therefore ideal samples for testing the lunar dynamo hypothesis late in lunar history.

NRM

We carried out AF demagnetization up to 85–290 mT on eight mutually oriented subsamples of 10017,378 and on three mutually oriented subsamples of 10049,102 (all samples without JSC saw cut faces). Because 10017 and 10049 were collected as regolith float by the Apollo astronauts, they are not mutually oriented, although their individual subsamples are mutually oriented with respect to their parent rock. We found that the subsamples had NRM intensities of 5.5 × 10⁻⁶–3.5 × 10⁻⁵ Am²⋅kg⁻¹ for 10017 and 1.1 × 10⁻⁵ to 2.3 × 10⁻⁵ Am²⋅kg⁻¹ for 10049. All demagnetized samples were observed to have two components of magnetization (Fig. 1, Table 1, and SI Appendix). All samples had a low coercivity (LC) and a high coercivity (HC) component. The LC component was removed by AF demagnetization up to somewhere between 9 and 20 mT for subsamples of 10017, with the exception of subsample 378-10, for which the LC and HC components demagnetized concurrently up to several tens of microteslas. The LC component was removed by AF demagnetization between 4 and 11.5 mT for subsamples of 10049. For all samples (with the exception of subsample 378-10), these values are lower than or comparable to those observed by previous studies: The LC component was removed at ∼50 mT for 10017 (16) and at ∼20 mT for 10049 (17). The LC component is inconsistent in direction between subsamples (Fig. 2) and decays like an isothermal remanent magnetization (IRM) during AF demagnetization (SI Appendix). The ratio of the LC component to an IRM (19) ranges between 0.026 and 0.083 over its coercivity range. These results indicate that the LC components in each basalt are likely to be overprints acquired in a strong artificial field during transportation (25) or preparation of the samples at the JSC.

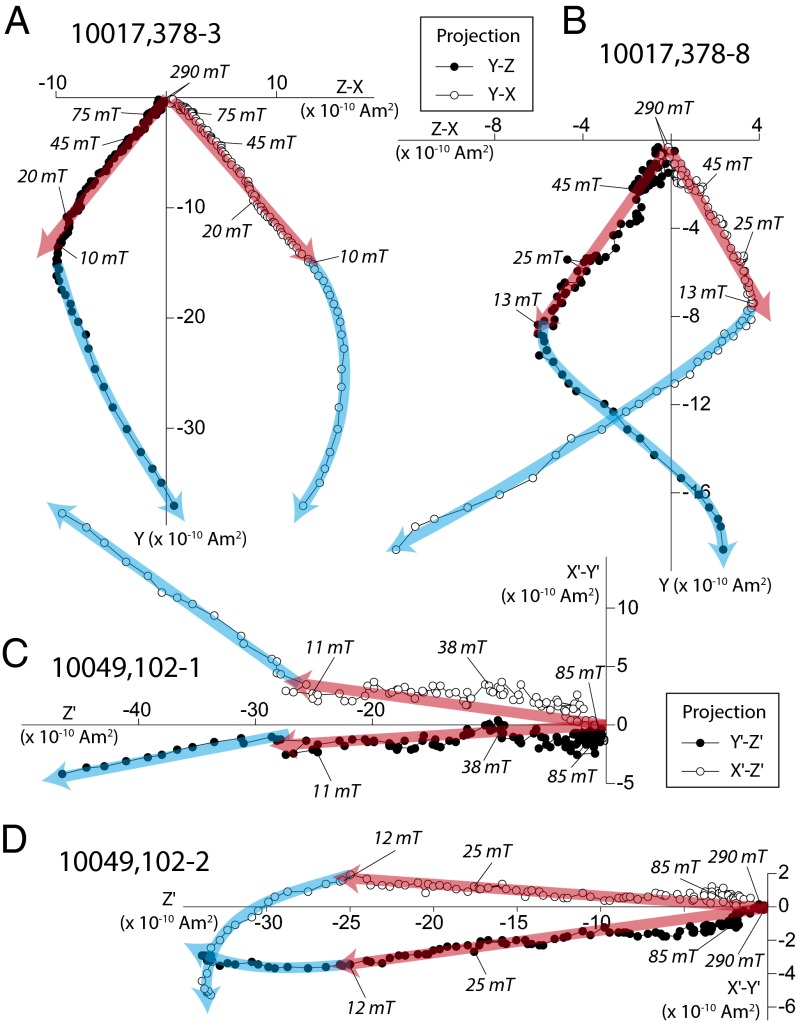
Fig. 1.

NRM in mare basalts 10017 and 10049. Shown is a 2D projection of the NRM vectors of subsamples 10017,378-3; 10017,378-8; 10049,102-1; and 10049,102-2 during AF demagnetization. Solid (●) [open (○)] circles represent end points of magnetization projected onto the Y–Z (X–Y) planes for 10017 and onto the Y′–Z′ (X′–Z′) planes for 10049. Peak fields for selected AF steps are labeled in microteslas. Red arrows denote HC component directions determined from principal component analyses. Subsample 10017,378-3 (A); subsample 10017,378-8 (B); subsample 10049,102-1 (C); and subsample 10049,102-2 (D).

Table 1.

Summary of LC and HC components for subsamples from 10017,378 and 10049,102 obtained with principal component analysis

Sample	Component	AF range, mT	Type	Dec., Inc.; °	MAD, °	DANG, °	N	Paleointensity, μT
								ARM, 50 μT	ARM, 100 μT	IRM
10017,378-1	LC	NRM-10	L	52.0, −30.9	2.3		19
	HC	10.5–85	AL	310.6, −44.0	4.1/4.8	3.5	90
10017,378-2	LC	NRM-9	L	322.0, 43.5	23.3		17
	HC	9.5–120	AL	310.0, −35.6	2.8/3.6	1.3	102	83.5 ± 1.2	80.6 ± 0.8	95.1 ± 4.6
10017,378-3	LC	NRM-10	L	271.3, 25.4	7.9		19
	HC	10.5–290	AL	312.6, −30.1	4.8/5.7	3.0	101	78.2 ± 1.7	76.7 ± 1.1	82.9 ± 1.6
10017,378-6	LC	NRM-20	L	232.6, 25.6	7.8		39
	HC	20.5–85	AL	303.6, −34.0	7.0/12.3	1.9	70
10017,378-7	LC	NRM-10	L	186.8, 16.0	3.0		19
	HC	10.5–85	AL	308.7, −35.4	3.9/5.7	2.3	90	64.9 ± 1.2	55.5 ± 0.8	61.9 ± 3.0
10017,378-8	LC	NRM-13	L	213.1, 26.7	5.2		25
	HC	13.5–110	AL	297.1, −28.8	10.0/14.0	5.8	95	50.5 ± 1.5	47.2 ± 1.6	43.2 ± 2.3
10017,378-10	LC	NRM-20	L	219.2, −24.1	7.3		39
	HC	20–180	AL	271.7, −51.4	3.8/4.9	2.5*	128
	HC	20–180	C	78.1, −37.9	18.2		128
	All	NRM-180	C	95.3, −37.6	15.7		166
10017,378-11	LC	NRM-15	L	243.3, −58.6	8.2		30
	HC	15–180	AL	313.5, −40.1	3.0/4.2	4.1*	137
10049,102-1	LC	NRM-10.5	L	353.1, −53.3	5.7		20
	HC	11–85	AL	332.5, −77.9	10.6/13.7	4.7	89	69.7 ± 5.3	86.3 ± 4.6	95.2 ± 4.3
10049,102-2	LC	NRM-11.5	L	175.2, −51.2	12.6		22
	HC	12–290	AL	294.2, −80.2	5.2/6.0	2.9	96	55.2 ± 1.3	49.3 ± 1.0	59.1 ± 3.2
10049,102-3	LC	NRM-4	L	268.6, −1.1	23.8		3
	HC	6–85	AL	339.7, −79.1	6.6/9.1	7.6	20

The first column gives the subsample name and component name; the second column gives the magnetization component; the third column gives the range of AF steps used for the fit; the fourth column gives the fit type (AL, line anchored to the origin; C, circle fit forced through the origin, poles reported; L, line); the fifth column gives the declination (Dec.) and inclination (Inc.) of the fit direction (for line fits) or great circle pole (for circle fits); the sixth column gives the MAD of the component forced through the origin/not forced through the origin; the seventh column gives the DANG; and the eighth column gives the number of AF steps used in fit (N). The last three columns give paleointensities: ARM paleointensity (in microteslas) = (NRM lost)/(ARM lost)/f′ × [bias field (in microteslas)] × anisotropy correction factor, IRM paleointensity (in microteslas) = (NRM lost)/(IRM lost) × a × anisotropy correction factor. We used f′ = 1.34 and a = 3,000. Uncertainties on each paleointensity value are formal 95% confidence intervals on the slope fit using the Student t test (31) and do not include the factor of ∼3–5 uncertainty associated with the unknown ratios of ARM and IRM to TRM.

^*DANG calculated using first point of fit.

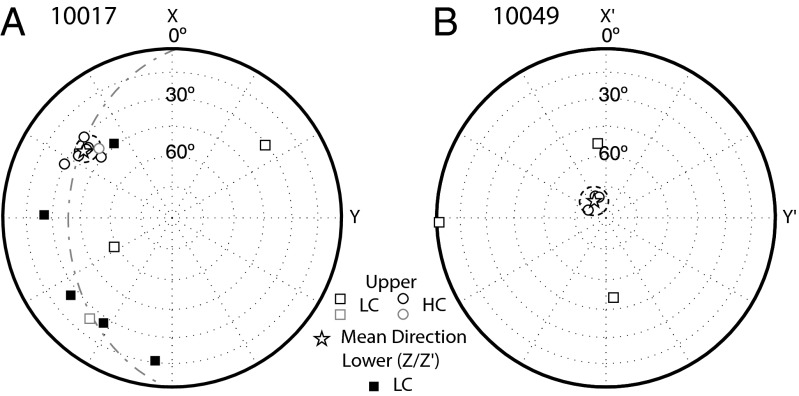
Fig. 2.

Equal area stereographic projection of NRM component fits. Circles denote HC directions (primary magnetization) for each subsample, and squares denote LC directions (overprint). The stars are the Fisher mean HC direction from principal component analyses, with surrounding dashed ellipses indicating 95% formal confidence intervals on mean directions (not accounting for additional ∼3–5° mutual orientation uncertainty). (A) Sample 10017,378. Black and gray symbols correspond to samples measured at the Massachusetts Institute of Technology and University of California, Santa Cruz, respectively. The dashed great circle denotes a circle fit forced through the origin for the HC data of subsample 10. (B) Sample 10049,102.

The HC component was observed to decay throughout the demagnetization up to at least 85 mT for all subsamples. Stepwise demagnetization was carried out up to even higher fields for samples 10017,378-2, 10017,378-3, 10017,378-8, and 10049,102-2 (SI Appendix). We found that subsample 378-3 had a directionally stable HC magnetization that continued to decay in intensity up to 120 mT, beyond which it remained directionally stable but without further decay up to 290 mT [likely due to anhysteretic remanent magnetization (ARM) noise]. We found that the HC magnetization in subsample 378-2 was stable in direction and continued to decay in intensity up to 120 mT, at which point the sample had completely demagnetized (i.e., became directionally unstable). Subsample 378-8 was stable in direction and decaying in intensity up to 110 mT, beyond which it remained relatively stable in direction with a superposed random component, again likely due to ARM noise. Subsample 102-2 was stable in direction and decaying in intensity up to 290 mT, whereas subsamples 102-1 and 102-3 were directionally stable and decayed in intensity up to at least 85 mT. The HC components are unidirectional within both 10017,378 and 10049,102. The maximum angle between the HC directions is 18° for 10017 and 8° for 10049. For 10017, the Fisher mean direction 95% confidence angle is 6.0° and the Fisher precision parameter is k = 153 (number of samples, n = 6). For 10049, the Fisher mean direction 95% confidence angle is 6.9° and the Fisher precision parameter is k = 478 (n = 3). Given the orientation uncertainty of ∼5–10° and maximum angular deviation (MAD) values in the range of 2.8–10.0° for 10017 and 5.2–10.6° for 10049, the HC directions are therefore indistinguishable from one another within both samples. In the absence of a statistical method to estimate whether a magnetization component is origin-trending with a confidence interval, we compared the angle between the best-fitting line through the data and the line connecting the origin with the center of mass of the data [deviation angle (DANG) (26)] with the MAD. We found a DANG < MAD for all HC components for both basalt samples, suggesting that the magnetizations are origin-trending, and are therefore the characteristic magnetizations.

To determine whether the NRMs of 10017 and 10049 were contaminated by viscous remanent magnetization (VRM) acquired during their 40-y exposure to the geomagnetic field since return to Earth, and how much of this VRM subsequently decayed during storage in our shielded room before our NRM measurements, we conducted VRM acquisition and decay experiments (SI Appendix). For 10017, we found that the residual VRM would be 9.4 × 10⁻¹¹ Am², equivalent to only 2.4% of the observed initial NRM. For 10049, we found that the residual VRM would be 9.3 × 10⁻¹¹ Am², equivalent to only 2.7% of the initial NRM. Therefore, neither the LC nor HC components of 10017 and 10049 are likely to be VRM-acquired in the Earth’s magnetic field.

Although our petrographic observations exclude shocks with pressures >5 GPa, even shocks with lower peak pressures could produce magnetization if a field were present. To investigate this possibility, we conducted pressure remanent magnetization (PRM) acquisition experiments (SI Appendix) for subsamples 378-3 and 102-1 following the method used by Gattacceca (27). Like previous such studies of lunar rocks (27), we found that PRM was acquired dominantly by LC grains (<∼30–40 mT) with even the 2.0-GPa PRM significantly softer than the NRM (SI Appendix). This suggests that neither the LC nor HC components are likely shock remanent magnetizations (SRM). We found that a 1-mT field and a 2-mT field would have been necessary to produce the LC and HC components of 378-3, respectively. Similarly, a 0.1-mT field and a 0.3-mT field would have been necessary to produce the LC and HC components of 102-1, respectively. Such fields are well above theoretical estimates of maximum dynamo fields for the Moon and at the upper end of predicted impact-generated fields (e.g., refs. 28, 29). Therefore, these field values provide further evidence against an SRM origin for either NRM component.

We conducted AF demagnetization of laboratory-induced magnetizations and compared them with that of the NRM. The HC component in each rock demagnetizes like an ARM [an analog of TRM (30)] and unlike either a PRM or an IRM (SI Appendix). Therefore, the HC components of 10017 and 10049 are likely TRMs acquired during cooling in a stable field on the Moon.

Paleointensity

The HC components of 10017,378 yielded anisotropy-corrected paleointensities ranging between 47 and 84 μT from the ARM method and between 43 and 95 μT from the IRM method; 10049,102 yielded anisotropy-corrected HC component paleointensities ranging between 49.3 and 86.3 μT from the ARM method and between 59.1 and 95.2 μT from the IRM method (Table 1 and SI Appendix). The range of variability between subsamples is expected, given the uncertainty in the calibration factors for these methods. Furthermore, the similarity between the ARM and IRM values gives confidence that each method is producing relatively accurate results. Given that each individual paleointensity is uncertain by a factor of 3–5, the multispecimen mean values should be significantly less uncertain than this factor. The average values for the ARM method are 67 ± 15 μT for 10017 and 65 ± 14 μT for 10049 [uncertainties are formal 95% confidence intervals on the slope fit using the Student t test (31) and do not include the factor of ∼3–5 uncertainty associated with the unknown ratios of ARM and IRM to TRM]. The average values for the IRM method are 71 ± 21 μT for 10017 and 77 ± 18 μT for 10049 (uncertainties on mean values are observed 1 SD from multiple samples). These paleointensities are indistinguishable within the uncertainty and give a mean value for all experiments on both samples of 69 ± 16 μT, which corresponds to a very conservative minimum paleofield of ∼13 μT. These values are also within error of the paleointensity inferred at 3.7 Ga from mare basalt 10020 (7) and consistent with values recently obtained for other samples with crystallization ages from 3.7 to 3.94 Ga (18) (although the age and origin of the magnetization in the latter samples are not well constrained). These paleointensities are higher than previous estimates for 10049, likely due to lack of complete NRM demagnetization in these earlier studies (SI Appendix).

Thermochronology

The 3.56-Ga crystallization ages of 10017 and 10049 place an upper limit on the time at which they acquired their magnetization. It is possible that the magnetization of these rocks could have been acquired or reset during thermal excursions following their formation. Although the lack of shock features in these rocks precludes direct shock heating, they could have experienced temperature excursions from burial in a hot ejecta blanket or nearby volcanic activity. To assess this possibility, we conducted ⁴⁰Ar/³⁹Ar and ³⁸Ar/³⁷Ar thermochronometry on two whole-rock subsamples of 10017 and 10049 (Fig. 3 and SI Appendix).

Fig. 3.

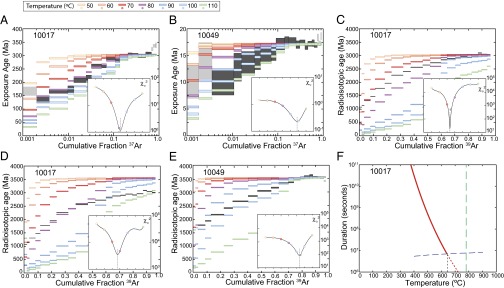
Radiogenic ⁴⁰Ar and cosmogenic ³⁸Ar thermochronometry of whole-rock mare basalts 10017 and 10049. Production and diffusion of ³⁸Ar_cos for 10017 (A) and 10049 (B). The observed exposure ages ± 1 SD (gray boxes) are plotted against the cumulative release fraction of ³⁷Ar. ³⁸Ar_cos was produced in situ while the rocks were exposed at the surface of the Moon. The colored steps are model release spectra calculated using the multiphase, multidomain model (model parameters are provided in SI Appendix) for the production and diffusion of ³⁸Ar_cos, assuming the rocks were subjected to various constant effective daytime temperatures ranging from 50 to 110 °C during the last 303.1 Ma for 10017 or during the last 17.2 Ma for 10049 (i.e., ³⁸Ar_cos is produced continuously over this duration, whereas diffusion occurs only over half of this period during elevated daytime temperatures). (Insets) Reduced χ² fit statistic for each model, identifying ∼80 °C as the best-fit effective mean temperature for 10017 and ∼95 °C as that for 10049. The diffusion of ⁴⁰Ar* due to solar heating for 10017 is shown, calculated assuming the K/Ar system was reset at 3.03 Ga (C) or 3.56 Ga (D) (symbols and model parameters are the same as in A). (E) Diffusion of ⁴⁰Ar* due to solar heating, calculated assuming the crystallization age is 3.56 Ga (symbols and model parameters are the same as in B). (F) Duration-temperature conditions required to cause >95% loss of ⁴⁰Ar* from the most retentive plagioclase domains in 10017 during the proposed 3.0-Ga thermal event (red curve). The dashed blue curve predicts the time required to cool diffusively from an initial temperature, T, to <100 °C in the center of a 6-m-thick ejecta blanket. The intersection of this curve with the solid curve gives the peak temperature that would explain the Ar data under this scenario. The green dashed line represents the Curie temperature of kamacite (780 °C).

Our analyses confirm that like other Apollo group A basalts (32), 10049 has a weighted average ⁴⁰Ar/³⁹Ar plateau age of 3,556 ± 8 Ma [uncertainty is 1 SD; uncertainty in the decay constant and age of the fluence monitor is excluded (33)]. However, 10017’s ⁴⁰Ar/³⁹Ar plateau age of 3,037 ± 7 Ma is ∼600 My younger than its crystallization age (34). Our thermochronological calculations suggest that 10017 may have been heated to several hundred °C at ∼3.05 Ga. Although this event may have partially remagnetized or demagnetized low blocking temperature grains in this rock (depending on whether a field was present at this time), many of these grains would have subsequently been demagnetized during zero-field residence on the lunar surface over the intervening 3 Ga and during residence in our laboratory’s shielded room. As has been inferred for many other Apollo 11 basalts (7, 35), both 10017 and 10049 also apparently experienced modest gas loss due to solar heating over the last 304.7 ± 2.0 Ma and 17.5 ± 0.1 Ma, respectively. In particular, numerical models of simultaneous production and diffusion of both radiogenic ⁴⁰Ar and cosmogenic ³⁸Ar indicate that sample 10049 only experienced temperatures in excess of the ambient crustal conditions because it was exposed near the lunar surface.

Implications for the Power Source of the Lunar Dynamo

Large impacts have the potential to unlock the Moon from synchronous rotation (36), such that the resulting differential motion between the librating mantle and core could generate a dynamo lasting for up to 10⁴ y (10). It is estimated that this can only occur for impactors that are larger than that required to produce a crater with a diameter of ∼300 km (assuming an Earth-Moon distance of 25 Earth radii) (36). The youngest such basin is Orientale, which formed at 3.73 Ga and marks the end of the Early Imbrian epoch (37, 38). Because this event occurred ∼160 Ma before the Late Imbrian eruption of 10017 and 10049, this likely excludes unlocking from synchronous rotation as a field source at 3.6 Ga.

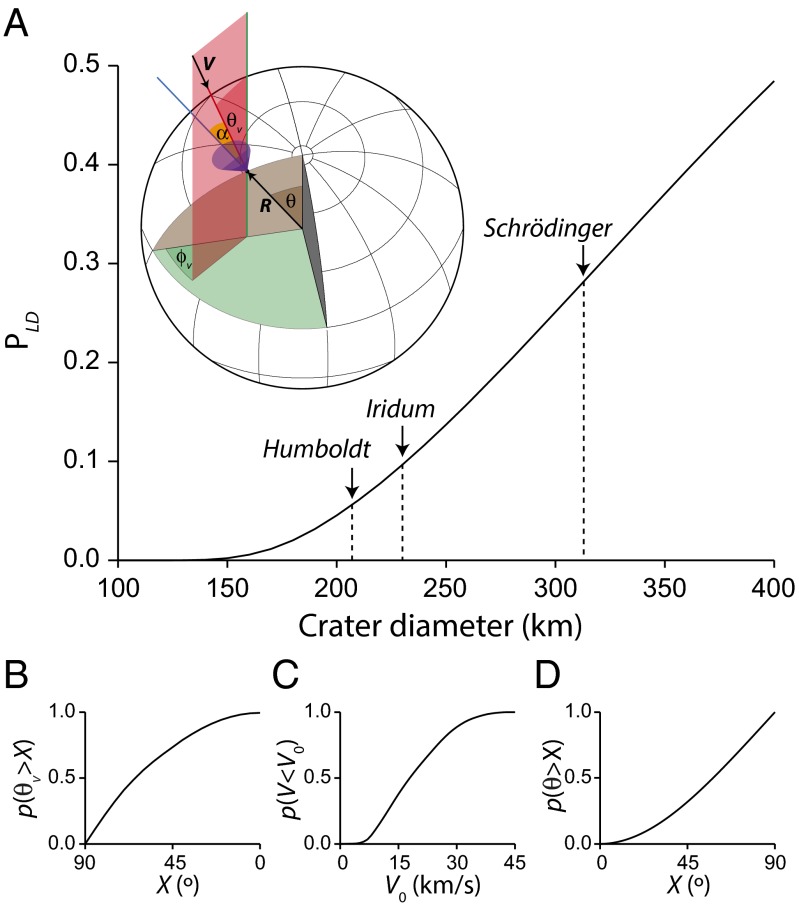
Smaller impacts that are insufficient to unlock the Moon from synchronous rotation could still generate a mechanical dynamo by inducing longitudinal free librations (10). However, it is estimated that this was only possible while the Earth-Moon separation was <∼40 Earth radii. Orbital history models constrained by geological evidence for the past 0.6 Ga (39, 40) suggest that the Earth-Moon separation was 37–44 Earth radii at 3.6 Ga, whereas uniformly scaled models give a range of 47–51 Earth radii (41). Therefore, the conditions for the existence of a libration dynamo might have been met during the eruption of the high-K basalts. Assuming this is the case, it is estimated that for the smallest Earth-Moon separation (37 Earth radii), an impact would have to produce a libration amplitude of at least 70° to trigger a libration dynamo (10). Using equations 1 and 6 in ref. 42, we determined the minimum impactor diameter [assuming a spherical bolide with uniform density of 3,500 kg⋅m⁻³ and a lunar crustal density of 2,691 kg⋅m⁻³ (43)] required to induce a libration dynamo as a function of impact location colatitude θ, impact trajectory inclination relative to the lunar spin axis θ_v, impact trajectory declination relative to the impact location ϕ_v, and velocity V (angles are defined in Fig. 4, Inset). Using the crater-scaling equation 5.6 in ref. 44, we calculated the corresponding crater size D_min. Using the impact velocity probability distribution p(V) of Le Feuvre and Wieczorek (37), the probability distribution p(θ_v) of impact inclinations of Le Feuvre and Wieczorek (45), and the probability distribution of impact geographic colatitude p(θ) calculated from the relative cratering rate variations with latitude of Le Feuvre and Wieczorek (45); assuming a uniform distribution for impact declinations ϕ_v; and ignoring the curvature of impact trajectories and acceleration due to the gravity of the Moon (which would tend to make trajectories more vertical and larger craters, and therefore reduce the effect on librations for a given crater size), we computed the probability P_LD for an impact that produces a crater with diameter D to induce a libration dynamo (Fig. 4):

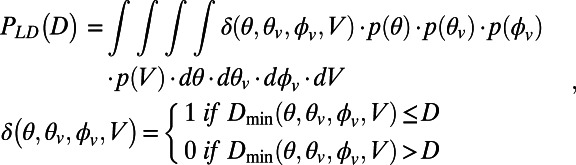where δ selects impact parameters that produce craters larger than the threshold value D_min. Impacts with incidence angles α > 80° [where α = acos(RV/|R||V|); angle and vector definitions are provided in Fig. 4, Inset] are expected to produce elliptical craters (46). Because no such crater is known to have formed in the Late Imbrian era, we excluded these trajectories. We find that only craters with a diameter >∼230 km have a probability to induce a libration dynamo >10% (Fig. 4). All the craters with a diameter >230 km identified in a recent Lunar Reconnaissance Orbiter survey* (47) are presented in SI Appendix, Table S1. The largest crater identified in the Late Imbrian era is Humboldt (38, 47); its diameter is ∼207 km, which corresponds to a probability of ∼6% to induce a libration dynamo. The youngest impacts that had a significant (>25%) probability to trigger a libration dynamo are the Early Imbrian basins Schrodinger and Orientale (47)*.

Fig. 4.

(A) Probability to have induced a libration dynamo as a function of crater diameter. The diameters of the Late Imbrian crater Humboldt and Early Imbrian craters Iridum and Schrödinger are shown. (Inset) Impact geometry. The red line is the impact trajectory; the red surface is the plane defined by the impact trajectory and a line parallel to the lunar spin axis at the impact location. The blue line is the local vertical. The purple cone represents trajectories with α > 80°. (B) Cumulative probability distribution for the inclination of the impact trajectory, θ_v (45). (C) Cumulative probability distribution for the impact velocity, V (37). (D) Cumulative probability distribution for the impact location colatitude, θ (45).

The Late Imbrian 3.56-Ga crystallization age of the high-K basalts means that they are very likely too young to have been magnetized by an impact-driven dynamo. Furthermore, attributing the paleomagnetic records of 76535 at 4.2 Ga (6), 10020 at 3.7 Ga (7), and 10017 and 10049 at 3.6 Ga to an impact-driven dynamo would require a series of transient impact-driven dynamos. The fact that the 10017 and 10049 paleointensities are so similar to one another, as well to those of the 3.72-Ga basalt 10020 (7), argues strongly in favor of a stable lunar dynamo at least between 3.72 and 3.56 Ga. This lifetime is inconsistent with existing models of core convection, which have been unable to power a dynamo unambiguously after 4.1 Ga by thermal convection alone (48). Rather, these results support the possibility of a longer-lived power source for the lunar dynamo, such as precession (9) or thermochemical convection due to core crystallization, although impact-induced core dynamos could have operated earlier in lunar history. Nevertheless, the high paleointensities of 10017 and 10049 [and 10020 (7)] still present a major challenge, given that all current lunar dynamo models are only thought to be capable of producing surface fields <15 μT (9). It currently remains unclear when the dynamo finally decayed.