True scale-invariant random spatial networks

Abstract

Some aspects of real-world road networks seem to have an approximate scale invariance property, motivating study of mathematical models of random networks whose distributions are exactly invariant under Euclidean scaling. This requires working in the continuum plane, so making a precise definition is not trivial. We introduce an axiomatization of a class of processes we call scale-invariant random spatial networks, whose primitives are routes between each pair of points in the plane. One concrete model, based on minimum-time routes in a binary hierarchy of roads with different speed limits, has been shown to satisfy the axioms, and two other constructions (based on Poisson line processes and on dynamic proximity graphs) are expected also to do so. We initiate study of structure theory and summary statistics for general processes in the class. Many questions arise in this setting via analogies with diverse existing topics, from geodesics in first-passage percolation to transit node-based route-finding algorithms.

We introduce and study a mathematical structure inspired by road networks. Although not intended as literally realistic, we do believe it raises and illustrates several interesting conceptual points and potential connections with other fields, summarized in the final section. Details will appear in a long technical paper (1). Here, we seek to explain in words rather than mathematical symbols.

Consider two differences between traditional paper maps and modern online maps for roads, which will motivate two conceptual features of our model. On paper, one needs different maps for different scales—for the intercity network and for the street network in one town. The usual simplified mathematical models involve different mathematical objects at the two scales, for instance representing cities as points for an intercity network model (2). Online maps allow you to “zoom in” so that the window you see covers less real-world area but shows more detail, specifically (for our purpose) showing comparatively minor roads that are not shown when you “zoom out” again. As a first conceptual feature, we seek a mathematical model that represents roads consistently over all scales. Next, a paper map shows roads, and the user then chooses a “route” between start and destination. In contrast, a typical use of an online map is to enter the start and destination address and receive a suggested route. As a second conceptual feature, our model will treat routes as the basic objects. That is, somewhat paradoxically, in our model routes determine roads.

Returning to the image of zooming in and out, the key assumption in our models is that statistical features of what we see in the map inside a window do not depend on the real-world width of the region being shown—on whether it is 5 miles or 500 miles. We call this property “scale invariance,” in accord with the usual meaning of that phrase within physics. Of course, our phrase “what we see” is very vague; we mean quantifiable aspects of the road network, and this is best understood via examples of quantifiable aspects described in the following section, and then the mathematical definition in the subsequent section. Note that scale invariance is not “scale-free network,” a phrase that has become attached (3) to the quite different notion of a (usually nonspatial) network in which the proportion 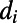of vertices with i edges scales for large i as 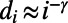for some γ. Our title reads “true scale invariance” to emphasize the distinction.

More precisely, the property is “statistical” scale invariance, and two analogies with classical subjects may be helpful. Modeling English text as “random” seems ridiculous at first sight—authors are not monkeys on typewriters. However, the Shannon theory of “information” (4) (better described as “data compression”) does assume randomness in a certain sense, called “stationarity” or “translation invariance.” Roughly, the assumption is that the frequency of any particular word such as “the” does not vary in different parts of a text. Such an assumption is intuitively plausible and is very different from any sort of explicit dice-throwing model of pure randomness. Analogously, roads are designed rather than arising from some explicit random mechanism, but this does not contradict the possibility that statistical properties of road networks are similar in different locations and on different scales. So, just as information theory imagines the actual text of Pride and Prejudice as if it were a realization from some translation-invariant random process, we will imagine the actual road network of the United States as if it were a realization from some random process with certain invariance properties.

A second analogy is with the “Wiener process,” a mathematical model in topics as diverse as physical Brownian motion, stock prices, and heavily-loaded queues. The mathematical model is exactly scale invariant (as explained and illustrated in a dynamic simulation in ref. 5) even though the real-world entities it models cannot be scale invariant at very small scales. Analogously, the exact scale invariance of our models is unrealistic at very small scales—we do not really have an arbitrarily dense collection of arbitrarily minor roads—but this is not an obstacle to interpreting the models over realistic distances.

Understanding Scale Invariance

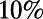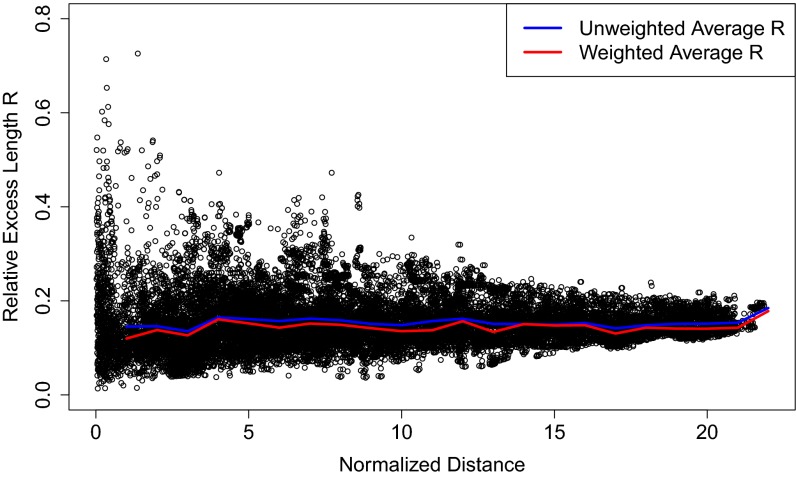
To what extent is scale invariance observed in the real road network? Here, we briefly compare some real data with two predictions based on scale invariance. Consider two city centers. The distance by road will be somewhat longer—maybe or 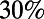longer—than straight-line distance. Fig. 1 shows, for each pair of cities from the largest 200 US cities, this “relative excess” R (vertical axis) and the normalized distance between cities (horizontal axis).

Fig. 1.

Scatter diagram of relative excess route lengths R between each pair from the 200 largest US cities. The horizontal scale is distance, normalized so that there is on average one city per unit area. The two lines show unweighted and population-weighted average excess, as a function of normalized distance. Each average is around 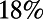at all distances.

These data show that the average excess is about 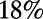throughout the range of distances, whereas the spread of this excess decreases noticeably as distance increases. This is consistent with previous related published data surveyed in ref. 6 and with many possible theoretical models for intercity networks (7). Now the prediction of scale invariance is that, for the road distance 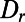between two “typical” points at (straight line) distance r, the probability distribution of 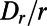does not depend on r. In other words, in a scatter diagram like Fig. 1 for typical points one would see a similar distribution in each vertical strip. What does “typical” mean? Within our mathematical models, the assumed translation invariance and rotation invariance imply that the statistical properties of the random network are the same relative to each pair of prespecified points at distance r. For real data for the US network, we just pick uniformly at random two points at distance r to define 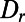; the randomness arises from this sampling, analogous to the randomness in opinion polls arising from random sampling of voters. However, of course the centers of large cities are not typical points relative to the road network, which is designed to have fairly direct links between large cities. We suspect that data for truly random points would show a pattern somewhat more similar to that predicted by scale invariance, but we leave this for future study.

Most recent studies of road networks in the physics literature (e.g., ref. 8 on urban networks) have sought to work within the “scale-free” paradigm by studying numbers of intersections of a given road with other roads (interpretable as degree in a dual graph), rather than directly formalizing spatial scale invariance as we do. The only directly relevant published data we know, in ref. 9, studies proportions of route length, within distance-r routes, spent on the ith longest road segment in the route (identifying roads by their highway number designation). In the United States, the averages of these ordered proportions are found to be around 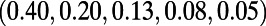as r varies over a range of medium-to-large distances. That these proportions do not vary with r is another prediction of scale invariance, as observed in ref. 9, section 4.

Class of Scale-Invariant Random Spatial Network Models

Here, we outline the mathematical definition of a class of models we call “scale-invariant random spatial networks” (SIRSNs). See ref. 1 for details.

We need to work in the continuum plane (in order for exact scale invariance to be possible; compare the Wiener process). For a realization of a SIRSN, imagine an idealization of an online mapping service that, for each pair of points 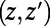in the plane, will specify a route 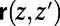between z and 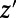. These routes, for different points, are required to satisfy several intuitively obvious consistency conditions [e.g., if y is in the route 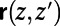, then that route is the concatenation of routes 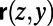and 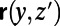], which we will not list here. 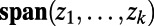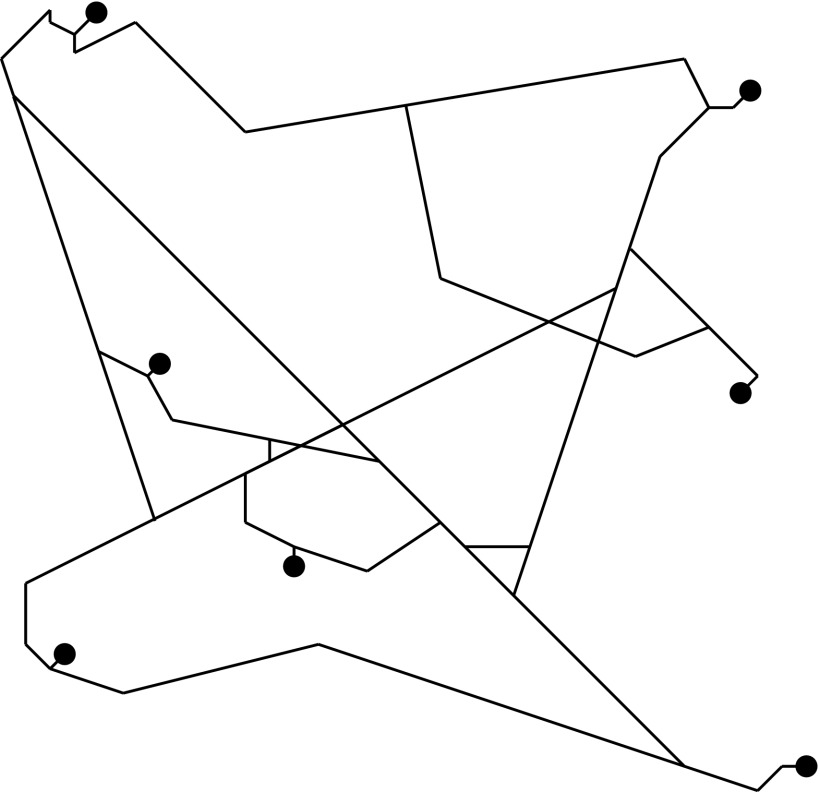So given a finite number of points we get a “spanning subnetwork” , consisting of the union of the routes 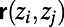. Fig. 2 shows a schematic. The full network itself is hard to envisage—there are routes specified between (almost) every pair of points—but we envisage it as a limit of subnetworks on increasingly dense collections of points.

Fig. 2.

Schematic for the subnetwork of a SIRSN on seven points ().

We study random such networks, and the statistical properties we impose are (i) translation and rotation invariance and (ii) scale invariance.

To elaborate the latter, consider the “scale by c” map 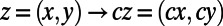on the plane. Scale invariance of routes is the property that the distribution of the subnetwork 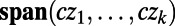on scaled points is the same as that obtained after scaling by c the original subnetwork 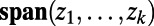. Because the model is defined entirely in terms of routes, one can immediately deduce scaling relationships for other quantities we shall consider.

It is important to note that these are the only assumptions (aside from assuming finiteness of the three statistics described below) we make for a SIRSN. In particular, we do not assume that a notion of a major road–minor road spectrum is given, although such a notion will soon be derived from our assumptions. Also, real-world routes are typically chosen as the optimal route under some criterion (e.g., estimated journey time), but we do not assume any such optimality.

We next define three numerical statistics 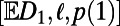associated with a SISRN model, and our final technical assumption is that all three are finite. As before, write 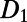for the length of the route between two random points at (straight line) distance 1. We require that its expectation 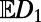is finite; this prevents fractal-like routes. Second, take a set of points of density 1 per unit area in the infinite plane (one could take the vertices of a unit-spaced square grid, but for technical reasons it is more convenient to take a Poisson point process of density 1). Write for the average length per unit area of the subnetwork spanning these points. We require that 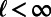; this disallows the “complete” network in which each route 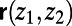is the straight-line segment between those endpoints. Finally, take 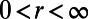. For each route 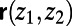, imagine deleting the parts of the route that are within distance r of eithe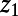r or 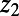, leaving a subroute 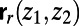; then take the union of 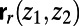over all pairs 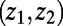. Call the union 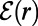and let 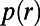be its length per unit area. Scale invariance implies a scaling relationship 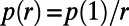and we require .

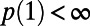This last fact provides a first glimpse of how structure emerges from the assumption of scale invariance. There are several possible real-world measures of “size” of a road segment, quantifying the minor road to major road spectrum—e.g., number of lanes; level in a highway classification system; traffic volume. We do not specify any such notion of size in specifying a SIRSN model, but then within a specified model we can define “size” of a short road segment as the largest r such that the segment is in 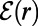, that is the largest r such that the segment is in the route between some two points at distance 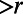from the segment. So we can interpret 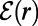as the network of roads of size at least r. This provides another interpretation of the whole network as the 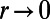limit of 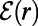. It also makes a quantitative connection with the zoom-in image for online maps. Explicitly, if the real-world network were scale invariant, then a map of a real-world square region of side L, presented in a unit square on your screen, could be drawn to show roads of size 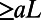, and the average length (of lines indicating roads on the map) you would see on the screen would be 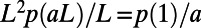, independent of the scale L.

Three Examples of SIRSNs

It is important to remember that SIRSN does not refer to a particular model but to the class of models satisfying the conditions specified above. Analogous to the class of stationary processes featuring in classical information theory, one expects there to be many different SIRSN models, and we indicate three constructions below. These involve defining routes as the “optimal” route in some sense. Because we must work in the continuum there are great technical difficulties in proving rigorously that optimal routes are unique, and in fact this has only been proved (1) for the first construction.

1. Lattice-Based Model.

Start with a square grid of roads, but impose a “binary hierarchy of speeds”: on a road meeting an axis at 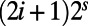, one can travel at speed 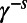for a parameter 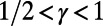(Fig. 3). Define the route between grid points to be a shortest-time path.

Fig. 3.

First stage of the construction in model 1. Line thickness indicates speed.

The key point of this construction is that given a minimum cost path from 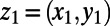to 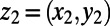, scaling by 2 gives a minimum cost path from 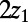to 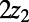. So we are starting with a deterministic construction that is invariant under scaling by 2. Aside from the (technically hard) issue of uniqueness of routes, “soft” arguments extend this construction to a scale-invariant network on the plane, via the following steps: (i) The construction is consistent under binary refinement of the lattice, so taking limits defines routes between points in the continuum. (ii) One can force translation invariance by applying a large-spread random translation. (iii) One can force rotation invariance by applying a random rotation. (iv) Because the construction is invariant under scaling by 2, applying a suitable random scaling gives full scaling invariance.

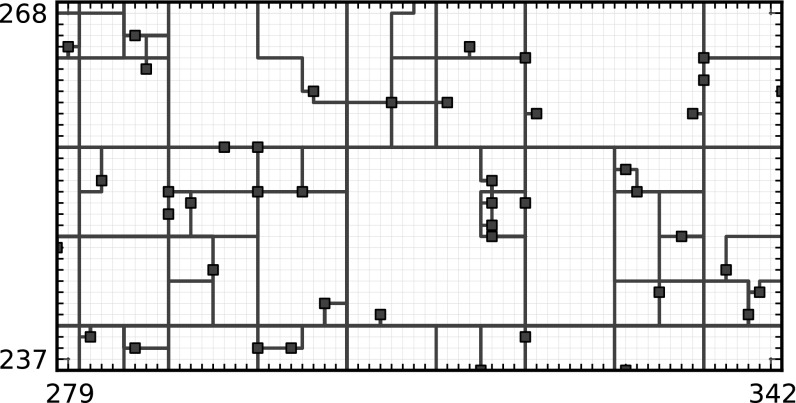
Intuitively, this construction seems like cheating, because in a realization one sees the lattice structure, but it does satisfy the formal conditions. Fig. 4 shows a realization of routes within this model (before the rotation step is applied). Fig. 5 shows simulation estimates of the three statistics 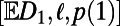as functions of the model parameter γ. Qualitatively, when γ is near 1, routes tend to stay within the rectangle defined by starting and ending points as corners; as γ decreases, routes exploit faster roads outside the rectangle, resulting in longer routes but a less dense network.

Fig. 4.

The spanning subnetwork (within a rectangular window) on sampled points () in a discrete approximation to model 1.

Fig. 5.

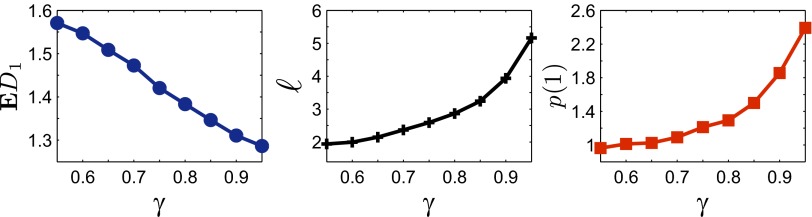
Simulation estimates of the three statistics 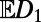and and 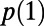as functions of the model 1 parameter γ. As explained in the SI Text, the case of 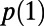is particularly difficult to estimate from discrete approximations so our results in that case may not be accurate.

2. Using Randomly Oriented Lines.

A variant of the first construction is to start with a Poisson line process (10) of roads and assign speeds to these roads in the appropriate scale-invariant way. Continue with denser and denser lines with lower and lower speeds, and as before define routes as shortest-time paths. This is more elegant in that it automatically has the desired invariance properties, which had to be “forced” in the first construction.

3. Dynamic Proximity Graphs.

Create random points in the plane sequentially; for each new point ξ, create new edges as line segments from ξ to each existing point 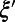for which the disk with diameter 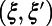contains no third existing point. Continue with denser and denser points, and define routes as shortest-length paths. From the property that the rule for creating edges depends only on relative distances to nearby points, one can deduce scale invariance for the limiting network. Fig. 6 shows the first stage of the construction, the “main roads” analogous to those in Fig. 3.

Fig. 6.

First stage of a dynamic proximity graph construction.

Future Work: Connections and Analogies

This article describes a mathematical structure, and let us conclude by indicating what aspects we find interesting for future development. As already mentioned, at the technical level the most pressing issue is to make rigorous proofs of the (intuitively rather obvious) “uniqueness” of optimal routes in the second and third constructions above, and it would be interesting to find conceptually different constructions. Also as technical mathematics, a start is made in ref. 1 on developing some theory of SIRSNs from the axiomatic setup. One aspect of this involves infinite “geodesics,” paths containing arbitrarily long routes. In somewhat analogous continuum models of first-passage percolation (11), it is an open problem to prove that no doubly infinite geodesics exists, but for SIRSNs this is an easy consequence of scale invariance.

There is substantial mathematical literature over the last decade concerning infinite discrete random networks in the plane arising as limits of finite graphs chosen uniformly over isomorphism classes of triangulations or quadrangulations on n vertices. The recent paper (12) studies scaling limits in that context, giving a model of “continuum network” with very different properties from the models in the paper.

A question with more applied flavor (discussed for intercity networks in ref. 2) concerns networks that make an optimal trade-off between notions of cost and benefit. For SIRSNs, a broad question is what values of the triple 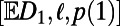are possible; more specifically, what is the optimal trade-off between 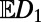(benefit) and (cost), both of which we want to make small. Lower bounds on what is possible, obtained via stochastic geometry methods, are given in ref. 1.

Our work has indirect connections with some actual algorithms used by automobile global positioning system devices to find routes. One key idea (13) is that there is a set of about 10,000 major road intersections in the United States (they write “transit nodes”) with the property that, unless the start and destination points are close, the shortest route goes via some transit node near the start and some transit node near the destination. Given such a set, one can precompute shortest routes and route lengths between each pair of transit nodes, and then answer a query by using the classical algorithm to calculate route lengths from starting (and from destination) point to each nearby transit node, and finally minimize over pairs of such transit nodes. In a “worst-case” analysis of such schemes (14), define “highway dimension” 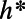as 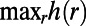, where 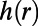is the smallest integer such that, for every ball of radius 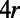, there exists a set of 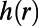vertices such that every shortest route of length 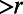within the ball passes through some vertex in the set. They analyze algorithms exploiting transit nodes and other structure, giving performance bounds involving h and number of vertices and network diameter. However, note that, in order for 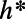to be usefully small, we would need 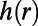not to vary greatly with r, and this is an aspect of approximate scale invariance. How one might repeat such analyses in terms of SIRSN models of the road network is outlined in ref. 1, and here it is the statistic 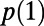that is relevant to algorithm performance. Indeed, the way we defined the network 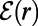in terms of routes is closely related to the notion of “reach” in the algorithmic literature (15).

Relevant data on the statistics of real road networks are scattered through the literature of transportation economics and urban economics. In the latter setting, our 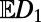is called “circuity.” See ref. 6 for an introduction to this literature, and for data on circuity of commute distances in different metropolitan areas showing that circuity tends to decrease with commute distance.