Emergence of hierarchy in cost-driven growth of spatial networks

Abstract

One of the most important features of spatial networks—such as transportation networks, power grids, the Internet, and neural networks—is the existence of a cost associated with the length of links. Such a cost has a profound influence on the global structure of these networks, which usually display a hierarchical spatial organization. The link between local constraints and large-scale structure is not elucidated, however, and we introduce here a generic model for the growth of spatial networks based on the general concept of cost–benefit analysis. This model depends essentially on a single scale and produces a family of networks that range from the star graph to the minimum spanning tree and are characterized by a continuously varying exponent. We show that spatial hierarchy emerges naturally, with structures composed of various hubs controlling geographically separated service areas, and appears as a large-scale consequence of local cost–benefit considerations. Our model thus provides the basic building blocks for a better understanding of the evolution of spatial networks and their properties. We also find that, surprisingly, the average detour is minimal in the intermediate regime as a result of a large diversity in link lengths. Finally, we estimate the important parameters for various world railway networks and find that, remarkably, they all fall in this intermediate regime, suggesting that spatial hierarchy is a crucial feature for these systems and probably possesses an important evolutionary advantage.

Our societies rely on various networks for the distribution of energy and information as well as for transportation of individuals. These networks shape the spatial organization of our societies, and their understanding is a key step toward the understanding of the characteristics and the evolution of our cities (1). Despite their apparent diversity, these networks are all particular examples of a broader class of networks—spatial networks, which are characterized by the embedding of their nodes in space. As a consequence, there is usually a cost associated with a link, leading to particular structures that are now fairly well understood (2) thanks to the recent availability of large sets of data. Nevertheless, the mechanisms underlying the formation and temporal evolution of spatial networks have not been much studied. Different kinds of models aiming at explaining the static characteristics of spatial networks have been suggested previously in quantitative geography, transportation economics, and physics (reviewed in ref. 3). Concerning the time evolution of spatial networks, only a few models exist to describe, in particular, the growth of road and rail networks (4–8), but a general framework is yet to be discovered.

The earliest attempts can be traced back to the economic geography community in the 1960s and 1970s [a fairly comprehensive review of these studies can be found in the work of Hagget and Chorley (9)]. However, due to the lack of available data and computational power, the proposed models were based on intuitive, heuristic rules and have not been studied thoroughly.

A more recent trend is that of optimization models. The common point among all these models is that they try to reproduce the topological features of existing networks, by considering the network as the realization of the optimum of a given quantity (an overview is provided in section IV.E in ref. 2). For instance, the hub-and-spoke models (10) reproduce correctly with an optimization procedure the observed hierarchical organization of city pair relations. However, the vast majority of the existing spatial networks do not seem to result from a global optimization but, instead, from the progressive addition of nodes and segments resulting from a local optimization. By modeling (spatial) networks as resulting from a global optimization, one overlooks the usually limited time horizon of planners and the self-organization underlying their formation.

Self-organization of transportation networks has already been studied in transportation engineering (11). Using an agent-based model, including various economical ingredients, Levinson and Yerra (5) modeled the emergence of the networks properties as a degeneration process. Starting from an initial grid, traffic is computed at each time step, and each edge computes its costs and benefits accordingly, using any excess to improve its speed. After several iterations, a hierarchy of roads emerges. Our approach is very different: We start from nodes and do not specify any initial network. Also, and most importantly, we deliberately do not represent all the causal mechanisms at work in the system. Indeed, the aim of our model is to understand the basic ingredients for emergence of patterns that can be observed in various systems, and we thus focus on a single, very general economical mechanism and its consequence on the large-scale properties of the networks.

Concerning spatial networks, as is the case for many spatial structures, there is a strong path dependency. In other words, the properties of a network at a certain time can be explained by the particular historical path leading to it. It thus seems reasonable to model spatial networks in an iterative way. Some iterative models, following ideas for understanding power laws in the Internet (12) and describing the growth of transportation networks (4, 6, 7), can be found in the literature. In these models, the graphs are constructed via an iterative greedy optimization of geometrical quantities. However, we believe that the topological and geometrical properties of networks are consequences of the underlying processes at stake. At best, geometrical and topological quantities can be a proxy for other, more fundamental properties; for instance, it will be clear in what follows that the length of an edge can be taken as a proxy for the cost associated with the existence of that edge. Finding those underlying processes is a key step toward a general framework within which the properties of networks can be understood and, hopefully, predicted.

In this respect, cost–benefit analysis (CBA) provides a systematic method to evaluate the economical soundness of a project. It allows one to appreciate whether the costs of a decision will outweigh its benefits, and therefore to evaluate quantitatively its feasibility and/or suitability. CBA has only been officially used to assess transport investments since 1960 (13). However, the concept comes across as so intuitive in our profit-driven economies that it seems reasonable to wonder whether CBA is at the core of the emergent features of our societies, such as distribution and transportation systems. If the temporal evolution of spatial networks is rarely studied, arguments mentioning the costs and benefits related to such networks are almost absent from the physics literature [the study by Popović et al. (14) is a notable exception, although they do not consider the time evolution of the network]. However, we find it intuitively appealing that in an iterative model, the formation of a new link should, at least locally, correspond to a CBA. We therefore propose here a simple CBA framework for the formation and evolution of spatial networks. Our main goal within this approach is to understand the basic processes behind the self-organization of spatial networks that lead to the emergence of their large-scale properties.

Theoretical Formulation

We consider here the simple case in which all the nodes are distributed uniformly in the plane (a detailed description of the algorithm is provided in Materials and Methods). For a rail network, the nodes would correspond to cities and the network grows by adding edges between cities iteratively; the edges are added sequentially to the graph, as a result of a CBA, until all the nodes are connected (4). For the sake of simplicity, we limit ourselves to the growth of trees, which allows us to focus on the emergence of large-scale structures due to the cost–benefit ingredient alone. Furthermore, we consider that all the actors involved in the building process are perfectly rational, and therefore that the most profitable edge is built at each step. More precisely, at each time step, we build the link connecting a new node i to a node j that already belongs to the network, such that the following quantity is maximum:

The quantity 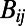is the expected benefit associated with the construction of the edge between node i and node j, and 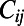is the expected cost associated with such a construction. Eq. 1 defines the general framework of our model, and we now discuss specific forms of 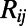. In the case of transportation networks, the cost will essentially correspond to some maintenance cost and will typically be proportional to the Euclidean distance 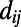between i and j. We thus write:

where κ represents the cost of a line per unit of length per unit of time. Benefits are more difficult to assess. For rail networks, a simple yet reasonable assumption is to write the benefits in terms of distance and expected traffic 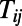between cities i and j:

where η represents the benefits per passenger per unit of length. We have to estimate the expected traffic between two cities, and for this, we will follow the common and simple assumption used in the transportation literature of having the so-called “gravity law” (15, 16):

where 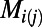is the population of city 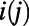and k is the rate associated with the process. We will choose here a value of the exponent 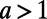( 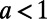would correspond to an unrealistic situation in which the benefits associated with passenger traffic would increase with the distance). This parameter a determines the range at which a given city attracts traffic, regardless of the density of cities. The accuracy and relevance of this gravity law are still controversial, and improvements have recently been proposed (17, 18). However, it has the advantage of being simple and being able to capture the essence of the traffic phenomenon: the decrease of the traffic with distance and the increase with population. Within these assumptions, the cost–benefit budget 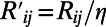now reads:

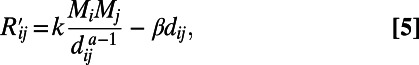where 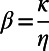represents the relative importance of the cost with regard to the benefits. We will assume that populations are power law-distributed with exponent 1+ μ (with 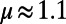for cities; Materials and Methods), and the model thus depends essentially on the two parameters a and β (a detailed description of parameters used in this paper is provided in Materials and Methods). In the following, we will be working with fixed values of μ and a. The exact values we choose, however, are not important (as long as they are chosen in a given range, as discussed in the previous section and in Materials and Methods) because the obtained graphs would have the same qualitative properties.

Results

Typical Scale.

The average population is , and the typical intercity distance is given by 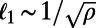, where 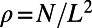denotes the city density (L is the typical size of the whole system). The two terms of Eq. 5 are thus of the same order for 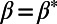, defined as:

In the theoretical discussion that follows, we will take 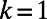for simplicity (but it should not be forgotten in empirical discussions). Another way of interpreting 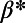, which makes it more practical to estimate from empirical data (Discussion), is to say that it is of the order of the average traffic per unit time:

From Eq. 6, we can guess the existence of two different regimes depending on the value of β:

• i) 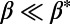: The cost term is negligible compared with the benefits term. Each connected city has its own influence zone depending on its population, and the new cities will tend to connect to the most influential city. In the case where 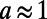, every city connects to the most populated cities and we obtain a star graph constituted of one single hub connected to all other cities.

• ii) 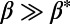: The benefits term is negligible compared with the cost term. All new cities will connect sequentially to their closest neighbor. Our algorithm is then equivalent to an implementation of Prim’s algorithm (19), and the resulting graph is a minimum spanning tree (MST).

The intermediate regime 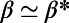needs to be elucidated, however. In particular, we have to study if there is a transition or a crossover between the two extreme network structures, and if we have a crossover, what the network structure is in the intermediate regime. In the following, we answer these questions by simulating the growth of these spatial networks.

Crossover Between the Star Graph and the MST.

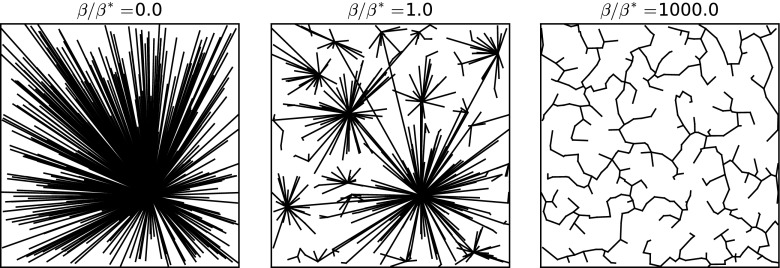
Fig. 1 shows three graphs obtained for the same set of cities for three different values of 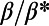(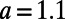, 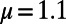), confirming our discussion about the two extreme regimes in the previous section. A visual inspection seems to show that a different type of graph appears for 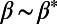, which suggests the existence of a crossover between the star graph and the MST. This graph is reminiscent of the hub-and-spoke structure that has been used to describe the interactions between city pairs (11, 20). However, in contrast to the rest of the literature about hub-and-spoke models, we show that this structure is not necessarily the result of a global optimization: indeed, it emerges here as the result of the autoorganization of the system.

Fig. 1.

Graphs obtained with our algorithm for the same set of cities (nodes) for three different values of 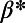(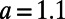, , 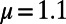400 cities). We show a star graph, where the most populated node is the hub (Left), and we recover the MST (Right).

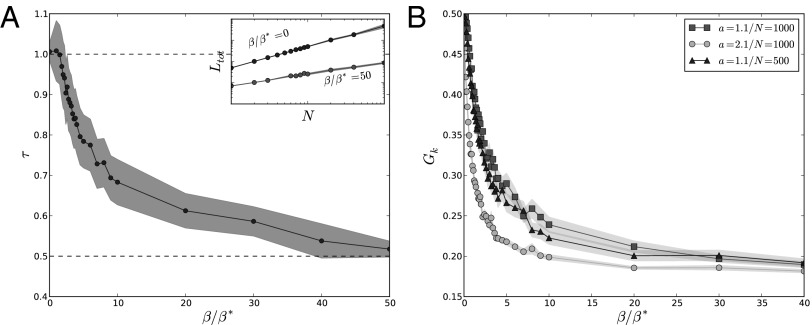
The MST is characterized by a peaked degree distribution, whereas the star graph’s degree distribution is bimodal, and we therefore choose to monitor the crossover with the Gini coefficient for the degrees defined as in the study by Dixon et al. (21):

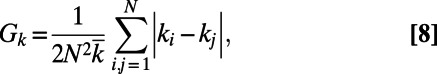where 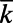is the average degree of the network. The Gini coefficient is in 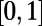, and if all the degrees are equal, it is easy to see that 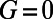. On the other hand, if all the nodes but one are of degree 1 (as in the star graph), a simple calculation shows that 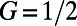. Fig. 2B displays the evolution of the Gini coefficient vs. 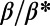(for different values of 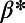obtained by changing the value of a, μ, and N). This plot shows a smooth variation of the Gini coefficient pointing to a crossover between a star graph and the MST, as one could expect from the plots in Fig. 1. (Also, we note that for given values of a and μ, all the plots collapse on the same curve, regardless of the number N of nodes. However, for different values of a or μ, we obtain different curves.)

Fig. 2.

(A) Exponent τ vs. β. For , we recover the star graph exponent 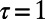, and for the other extreme 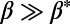, we recover the MST exponent 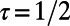. In the intermediate range, we observe a continuously varying exponent suggesting a nontrivial structure. The shaded area represents the SD of τ. (Inset) To illustrate how we determined the value of τ, we represent 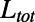vs. N for two different values of β. The power law fit of these curves gives τ. (B) Evolution of the Gini coefficient (Eq. 8) with 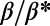for different values of 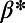. The shaded area represents the SD of the Gini coefficient.

Another important difference between the star graph and the MST lies in how the total length of the graph scales with its number of nodes. Indeed, in the case of the star graph, all the nodes are connected to the same node and the typical edge length is L, the typical size of the system the nodes are enclosed in. We thus obtain:

On the other hand, for the MST, each node is connected roughly to its nearest neighbor at a distance typically given by 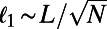, leading to:

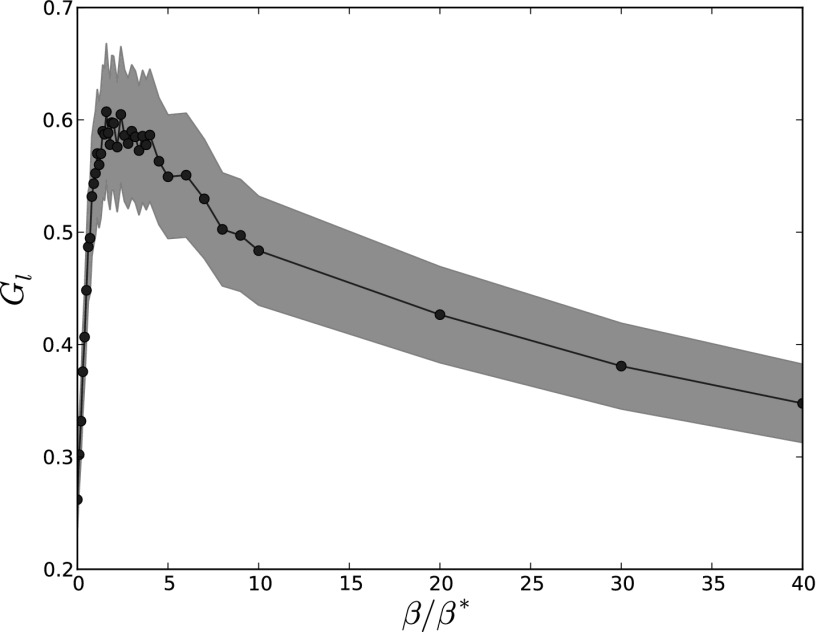
More generally, we expect a scaling of the form 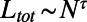, and in Fig. 2A, we show the variation of the exponent τ vs. β. For 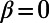, we have 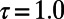, and we recover the behavior 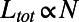typical of a star graph. In the limit 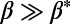, we also recover the scaling 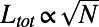, typical of an MST. For intermediate values, we observe an exponent that varies continuously in the range 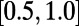. This rather surprising behavior is rooted in the heterogeneity of degrees, and in the following, we will show that we can understand this behavior as resulting from the hierarchical structure of the graphs in the intermediate regime.

It is interesting to note that a scaling with an exponent 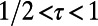has been observed (2, 22) for the total number 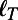of miles driven by the population (of size P) of city scales: 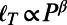with 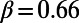. Understanding the origin of those intermediate numbers might thus also give us insights into important features of traffic in urban areas and the structure of cities.

It thus seems that from the point of view of interesting quantities, such as the Gini coefficient or the exponent τ, there is no sign of a critical value for β and we are in presence of a crossover rather than a transition.

Spatial Hierarchy and Scaling.

The graph corresponding to the intermediate regime 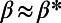depicted in Fig. 1 exhibits a particular structure corresponding to a hierarchical organization, as is observed in many complex networks (23). Inspired from the observation of networks in the regime 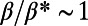, we define a particular type of hierarchy, which we call spatial hierarchy, as follows. A network will be said to be spatially hierarchical if:

• i) We have a hierarchical network of hubs that connect to nodes less and less far away as one goes down the hierarchy.

• ii) Hubs belonging to the same hierarchy level have their own influence zone clearly separated from those of others. In addition, the influence zones of a given level are included in the influence zones of the previous level.

The relevance of this concept of hierarchy in the present context can be qualitatively assessed in Fig. S1, where we represent the influence zones by colored circles, with the colors corresponding to different hierarchical levels. To go beyond this simple qualitative description of the structure, we provide in the following sections quantitative proof that networks in the regime 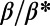exhibit spatial hierarchy.

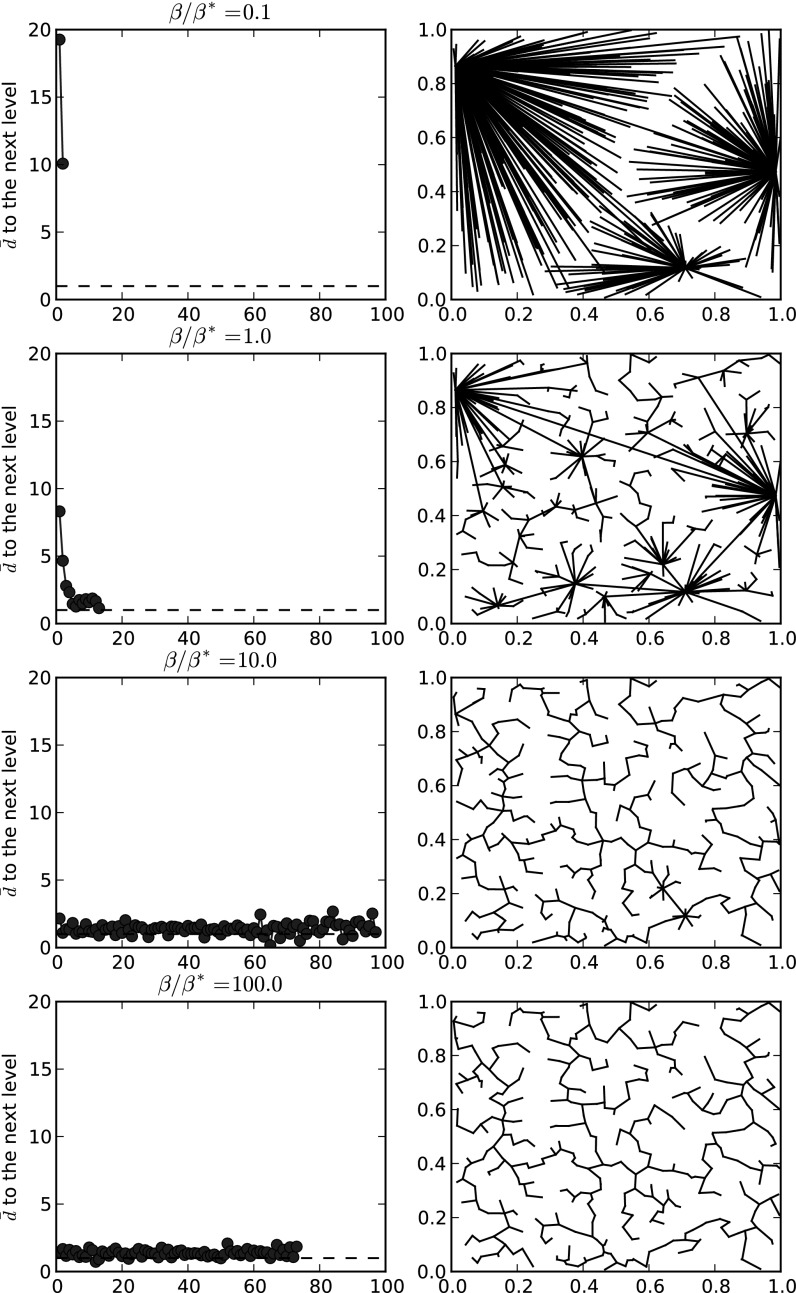
Distance between hierarchical levels.

We propose here a quantitative characterization of part i in the definition of spatial hierarchy. The first step is to identify the root of the network, which allows us to characterize a hierarchical level naturally by means of its topological distance to the root. We choose the most populated node as the root (which will be the largest hub for 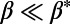), and we can now measure various quantities as a function of the level in the hierarchy. In Fig. 3, we plot the average Euclidean distance 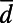between the different hierarchical levels as a function of the topological distance from the root node (for the sake of clarity, we also draw the corresponding graphs next to these plots). For reasonably small values of 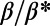(i.e., when the graph is not far from being a star graph), the average distance between levels decreases as we go further away from the root node. This confirms the idea that the graphs for 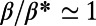exhibit a spatial hierarchy in which nodes from different levels are getting closer and closer to each other as we go down the hierarchy. Eventually, as 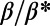becomes larger than 1, the distance between consecutive levels just fluctuates around 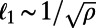, the average distance between nearest neighbors for a Poisson process, which indicates the absence of hierarchy in the network.

Fig. 3.

Average distance between the successive hierarchy levels for different values of 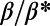(Left), next to the corresponding graphs (Right). The most populated node is taken as the root node.

Geographical separation of hubs zones.

We now discuss part ii of the definition of spatial hierarchy, that is, how the hubs are located in space. Indeed, another property that we can expect from spatially hierarchical graphs is that of geographical separation, as defined in SI Text. We define a separation index (a definition is provided in SI Text) which quantifies the separation between the respective influence zones of hubs belonging to the same level (see Fig. S2). The separation index is equal to 1 if the nodes’ influence zones do not overlap at all, and it is 0 if they perfectly overlap. We plot this quantity averaged over the all the graph’s levels for different values of 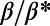in Fig. S3. One can observe on this graph that the separation index reaches values above 0.90 when 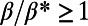, which means that the corresponding graphs indeed have a structure with hubs controlling geographically well-separated regions. Obviously, the choice of the shape of the influence zone (which is chosen here to be a disk; SI Text) has a strong impact on the results, but the same qualitative behavior will be obtained for any type of convex shapes.

In conclusion, the graphs produced by our model in the regime 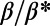satisfy the two points of the definition. They exhibit a spatially hierarchical structure, characterized by a distance ordering and geographical separation of hubs. In this regime, we saw earlier that we have specific, nontrivial properties, such as 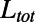scaling with an exponent depending continuously on 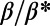. Using a simple toy model defined by a fractal tree (see Fig. S4), we can show that the spatial hierarchy can explain this varying exponent for the regime 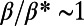(details are provided in SI Text, Understanding the Scaling with a Toy Model).

Efficiency.

Most transportation networks are not obtained by a global optimization but result from the addition of various, successive layers. The question of the efficiency of these self-organized systems is therefore not trivial and deserves some investigation. The model considered here allows us to test the effect of various parameters and how efficient a self-organized system can be. In particular, we would like to characterize the efficiency of the system for various values of β. For this, we can assume that the construction cost per unit length is fixed (i.e., the factor η in Eq. 2 is constant), and because 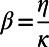, a change of value for β is equivalent to a change in the benefits per passenger per unit of length.

A first natural measure of how optimal the network is can be given by its total cost proportional to the total length : The shorter a network is, the better it is for the company in terms of building and maintenance costs. In our model, the behavior of the total cost is simple and expected: For small values of 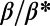, the obtained networks correspond to a situation in which the users are charged a lot compared with the maintenance cost and the network is very long 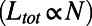. In the opposite case, when , the main concern in building this network is concentrated on construction cost and the network has the smallest total length possible (for a given set of nodes).

The cost is not enough to determine how efficient the network is from the users’ point of view, however: A very-low-cost network might indeed be very inefficient. A simple measure of efficiency is then given by the amount of detour needed to go from one point to another. In other words, a network is efficient if the shortest path on the network for most pairs of nodes is very close to a straight line. The detour index for a pair of nodes 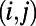is conveniently measured by 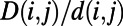, where 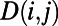is the length of the shortest route between i and j, and 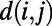is the Euclidean distance between i and j. To have detailed information about the network, we use the quantity introduced by Aldous and Shun (24):

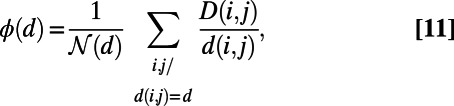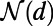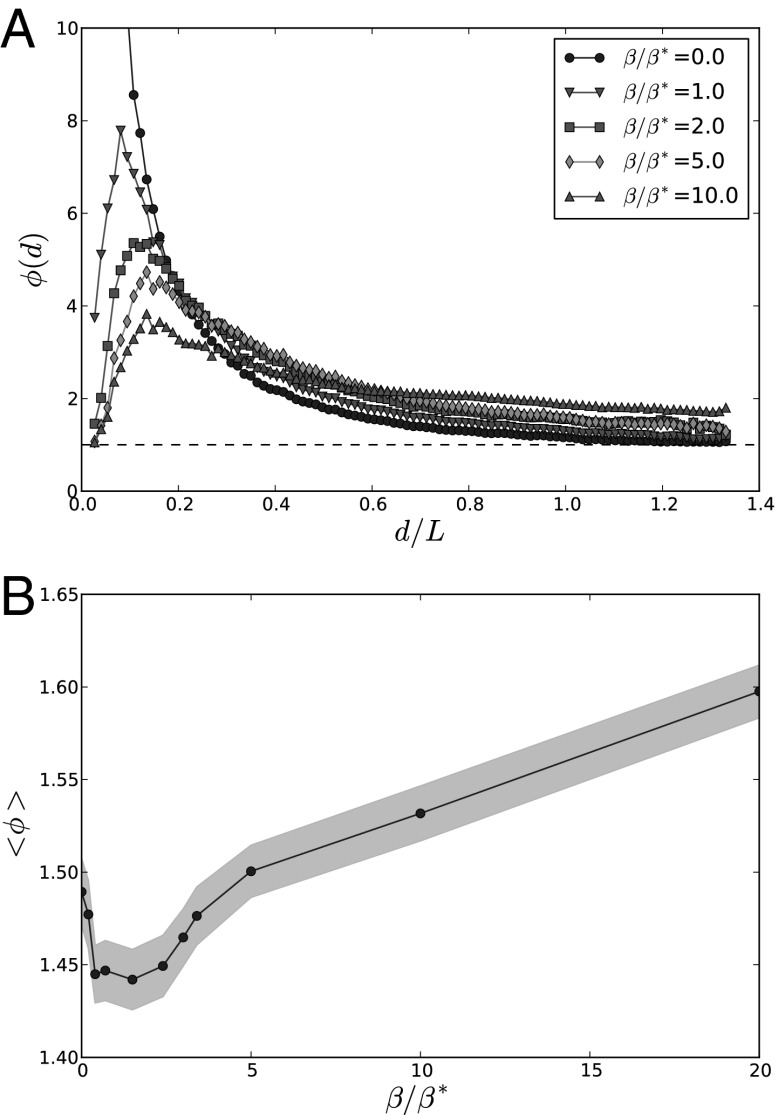
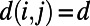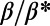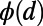where the normalization is the number of pairs with . We plot this “detour function” for several values of in Fig. 4A. For , the function takes high values for small d and low values for large d, meaning that the corresponding networks are very inefficient for relatively close nodes, although being very efficient for distant nodes. On the other hand, for , we see that the MST is very efficient for neighboring nodes but less efficient than the star graph for long distances. Surprisingly, the graphs for 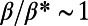exhibit a nontrivial behavior: For small distances, the detour is not as good as for the MST but not as bad as for the star graph, and for long distances, it is the opposite. To make this statement more precise, we compute the average of 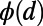over d (a quantity that has a clear meaning for trees; objections to the use of 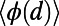as a good efficiency measure in general are reviewed in ref. 24) and plot it as a function of 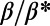. The results are shown in Fig. 4B and confirm this surprising behavior in the intermediate regime: We observe a minimum for . In other words, there exists a nontrivial value of β (i.e., a value of the benefits per passenger per unit of length) for which the network is optimal from the point of view of the users.

Fig. 4.

(A) Detour function 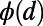vs. the relative distance between nodes for different values of 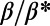. (B) Average detour index 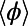for several realizations of the graphs as a function of 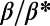. The shaded area represents the SD of 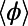. This plot shows that there is a minimum for this quantity in the intermediate regime .

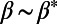The existence of such an optimum is far from obvious, and to gain more understanding about this phenomenon, we plot the Gini coefficient 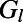relative to the length of the edges between nodes in Fig. 5. We observe that the Gini coefficient peaks around 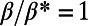, which means that in this regime, the diversity in terms of edge length is the highest. The large diversity of lengths explains why the network is most efficient in this regime: Indeed, long links are needed to cover large distances, whereas smaller links are needed to reach all the nodes efficiently. It is interesting to note that this argument is similar to the one proposed by Kleinberg (25) to explain the existence of an optimal delivery time in small-world networks.

Fig. 5.

Evolution of the Gini coefficient for the length vs. 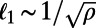(for different values of 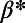). The shaded area represents the SD.

Discussion

We have presented a model of a growing spatial network based on a CBA. This model allows us to discuss the effect of a local optimization on the large-scale properties of these networks. First, we showed that the graphs exhibit a crossover between the star graph and the MST when the relative importance of the cost increases. This crossover is characterized by a continuously varying exponent that could give some hints about other quantities observed in cities, such as the total length traveled by the population. Second, we showed that the model predicts the emergence of a spatial hierarchical structure in the intermediate regime, where costs and benefits are of the same order of magnitude. We showed that this spatial hierarchy can explain the nontrivial behavior of the total length vs. the number of nodes. Finally, this model shows that in the intermediate regime, the vast diversity of links lengths entails a large efficiency, an aspect that could of primary importance for practical applications.

An interesting playground for this model is given by railways, and we can estimate the value of 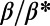for these systems. In some cases, we were able to extract the data from various sources (particularly financial reports of railway companies), and the results are shown in Table 1. We estimate β for different real-world networks, including some of the oldest railway systems, using its definition (total maintenance costs per year divided by the total length and by the average ticket price per kilometer). To estimate 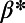, we use Eq. 7 in the following way:

where 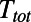is the total traveled length (in passengers per kilometers per year) and 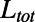is the total length of the network under consideration. Remarkably, the computed values for the ratio 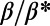shown in Table 1 are all of the order of 1 (ranging from 0.20 to 1.56). In the framework of this model, this result shows that all these systems are in the regime where the networks possess the property of a spatial hierarchy, suggesting it is a crucial feature for real-world networks. We note that in our model, the value of 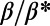is given exogenously, and it would be extremely interesting to understand how we could construct a model leading to this value in an endogenous way.

Table 1.

Empirical estimates for β and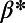

Country	Total distance traveled, passengers per kilometer per year	Total length, kilometers	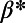, passengers per year	Maintenance cost, Euros per year	Average ticket price, Euros per kilometer	β, passengers per year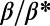
France				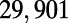	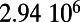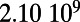0.12		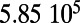0.20
Germany		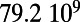		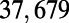	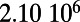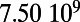0.30		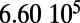0.32
India		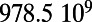		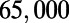	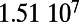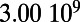0.01		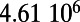0.31
Italy		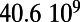		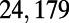	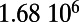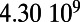0.20		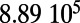0.53
Spain		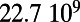		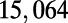	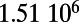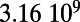0.11		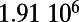1.26
Switzerland		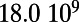		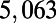	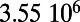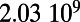0.17		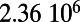0.66
United Kingdom		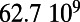		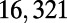	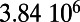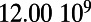0.16		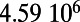1.19
United States		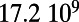		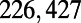	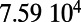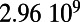0.11		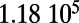1.56

This table gives the total ride distance (in kilometers), the total network length (in kilometers), the total annual maintenance expenditure (in Euros per year), and the average ticket price (in Euros per kilometer). All the given values correspond to the year 2011. From these data, we compute the empirical values of β and 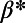, as well as their ratio (data obtained from various sources, such as financial reports of railway companies).

There are also several directions that seem interesting. First, various forms of cost and benefits functions could be investigated to model specific networks. In particular, there are several choices that can be taken for the expected traffic. In this paper, we limit ourselves to estimate the traffic as direct traffic from a node i to a node j, but it is likely that part of the traffic will come from other nodes. To take this into account, we think that the following extensions are probably interesting:

• i) A given city (denoted by 0 with population 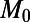) plays a particular role in the network (e.g., the capital city in a relatively small country). In that case, it is beneficial to be close to that city through the network, and we write:

  

  where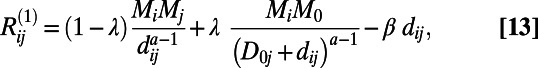 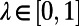is a coefficient weighing the relative importance of the traffic coming from the particular city.
• ii) The most general case in which all the network-induced traffic is taken into account. We then consider:

  

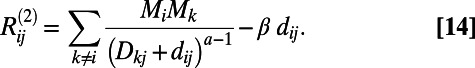
Other ingredients, such as the presence of different rail companies or the difference between a state-planned network and a network built by private actors, could easily be implemented, and the corresponding models could possibly lead to interesting results.

More importantly, we limit ourselves here to trees to focus on the large-scale consequences of the cost–benefit mechanism. Further studies are needed to uncover the mechanisms of formation of loops in growing spatial networks, and we believe that the model presented here might represent a suitable modeling framework.

Finally, it seems plausible that the general cost–benefit framework introduced at the beginning of this article could be applied to the modeling of systems other than transportation networks. We believe it captures the fundamental features of a spatial network while being versatile enough to model the growth of a great diversity of systems shaped by space.

Materials and Methods

Simulations.

The simulation starts by distributing nodes uniformly in a square. We then attribute to each node a random population distributed according to the power law:

The choice of this distribution is motivated by Zipf’s empirical results on city populations (26) (which motivates the choice 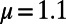in our simulations) but also because we can go from a peaked to a broad distribution by tuning the value of μ. Indeed, for 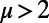, both the first and second moments of this distribution exist and the distribution can be considered as peaked. In contrast, for 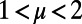, only the first moment converges and the distribution is broad.

Once the set of nodes is generated, we choose a random node as the root and add nodes recursively until all the nodes belong to the graph. At each time step, the nodes belonging to the graph constitute the set of “inactive” nodes and the other, not yet connected nodes constitute the “active” nodes. At each time step, we connect an active node to an inactive node, such that their value of R defined in Eq. 5 is maximum.