Abstract
Phylogenetic networks can model reticulate evolutionary events such as hybridization, recombination, and horizontal gene transfer. However, reconstructing such networks is not trivial. Popular character-based methods are computationally inefficient, whereas distance-based methods cannot guarantee reconstruction accuracy because pairwise genetic distances only reflect partial information about a reticulate phylogeny. To balance accuracy and computational efficiency, here we introduce a quartet-based method to construct a phylogenetic network from a multiple sequence alignment. Unlike distances that only reflect the relationship between a pair of taxa, quartets contain information on the relationships among four taxa; these quartets provide adequate capacity to infer a more accurate phylogenetic network. In applications to simulated and biological data sets, we demonstrate that this novel method is robust and effective in reconstructing reticulate evolutionary events and it has the potential to infer more accurate phylogenetic distances than other conventional phylogenetic network construction methods such as Neighbor-Joining, Neighbor-Net, and Split Decomposition. This method can be used in constructing phylogenetic networks from simple evolutionary events involving a few reticulate events to complex evolutionary histories involving a large number of reticulate events. A software called “Quartet-Net” is implemented and available at http://sysbio.cvm.msstate.edu/QuartetNet/.
Keywords: phylogenetic network, split network, quartet, 2-weakly compatible, consistency
Introduction
In natural history, reticulate events, such as horizontal gene transfer (HGT), hybridization, and recombination, have been demonstrated to be important in contributing to speciation, drug resistance, and DNA repair (Bruce 2002). For example, HGT is a significant evolutionary mechanism in shaping the diversification of bacterial genomes (Doolittle et al. 2003), hybridization plays a key role in the evolution of plants and fish (Linder and Rieseberg 2004), whereas recombination is very important in human genome evolution (Meunier and Duret 2004). Phylogenetic tree construction is a conventional method used to demonstrate evolutionary relationships among genes and species (Felsenstein 2004). However, detection of reticulate events, such as HGT, hybridization, and recombination, using phylogenetic trees is not straightforward, as it involves comparison of tree topologies, which is not trivial due to cluster confidence assessment. Parallel evolution, model heterogeneity, and sample or inference errors complicate phylogenetic tree construction.
Phylogenetic networks, a generalization of phylogenetic trees, allow non-tree-like structures to represent conflicting signals or alternative evolutionary histories for a group of taxa. Thus, phylogenetic networks provide additional capacity to detect reticulate events by illustrating the conflicting tree topologies as reticulate blocks in a network. In the past few years, various phylogenetic network construction methods have been developed (Posada and Crandall 2001; Semple and Steel 2003; Morrison 2005; Gascuel and Steel 2006). These methods can be explicit network construction describing explicit evolutionary events, such as hybridization networks (Linder and Rieseberg 2004; Yu et al. 2011), recombination networks (Gusfield et al. 2004; Huson and Kloepper 2005) and HGT networks (Kunin et al. 2005; Jin et al. 2006; Park et al. 2010). Implicit network construction, for example, split networks (Bandelt and Dress 1992a, 1992b), captures conflicting signals without specifically identifying reticulate evolutionary events. Most of these explicit and implicit network methods can be grouped into two categories: distance-based methods (Bandelt and Dress 1992a, 1992b; Bryant and Moulton 2004; Huson and Bryant 2006; Willson 2006) or character-based methods (Templeton et al. 1992; Bandelt et al. 1995, 1999; Fitch 1997; Huber et al. 2002; Gusfield et al. 2004; Song and Hein 2005). Character-based methods infer a phylogenetic network directly from the sequence information through usually a parsimony or maximum-likelihood criterion, whereas distance-based methods first construct a genetic distance matrix of the taxa set and then build the network from this distance matrix. Distance-based methods are often computationally more efficient than character-based ones. However, distance-based methods can cause potential loss of accuracy because the information embedded in genetic distances is less complete than those extracted from raw character data (Felsenstein 2004).
To balance accuracy and computational efficiency, a compromise strategy is to construct phylogenetic trees or networks from (weighted) triplets, for example, TripleML (Ranwez and Gascuel 2002) and level 2 phylogenetic networks (van Iersel et al. 2009), or from (weighted) quartets, for example, Tree-Puzzle (Strimmer and von Haeseler 1996), a dynamic programming approach (Ben-Dor et al. 1998), quartet cleaning (Berry et al. 1999), Addquart (Berry and Gascuel 2000), QNet and SuperQ (Grünewald et al. 2007, 2013), a stochastic method (Tria et al. 2010), and some explicit methods (Posada and Crandall 2001; Lemey et al. 2009), or from clusters (van Iersel et al. 2010). Weighted triplets and quartets keep more information and cause less reduction of raw data than distances. However, most prevailing methods use unweighted triplets and quartets, which has been proven by St. John et al. (2003) to be less sensitive than efficient distance based methods like Neighbor-Joining (Saitou and Nei 1987). In consequence, triplet- and quartet-based methods are not as popular as their distance-based competitors.
In this article, a novel method, Quartet-Net is presented to reconstruct split networks from a collection of weighted triplets and quartets. It can be viewed as a quartet analog of Split-Decomposition (Bandelt and Dress 1992a, 1992b). Quartet-Net first calculates triplet and quartet weights directly from multiple sequence alignments (MSAs) by a parsimony method using only parsimony informative sites and then functions by agglomeratively decomposing all triplet and quartet weights into simple components based on full splits. Consistency is an important criterion for evaluating a reconstruction method. A reconstruction method is called consistent on a special set of trees or networks if the method reconstructs precisely every tree or network in the set provided that the input data are generated from it and that sufficient data are available. For example, Neighbor-Joining (Saitou and Nei 1987) is consistent on all trees, Split-Decomposition (Bandelt and Dress 1992a, 1992b) is consistent on weakly compatible systems (Bandelt and Dress 1992a, 1992b), and Neighbor-Net (Bryant and Moulton 2003) and QNet (Grünewald et al. 2007, 2009) are consistent on circular split systems. We prove that Quartet-Net is consistent on “2–weakly compatible” split systems, a more general class of split systems than trees, weakly compatible systems and circular split systems. Thus, Quartet-Net is capable of accurately reconstructing a larger set of split networks than other methods. In addition, Quartet-Net is effective in inferring phylogenetic distances.
Results and Discussion
We perform an analysis on artificial DNA sequence data generated from a phylogenetic history containing two reticulation events and two published DNA sequence data sets: a bacterial data set used by Takahashi et al. (2009) to classify bacterial species and estimate their phylogenetic relationships and a collection of complete mitochondrial genomes of 31 squamata (or scaled reptiles) species. The study of bacterial data sheds light on the classification of bacteria, whereas that of squamata data serves as an illustration that Quartet-Net has the ability to reconstruct complex networks for data from taxa sets known to have many reticulate events (Townsend et al. 2004). We also compare the results with four widely used phylogenetic tree and network reconstruction methods: Neighbor-Joining (Saitou and Nei 1987), Split Decomposition (Bandelt and Dress 1992a, 1992b), Neighbor-Net (Bryant and Moulton 2004), and QNet (Grünewald et al. 2007).
Analysis on Artificial Data
We use the software Dawg (Cartwright 2005) with the GTR + Gamma + I model to generate six DNA sequences from the four feasible trees contained in a phylogenetic scenario shown in figure 1. The substitution rate was set to be 0.01 and the sequence length 40,000 bp.
Fig. 1.
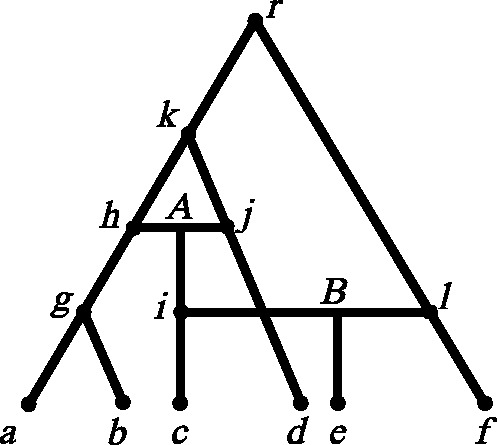
A phylogenetic history containing two reticulations at A and B, respectively; the artificial sequence data are generated from this phylogeny.
This phylogenetic history is basically tree-like with two reticulations at A and B. We completed 100 runs using Dawg (Cartwright 2005), which generates 100 alignments from the phylogenetic history. The alignments of six DNA sequences at a, b, c, d, e, and f were used as inputs to Quartet-Net, QNet (Grünewald et al. 2007), Neighbor-Net (Bryant and Moulton 2004), Split-Decomposition (Bandelt and Dress 1992a, 1992b), and Neighbor-Joining (Saitou and Nei 1987). For the distance-based methods, we used the uncorrected P distance as implemented by SplitsTree v4 (Huson and Bryant 2006) and for QNet we used the “expected branch lengths,” a maximum-likelihood–based estimation of the quartet weights.
To perform a better comparison, we list in table 1 all nontrivial true splits and splits reconstructed by the five methods with bootstrap value larger than or equal to 10 together with their averaged weights. The trivial splits are ignored because all methods reconstruct them correctly. Because of the different strategies to calculate weights from the MSA, the edge lengths can only be compared according to proportions. For convenience, we normalize each weight by 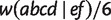 because the split
because the split 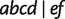 is detected by all methods.
is detected by all methods.
Table 1.
True Nontrivial Splits and Splits Reconstructed from the Phylogenetic History in Figure 1 by Quartet-Net, QNet (Grünewald et al. 2007), Neighbor-Net (Bryant and Moulton 2004), Split-Decomposition (Bandelt and Dress 1992a, 1992b), and Neighbor-Joining (Saitou and Nei 1987).
| True Phylo |
Quartet-Net |
QNet |
Neighbor-Net |
Spit-Decomposition |
Neighbor-Joining |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Split | Weight | Split | Weight | Bval | Split | Weight | Bval | Split | Weight | Bval | Split | Weight | Bval | Split | Weight | Bval |
| ab | 6 | ab | 6 | 100 | ab | 6 | 100 | ab | 6 | 100 | ab | 6 | 100 | ab | 6 | 100 |
| abc | 1 | abc | 1.04 | 100 | abc | 0.79 | 88 | abc | 0.48 | 72 | abc | 0.10 | 48 | abc | 0.26 | 57 |
| abcd | 8 | abcd | 8.04 | 100 | abcd | 4.46 | 100 | abcd | 6.47 | 100 | abcd | 6.87 | 100 | abcd | 5.49 | 100 |
| abce | 1 | abce | 0.99 | 100 | abce | 1.10 | 52 | abce | 0.58 | 46 | abce | 0.12 | 54 | |||
| abdf | 2 | abdf | 2.00 | 100 | abdf | 1.65 | 47 | abdf | 1.69 | 39 | abdf | 1.06 | 100 | |||
| abef | 1 | abef | 1.07 | 100 | abef | 1.12 | 65 | abef | 0.34 | 40 | abef | 0.12 | 41 | abef | 0.26 | 43 |
| abf | 1 | abf | 0.98 | 100 | abf | 1.35 | 48 | abf | 1.08 | 54 | abf | 0.11 | 41 | |||
| abd | 0.08 | 90 | adef | 0.24 | 48 | ac | 0.04 | 36 | acd | 0.03 | 15 | |||||
| abcf | 0.02 | 53 | ac | 0.24 | 40 | adef | 0.02 | 25 | ace | 0.02 | 14 | |||||
| ae | 0.01 | 23 | aef | 0.22 | 36 | af | 0.03 | 18 | af | 0.03 | 14 | |||||
| acdf | 0.02 | 20 | acd | 0.23 | 29 | acde | 0.03 | 16 | ac | 0.03 | 12 | |||||
| ad | 0.11 | 24 | acd | 0.04 | 11 | adef | 0.02 | 11 | ||||||||
| acef | 0.09 | 23 | aef | 0.04 | 10 | |||||||||||
Note.—The column “True phylo” represents the real phylogenetic history, whereas the other columns show the reconstructed splits by each method. There are three subcolumns: 1) the column “split” represents the nontrivial full splits; only left blocks of the splits are listed, 2) “bval” denotes the bootstrap value of a split in the 100 runs; only the splits with bootstrap value larger than or equal to 10 are shown, and 3) “weight” calculates the average weight of a split in bval runs.
As can be seen from table 1, Quartet-Net is able to accurately reconstruct all seven nontrivial splits in all 100 runs; however, the other four methods fail to reconstruct some nontrivial splits in most runs. For example, QNet (Grünewald et al. 2007) fails to reconstruct full splits 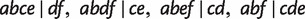 in almost half of the runs, and the other three methods perform even worse. Except for Neighbor-Joining (Saitou and Nei 1987), all other methods reconstruct some false-positive nontrivial splits with small weights. The reason might be random noise and a bias of the methods to compute distances and quartet weights from an MSA. Though the splits predicted by Neighbor-Joining (Saitou and Nei 1987) are true splits, it fails in inferring three splits
in almost half of the runs, and the other three methods perform even worse. Except for Neighbor-Joining (Saitou and Nei 1987), all other methods reconstruct some false-positive nontrivial splits with small weights. The reason might be random noise and a bias of the methods to compute distances and quartet weights from an MSA. Though the splits predicted by Neighbor-Joining (Saitou and Nei 1987) are true splits, it fails in inferring three splits 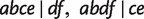 , and
, and 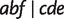 resulting from reticulations in all 100 runs and two splits
resulting from reticulations in all 100 runs and two splits 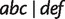 and
and 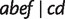 in almost half of the runs. It is due to the fact that Neighbor-Joining (Saitou and Nei 1987) only keeps the strongest compatible splits. In addition, the proportions of phylogenetic distances inferred by Quartet-Net are almost identical to the real phylogenetic history and is better than those inferred by the other four methods.
in almost half of the runs. It is due to the fact that Neighbor-Joining (Saitou and Nei 1987) only keeps the strongest compatible splits. In addition, the proportions of phylogenetic distances inferred by Quartet-Net are almost identical to the real phylogenetic history and is better than those inferred by the other four methods.
Analysis on Bacterial Data
The bacterial data set consists of concatenated sequences of seven genes (16S rRNA, 23S rRNA, gyrB, phyH, recA, rpoA, and rpoD) from 36 bacterial species, with lengths approximately 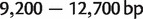 (Takahashi et al. 2009). GC-content is a very important criterion for bacterial classification. It is defined as the percentage of guanine and cytosine in a sequence. The 36 bacterial sequences fall into three groups (GC-poor, GC-median, and GC-rich) according to their GC-content levels (
(Takahashi et al. 2009). GC-content is a very important criterion for bacterial classification. It is defined as the percentage of guanine and cytosine in a sequence. The 36 bacterial sequences fall into three groups (GC-poor, GC-median, and GC-rich) according to their GC-content levels (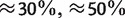 , and
, and 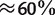 ). There are 14 GC-poor, 11 GC-median, and 11 GC-rich bacteria, respectively. The readers are referred to Takahashi et al. (2009) for the detailed information about concatenated sequences as well as the single genes of the species.
). There are 14 GC-poor, 11 GC-median, and 11 GC-rich bacteria, respectively. The readers are referred to Takahashi et al. (2009) for the detailed information about concatenated sequences as well as the single genes of the species.
We use ClustalW (Larkin et al. 2007) to align 11 GC-rich sequences, 25 GC-poor and GC-rich sequences, and all 36 sequences, respectively. The obtained multiple alignments are taken as inputs to Neighbor-Joining (Saitou and Nei 1987), Split-Decomposition (Bandelt and Dress 1992a, 1992b), Neighbor-Net (Bryant and Moulton 2004), and Quartet-Net. We run the programs on a Lenovo laptop with 2.53 GHz processor and 4 GB memory. In practice, the running time of Quartet-Net is longer than all three other methods. It takes from a few seconds to 3 minutes for different MSAs. We list the number of splits in table 2, and visualize the results by SplitsTree4 (Huson and Bryant 2006). Because of the limitation of pages, only some of the networks are shown in figures 2–7.
Table 2.
The Number of Full Splits Reconstructed from Four Methods, Namely Neighbor-Joining (Saitou and Nei 1987), Split-Decomposition (Bandelt and Dress 1992a, 1992b), Neighbor-Net (Bryant and Moulton 2004) and Quartet-Net on Three Bacterial Data Sets, GC-Poor Data Consisting of 11 GC-Poor Bacteria, GC-Poor, and GC-Rich Data Consisting of 25 Bacteria and all 36 Bacteria.
| Methods | GC-Poor | GC-Poor and Rich | All |
|---|---|---|---|
| Neighbor-joining | 19 | 47 | 69 |
| Split-decomposition | 23 | 48 | 66 |
| Neighbor-net | 29 | 77 | 114 |
| Quartet-net | 22 | 45 | 60 |
Fig. 2.
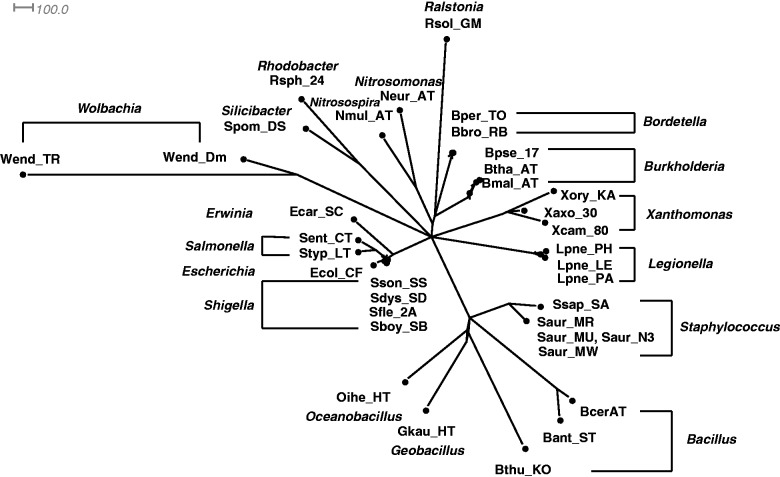
A Quartet-Net phylogenetic network of 25 GC-poor and GC-rich bacteria.
Fig. 3.
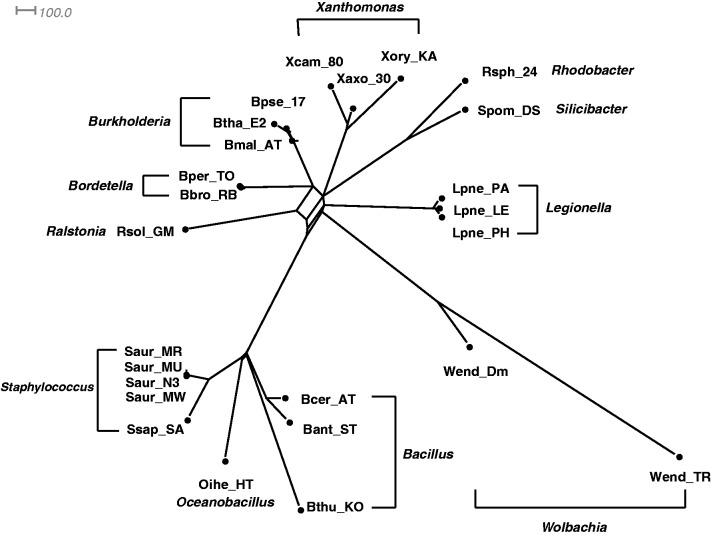
A Quartet-Net phylogenetic network of all 36 bacteria.
Fig. 4.
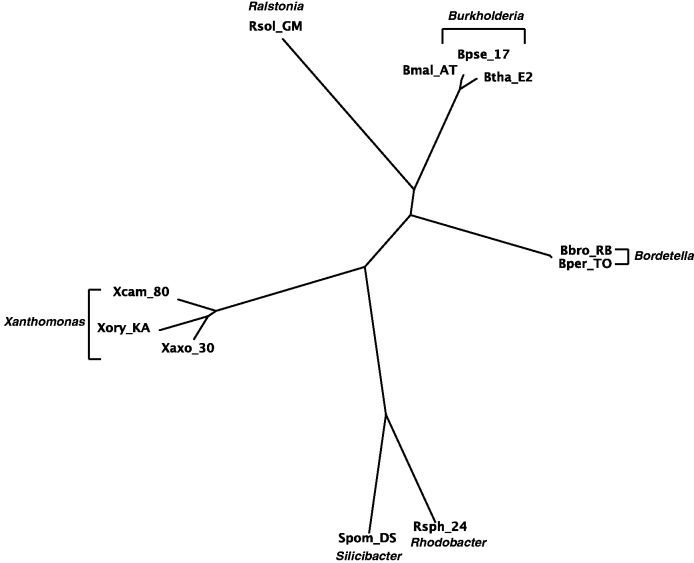
The Neighbor-Joining tree of 11 GC-rich bacteria with concatenated sequences of 7 genes.
Fig. 5.
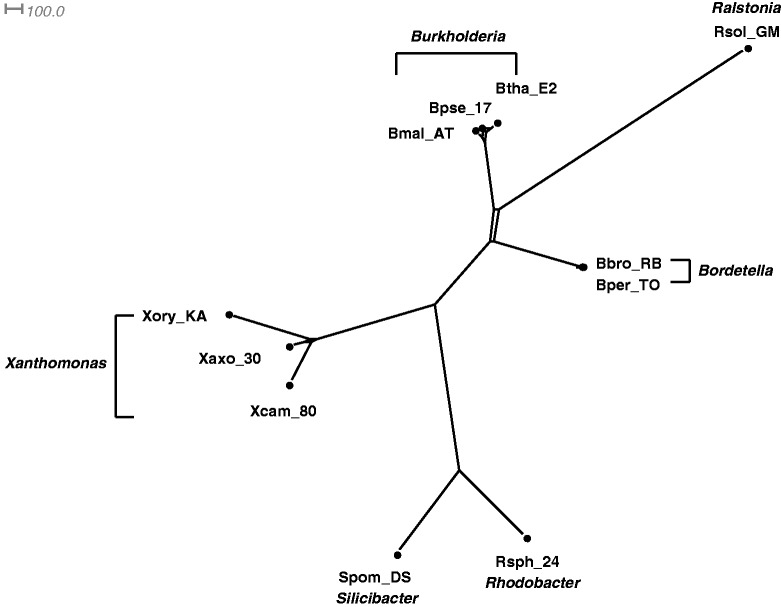
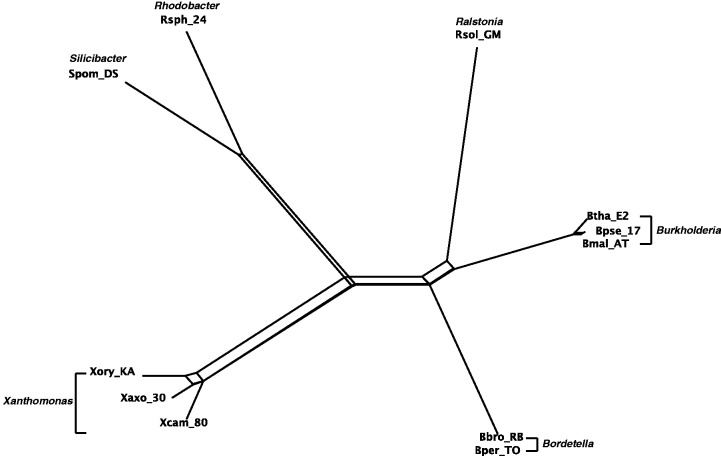
The Quartet-Net network of 11 GC-rich bacteria with concatenated sequences of 7 genes.
Fig. 6.
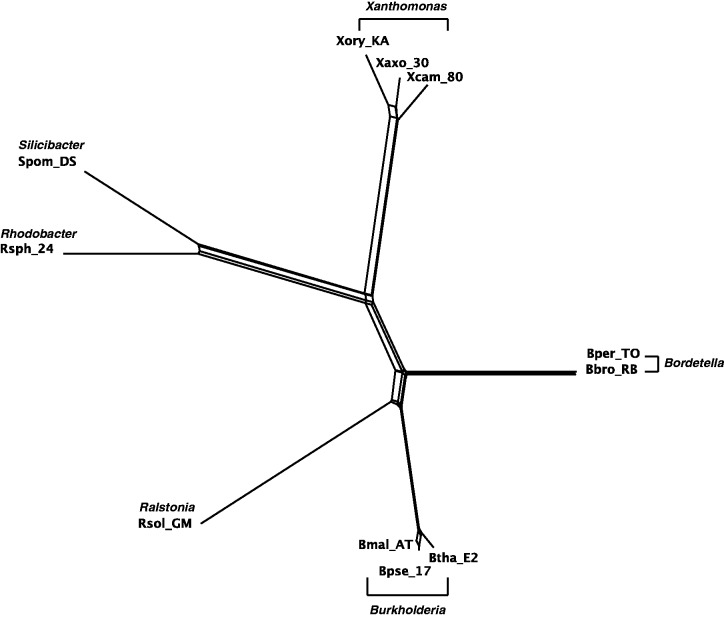
The Split-Decomposition network of 11 GC-rich bacteria with concatenated sequences of 7 genes.
Fig. 7.
The Neighbor-Net network of 11 GC-rich bacteria with concatenated sequences of 7 genes.
Figures 2 and 3 show two Quartet-Net networks on 25 GC-poor and GC-rich bacteria, and all 36 bacteria, respectively. An interesting observation is that there is a split in figure 2, which divides the GC-poor and GC-rich bacteria. However, this split disappears with the addition of GC-median bacteria. There are two implications from the result: 1) Extinct species might have effect on the classification of present species, and 2) it might not be appropriate to classify species only by their GC-contents.
Figures 4–7 show the phylogenetic networks of 11 GC-rich bacteria by using four methods: 1) Neighbor-Joining (Saitou and Nei 1987), 2) Quartet-Net, 3) Split-Decomposition (Bandelt and Dress 1992a, 1992b), and 4) Neighbor-Net (Bryant and Moulton 2004). As one can see, Quartet-Net presents a network quite close to the Neighbor-Joining tree but with some small additional non-tree like blocks. The results support the commonly accepted classification of these bacteria (Takahashi et al. 2009) and suggest that, for the genes considered here, the number of reticulate events in bacteria might be relatively low. In addition, the comparison of the networks produced by Quartet-Net, Split-Decomposition, and Neighbor-Net shows that Quartet-Net tends to keep only those splits with large weights and ignore the small ones. This can be considered beneficial because those very weak contradicting signals often result from experimental or inference errors. Furthermore, an interesting observation from table 2 is that Split-Decomposition and Quartet-Net sometimes produce even fewer splits than Neighbor-Joining. The main reason may be that both Split-Decomposition and Quartet-Net set weights by taking a minimum over possible values whereas Neighbor-Joining takes averages. Experimental or inference errors on these data might also contribute to this behavior.
Analysis on Mitochondrial Genomes of Squamatas
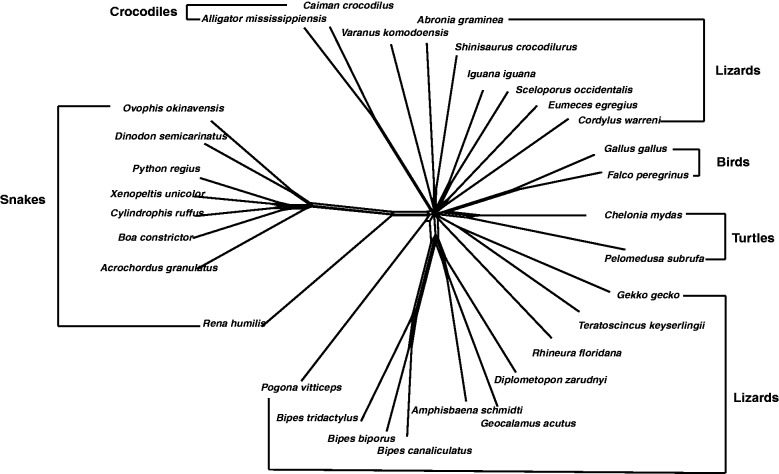
These squamata data consist of mitochondria genomes of 31 squamata species with lengths of approximately 20,000 bp. It is known to be a difficult data set where model-based tree reconstruction methods tend to struggle. The networks reconstructed by Quartet-Net and Split-Decomposition (Bandelt and Dress 1992a, 1992b) are shown in figures 8 and 9, respectively. Quartet-Net reconstructs 98 full splits, whereas Split-Decomposition reconstructs a history with only 69 full splits. Though the graph from Split-Decomposition looks better, it might suggest more compatibility than there is in the data. Many of the splits in the Quartet-Net are 2-splits, that is, splits grouping exactly two taxa together. Such splits will typically occur when, due to randomization of parts of the sequences and high number of backward or parallel mutations, the weights of all quartets are high. Here, Quartet-Net can indicate that the pattern-counting approach might be problematic while Split-Decomposition can not discriminate this situation from data that fits well on a tree with long pendant edges.
Fig. 8.
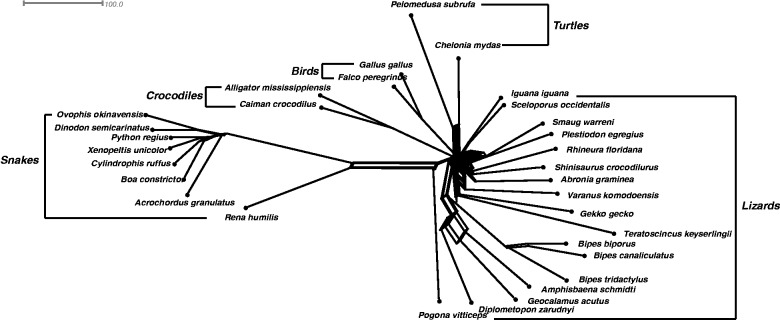
The Quartet-Net phylogenetic network of 31 squamata species.
Fig. 9.
The Split-Decomposition network of 31 squamata species.
Conclusion
We have introduced and implemented a novel method called Quartet-Net to infer phylogenetic networks from weighted triplets and quartets. The applications of Quartet-Net showed that this method reconstructs a wide range of networks, sometimes clear tree-like histories, for example, for bacterial data and sometimes complex networks, for example, for squamata data. A simulation study shows that Quartet-Net has the potential to reconstruct accurate splits and weights. Theoretically, we prove that it is consistent on 2–weakly compatible split systems. However, Quartet-Net is relatively slow. It is most efficient in reconstructing the phylogenetic history of a taxa set with size less than 100 at present.
Materials and Methods
Splits and Split Systems
A split on a taxa set X consists of two nonempty disjoint subsets (or blocks) of X. We denote the split whose blocks are A and B by 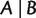 . If
. If 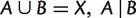 is called a full split; otherwise, it is called a partial split. A split is called trivial if one of its blocks contains only a single taxon. Splits are the building blocks of unrooted phylogenetic trees. As shown in figure 10, each branch of an unrooted tree defines a natural split of the taxa set, in which taxa on different sides of the branch compose the two blocks. In addition, if the tree is weighted, then we associate the length of a branch to its natural split and call it the weight of that split. In general, for any (partial or full) split
is called a full split; otherwise, it is called a partial split. A split is called trivial if one of its blocks contains only a single taxon. Splits are the building blocks of unrooted phylogenetic trees. As shown in figure 10, each branch of an unrooted tree defines a natural split of the taxa set, in which taxa on different sides of the branch compose the two blocks. In addition, if the tree is weighted, then we associate the length of a branch to its natural split and call it the weight of that split. In general, for any (partial or full) split  , the weight of
, the weight of  , denoted by
, denoted by  represents the evolutionary distance between the taxa sets A and B.
represents the evolutionary distance between the taxa sets A and B.
Fig. 10.
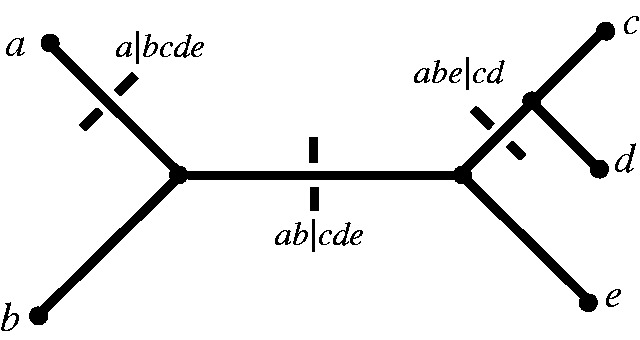
A phylogenetic tree and some splits in the corresponding compatible split system.
A (weighted) split system is a collection of (weighted) full splits. We call a split system compatible if all its splits can be fitted into an unrooted phylogenetic tree; otherwise, we call it incompatible. Alternatively, a split system is compatible if any two splits 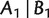 and
and 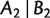 are compatible in the sense that, at least one of the sets
are compatible in the sense that, at least one of the sets 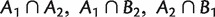 , and
, and 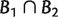 is empty (Buneman 1971). A compatible split system contains all the branching information of its corresponding phylogenetic tree. On the other hand, a phylogenetic tree naturally defines a compatible split system. So, there is a one-to-one correspondence between compatible split systems and unrooted phylogenetic trees (Buneman 1971; Bandelt and Dress 1992a).
is empty (Buneman 1971). A compatible split system contains all the branching information of its corresponding phylogenetic tree. On the other hand, a phylogenetic tree naturally defines a compatible split system. So, there is a one-to-one correspondence between compatible split systems and unrooted phylogenetic trees (Buneman 1971; Bandelt and Dress 1992a).
To classify splits from networks rather than from trees, a more general class of systems called weakly compatible split systems is employed. A split system on X is weakly compatible if any three splits 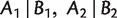 , and
, and  are weakly compatible in the sense that, at least one of the intersections
are weakly compatible in the sense that, at least one of the intersections 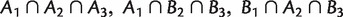 , and
, and 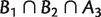 is empty (Bandelt and Dress 1992a). It is clear from the definition that a compatible system is also weakly compatible. So, weakly compatible split systems are indeed a generalization of compatible split systems.
is empty (Bandelt and Dress 1992a). It is clear from the definition that a compatible system is also weakly compatible. So, weakly compatible split systems are indeed a generalization of compatible split systems.
Furthermore, to analyze the consistency of Quartet-Net, we introduce 2-weakly compatible split systems. A split system on X is 2-weakly compatible if any four splits 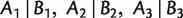 , and
, and 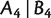 are 2–weakly compatible in the sense that,
are 2–weakly compatible in the sense that,  implies that at least one of the intersections
implies that at least one of the intersections 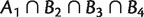 ,
, 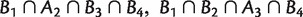 , and B1 ∩ B2 ∩ B3
, and B1 ∩ B2 ∩ B3
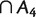 is empty. In the first section of supplementary material, Supplementary Material online, we define a more general collection of splits called k-weakly compatible system, and show that 2-weakly compatible systems are a proper generalization of weakly compatible systems.
is empty. In the first section of supplementary material, Supplementary Material online, we define a more general collection of splits called k-weakly compatible system, and show that 2-weakly compatible systems are a proper generalization of weakly compatible systems.
Triplets, Quartets, and Their Weights
A quartet (triplet) is a split of four (three) taxa into two pairs (a pair and a singleton). Let a, b, c, and d be these four taxa, then there are three different quartets denoted by 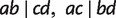 , and
, and 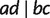 , respectively. In general, there are overall
, respectively. In general, there are overall 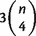 different quartets for a taxa set of size n. A split
different quartets for a taxa set of size n. A split 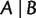 is said to display another split
is said to display another split 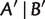 if either
if either 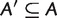 and
and 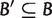 , or
, or 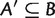 and
and 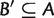 . As shown in figure 11, quartet
. As shown in figure 11, quartet 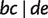 is displayed by three full splits
is displayed by three full splits 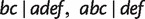 , and
, and 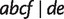 .
.
Fig. 11.
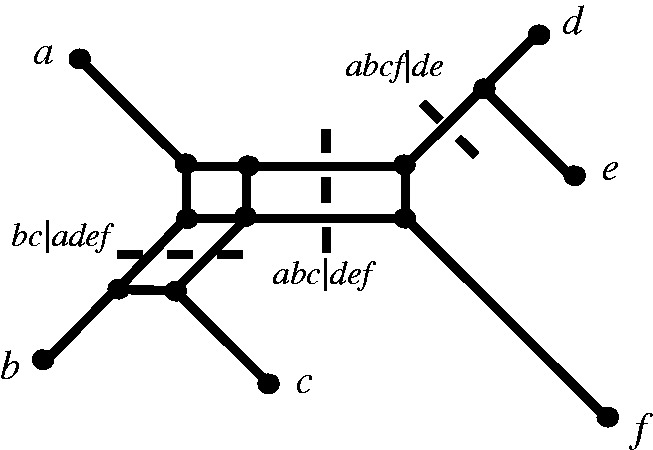
A phylogenetic network showing the relation “display”. Three full splits 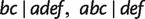 and
and 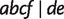 displaying a quartet
displaying a quartet 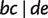 are shown by dashed lines. For simplicity, other full and partial splits that display
are shown by dashed lines. For simplicity, other full and partial splits that display 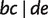 are not shown.
are not shown.
In Quartet-Net, we calculate quartet weights directly from an MSA using parsimony informative sites as follows. For any quartet 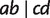 , we first collect the four sequences of taxa a, b, c, and d from the MSA. A site is defined to support
, we first collect the four sequences of taxa a, b, c, and d from the MSA. A site is defined to support 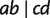 if the character states (e.g., nucleotides for DNA) in this site coincide for taxon a and b, and for taxon c and
if the character states (e.g., nucleotides for DNA) in this site coincide for taxon a and b, and for taxon c and 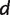 , but not for a and c. The quartet weight
, but not for a and c. The quartet weight 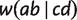 is then calculated as the number of sites that support
is then calculated as the number of sites that support 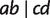 . As trivial splits do not display any quartet, we also incorporate triplet weights from the MSA using parsimony informative sites to calculate the weights of trivial full splits.
. As trivial splits do not display any quartet, we also incorporate triplet weights from the MSA using parsimony informative sites to calculate the weights of trivial full splits.
It is worth noting that we consider a quartet weight as an estimation of the sum of the weights of all splits displaying that quartet. This corresponds to the length of the middle edge of the corresponding quartet tree (see also Grünewald et al. 2007). There are a number of studies that define a quartet weight to be the confidence in or likelihood of a quartet topology under various models of sequence evolution (Willson 1999; Ranwez and Gascuel 2001; Huson et al. 2004; Sumner et al. 2008; Holland et al. 2007, 2008, 2013; Snir and Rao 2012). In the implementation of Quartet-Net, the following two options are provided: 1) construct a split network directly from the sequence alignment file using the parsimony method on informative sites to calculate triplet and quartet weights; and 2) construct a split network from a triplet and quartet file in a given format (see user’s manual), specifying the triplet and quartet weights precomputed by the user.
The main purpose of the second option is to separate the two steps of the algorithm, the computation of triplet and quartet weights from an MSA and the computation of a split system from this intermediate data. We simply count site patterns to assign quartet weights. Similarly, the simple uncorrected P distance is commonly used for Neighbor-Net and Split Decomposition, for example, it is the default distance of SplitsTree v4 (Huson and Bryant 2006). Other quartet weights have been suggested. QNet (Grünewald et al. 2007) comes with a procedure that utilizes the maximum likelihood framework of Tree Puzzle (Strimmer and von Haeseler 1997) to compute “expected branch lengths,” quartet weights that converge to the true value, if the sequences evolve along a tree under the GTR model. More recently, (Holland et al. 2013) used “squangles” to estimate quartet weights under the general Markov model. These model-based ways to compute quartet weights might be very useful, if the true underlying split system is a tree. If not, then the violation of the underlying compatibility assumption of the models can be a problem. This is indicated by the relatively high weight of the wrong splits for QNet with “expected branch lengths” in our simulation.
To give a better understanding of the Quartet-Net algorithm, we first present some recurrence formulas for calculating split weights from distances.
Computing Split Weights from Distances
Before introducing the formulas, it will be beneficial to restate that the objective is to decompose pairwise distances into the weights of full splits such that the summation over the weights of all full splits displaying a pair 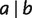 is as close as possible but not exceeding the distance between a and b. Thus, we always take the minimum for all possible choices in each decomposition step.
is as close as possible but not exceeding the distance between a and b. Thus, we always take the minimum for all possible choices in each decomposition step.
For any taxa set X and 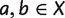 , we use ab to denote
, we use ab to denote 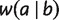 , the distance between taxa a and b. We associate any split
, the distance between taxa a and b. We associate any split 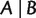 with a weight
with a weight  in an agglomerative process. The association begins with any triplet, say
in an agglomerative process. The association begins with any triplet, say 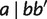 . Similar to split decomposition (Bandelt and Dress 1992a), we have
. Similar to split decomposition (Bandelt and Dress 1992a), we have
| (1) |
For any trivial split 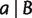 with
with 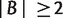 , we take the minimum over all
, we take the minimum over all 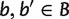 ,
,
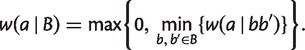 |
(2) |
As for 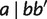 , a new taxon
, a new taxon 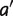 can be added to either side, we have
can be added to either side, we have 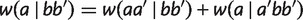 , which implies
, which implies 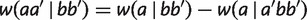 . Similarly, there are three other equations for
. Similarly, there are three other equations for 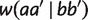 and we take the minimum,
and we take the minimum,
 |
(3) |
For any split  , with
, with  and
and  , we have
, we have
| (4) |
Equations (1)–(4) form a recurrence system to calculate split weights from distances, which is equivalent to the Split Decomposition algorithm (Bandelt and Dress 1992a, 1992b). The readers are referred to supplementary material, Supplementary Material online (second section) for the proof of the equivalence. The recurrence system can be readily generalized from distances to triplet and quartet weights.
Computing Split Weights from Triplet and Quartet Weights
For a taxa set X of size n, suppose that we have already calculated all 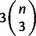 triplet weights and
triplet weights and 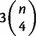 quartet weights from an MSA or from distances. Then, we associate any split
quartet weights from an MSA or from distances. Then, we associate any split 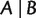 with a weight
with a weight  as follows.
as follows.
First, by applying w(aa′|bb′b″) = w(aa′|bb′)-w(bb′|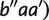 iteratively, we have
iteratively, we have
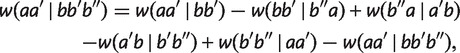 |
which implies
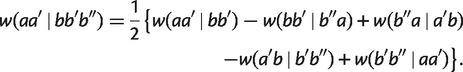 |
Taking minimum over all possible cases, we have for any split 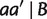 with
with 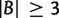 ,
,
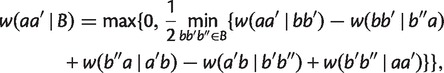 |
(5) |
Similar to equation (3), we have for any split 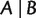 with
with 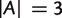 and
and 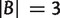 ,
,
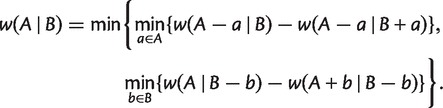 |
(6) |
And for any split 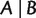 with
with 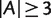 and
and 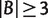 ,
,
| (7) |
The above process generates the weights of all nontrivial full splits, we then calculate the weights of trivial splits 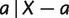 as
as
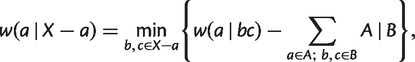 |
(8) |
where 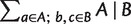 calculates the sum of the weights of all nontrivial full splits that display
calculates the sum of the weights of all nontrivial full splits that display 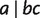 here.
here.
It is worth noting that taking minimum functions will potentially cause the loss of some full splits for noisy data. So, it is also reasonable to replace the minimum function in equation (5) with an average function, which will produce more full splits with a higher false-positive rate.
Equations (5)–(8) decompose triplet and quartet weights iteratively to weights of full splits. However, a brute force implementation is not advisable. We first present a lemma. Its proof is the same as in (Bandelt and Dress 1992a).
Lemma 1. —
If a split
displays another split
, then
.
By this lemma, if a partial split receives weight 0, then all the splits displaying this split will be associated with weight 0. This observation reduces the running time of Quartet-Net.
The Quartet-Net Algorithm
Quartet-Net accepts two kinds of inputs: an MSA or a file specifying all triplet and quartet weights. The reader is referred to the manual at http://sysbio.cvm.msstate.edu/QuartetNet/. For simplicity, we use 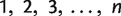 to represent the taxa.
to represent the taxa.
In the initialization step, all triplet and quartet weights are calculated from the MSA or read from the input file. Then, three quartets 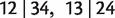 , and
, and 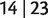 together with their weights are stored in a set, say S. After that, iteratively we add
together with their weights are stored in a set, say S. After that, iteratively we add 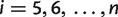 to the left and right blocks of the splits stored in S and calculate the weights of newly generated splits from those splits already resolved by equations (5)–(7). Noting that the only splits which can not be generated in this way are
to the left and right blocks of the splits stored in S and calculate the weights of newly generated splits from those splits already resolved by equations (5)–(7). Noting that the only splits which can not be generated in this way are 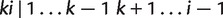 for
for  , we also calculate their weights by equation (5) and add them to S. At the end of each iteration, we remove from S the splits with weight 0 because they cannot be further extended to splits with positive weights. After the last iteration, only nontrivial full splits with nonzero weights are left in S. The weights of trivial full splits are also calculated by equation (8). A NEXUS file is created to store them and “SplitsTree4” (Huson and Bryant 2006) can be used to visualize the network.
, we also calculate their weights by equation (5) and add them to S. At the end of each iteration, we remove from S the splits with weight 0 because they cannot be further extended to splits with positive weights. After the last iteration, only nontrivial full splits with nonzero weights are left in S. The weights of trivial full splits are also calculated by equation (8). A NEXUS file is created to store them and “SplitsTree4” (Huson and Bryant 2006) can be used to visualize the network.
As we can see, only the splits of length 5 and the full splits over 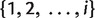 with nonzero weights are stored in iteration i. For every i, the set of all full splits with nonzero weight is a 2–weakly compatible split system. Using our consistency result and applying a similar argument as in (Bandelt and Dress 1992a), it can be shown that the number of splits in a 2–weakly compatible split system on n taxa can not exceed
with nonzero weights are stored in iteration i. For every i, the set of all full splits with nonzero weight is a 2–weakly compatible split system. Using our consistency result and applying a similar argument as in (Bandelt and Dress 1992a), it can be shown that the number of splits in a 2–weakly compatible split system on n taxa can not exceed 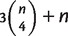 . Therefore, the Quartet-Net algorithm is polynomial in space and time. Indeed the space complexity of Quartet-Net is
. Therefore, the Quartet-Net algorithm is polynomial in space and time. Indeed the space complexity of Quartet-Net is 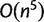 and the time complexity is
and the time complexity is 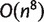 .
.
Consistency and Implementation
Consistency is a very important criterion to evaluate a reconstruction algorithm. We present the consistency of Quartet-Net in the following theorem, the proof of which can be found in the third section of supplementary material, Supplementary Material online.
Theorem 1. —
If the Quartet-Net algorithm is applied to triplet and quartet weights that are induced by a weighted 2–weakly compatible split system
on X, then it will output the splits in
with correct weights.
As the class of 2–weakly compatible split systems strictly contains compatible and weakly compatible split systems as special cases, Quartet-Net has the potential to accurately reconstruct a larger set of weighted split systems than previous algorithms such as Split-Decomposition (Bandelt and Dress 1992a, 1992b), Neighbor-Net (Bryant and Moulton 2004), and QNet (Grünewald et al. 2007). Quartet-Net has been implemented in C++ and is available for download for both Windows and Linux at http://sysbio.cvm.msstate.edu/QuartetNet/.
Supplementary Material
Supplementary material is available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).
Acknowledgments
The authors thank Naruya Saitou for providing the bacteria sequence data. This work was partially supported by the Natural Science Foundation of China (No. 10971213) to S.G., and Department of Justice (2010-DD-BX-0596) and National Institutes of Health (NIAID RC1AI086830) to X.-F.W.
References
- Bandelt HJ, Dress AWM. A canonical decomposition theory for metrics on a finite set. Adv Math. 1992a;92:47–105. [Google Scholar]
- Bandelt HJ, Dress AWM. Split-decomposition: a new and useful approach to phylogenetic analysis of distance data. Mol Phylogenet Evol. 1992b;1:242–252. doi: 10.1016/1055-7903(92)90021-8. [DOI] [PubMed] [Google Scholar]
- Bandelt H, Forster P, Röhl A. Median-joining networks for inferring intraspecific phylogenies. Mol Biol Evol. 1999;16:37–48. doi: 10.1093/oxfordjournals.molbev.a026036. [DOI] [PubMed] [Google Scholar]
- Bandelt H, Forster P, Sykes B, Richards M. Mitochondrial portraits of human population using median networks. Genetics. 1995;141:743–753. doi: 10.1093/genetics/141.2.743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berry V, Gascuel O. Inferring evolutionary trees with strong combinatorial evidence. Theor Comput Sci. 2000;240:271–298. [Google Scholar]
- Berry V, Jiang T, Kearney P, Li M, Wareham T. Quartet cleaning: improved algorithms and simulations. In: Nesetril J, editor. Proceedings of the 7th European Symposium on Algorithm (ESA99), Prague, Czech Republic. New York: Springer; 1999. pp. 313–324. [Google Scholar]
- Ben-Dor A, Chor B, Graur D, Ophir R, Pelleg D. Constructing phylogenies from quartets: elucidation of eutherian superordinal relationships. J Comput Biol. 1998;5:377–390. doi: 10.1089/cmb.1998.5.377. [DOI] [PubMed] [Google Scholar]
- Bruce A. Molecular biology of the cell. 4th ed. New York: Garland Science; 2002. [Google Scholar]
- Buneman P. The recovery of trees from measures of dissimilarity. In: Hodson FR, Kendall DG, Tautu P, editors. Mathematics in the archaeological and historical sciences. Providence (RI): American Mathematical Society; 1971. pp. 387–395. [Google Scholar]
- Bryant D, Moulton V. Neighbor-net: an agglomerative method for the construction of phylogenetic networks. Mol Biol Evol. 2004;21:255–265. doi: 10.1093/molbev/msh018. [DOI] [PubMed] [Google Scholar]
- Cartwright R. DNA assembly with gaps (Dawg): simulating sequence evolution. Bioinformatics. 2005;21(3 Suppl):iii31–iii38. doi: 10.1093/bioinformatics/bti1200. [DOI] [PubMed] [Google Scholar]
- Doolittle W, Boucher Y, Nesbø CL, Douady CJ, Andersson JO, Roger AJ. How big is the iceberg of which organellar genes in nuclear genomes are but the tip? Philos Trans R Soc Lond B Biol Sci. 2003;358:39–57. doi: 10.1098/rstb.2002.1185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felsenstein J. Inferring phylogenies. Sunderland (MA): Sinauer Associates; 2004. [Google Scholar]
- Fitch W. Networks and viral evolution. J Mol Evol. 1997;44:S65–S75. doi: 10.1007/pl00000059. [DOI] [PubMed] [Google Scholar]
- Gascuel O, Steel M. Reconstructing evolution: new mathematical and computational advances. New York: Oxford University Press; 2006. [Google Scholar]
- Grünewald S, Forslund K, Dress AWM, Moulton V. QNet: an agglomerative method for the construction of phylogenetic networks from weighted quartets. Mol Biol Evol. 2007;24:532–538. doi: 10.1093/molbev/msl180. [DOI] [PubMed] [Google Scholar]
- Grünewald S, Moulton V, Spillner A. Consistency of the QNet algorithm for generating planar split networks from weighted quartets. Discrete Appl Math. 2009;157:2325–2334. [Google Scholar]
- Grünewald S, Spillner A, Bastkowski S, Bogershausen A, Moulton V. SuperQ: Computing Supernetworks from Quartets. IEEE/ACM Trans Comput Biol Bioinform. 2013 doi: 10.1109/TCBB.2013.8. Advance Access published January 30, 2013, doi:10.1109/TCBB.2013.8. [DOI] [PubMed] [Google Scholar]
- Gusfield D, Eddhu S, Langley C. Optimal, efficient reconstruction of phylogenetic networks with constrained recombination. J Bioinform Comput Biol. 2004;2:173–213. doi: 10.1142/s0219720004000521. [DOI] [PubMed] [Google Scholar]
- Huber K, Langton M, Penny D, Moulton B, Hendy M. Spectronet: a package for computing spectra and median networks. Appl Bioinformatics. 2002;1:159–161. [PubMed] [Google Scholar]
- Huson D, Bryant D. Application of phylogenetic networks in evolutionary studies. Mol Biol Evol. 2006;23:254–267. doi: 10.1093/molbev/msj030. Available from: www.splitstree.org. [DOI] [PubMed] [Google Scholar]
- Huson D, Dezulian T, Klöpper T, Steel M. Phylogenetic super-networks from partial trees. IEEE ACM T Comput Biol. 2004;1:151–158. doi: 10.1109/TCBB.2004.44. [DOI] [PubMed] [Google Scholar]
- Huson D, Kloepper T. Computing recombination networks from binary sequences. Bioinformatics. 2005;21(2 Suppl):ii159–ii165. doi: 10.1093/bioinformatics/bti1126. [DOI] [PubMed] [Google Scholar]
- Holland B, Benthin S, Lockhart P, Moulton V, Huber K. Using super-networks to distinguish hybridization from lineage-sorting. BMC Evol Biol. 2008;8:202. doi: 10.1186/1471-2148-8-202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holland B, Conner G, Huber K, Moulton V. Imputing supertrees and supernetworks from quartets. Syst Biol. 2007;56:57–67. doi: 10.1080/10635150601167013. [DOI] [PubMed] [Google Scholar]
- Holland BR, Jarvis PD, Sumner JG. Low-parameter phylogenetic inference under the general Markov model. Syst Biol. 2013;62(1):78–92. doi: 10.1093/sysbio/sys072. [DOI] [PubMed] [Google Scholar]
- Jin G, Nakhleh L, Snir S, Tuller T. Efficient parsimony-based methods for phylogenetic network reconstruction. Bioinformatics. 2006;23:e123–e128. doi: 10.1093/bioinformatics/btl313. [DOI] [PubMed] [Google Scholar]
- Kunin V, Goldovsky L, Darzentas N, Ouzounis CA. The net of life: reconstructing the microbial phylogenetic network. Genome Res. 2005;15:954–959. doi: 10.1101/gr.3666505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larkin M, Blackshields G, Brown N, et al. (13 co-authors) Clustal W and Clustal X version 2.0. Bioinformatics. 2007;23(21):2947–2948. doi: 10.1093/bioinformatics/btm404. [DOI] [PubMed] [Google Scholar]
- Lemey P, Lott M, Martin DP, Moulton V. Identifying recombinants in human and primate immunodeficiency virus sequence alignments using quartet scanning. BMC Bioinformatics. 2009;10:126. doi: 10.1186/1471-2105-10-126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Linder R, Rieseberg L. Reconstructing patterns of reticulate evolution in plants. Am J Bot. 2004;91:1700–1708. [PMC free article] [PubMed] [Google Scholar]
- Meunier J, Duret L. Recombination drives the evolution of GC-content in the human genome. Mol Biol Evol. 2004;21(6):984–990. doi: 10.1093/molbev/msh070. [DOI] [PubMed] [Google Scholar]
- Morrison D. Networks in phylogenetic analysis: new tools for population biology. Int J Parasitol. 2005;35:567–582. doi: 10.1016/j.ijpara.2005.02.007. [DOI] [PubMed] [Google Scholar]
- Park HJ, Jin G, Nakhleh L. Bootstrap-based support of HGT inferred by maximum parsimony. BMC Evol Biol. 2010;10:131. doi: 10.1186/1471-2148-10-131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Posada D, Crandall K. Intraspecific gene genealogies: trees grafting into networks. Trends Ecol Evol. 2001;16:37–45. doi: 10.1016/s0169-5347(00)02026-7. [DOI] [PubMed] [Google Scholar]
- Ranwez V, Gascuel O. Quartet-based phylogenetic inference: improvements and limits. Mol Biol Evol. 2001;18(6):1103–1116. doi: 10.1093/oxfordjournals.molbev.a003881. [DOI] [PubMed] [Google Scholar]
- Ranwez V, Gascuel O. Improvement of distance-based phylogenetic methods by a local maximum likelihood approach using triplets. Mol Biol Evol. 2002;19(11):1952–1963. doi: 10.1093/oxfordjournals.molbev.a004019. [DOI] [PubMed] [Google Scholar]
- Saitou N, Nei M. The neighbor-joining method: a new method for reconstructing phylogenetic trees. Mol Biol Evol. 1987;4:406–425. doi: 10.1093/oxfordjournals.molbev.a040454. [DOI] [PubMed] [Google Scholar]
- Semple C, Steel M. Oxford: Oxford University Press; 2003. Phylogenetics. [Google Scholar]
- Snir S, Rao S. Quartet MaxCut: a fast algorithm for amalgamating quartet trees. Mol Phylogenet Evol. 2012;62(1):1–8. doi: 10.1016/j.ympev.2011.06.021. [DOI] [PubMed] [Google Scholar]
- Song YS, Hein J. Constructing minimal ancestral recombination graphs. J Comput Bioecol. 2005;12:147–169. doi: 10.1089/cmb.2005.12.147. [DOI] [PubMed] [Google Scholar]
- St. John K, Warnow T, Moret B, Vawter L. Performance study of phylogenetic methods: (unweighted) quartet methods and neighbor-joining. J Algorithms. 2003;48:174–193. [Google Scholar]
- Strimmer K, von Haeseler A. Quartet puzzling: a quartet maximum likelihood method for reconstructing tree toplogies. Mol Biol Evol. 1996;13:964–969. [Google Scholar]
- Sumner JG, Charleston MA, Jermiin LS, Jarvis PD. Markov invariants plethysms, and phylogenetics. J Theor Biol. 2008;253:601–615. doi: 10.1016/j.jtbi.2008.04.001. [DOI] [PubMed] [Google Scholar]
- Takahashi M, Kryukov K, Saitou N. Estimation of bacterial species phylogeny through oligonucleotide frequency distances. Genomics. 2009;93:525–533. doi: 10.1016/j.ygeno.2009.01.009. [DOI] [PubMed] [Google Scholar]
- Templeton A, Crandall K, Sing C. A cladistics analysis of phenotypic associations with haplotypes inferred from restriction endonuclease mapping and DNA sequence data. III. Cladogram estimation. Genetics. 1992;132:619–633. doi: 10.1093/genetics/132.2.619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Townsend T, Larson A, Louis E, Macey JR. Molecular phylogenetics of Squamata: the position of snakes, amphisbaenians,and dibamids, and the root of the squamate tree. Syst Biol. 2004;53(5):735–757. doi: 10.1080/10635150490522340. [DOI] [PubMed] [Google Scholar]
- Tria F, Caglioti E, Loreto V, Pagnani A. A stochastic local search algorithm for distance-based phylogeny reconstruction. Mol Biol Evol. 2010;27:2587–2595. doi: 10.1093/molbev/msq154. [DOI] [PubMed] [Google Scholar]
- van Iersel L, Keijsper J, Kelk S, Stougie L. Constructing level-2 phylogenetic networks from triplets. IEEE/ACM Trans Comput Biol Bioinform. 2009;6(4):667–681. doi: 10.1109/TCBB.2009.22. [DOI] [PubMed] [Google Scholar]
- van Iersel L, Kelk S, Rupp R, Huson D. Phylogenetic networks do not need to be complex: using fewer reticulations to represent conflicting clusters. Bioinformatics. 2010;26(12):i124–i131. doi: 10.1093/bioinformatics/btq202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willson S. Building phylogenetic trees from quartets by using local inconsistency measures. Mol Biol Evol. 1999;16:685–693. [Google Scholar]
- Willson S. Unique reconstruction of tree-like phylogenetic networks from distances between leaves. Bull Math Biol. 2006;68:919–944. doi: 10.1007/s11538-005-9044-x. [DOI] [PubMed] [Google Scholar]
- Yu Y, Than C, Degnan JH, Nakhleh L. Coalescent histories on phylogenetic networks and detection of hybridization despite lineage sorting. Syst Biol. 2011;60(2):138–149. doi: 10.1093/sysbio/syq084. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.