SUMMARY
Proper control of confounding due to population stratification is crucial for valid analysis of case-control association studies. Fine matching of cases and controls based on genetic ancestry is an increasingly popular strategy to correct for such confounding, both in genome-wide association studies (GWAS) as well as studies that employ next-generation sequencing, where matching can be used when selecting a subset of participants from a GWAS for rare-variant analysis. Existing matching methods match on measures of genetic ancestry that combine multiple components of ancestry into a scalar quantity. However, we show that including non-confounding ancestry components in a matching criterion can lead to inaccurate matches, and hence to an improper control of confounding. To resolve this issue, we propose a novel method that assigns cases and controls to matched strata based on the stratification score (Epstein et al., 2007, AJHG: 80: 921–930), which is the probability of disease given genomic variables. Matching on the stratification score leads to more accurate matches because case participants are matched to control participants who have a similar risk of disease given ancestry information. We illustrate our matching method using the African-American arm of the GAIN GWAS of schizophrenia. In this study, we observe that confounding due to stratification that can be resolved by our matching approach but not by other existing matching procedures. We also use simulated data to show our novel matching approach can provide a more appropriate correction for population stratification than existing matching approaches.
INTRODUCTION
Case-control association studies of complex disease have successfully identified genetic variants within the human genome that increase risk for complex diseases, including type II diabetes (Saxena et al., 2007; Scott et al., 2007; Sladek et al., 2007) and breast cancer (Easton et al., 2007; Hunter et al., 2007). When designing and analyzing case-control studies, care must be taken to ensure that significant results are true signals and not spurious findings attributable to confounding. In particular, genetic association studies may encounter confounding due to population stratification, which arises when genetic variation is correlated with variation in disease risk across latent subpopulations or geographic gradients. Failure to properly account for this correlation can lead to false associations between genetic markers and disease, as had been noticed in genetic studies of height (Campbell et al., 2005) and type II diabetes (Knowler et al., 1988).
A common strategy to resolve confounding due to population stratification uses large sets of genetic markers (typically single-nucleotide polymorphisms or SNPs) to infer influential components of ancestry, often using eigenvectors based on the principal components of the sample correlation matrix of SNP genotypes (Chen et al., 2003; Patterson et al., 2006; Price et al., 2006) as components of ancestry. More recently, Lee et al. (2009) used spectral-graph theory to form ancestry components consisting of eigenvectors derived from the normalized Laplacian matrix of the sample genotype data. Using either procedure, investigators then can adjust for confounding by using the ancestry components as covariates in regression-based tests of disease-marker association. We refer to this strategy as ‘direct adjustment’ for confounding due to population stratification.
As an alternative to direct-adjustment methods, an increasingly popular strategy to correct for population stratification involves tight matching of cases and controls into matched sets having similar genetic ancestry. One can then test for association between disease and genetic markers using a statistic appropriate for highly-stratified data, such as Cochran-Mantel-Haenszel tests or tests derived from conditional logistic regression. For a genome-wide association study, matching has advantages if a study recruits control subjects from large public databases, such as the POPRES database (Nelson et al., 2008) or uses control participants from other association studies made available through dbGaP (see Web Resources), since it ensures that only controls that have similar ancestry to those of case subjects are used in the analysis. Inclusion of controls with substantially dissimilar ancestry from cases can lead to improper corrections for population stratification when using direct-adjustment procedures (Luca et al., 2008; Allen et al., 2010). Furthermore, analysis of properly matched case and control participants adjusts for confounding with fewer assumptions than direct adjustment, which assumes disease risk is a linear or log-linear function of ancestry components. Finally, matching can provide a better correction for confounding in the presence of outliers (Luca et al., 2008).
Many genomewide association studies (GWAS) of complex diseases, including studies of ulcerative colitis (Silverberg et al., 2009), asthma (Himes et al., 2009), and presenile dementia (Van Deerlin et al., 2010), have employed fine matching to deal with confounding due to population stratification. We note that matching also will be valuable for studies that use next-generation sequencing of existing samples from a GWAS study. The current costs of massively-parallel sequencing technology typically prevents an entire GWAS sample from being sequenced. It is advantageous to select matched case and control participants for sequencing to ensure control of confounding due to population stratification. After such sampling, an unmatched analysis using direct adjustment can be problematic (Rothman et al., 2008) while a matched analysis is valid. Therefore, we anticipate matching will become even more important with the increased popularity of next-generation sequencing studies of complex disease.
Epidemiological studies that use matching often match on categorical variables such as race and gender. A complication of genetic matching is that ancestry components are continuous rather than categorical in nature. Furthermore, many ancestry components may be required to adequately summarize genetic variation within the dataset. For example, Tishkoff et al. (2009) identified 43 significant principal components (based on Tracy-Widom statistics (Patterson et al., 2006) within a sample of 2432 African subjects. As a result, matching based on ancestry components can be problematic. One approach is to combine all the ancestry components into a single scalar measure. The GEM approach (Luca et al., 2008) uses the Euclidean distance between the principal components of case and control participants to determine genetic similarity when assigning matched sets. GEM can include up to 50 principal components that are significant based on Tracy-Widom statistics. Lee et al. (2009) proposed a variation of GEM called SpectralGEM that replaces the principal components used in GEM with significant ancestry components derived from the spectral-graph approach (with the authors determining the number of significant ancestry components using an eigengap statistic). A different approach was taken by Guan et al. (2009) who developed a matching algorithm called GSM that matches subjects based on the average proportion of alleles (weighted by allele frequency) shared identical-by-state (IBS) over tens of thousands of SNPs.
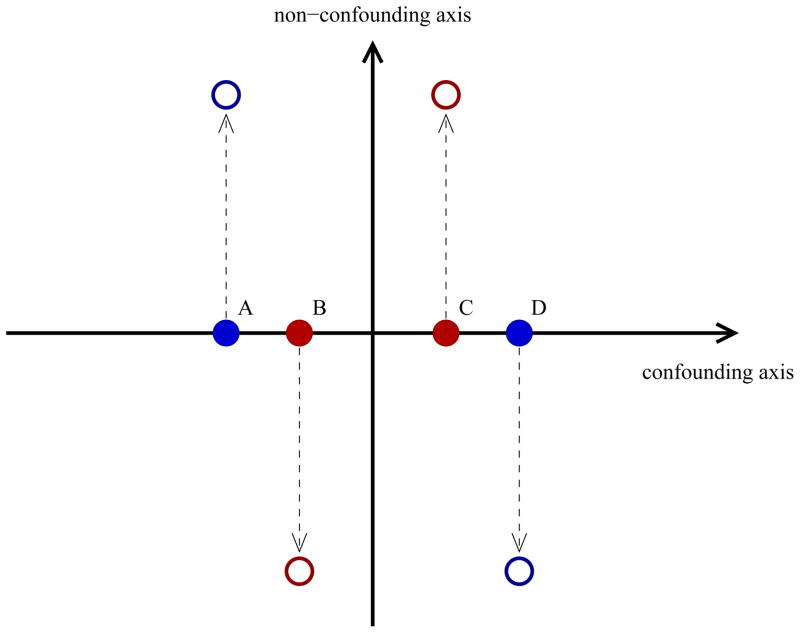
Existing matching methods summarize multiple ancestry components into a single scalar measure without regard to which components of ancestry actually contribute to confounding. For example, GEM and SpectralGEM methods attempt to match on all significant ancestry components but only a small fraction of these may be correlated with disease risk and therefore be potential confounders. Ancestry components that are uncorrelated with disease risk are simply noise for the purpose of adjusting for confounding due to population stratification. Of more concern when matching, the inclusion of non-confounding ancestry components in a scalar measure used for fine matching can lead to unsuitable matches of cases and controls that could result in improper correction for the confounding. To illustrate this issue, consider the example in Figure 1. We would like to match a red (case) subject to a blue (control) subject for the purpose of the analysis. Examining ancestry components only along the confounding axis of genetic variation, it is evident using a measure such as Euclidean distance (employed by GEM and SpectralGEM) that case participant B should be matched to control participant A and case participant C should be matched to control participant D. However, suppose we now introduce an additional axis of genetic variation that is not a confounder and proceed to conduct the matching in two-dimensional space. As participants A and B (and, likewise C and D) have quite dissimilar values along the non-confounding axis of genetic variation, they are less likely to be properly paired together. Subsequently, using Euclidean distance, we would end up matching A and C together and B and D together, which is a less optimal match than the original matching if we ignored the non-confounding axis. We would anticipate improper matching to be further exacerbated with the introduction of more components of ancestry that are not confounders within the sample.
Figure 1.
Impact of inclusion of non-confounding ancestry components on matching. If matching on confounding axis only, a study would pair subject A with subject B and subject C with subject D. Inclusion of a non-confounding axis would likely result in the less-optimal matching of subject A with subject C and subject B with subject D.
To ensure fine matching of cases and controls on only those ancestry components that are potential confounders, we propose a novel matching method based on a measure called the stratification score (Epstein et al., 2007). The stratification score for each participant is the estimated odds of disease conditional on potential confounders. Here we estimate the stratification score conditional on components of ancestry, which we infer from SNP data. Previously, we had used the stratification score to assign subjects to a small number of strata and then used stratified tests of association between disease and the test genotype. However, as we show, the stratification score is also amenable to use in tight matching of case and control subjects into fine strata. The stratification score is appealing for fine matching because it is an inherently scalar measure that accounts for the correlation between each ancestry component and disease risk. We can easily match on the stratification score regardless of the number of significant ancestry components identified within the sample. To see the advantage of matching based on the stratification score in a situation like that considered in Figure 1, note that the stratification score should vary most strongly along the confounding axis while varying little along the non-confounding axis. Consequently, matching on the stratification score should properly assign A and B into one stratum and C and D into a different stratum.
In subsequent sections, we review the stratification score and discuss methods for fine matching based on this quantity. We then illustrate our matching approach with an application to a genome-wide association study of schizophrenia sampled from an African-American population. Within the case-control sample, we observe confounding due to stratification that can be resolved by our stratification-score matching approach but not by GEM, SpectralGEM, or GSM. We also use simulated data to show our novel matching approach can provide a more appropriate correction for population stratification than a matched analysis using GEM or SpectralGEM.
MATERIALS AND METHODS
Assumptions and Notation
We assume a case-control study with N1 case participants and N0 control participants and let N = N0 + N1. For j = 1, …, N, we let Dj indicate the jth study participant’s disease status with Dj = 1 representing a case participant and Dj = 0 representing a control participant. We assume each participant is genotyped for a (possibly high-density) panel of M SNPs; for clarity of presentation we focus on the association between case/control status Dj and genotype at a single test locus of interest (denoted Gj ). We also let Zj = (Zj,1, Zj,2, …, Zj,K)T denote the vector of genotypes for K SNPs that we use to infer ancestry in the sample. There may be situations where K < M; for example, Fellay et al. (2007) used a thinned SNP set having low pairwise linkage disequilibrium (LD) to calculate principal components to avoid identifying significant axes that merely reflect LD among SNPs.
The Stratification Score
The foundation of our method involves the construction of the stratification score for each participant, which is the estimated odds of disease of a subject conditional on potential confounders (Epstein et al., 2007). Here the potential confounders of interest are related to ancestry information provided by the SNPs in Zj. We summarize ancestry information in Zj using a small number of ancestry components Cj derived from either the principal-component procedure of Patterson et al. (2006) or the spectral-graph method of Lee et al. (2009). To calculate the stratification score, we use logistic regression and write
| (1) |
where Θ(Cj) is the odds of disease conditional on ancestry components Cj, α is an intercept, and β is a vector of disease-risk parameters corresponding to ancestry components Cj. Fitting model (1) to the case-control data we estimate the coefficients α̂ and β̂ and hence estimate Θj:= Θ̂(Cj) = exp(α̂ + β̂T · Cj) which is the stratification score for the jth participant.
In Epstein et al. (2007), we used the stratification score to assign subjects (independent of disease status) to a small number of strata of approximately equal size, and subsequently tested association between D and G using stratified logistic regression or Cochran-Mantel-Haenszel statistics. Assuming the stratification score changes little within strata, Epstein et al. showed this stratified analysis controlled confounding by population stratification. Here, we propose matching on the value of the stratification score. Such matching constitutes a form of (fine) stratification, and thus controls for confounding by population stratification by the results of Epstein et al. (2007). Further, fine matching relaxes the assumption that the stratification score varies little within large strata.
In our original stratification-score paper, we proposed constructing the ancestry components Cj using partial-least squares (PLS), which constructs loadings using a combination of the SNPs Zj and disease information Dj. However, as noted by Lee et al. (2008), the use of PLS to construct the stratification score may lead to strata consisting of cases only or controls only, since the PLS-based ancestry components are constructed using information on disease status. Such strata are uninformative for association testing and lead to a decrease in power to detect SNP-disease association. For this reason, in this article and in other publications where we have used the stratification score to analyze GWAS data (Allen et al., 2010; Allen and Satten, 2009a,b, 2010; Sarasua et al., 2009), we use principal components or spectral-graph analysis (which produces ancestry components that are constructed without using information on disease) to construct Cj.
Fine Matching Based on the Stratification Score
We perform fine matching of cases and controls based on the stratification score using a matching strategy first proposed by Rosenbaum and Rubin (1985) for matching with the propensity score. Following Rosenbaum and Rubin, we calculate a dissimilarity measure Uij between a case i (i = 1, …, Nd) and a control j (j = 1, …, Nc) as the absolute difference between the log-transformed value of the stratification score derived from (1) scaled by the pooled standard deviation; that is, we define Uij as
| (2) |
where sd1 log(Θ(1)) and sd0 log(Θ(0)) denote the standard deviations of the log-transformed values of the stratification score in the cases and controls, respectively. Because Uij = 0 when case participant i and control participant j have the same value of the stratification score, and Uij > 0 otherwise, we ideally match a case i to a control j with a small (and possibly zero) value of Uij. Identification of optimal matches between cases and controls requires identifying the specific partitioning that minimizes the total dissimilarity of cases and controls within strata Guan et al. (2009). Here we follow the full matching strategy of Rosenbaum (1991) and minimize
| (3) |
where Aℓ and Bℓ denote the group of cases and controls, respectively, found in stratum ℓ(ℓ = 1, …, L). For details of the minimization, see Appendix A of Guan et al. (2009). As showed by Rosenbaum (1991), the matches that minimize T in (3) consist of either one case and ≥ 1 control (1:m matching) or ≥ 1 case and 1 control (m:1 matching). The set of optimal matches that minimize (3) can be obtained by using the R package optmatch. We note that GEM and SpectralGEM also utilize optmatch, while GSM uses a C implementation of the same algorithm as used in optmatch to identify matched strata. However, for these methods, the Uij measure in (3) is either a Euclidean distance that uses all the significant ancestry components (for GEM and SpectralGEM) or is a function of identity-by-state sharing across SNPs used to identify structure (for GSM).
After creating matched strata based on the stratification score, we use statistical methods tailored for finely-stratified data to perform association testing between disease outcome Y and test-locus genotype G. Here, we use the Cochran-Mantel-Haenszel to test for disease-SNP association in the finely-stratified data. If we must adjust for any additional covariates not incorporated within the matching measure, we could also implement a score test (Rao, 1965) based on a conditional logistic regression model for inference.
Software Implementation
We implemented our stratification score matching procedure in R code using existing R packages. Assuming availability of ancestry components for each study participant, our approach is easily implemented using the sample R code provided in Appendix A. We first construct the stratification score in (1) using the logistic-regression model implemented in the glm() function available in the R package stats. Next, we construct the dissimilarity measures for each case-control pairing in (2) using the pscore.dist() function available in the R package optmatch. Finally, we perform matching of cases and controls based on the dissimilarity measure in (2) using the fullmatch() function within the R package optmatch. Once we complete matching, we perform Cochran-Mantel-Haenszel tests of SNP-disease association across the finely-matched strata using the cmh test() function in the R package coin.
RESULTS
Analysis of the GAIN Schizophrenia GWAS
We applied our stratification-score matching approach to the GAIN case-control GWAS of African-American subjects with schizophrenia (Manolio et al., 2007) available for download from dbGaP (see Web Resources and Acknowledgements). As African-Americans are an admixed population and the prevalence of schizophrenia can vary among different ethnic groups (Kirkbride et al., 2006), we expect both population stratification and confounding by population stratification within the GWAS. The study dataset consisted of 921 cases and 954 controls genotyped for 845,814 SNPs. Prior to analysis, we implemented quality-control procedures using the software package PLINK version 1.07 (Purcell et al., 2007, see Web Resources). We removed SNPs that either had a minor-allele frequency less than 0.01, failed an exact test of HWE within the control subjects (assuming a significance level of 0.001), or were missing genotype calls in over 10% of the sample. Moreover, we excluded SNPs from the sex chromosomes from the analyses. We also removed any subjects that were missing more than 3% of their genotypes and further removed a small subset of subjects showing evidence of familial relationships within the sample based on excessive sharing of alleles identical by descent. After completion of quality-control checks, our revised sample consisted of 907 cases and 937 controls genotyped for 808,169 SNPs across the autosomes.
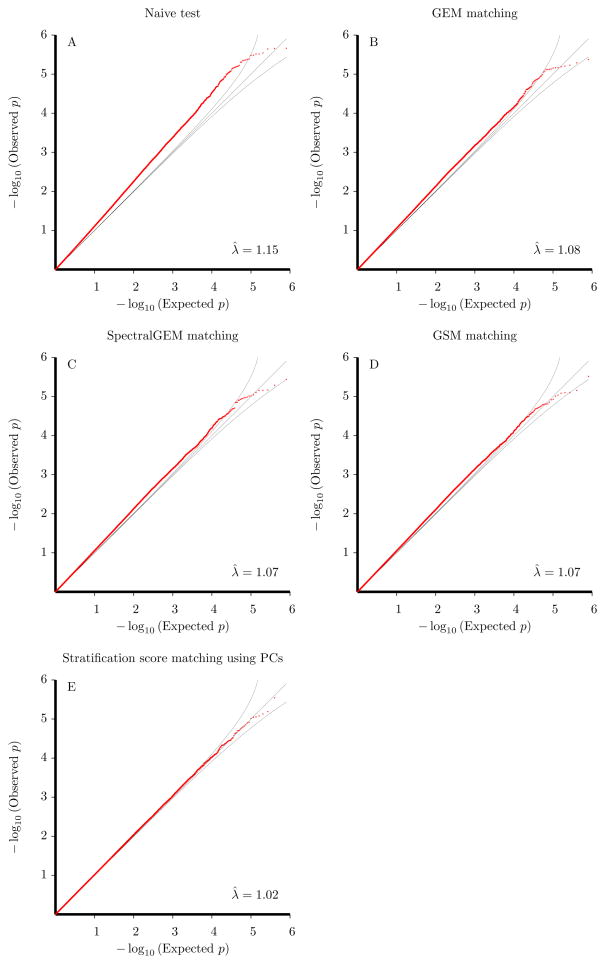
We initially used PLINK to perform SNP-disease association testing without any adjustment for population stratification. We performed testing using Cochran-Armitage trend statistics and present a QQ plot contrasting the observed p-values (on the −log10 scale) with those expected under the null hypothesis of no association in Figure 2A. The QQ plot departs from the 45° line and demonstrates marked confounding of association results due to population stratification within the test sample. We also calculated the inflation factor of the Cochran-Armitage trend statistics to be λ̂ = 1.15. Results using the allelic test (not shown) revealed a similar QQ plot and inflation factor.
Figure 2.
QQ plots of observed p-values versus expected p-values under the null hypothesis (on −log10 scale). Panel A: Naive analysis using Armitage trend test. Panel B: GEM matching analysis. Panel C: SpectralGEM matching analysis. Panel D: GSM matching analysis. Panel E: Analysis using stratification-score matching with 8 significant principal components. λ̂ denotes the inflation factor (calculated as the mean value of the observed chi-square statistics).
We next identified components of genetic ancestry within the test sample using the genomewide SNP data. We used GEM to infer significant eigenvectors from principal-component analysis (Chen et al., 2003; Patterson et al., 2006) and also used SpectralGEM to identify significant eigenvectors derived from spectral-graph theory (Lee et al., 2009). To ensure that significant components of ancestry were not a result of linkage disequilibrium among SNPs, we performed the eigenvector decompositions using a reduced set of SNPs that were in approximate linkage equilibrium. To construct this reduced SNP set, we pruned the set of SNPs having a genotype call rate of 100% and a minor-allele frequency greater than 5% with PLINK so that the pairwise r2 was ≤ 0.04 (similar to the criterion used by Luca et al. (2008). Using the resulting 41,182 SNPs to construct ancestry components, GEM identified 8 significant eigenvectors from principal-component analysis (based on Tracy-Widom statistics declared significant at α = 0.01) and SpectralGEM identified 12 significant eigenvectors from spectral-graph analysis (using the eigengap cutoff suggested by Lee et al. (2009)). We searched for potential outliers in our sample who had eigenvector values whose magnitude exceeded 6 times the standard deviation in any one of the significant axes (based on the suggestion of Luca et al. (2008)), but did not identify any such participants.
Using these ancestry components, we applied existing matching procedures to correct for potential confounding in the dataset. We applied the matching algorithms in GEM and SpectralGEM to perform full matching of cases and controls based on principal components and the significant eigenvectors from spectral-graph analyses, respectively. We also applied the GSM approach of Guan et al. (2009) that performed full matching based on weighted pairwise allele sharing at the 41,182 SNPs used for eigenvector decomposition. GEM yielded 906 strata (881 of size 2, 19 of size 3, 5 of size 4, 1 of size 5) while SpectralGEM yielded 907 strata (887 of size 2, 13 of size 3, 5 of size 4, 1 of size 5, 1 of size 6). GSM also yielded 907 strata (902 of size 2, 1 of size 5, 2 of size 6, 1 of size 8, 1 of size 15). Figures 2B, 2C, and 2D present the QQ plots for Cochran-Mantel-Haenszel tests based on the matched strata formed by GEM, SpectralGEM, and GSM, respectively. The QQ plots clearly indicate that these three methods inadequately adjust for the confounding within the dataset with GEM yielding an estimated inflation factor of λ̂ = 1.08 and SpectralGEM and GSM each yielding an inflation factor of λ̂ = 1.07.
We next applied our stratification-score matching algorithm using significant eigenvectors from either principal-component or spectral-graph analysis to the schizophrenia GWAS. Stratification-score matching yielded fewer strata than GEM, SpectralGEM, and GSM matching methods. Using eigenvectors from principal-component analysis, stratification-score matching yielded 661 strata (357 of size 2, 179 of size 3, 72 of size 4, 32 of size 5, 10 of size 6, 7 of size 7, 2 of size 8, 2 of size 10). Figure 2E shows the QQ plot of Cochran-Mantel-Haenszel tests based on the stratification score using the 8 significant eigenvectors from principal-component analysis. We found the observed p-values matched closely to those expected under the null (inflation factor of λ̂ = 1.02), indicating stratification-score matching properly corrected for confounding due to population stratification within the sample. Results based on the stratification score using 12 significant eigenvectors from spectral-graph analysis were similar (results not shown).
To gain a better understanding of why stratification-score matching based on the significant eigenvectors from principal-component/spectral-graph analyses corrected for confounding whereas GEM and Spectral-GEM did not, we examined the correlation of the significant eigenvectors with disease in the schizophrenia GWAS. Table 1 shows p-values of association tests examining the correlation between disease status and significant eigenvectors from principal-component analysis using a logistic-regression model. Results indicate that only 2 of the 8 eigenvectors that GEM used for matching were correlated with disease whereas the remaining 6 eigenvectors were uncorrelated with the outcome. Consequently, the inclusion of the 6 eigenvectors that are not confounders in analysis likely led GEM to select suboptimal matches. Stratification-score matching, on the other hand, relies on a measure that upweights the contribution of eigenvectors 1 and 4 (which are correlated with disease) and downweights the contribution of the remaining eigenvectors that are not confounders. Table 2 shows similar p-values of association tests examining the correlation between disease status and significant eigenvectors from spectral-graph analysis. Similar to the results shown in Table 1, we found that only 2 of the 12 significant eigenvectors from spectral-graph decomposition were correlated with disease risk in the schizophrenia GWAS, thereby increasing the chance of suboptimal matching using SpectralGEM.
Table 1.
Correlation of eigenvectors from principal component analysis with disease outcome in GAIN schizophrenia GWAS. Here the p-values were obtained from logistic-regression analysis that regresses disease outcome on significant eigenvectors from principal component analysis.
| Eigenvector | p-value |
|---|---|
|
| |
| 1 | 5.00 × 10−5 |
| 2 | 0.486 |
| 3 | 0.293 |
| 4 | 0.016 |
| 5 | 0.662 |
| 6 | 0.732 |
| 7 | 0.543 |
| 8 | 0.707 |
Table 2.
Correlation of eigenvectors from spectral-graph analysis with disease outcome in GAIN schizophrenia GWAS. Here the p-values were obtained from a logistic-regression model that regresses disease outcome on significant eigenvectors from spectral-graph analysis.
| Eigenvector | p-value |
|---|---|
|
| |
| 1 | 0.614 |
| 2 | 6.670 × 10−5 |
| 3 | 0.395 |
| 4 | 0.417 |
| 5 | 0.822 |
| 6 | 0.284 |
| 7 | 0.050 |
| 8 | 0.717 |
| 9 | 0.556 |
| 10 | 0.326 |
| 11 | 0.829 |
| 12 | 0.950 |
As shown in Figures 2B and 2C, we observed similar inflation in test statistics for both GEM and SpectralGEM even though the latter matches on more unnecessary variables than the former procedure. We believe this arises because GEM weights the eigenvectors used in the matching criterion by their corresponding eigenvalue whereas SpectralGEM does not perform such weighting. Consequently, while GEM is matching on fewer eigenvectors than SpectralGEM, it actually assigns higher weight to eigenvectors 2 and 3 (which are not confounders according to Table 1) than eigenvector 4 (which is a confounder). SpectralGEM weights all eigenvectors equally. Hence, although GEM uses fewer unnecessary eigenvectors, its choice of weights diminishes its performance in this simulation, with the net result that inference using GEM is similar to that obtained using SpectralGEM.
To assess whether the choice of matching method used in the GAIN schizophrenia GWAS would affect the selection of SNPs for potential follow-up studies, we compared the rankings of the top SNPs based on stratification-score matching with the rankings obtained from using GEM, SpectralGEM, and GSM. Overall, we found that the top-ranked SNPs identified by our matching approach had only minor overlap with the top-ranked SNPs identified by GEM/SpectralGEM/GSM. Among the top 10 SNPs identified by each approach, our matching approach shared only 1 SNP in common with GEM, SpectralGEM, and GSM. Among the top 100 SNPs identified by the various methods, our matching approach shared 20 SNPs in common with GEM, 24 SNPs with SpectralGEM, and 25 SNPs with GSM. Consequently, replication studies would be affected by the choice of matching method used for initial analysis.
Simulations based on GAIN Schizophrenia GWAS
We further used the schizophrenia GWAS considered above as the basis of additional simulations to further elucidate the differences in inference based on different matching approaches. In particular, we created a simulated dataset that generated new disease and test-SNP genotype data for each of the 1844 subjects within the schizophrenia GWAS using the subject’s significant ancestry components. For each simulated dataset, we constrained the number of cases and controls to be the same as the schizophrenia GWAS (907 cases, 937 controls) and further constrained the allele counts of the test SNP to be equal to a SNP chosen from the study.
We assumed the ancestry components to be the 8 significant eigenvectors from principal-component analysis. To generate a new disease outcome for each subject j (j = 1, …, 1844) in the schizophrenia study, we used the ancestry components Cj to create a new odds of disease Θ*(Cj ) using
| (4) |
where α* denotes an intercept, β* denotes an 8-dimensional vector of values for the disease-risk parameters related to the 8 significant principal components that constitute Cj, and γ* denotes a disease-risk parameter related to the test-locus genotype Gj. Based on the results of our schizophrenia analysis that showed that only the first and fourth principal components were correlated with disease, we assumed in (4) and chose . We used γ* = 0 when investigating size and γ* = 1.2 when examining power.
We used the odds model in (4) to sample disease status for each study participant, conditional on the presence of 907 case participants and 937 control participants in the dataset, by drawing a random vector from Fisher’s multivariate noncentral hypergeometric distribution with noncentrality parameter Θ* = (Θ*(C1), Θ*(C2), …, Θ*(C1844)). Note that the multivariate noncentral hypergeometric distribution arises when drawing balls with differing odds of selection from an urn conditional on the event of the total number of balls chosen. As the distribution depends only on the ratio of the individual elements of Θ*, we do not need to specify the intercept α* in (4).
To generate the genotype at the test locus, we assumed independence of alleles conditional on the ancestry components, and then modeled the odds of possessing the minor SNP allele over the major SNP allele given Cj. We denote this odds parameter by Ψ(Cj) and model it using
| (5) |
where η denotes a 8-dimensional vector of coefficients relating the 8 significant principal components that constitute Cj to the odds of the minor allele. To determine η, we used the estimated coefficients from a logistic-regression model that regressed the presence of the minor allele for rs6667248 in the schizophrenia GWAS (overall minor-allele frequency of 0.20 in the sample) on the 8 significant eigenvectors from principal-component analysis. Based on this analysis, we assumed η = (−4.92, 1.06, −0.77, −3.87, 2.59, −1.01, −2.49, 0.07)T. Note that the first and fourth principal components of Cj are confounders, as their corresponding elements of β* in (4) and η in (5) are both non-zero and therefore affect both the disease risk and allele frequencies at the test SNP. To maintain the same number of risk alleles in each simulation, we assumed the total number of minor alleles in the sample was equivalent to the total number observed for SNP rs6667248 in the schizophrenia GWAS. We then generated test-SNP genotypes using Fisher’s noncentral hypergeometric distribution with noncentrality parameter Ψ = (Ψ(C1), Ψ(C2), …, Ψ(C1844)).
For the model specified using (4) and (5), we generated 10,000 datasets based on Fisher’s multivariate noncentral hypergeometric distribution using the R package BiasedUrn (Fog, 2008), which we recompiled to allow for the generation of random vectors with dimension equal to the number of study participants (see Web Resources). Table 3 provides the empirical type-I error rates under our model. As expected, we observed confounding in our simulated datasets as noted by the inflated type-I error rates of the naive tests. We also found that our proposed stratification-score matching approach using principal components adequately corrected for the confounding in the datasets. However, we found that GEM had highly inflated type-I error rates in the simulated datasets, indicating that the method yielded inaccurate matches when combining the principal components that were confounders (i.e. the first and fourth components) with those components that were not confounders. SpectralGEM also yielded inflated type-I error rates, which we believe is due to only 3–4 of the 12 significant eigenvectors from spectral-graph decomposition being correlated with disease risk across the simulated datasets examined. To support these hypotheses, we applied modified forms of GEM and SpectralGEM to our simulation example in Table 3 where we constructed the matching measure of the procedures incorporating only the confounding axes of variation into the measure (defined as axes associated with disease with a p-value less than 0.05). We observed that these ‘modified’ forms of GEM and SpectralGEM had appropriate type-I error in the presence of confounding (results not shown).
Table 3.
Type-I error results for 10,000-replicate simulations conducted using SNP rs6667248 (overall MAF of 0.20) from the schizophrenia GWAS study. Stratification score matches were constructed using significant eigenvectors from principal component analysis.
| Method | Type-I Error | |
|---|---|---|
| α = 0.05 | α = 0.005 | |
| Naive | 0.141 | 0.0290 |
| Stratification Score Matching | 0.048 | 0.0047 |
| GEM | 0.094 | 0.0148 |
| SpectralGEM | 0.112 | 0.0200 |
Table 4 shows power estimates of stratification-score matching, GEM, and SpectralGEM under a model where there is population stratification in the sample but no confounding due to stratification (achieved by modeling β* = (0, 0, 0, 0, 0, 0, 0, 0)T in (4), since the power of the latter two methods is invalid in the presence of confounding. Overall, we found the power of the three procedures to be similar, although we observe GEM and SpectralGEM have a slight power increase over stratification-score matching. We believe this minor power increase is due to our observation in the simulated data that stratification-score matching sometimes yield larger strata that are more imbalanced with regards to case and control participants than GEM and SpectralGEM. Such imbalanced strata tend to be less informative for analysis (Hansen, 2004).
Table 4.
Power results based on 10,000-replicate simulations conducted using SNP rs6667248 (overall MAF of 0.20) from the schizophrenia GWAS study. Assumed here is a relative risk of 1.2 per copy of the minor allele. Datasets were generated assuming population stratification but no confounding due to stratification. Stratification score matches were constructed using significant eigenvectors from principal-component analysis.
| Method | Power | |
|---|---|---|
| α = 0.05 | α = 0.005 | |
| Naive | 0.626 | 0.312 |
| Stratification Score Matching | 0.583 | 0.279 |
| GEM | 0.617 | 0.304 |
| SpectralGEM | 0.621 | 0.310 |
DISCUSSION
With the recent availability of large public databases of healthy controls for use in genetic studies, fine matching of cases and controls on a measure of genetic ancestry has become an increasingly common procedure to correct for confounding due to population stratification and will become even more valuable with the increased popularity of massively-parallel sequencing studies. In this article, we describe a novel matching procedure to correct for confounding based on a measure called the stratification score that is the predicted odds of disease conditional on components of ancestry (Epstein et al., 2007). Using both a real case-control GWAS of schizophrenia in an African-American population, as well as simulated datasets, we showed our proposed matching method provides a better correction for confounding due to population stratification than existing matching methods. Our proposed matching method provides an improved correction because the stratification score automatically upweights the contribution of components of ancestry that are potential confounders and downweights those components that are not. Existing matching methods use all components of genetic variation regardless of whether they are potential confounders, thereby increasing the chance of inaccurate matches and weaker correction for confounding due to population stratification.
Matching on the stratification score in case-control association studies has parallels to matching on the propensity score in prospective studies (Rosenbaum and Rubin, 1983, 1984). The propensity score is defined as the probability (or odds) of an exposure conditional on confounder variables. It is well established that stratification on the propensity score removes confounding when examining the relationship between a binary exposure and disease in prospective studies. In the same way, matching on the propensity score is also known to remove confounding (Rosenbaum and Rubin, 1985).
Association studies have increasingly moved beyond the testing for common SNP variants; many analyses are focused on rare variants (Li and Leal, 2008; Madsen and Browning, 2009; Li et al., 2010; Ionita-Laza et al., 2011). In this paper we have considered the effect of genotype on case-control status. In fact, genotype G can refer to any kind of genotypic effect we wish to model. For example, G could count the number of rare variants in a window centered at a specific locus; a series of such sliding window analyses would allow for a genome-wide scan for rare variant effects that used matching to control for confounding by population stratification.
A limitation of our stratification-score matching procedure is that, while the approach is valid for testing the null hypothesis of no association between a test locus and disease, parameter estimates correspond to a marginal model in which case and control participants have the same distribution of confounding covariates, so that covariates can be ignored (Allen and Satten, 2011). However, under the null hypothesis, parameters in this marginal model coincide with those in the more-standard conditional model that explicitly includes confounding covariates, so that hypothesis tests of parameters in the marginal model are valid for inference on parameters in the conditional model. Nevertheless, we believe our approach still has substantial value for initial GWAS studies (where the focus is on testing of SNPs rather than estimation due to the upward bias of effect-size estimates of the most significant SNPs due to the phenomenon of Winner’s Curse) as well as resequencing studies (where the odds ratios of individual rare variants are difficult to estimate and rare-variant grouping variables are often difficult to interpret).
Acknowledgments
We thank Drs. Michael Boehnke, Weihua Guan, and Liming Liang as well as two anonymous reviewers for helpful comments on a previous version of this article. This work was supported by National Institutes of Health grants HG003618 (to M.P.E and R.D.) and HL077663 (to A.S.A). Funding support for ‘Genome-Wide Association Study of Schizophrenia’ was provided by National Institutes of Health and the genotyping of samples was provided through the Genetic Association Information Network (GAIN). The dataset used for the analyses described in this manuscript were obtained from the database of Genotype and Phenotype (dbGaP) found at http://www.ncbi.nlm.nih.gov/gap through dbGaP accession number phs000021.v2.p1. Samples and associated phenotype data for ‘Genome-Wide Association Study of Schizophrenia ’ were provided by Pablo V. Gejman, MD.
APPENDIX A: SAMPLE R CODE FOR IMPLEMENTING STRATIFICATION-SCORE MATCHING
Listing 1: R code
# required libraries ‘optmatch’ and ‘survival’
# must be installed prior to upload:
\library(‘stats’)
\library(‘optmatch’)
\library(‘survival’)
\library(‘coin’)
# Assume one has already scanned in required dataset. This includes:
# dis: array of length N consisting of disease outcomes for N subjects
# (1: affected, 0: unaffected)
# g: array of length N consisting of test-SNP genotypes for N subjects
# (\# of copies of reference allele, NA for missing)
# pc: N x p matrix consisting of the p significant eigenvectors for the N subjects
# Step 1: Construct the stratification score in \eqref{eqn-1}
# using the significant eigenvectors:
sscore_pc <- glm(dis∼pc,family=binomial())
# Step 2: Calculate the dissimilarity measure in \eqref{eqn-2} based on the
# stratification score:
ssd_pc <- pscore.dist(sscore_pc)
#Step 3: Perform full matching of cases and controls:
fmatch_ssd_pc <- fullmatch(ssd_pc)
#Step 4: Form a new dataframe combining the disease, test-SNP genotype,
# and matched-stratum indicator:
full_match_dat_pc <- data.frame(cbind(dis,g,fmatch_ssd_pc))
#Step 5: Perform Cochran-Mantel-Haenszel (CMH) Test of SNP-Disease Association:
# Must first remove strata with fewer than two observations
# (possible if SNP vector g contains missing data)
orig_table <- table(full_match_dat_pc)
orig_table_strat <- max(full_match_dat_pc[,3])
miss_strat <- 0
for(i in 1:orig_table\strat) {
if(sum(orig_table[,,i]) <= 1)
miss_strat <- c(miss_strat,i)
}
if(length(miss_strat) > 1) {
miss_strat <- miss_strat[-1]
final_table <- orig_table[,,-c(miss_strat)]
nstrat <- orig_table_strat - length(miss_strat)
}
else if(length(miss_strat)==1) {
final_table <- orig_table
nstrat <- orig_table_strat
}
ng <- length(table(full_match_dat_pc[,2]))
gscore <- seq(0,(ng-1))
#Implement CMH test
cmh_analysis <- cmh_test(as.table(final_table), scores=list(dis=0:1,g=gscore))
#Obtain p-value from CMH test
pvalue_cmh <- pvalue(cmh_analysis)
Footnotes
Disclaimer: The findings and conclusions in this article are those of the authors and do not necessarily represent the official position of the Centers for Disease Control and Prevention
WEB RESOURCES
| dbGaP | http://view.ncbi.nlm.nih.gov/dbgap |
| Epstein Software | http://www.genetics.emory.edu/labs/epstein |
| GEM and SpectralGEM | http://wpicr.wpic.pitt.edu/WPICCompGen |
| GSM | http://www.sph.umich.edu/csg/liang/gsm/ |
| PLINK version 1.07 | http://pngu.mgh.harvard.edu/~purcell/plink/ |
References
- Allen A, Epstein M, Satten G. Score-based adjustment for confounding by population stratification in genetic association studies. Genetic Epidemiology. 2010;34:383–385. doi: 10.1002/gepi.20487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen A, Satten G. Genome-wide association analysis of rheumatoid arthritis data via haplotype sharing. BMC Proceedings. 2009a;3(Suppl 7):S30. doi: 10.1186/1753-6561-3-s7-s30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen A, Satten G. Control for confounding in case-control studies using the stratification score, a retrospective balancing score. American Journal of Epidemiology. 2011;173:752–760. doi: 10.1093/aje/kwq406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen AS, Satten GA. A novel haplotype-sharing approach for genome-wide case-control association studies implicates the calpastatin gene in parkinson’s disease. Genetic Epidemiology. 2009b;33(8):657–667. doi: 10.1002/gepi.20417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen AS, Satten GA. SNPs in CAST are associated with parkinson disease: A confirmation study. American Journal of Medical Genetics Part B: Neuropsychiatric Genetics. 2010;153B(4):973–979. doi: 10.1002/ajmg.b.31061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campbell CD, Ogburn EL, Lunetta KL, Lyon HN, Freedman ML, Groop LC, Altshuler D, Ardlie KG, Hirschhorn JN. Demonstrating stratification in a European American population. Nature Genetics. 2005;37(8):868–872. doi: 10.1038/ng1607. [DOI] [PubMed] [Google Scholar]
- Chen HS, Zhu X, Zhao H, Zhang S. Qualitative semiparametric test to detect genetic association in case-control design under structured population. Annals of Human Genetics. 2003;67:250–264. doi: 10.1046/j.1469-1809.2003.00036.x. [DOI] [PubMed] [Google Scholar]
- Easton DF, Pooley KA, Dunning AM, Pharoah PDP, Thompson D, Ballinger DG, Struewing JP, Morrison J, Field H, Luben R, Wareham N, Ahmed S, et al. Genome-wide association study identifies novel breast cancer susceptibility loci. Nature. 2007;447(7148):1087–1093. doi: 10.1038/nature05887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Epstein MP, Allen AS, Satten GA. A simple and improved correction for population stratification in case-control studies. American Journal of Human Genetics. 2007;80(5):921–930. doi: 10.1086/516842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fellay J, Shianna KV, Ge D, Colombo S, Ledergerber B, Weale M, Zhang K, Gumbs C, Castagna A, Cossarizza A, Cozzi-Lepri A, De Luca A, et al. A whole-genome association study of major determinants for host control of HIV-1. Science. 2007;317(5840):944–947. doi: 10.1126/science.1143767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fog A. Sampling methods for Wallenius’ and Fisher’s noncentral hypergeometric distributions. Communications in Statistics, Simulation and Computation. 2008;37(2):241–257. [Google Scholar]
- Guan W, Liang L, Boehnke M, Abecasis GR. Genotype-based matching to correct for population stratification in large-scale case-control genetic association studies. Genetic Epidemiology. 2009;33(6):508–517. doi: 10.1002/gepi.20403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen BB. Full matching in an observational study of coaching for the sat. Journal of the American Statistical Association. 2004;99(467):609–618. [Google Scholar]
- Himes B, Hunninghake G, Baurley J, Rafaels N, Sleiman P, Strachan D, Wilk J, Willis-Owen S, Klanderman B, Lasky-Su J, Lazarus R, Murphy A, et al. Genome-wide association analysis identifies PDE4D as an asthma-susceptibility. Americal Journal of Human Genetics. 2009;84:581–593. doi: 10.1016/j.ajhg.2009.04.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hunter DJ, Kraft P, Jacobs KB, Cox DG, Yeager M, Hankinson SE, Wacholder S, Wang Z, Welch R, Hutchinson A, Wang J, Yu K, et al. A genome-wide association study identifies alleles in FGFR2 associated with risk of sporadic postmenopausal breast cancer. Nature Genetics. 2007;39(7):870–874. doi: 10.1038/ng2075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ionita-Laza I, Buxbaum JD, Laird NM, Lange C. A new testing strategy to identify rare variants with either risk or protective effect on disease. PLoS Genet. 2011 Feb;7(2):e1001289. doi: 10.1371/journal.pgen.1001289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirkbride JB, Fearon P, Morgan C, Dazzan P, Morgan K, Tarrant J, Lloyd T, Holloway J, Hutchinson G, Leff JP, Mallett RM, Harrison GL, et al. Heterogeneity in incidence rates of schizophrenia and other psychotic syndromes: findings from the 3-center ÆSOP study. Archives of General Psychiatry. 2006;63(3):250–258. doi: 10.1001/archpsyc.63.3.250. [DOI] [PubMed] [Google Scholar]
- Knowler W, Williams R, Pettitt D, Steinberg A. Gm3;5,13,14 and type 2 diabetes mellitus: an association in American Indians with genetic admixture. American Journal of Human Genetics. 1988;43:520–526. [PMC free article] [PubMed] [Google Scholar]
- Lee AB, Luca D, Klei L, Devlin B, Roeder K. Discovering genetic ancestry using spectral graph theory. Genetic Epidemiology. 2009;34(1):51–59. doi: 10.1002/gepi.20434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S, Sullivan P, Zou F, Wright F. Comment on a simple and improved correction for population stratification. Americal Journal of Human Genetics. 2008;82:524–526. doi: 10.1016/j.ajhg.2007.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li B, Leal SM. Methods for detecting associations with rare variants for common diseases: Application to analysis of sequence data. American Journal of Human Genetics. 2008;83(3):311–321. doi: 10.1016/j.ajhg.2008.06.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Byrnes A, Li M. To identify associations with rare variants, just WHaIT: weighted haplotype and imputation-based tests. American Journal of Human Genetics. 2010;87(5):728–735. doi: 10.1016/j.ajhg.2010.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luca D, Ringquist S, Klei L, Lee AB, Gieger C, Wichmann HE, Schreiber S, Krawczak M, Lu Y, Styche A, Devlin B, Roeder K, et al. On the use of general control samples for genome-wide association studies: Genetic matching highlights causal variants. Americal Journal of Human Genetics. 2008;82(2):453–463. doi: 10.1016/j.ajhg.2007.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madsen BE, Browning SR. A groupwise association test for rare mutations using a weighted sum statistic. PLoS Genet. 2009 Feb;5(2):e1000384. doi: 10.1371/journal.pgen.1000384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manolio TA, Rodriguez LL, Brooks L, Abecasis G. New models of collaboration in genome-wide association studies: the Genetic Association Information Network. Nature Genetics. 2007;39(9):1045–1051. doi: 10.1038/ng2127. [DOI] [PubMed] [Google Scholar]
- Nelson M, Bryc K, King K, Indap A, Boyko A, Novembre J, Briley L, Maruyama Y, Waterworth D, Waeber G, Vollenweider P, Oksenberg J, et al. The population reference sample, POPRES: a resource for population, disease, and pharmacological genetics research. Americal Journal of Human Genetics. 2008;83:347–358. doi: 10.1016/j.ajhg.2008.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patterson N, Price AL, Reich D. Population structure and eigenanalysis. PLoS Genet. 2006 Dec;2(12):e190. doi: 10.1371/journal.pgen.0020190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D. Principal components analysis corrects for stratification in genome-wide association studies. Nature Genetics. 2006;38(8):904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MA, Bender D, Maller J, Sklar P, de Bakker PI, Daly MJ, Sham PC. PLINK: A tool set for whole-genome association and population-based linkage analyses. American Journal of Human Genetics. 2007;81:559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rao C. Linear Statistical Inference and its Applications. New York: Wiley; 1965. pp. 350–352. [Google Scholar]
- Rosenbaum PR. A characterization of optimal designs for observational studies. Journal of the Royal Statistical Society, Series B (Methodological) 1991;53(3):597–610. [Google Scholar]
- Rosenbaum PR, Rubin DB. The central role of the propensity score in observational studies for causal effects. Biometrika. 1983;70(1):41–55. [Google Scholar]
- Rosenbaum PR, Rubin DB. Reducing bias in observational studies using subclassification on the propensity score. Journal of the American Statistical Association. 1984 Sep;79(387):516–524. [Google Scholar]
- Rosenbaum PR, Rubin DB. Constructing a control group using multivariate matched sampling methods that incorporate the propensity score. The American Statistician. 1985 Feb;39(1):33–38. [Google Scholar]
- Rothman KJ, Greenland S, Lash TL. Modern Epidemiology. 3. Philadelphia, PA: Lippincott Williams & Wilkins; 2008. [Google Scholar]
- Sarasua S, Collins J, Williamson D, Satten G, Allen A. Effect of population stratification on the identification of significant single-nucleotide polymorphisms in genome-wide association studies. BMC Proceedings. 2009;3(Suppl 7):S13. doi: 10.1186/1753-6561-3-s7-s13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saxena R, Voight BF, Lyssenko V, Burtt NP, de Bakker PIW, Chen H, Roix JJ, Kathiresan S, Hirschhorn JN, Daly MJ, Hughes TE, Groop L, et al. Genome-wide association analysis identifies loci for type 2 diabetes and triglyceride levels. Science. 2007;316(5829):1331–1336. doi: 10.1126/science.1142358. [DOI] [PubMed] [Google Scholar]
- Scott LJ, Mohlke KL, Bonnycastle LL, Willer CJ, Li Y, Duren WL, Erdos MR, Stringham HM, Chines PS, Jackson AU, Prokunina-Olsson L, Ding CJ, et al. A genome-wide association study of type 2 diabetes in Finns detects multiple susceptibility variants. Science. 2007;316(5829):1341–1345. doi: 10.1126/science.1142382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silverberg MS, Cho JH, Rioux JD, McGovern DPB, Wu J, Annese V, Achkar JP, Goyette P, Scott R, Xu W, Barmada MM, Klei L, et al. Ulcerative colitis–risk loci on chromosomes 1p36 and 12q15 found by genome-wide association study. Nature Genetics. 2009;41(2):216–220. doi: 10.1038/ng.275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sladek R, Rocheleau G, Rung J, Dina C, Shen L, Serre D, Boutin P, Vincent D, Belisle A, Hadjadj S, Balkau B, Heude B, et al. A genome-wide association study identifies novel risk loci for type 2 diabetes. Nature. 2007;445(7130):881–885. doi: 10.1038/nature05616. [DOI] [PubMed] [Google Scholar]
- Tishkoff SA, Reed FA, Friedlaender FR, Ehret C, Ranciaro A, Froment A, Hirbo JB, Awomoyi AA, Bodo JM, Doumbo O, Ibrahim M, Juma AT, et al. The genetic structure and history of Africans and African Americans. Science. 2009;324(5930):1035–1044. doi: 10.1126/science.1172257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Deerlin VM, Sleiman PMA, Martinez-Lage M, Chen-Plotkin A, Wang LS, Graff-Radford NR, Dickson DW, Rademakers R, Boeve BF, Grossman M, Arnold SE, Mann DMA, et al. Common variants at 7p21 are associated with frontotemporal lobar degeneration with TDP-43 inclusions. Nature Genetics. 2010;42(3):234–239. doi: 10.1038/ng.536. [DOI] [PMC free article] [PubMed] [Google Scholar]