Sequence and Temperature Dependence of the End-to-End Collision Dynamics of Single-Stranded DNA

Abstract

Intramolecular collision dynamics play an essential role in biomolecular folding and function and, increasingly, in the performance of biomimetic technologies. To date, however, the quantitative studies of dynamics of single-stranded nucleic acids have been limited. Thus motivated, here we investigate the sequence composition, chain-length, viscosity, and temperature dependencies of the end-to-end collision dynamics of single-stranded DNAs. We find that both the absolute collision rate and the temperature dependencies of these dynamics are base-composition dependent, suggesting that base stacking interactions are a significant contributor. For example, whereas the end-to-end collision dynamics of poly-thymine exhibit simple, linear Arrhenius behavior, the behavior of longer poly-adenine constructs is more complicated. Specifically, 20- and 25-adenine constructs exhibit biphasic temperature dependencies, with their temperature dependences becoming effectively indistinguishable from that of poly-thymine above 335 K for 20-adenines and 328 K for 25-adenines. The differing Arrhenius behaviors of poly-thymine and poly-adenine and the chain-length dependence of the temperature at which poly-adenine crosses over to behave like poly-thymine can be explained by a barrier friction mechanism in which, at low temperatures, the energy barrier for the local rearrangement of poly-adenine becomes the dominant contributor to its end-to-end collision dynamics.

Introduction

Intramolecular collision dynamics play an essential role in biomolecular folding (1,2) and function (3,4) and, increasingly, in the performance of some biomimetic technologies (5–8). Thus motivated, the intramolecular collision dynamics of unstructured polypeptides have seen extensive study (9–15). In comparison, however, relatively little attention has been paid to the dynamics of single-stranded oligonucleotides (16–19), despite the significant roles that such dynamics play in the folding of RNA (1,4), in the regulation of gene expression (20,21), and in a range of sensing technologies based on the binding-induced folding of nucleic acids (6–8).

Among the few studies reported to date regarding the dynamics of single-stranded oligonucleotides, a persistent suggestion has emerged that, not surprisingly given their charge, electrostatic effects dominate the dynamic properties of short, single-stranded DNAs. For example, we have previously found that the end-to-end collision rates of polymers of thymine deoxyoligonucleotide (poly-thymine) ranging from 6 to 26 bases scales with the number of monomers to the −3.49 ± 0.13 power (22), which is a significantly stronger length dependence than those observed experimentally for the end-to-end collision kinetics of polypeptides (13–15) or estimated theoretically using polymer scaling laws (23–33). Based on the results of extensive simulations, we have previously argued that this large exponent arises due to electrostatic effects specific to short, highly charged polymer chains (22).

In addition to electrostatic effects, several groups have reported that sequence-specific base stacking interactions also play a significant role in defining the internal dynamics of short, single-stranded oligonucleotides. Majima and co-workers, (34) for example, have reported that the end-to-end collision dynamics of a 9-base adenine deoxyoligonucleotide (poly-adenine) are slower than those of the equivalent length of thymine oxyoligonucleotide; an observation they attribute to higher intrinsic rigidity in the former. Studying di- and tetranucleotide constructs Nau and co-workers (35) have likewise argued that, although the end-to-end collision dynamics of thymine oligonucleotides are limited by the entropic cost of loop closure, those of adenine constructs are limited by the energetic cost of breaking base stacking interactions. To date, however, no detailed, quantitative studies have been reported of, for example, how the length and temperature dependence of the end-to-end collision dynamics of single-stranded DNA vary with sequence composition, work that could clarify the relative contributions of electrostatics and base stacking to oligonucleotide dynamics. Specifically, whereas the strong chain-length dependence of the end-to-end collision rate is a signature of electrostatic interactions, base-base interactions should affect the temperature dependence of the rate, as the stacking of, for example, poly-riboadenine decreases significantly with increasing temperature (36). Thus motivated, here we have investigated chain length, sequence composition, and temperature dependencies of the end-to-end collision dynamics of single-stranded DNAs.

Materials and Methods

Estimation of the end-to-end collision rate of single-stranded DNAs

We determined end-to-end collision rates using the effectively contact quenching of a long-lived ruthenium tris(bipyridine) luminophore as previously reported (22,35), except that we employed DABSYL (see Abbreviations in the Supporting Material for the systematic IUPAC name) rather than methyl bipyridine (see Abbreviations) as our quencher. Methyl bipyridine exhibits diffusion-limited quenching via electron transfer, a near contact process (37,38). Unfortunately, due to the strong absorption of DABSYL the bimolecular quenching rate of DABSYL is not experimentally accessible rendering it difficult to demonstrate directly that this quenching is similarly a near-contact process. Several indirect lines of evidence, however, argue that this is the case and thus that we can employ DABSYL in our studies: First, the redox potentials of a closely related derivative, DABCYL (see Abbreviations) are, at −0.20 and −0.40V vs. SHE (39), somewhat higher than that of the −0.45V of methyl bipyridine (40), suggesting that electron transfer from the exited luminophore to DABSYL will be still more favorable. Second, although a subtle overlap between the absorption spectrum of DABSYL and luminescence spectrum of ruthenium luminophore (Fig. S1 in the Supporting Material) suggests that quenching via resonance energy transfer may be possible; the overlap is so slight that the calculated Förster radius is only 11 Å, which is quite similar to the dimensions of the reporters themselves. DABSYL, for example, approximates a cylinder ∼1.4 Å in diameter and ∼6 Å in length, and the ruthenium complex to approximate a sphere ∼8 Å in diameter. Thus, even if resonance energy transfer contributes to the observed quenching, the two termini must nevertheless still be in near contact for quenching to occur.

Consistent with the previous arguments, the end-to-end collision rates we have determined using DABSYL are only slightly greater (e.g., 8.3 × 10⁵ s⁻¹ for DABSYL modified 27-thymine construct versus 3.2 × 10⁵ s⁻¹ for methyl-bipyridine modified 26-thymine construct at 302 ± 2 K) than those obtained using methyl bipyridine as the quencher. This said, of course, the absolute collision rates depend on the size of the reporters employed, as if we employ larger reporters (reporters with a larger collisional cross section) the two termini need not approach as closely for a collision to be reported. Fortunately, however, comparative studies of relative collision dynamics, such as the studies presented here regarding how relative collision rates change as functions of various parameters, such as polymer length, base composition, and temperature, are insensitive to the precise details of how a collision is defined by the experimental setup we have employed. Consistent with this second argument, the scaling exponents we observe for the chain-length dependence of end-to-end collision rates of poly-thymine are experimentally indistinguishable if we use DABSYL (this work) or methyl bipyridine (22) as the quencher. The viscosity dependence of the end-to-end collision rate is likewise independent of the nature of the quencher (Fig. S2). Finally, it is important to note that intermolecular quenching is not a significant contributor to the quenching rate associated with DABSYL and from that the quenching rate is independent of the concentration of the ruthenium complex (data not shown).

All DNA constructs were purchased from Biosearch (Novato, CA) as purified, modified oligonucleotides and used as received. We employed ∼5 μM DNA constructs in 100 mM NaCl/20 mM sodium phosphate pH 7 for all experiments. The temperature of the sample to generate the Arrhenius plot was controlled within ± 0.1°C.

Luminescence lifetime measurements were performed using a picosecond luminescence measurement system (Hamamatsu, C4780 system; Hamamatsu, Japan) equipped with a nitrogen laser (Laser Photonics, LN203S2; Lake Mary, FL). We excited the ruthenium luminophore at 450 nm and collected integrated emission between 625 and 675 nm, which lead to improved signal/noise ratios (we confirmed the validity of collecting the emission from this broad wavelength by comparing the decay rate obtained from the emission at 650 nm; data not shown). Part of the luminescence lifetime measurement was performed using a different setup equipped with a femtosecond wavelength-tunable laser system composed of an optical parametric amplifier (OPA-9400, Coherent, Santa Clara, CA) pumped with a Ti:sapphire regenerative amplifier (RegA, Coherent), and mode-locked Ti:sapphire laser (MIRA 900, Coherent). We excited the ruthenium luminophore at 490 nm and measured luminescence spectrum using a streak camera (C5680, Hamamatsu). The natural logarithms of the obtained data were fit with linear using Igor pro (Wavematrix, Lake Oswego, OR). All reported error bars reflect estimated 95% confidence intervals as determined using at least triplicate measurements unless otherwise noted.

Results and Discussion

Determination of the end-to-end collision rate

We have measured end-to-end collision rates by monitoring the near-contact quenching of a long-lived luminophore at the 3′ termini of single-stranded constructs by a quencher attached to their 5′ termini (Fig. 1). Specifically, we have employed the quenching of a long-lifetime ruthenium tris(bipyridine) derivative (Ru, see Abbreviations) attached to a thymine at the 3′ terminus of each construct (-(T)Ru) by a DABSYL moiety (Dab) attached to a thymine at the 5′ terminus of each construct (Dab(T)-) (see Fig. 1).

Figure 1.

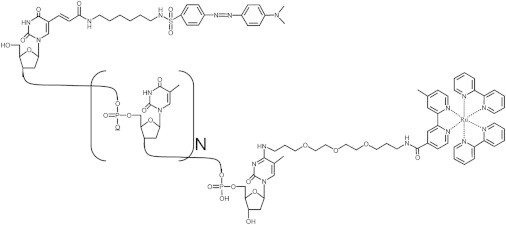
Shown is the structure of Dab(T)-T_N-(T)Ru, which is typical of the constructs employed here. The quencher, 4-dimethylaminoazobenzene (DABSYL), is attached to the base of the 5′ terminal thymine and the luminophore, a ruthenium tris(bipyridine) variant, is attached to the base of the 3′ terminal thymine. (Thus, all constructs, irrespective of their sequence, begin and end with a thymine.)

The base composition dependence of end-to-end collision rates is seen in the excited state lifetime of the Ru luminophore attached to our various DABSYL-terminated constructs (Table S1). Specifically, at 22 ± 1°C (295 K) a 20-thymine ruthenium- and quencher-modified oligonucleotide (Dab(T)-T₂₀-(T)Ru) produces single exponential luminescence decay with an excited state lifetime of 284 ± 13 ns (Fig. 2). The luminophore lifetime of a 20-cytosine construct (Dab(T)-C₂₀-(T)Ru) is, at 312 ± 4 ns (here the reported error reflects standard deviation derived from the fit) quite similar, suggesting the effects of base stacking are similar in both constructs. In contrast the excited-state lifetime of the 20-adenine construct (Dab(T)-A₂₀-(T)Ru) is, at 377 ± 10 ns, significantly longer, suggesting that the much stronger base stacking interactions of this nucleotide (35) reduce the observed end-to-end collision rate. (Unfortunately, attempts to probe this question further using a 20-guanine construct met with failure due to the poor solubility of this homopolymer.) The excited-state lifetime of the mixed-sequence construct Dab(T)-(AGTC)₅-(T)Ru, however, is, at 280 ± 16 ns, within error of that for Dab(T)-T₂₀-(T)Ru. This similarity, which occurs despite the large fraction of purine bases in the mixed sequence construct, suggests that the longer excited-state lifetime seen for Dab(T)-A₂₀-(T)Ru likely does not arise as a simple consequence of the difference of base size, but rather in base-base interaction strength.

Figure 2.

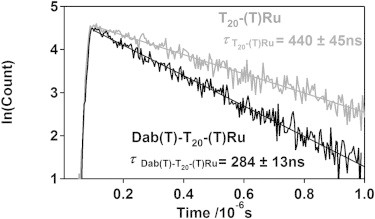
The presence of a DABSYL quencher on one end of a short, single-stranded DNA reduces the lifetime of a long-lived ruthenium luminophore on the opposite end, with the magnitude of the reduction dependent on the end-to-end collision rate.

Using measurements of the excited-state lifetime in the presence and absence of the DABSYL quencher we can derive end-to-end collision rates for our constructs (22,35) (Table S2). For example, the excited-state lifetime observed for a 20-thymine construct lacking a quencher (T₂₀-(T)Ru) is 440 ± 45 ns (Fig. 2). The quenching that occurs upon the addition of DABSYL to the 5′ terminus of this construct (Dab(T)-T₂₀-(T)Ru) shortens its excited-state lifetime to 284 ± 13 ns (Fig. 2). From these two values we calculate end-to-end collision rates as (35):

$$k_T\left(20\right)=\frac{1}{{\tau }_{\text{Dab}\left(\text{T}\right){\text{-}\text{T}}_{20}\text{-}\left(\text{T}\right)\text{Ru}}}-\frac{1}{{\tau }_{{\text{T}}_{20}\text{-}\left(\text{T}\right)\text{Ru}}},$$ (1)

giving rates of 12.5(±1.1) × 10⁵ s⁻¹ (1/803 ns) for the 20-thymine construct (T₂₀) at 22 ± 1°C.

Chain-length dependence of end-to-end collision dynamics

We have previously found that the chain-length dependence of the end-to-end collision rate of single-stranded poly-thymine is well described by a power law with an exponent of −3.49 ± 0.13 (22). As noted previously, this exponent is considerably larger than the exponent observed for the end-to-end collision kinetics of polypeptides (13–15) or estimated theoretically from polymer scaling laws (23–33), an observation that we have previously attributed to electrostatic effects limited to the relatively short polymers we employed. Here, we confirm this unexpectedly large exponent, observing a value of −3.52 ± 0.87 for poly-thymine (Fig. 3), which is within error of the previously determined value (despite our having employed a methyl-bipyridine quencher in the prior work (22) rather than the DABSYL quencher employed here). This said, the end-to-end collision dynamics of poly-thymine deviate from the power-law behavior for polymers of <14 bases (Fig. 1). Previously, we have argued that this deviation arises due to the relatively long, flexible linkers used to attach the ruthenium complex and quencher to the oligonucleotide (22). For example, the alkane linkers in total approximate the length of five contiguous thymines. This should lead to a plateau at shorter lengths of oligonucleotide when collisions between the ruthenium complex and DABSYL become limited by the dynamics of the linkers.

Figure 3.

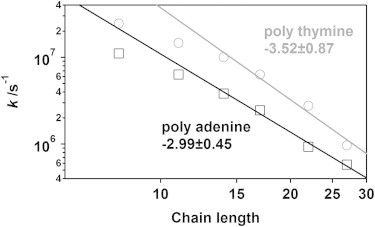
The end-to-end collision rates of single-stranded poly-thymine and poly-adenine at 22 ± 1°C (295 K) show similar power law dependencies. The rollovers observed at very short polymer lengths reflect the presence of the highly flexible linkers (22). Note that our poly-adenine constructs include a thymine at each end to which the luminophore and quencher are attached; each construct is thus 2 bases longer than the number of internal adenines it contains (for example, the A25 construct is 27 bases long and has the sequence TA₂₅T).

Consistent with the argument that this exponent arises due to electrostatic effects (which are, of course, independent of base composition) we find that the end-to-end collision rates of poly-adenine constructs of 14 or more bases (including two terminal thymines to modify ruthenium complex and the quencher) scale as chain length to the −2.99 ± 0.45 power, which is within error of that observed for poly-thymine (Fig. 3). Likewise, similar to the behavior of poly-thymine, the end-to-end collision rates of shorter poly-adenine constructs become length independent. Again, this presumably occurs when the length of the oligonucleotide becomes comparable to the length of the flexible linkers used to attach the ruthenium and the quencher (22).

Sequence composition and the energy barrier for end-to-end collisions

The energetic barrier limiting end-to-end collision dynamics is a strong function of the base composition of the oligonucleotide. To see this, we have generated Arrhenius plots (log(k) versus 1/T) for all of our poly-thymine and poly-adenine constructs (Fig. 4). For our poly-thymine constructs the resultant plots are linear and share a common slope (activation energy) of 27.7 ± 2.5 kJ/mol (Fig. 4 and Fig. 5). The viscosity of water, however, decreases significantly with increasing temperature, an effect that produces an apparent 16 kJ/mol barrier for process—such as intrachain dynamics—under diffusion control (35). The similarity of these values suggests that the end-to-end collision dynamics of poly-thymine are largely defined by the entropy associated with the search through the solvent rather than by any significant enthalpic barrier. Our two shortest poly-adenine constructs (A₁₂ and A₁₅) also produce linear Arrhenius behavior, the slopes of each are within error of 46.7 ± 3.3 kJ/mol. This is significantly greater than the value observed for poly-thymine, implying a much larger enthalpic barrier. In contrast, our two longest poly-adenine constructs, which contain 20- and 25-adenines, exhibit nonlinear Arrhenius behavior. Specifically, although at lower temperatures (below 335 K for 20-adenines and 328 K for 25-adenines) both constructs exhibit the same high barrier as their shorter poly-adenine brethren, their barriers become effectively indistinguishable from that of poly-thymine at higher temperatures (Fig. 4). Of note, circular dichroism studies suggest that the nonlinear behaviors do not correspond to any obvious, temperature-dependent change in their net secondary structure content (Fig. S3).

Figure 4.

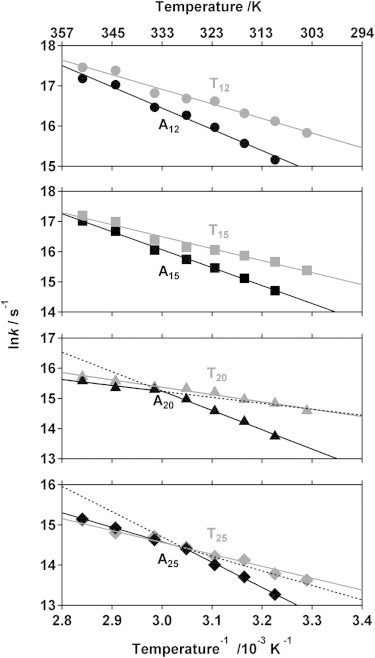
The end-to-end collision rates of all constructs save our two longest poly-adenine constructs exhibit Arrhenius temperature dependencies (i.e., ln k is linear in 1/T at R² > 0.97 for all but our two longest poly-adenine constructs). The steeper curves generally observed for poly-adenine suggest that the energy barrier for end-to-end collisions in this polymer is much greater than that of poly-thymine, presumably due to base-stacking effects absent in the latter (58). The two longest poly-adenine constructs, in contrast, exhibit biphasic (bilinear) behavior; whereas they behave like shorter adenine chains at lower temperatures (to the right) their barrier becomes effectively indistinguishable from that of the equivalent length of poly-thymine above some crossover temperature that is, itself, chain-length dependent. This nonlinear behavior and the chain-length dependence of the crossover temperature are consistent with the barrier friction mechanism (see discussion in text).

Figure 5.

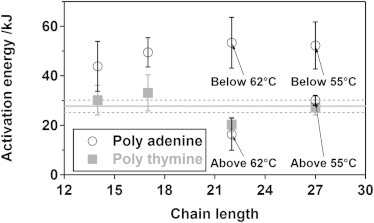
Whereas the activation energy of poly-thymine is effectively chain-length independent, longer poly-adenine constructs differ from shorter poly-adenine constructs in exhibiting a bilinear temperature dependence to their collision dynamics. The ∼16 kJ/mol activation energy that arises due to the temperature dependence of the viscosity of water (35) accounts for the large majority of the 27.7 ± 2.5 kJ/mol activation energy of poly-thymine (black line). This suggests that the end-to-end collision dynamics of poly-thymine are largely limited by the entropy associated with the search through the solvent. The activation energies of shorter poly-adenine constructs, in contrast, exhibit a significantly greater barrier (46.7 ± 3.3 kJ/mol). Finally, the behavior of our two longest poly-adenine constructs is biphasic; whereas their barriers are similar to that of shorter poly-adenine constructs at low temperatures, it coincides with the (smaller) activation energy of poly-thymine at higher temperatures. Of note, circular dichroism studies suggest that the nonlinear behaviors do not correspond to any obvious, temperature-dependent change in their net secondary structure content (Fig. S3).

Possible origins of nonlinearity of the Arrhenius plots for poly-adenine

Several mechanisms may account for the observation of nonlinear Arrhenius behavior. Such behavior, for example, is often attributed to a nonzero change in heat capacity (ΔC_p^‡) associated with the formation of the transition state. Convex Arrhenius plots similar to those observed in the current study, for example, are observed for protein folding kinetics (41,42), where the requisite decrease in the heat capacity upon achieving the transition state is thought to arise due to the burial of the hydrophobic residues relative to the expanded, fully solvated unfolded state (43,44). Here, however, nonlinear Arrhenius plots are observed for a diffusion-controlled process involving reconfiguration dynamics of relatively flexible poly-adenine chains as they sample random conformations. Under these circumstances it appears more likely that hydrophobic surface would be exposed rather than buried, due to the disruption of base stacking upon the formation of a relatively tight loop. This suggests that the mechanism responsible for nonlinear Arrhenius behavior observed for protein folding does not underlie the nonlinear Arrhenius behavior we observe. A second possibility is that the nonlinear Arrhenius plot arises from the temperature dependence of the persistence length (as is seen for polystyrene, albeit with temperature dependence opposite that required to produce the behavior of poly-adenine (45)). This hypothesis, however, fails to explain why the crossover temperature between the low and high activation energy regimes depends on the length of the construct (Fig. 4).

The nonlinear Arrhenius dependence and the lower loop formation rates observed for poly-adenine (as compared to poly-thymine) may have a dynamic, rather than (as above) structural origin. Specifically, base-stacking interactions in poly-adenine may result in a rough energy landscape, where local conformational rearrangements of the chain (e.g., hindered bond rotations) require surmounting energy barriers. Such barriers would then slow the dynamics of the chain relative to the idealized, barrierless case adopted by common polymer models (such as the freely jointed chain and simple bead-and-spring models). In the polymer literature, this slowdown is commonly referred to as barrier friction or internal friction (see (46,47) for reviews). The overall effect of barrier friction on the dynamics of a polymer chain depends on its length. In particular, in a seminal study (48), Kuhn and Kuhn proved that barrier friction has a negligible effect on the global reconfiguration dynamics of a sufficiently long chain. This somewhat counterintuitive conclusion stems from the observation that, in contrast to short polymer chains that require many local conformational rearrangements to bring about large relative displacement of the chain termini, global relaxation modes of long chains may involve fewer collective, translation-like movements of large segments of the chain. For these reasons the barrier friction effect becomes negligible both at high temperatures (where local chain rearrangements are rapid) and for longer chains, thus perhaps explaining why the dynamics of poly-adenine are slower than those of poly-thymine under some circumstances but that this difference disappears at high temperatures and/or for longer constructs.

Validation of the barrier friction hypothesis

Although the notion of internal, or barrier friction is widely adopted in polymer literature, its mathematical description at the level of standard bead-and-spring models of polymer dynamics and its connection to the atomistic-level dynamics remains a controversial issue (46). Nevertheless, a number of theoretical studies converge on a model, where the intrinsic roughness of a polymer’s energy landscape results in an additional, internal friction force that opposes the relative motion of adjacent monomers (see (46,47,49) for further discussion of relevant literature). Quantitatively, this frictional force has been studied in the framework of the Rouse model with internal friction, which incorporates both the internal friction and the Stoke-type viscous drag forces acting on the monomers in solution. Similarly to other models of polymer dynamics, the motion of the polymer chain in this model is decomposed into independent modes, each exhibiting its own characteristic relaxation timescale. The effect of internal barrier friction is then found to increase the timescale for each relaxation mode by exactly the same amount, τ_i, which is proportional to the internal friction coefficient (49). Because the time, τ_i, is independent of chain length and because the timescale of end-to-end collisions is essentially controlled by the longest relaxation timescale (26), which increases with increasing chain length, the relative effect of internal friction on the chain dynamics decreases for longer chains, in agreement with (46,47). Of relevance to our study, this model was recently found to quantitatively account for reconfiguration dynamics of unfolded proteins as measured by single-molecule nanosecond fluorescence correlation spectroscopy (50).

To adapt these ideas to the current study, we note that the Rouse model by itself does not provide a good description of the end-to-end collision dynamics of single-stranded oligonucleotides, as our own results indicate. Nevertheless, it is plausible that the additivity of the internal friction timescale is more general. In further support of this idea, similar additivity of the internal friction timescale has been proposed to explain internal friction effects on protein folding rates (51,52). We then attribute the difference between the end-to-end collision rates for poly-thymine, k_T(N), and poly-adenine, k_A(N), to barrier friction (which is negligible in the former case) and write

$$k_A^{-1}\left(N\right)={\tau }_i+k_T^{-1}\left(N\right).$$ (2)

We note that computer simulations (53) suggest a more general relationship, where ${\tau }_i$ is replaced in Eq. 2 by ${\mathit{\tau }}_{i}f\left(N\right)$, with $f\left(N\right)$ being a weak power law. In our case, however, we find $f\left(N\right)$ to be nearly constant (see below).

Although the relationship between the internal friction time constant τ_i and the microscopic barriers causing the internal friction effect can only be established through extensive numerical computation (54), it is obvious on physical grounds that τ_i should increase with decreasing temperature. We thus adopt the Arrhenius formula to describe the temperature dependence of this time constant:

$${\tau }_i^{-1}=\nu \text{exp}\left(\frac{-E_a}{k_{\mathrm{B}}T}\right).$$ (3)

If the temperature dependence of τ_i is stronger than that of the end-to-end collision rate k_T(N), the relative effect of internal friction on the end-to-end collision dynamics becomes negligible at a high enough temperature and the end-to-end collision rates for poly-adenine and poly-thymine will coincide (Eq. 2). As the temperature is lowered, however, the barrier friction becomes the dominant contributor to the end-to-end collision rate k_A(N) (Eq. 2). The crossover between the barrier-friction-dominated and the Kuhn regime (where the barrier friction is negligible) depends on chain length N. The longer the chain, the slower the collision timescale will be and, consequently, the lower the expected crossover temperature.

Several lines of evidence support the validity of Eq. 2 and the barrier friction model. First, from the Arrhenius plot of the internal friction time (Fig. 6) we estimate E_a to be 70.7 ± 6.3 kJ/mol. In agreement with Eq. 2 this is greater than the activation barriers for end-to-end collision dynamics, which, as described previously, are 46.7 and 27.7 kJ/mol for poly-adenine and poly-thymine, respectively. Similarly, large activation energies have been reported for the intrinsic rotational barriers of isotactic polystyrene (63 kJ/mol) (55), for which, due to the interaction of phenyl rings separated by three and four monomer units, skeletal rotation around five consecutive chain bonds must be driven together. By analogy, it would appear reasonable that the large activation energy we observe for poly-adenine likely arises due to the barrier friction associated with adenine base stacking. Further validation of Eq. 2 and the barrier friction model is given by the observation that τ_i is, to within experimental error, independent of chain length (Fig. 6).

Figure 6.

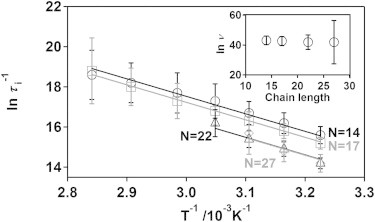
Global fitting for the Arrhenius temperature dependencies of the barrier friction time constant, τ_i, provide evidence in support of the barrier friction model. Using this model to fit all of our barrier friction time constant simultaneously, we derive universal activation energy of 70.7 ± 6.3 kJ/mol which, as predicted by the model, is greater than the 46.7 ± 3.3 kJ/mol activation energy derived from simple Arrhenius analysis (which ignores barrier friction). The 95% confidence for each point is estimated from linear fitting in Fig. 4. The apparent errors for the longest two constructs are presumably underestimated due to the limited number of linear fitted data points for A₂₀ and A₂₅ in Fig. 4. (Inset) The preexponential factor obtained from the global fitting is independent of chain length, suggesting that the biphasic behavior observed for the two longest poly-adenine constructs can be explained by barrier friction mechanism.

We would note that the transition from the Kuhn regime to the barrier friction regime has significant implications for our understanding of reconfiguration dynamics and folding in biopolymers. Specifically, the time it takes the unfolded biomolecule to explore available configuration space sets the fundamental limit on how fast it can fold (13,56,57). In the Kuhn regime this reconfiguration timescale can be simply estimated (47) as R²/D, where R is the coil size and D is the translational diffusion coefficient of the entire chain, and is thus essentially independent of the details of polymer’s energy landscape, an observation confirmed by a recent study of unfolded proteins (50). Such a simple view, however, becomes invalid in the barrier friction dominated regime, where explicit consideration of intramolecular interactions becomes necessary. More broadly, the validity of Eq. 2 supports the barrier-friction mechanism as an explanation of the difference between the end-to-end collision dynamics of poly-thymine and poly-adenine, a conclusion that we hope will motivate future studies aimed at elucidating precise mechanistic origins of the roughness of the energy landscape through fully atomistic simulations of single-stranded oligonucleotides. Such studies will likely contribute to our (currently incomplete) understanding of the more general question of internal friction in polymers.