Abstract
Viscoelastic characteristics of many materials falling under the category of soft glassy substances, including biological tissue, often exhibit a mechanical complex modulus Y(ω) well described by a fractional derivative model: Y(ω) = E(iω/ϕ)k, where E = a generalized viscoelastic stiffness; i = (−1)1/2; ω = angular frequency; ϕ = scaling factor; and k = an exponent valued between 0 and 1. The term “fractional derivative” refers to the value of k: when k = 0 the viscoelastic response is purely elastic, and when k = 1 the response is purely viscous. We provide an analytical derivation of the fractional derivative complex modulus based on the hypothesis that the viscoelastic response arises from many intermittent molecular crosslinks, whose lifetimes longer than a critical threshold lifetime, tcrit, are distributed with an inverse power law proportional to t-(k+2). We demonstrate that E is proportional to the number and stiffness of crosslinks formed at any moment; the scaling factor ϕ is equivalent to reciprocal of tcrit; and the relative mean lifetime of the attached crosslinks is inversely proportional to the parameter k. To test whether electrostatic molecular bonds could be responsible for the fractional derivative viscoelasticity, we used chemically skinned human skeletal muscle as a one-dimensional model of a soft glassy substance. A reduction in ionic strength from 175 to 110 mEq resulted in a larger E with no change in k, consistent with a higher probability of interfilament molecular interactions. Thick to thin filament spacing was reduced by applying 4% w/v of the osmolyte Dextran T500, which also resulted in a larger E, indicating a greater probability of crosslink formation in proportion to proximity. A 10°C increase in temperature resulted in an increase in k, which corresponded to a decrease in cross-bridge attachment lifetime expected with higher temperatures. These theoretical and experimental results suggest that the fractional derivative viscoelasticity observed in some biological tissue arises as a mechanical consequence of electrostatic interactions, whose longest lifetimes are distributed with an inverse power law.
Introduction
Through several decades of material science research, the fractional derivative description of viscoelastic behavior has arisen empirically to describe the mechanical characteristics of numerous materials including creams, gels, polymers, and biological tissue often falling within the category of soft glassy substances (1–8). These materials exhibit a mechanical complex modulus in frequency space described well by the following mathematical expression (1,2,9,10):
| (1a) |
The parameter E signifies the generalized viscoelastic stiffness of the material in units of stress. The terminology “fractional derivative” should not be taken to indicate that a fractional derivative operation has occurred, but signifies only that, for those materials exhibiting a complex modulus described by Eq. 1a, the exponent k applied to the complex angular frequency iω is found valued between 0 and 1. When k = 0 the stress is directly proportional to the strain and indicates purely elastic behavior of the material. When k = 1 the stress is proportional to the first derivative of the strain with respect to time and reflects purely viscous behavior. The scaling factor ϕ in units of angular frequency is often applied to iω to satisfy the appropriate units of the complex modulus. Written in terms of its real and imaginary parts, the complex modulus takes the form
| (1b) |
The real and imaginary parts are termed the elastic or storage modulus (G′) and the viscous or loss modulus (G″), respectively. Fig. 1 illustrates the characteristics of a complex modulus following this fractional derivative description.
Figure 1.
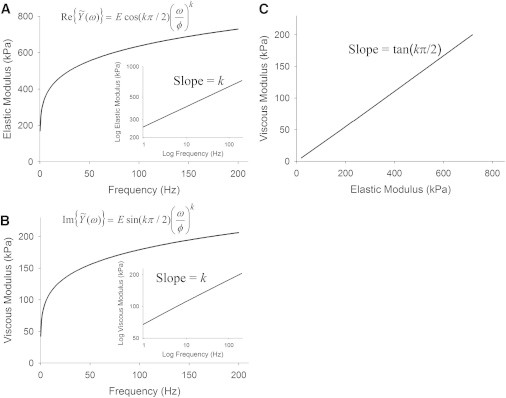
Properties of fractional derivative complex modulus. (A and B) The real part (A) and the imaginary part (B) are of the complex modulus are referred to as the elastic (or storage) modulus and the viscous (or loss) modulus, respectively. (Insets) Log-log plots of elastic and viscous moduli against frequency exhibit linear relationships with a slope of k. (C) A plot of viscous versus elastic moduli likewise shows a linear relationship that intercepts the origin and has slope tan(kπ/2).
What molecular-level mechanisms could result in a fractional derivative description of viscoelasticity measured at a macroscopic level? Physical and conceptual models have been proposed to explain this representation, especially with regard to biological tissue (11,12). Bates (13) suggests a series of viscoelastic elements whose sequential coupling via internal stresses leads to a power-law description of stress relaxation, which is consistent with the fractional derivative complex modulus. Donovan et al. (14) propose a model of molecular crosslinks whose interactions are governed by spatially nonlinear, first-order rates of attachment and detachment. Semmrich et al. (15) demonstrate that glassy behavior at the macroscopic level may emerge from nonlinear stress-strain relationships of worm-like chains at the molecular level.
In this article, we consider the hypothesis forwarded by Sollich (3) and reiterated by Fabry et al. (4), Djordjević et al. (5), and Gunst and Fredberg (12) to explain the viscoelastic behavior observed in biological materials. These authors suggest that molecules within the material pass through multiple mechanical potential wells as the material is deformed. Furthermore, these potential wells are discrete, numerous, and universal in character so as to underlie the viscoelasticity of many disparate materials. We interpret this to mean that the mechanical consequences of many temporary elastic crosslinks due to nonspecific binding between molecules will give rise to the fractional derivative complex modulus at the macroscopic level. This concept of temporary molecular interactions taking place within a viscoelastic material is a common thread among several of the aforementioned works and others (1,3–5,11,13,14,16–20). We hypothesize that these nonspecific bonds among molecules are electrostatic interactions due to hydrogen bonds, ionic bonds, and van der Waals forces and that the temporary nature of these interactions underlie the frequency dependence of viscoelastic properties represented by the fractional derivative complex modulus.
In this article, we develop a model of the mechanical consequences at the macroscopic level of temporary elastic crosslinks formed at the molecular level. We assume that the mechanical perturbation of a material is small enough to elicit a linear mechanical response from crosslinks formed at the molecular level and that linear systems analysis is warranted. We then derive an analytical relationship between the complex modulus as would be measured at the macroscopic level and the distribution of crosslink lifetimes at the molecular level. We demonstrate that the fractional derivative representation of the complex modulus can arise from an inverse power-law distribution of intermolecular crosslink lifetimes. We also demonstrate that the parameters of Eq. 1, namely E, k, and ϕ, can be interpreted in terms of the crosslink number, stiffness, and lifetime. Our approach differs from previous modeling attempts in that we do not use differential equations or ascribe rates of attachment and detachment to the crosslinks, and we do not make any a priori assumptions regarding the length of time that molecular crosslinks remain formed.
Methods
All volunteers signed informed consent forms and protocols were approved by the Committees on Human Research of the University of Vermont. Human skeletal muscle tissue was obtained by percutaneous biopsy of vastus lateralis muscle. Muscle tissue processing immediately postbiopsy until isolation of single fibers for mechanical experiments was performed as described previously in Miller et al. (21). Segments (∼2.5–3 mm) of single fibers were isolated from muscle bundles, and with aluminum T-clips placed at both ends, these segments were then mounted onto the experimental apparatus, as previously described in Miller et al. (21) and submerged in relaxing solution: 65 mM Na-MS (Na-methyl sulfonate); 20 mM BES (n,n-bis[2-hydroxyethyl]-2-aminoethanesulfonic acid); 5 mM EGTA; 5 mM MgATP; 1 mM free Mg2+; 1 mM DTT (dithiothreitol); 15 mM creatine phosphate; 40 mM BDM (2,3-butanedione monoxime); 5 mM Pi (phosphate); and 300 units mL−1 of creatine phosphokinase with an ionic strength of 175 mEq, pH 7.0 and pCa 8. Notably, relaxing solution contained BDM, which inhibits the formation of strongly bound myosin crossbridges (22).
Viscoelastic properties of relaxed skeletal muscle were detected using sinusoidal length perturbations with amplitudes of 0.25%, which were small enough to assure a linear viscoelastic response. All fibers from the mechanical experiments were run on sodium dodecyl sulfate-polyacrylamide gel electrophoresis gels to determine myosin heavy chain (MHC) isoform, as previously described in Miller et al. (21). The most common fiber type for any experiment was chosen to represent the results of the experiment. MHC IIA fibers (n = 4) isolated from one subject were examined as ionic strength was reduced from 175 (control) to 110 mEq by essentially removing Na-MS. MHC I fibers (n = 4) from another subject were examined for Dextran T500 experiments with 0% (control) and 4% w/v T500 (molecular mass 500 kDa) added to osmotically compress the myofilament lattice, thereby reducing the thick-to-thin filament distance, and for Dextran T10 experiments with 0% (control) and 0.34% w/v T10 (molecular mass 10 kDa) added to reduce myofilament protein hydration and match the hydration conditions of 4% w/v T500 (23). Another set of MHC I fibers (n = 4) from another subject were examined with a temperature change from 15°C to 25°C.
Recorded elastic and viscous moduli were corrected for phase shift associated with the delay of the force signal relative to the length signal due to differences in the number and design of amplifier stages (24). All measured complex moduli of relaxed striated muscles appeared to exhibit fractional derivative characteristics. In estimating values for E and k, we set ϕ equal to a constant, 108 s−1, and fit the data to Eq. 1 using a Levenberg-Marquardt nonlinear least-squared fitting algorithm (Exelis, Boulder, CO). Without such an assumed value for ϕ, estimates of E would have covaried unpredictably with those of ϕ.
Mathematical Modeling
We consider here a material segment of infinitesimally small length, dx, which contains several intermittently interacting molecules. When the material is subjected to a length perturbation, we assume that force propagates across the segment via molecular crosslink. Fig. 2 illustrates such a segment of material as would be found in striated muscle containing interdigitating thick and thin filaments. Striated muscle represents a three-dimensional experimental system, whose paracrystalline structure reduces in effect to a one-dimensional material when measuring viscoelastic properties along its longitudinal axis. The intermolecular distances and probability of interaction between the thick and thin filaments in striated muscle can be manipulated so as to adjust crosslink number and illustrate the efficacy of our model. As depicted in Fig. 2, the force propagated across the segment dx by a crosslink is considered to be proportional to the relative change in length of the segment,
| (2) |
where f = force propagated across the segment via one crosslink having an effective cross-sectional area a, λ = elastic modulus of this one crosslink, and dl/dx = the relative change in length of the segment dx. Equation 2 simply represents the linear relationship between stress, σ = f/a, and strain, ε = dl/dx, of a purely elastic crosslink, σ/ε = λ. The crosslink represented in Eq. 2 probably best reflects a myosin head of the thick filament undergoing a brief electrostatic interaction with actin of the thin filament. Although the filaments certainly contribute to the effective stiffness of a crosslink, its net stiffness is essentially equivalent to the most compliant structure, which in this case is the myosin neck. We would further expect there to be a distribution of many possible values for λ and a, which would be based in part on the many possible alignments of myosin and actin as well as their location in the sarcomere. These inhomogeneities will be addressed by using random variables to describe values for λ and a and eventually also the lifetimes of each crosslink.
Figure 2.
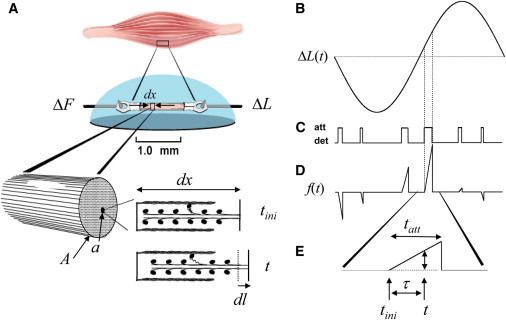
Examination of muscle. (A) A section of skeletal muscle is shown here placed between a length motor (ΔL) and force transducer (ΔF). A very short segment of the muscle, dx, with cross-sectional area A contains molecules whose crosslinks allow the transfer of force across the segment. For striated muscle, one such crosslink could result from myosin of the thick filament forming a weak molecular bond (e.g., hydrogen bond or ionic bond) with actin of the thin filament. (B–E)Any change in length (B) while the crosslink is attached (att) but not detached (det) (C) would result in the development of a force (D and E) across the segment. dl = Length change at the level of the segment dx; dl/dx = strain or change in length relative to segment length; a = effective cross-sectional area of the crosslink; A = cross-sectional area of the sample; ΔL(t) = length perturbation applied to the muscle; f(t) = force developed across the segment by one crosslink due to imposed strain; tini = initial time of the most recent crosslink formation; τ = duration that crosslink has survived up to time t; and tatt = total lifetime of attached crosslink.
We demonstrate below that a fractional derivative complex modulus of a one-dimensional system like relaxed striated muscle can arise as a consequence of many such intermolecular interactions whose lifetimes are distributed by an inverse power law.
Complex modulus due to temporary crosslinks
Total force propagated across the segment length dx is the sum of the many individual forces generated by many crosslinks. The force of the ith intermolecular crosslink, denoted f(i)(t), arises from the effective elastic modulus of the crosslink, λ(i), and the net relative length change, dl(t)/dx, because the most recent initial time of attachment, tini, is
| (3) |
where a(i) = the effective cross-sectional area of the ith crosslink. Every possible crosslink is assumed to be in either an attached or detached state at any given time. The time periods of attachment, tatt, and detachment, tdet, are random variables whose values are governed by stochastic processes independent of force, stress, strain, length, velocity, and each other, which we consider a reasonable assumption for very small deformations resulting in a linear relationship between stress and strain.
The total force response of the material segment, F(t), would be equal to the sum of the individual forces arising from the length displacement. We now substitute dl(t)/dx, i.e., change in segment length relative to its initial length, with (L(t)−L0)/L0, which represents the relative change in total muscle length, L(t), from its initial length L0, and is a valid substitution for small perturbations:
| (4) |
If we use the inverse Fourier transform definitions for F(t) and L(t), namely
| (5a) |
| (5b) |
where and are the Fourier transforms of F(t) and L(t), respectively, we then obtain from Eq. 4 that
| (6) |
We now introduce a variable, τ = t − tini, as the time period from any given time t to the instant of initiation of the most recent interaction tini. For the ith interaction, tini(i) = t − τ(i), and the term becomes . We can now remove the Inverse Fourier transform integrals of Eq. 6:
| (7) |
If we introduce the total cross-sectional area of the material, A, the complex ratio in terms of force and length can be written in terms of macroscopic stress and macroscopic strain as
| (8) |
The left-hand side of Eq. 8 defines the complex modulus of the material at the macroscopic level, i.e., . With the assumption that the random variables λ, a, and τ are stationary, i.e., do not vary with time, and are independent of each other, the summation over a large number of crosslinks attached at any time, M, on the right-hand side of Eq. 8 can be replaced as the product of M and the expected value of the terms subject to the summation,
| (9) |
where = mean elastic modulus of intermolecular links, = mean area of the intermolecular links, and P(τ) = the probability density function for the random variable τ.
As we have demonstrated in a previous analysis (25), the number of crosslinks attached at any time, M, can also be replaced by the total number of molecular crosslinks possible, N, multiplied by the probability that any given crosslink has formed at any instant in time, i.e., , where and are the mean time periods of a crosslink being attached and detached, respectively. Our representation of the complex modulus due to intermittently formed molecular crosslinks is then
| (10) |
Equation 10 provides an analytical expression relating the distribution of lifetimes of molecular-level crosslinks to the mechanical complex modulus observed at the macroscopic level. A similar representation of the mechanical consequences of enzymatic myosin crossbridges in calcium-activated striated muscle has been presented previously and verified by computer simulations and experimental data (25,26).
Survival function
The random variable τ represents the time duration any already bound crosslink has survived since the moment of its initial formation (see Fig. 2). The probability that a crosslink has survived at least a time period τ is described by the survival function S(τ). All crosslinks survive for an infinitesimally short duration, thus S(0) has unity value and S(τ) decreases monotonically as τ increases. The survival function S(τ) is related to the probability density function for crosslink lifetimes, which we will call Tatt(τ), as the probability (Pr) that the lifetime random variable tatt is greater than duration τ (27). Note that θ is used only as a variable of integration:
| (11a) |
| (11b) |
The P(τ) needed in Eq. 10 is simply a normalization of S(τ) and is calculated as the survival function of Eq. 11a divided by its integral over 0 ≤ τ ≤ ∞, which is the mean lifetime, :
| (12) |
As mentioned above, all crosslinks are bound for duration 0, S(0) = 1. By extension, the value of P(0) must be finite and equal to the reciprocal of the mean lifetime. These points will be important in the following development.
Inverse power-law distribution
We would like to find the P(τ) evaluated in Eq. 10 that would result in a complex modulus conforming to a fractional derivative response represented by Eq. 1. We ask, what is P(τ) that satisfies the following equation:
| (13) |
We will let and use the identities ik = eikπ/2 and e±ix = cos(x) ± isin(x) to write Eq. 13 in terms of its real and imaginary parts:
| (14a) |
| (14b) |
As demonstrated in Appendix A, both Eqs. 14a and 14b can be solved with the same P(τ), which is proportional to an inverse power law of τ, as
| (15) |
According to the relationships provided in Eqs. 11b and 12, the probability density function for the lifetimes of crosslink attachment Tatt(τ) would be given as follows:
| (16) |
The result of Eq. 16 suggests that an inverse power-law distribution of crosslink lifetimes underlies the fractional derivative viscoelasticity observed for many substances, including some biological tissues.
There are, however, significant practical problems associated with the expressions given in Eqs. 15 and 16. The densities P(τ) and Tatt(τ) must exhibit specific properties; namely, P(0) and Tatt(0) must be finite in value, and the definite integrals of P(τ) and Tatt(τ) over 0 ≤ τ ≤ ∞ must be equal to unity. The P(τ) and Tatt(τ) provided by Eqs. 15 and 16 do not satisfy either of these requirements due to the approach to infinite value at τ = 0.
Nevertheless, because Eq. 15 does provide a solution to Eqs. 14a and 14b, it would be appropriate to develop expressions for P(τ) and Tatt(τ) similar in form to those given in Eqs. 15 and 16, but finite-valued over the range 0 ≤ τ ≤ ∞.
Approximate inverse power-law distribution
Using the suggestion of Newman (28) and Clauset et al. (29), we can write an approximate inverse power-law function by considering the inverse power law applicable only for those times longer than a critical time threshold, tcrit. For time durations shorter than tcrit, an exponential description is used. A probability density function Tatt(τ) bearing this approximation could have the following form:
| (17) |
Equation 17 is finite-valued over the range 0 ≤ τ ≤ ∞, and it is normalized such that its definite integral over this range is equal to unity. The corresponding survival function is then calculated using Eq. 11a, and results as
| (18) |
Equation 18 satisfies the requirement for a survival function of unity value at τ = 0.
According to Eq. 12, P(τ) arises from normalizing the survival function with the mean lifetime of attachment, which is found by integration of S(τ) and results as follows:
| (19) |
For values of k in the range 0.05–0.25, which approximately covers the range for soft biological tissue (7,30), the bracketed term in Eq. 19 is within 7% of the value 0.267. This estimate permits a more intuitive interpretation of k as a descriptor of the mean time of attachment: when k is small at ∼0.05, the mean time of attachment is long—roughly 5 × tcrit—and describes a relatively more elastic response; when k is larger at ∼0.25, the mean time of attachment is shorter—roughly equal to tcrit—and describes a relatively more viscous response. We now write P(τ):
| (20) |
Equations 17, 18, and 20 offer continuously smooth curves at tcrit and a finite value for the mean time of attachment. In using this approximation to the inverse power-law distribution, the value to tcrit must be short enough to emphasize the inverse power-law representation of P(τ) in the underlying actual measures of the complex modulus. Frequencies up to 1 kHz are often used to record the complex modulus of materials, which would suggest tcrit ≪ 1 ms.
Using first principles, others have estimated that and therefore tcrit are ∼10−12–10−11 s if molecular crosslinks are adequately represented as hydrogen bonds in aqueous solution near ambient temperature (31–35). Still others have estimated the scaling factor ϕ for biological tissue to be ∼108 s−1 (4,5,7). The corresponding tcrit and average crosslink lifetime based on our analysis would be ∼10 ns. In either case, the expected tcrit would certainly satisfy the requirement of being much less than 1 ms. In Fig. 3, we have provided example sets of curves for S(τ), P(τ), and Tatt(τ), with tcrit = 10 ns and k = 0.05, 0.15, and 0.25.
Figure 3.
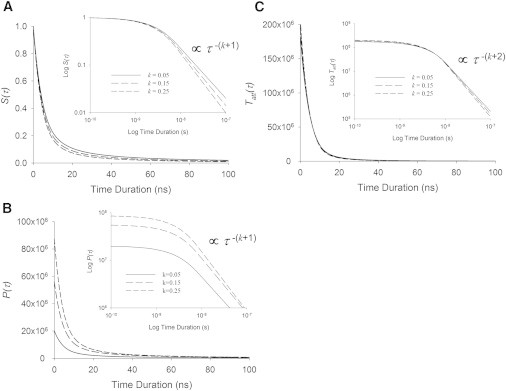
Probability density functions. (A) The probability that any already attached crosslink has been formed or has survived for a specific duration, τ, is described by S(τ), which we model with an inverse power law after a critical time tcrit. For illustration purposes, we use tcrit = 10 ns as might be expected from ionic bonds. This survival function always has unitary value at time zero. (B) The corresponding probability density function for the survival duration τ is given by P(τ), which is equivalent to S(τ) divided by the mean crosslink lifetime. (C) The probability density function for attached crosslink lifetimes, Tatt(τ), is proportional to the time-derivative of S(τ). (Insets) Log-log plots of these functions versus duration show linear relationships for crosslink durations longer than tcrit.
Complex modulus based on approximate inverse power-law distribution
We now evaluate the complex modulus defined by Eq. 10 using the P(τ) provided by Eq. 20. We notice that the definite integral of P(τ) is equal to unity, and we can rewrite Eq. 10 in the following form:
| (21) |
Upon applying the approximate inverse power-law distribution provided in Eq. 20, we must solve the following:
| (22) |
The Supporting Material presents the details of the evaluation of Eq. 22, which results in the following approximation for the complex modulus due to the second integral term:
| (23) |
Equation 23 demonstrates that the approximate inverse power-law distribution of intermolecular bond lifetime described in Eq. 17 can give rise to the measurable fractional derivative viscoelasticity described in Eq. 1. It should be noted, that for the values of k between 0.05 and 0.25, the value of the k-bearing bracketed term in Eq. 23 ranges between 0.93 and 0.83 and can be approximated within only a small percentage of error, by 0.88.
Upon comparing Eqs. 1 and 23, we have an interpretation of the scaling factor ϕ as the reciprocal of tcrit: ϕ = tcrit−1. The form of Eq. 23 further suggests that the magnitude E of the empirically determined Eq. 1 is approximately equivalent to ξ:
| (24) |
Results
Ionic strength
To test whether electrostatic interactions could underlie the interfilament crosslinks, we lowered the ionic strength from 175 to 110 mEq. This reduction in ionic strength enhances the probability of electrostatic bond formation due to the relative loss of free ions that can block intermolecular ionic interactions due to Debye shielding (36,37). We found no significant change in parameter k with the reduction in ionic strength, but the magnitudes of the elastic and viscous moduli (Fig. 4) and of parameter E rose significantly (Table 1). A similar result has been reported previously for activated muscle (38). Our results are consistent with E representing an increased number of electrostatic interactions formed when ionic strength is lowered, and suggests that electrostatic interactions constitute the specific molecular interactions that underlie the fractional derivative viscoelasticity measured at the macroscopic level.
Figure 4.
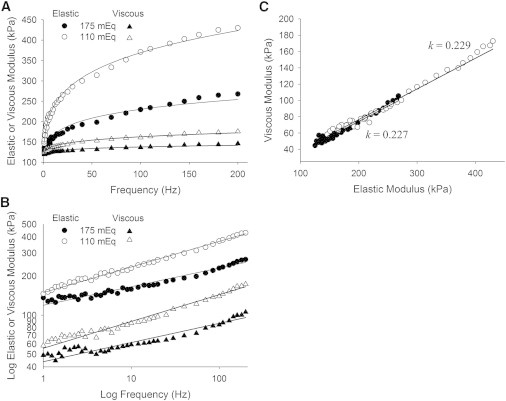
Recorded elastic and viscous moduli from human MHC IIA skeletal muscle at different ionic strengths. (A) The reduction in ionic strength from 175 to 110 mEq resulted in a significant elevation in the elastic and viscous moduli reflected in a higher value for parameter E (see Table 1). (B) The log-log plots of the elastic and viscous moduli versus frequency demonstrate nearly parallel lines for each condition, which lends support to the use of the fractional derivative description of the complex modulus for relaxed skeletal muscle. (C) The phase plot of viscous versus elastic moduli illustrates a significant change in magnitudes of the moduli with no appreciable change in k. The enhanced magnitudes of the moduli reflect a greater probability of crosslink formation when the ionic barriers have been removed. These data suggest that ionic bonds underlie, in large part, the fractional derivative viscoelasticity observed in biological tissue.
Table 1.
Dependency of model parameters of Eq. 1 on ionic strength in MHC IIA fibers, and temperature, myofilament lattice compression, and hydration in MHC I fibers
| Condition | E (kPa) | k | tatt (ns) |
|---|---|---|---|
| 175 mEq | 4460 ± 784 | 0.227 ± 0.009 | 11.8 ± 0.5 |
| 110 mEq | 6765 ± 230a | 0.229 ± 0.004 | 11.7 ± 0.2 |
| 15°C | 4223 ± 1134 | 0.151 ± 0.011 | 17.8 ± 0.9 |
| 25°C | 5304 ± 1756 | 0.180 ± 0.013a | 15.2 ± 1.2a |
| pre-T500 | 3467 ± 991 | 0.179 ± 0.011 | 15.0 ± 0.9 |
| 4% T500 | 9000 ± 2293a | 0.207 ± 0.008a | 13.0 ± 0.5a |
| pre-T10 | 3435 ± 1151 | 0.169 ± 0.023 | 16.1 ± 2.2 |
| 0.34% T10 | 3728 ± 1679 | 0.190 ± 0.007a | 14.1 ± 0.5a |
Assumed value for ϕ = 108 s−1. Data presented as mean ± SE (n = 4 for each case).
P < 0.05 by paired t-test against initial control condition.
Temperature
As indicated in Table 1 and illustrated in Fig. 5, we observed a ∼19% increase in parameter k with the 10°C increase in temperature from 15°C to 25°C. This change in k corresponded to a shortening in the average lifetime of crosslinks of ∼19% according to Eq. 19 and therefore a Q10 of 1.19, which is within the expected range for nonenzymatic phenomena. The change in temperature did not significantly change the generalized stiffness E.
Figure 5.
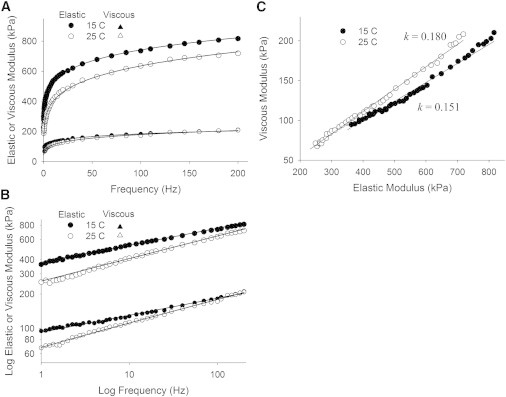
Recorded elastic and viscous moduli from human MHC I skeletal muscle at different temperatures. (A) An increase in temperature from 15°C to 25°C did not result in a statistically significant change in E. (B) The log-log plot of each moduli pair again demonstrates parallel lines for each condition. (C) The 10°C rise in temperature resulted in a ∼19% rise in parameter k and a corresponding reduction in the average crosslink lifetime. A Q10 of 1.19 is within the range of expected sensitivities to temperature for nonenzymatic processes.
Lattice spacing and hydration
Bathing the skinned fiber in 4% wt/vol T500, which is excluded from the myofilament lattice, compressed the lattice such that the thick and thin filaments moved into closer proximity, approximately from 28-nm to 25-nm apart (39). The cross-sectional area was reduced by a similar amount, and we assumed the ratio (a/A) did not change due to osmotic compression. Therefore, we did not adjust the recorded forces for a new cross-sectional area. Under these conditions, the value of E rose at least 200% with lattice compression due to T500 (Fig. 5 and Table 1). This rise in stiffness must be due to an increased number of crosslinks formed as thick and thin filaments came closer together. These data support the idea that interfilament crosslinks are a significant source of material stiffness in relaxed striated muscle.
We also found that T500 produced a rise in the parameter k that corresponded to a shortening of the average crosslink lifetime by 12% (Fig. 5 and Table 1). A similar response was found for k when adding 0.34% Dextran T10 to the bathing solution, which matches the osmotic pressure of 4% T500 (23). Dextran-T10 is small enough to infiltrate the myofilament lattice of vertebrate striated muscle (39) and therefore does not change myofilament lattice spacing. The equivalent osmotic pressures (4% T500 and 0.34% T10) correspond to equivalent reductions in the density of water molecules in the myofilament proteins resulting in the same response for parameter k. We infer that the crosslinks are probably not represented as hydrophobic bonds. Notably, the addition of T10 did not change parameter E, and therefore did not likely change the number, fraction bound, or stiffness of the crosslinks. If hydrophobic bonds represented the molecular crosslinks, we would have expected dehydration to have affected E.
Discussion
We present a mathematical relationship between molecular-level crosslinks undergoing small length perturbations and their mechanical consequences at the macroscopic level. We demonstrate that viscoelastic behavior at the macroscopic level, represented well by a fractional derivative complex modulus, could be accounted for by molecular-level crosslinks exhibiting lifetimes distributed with an inverse power law. This inverse power-law distribution applies only for those lifetimes longer than some very short time threshold tcrit and therefore describes the long tail of the crosslink lifetime distribution. Our experimental results further suggest that the specific molecular level crosslinks are due at least in part to electrostatic interactions, which are so ubiquitous as to conceivably underlie the many disparate materials, including biological tissue, that exhibit a fractional derivative viscoelasticity (2–8). Our findings are relevant to biological tissues in particular, because they suggest that intracellular ionic concentrations can play a significant role in dictating tissue viscoelasticity, which is altered by disease, aging, hydration, and other conditions (30). (See Fig. 6.)
Figure 6.
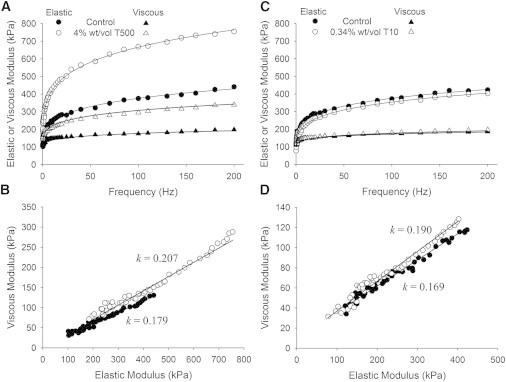
Recorded elastic and viscous moduli from human MHC I skeletal muscle at 4% w/v Dextran T500 and 0.34% w/v DextranT10, which are osmolytes. (A and B) With the application of 4% w/v Dextran T500, the myofilament lattice was compressed and distances between thick and thin filaments were shortened. The magnitudes of the elastic and viscous moduli were significantly increased with the compressed lattice spacing, which we attribute to the enhanced probability of crosslink formation due to the closer proximity of thick and thin filaments. (C and D) The application of 0.34% w/v Dextran T10 caused dehydration of protein structures similar to that of 4% w/v of T500 without changing myofilament lattice spacing and resulted in a rise in parameter k, which corresponded to a reduction in mean crosslink lifetime due to dehydration.
Our finding an inverse power-law distribution of crosslink lifetimes differs fundamentally from that expected from first-order rates of detachment, such as exemplified by the enzymatic activity of strongly bound myosin crossbridges of activated muscle. In that scenario, a significant portion of molecular crosslink lifetimes are best described by an exponential distribution (40), and the macroscopic viscoelasticity would take the form iω/(iω + α) with α as the detachment rate constant (25,41). This representation of the complex modulus is very different from the fractional derivative expression; specifically, the exponential response exhibits a semicircle relationship between the elastic and viscous moduli, while the fractional derivative response exhibits a straight line (41). Thus, a first-order rate of detachment cannot underlie a linear viscoelasticity described by a fractional derivative complex modulus.
Interpretation of model parameters
As stated in Eq. 24, we find the stiffness magnitude E represents the product of:
-
1.
The number of possible crosslinks (N);
-
2.
The fraction of possible crosslinks formed at any instance ;
-
3.
The average fraction of cross-sectional area taken up by one crosslink (ā/A); and
-
4.
The average elastic stiffness of any one crosslink ().
This interpretation bears both the temporal (point 2) and spatial (point 3) fractions of crosslinks contributing to the stiffness magnitude E. We were able to use this interpretation to infer that compression of the myofilament lattice likely caused an increased probability of crosslink formation. Our physical interpretation reflects what one might intuitively expect from the proximity of proteins as occurs with osmotic compression of myofilament lattice in striated muscle. We take from these results that the viscoelastic behavior of relaxed striated muscle is due in large part to a significant number of weakly bound interactions between myosin and actin (38) or between actin other molecules, such as myosin binding protein-C and unbound segments of titin, that may span between the thick and thin filaments and interact only intermittently (42,43). Any covalent bonds of molecules that span between the filaments would not be subject to the analysis provided here.
According to our analysis, the parameter k is reciprocally related to the mean lifetime of crosslink attachment (see Eq. 19). Our data demonstrating the effects of a temperature change are qualitatively consistent with this interpretation. Because k is a unitless exponent, it can reflect the mean lifetime only in relative terms and not in absolute terms. A measure of lifetime in absolute terms is not possible at this time without a clearer understanding of the processes involved in the maintenance of crosslink lifetimes closer to and shorter than tcrit.
Our analysis predicts that ϕ is equal to the reciprocal of tcrit. What is the meaning of tcrit, and is it a physical or experimental constant? According to our analysis, tcrit is the lifetime threshold, under which the inverse power law no longer applies and roughly corresponds to the mean lifetime of the crosslinks. Models of hydrogen-bond lifetimes would suggest that tcrit has a value of ∼10 ps that can be visualized as the survival function approaching unity value as τ→0 (27–31). We have opted not to fit this parameter because, under our experimental conditions and assumptions, we are unable to make an estimate of ϕ independently from that of E. Others, however, have estimated the scaling factor ϕ for biological tissue to be ∼108 s−1, which would correspond to tcrit of 10 ns (4,5). We are unfortunately unable to offer a more specific inference into a physical interpretation of tcrit based on the work in this article. Others have demonstrated that the dynamic structure factor, which reflects thermal fluctuations or structural disorder within a material, is initially high after a perturbation of actin filaments in solution and then follows a logarithmic relaxation after some characteristic time period (15,44). We can only speculate at this point that tcrit may similarly reflect a time duration, after which the relaxation of structural disorder within the material begins to follow an inverse power law.
Limitations of interpretation
In providing physical interpretations to the parameters E, k, and ϕ used to describe the fractional derivative complex modulus, it was necessary to assume a description of Tatt(τ) in Eq. 17 that allowed for an inverse power-law representation of relatively long lifetimes, i.e., longer than tcrit. Furthermore, measurements of the mechanical complex modulus up to frequencies of ∼1 kHz are only able to provide information regarding the distribution of crosslink lifetimes longer than ∼1 ms. Therefore, the lifetimes reflected in a measured complex modulus are very much longer than the majority of lifetimes of electrostatic interactions, such as hydrogen or ionic bonds. To the extent that our analysis is correct, our measures of viscoelastic behavior reflect the mechanical consequences of the longest-lived crosslinks represented in the tail of a distribution of lifetimes, and we have no basis to discern or infer the distribution of lifetimes below ∼1 ms and certainly not below tcrit. Exactly how a population of crosslink lifetimes might be expected to exhibit an inverse power-law distribution is not clear. We would speculate that this form of distribution tail arises because electrostatic crosslink detachment requires many independent random processes, as has been suggested for other phenomena resulting in an inverse power-law tail (45). A more specific theoretical basis for the question at hand, however, is clearly warranted, but beyond the scope of this work.
Perhaps the most significant limitation of our model lies in its dependence upon linear systems analysis. We have assumed purely elastic crosslinks, which would not likely apply for cases with greater amplitudes of length perturbations (14), but appear reasonable for the very small length perturbations used in this work. We have also assumed no strain dependency placed on the crosslink lifetime. However, there would likely be a redistribution of internal strains once any crosslink has formed or terminated, and the crosslink lifetime is likely to be shortened due to strain. Incorporation of strain-dependent processes is warranted, as suggested by others (13,14), as models of the molecular underpinnings of macroscopic viscoelasticity are further examined and developed. Our model, which is based on brief electrostatic interactions, does not obviate the possibility that other phenomena, such as an exponential elasticity of worm-like proteins (15,44), may underlie at least in part the viscoelastic characteristics of soft glassy materials and other materials that demonstrate a fractional derivative complex modulus.
Implications of the model
The mathematical model described in Eq. 10 suggests that a single underlying phenomenon at the molecular level, namely the distribution of crosslink survival times P(τ), gives rise to the mechanical complex modulus at the macroscopic level. This model, like other mathematical models, represents a hypothesis of the molecular basis of viscoelastic properties observed at a macroscopic level. The implication of our model is that a single distribution of crosslink survival times underlies both the elastic and viscous moduli of the measured viscoelasticity. As suggested in the common solution for Eqs. 14a and 14b, the elastic and viscous moduli of the fractional derivative description of viscoelasticity could be considered different reflections of the same underlying distribution of crosslink survival times P(τ). Contrast this concept against a complex modulus due to a perfect spring and dashpot aligned in parallel; the elastic and viscous moduli would be independent of each other and a single underlying distribution of survival times could not possibly be found to produce the complex modulus.
We propose that the common solution for Eqs. 14a and 14b with the same P(τ) lends validity to Eq. 10 and to the accuracy of the empirically produced Eq. 1, because it is highly unlikely these equations could be solved with the same P(τ) by coincidence. The concept of a single underlying source giving rise to both the elastic and viscous moduli is perhaps more intuitively apparent for activated striated muscle, where the overwhelming number and enzymatic nature of strongly bound myosin crossbridges are clearly reflected in the dependence of the complex modulus upon calcium and MgATP concentrations (24–26,46). If we accept that a single density of crosslink survival duration underlies a measured complex modulus, this density of molecular crosslink survival duration could theoretically be directly calculated from the recorded elastic and viscous moduli of a material without any need for an empirically produced mathematical description of the complex modulus like that of Eq. 1 or like that resulting from assuming a single exponential process, iω/(iω + α), presented by Kawai and Brandt (24), Machin (41), Kawai et al. (46), and Pringle (47). One would only need to solve Eq. 10 using inverse Fourier methods to numerically produce P(τ) from the recorded elastic and viscous moduli.
Based on the above arguments, we contend that Eq. 10 represents a rational and practical description of the relationship between the molecular and macroscopic phenomena of materials, whose macroscopic viscoelasticity arise from the brief intermittent interactions of elastic-like molecules. There may be applicability of this approach for analysis of biological tissues other than striated muscles. Its application to smooth muscle and collagen networks, which possess long filamentous structures of actin, myosin, and collagen, would appear appropriate, although the isotropic or partially isotropic orientations and possibly nonlinear elasticity of the filaments would have to be considered more thoroughly.
Conclusion
Our analysis suggests that the elastic and viscous moduli of viscoelastic materials provide different yet related information about the underlying distribution of crosslink lifetimes and that the nature of the fractional derivative viscoelasticity arises from an inverse power law of crosslink lifetimes that exist within disparate materials often falling under the soft glassy substance classification including biological tissue (3,12). Our experimental results, particularly with differing ionic strengths and temperatures, suggest that molecular electrostatic interactions and the inverse power-law distribution of their lifetimes longer than ∼10−8 s represent the underlying features common to the many different materials exhibiting fractional derivative viscoelasticity.
Acknowledgments
This manuscript is dedicated in honor of my father, Bruce Reed Palmer.
We are grateful to Joan Braddock for her expert technical assistance and to Drs. Jason Bates, David Maughan, Shane Nelson, and Pamela Vacek for helpful discussions during the preparation of this manuscript.
This work was supported by grants from National Institutes of Health grants No. P01-HL59408 (to B.M.P.), No. T32-HL007647 (to B.C.W.T.), No. R01-HL077418 (to M.J.T.), and No. K01-AG031303 (to M.S.M.).
Appendix A
In this Appendix we provide a more detailed derivation of P(τ) in Eqs. 14a and 14b. We solve for P(τ) in Eq. 14a starting with the following equality provided in Gradshteyn and Ryzhik (48) as
| (A1) |
We substitute θ = ω/2 and use the identity sin2ωτ/2 = 1/2(1−cosωτ),
| (A2) |
We substitute μ = −k. Upon canceling the factors of 2 in the denominators of Eq. A2, we have
| (A3) |
Upon noting the identities Γ(−k) = −Γ(1−k)/k and cos(−kπ /2) = cos(kπ/2), we have
| (A4) |
Equation A4 has the same form as Eq. 14a, and suggests
| (A5) |
We solve for P(τ) in Eq. 14b starting with the following equality provided in Gradshteyn and Ryzhik (48),
| (A6) |
We substitute μ = −k. Then,
| (A7) |
We now note the identities Γ(−k) = −Γ(1−k)/k and sin(−kπ /2) = −sin(kπ/2), and we have
| (A8) |
Equation A7 has the same form as Eq. 14b, and suggests again
| (A9) |
In both Eqs. A5 and A9, the solution permits the acceptable range of values for k: 0 < k < 1.
Supporting Material
References
- 1.Bagley R.L., Torvik P.J. The theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol. 1983;27:201–210. [Google Scholar]
- 2.Torvik P.J., Bagley R.L. On the appearance of the fractional derivative in the behavior of real materials. J. Appl. Mech. 1984;51:294–298. [Google Scholar]
- 3.Sollich P. Rheological constitutive equation for a model of soft glassy material. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1998;58:738–759. [Google Scholar]
- 4.Fabry B., Maksym G.N., Fredberg J.J. Scaling the microrheology of living cells. Phys. Rev. Lett. 2001;87:148102. doi: 10.1103/PhysRevLett.87.148102. [DOI] [PubMed] [Google Scholar]
- 5.Djordjević V.D., Jarić J., Stamenović D. Fractional derivatives embody essential features of cell rheological behavior. Ann. Biomed. Eng. 2003;31:692–699. doi: 10.1114/1.1574026. [DOI] [PubMed] [Google Scholar]
- 6.Fabry B., Fredberg J.J. Remodeling of the airway smooth muscle cell: are we built of glass? Respir. Physiol. Neurobiol. 2003;137:109–124. doi: 10.1016/s1569-9048(03)00141-1. [DOI] [PubMed] [Google Scholar]
- 7.Fabry B., Maksym G.N., Fredberg J.J. Time scale and other invariants of integrative mechanical behavior in living cells. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2003;68:041914. doi: 10.1103/PhysRevE.68.041914. [DOI] [PubMed] [Google Scholar]
- 8.Lenormand G., Millet E., Fredberg J.J. Linearity and time-scale invariance of the creep function in living cells. J. Roy. Soc. Interface. 2004;1:91–97. doi: 10.1098/rsif.2004.0010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Koeller R.C. Applications of fractional calculus to the theory of viscoelasticity. J. Appl. Mech. 1984;51:299–307. [Google Scholar]
- 10.Bagley R.L., Torvik P.J. On the fractional calculus model of viscoelastic behavior. J. Rheol. 1986;30:133–155. [Google Scholar]
- 11.Suki B., Barabási A.L., Lutchen K.R. Lung tissue viscoelasticity: a mathematical framework and its molecular basis. J. Appl. Physiol. 1994;76:2749–2759. doi: 10.1152/jappl.1994.76.6.2749. [DOI] [PubMed] [Google Scholar]
- 12.Gunst S.J., Fredberg J.J. The first three minutes: smooth muscle contraction, cytoskeletal events, and soft glasses. J. Appl. Physiol. 2003;95:413–425. doi: 10.1152/japplphysiol.00277.2003. [DOI] [PubMed] [Google Scholar]
- 13.Bates J.H. A recruitment model of quasi-linear power-law stress adaptation in lung tissue. Ann. Biomed. Eng. 2007;35:1165–1174. doi: 10.1007/s10439-007-9291-0. [DOI] [PubMed] [Google Scholar]
- 14.Donovan G.M., Bullimore S.R., Sneyd J. A continuous-binding cross-linker model for passive airway smooth muscle. Biophys. J. 2010;99:3164–3171. doi: 10.1016/j.bpj.2010.09.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Semmrich C., Storz T., Kroy K. Glass transition and rheological redundancy in F-actin solutions. Proc. Natl. Acad. Sci. USA. 2007;104:20199–20203. doi: 10.1073/pnas.0705513104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Mijailovich S.M., Stamenović D., Fredberg J.J. Toward a kinetic theory of connective tissue micromechanics. J. Appl. Physiol. 1993;74:665–681. doi: 10.1152/jappl.1993.74.2.665. [DOI] [PubMed] [Google Scholar]
- 17.Forgacs G. On the possible role of cytoskeletal filamentous networks in intracellular signaling: an approach based on percolation. J. Cell Sci. 1995;108:2131–2143. doi: 10.1242/jcs.108.6.2131. [DOI] [PubMed] [Google Scholar]
- 18.Ingber D.E. Tensegrity-based mechanosensing from macro to micro. Prog. Biophys. Mol. Biol. 2008;97:163–179. doi: 10.1016/j.pbiomolbio.2008.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Luo Y., Xu X., Ingber D.E. A multi-modular tensegrity model of an actin stress fiber. J. Biomech. 2008;41:2379–2387. doi: 10.1016/j.jbiomech.2008.05.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bazant Z.P., Le J.L., Bazant M.Z. Scaling of strength and lifetime probability distributions of quasibrittle structures based on atomistic fracture mechanics. Proc. Natl. Acad. Sci. USA. 2009;106:11484–11489. doi: 10.1073/pnas.0904797106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Miller M.S., van Buren P., Toth M.J. Chronic heart failure decreases cross-bridge kinetics in single skeletal muscle fibers from humans. J. Physiol. 2010;588:4039–4053. doi: 10.1113/jphysiol.2010.191957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Mulieri L.A., Hasenfuss G., Alpert N.R. Protection of human left ventricular myocardium from cutting injury with 2,3-butanedione monoxime. Circ. Res. 1989;65:1441–1449. doi: 10.1161/01.res.65.5.1441. [DOI] [PubMed] [Google Scholar]
- 23.Tanner B.C., Farman G.P., Miller M.S. Thick-to-thin filament surface distance modulates cross-bridge kinetics in Drosophila flight muscle. Biophys. J. 2012;103:1275–1284. doi: 10.1016/j.bpj.2012.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kawai M., Brandt P.W. Sinusoidal analysis: a high resolution method for correlating biochemical reactions with physiological processes in activated skeletal muscles of rabbit, frog and crayfish. J. Muscle Res. Cell Motil. 1980;1:279–303. doi: 10.1007/BF00711932. [DOI] [PubMed] [Google Scholar]
- 25.Palmer B.M., Suzuki T., Maughan D.W. Two-state model of acto-myosin attachment-detachment predicts C-process of sinusoidal analysis. Biophys. J. 2007;93:760–769. doi: 10.1529/biophysj.106.101626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Palmer B.M., Wang Y., Miller M.S. Distribution of myosin attachment times predicted from viscoelastic mechanics of striated muscle. J. Biomed. Biotechnol. 2011;2011:592343. doi: 10.1155/2011/592343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Evans M., Hastings N., Peacock B. 3rd ed. Wiley; New York: 2000. Statistical Distributions. [Google Scholar]
- 28.Newman M.E.J. Power laws, Pareto distributions and Zipf’s law. Contemp. Phys. 2005;46:323–351. [Google Scholar]
- 29.Clauset A., Shalizi C.R., Newman M.E.J. Power-law distributions in empirical data. SIAM Rev. 2009;51:661–703. [Google Scholar]
- 30.Rembold C.M., Tejani A.D., Han S. Paxillin phosphorylation, actin polymerization, noise temperature, and the sustained phase of swine carotid artery contraction. Am. J. Physiol. Cell Physiol. 2007;293:C993–C1002. doi: 10.1152/ajpcell.00090.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Sciortino F., Poole P.H., Havlin S. Lifetime of the bond network and gel-like anomalies in supercooled water. Phys. Rev. Lett. 1990;64:1686–1689. doi: 10.1103/PhysRevLett.64.1686. [DOI] [PubMed] [Google Scholar]
- 32.Luzar A., Chandler D. Effect of environment on hydrogen bond dynamics in liquid water. Phys. Rev. Lett. 1996;76:928–931. doi: 10.1103/PhysRevLett.76.928. [DOI] [PubMed] [Google Scholar]
- 33.Keutsch F.N., Saykally R.J. Water clusters: untangling the mysteries of the liquid, one molecule at a time. Proc. Natl. Acad. Sci. USA. 2001;98:10533–10540. doi: 10.1073/pnas.191266498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Mallik B.S., Chandra A. Hydrogen bond and residence dynamics of ion-water and water-water pairs in supercritical aqueous ionic solutions: dependence on ion size and density. J. Chem. Phys. 2006;125:234502. doi: 10.1063/1.2403867. [DOI] [PubMed] [Google Scholar]
- 35.Park S., Fayer M.D. Hydrogen bond dynamics in aqueous NaBr solutions. Proc. Natl. Acad. Sci. USA. 2007;104:16731–16738. doi: 10.1073/pnas.0707824104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.von Hippel P.H., Berg O.G. Facilitated target location in biological systems. J. Biol. Chem. 1989;264:675–678. [PubMed] [Google Scholar]
- 37.Smith D.A., Stephenson D.G. An electrostatic model with weak actin-myosin attachment resolves problems with the lattice stability of skeletal muscle. Biophys. J. 2011;100:2688–2697. doi: 10.1016/j.bpj.2011.04.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kawai M., Wray J.S., Güth K. Effect of ionic strength on crossbridge kinetics as studied by sinusoidal analysis, ATP hydrolysis rate and x-ray diffraction techniques in chemically skinned rabbit psoas fibers. J. Muscle Res. Cell Motil. 1990;11:392–402. doi: 10.1007/BF01739760. [DOI] [PubMed] [Google Scholar]
- 39.Kawai M., Wray J.S., Zhao Y. The effect of lattice spacing change on cross-bridge kinetics in chemically skinned rabbit psoas muscle fibers. I. Proportionality between the lattice spacing and the fiber width. Biophys. J. 1993;64:187–196. doi: 10.1016/S0006-3495(93)81356-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Baker J.E., Brosseau C., Warshaw D.M. The biochemical kinetics underlying actin movement generated by one and many skeletal muscle myosin molecules. Biophys. J. 2002;82:2134–2147. doi: 10.1016/S0006-3495(02)75560-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Machin K.E. Feedback theory and its application to biological systems. Symp. Soc. Exp. Biol. 1964;18:421–445. [PubMed] [Google Scholar]
- 42.Luther P.K., Winkler H., Liu J. Direct visualization of myosin-binding protein C bridging myosin and actin filaments in intact muscle. Proc. Natl. Acad. Sci. USA. 2011;108:11423–11428. doi: 10.1073/pnas.1103216108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Weith A., Sadayappan S., Warshaw D.M. Unique single molecule binding of cardiac myosin binding protein-C to actin and phosphorylation-dependent inhibition of actomyosin motility requires 17 amino acids of the motif domain. J. Mol. Cell. Cardiol. 2012;52:219–227. doi: 10.1016/j.yjmcc.2011.09.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Glaser J., Hallatschek O., Kroy K. Dynamic structure factor of a stiff polymer in a glassy solution. Eur. Phys. J. E. Soft Matter. 2008;26:123–136. doi: 10.1140/epje/i2007-10321-2. [DOI] [PubMed] [Google Scholar]
- 45.Reed W.J., Hughes B.D. From gene families and genera to incomes and internet file sizes: why power laws are so common in nature. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2002;66:067103. doi: 10.1103/PhysRevE.66.067103. [DOI] [PubMed] [Google Scholar]
- 46.Kawai M., Zhao Y., Halvorson H.R. Elementary steps of contraction probed by sinusoidal analysis technique in rabbit psoas fibers. Adv. Exp. Med. Biol. 1993;332:567–580. doi: 10.1007/978-1-4615-2872-2_51. [DOI] [PubMed] [Google Scholar]
- 47.Pringle J.W. The Croonian Lecture, 1977. Stretch activation of muscle: function and mechanism. Proc. R. Soc. Lond. B Biol. Sci. 1978;201:107–130. doi: 10.1098/rspb.1978.0035. [DOI] [PubMed] [Google Scholar]
- 48.Gradshteyn I.S., Ryzhik I.M., editors. Tables of Integrals, Series, and Products. 4th Ed. Academic Press; London: 1980. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


