Exponential Sum-Fitting of Dwell-Time Distributions without Specifying Starting Parameters

Abstract

Fitting dwell-time distributions with sums of exponentials is widely used to characterize histograms of open- and closed-interval durations recorded from single ion channels, as well as for other physical phenomena. However, it can be difficult to identify the contributing exponential components. Here we extend previous methods of exponential sum-fitting to present a maximum-likelihood approach that consistently detects all significant exponentials without the need for user-specified starting parameters. Instead of searching for exponentials, the fitting starts with a very large number of initial exponentials with logarithmically spaced time constants, so that none are missed. Maximum-likelihood fitting then determines the areas of all the initial exponentials keeping the time constants fixed. In an iterative manner, with refitting after each step, the analysis then removes exponentials with negligible area and combines closely spaced adjacent exponentials, until only those exponentials that make significant contributions to the dwell-time distribution remain. There is no limit on the number of significant exponentials and no starting parameters need be specified. We demonstrate fully automated detection for both experimental and simulated data, as well as for classical exponential-sum-fitting problems.

Introduction

Exponential sum-fitting is often used to describe distributions of various natural phenomena (1–5). In exponential sum-fitting, the distributions of interest are described by the sums of exponentials, such that

$$f\left(t\right)=\sum _{k=1}^N\left(\frac{a_k}{{\tau }_k}\right)\exp \left(\frac{-t}{{\tau }_k}\right),$$ (1)

where f(t) is the function of the fitted sum of exponentials used to describe the dwell-time distribution, N is the number of summed exponentials, a_k is the area (the fraction of the total area of the dwell-time distribution) of exponential k, τ_k is the time constant of exponential k, and the quotient a_k/τ_k gives the magnitude of exponential k at 0 time. The time constant τ_k is the time for exponential k to decay to 1/e (0.368) of its 0 time value, which is the same as the mean duration of all the dwell times in exponential k. An inherent difficulty in exponential fitting is to identify the number of summing exponentials and their parameters (1,6–8). We now extend previous approaches of exponential sum-fitting for the specific case of fitting dwell-time distributions obtained from single ion channels.

Ion channels are integral membrane proteins comprised of subunits that allow the passage of ions through cell membranes (9). Ion channels gate their pores by changing their conformation, with typically one or more open (conducting) states and many closed (nonconducting) states (9). Such gating has been successfully modeled with discrete-state Markov-chain models (10–15). Such models predict that the distributions of open and closed dwell times will be described by the sums of exponentials (16,17). A determination of the number of significant exponentials that sum to describe the open and closed dwell-time distributions provides an estimate of the minimal numbers of open and closed states (16,17), respectively, but there is not typically a one-to-one relationship between designated exponential components and states (16–18). Nevertheless, the exponentials and their sum provide a convenient means to describe the dwell-time distributions consistent with the underlying theory.

A difficulty with exponential sum-fitting of dwell-time distributions, just as with the exponential sum-fitting of other phenomena, has been to find all the significant exponentials that contribute to the distributions (1,6,7), The problem is further complicated because large numbers of exponentials, often closely spaced, can be required to describe the dwell-time distributions from single-channels (19–21), consistent with theoretical predictions that large numbers of kinetic states can contribute to gating (22–24). Detecting such exponentials can be especially difficult, because search routines often get trapped in local maxima, preventing them from finding all exponentials. To overcome these difficulties, we now present an automated analysis method that consistently finds all of the significant exponentials contributing to dwell-time distributions for simulated single-channel data. A key feature of our automated analysis is based on previous examples of exponential sum-fitting (4,25–27). Instead of searching for the exponentials, the fitting starts with essentially all possible exponentials so that none are missed.

In practice, we have found that 20–40 initial exponentials equally spaced in log time have been sufficient to find the significant exponentials contributing to dwell-time distributions from single channels. In the automated analysis, once the time constants of the equally log-spaced initial exponentials are set, the areas of the initial exponentials are determined with maximum-likelihood fitting. In an iterative manner, the analysis then removes exponentials with negligible area and combines adjacent exponentials with refitting to optimize the areas and time constants of the exponentials until only those exponentials that make significant contributions to the description of the dwell-time distributions remain. There is no practical limit on the number of significant exponentials, and no starting parameters need be specified.

Materials and Methods

Measuring, log binning, and plotting single-channel dwell times

Methods for measuring dwell times from single ion channels, log binning the dwell times to generate frequency histograms, and the theory and application of maximum-likelihood fitting of dwell-time distributions with sums of exponentials (or mixtures of exponentials when the data are converted to probability density functions) have been extensively described (19,28–31). Log binning allows dwell times from microseconds to hours to be binned in just a few hundred bins with a constant relative time resolution (19,29,30). Although it would be possible to analyze the data for the analysis to be presented here without log binning, the log binning allows meaningful plots of distributions spanning up to seven orders of magnitude of the dwell times examined here, and it reduces the time required for fitting 10⁷ intervals by ∼60,000 fold, from months to just a few minutes on a Windows-based desktop computer as the fitting time depends mainly on the number of bins (∼150) rather than the number of intervals. Plots of the dwell-time distributions in this article use the Sigworth and Sine transform (29) which plots the square root of the number of intervals per bin versus log time, with the peak amplitude of each transformed exponential located at its time constant.

To find the appropriate bin for an observed interval, the log of the interval duration in sample periods is multiplied by the number of bins per log unit (30). The result of this operation is that some bins have no events and other bins may have greater or fewer events than indicated by the magnitude of the fitted dwell-time distribution at the midtime of the bins. This distortion of the data, which is only significant at short times, has negligible effect on the fitting but can distort the plots of the simulated and binned data, making it difficult to visually compare simulated and fitted distributions at short times. To reduce the visual discontinuities in the plots from log binning, a small sample interval of typically 0.0001–0.001 ms was used when binning the dwell times, and corrections of the binned data at brief times were applied (19,30). The fitting was always performed on uncorrected data.

Simulation of dwell-time distributions

The dwell times for a simulated dwell-time distribution were generated with an algorithm (in abbreviated format)

• For k = 1 to N

• While na_k > 0.5

• $\text{dwell}={\mathit{\tau }}_k\left(-{\log }_e\left(\text{RND}\right)\right)$

• $\mathit{n}{\mathit{a}}_{\mathit{k}}=\mathit{n}{\mathit{a}}_{\mathit{k}}-1$

• Wend

• Next k,

where N is the number of exponentials, n is the total number of dwell times to simulate, a_k, and τ_k are the area and time constants, respectively, of exponential k, dwell is the duration of each successively generated dwell time, RND is a random number between 0+ (∼5 × 10⁻⁸) and 1.0, −log_e(RND) converts the linear random numbers to exponentially distributed dwell times with a mean of 1.0, and Wend returns the loop to While. If the last value of na_k before exiting the loop is >0.5, then an interval is generated. Unless stated otherwise, 10⁷ intervals were simulated for each dwell-time distribution to reduce stochastic variation to low levels, as the major focus of the fitting was to determine whether the automated analysis program could find the significant exponentials, not to explore the effects of stochastic variation. As a second method of generating near-perfect dwell-time distributions, we calculated the number of intervals in each bin rather than using a random number generator. The distributions generated by the two methods visually superimposed, and near-identical visual results were obtained when fitting the distributions, but as would be expected, the errors for fitting the near-perfect distributions were reduced somewhat compared to fitting the stochastic distributions. The results presented in this article for the four classic examples of exponential sum-fitting are for fitting calculated distributions of near-perfect data for comparison to previous studies where near-perfect data were fit, whereas the results based on experimental data are for simulated distributions, so that the consequences of decreasing the number of dwell times in a distribution, which would increase stochastic variation, could be examined. Binning for both simulated and calculated distributions was at 25 bins/log unit (30).

Significance of an additional exponential and the number of dwell times required for significance

Whether an additional exponential was significant when fitting distributions with sums of exponentials was determined from the log_e of the likelihood ratio, LLR, given by

$$\text{LLR}={\text{LL}}_{\text{N}}-{\text{LL}}_{\text{N}-1},$$ (2)

where LL_N and LL_N−1 are the log_e of the likelihoods that the experimental data were drawn from a distribution described by N or N − 1 exponentials, respectively. Twice the value of the LLR is distributed as χ², with the number of degrees of freedom equal to 2 for an additional exponential (19,32,33). On this basis, an additional exponential was considered significant with P < 0.05, P < 0.01, P < 0.001, P < 0.0001, and P < 0.00001 when the LLR was >2.995, >4.605, >6.908, >9.210, and >11.51, respectively.

Having determined with Eq. 2 that there are N significant exponential components in a distribution containing n_D intervals, it can be useful to estimate the minimum number of intervals n_N drawn from the same distribution that would be required to detect all N significant exponentials, as is done in the Results and Discussion section. Such a calculation is possible because (for perfect data) the LLR ratio scales directly with the number of intervals in a dwell-time distribution (19,28), such that (19)

$$n_{\mathrm{N}}=n_{\mathrm{D}}\frac{2.995}{\text{LLR}},$$ (3)

where LLR is defined by Eq. 2.

Definition of relative error

Relative error in estimating an exponential parameter is defined as the absolute value of the fractional difference between true and fitted values, such that

$$\text{Relative}\text{error}=\left|\left(\frac{\text{True}-\text{Fitted}}{\text{True}}\right)\right|,$$ (4)

where the true values are the values used to simulate the data. Where indicated, average relative error estimates are presented as the mean ± SD of individual relative error estimates.

Approach for automated determination of all significant exponentials

Many different approaches have been considered to search for the number of exponentials and their parameters for exponential sum-fitting of distributions (1–4,7,8,19,25–28,34–37). We apply and extend various aspects of some of these previous approaches to develop an automated analysis for exponential sum-fitting of dwell-time distributions obtained from single ion channels. A key feature of our automated analysis is that the fitting starts with essentially all possible detectable exponentials as defined by their time constants, so that none are missed, a technique applied previously (4,26,27). Exponentials with negligible areas are then removed, those with time constants so close that they cannot be distinguished are combined, and those that make statistically insignificant contributions are removed, leaving only those exponentials that significantly improve the likelihood. Hence, it is not necessary when using the automated analysis to specify either the number of exponentials or their starting parameters.

The analysis method is summarized below in 10 steps. Fitting, when indicated in the various steps, is done using the method of maximum likelihood, as described previously (19,28).

• 1.Log bin the data. The experimentally observed dwell times are log binned into open and closed dwell-time distributions (30). These distributions are then analyzed separately.
• 2.Generate the time constants for essentially all possible significant exponentials. The time constants of the fastest and slowest initial exponentials are assigned the values of the briefest and longest observed dwell times, respectively. The time constants of the exponentials in between are then equally spaced on a logarithmic time axis and given equal areas that sum to 1.0. We found that 20 initial exponentials were sufficient for the examples in this article. An examination of fitted dwell-time distributions in published single-channel dwell-time distributions suggests that 20 initial exponentials would also be sufficient to find the significant exponentials in those distributions. For 20 exponentials, the initial area of each exponential was set to 0.05 (Fig. 1 B). Having the ratios of the time constants of adjacent initial exponentials no greater than the minimal ratio of significant adjacent exponentials in the experimental data should assure that the significant exponentials in the data are detected. This would be the case because the fitting would start with approximations of all possible significant exponentials identified on the basis of their time constants. The number of significant exponentials in experimental data is not known, so the number of initial exponentials could be increased for the initial analysis. There is no drawback to starting with more initial exponentials than might be needed to detect the significant exponentials, except for a time penalty in the fitting. An approach toward estimating the number of initial exponentials to use for fitting is presented in the Supporting Material.
• 3.With the time constants fixed, a maximum-likelihood fit to find the most likely area for each of the 20 initial exponentials is performed. With the time constants fixed, fitting areas is a well-conditioned problem that readily converges (6).
• 4.Delete the end exponentials with insignificant area. The two to three fastest and slowest exponentials typically have areas of 0.0. To delete these end exponentials, the fastest and slowest exponentials with areas greater or equal to 10⁻⁵ are taken as the new fastest and slowest exponentials. Steps 2 and 3 are then repeated, but with the new fastest and slowest exponentials setting the range to distribute the exponentials. We found that setting the minimal area to 10⁻⁵ for retention of an exponential was sufficient for all the examples presented in this study (the smallest area was 0.000046) and should be sufficient for the large number of published distributions we have examined, because the areas of the smallest fitted exponentials in those distributions were >10⁻⁵. Hence, retention of exponentials with areas ≥10⁻⁵ for step 4 and step 5 should be suitable for the analysis of most (if not all) single-channel data published so far, without the need to adjust this parameter. To look for significant exponentials with areas <10⁻⁵ in distributions with >100,000 intervals, this value could be reduced (see Supporting Material).
• 5.Delete all exponentials with negligible (<10⁻⁵) area. (For the data in Fig. 1, six exponentials were automatically deleted, leaving 14.) A plot of the fit at the end of step 5 is presented in Fig. S1 A in the Supporting Material.
• 6.Apply maximum-likelihood fitting to find the most likely areas and time constants of the remaining exponentials. This is the first time that the time constants are free parameters. The fitting makes small adjustments in the time constants to move them to the most likely values while adjusting the areas to match the new time constants. The number of exponentials after step 6 are the same as in step 5, as step 6 step does not eliminate exponentials. A plot of the fit at the end of step 6 is presented in Fig. S1 B in the Supporting Material.
• 7.Combine exponentials with very close time constants. Adjacent exponentials whose time constants differ by <2% are combined into a single exponential with an area equal to the sum of the two areas and a time constant between the two weighted for the difference in areas. This process is carried out by systematically moving down the list of exponentials arranged in order of decreasing time constant, with refitting after every combination. For the data in Fig. 1, four exponentials were removed through combining adjacent exponentials, leaving 10. Less than 2% was selected for the criterion for combining exponentials, as the likelihood was essentially unchanged after such combinations for 10⁷ fitted intervals. Consequently there is essentially no chance that a significant exponential would be excluded through combination for single-channel data by using this criterion.
• 8.Determine the best fit with one less exponential. Each exponential is then removed one at a time, followed by refitting (after which the exponential is replaced), with each fit and its likelihood value saved. The fit with the best likelihood then gives the maximum-likelihood value and exponential parameters for fitting with one less exponential.
• 9.Determine the number of significant exponentials and their parameters. Step 8 is repeated until a decrease in the number of exponentials by one makes the likelihood of the fit significantly worse, as indicated when the LLR of fits for N, compared to N − 1, exponentials is >2.995 (19,33). The fit with N exponentials then indicates the number of significant exponentials and the most likely parameters for each of those exponentials.
• 10.Exclusion of brief erroneous exponentials. For single-channel recording, very brief dwell times are not detected due to the limited frequency response of the recording systems. Hence, the maximum-likelihood fitting does not start at 0 time but at a time equal to typically twice the dead time, where dead time is the duration of the briefest detected intervals (28,30). For such fitting, an erroneous exponential with a time constant typically much shorter than the dead time can occasionally be reported by the fitting program if the tail of the erroneous exponential improves the likelihood. Such erroneous exponentials are possible with missed events, because the majority of the area of the erroneous exponential is not fitted, so it provides no penalty. Such erroneous brief exponentials were automatically eliminated by excluding reported exponentials with time constants less than the dead time whose fitted area contributes <10⁻⁵ of the total fitted area of the dwell-time distribution, and then refitting. Erroneous exponentials do not arise for exponentials with longer time constants, because the vast majority of the area of the longer exponentials is included in the fitting. If apparent erroneous exponentials are not excluded by these criteria, then the user could change the parameters for exclusion.

Figure 1.

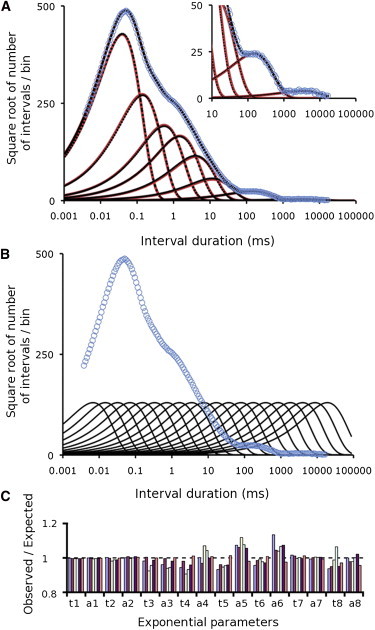
Detecting the exponentials summing to describe a simulated dwell-time distribution for closed intervals based upon an idealized single-channel recording. (A) The simulated dwell-time distribution (blue open circles) and the eight underlying exponential components from Table 1 (red lines) are presented with the Sigworth and Sine transform (29), which plots the square root of the number of closed intervals in each bin versus the duration of the closed intervals on a logarithmic time axis. Bin width remains constant on the logarithmic time axis, giving an exponential increase in bin width as interval duration increases. The peak of each transformed exponential indicates the time constant of that exponential. The automated fitting of the dwell-time distribution detected eight exponentials (dashed black lines) that superimposed the exponentials used to simulate the distribution. The fitted distribution (solid black line) superimposed the simulated distribution (blue open circles). The eight underlying exponentials were detected without the user specifying either the number of exponentials or the starting parameters for the exponentials. N = 10⁷ intervals simulated. (B) The 20 starting exponentials automatically generated by the program are plotted (black lines). The fitting for this and the other figures typically started at 0.003981 ms. (C) Normalized estimates of the time constants (t1–t8) and areas (a1–a8) of the eight exponential components for six different simulations and fittings (Table S1). The data are plotted as the observed (fitted) values divided by the values used to simulate the distribution from Table 1. The same eight exponentials were detected in each case.

Whereas the fixed parameters in the previous steps have been sufficient for all the examples examined in this study, they may need adjustment for other types of channels and data. As is the case for all fitting programs, fitting of data simulated with parameters similar to those obtained for the experimental data can be used to test the ability of the program to detect exponentials for different types of data, and adjustments can be made if necessary.

Search routine for automated maximum likelihood fitting

The theory and method of maximum-likelihood fitting of dwell-time distributions with sums of exponentials (or mixtures of exponentials when the data are converted to probability density functions) have been described previously (19,28). The search routine used for maximum-likelihood fitting in the various steps above does not have to find the exponentials, only adjust the parameters of each of the starting exponentials to maximize the likelihood that the data were drawn from a dwell-time distribution described by the sum of the exponentials. This is the case because all possible significant exponentials, which are the starting exponentials, are approximated by the end of step 3 in the previous section. Steps 4–9 then remove the extra exponentials while retaining the significant exponentials. Search routines that jump one or more parameters large distances would not be suitable for the maximum-likelihood fitting in the steps above because they may get trapped in local maxima by moving the parameters for an exponential away from one of the potentially significant exponentials defined in the initial starting parameters. A direct search approach based on Patternsearch (38) was used to avoid this possibility by adjusting the parameters one at a time in small steps.

Results and Discussion

Automated detection of the exponentials in simulated dwell-time distributions based on experimental data without the need to specify starting parameters

Fig. 1 A presents an example of automated detection of the eight exponential components that sum to form a dwell-time distribution. The eight exponential components (Table 1) are plotted as red lines in Fig. 1 A and are based on the eight significant exponential components fitted to experimental data recorded from a large-conductance Ca²⁺-activated K⁺ channel (19). Using the areas and time constants of the components, 10⁷ intervals were simulated, log binned, and plotted as blue open circles to obtain the distribution predicted by the sum of the exponentials. The plots in Fig. 1, A and B, are presented in the Sigworth and Sine transform (29), where the square root of the number of intervals in each bin is plotted against the mean duration of the intervals in that bin on a logarithmic time axis. The bin width increases logarithmically, giving constant bin width on the logarithmic timescale. With this transform the time of the peak amplitude of each exponential component indicates the time constant of that component (29).

Table 1.

Eight exponentials used to simulate the dwell-time distribution in Fig. 1

Exponential	τ (ms)	Area
1	0.039	0.539
2	0.139	0.220
3	0.547	0.111
4	1.48	0.0815
5	4.12	0.0379
6	11.9	0.00880
7	146.0	0.00170
8	3390.0	0.000046

The time constants (τ) and areas are from Table 4 in McManus and Magleby (19).

The simulated dwell-time distribution was fitted with sums of exponentials to find the significant underlying exponential components. The fitted components (Fig. 1 A, black dashed lines) superimposed the initial components (Fig. 1 A, red lines), and the sum of the fitted components (Fig. 1 A, solid black line) superimposed the simulated distribution (Fig. 1 A, black line with blue circles), indicating that the eight exponential components used to simulate the distribution of dwell times were found by the automated analysis without specifying either the number of exponentials or their starting parameters. It was not necessary to specify starting exponentials for the fit because the automated analysis generated a sufficient number of starting exponentials logarithmically spaced in time so that there would be one or more starting exponentials with time constants close to those of any possible underlying exponentials. This can be seen by comparing the time constants (peaks of the exponentials) of the starting exponentials in Fig. 1 B to the time constants of the exponential components that sum to generate the dwell-time distribution in Fig. 1 A.

Repeating the analysis in Fig. 1 A for five additional data sets, each simulated with a different random number seed, detected the same eight exponentials used to simulate the data (Fig. 1 C and Table S1), with relative errors (Eq. 4) in the estimates of the 16 parameters for the areas and time constants of the eight exponentials of 0.023 ± 0.028 (mean ± SD) based on estimates obtained from the 16 parameters estimated from each of the six different simulations and fittings. In >1000 simulations and fittings of distributions with 1–10 exponentials with a wide range of time constants and areas, all significant exponential components were found using the automated analysis.

How is it possible to detect the significant exponentials in the simulated data including the eight exponentials that sum to describe the distribution in Fig. 1, when it has been stated (and restated) in the literature that determining both the areas and time constants for fitting sums of exponentials can be hopeless or require an increase in the accuracy of the data to limits that are far beyond the capability of present measuring devices (6,7). Certainly, exponential sum-fitting can be ill-conditioned when the data are inadequate, with very few data points, or when data are obtained over limited time ranges or with very closely spaced exponentials or with much noise (7,8). However, for single-channel data, tens of thousands to many hundreds of thousands of open and closed intervals can be recorded over wide time ranges to reduce the stochastic variation and increase the ability to detect exponentials (19,31). For example, the eight exponentials in Table 1 were determined from analysis of 114,350 closed intervals recorded from a BK channel, where the experimentally observed dwell times spanned nine orders of magnitude in frequency of observation and six orders of magnitude in duration (19). The dwell-time distribution of the experimental data fitted with eight significant exponentials is presented in Fig. 8 A in McManus and Magleby (19). (For the experimental data, intervals with true durations <30 μS were not detected (missed events) due to filtering (28). Including the missed events in the distribution gives ∼170,000 true intervals underlying the experimental data.)

Testing the automated fitting program for less than ideal data

To test whether the automated analysis could also find the significant exponentials for less-than-ideal data, the analysis was applied directly to experimental dwell-time distributions from BK channels, and the results were compared to those from applying our previous fitting programs to the same experimental data. This analysis is different from the one represented in Fig. 1, for which a known number of specified exponentials was used to simulate ideal data. When fitting experimental data, the number of exponentials is not known, but theoretical considerations suggest that large numbers of open and closed states (>50) may contribute to dwell-time distributions from BK channels (22–24). Application of the automated analysis to experimental data from BK channels found either the same significant exponentials as found using our previous programs or, in two cases, one additional significant exponential, suggesting that our previous programs did not always have a sufficient number of starting parameters to find all significant exponentials. There was not one case where the automated analysis found fewer significant exponentials than had our previous analysis methods. Hence, our automated analysis, without the need to specify starting parameters, was as good or better at finding the significant exponentials than our previous programs, which used >100 different sets of starting parameters based on years of fitting data from BK channels.

We also compared the results obtained by the automated fitting program to results obtained when the fitting was with programs in which fitting could be started with the parameters used to simulate the data. The significant exponentials found by the automated analysis program were essentially identical to those obtained when the fitting was started with the simulation parameters, and this was the case for smaller data sets of 1000 intervals as well as for larger ones, indicating the robustness of the fitting algorithm to find the significant exponentials.

Errors in exponential sum-fitting introduced by fitting too few dwell times

The previous sections indicated the consistent ability of the automated fitting algorithm to find the significant exponentials in simulated and experimental single-channel data. Nevertheless, there are limitations to the detection of exponentials based on the number of fitted intervals (19). We now consider the limits of detection as related to the number of fitted intervals for simulated distributions based on the eight exponentials in Table 1 that were used to simulate the data for Fig. 1. Eq. 3 is first examined to determine whether it can provide an estimate of the number of intervals needed for detection of the eight significant exponentials. Errors associated with reducing the number of intervals below the number required to detect all eight exponentials are then examined.

Log-likelihood estimates from the six simulations and fittings of 10⁷ intervals presented in Table S1 indicated that the LLR (see Eq. 2) for nine versus eight exponentials ranged from 0.5 to 2.5. These LLR values are less than the 2.995 required for significance at P < 0.05 (see Materials and Methods), indicating that nine exponentials were not significantly better than eight in any of the six simulations. Hence, no false exponentials were detected. The LLR for eight over seven significant exponentials ranged from 195 to 258, indicating eight significant exponentials versus seven at P ≪ 0.00001 for each simulation. Hence, all eight significant exponentials were detected in each simulation of 10⁷ intervals.

Given LLRs of 195–258 for eight significant exponentials over seven for fitting 10⁷ intervals, Eq. 3 indicated that ∼116,000–154,000 dwell times would be required to detect eight significant exponentials. To test this prediction, we simulated four separate distributions, as in Fig. 1 A, but with 135,000 dwell times each (the median between 116,000 and 154,000), and found that eight significant exponentials were detected in two of the four simulated distributions, and that seven were detected in the other two. Hence, with ∼135,000 dwell times, all eight significant exponentials would be detected in about half the experiments, consistent with the approximate number of dwell times required for the threshold of detection calculated from Eq. 3. When the number of simulated dwell times was increased to 170,000, eight significant exponentials were consistently detected (Fig. S2 A), and when the number of simulated dwell times was reduced to 30,000, seven significant exponentials were consistently detected. With 30,000 dwell times, the two exponentials with time constants of 4.12 and 11.9 ms were combined into a single exponential with an intermediate time constant and combined area. With 10,000 simulated dwell times, only six significant exponentials were found (Fig. S2 B), with the slowest exponential of 3390 ms now also missing, as expected, because there would be, on average, <1 dwell time (0.000046 × 10,000) from the slowest exponential in the distribution because of its very small area (Table 1). In the severe case of only 1000 simulated dwell times, only four of the eight significant exponentials were found (Fig. S2 C). The slowest exponential of 3390 ms was missing, as expected, the next two slowest exponentials of 148 ms and 11.9 ms were combined into an exponential at ∼50 ms, and the other three significant exponentials were combinations of the five remaining underlying exponentials. Thus, decreasing the number of dwell times in a distribution can be expected to decrease the number of significant exponentials (19) for both the automated analysis presented here and for all methods of exponential sum-fitting, depending on the complexity of the gating mechanism. It follows that the number of significant exponentials then places a lower limit on the number of exponentials contributing to the distribution, as there may be insufficient data to detect all the exponentials, and because some of the exponentials may have too small of an area for detection or have time constants too close to those of other exponentials to be detected.

The automated analysis can find the exponentials in classic examples of exponential sum-fitting

As a further test of the ability of the automated fitting program to find the significant exponentials, we examined whether it could find the exponentials in four different classic exponential-sum-fitting problems, where detection of the exponentials can be difficult. The first two classic examples were Boliden 3 and Boliden 4 from Table 2 in Watson (34). The results are presented in Fig. 2 and Table 2. The parameters defining the exponential components were used to simulate dwell-time distributions with log binning, which were then fit with the automated analysis. Boliden 3 examines detection of four exponentials with progressively increasing areas and time constants, and Boliden 4 examines detection when one of the exponentials has less area than the two adjacent exponentials. For both examples, the automated analysis found the four exponentials used to simulate the dwell-time distributions, with minimal relative error in the areas and time constants of ∼0.001 ± 0.001. For both Boliden 3 and Boliden 4, each with four significant exponentials, the LLR for five versus four significant exponentials was ∼0, indicating that five exponentials were not better than four, and the LLR for four versus three significant exponentials was 22,020 for Boliden 3 and 5580 for Boliden 4, indicating that the four exponentials were found in each case and were highly significant (P ≪ 0.00001). The true exponentials, fitted values, and relative errors are given in Table 2.

Table 2.

Identifying the four exponentials in Boliden 3 and Boliden 4

Boliden 3
Magnitude	Rate (ms−1)	τ (ms)	Nor. Area	Fit area	Error	Fit τ	Error
0.714866	10.00000	0.100000	0.016770	0.016762	0.000460	0.100311	0.003110
0.183963	0.734125	1.362166	0.058784	0.058686	0.001673	1.361681	0.000356
0.078444	0.105668	9.463603	0.174148	0.174068	0.000457	9.45156	0.001273
0.022392	0.007001	142.8367	0.750298	0.750485	0.000249	142.8085	0.000198
Boliden 4
Magnitude	Rate	τ	Nor. Area	Fit area	Error	Fit τ	Error
0.841884	3.478609	0.287471	0.091044	0.091098	0.000593	0.287973	0.001745
0.098694	0.702992	1.422491	0.052813	0.052618	0.003702	1.422578	0.000061
0.049751	0.146201	6.839898	0.128014	0.128046	0.000253	6.830302	0.001403
0.009850	0.005089	196.5023	0.728129	0.728237	0.000148	196.4776	0.000125

Magnitudes and rate constants are from Table 2 of Watson (34). The time constant (τ) is given by 1/rate. Nor. area is the area of the four exponentials after normalizing to an area of 1.0. The relative errors (Eq. 4) for the eight estimated parameters for Boliden 3 and for Boliden 4 were similar at ∼0.001 ± 0.001 (mean ± SD). N = 10⁷ simulated dwell times.

Figure 2.

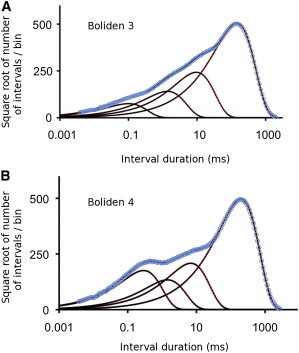
Automated fitting detects the exponentials underlying simulated dwell-time distributions based on Boliden 3 and Boliden 4 in Table 2 in Watson (34). The time constants and areas of exponentials used to simulate the dwell-time distributions are in columns “τ” and “Nor. Area” in Table 2. (A and B) Red lines plot the exponential components used for the simulation, blue open circles the simulated distributions, black dashed lines the exponentials detected by fitting the simulated distributions, and solid black lines the sum of the detected exponentials. For both Boliden 3 and Boliden 4, the four underlying exponentials are detected with minimal error (Table 2).

The next classic example of exponential sum-fitting examined was Evans GV from Table 2 of Watson (34). Evans GV tests the ability to detect an exponential of small area (0.004979) whose time constant is only threefold longer than that of the preceding exponential. The findings are in Fig. 3 and Table 3, where the three underlying exponentials were detected with negligible relative error in the estimated parameters (0.0059 ± 0.0042). The LLR for four versus three exponentials was ∼0, and for three versus two was 2123, giving the three highly significant exponentials (P ≪ 0.00001).

Figure 3.

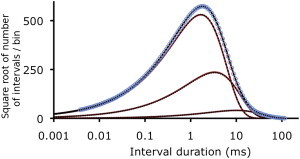
Automated fitting detects the exponentials underlying a simulated dwell-time distribution based on Evans GV in Table 2 in Watson (34). The time constants and areas of exponentials used to simulate the dwell-time distributions are in columns “τ” and “Nor. Area” in Table 3. Red lines plot the exponential components used for the simulation, blue open circles the simulated distributions, black dashed lines the exponentials detected by fitting the simulated distribution, and the solid black line the sum of the detected exponentials. The three underlying exponentials are detected with minimal error (Table 3).

Table 3.

Identifying the three exponentials in Evans GV

Magnitude	Rate (ms−1)	τ (ms)	Nor. Area	Fitted area	Area error	Fitted τ	τ error
0.100043	0.599936	1.66684	0.829566	0.831361	0.002164	1.67126	0.002649
0.009985	0.300123	3.33197	0.165508	0.163660	0.011163	3.32364	0.002499
0.000099	0.099965	10.0035	0.004927	0.004979	0.010615	9.93884	0.006464

Magnitudes and rate constants are from Table 2 in Watson (34). The time constant (τ) is given by 1/rate. Nor. area is the area of the three exponentials after normalizing to an area of 1.0. The relative error (Eq. 4) for the six estimated parameters was 0.0059 ± 0.0042 (mean ± SD). Estimates are based on 10⁷ simulated dwell times.

In the fourth classic example examined with the automated method, we simulated and fit a distribution of dwell times based on Eq. 4-23.17 used for the classic Lanczos example (7). It is the Lanczos example that has often been referred to when stating that it can be hopeless to estimate both magnitudes and time constants with exponential sum-fitting. The Lanczos example tests the ability to detect three exponentials when two are highly overlapping and the third has a smaller area and longer time constant (Fig. 4 and Table 4). When the entire time range of the simulated distribution was fit from ∼0.004 to 12.6 ms, the areas and time constants of the three exponentials in the Lanczos example were found with minimal relative error of 0.0022 ± 0.0008 (Fig. 4 and Table 4). The LLR for four versus three significant exponentials was ∼0 and for three versus two significant exponentials it was 1651, giving three highly significant exponentials (P ≪ 0.00001).

Figure 4.

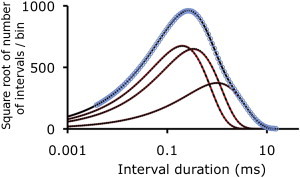
Automated fitting detects the exponentials underlying a simulated dwell-time distribution based on Eq. 4-12.17 in Lanczos (7). The time constants and areas of exponentials used to simulate the dwell-time distributions are in columns “τ” and “Nor. Area” in Table 4. Red lines plot the exponential components used for the simulation, blue open circles the simulated distribution, black dashed lines the exponentials detected by fitting the simulated distribution, and the solid black line the sum of the detected exponentials. The three underlying exponentials are detected with minimal error (Table 4).

Table 4.

Identifying the three exponentials from Lanczos

Magnitude	Rate (ms−1)	τ (ms)	Nor. Area	Fitted area	Area error	Fitted τ	τ error
1.5576	5	0.2	0.449187	0.449854	0.001485	0.200481	0.002405
0.8607	3	0.3333333	0.413687	0.412555	0.037820	0.332843	0.001471
0.0951	1	1	0.137126	0.137591	0.000937	0.998382	0.001618

Magnitudes and rate constants are from scheme 4-12.17 of Lanczos (7). The time constant (τ) is given by 1/rate. Nor. area is the area of the three exponentials after normalizing to an area of 1.0. The relative error (Eq. 4) for the six estimated parameters was 0.0022 ± 0.0008 (mean ± SD). Estimates are based on 3 × 10⁷ simulated dwell times.

If the simulated distribution for the Lanczos example was fit from ∼0.004 ms to shorter times of 3.6 and 2.1 ms rather than to 12.6 ms, then the three exponentials in the Lanczos function were still found, but with increased average relative errors of ∼0.02 and ∼0.46, respectively. Fitting the distribution to 1.15 ms found only two significant exponentials with large errors, just as in the classic Lanczos example where the data were fit to 1.15 ms. Hence, the Lanczos sum-fitting example as originally presented (7) is highly ill conditioned because of the lack of data at longer times needed to define the longer exponentials, not because all applications of exponential sum-fitting are ill conditioned.

Consistent with our findings and this conclusion, a fitting of the Lanczos example to 3.6 time units in a previous study using a rather different method also found the three exponentials (36), just as our automated analysis did.

Uses and limitations of exponential sum-fitting

Our automated fitting method found the eight exponentials summing to form the dwell-time distribution in Fig. 1. It also found the exponentials in additional large numbers of tests of simulated data (not presented), as well as the exponentials in distributions based on four different classic exponential-sum-fitting problems. Nevertheless, there are limits to the detection of exponentials. The limits are set by the number, relative areas, and relative time constants of the exponentials, the time range of the data compared to the time constants of the exponentials, the number of fit dwell times (Eq. 3), and the stochastic and experimental variation in the data, including experimental noise (7,8,19,26,34). Some of these limits were illustrated in the previous sections and in Fig. S2. Consequently, for complex gating mechanisms, or even for simple ones, and especially when the analysis is based on a thousand or even ten thousand intervals rather than hundreds of thousands, there are likely to be exponentials arising from the gating that are not detected in the dwell-time distributions. Why bother, then, with the fitting of significant exponential components to dwell-time distributions? 1), Exponential sum-fitting provides a quantitative method to describe dwell-time distributions to summarize experimental data for publication and for comparison to data obtained under different experimental conditions and from other studies. 2), Exponential sum-fitting can provide an estimate of the minimum number of states that contribute to the gating of the channel, with one state per exponential, although components and states are not necessarily directly related (16–18). The minimal number of states can serve as a starting point to develop gating mechanisms. 3), Alternatively, any viable proposed gating mechanism should generate at least as many exponential components as the number of significant exponentials determined with exponential sum-fitting. Whereas exponential sum-fitting is useful initially as a tool in kinetic analysis, further development of kinetic gating mechanisms from single-channel data typically involves global fitting of data obtained over a range of experimental conditions, including taking the correlation information in the data into account, to obtain sufficient information to define the models and parameters (10–13,15,21,32).

In conclusion, we have presented an automated method that can be used to detect all of the significant exponentials contributing to dwell-time distributions from single-channel data without the need to specify starting parameters.