Modeling Stochastic Kinetics of Molecular Machines at Multiple Levels: From Molecules to Modules

Abstract

A molecular machine is either a single macromolecule or a macromolecular complex. In spite of the striking superficial similarities between these natural nanomachines and their man-made macroscopic counterparts, there are crucial differences. Molecular machines in a living cell operate stochastically in an isothermal environment far from thermodynamic equilibrium. In this mini-review we present a catalog of the molecular machines and an inventory of the essential toolbox for theoretically modeling these machines. The tool kits include 1), nonequilibrium statistical-physics techniques for modeling machines and machine-driven processes; and 2), statistical-inference methods for reverse engineering a functional machine from the empirical data. The cell is often likened to a microfactory in which the machineries are organized in modular fashion; each module consists of strongly coupled multiple machines, but different modules interact weakly with each other. This microfactory has its own automated supply chain and delivery system. Buoyed by the success achieved in modeling individual molecular machines, we advocate integration of these models in the near future to develop models of functional modules. A system-level description of the cell from the perspective of molecular machinery (the mechanome) is likely to emerge from further integrations that we envisage here.

Introduction

Some of the greatest thinkers of all time, ranging from Aristotle to Descartes and Leibnitz, have been drawn by some of the striking analogies between a living organism and a man-made machine. However, the existence of molecular machines in living bodies was first speculated in the 17th century by Marcelo Malpighi (1). A molecular machine is either a single protein or a macromolecular complex (2–10). For its operation, a molecular machine needs an energy input. It has an engine that transduces energy. In this mini-review, we focus almost exclusively on specific types of molecular machines, called molecular motors, whose output is mechanical work (11–21).

The cytoskeletal motor proteins drive motility and contractility at the subcellular level. However, cell motility and morphogenesis, which are also driven by these motors, are beyond the scope of this mini-review. Many other specialized enzymes involved in the manipulation, synthesis, and degradation of macromolecules (e.g., proteins and nucleic acid strands) can also be regarded as molecular motors (4,22).

A cell has, at least superficially, similarities with a microfactory (5) in which most of the crucial intracellular functions require the coordination, cooperation, and competition of several machines that together form a functional module (23). The interactions between different modules are relatively weak, and the component machines of a single functional module need not be contiguous in space.

Theoretical models are not only useful for systematic analyses of the vast amounts of experimental data obtained at different levels of spatiotemporal resolution, they can also be used to predict new results and guide further experiments (24). In a recent review published elsewhere (21), I have presented a detailed overview of the results of multidisciplinary research on the kinetic models of molecular motors and motor-driven processes, as well as models of a few important modules. This mini-review is a nontechnical summary of that long review. Here I cite mostly books and review articles; interested readers can refer to Chowdhury (21) for technical details and a comprehensive bibliography.

Catalog of Molecular Machines and Fuels

Microtubules (MTs) and filamentous actin (F-actin) are the two types of cytoskeletal polar filaments that also serve as tracks for the cytoskeletal motor proteins (11). These motors, which are listed in Table 1, function as intracellular porters (25). These proteins carry intracellular cargoes (e.g., vesicles and organelles) over long distances by walking along their respective tracks (Fig. 1). The porters power their walk by hydrolyzing ATP, which is the most widely used fuel for molecular machines.

Table 1.

Examples of ATP-driven porters along with their corresponding tracks

Motor family (Ref.)	Ancestor	Track	Step size	Location and functions
Myosin-V and myosin-VI (73–75)	G-protein	F-actin	36 nm	melanophore transport
Kinesin-1 (76,77)	G-protein	MT	8 nm	transport in axons and fungal hyphae
Cytoplasmic dynein (77,78)	AAA+ proteins	MT	8 nm	transport in axons and flagella

The actual step size can be an integral multiple of the minimum value quoted in this table.

Figure 1.

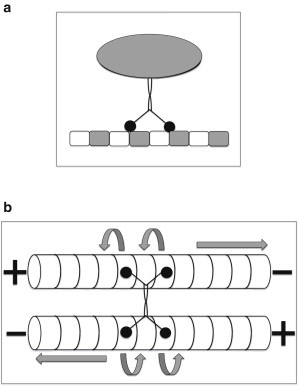
Schematic representation of (a) porters and (b) sliders. In panel a, a vesicular cargo (represented by the gray ellipse) is being hauled by a two-headed kinesin (with the two heads denoted by black circles) walking on an MT protofilament that consists of periodic repetition of $\alpha -\beta$ tubulin dimers. In b, the sliding of the two MTs, which are antiparallel to each other, takes place when the heads of a four-headed kinesin (say, Eg5) step toward the + ends of the respective MTs, as indicated by the curved arrows. The directions of the resulting movement of the MTs are indicated by the straight arrows.

In contrast, the motors listed in Table 2 slide one cytoskeletal polar filament with respect to another (15,20). The sliding occurs when a slider motor that cross-links the two filaments tends to walk on both simultaneously, hydrolyzing ATP (Fig. 1). Some sliders work in groups, and each group detaches from the filament after every single stroke. These are often referred to as rowers because of the obvious analogy to rowing, where the oars remain in contact with water for a very brief period during each stroke (25). Sliders and rowers drive contractility at cellular and subcellular levels.

Table 2.

Examples of rowers and sliders, and their locations and biological functions

Motor family (Ref.)	Filament	Location and function
Myosin-II (79)	F-actin	actomyosin cross-bridge, muscle contraction
	F-actin	stress fiber, contraction of nonmuscle cells
	F-actin	contractile ring, eukaryotic cell division
Kinesin-5, kinesin-14 (80)	MT	cross-linked MT, mitotic spindle size control
Axonemal dynein (81)	MT	axoneme, eukaryotic flagellar beating
Dynein (82)	MT	megakaryocytes, blood plateletformation

Some cytoskeletal motor proteins are neither porters nor rowers. Instead, they target MT tips and upon arrival start to depolymerize the MT itself. For obvious reasons, these are called depolymerases (26); their filament-chipping activities are also powered by ATP hydrolysis. Two families of these motors and their distinct characteristics are listed in Table 3.

Table 3.

Examples of MT depolymerase motors and their distinct features

Motor family (Ref.)	Target direction	Mode of reaching the target	Purpose of ATP hydrolysis
Kinesin-13 (26)	either end of MT	unbiased diffusion	only for depolymerization
Kinesin-8 (26)	only + end of MT	directed walking	for both walking and depolymerization

A polymerizing filamentous biopolymer can exert a pushing force against a light object (e.g., a membrane), thereby mimicking a nanopiston (6) (Fig. 2). Similarly, a depolymerizing MT can pull a light, ring-like object by inserting its hook-like, outwardly curled, depolymerizing tip into the ring (27) (Fig. 2). A few typical examples of such force generators are listed in Table 4.

Figure 2.

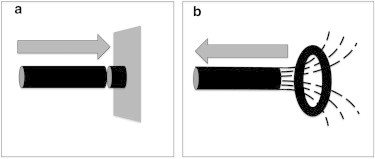
(a and b) Schematic representation of (a) a nanopiston and (b) a nanohook. In panel a, a polymerizing MT pushes a membrane (represented by the gray plane) in the direction indicated by the arrow. In b, the curved tips of a depolymerizing MT pull a ring in the direction indicated by the arrow.

Table 4.

Examples of nanopistons and nanohooks

Polymer (Ref.)	Mode of force generation	Function
MT (83)	polymerization	organizing cell interior
F-actin (6)	polymerization	cell motility
MT (27)	depolymerization	chromosome segregation

Some motors, while anchored on a fixed support, can import or export macromolecules across either the plasma membrane or, in the case of eukaryotes, the internal membranes of a cell. Packaging of the genome inside a prefabricated empty viral capsid is facilitated by packaging motors, located at the entrance of a viral capsid, that push the viral genome into the capsid (9). These movers and packers are among the strongest molecular motors discovered so far—the force generated can be as large as ∼60 pN. Helicases, which unwind double-stranded DNA, also share the defining characteristics of molecular motors (13). Topoisomerases are molecular machines that untangle DNA by passing one DNA strand through a transient cut in another (4).

Polynucleotides (DNA and RNA) and polypeptides (proteins) are linear polymers. The sequence of the monomeric subunits of each of these polymers is dictated by that of the corresponding template. A polymerizing machine selects the successive monomers, as directed by the corresponding template, and adds these step by step, thereby elongating the product polymer. Depending on the nature of the template and product polymers, specific machines for template-directed polymerization are used (10); these are listed in Table 5. Because the template also serves as the track for the polymerizing machine, and movement of the machine along the track is powered by input chemical energy, these machines are also regarded as motors (4,22) (Fig. 3).

Table 5.

Types of polymerizing machines, the templates that dictate the sequence of monomers of the polymeric products, and the corresponding function

Machine (Ref.)	Template	Product	Function
DNA-dependent DNA polymerase (84)	DNA	DNA	DNA replication
DNA-dependent RNA polymerase (85,86)	DNA	RNA	transcription
RNA-dependent DNA polymerase (87)	RNA	DNA	reverse transcription
RNA-dependent RNA polymerase (88)	RNA	RNA	RNA replication
Ribosome (89)	mRNA	protein	translation

Figure 3.

Schematic representation of template-directed polymerization of a DNA chain using another DNA strand as the template (i.e., DNA replication). Only a short stretch of the partially replicated template, excluding the site of initiation and termination of replication, is shown. Moreover, the strands are depicted as straight tapes, ignoring their actual conformations.

The cell also uses specialized machines for degradation of the polymers. The exosome and proteasome are nanocages into which RNA and proteins, respectively, are translocated and shredded into smaller fragments (28).

Two extensively studied rotary motors are ATP synthase (29) and the bacterial flagellar motor (30); the former synthesizes ATP from ADP, whereas the latter rotates the flagellum that propels swimming bacteria in bulk fluid medium (13). The ion-motive force (IMF) created by the concentration gradient of ionic charges across membranes drives most of these rotary motors, exploiting the spatial arrangement of some static charges and the trajectories of mobile charges (Figs. 4 and 5).

Figure 4.

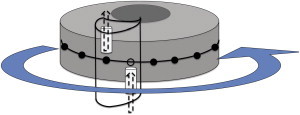
Schematic representation of the turnstile model of rotary motors. Upon entering from the bottom entrance, the mobile ions take a ride on the rotor. The electrostatic interactions among the charges on the stator and the rotor, as well as the rotational Brownian motion of the rotor, result in the noisy directed rotation of the rotor. Each hitchhiking ion disembarks from the rotor after being transported up to a certain distance by the rotor. Once the ion leaves, the rotor remains locked in its current position and waits for the arrival of the next ion. The F0 part of the ATP synthase exploits this mechanism (adapted from Chapter4 of Schliwa (13)).

Figure 5.

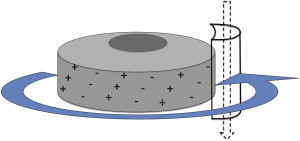
Schematic representation of the turbine model of rotary motors. The rotor is decorated with rows of charges that are tilted with respect to the stator. Protons are constrained to move straight, hopping from one binding site to the next in the stator. Thus, as the protons flow down the stator along their concentration gradient, their interactions with tilted rows of charges on the rotor rotate the rotor in a plane perpendicular to the stator. The flagellar motor of bacteria is believed to be a physical realization of this mechanism (adapted from Chapter4 of Schliwa (13)).

Some Fundamental Biophysical Questions about Molecular Machines

Operational mechanism of a single motor

Biophysical characteristic properties of a molecular machine

Directionality and processivity are two characteristic properties of a family of motors. Members of the same family move in the same direction on a polar filamentous track. Loosely speaking, the higher the processivity of a motor, the longer is the distance it covers in a single run in between its attachment to the track and its complete detachment from it. The average fraction of the cycle time in which each head remains attached to the track is called its duty ratio.

An external force that opposes the natural walk of a motor is called a load force. The average velocity of a motor decreases with increasing magnitude of the load force, eventually vanishing at a value that is called the stall force. The force-velocity relation is one of the most fundamental characteristics of a molecular motor. Two different motors with identical average velocities may exhibit widely different types of fluctuations. Therefore, one can obtain a more detailed characterization of the stochastic stepping kinetics of a motor by examining the distribution of its dwell times at successive spatial positions on its track.

Over the last two decades, it has become possible to account for the above-mentioned characteristic properties of a given family of motors in terms of the structure and dynamics of its members. Model building has been assisted by insights gained from experimental studies of these motors, and in the next three sections we discuss the theoretical and experimental approaches used in such studies.

Energy transduction: power stroke and Brownian ratchet

For a force-generating motor, efficiency and power output are good measures of its performance. In fact, efficiency at maximum power, rather than the maximum of the efficiency itself, is the main quantity of interest for all real motors whose cycle time is finite (31). However, in contrast to the unique definition of efficiency of transduction of macroscopic engines, several alternative definitions are possible in the case of nanomachines operating against a viscous drag of the surrounding aqueous medium. Different efficiencies characterize different aspects of energy transduction.

The power stroke of a molecular motor is bound to be noisy because of the Brownian forces acting on it. Interestingly, it is possible for a molecular motor to transduce energy by a different mechanism, called Brownian ratchet (32,33), that does not have any macroscopic counterpart. Suppose the motor suffers unbiased forward and backward displacements randomly because of the Brownian forces acting on it. If input energy is utilized to operate a device that prevents (or suppresses) backward movements without affecting the forward displacements, then, on average, the motor will move forward. The actual mechanism for a real molecular motor may be a combination of the two idealized extremes, namely, power stroke and Brownian ratchet.

The original actomyosin cross-bridge model of muscle contraction, proposed by Andrew Huxley, was later interpreted as a Brownian ratchet. Other well-known examples of (approximate) physical realizations of Brownian ratchet include the movement of single-headed kinesin KIF1A along the MT track in vitro, messenger RNA (mRNA) export from the nucleus, transcription by T7 RNA polymerase, translocation of ribosome during translation, and rotation of the F0-motor of mitochondria (see Chowdhury (21) for references and details of the original works).

Speed versus fidelity: quality-control mechanism

Not all molecular motors are primarily force generators. For example, for polymerases and ribosomes, the quality of performance is best characterized in terms of the accuracy of the template-directed polymerization that they carry out (10). Such motors have to optimize the opposing demands of speed and accuracy.

While selecting the monomeric subunits of the elongating polymer, if the machine were to discriminate between the correct and incorrect subunits based solely on the differences in the free energies of binding with the corresponding substrates, the error rates would be orders of magnitude higher than the observed values. Kinetic proofreading (34,35) is one of the kinetic mechanisms that amplify the achievable accuracy of template-directed polymerization. This process involves dissipation of energy, a typical example being the hydrolysis of one GTP molecule by a ribosome for selection of the amino acid substrate during translation.

The quality-control system of the machines for template-directed polymerization is not restricted only to the stage of subunit selection (10). Quality-control mechanisms have been captured in kinetic models of transcription, translation, and replication (21).

Coordination, cooperation, and competition among several motors

Cooperative phenomena involving multiple molecular motors are observed at several different spatiotemporal scales in an organism. A packaged cargo (e.g., a vesicle) is normally hauled by a team of motors. Often organelles exhibit bidirectional movements on a track. The fluctuation in the direction of the resultant force experienced by the cargo indicates the involvement of two teams of oppositely directed motors (e.g., kinesins and dyneins) and may be a manifestation of an ongoing tug-of-war between these two teams (36). Given the force-velocity relation of the individual motors, how would the average velocity of a cargo and the force required to stall it vary with the number of motors (37)? How do these results change with the decreasing processivity of the motors and increasing softness of the cargo (38)?

When many motors translocate simultaneously along the same track, their collective movement resembles vehicular traffic on a highway. The theoretically predicted possibility of a molecular motor traffic jam is being pursued experimentally. Although jamming of the cytoskeletal motors would have important implications for cargo transport, jamming of RNA polymerases and ribosomes would severely affect gene expression.

Several complex machineries in a living cell may be regarded as machines within a machine (39), typical examples being a replisome that replicates genomic DNA, and a mitotic spindle that segregates postreplication eukaryotic chromosomes (40). A replisome consists of a DNA-dependent DNA polymerase and a few other accessory machines. This is in contrast to genome-wide replication in eukaryotic cells, which requires the coordination of many replisomes that are spatially distributed instead of being segregated contiguously. A mitotic spindle self-organizes by integrating several different types of machines, which include porters, sliders, chippers, nanopistons and nanohooks, etc., within a single assembly (41).

Theoretical Modeling of Molecular Motors at Different Scales

In the following subsections, we mention a few alternative formalisms that model molecular motors and motor-driven processes at different levels of spatiotemporal resolution. We also explore the possible relations between them. Moreover, whenever possible, we mention a few alternative formalisms at the same level of spatiotemporal resolution and explain their relative advantages and disadvantages.

In general, to model molecular motors, one must make four key choices: 1), the choice of the degrees of freedom, or dynamical variables, consistent with the intended level of spatiotemporal resolution; 2), the choice of the form of the interactions between the variables; 3), the choice of which dynamical equations to use depending on the nature of the dynamical variables; and 4), the choice of which solution methods to use to calculate the quantities of interest under the given initial and/or boundary conditions. These choices are normally guided by the questions intended to be addressed by the model. Once these selections are made, the aim of the theoretical model might be merely to explain the fundamental principles underlying some generic phenomena exhibited by all (or at least a class of) motors at that level. However, it is equally (if not more) important to understand the reasons for the observed diversities among different motors in terms of the key structural and/or dynamical features of those motors. Examples of both types of models are discussed critically in my long review (21).

Fully atomistic and coarse-grained models

The relevant timescales for the kinetics of an entire molecular motor are too long to be accessed by a molecular-dynamics (MD) simulation of an atomistic model with the currently available computational resources. However, MD has been used successfully to study subprocesses of shorter durations. Moreover, normal-mode analysis (NMA) of a fully atomistic model, assisted by experimental insight, helps to elucidate the collective conformational dynamics of a molecular motor. Because of the macromolecular nature of the motors, NMA of atomistic models are usually very computer intensive.

For a coarse-grained description of a motor, a group of atoms is represented by a single bead, and the beads are assumed to interact with each other through appropriate effective potentials. For example, one can develop an elastic network model for a molecular motor by assigning a bead to each amino acid and postulating that these beads are connected by harmonic springs. The collective modes of the coarse-grained model can be obtained by carrying out an NMA (42). NMA results have been reported for coarse-grained models of myosin, dynein, and ATP synthase, among others (21).

However, in the absence of additional experimental information, it is very difficult to identify unambiguously which of the normal modes is functionally relevant for the given motor. Obviously, NMA is not suitable for studying dynamical processes that involve a low degree of collectivity. A coarse-grained approach cannot resolve important chemical details. For example, ATP binding, ATP hydrolysis, and release of ADP and P_i are captured indirectly by the making and breaking of elastic links and relaxation of elastic strain in the ATP-binding region of the coarse-grained model of the motor. Therefore, a MD simulation of a fully atomistic model of the ATP-binding site and its immediate surroundings, together with that of the ligands, would be more appropriate for elucidating the molecular mechanism of the ATPase activity of a motor.

Stochastic mechanochemical model: wandering on landscapes

In this section, we discuss an alternative approach that involves far fewer dynamical variables than the methods discussed above and is capable of capturing noncollective dynamical processes. The key mathematical concepts at the foundation of this formalism are summarized in Section A of the Supporting Material.

The conformations of a molecular motor are described by specifying the positions of all the constituent atoms in the three-dimensional space. Since a motor is either a protein or a macromolecular complex, it has a large number of degrees of freedom. In the coarse-grained description that we discuss in this subsection, only a few dynamical variables are treated explicitly; the remaining degrees of freedom of the motor as well as those of the aqueous medium are assumed to constitute a bath. The effects of the bath enter into the equations of motion of the motor via two terms that represent a viscous damping force and a random (Brownian) force.

For chemically driven mechanical movements of a motor, let us now divide the explicit dynamical variables into two classes: mechanical variables and chemical variables. For simplicity, let us discuss only a minimal version of such a model. This version has only one mechanical variable, x, which denotes the position of the center of mass of the motor along its track, and a single chemical variable, ξ, which accounts for the progress of the chemical reaction that supplies the chemical input energy to the motor. The free energy, $U\left(x,\xi \right)$, which is also called the potential of mean force, can be graphically represented as a landscape (Fig. 6), where the height of the landscape at any point with coordinates $x,\xi$ represents the corresponding potential $U\left(x,\xi \right)$.

Figure 6.

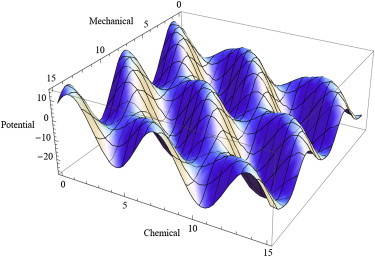
Schematic representation of a landscape where the height represents the potential of mean force (free energy) of a hypothetical molecular motor that is described by a single mechanical variable and a single chemical variable (adapted from Keller and Bustamante (43); courtesy Ajeet K. Sharma).

If the motor-binding sites on the track form a periodic array, a cross-section of the landscape parallel to x (i.e., for ξ = constant) must also be periodic; all the local minima, which coincide with the location of the motor-binding sites on the track, are equally deep (Fig. 7 a). However, within each period it is, in general, not symmetric about the location of the maximum. In contrast, a cross-section of this landscape parallel to ξ (i.e., for x = constant), which also consists of local minima separated by potential barriers, is tilted forward (Fig. 7 b) so that the bottom of the successive minima is deeper by $\left|\text{Δ}G\right|$, which accounts for the lowering of free energy caused, for example, by ATP hydrolysis.

Figure 7.

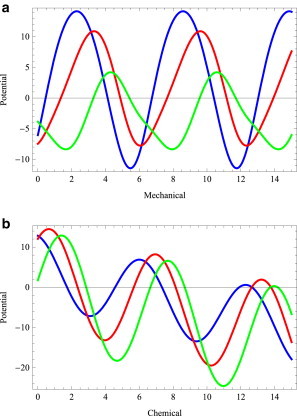
(a and b) Cross sections of the landscape shown in Fig. 6 parallel to (a) the mechanical coordinate (i.e., for a constant value of the chemical variable) and (b) the chemical variable (i.e., for a constant value of the mechanical variable; courtesy Ajeet K. Sharma).

The kinetics of the motor is mathematically described by the Brownian motion of a particle in this time-independent potential landscape. A coupling between the mechanical and chemical cycles in this space gives rise to a chemically driven mechanical motor. This formulation is useful for an intuitive physical explanation of the coupled mechanochemical kinetics of molecular motors (43).

Next, let us consider those special situations in which the chemical states of the motor change in discrete jumps from one long-lived state to another. We label the chemical states by the integer index μ $\left(1\le \mu \le m\right)$. As an example, m = 4 may be assigned to a motor powered by ATP hydrolysis to denote the following four distinct chemical states: 1), ligand free; 2), ATP bound; 3), ADP-P_i bound; and 4), ADP bound. During the period in which the motor dwells in the chemical state ν, its mechanical variable x can continue to change as dictated by the corresponding time-independent potential $U_{\nu }\left(x\right)$. The transition from one chemical state to another is so rapid that during such a transition, the mechanical variables remain frozen. No mixed mechanochemical transition takes place in such special situations because of the clear separation of the timescales of variation of the mechanical and chemical variables. A purely chemical transition $\nu \to \lambda$ causes the corresponding change $U_{\nu }\left(x\right)\to U_{\lambda }\left(x\right)$ of the potential profile. A sequence of chemical transitions is accompanied by the corresponding sequential change of the potential profile $U_{\mu }\left(x\right)$. The kinetics of the center of mass of the motor is described by the Brownian motion of a particle in the time-dependent potential $U_{\mu }\left(x\right)$, where μ varies with time by discrete jumps.

Mechanochemical models based on explicit interactions among the constituent parts of a motor have been developed to elucidate the mechanisms of myosin-V, myosin-VI, and dynein (21). The number of mechanical variables and their nature depends on the molecular motor under consideration. For example, an angle, rather than position, is the appropriate mechanical variable in the mechanochemical models of rotary motors such as F1-ATPase. Similarly, while developing models for myosin-V and myosin-VI, Lan and Sun (44) used two angular variables that were defined with respect to the monomer body axis and the F-actin plane.

For a track like MT, in the absence of any MT-associated protein, the potential $U_{\mu }\left(x\right)$ is periodic, but because of the intrinsic asymmetry of the $\alpha -\beta$-tubulin heterodimer, each period of this potential is expected to be spatially asymmetric. Interestingly, on average, a temporal sequence of such a periodic asymmetric potential can lead to directed movement of the motor, albeit noisily, in spite of the vanishing of spatially averaged force (32). This is one of the possible mechanisms of a Brownian ratchet. Rectification of the noise required for the Brownian ratchet mechanism can also be achieved, for example, by the binding of a ligand that stabilizes conformations in the forward direction (33).

Markov model: motor kinetics as a jump process on a network of fully discrete mechanochemical states

In this subsection we further simplify the continuum landscape-based scenario developed above to formulate a fully discrete scheme (45,46). The main equations of these formalisms are summarized in Section B of the Supporting Material.

Suppose $\mathcal{P}\left(Y\right)\text{Δ}Y$ is the probability of finding the system between Y and $Y+\text{Δ}Y$ on the continuous landscape. Now, with each local minimum of the free-energy landscape we associate a discrete state. The probability $P_i$ of finding the system in the i-th discrete state is obtained by integrating the probability $\mathcal{P}\left(Y\right)$ over the i-th zone, which is the immediate surroundings of the local minimum labeled by the discrete index i. Just like the continuum formulation, the minimal model must have one mechanical variable and a chemical variable, both of which are discrete.

Let $P_{\mu }\left(i,t\right)$ be the probability of finding the motor at the discrete position labeled by i and in the chemical state μ at time t. The time evolution of the system is described as discrete jumps on the network of the discrete states governed by the master equations for $P_{\mu }\left(i,t\right)$ (which are also referred to as stochastic rate equations).

The local minima in the free-energy landscape are separated by low-energy passes, such that thermal fluctuations occasionally cause the system to leave the neighborhood of one local minimum and arrive at that of a neighboring one. Such wanderings on the free-energy landscape are identified as transitions from one discrete state to another in the fully discrete formulation. The corresponding rate constants (i.e., the probabilities of transition per unit time) can also be obtained from an analysis of the probability fluxes on the continuous landscape (43,44). Obviously, the rate constants depend on the shape of the free-energy landscape; the dependence of the rate constants on the external force arise from that of the landscape shape on the external force. The discrete state space of this formulation can be regarded as a network. The mathematical properties of such networks are closely related to the formal properties of electrical networks pioneered by Kirchoff and others.

Markov modeling has been exploited successfully for many motors, including myosin-V, kinesin-1, KIF1A, RNA polymerase, DNA polymerase, and ribosome (21). One distinct advantage of this approach is that often one can solve the master equations to derive the main results analytically. However, in contrast to the landscape-based scenario, forces between different parts of the motor do not appear explicitly through any interaction potential. Consequently, the Markov models of motors are the most suitable for interpreting a wide range of empirical data without having to obtain the explicit form of the potentials of interactions among the constituent parts or those among the motor, ligand, and track.

Inverse Problem: From Data to Model by Probabilistic Reverse Engineering

So far in this mini-review, we have discussed the forward problem of modeling machine-driven kinetic processes. The forward problem is solved by starting with an a priori hypothesis (essentially, an educated guess) about the mechanochemical kinetics of the motor. An analytical or numerical approach (or a combination thereof) yields data that can be compared with the empirical data. In contrast, the inverse problem is to infer the model from the empirical data; this task is reminiscent of reverse engineering.

The likelihood $\mathcal{P}$ of a state trajectory is the conditional probability for this trajectory, given the rate constants for the interstate transitions. There are two alternative approaches for estimating the rate constants from the likelihood. Here we discuss these methods without mathematical equations. The main steps of these formalisms are summarized in Section C of the Supporting Material.

The maximum-likelihood (ML) approach is based on estimating the set of rate constants that maximizes the likelihood $\mathcal{P}$. In other words, the estimated rate constants are their most probable values.

In the Bayesian approach, both the rate constants and empirical data are treated on an equal footing, i.e., both are regarded as random variables. Starting from an assumed a priori distribution of the rate constants (called the prior, for obvious reasons), one estimates the a posteriori probability distribution of the rate constants by utilizing the distribution of the observed data. The choice of the prior can be based on physical intuition or general arguments based, for example, on symmetries. The choice of the prior can be simple if some experience has been gained from previous measurements. Often a uniform distribution of the model parameter(s) can be assumed over its allowed range if no additional information is available to bias its choice.

For both the frequentist and Bayesian approaches outlined above, the state trajectories are required. However, in practice, the actual sequence of states of the motor, generated by the underlying Markovian kinetics, is not directly available for analysis. For example, the distinct chemical states that correspond to the same mechanical state cannot be distinguished in a purely mechanical measurement on a single motor. The hidden Markov model is a powerful tool for extracting information about hidden trajectories from the trajectories that are visible in single-molecule experiments.

Most often, one can infer multiple models, all at the same level of spatiotemporal resolution, from a statistical analysis of the same set of data. Therefore, it would be desirable to follow Platt’s (47) principle of strong inference (which is an extension of Chamberlin’s (48) method of multiple working hypotheses). According to this principle, the level of success of a model can be quantified by a numerical score. The relative scores of the competing models (and the corresponding underlying hypotheses) would be a true reflection of their merits. Very few attempts have been made so far to rank the models of molecular motors inferred from the data according to their relative scores (21).

Experimental Studies of Molecular Machines

The main emphasis of this mini-review is on theoretical modeling of molecular machines. Nevertheless, the current rapid progress in theory has been stimulated by experimental observations, many of which were made possible by the invention of novel techniques coupled with precision technology. In this section, we present a micro-review of some of these techniques and their use for studying molecular machines.

X-ray crystallography, NMR, and electron microscopy (EM) (49) are the standard techniques for experimentally determining the structures of macromolecular systems, including molecular machines. However, the main hurdle in x-ray crystallography is the difficulty of achieving crystallization. Similarly, structure determination by NMR becomes very difficult for most molecular machines because these machines are usually large macromolecular complexes. Therefore, for many of the molecular machines for which x-ray crystallography has not been possible, high-resolution atomic structures of some of their important subunits have been obtained separately by x-ray crystallography. In more recent times, a combination of these techniques, particularly EM of the full machine and x-ray structures of component subunits, have been found to be more powerful than any of the individual techniques (50).

The results obtained by the above-mentioned techniques are averaged over an ensemble of machines. Similarly, rate constants for various chemical reactions involved in the operation of a molecular machine are averaged over an ensemble when extracted from the bulk sample. In contrast, single-molecule techniques developed in recent years avoid averaging over an ensemble (19,22,51–53). Some fluorescence-based, single-molecule imaging techniques (54) enable one to monitor the movement of the motor or relative motion between different parts of the motor. In some other single-molecule experiments, the motor is manipulated by application of an external force or torque; optical tweezers (52,55) and magnetic tweezers (56–58) are the most commonly used devices for this purpose.

Single-molecule studies (51,52) have provided deep insights into the mechanochemical kinetics of almost all types of molecular machines (59), including cytoskeletal motors (19), as well as machines for genomic processes (22,60), such as helicase motors (45) and machines for template-directed polymerization (e.g., RNA polymerases (46,61), replisomes (62,63), and ribosomes (64–66)). Single-molecule techniques have also been used to study machines for packaging of genome into viral capsids (67).

For a given motor, the data from single-molecule experiments can also be used to obtain the dwell-time distribution (DTD). The DTD can be utilized to extract a lower bound on the number of kinetic states (68). The DTD is essentially a distribution of first-passage times (69), an interesting concept in nonequilibrium statistical mechanics. The theoretically calculated DTDs for several motors are consistent with the corresponding experimental data (21).

Conclusions and Outlook

Over the last two decades, investigators have been able to produce a parts list of many motors by performing careful experiments (18), and consequently have developed models of single motors, at various levels of spatiotemporal resolution, by assembling those parts. However, dynamical studies of fully atomistic models of even single motors remain constrained by the current computational resources. I have sketched several alternative strategies for modeling molecular machines depending on the questions to be addressed and the level of spatiotemporal organization. Because of space limitations, I have not discussed any individual examples in this mini-review; interested readers are referred to my recent detailed review published elsewhere (21).

The catalog of the machines presented here can be divided into two parts: 1), machines for motility and contractility (e.g., exporters and importers, packers and porters, sliders and rowers); and 2), machines for genomic processes (e.g., unwrappers, unzippers, and untanglers, and synthesizers and degraders of DNA, RNA, and proteins; Fig. 8). The operation of both groups of machines is regulated by signaling and metabolic machineries (Fig. 8), which I have not discussed here or in the longer review (21). However, one can incorporate the switching on and off of a machine, as well as the supply of fuel and raw materials for its operation, within the model of its operation by linking it with signaling and metabolic machineries.

Figure 8.

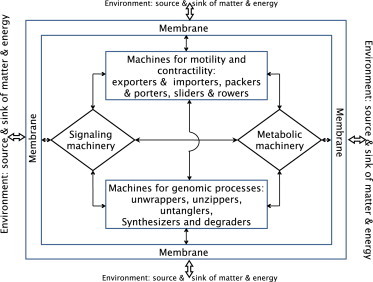
Interactions of the different types of machines with each other and with the signaling and metabolic machineries are indicated schematically by the two-headed arrows. The exchange of matter and energy between the cellular machineries and the cell exterior across the cell membrane is also indicated by two-headed double arrows.

When modeling the full operation of a module, one should incorporate all three stages of dynamic assembly: 1), assembly of the component devices at the right place and the right time; 2), the successive steps of its main operation; and 3), disassembly, if it occurs, after completion of its operation. Over the next decade, we can expect to see major efforts to integrate coarse-grained models of motors into dynamic modules. Next, further integration of weakly interacting dynamic modules is likely to pave the way for what may be called a system-level description (the mechanome (70)) of an entire cell, at least in the interphase, as a microfactory (5). Finally, modeling cellular homeostasis in molecular detail will require integration of the multimodule model of the cell interior with the external stressors at the exterior-interior interface (71) (Fig. 8). The cell is the functional unit of life. Therefore, this dream project, if it is ever completed even for a minimal synthetic cell (72), will take biophysicists closer to answering the eternal question: what is life?