Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2013 May 15;52(11):6260–6272. doi: 10.1021/ic4004824

Mechanism Elucidation of the cis–trans Isomerization of an Azole Ruthenium–Nitrosyl Complex and Its Osmium Counterpart

Anatolie Gavriluta †,‡, Gabriel E Büchel †,‡, Leon Freitag §, Ghenadie Novitchi †,∥,*, Jean Bernard Tommasino †, Erwann Jeanneau †, Paul-Steffen Kuhn ‡, Leticia González §,*, Vladimir B Arion ‡,*, Dominique Luneau †,*
PMCID: PMC3673021  PMID: 23675748

Abstract

graphic file with name ic-2013-004824_0013.jpg

Synthesis and X-ray diffraction structures of cis and trans isomers of ruthenium and osmium metal complexes of general formulas (nBu4N)[cis-MCl4(NO)(Hind)], where M = Ru (1) and Os (3), and (nBu4N)[trans-MCl4(NO)(Hind)], where M = Ru (2) and Os (4) and Hind = 1H-indazole are reported. Interconversion between cis and trans isomers at high temperatures (80–130 °C) has been observed and studied by NMR spectroscopy. Kinetic data indicate that isomerizations correspond to reversible first order reactions. The rates of isomerization reactions even at 110 °C are very low with rate constants of 10–5 s–1 and 10–6 s–1 for ruthenium and osmium complexes, respectively, and the estimated rate constants of isomerization at room temperature are of ca. 10–10 s–1. The activation parameters, which have been obtained from fitting the reaction rates at different temperatures to the Eyring equation for ruthenium [ΔHcis-trans‡= 122.8 ± 1.3; ΔHtrans-cis= 138.8 ± 1.0 kJ/mol; ΔScis-trans‡= −18.7 ± 3.6; ΔStrans-cis= 31.8 ± 2.7 J/(mol·K)] and osmium [ΔHcis-trans‡= 200.7 ± 0.7; ΔHtrans-cis= 168.2 ± 0.6 kJ/mol; ΔScis-trans‡= 142.7 ± 8.9; ΔStrans-cis= 85.9 ± 3.9 J/(mol·K)] reflect the inertness of these systems. The entropy of activation for the osmium complexes is highly positive and suggests the dissociative mechanism of isomerization. In the case of ruthenium, the activation entropy for the cis to trans isomerization is negative [−18.6 J/(mol·K)], while being positive [31.0 J/(mol·K)] for the trans to cis conversion. The thermodynamic parameters for cis to trans isomerization of [RuCl4(NO)(Hind)]−, viz. ΔH° = 13.5 ± 1.5 kJ/mol and ΔS° = −5.2 ± 3.4 J/(mol·K) indicate the low difference between the energies of cis and trans isomers. The theoretical calculation has been carried out on isomerization of ruthenium complexes with DFT methods. The dissociative, associative, and intramolecular twist isomerization mechanisms have been considered. The value for the activation energy found for the dissociative mechanism is in good agreement with experimental activation enthalpy. Electrochemical investigation provides further evidence for higher reactivity of ruthenium complexes compared to that of osmium counterparts and shows that intramolecular electron transfer reactions do not affect the isomerization process. A dissociative mechanism of cis↔trans isomerization has been proposed for both ruthenium and osmium complexes.

Short abstract

The cis and trans isomers of ruthenium and osmium nitrosyl complexes with general formulas (nBu4N)[MCl4(NO)(Hind)] (M = Ru or Os) have been synthesized and their crystal structures determined. NMR spectroscopy shows that the cis and trans complexes are stable in DMSO and C2D2Cl4 solutions at room temperature, and cis/trans isomerization occurs at high temperatures (80−100 °C) and follows a reversible first order process with a dissociative mechanism as supported by electrochemical and theoretical calculations investigations.

Introduction

Metal–nitrosyl complexes have attracted considerable attention because of their electron-transfer properties,1−6 light-induced linkage isomerism,7 and catalytic activities in organic synthesis.8,9 They are also among the essentials in teaching coordination chemistry. It is the noninnocent nitrosyl molecule (NO) that mainly causes their interesting properties. It is also what makes it often difficult to assign an oxidation number to the metal center, so the electronic structure of the {M(NO)} moiety remains a field of current interest.10−15 The relatively strong binding of the nitrosyl ligand to transition metal ions enables many substitution reactions on the metal centers. Along this, the strong trans effect of the nitrosyl ligand plays an important role in the chemical reactivity, electronic structure, and stereochemistry of the initial and final complexes.16,17 It follows a great versatility of the complexes. They have long been limited to transition metal ions,15,16,18 but have recently crossed the f-element border with the report of an actinide complex.19

Metal-nitrosyl complexes are not only interesting for their physical and chemical properties. They have also been increasingly investigated for biomedical applications as suppliers or scavengers of NO18,20−22 since being recognized as biologically relevant.23 In this regard, a very well documented example of a coordination compound containing NO in clinical use is sodium nitroprusside (Na2[Fe(CN)5(NO)]), which has been amply studied for its photochemical properties24 and is now the strongest available vasodilator.22,25

Metal–nitrosyl complexes, particularly those of the platinum group, are of interest to us as potential anticancer agents that may kill the cancer cells by releasing a cocktail of NO and metal complex.26 In the field of anticancer metal drugs, it is well-known that the reactivity and biological properties can vary significantly with the isomeric compounds. The classical example of contrasting biological activity is cisplatin, which is the first clinically used metal-based anticancer agent, whereas its trans isomer shows no biological activity.27,28 Two other platinum(II) complexes in clinical use today, namely cis-diamine(cyclobutane-1,1-dicarboxylato-O,O′)platinum(II) (carboplatin) and (1R,2R)-diaminocyclohexane-oxalatoplatinum(II) (oxaliplatin), are also cis-configured complexes. It follows that the cis geometry was for a long time considered as a prerequisite for anticancer activity,29,30 and therefore, the trans-configured complexes have attracted little attention of researchers. The situation has changed, however, in recent years after several classes of trans-configured complexes have been reported to exhibit higher cytotoxicity than the corresponding cis isomers31 with some of them exhibiting antitumor activity in vivo, with a lack of cross-resistance to cisplatin.32 Cellular accumulation experiments have shown that accumulation in the SW480 cells of trans-configured platinum(II) complexes with acetone oxime and 3-pentanone oxime was up to 50 times higher than that of platinum(II) complexes and resulted in pronounced DNA strand cleavage for trans complexes, and a lack of DNA degradation for cis complexes.33 All of these examples are concerned with square-planar platinum complexes. In the case of octahedral ruthenium and osmium complexes, the exploration of such structure–activity relationships is hindered by the low number of available compounds, although some rare examples of well-documented isomers have been reported in the literature.34−37 In particular, the antiproliferative activity of (H2trz)[trans-RuCl4(Htrz)2], where Htrz = 1H-1,2,4-triazole, was found higher than that of the corresponding cis isomer in human cancer cell lines SW480 (colon carcinoma), HT29 (colon carcinoma), and SK-BR-3 (mammary carcinoma). These examples show the crucial need in the field of antiproliferative complexes, as for any pharmaceutics, to control the stereochemistry and to know about the interconversion processes in between the isomeric forms. This goes well beyond the scope of metallopharmaceutics, given that stereochemistry studies are the basis of coordination chemistry.

With this in mind and as a tribute to Alfred Werner Nobel prize celebrations, we report herein on the synthesis, structure, and spectroscopic and electrochemical properties of the trans and cis isomers of the ruthenium– and osmium–nitrosyl complexes of the general formula (n-Bu4N)[MCl4(NO)(Hind)] where M = Ru or Os and Hind = 1H-indazole (Scheme 1). This is completed by in depth studies of their relative thermodynamic stabilities and of the trans ↔ cis isomerization mechanism that has been investigated experimentally by NMR and theoretically by DFT calculations in a complementary way.

Scheme 1. Compounds Reported in This Work.

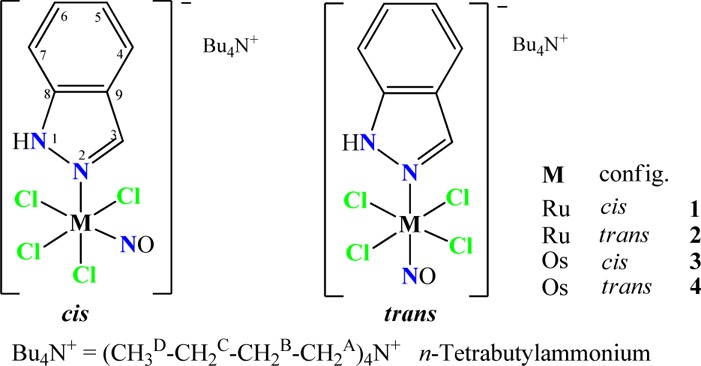
Scheme 1

Open in a new tab

Atom labeling was introduced for assignment of resonances in NMR spectra.

Experimental Section

Starting Materials

Na2[RuCl5(NO)]·6H2O was synthesized as previously reported in the literature.38 (H2ind)2[RuCl5(NO)] (Hind = 1H-indazole) was prepared by heating the sodium salt with indazole in a 1:2 molar ratio in 6 M HCl. The starting compound (n-Bu4N)2[OsCl5(NO)] was synthesized as previously reported in the literature.39 OsO4 (99.8%) was purchased from Johnson Matthey. NH2OH·HCl, K2C2O4·H2O, and indazole were from Aldrich.

(H2ind)[cis-RuCl4(NO)(Hind)] and (H2ind)[trans-RuCl4(NO)(Hind)]

A suspension of (H2ind)2[RuCl5(NO)] (230 mg, 0.36 mmol) in 1-propanol (8 mL) was heated at 75 °C for 6 h. The solvent was removed in vacuo, and the residue was extracted with chloroform. Fractioned crystallization afforded pink crystals of the trans isomer (first fraction), which was filtered off, washed with diethyl ether, and dried in vacuo. Yield: 47 mg, 21%. The second fraction crystallized as a cis isomer was filtered off, washed with diethyl ether, and dried in vacuo. Yield: 79 mg, 36%. Analytical data for cis isomer: Anal. Calcd for C14H13RuCl4N5O·0.25 CHCl3 (Mr = 540.01 g/mol): C, 31.69; H, 2.47; N, 12.96. Found: C, 31.64; H, 2.57; N, 13.28. ESI-MS in MeOH (negative): m/z 243 [RuCl4]−, 273 [RuCl4(NO)]−, 391 [RuCl4(NO)(Hind)]−. ESI-MS in MeOH (positive): m/z 119 (H2ind)+. MIR, ν, cm–1: 614, 649, 840, 925, 965, 999, 1091, 1125, 1150, 1175, 1214, 1237, 1278, 1358, 1379, 1435, 1475, 1513, 1582, 1629 (C=N), 1854 (NO), 2993, 3127 (NH), 3308. UV–vis (CH3CN), λmax, nm (ε, M–1 cm–1): 258 (21 517), 294 sh (15 948), 373 sh (154), 453 (68), 539 sh (46). 1H NMR (DMSO-d6, 500.32 MHz), δ, ppm: 7.10 (t, 1H5′, J = 7.01 Hz), 7.24 (t, 1H5, J = 7.21 Hz), 7.34 (t, 1H6′, J = 7.30 Hz), 7.49 (t, 1H6, J = 7.16 Hz), 7.52 (d, 1H7′, J = 7.45 Hz), 7.77 (d, 2H4′/7, J = 9.61 Hz), 7.90 (d, 1H4, J = 8.15 Hz), 8.06 (s, 1H3′), 8.62 (s, 1H3), 13.28 (s, 1H1). 13C{1H} NMR (DMSO-d6, 125.77 MHz), δ, ppm: 110.54 (C7′), 111.62 (C5′), 120.64 (C4′/7), 120.94 (C4′/7), 121.50 (C4), 121.92 (C9), 122.33 (C5), 123.24 (C9′’), 126.35 (C6′’), 129.07 (C6), 133.78 (C3′), 137.80 (C3), 140.10 (C8), 141.04 (C8′). 15N NMR (DMSO-d6, 50.68 MHz), δ, ppm: 163.44 (N1). Suitable crystals for the X-ray diffraction study were grown by slow evaporation of a solution of the cis isomer in chloroform. Analytical data for the trans isomer: Anal. Calcd for C14H13RuCl4N5O·CHCl3 (Mr = 629.54 g/mol): C, 28.62; H, 2.24; N, 11.12. Found: C, 28.83; H, 2.05; N, 10.97. ESI-MS in MeOH (negative): m/z 243 [RuCl4]−, 273 [RuCl4(NO)]−, 391 [RuCl4(NO)(Hind)]−. ESI-MS in MeOH (positive): m/z 119 (H2ind)+. MIR, ν, cm–1: 588, 615, 657, 731, 739, 861, 899, 962, 999, 1091, 1121, 1148, 1228, 1270, 1298, 1358, 1449, 1471, 1511, 1582, 1635 (C=N), 1891 (NO), 2995, 3158, 3232 (NH), 3317. UV–vis (CH3CN), λmax, nm (ε, M–1 cm–1): 260 (21 883), 283 sh (16 175), 383 sh (99), 504 (36), 597 (19). 1H NMR (DMSO-d6, 500.32 MHz), δ, ppm: 7.10 (t, 1H5′, J = 7.11 Hz), 7.22 (t, 1H5, J = 7.21 Hz), 7.34 (t, 1H6′, J = 7.23 Hz), 7.51 (t, 1H6, J = 7.34 Hz), 7.54 (d, 1H7′, J = 7.35 Hz), 7.76 (d, 1H4′, J = 7.76 Hz), 7.79 (d, 1H7, J = 7.75 Hz), 7.90 (d, 1H4, J = 8.25 Hz), 8.07 (s, 1H3′), 8.63 (s, 1H3), 12.95 (s, 1H1). 13C{1H} NMR (DMSO-d6, 125.77 MHz), δ, ppm: 110.54 (C7′), 112.13 (C7), 120.64 (C5′), 120.94 (C4′), 121.01 (C9), 121.94 (C4), 122.36 (C5), 123.23 (C9′), 126.36 (C6′), 129.40 (C6), 133.78 (C3′), 138.21 (C3), 140.14 (C8), 140.33 (C8′). 15N NMR (DMSO-d6, 50.68 MHz), δ, ppm: 161.97 (N1). Suitable crystals for the X-ray diffraction study were grown by slow evaporation of a solution of the trans isomer in chloroform.

(Bu4N)[cis-RuCl4(NO)(Hind)] (1)

To a solution of (H2ind)[cis-RuCl4(NO)(Hind)] (43 mg, 0.08 mmol) in 20 mL of water n-Bu4NCl was added (30 mg, 0.1 mmol). The solution becomes immediately cloudy and product 1 precipitates after several minutes. The pale pink precipitate was filtered off washed with diethyl ether (2 × 10 mL) and dried in vacuo. Yield: 33 mg, 61%. Anal. Calcd for C23H42Cl4N4ORu (Mr = 633.49 g/mol): C, 43.61; H, 6.68; N, 8.84. Found: C, 43.67; H, 6.50; N, 8.78. ESI-MS in MeOH (negative): m/z 391 [RuCl4(NO)(Hind)]−. ESI-MS in MeOH (positive): m/z 242 Bu4N+. IR, ν, cm–1: 658, 677, 729, 764, 782, 848, 869, 963, 1091, 1114, 1241, 1358, 1381, 1442, 1476, 1508, 1623, 1846 (NO), 2873, 2959, 3250. 1H NMR (DMSO-d6, 500.32 MHz), δ, ppm: 0.95 (t, 12HD, J = 7.2 Hz), 1.32 (sxt, 8HC, J = 7.2 Hz), 1.57 (qui, 8HB, J = 7.8 Hz), 3.17 (t, 8HA, J = 7.7 Hz), 7.23 (t, 1H5, J = 7.21 Hz), 7.49 (t, 1H6, J = 7.16 Hz), 7.77 (d, 1H4/7, J = 9.61 Hz), 7.89 (d, 1H4, J = 8.15 Hz), 8.62 (s, 1H3), 13.28 (s, 1H1). Suitable crystals for X-ray diffraction study were grown by slow evaporation of the mother liquor.

(Bu4N)[trans-RuCl4(NO)(Hind)] (2)

To a solution of (H2ind)[trans-RuCl4(NO)(Hind)] (40 mg, 0.08 mmol) in 20 mL of water n-Bu4NCl was added (30 mg, 0.1 mmol). The solution becomes immediately cloudy and product 2 precipitates after several minutes. The pale pink precipitate was filtered off washed with diethyl ether (2 × 10 mL) and dried in vacuo. Yield: 34 mg, 68%. Anal. Calcd for C23H42Cl4N4ORu (Mr = 633.49 g/mol): C, 43.61; H, 6.68; N, 8.84. Found: C, 43.53; H, 6.54; N, 8.74. IR, ν, cm–1: 591, 659, 737, 747, 757, 784, 833, 879, 965, 1002, 1097, 1238, 1282, 1360, 1378, 1459, 1476, 1514, 1629, 1875 (NO), 2872, 2960, 3302. ESI-MS in MeOH (negative): m/z 391 [RuCl4(NO)(Hind)]−. ESI-MS in MeOH (positive): m/z 242 Bu4N+. 1H NMR (DMSO-d6, 500.32 MHz), δ, ppm: 0.95 (t, 12HD, J = 7.2 Hz), 1.32 (sxt, 8HC, J = 7.2 Hz), 1.57 (qui, 8HB, J = 7.8 Hz), 3.17 (t, 8HA, J = 7.7 Hz), 7.23 (t, 1H5/6, J = 7.2 Hz), 7.51 (t, 1H5/6, J = 7.6 Hz), 7.78 (d, 1H4/7, J = 8.8 Hz), 7.92 (d, 1H4/7, J = 8.3 Hz), 8.68 (s, 1H3), 12.96 (s, 1H1). Suitable crystals for X-ray diffraction study were grown by slow evaporation of the mother liquor.

(Bu4N)[cis-OsCl4(NO)(Hind)] (3) and (Bu4N)[trans-OsCl4(NO)(Hind)] (4)

A mixture of indazole (100 mg, 0.85 mmol) and (n-Bu4N)2[OsCl5(NO)] (500 mg, 0.56 mmol) in n-butanol (10 mL) was heated at 105 °C for 24 h. The solution was allowed to stand in an open beaker, and after 2 days the red crystals of the cis isomer were filtered off, washed with 1:2 water/ethanol (3 × 10 mL) and diethyl ether (3 × 5 mL), and dried in vacuo. Yield: 210 mg, 52%. The volume of the filtrate was reduced to one-third, and slow diffusion of diethyl ether afforded the formation of blue crystals of the trans isomer. These were filtered off, washed with 1:2 water/ethanol (3 × 3 mL) and diethyl ether (3 × 1 mL), and dried in vacuo. Yield: 101 mg, 25%.

Analytical Data for 3

Anal. Calcd for C23H42OsCl4N4O (Mr = 722.65 g/mol): C, 38.23; H, 5.86; N, 7.75. Found: C, 38.48; H, 5.66; N, 7.62. ESI-MS in CH3CN (negative): m/z 332 [OsCl4]−, 362 [OsCl4(NO)]−, 480 [OsCl4(NO)(Hind)]−. IR, ν, cm–1: 437, 657, 761, 846, 878, 967, 1004, 1091, 1153, 1240, 1279, 1359, 1380, 1476, 1625, 1805 (NO), 2873, 2960, 3258. UV–vis (CH3CN), λmax, nm (ε, M–1 cm–1): 248 (11 573), 393 (sh, 6178), 511 (921). 1H NMR (DMSO-d6, 500.13 MHz), δ, ppm: 0.93 (t, 12HD, J = 7.3 Hz), 1.31 (sxt, 8HC, J = 7.3 Hz,), 1.57 (qui, 8HB, J = 7.7 Hz,), 3.16 (t, 8H, J = 8.4 Hz,), 7.26 (t, 1H, J = 7.5 Hz, H6), 7.49 (t, 1H, J = 7.6 Hz, H5), 7.78 (d, 1H, J = 8.1 Hz, H4), 7.91 (d, 1H, J = 8.2 Hz, H7), 8.62 (s, 1H, H3), 13.49 (s, 1H, H1). 13C40 NMR (DMSO-d6, 125.77 MHz), δ, ppm: 13.47 (CD), 19.18 (CC), 23.07 (CB), 57.54 (CA), 111.11 (C4), 121.33 (C7), 121.98 (C6), 129.12 (C5), 137.79 (C3), 140.78 (C8,9). 15N NMR (DMSO-d6, 50.69 MHz), δ, ppm: 65.6 (N from Bu4N+), 187.6 (N2), 194.2 (d, N1). X-ray diffraction quality single crystals of 3 were picked from the reaction vessel.

Analytical Data for 4

Anal. Calcd for C23H42OsCl4N4O (Mr = 722.65 g/mol): C, 38.23; H, 5.86; N, 7.75. Found: C, 38.49; H, 5.74; N, 7.61. ESI-MS in CH3CN (negative): m/z 332 [OsCl4]−, 362 [OsCl4(NO)]−, 480 [OsCl4(NO)(Hind)]−. IR, ν, cm–1: 437, 520, 594, 616, 660, 736, 757, 832, 878, 967, 1005, 1096, 1150, 1238, 1284, 1361, 1378, 1476, 1517, 1630, 1838, 2871, 2960, 3300. UV–vis (CH3CN), λmax, nm (ε, M–1 cm–1): 254 (9207), 270 (8145), 300 (sh, 3808), 579 (116). 1H NMR (DMSO-d6, 500.13 MHz), δ, ppm: 0.93 (t, 12HD, J = 7.3 Hz), 1.31 (sxt, 8HC, J = 7.3 Hz,), 1.56 (qui, 8HB, J = 7.2 Hz,), 3.16 (t, 8H, J = 8.3 Hz,), 7.23 (t, 1H, J = 7.5 Hz, H6), 7.52 (t, 1H, J = 7.7 Hz, H5), 7.76 (d, 1H, J = 8.5 Hz, H4), 7.90 (d, 1H, J = 8.2 Hz, H7), 8.58 (s, 1H, H3), 13.00 (s, 1H, H1). 13C40 NMR (DMSO-d6, 125.77 MHz), δ, ppm: 13.47 (CD), 19.18 (CC), 23.05 (CB), 57.53 (CA), 111.63 (C4), 120.26 (C9),121.56 (C7), 122.11 (C6), 129.39 (C5), 138.30 (C3), 139.69 (C8). 15N NMR (DMSO-d6, 50.69 MHz) δ, ppm: 65.6 (N from Bu4N+), 185.0 (N2), 238.7 (N1). Suitable crystals of 4 for X-ray diffraction analysis were obtained from mother liquor after isolation of 3 by slow diffusion of diethyl ether.

Physical Measurements

Elemental analyses were performed by the Microanalytical Service of the Faculty of Chemistry of the University of Vienna.

MIR spectra of 1 and 2 were obtained by using an ATR unit with a Perkin-Elmer 370 FTIR 2000 instrument (4000–400 cm–1), while ESI mass spectrometry was carried out with a Bruker Esquire 3000 instrument (Bruker Daltonics, Bremen, Germany) by using methanol as solvent. Expected and measured isotope distributions were compared. The 1H, 13C, and 15N NMR spectra were recorded at 500.32, 125.82, and 50.70 MHz on a Bruker DPX500 (Ultrashield Magnet) d6-DMSO (2.50 ppm) or C2D2Cl4 (5.98 ppm). 2D 13C1H HSQC, 15N1H HSQC, 13C1H HMBC, and 1H1H COSY experiments were performed.

IR spectra of 3 and 4 were recorded in the solid state on a NICOLET spectrophotometer in the 400–4000 cm–1 range, while UV–vis spectra were recorded on a Perkin-Elmer Lambda 35 UV–vis spectrophotometer using samples dissolved in CH3CN. Mass spectra were recorded on an ion trap mass spectrometer (LCQ, Thermo, Bremen, Germany) equipped with an electrospray (ESI) ion source in the positive and negative ion mode. The spray voltage for the positive and negative ion mode is respectively 4 kV and −3 kV. The capillary transfer temperature is 200 °C. For 1H and 13C NMR experiments, all samples were prepared under a N2 atmosphere in 5 mm NMR tubes. The chemical shifts were referred to TMS using the residual signals from the solvent d6-DMSO (2.50 ppm) or C2D2Cl4 (5.98 ppm). The 2D NMR spectra were recorded on a Bruker AV500 spectrometer and kinetic 1H NMR spectra on a Bruker DRX-300 spectrometer.

Electrochemical Measurements

Electrochemical measurements were performed using an AMEL 7050 all-in-one potentiostat, using a standard three-electrode setup with a glassy carbon electrode, a platinum auxiliary electrode, and a SCE (saturated calomel electrode) as the reference electrode. Deareation of solutions was accomplished by passing a stream of N2 through the solution for 30 min prior to the measurement and then maintaining a blanket atmosphere of N2 over the solution during the measurement. The complex solution in CH3CN was 1 or 2 mM in the supporting electrolyte of 0.1 M (n-Bu4N)PF6. Under these experimental conditions, the ferrocene/ferricinium couple, used as an internal reference for potential measurements, was located at E1/2ox = +0.425 V. The cyclic voltammetry of a mixture of 3 and 4 was characterized by two reversible oxidation waves corresponding to each isomer studied separately, whereas no separation oxidation peak was observed with a mixture of 1 and 2.

Kinetic Analysis

The integrals of NMR signals were obtained by fitting Lorentzian functions to the experimental spectra using the “NMRICMA 3.0”41 program for MATLAB (see Supporting Information, Figure S1). The adjustable parameters are the resonance frequency, intensity, line width, baseline, and phasing. Data analyses were carried out with the nonlinear least-squares fitting program VISUALIZEUR-OPTIMISEUR42 for MATLAB, using the Levenberg–Marquardt algorithm. Irreversible and reversible first-order reaction models were applied to analyze the time evolution of trans and cis Ru and Os isomer concentrations. The experimental data were fitted according to eqs 1–4 where A0T and B0 correspond to initial concentrations of trans and cis isomers, respectively. The samples were heated in an external constant temperature steam sterilizer at the desired temperature, whose value is assumed to be accurate within ±0.5 K. The temperature was monitored by a thermometer situated near the NMR sample tubes. NMR spectra of the investigated samples were measured at room temperature (20 °C) after rapid sample cooling using a water bath. Due to extremely low isomerization process rates in these systems, the time during NMR measurements is neglected. The time used in kinetic analysis (τ) corresponds to the heating time at indicated temperatures.

Crystallographic Structure Determination

X-ray diffraction measurements for ruthenium complexes 1 and 2 were performed on a Bruker X8 APEXII CCD diffractometer at 150 K with Mo Kα monochromated radiation. Diffraction data for osmium complexes 3 and 4 were collected on Gemini R and Gemini A Ultra diffractometers from Agilent Technologies Ltd. at 100 K with Cu Kα and Mo Kα graphite-monochromated radiation, respectively, both equipped with a CCD camera and controlled by the CrysAlisPro Software (Agilent Technologies, versions 1.171.33.55 and 1.171.34.49). The data on ruthenium complexes were processed using SAINT software,43 and those on osmium complexes with the CrysAlisPro package.44 For all crystals, an analytical absorption correction was applied using the modeled faces of the crystal.45 Crystal data, data collection parameters, and structure refinement details are given in Table 1. The structures were solved by direct methods and refined by full-matrix least-squares techniques. All non-hydrogen atoms in 1, 2, and 4 were refined with anisotropic displacement parameters, while the non-hydrogen atoms of indazole in 3 (vide infra) were refined isotropically. H atoms were inserted in calculated positions and refined with a riding model. The nitrosyl ligand in 1 and 3 was found to be disordered over three positions in the equatorial plane of the metal. One of three crystallographically independent complex anions in 1 and two of three in 3 were found to be affected by this disorder. In addition, the indazole ligand in one crystallographically independent anion of 3 was found to be disordered over two positions with a s.o.f. of 0.5:0.5. The disorder was solved by using SADI, DFIX, and EADP instructions implemented in SHELXL. The following software programs and computer were used: structure solution, SHELXS-97; refinement, SHELXL-97;46 molecular diagrams, ORTEP-3;47 computer, Intel CoreDuo. Selected bond distances and angles for 1–4 are listed in Table 2.

Table 1. Crystal Data, Data Collection Parameters, and Structure Refinement Details for (Bu4N)[cis-MCl4(NO)(Hind)] (M = Ru (1); Os (3)) and (Bu4N)[trans-MCl4(NO)(Hind)] (M = Ru (2); Os (4)).

compound 1 2 3 4
empirical formula C23H42Cl4N4ORu C23H42Cl4N4ORu C23H42Cl4N4OOs C23H42Cl4N4OOs
fw 633.48 633.48 722.61 722.62
space group P21/n P21/c P21/n P21/c
a [Å] 12.4091(4) 10.0975(5) 12.35414(12) 10.0836(7)
b [Å] 52.5720(15) 15.8422(9) 52.4121(4) 15.8530(10)
c [Å] 13.7339(4) 18.9705(10) 13.87637(13) 18.9740(10)
α [deg]        
β [deg] 100.7330(10) 100.759(2) 100.7569(9) 101.298(7)
γ [deg]        
V [Å3] 8802.9(5) 2981.3(3) 8827.14(14) 2974.3(3)
Z 12 4 12 4
λ [Å] 0.70713 0.71073 1.54184 0.71070
ρcalcd [g cm–3] 1.434 1.411 1.631 1.614
cryst size [mm3] 0.14 × 0.14 × 0.10 0.15 × 0.02 × 0.02 0.27 × 0.17 × 0.14 0.57 × 0.29 × 0.15
T [K] 150(2) 150(2) 100(2) 100(2)
μ [mm–1] 0.921 0.906 11.698 4.668
R1a 0.0715 0.0310 0.0316 0.0304
wR2b 0.1288 0.0641 0.0860 0.0697
GOFc 1.064 1.025 1.042 1.033
Open in a new tab
a

R1 = ∑∥Fo| – |Fc∥/∑|Fo|.

b

wR2 = {∑[w(Fo2 – Fc2)2]/∑[w(Fo2)2]}1/2.

c

GOF = {∑[w(Fo2 – Fc2)2]/(n – p)}1/2, where n is the number of reflections and p is the total number of parameters refined.

Table 2. Selected Bond Lengths (Å) and Angles (deg) (experimental and calculated) for Compounds cis-(Bu4N)[MCl4(NO)(Hind)] (M = Ru (1), Os (3)) and trans-(Bu4N)[MCl4(NO)(Hind)] (M = Ru (2), Os (4)).

  X-ray
 B3LYP/6-31G*
bond 1a 2 3a 4 1 2 3 4
M–N1 2.092(4) 2.104(2) 2.080(4) 2.114(3) 2.151 2.204 2.161 2.182
M–Cleq(av) 2.350(19) 2.360(3) 2.373(9) 2.368(3) 2.469 2.451 2.406 2.438
M–Clax 2.3675(13)   2.3728(11)   2.405   2.390  
M–N3 1.784(5) 1.717(2) 1.8220(9) 1.763(3) 1.747 1.735 1.732 1.715
N3–O1 1.041(6) 1.144(3) 1.1346(12) 1.133(4) 1.171 1.167 1.161 1.157
M–N3–O1 176.1(5) 178.2(2) 176.4(4) 178.0(4) 178.7 179.7 179.5 179.8
Open in a new tab
a

Quoted parameters refer to crystallographically independent complex anions not affected by the disorder.

Computational Details

The equilibrium geometries of the compounds 1–4 have been optimized in the gas phase combining the functional B3LYP48,49 and the 6-31G* basis set for the light atoms. For ruthenium complexes 1 and 2 and osmium compounds 3 and 4, the Stuttgart–Dresden 28-electron quasi-relativistic effective core potential (MWB28)50 and the analogous 60-electron pseudopotential (MWB60),50 respectively, have been used to account for the scalar relativistic effects. The possible transition state structures for the cis↔trans isomerization reaction of the Ru complexes were calculated at the same level of theory. In all the calculations, only the anions of all compounds have been considered, i.e., without any counterions. To verify the nature of the minima and the transition states, as well as to analyze the NO stretching frequency, harmonic vibrational frequency calculations have been carried out. Following the work of Scott and Radom,51 the calculated harmonic vibrational frequencies were refined with a scaling factor of 0.9614 to account for the anharmonicity.

The mechanistic study of the [RuCl4(NO)(Hind)]−cis↔trans isomerization requires high accuracy of the relative energies of the species. Therefore, additional single-point calculations on the optimized structures have been carried out on all Ru species using the double-hybrid B2GP-PLYP52 functional and the 6-311G* basis set and MWB28 pseudopotential. The B2GP-PLYP functional has been used previously for accurate calculations of thermochemical data of late transition metal reactions.53 These single point calculations have been carried out both in the gas phase and incorporating solvent effects in DMSO using the integral equation formalism (IEF)54,55 of the polarizable continuum model (PCM).56−58 To estimate the overall effect of the solvent on the relative energies and geometries of the species, two additional calculations have been carried out: (i) a B3LYP/6-311G* single-point calculation using the PCM on the B3LYP/6-31G* gas-phase optimized geometries (labeled as PCM-B3LYP/6-311G*//B3LYP/6-31G*) and (ii) a PCM-B3LYP/6-31G* optimization (on compounds 1 and 2 and one transition state for the dissociative mechanism). The PCM-B3LYP/6-31G* geometries showed negligible differences from the gas-phase B3LYP/6-31G* ones, and relative PCM-B3LYP/6-31G* energies deviated by less than 3 kJ/mol from the values calculated at the PCM-B3LYP/6-311G*//B3LYP/6-31G* level of theory. Therefore, gas-phase B3LYP/6-31G* geometries have been used for all subsequent calculations in the whole study. All calculations have been carried out with the Gaussian 09 program package.59

Results and Discussion

Syntheses

Anderson rearrangement reaction of (H2ind)2[RuCl5(NO)] in alcohols at elevated temperatures yielded (H2ind)[cis-RuCl4(NO)(Hind)] and (H2ind)[trans-RuCl4(NO)(Hind)], which were separated by fractioned crystallization. A metathesis reaction with a small excess of (n-Bu4N)Cl afforded complexes 1 and 2, respectively.

The isomeric osmium–nitrosyl complexes 3 and 4 were obtained by reaction of (n-Bu4N)2[OsCl5(NO)] with 1H-indazole in a 1:1.5 molar ratio in n-butanol at 105 °C for 24 h with an overall yield between 75 and 80%. Fractioned crystallization of the reaction mixture afforded 2/3 of the red cis isomer 3, and then by slow diffusion of diethyl ether into the concentrated filtrate, 1/3 of blue crystals of the trans-isomer 4 were afforded.

The reactivity of pentahalonitrosyl metalate [MX5(NO)]2– (M = Ru, Os; X = Cl, Br, I) increases in the order Cl– < Br– < I– and Os < Ru, and the ligand substitution should be favored in the trans position to the NO group due to the well-known trans effect.17 However, in our case, the main compounds isolated were the cis isomers 1 and 3. The lower yield of trans isomers 2 and 4 suggests that they are transient species, transforming into the cis forms under reaction conditions (n-propanol at 75 °C for ruthenium, n-butanol at 105 °C for osmium). This prompted us to study the trans/cis conversion by 1H NMR in detail.

The peak with m/z 391 in the negative ion mode ESI mass spectra of 1 and 3 was assigned to [RuCl4(NO)(Hind)]−, while signals at m/z 480, 362, and 332 for 2 and 4 were attributed to [OsCl4(NO)(Hind)]−, [OsCl4(NO)]−, and [OsCl4]−, respectively. All compounds possess an S = 0 ground state as confirmed by magnetic measurements and NMR spectra. In IR spectroscopy, cis isomers are characterized by lower ν(NO) wavenumbers than the trans species. In particular, the ν(NO) for 1 and 3 is seen at 1846 and 1805 cm–1, while that of 2 and 4 are at 1875 and 1838 cm–1, respectively.

Crystal Structures

The crystal structures of 1–4 contain essentially octahedral Ru and Os complexes of the general formula (n-Bu4N)[MCl4(NO)(Hind)] (M = Ru or Os; Hind = 1H-indazole; Figure 1). Complexes 1 and 3 crystallized in the monoclinic space group P21/n, while 2 and 4 crystallized in the monoclinic space group P21/c. Compounds 1 and 3 are cis isomers, in which three chlorido ligands and one NO molecule are bound to ruthenium (1) or osmium (3) in the equatorial plane, and the axial sites are occupied by an indazole heterocycle and a fourth chlorido ligand. In trans isomers 2 and 4, the equatorial plane is occupied by four chlorides and the axial positions by NO and the indazole heterocycle. Crystal data and structure refinement parameters for 1–4 are shown in Table 1.

Figure 1.

Figure 1

Open in a new tab

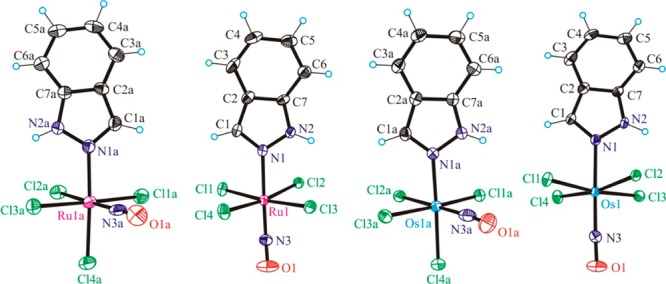
ORTEP views of the [cis-RuCl4(NO)(Hind)]−, [trans-RuCl4((NO)(Hind)]−, cis-[OsCl4(NO)(Hind)]−, and trans-[OsCl4(NO)(Hind)]− complex anions in 1–4 (from left to right). Thermal ellipsoids are drawn at the 50% probability level.

Selected bond lengths and angles of the compounds 1–4, as obtained from the crystal structures and theoretical calculations, are shown in Table 2. All complexes show a distorted octahedral coordination geometry around the metal center and a linear NO binding. In the cis compounds, NO lies in one plane with the equatorial Cl– ligands, while in the trans compounds the Cl– ligands are slightly bent out-of-plane toward the indazole ligand. In the calculated structures, we observe slightly longer (by ca. 0.1 Å) M–Cl bonds and a slightly more linear NO coordination compared to the crystal structures (Table 2). Otherwise, the optimized geometries are in good agreement with the X-ray structures.

Kinetic Study by NMR Spectroscopy

It is well-known that isomerization processes60−76 as well as exchange/substitution reactions77−80 at the metal center in platinum group (Ru, Rh, Pd, Os, Ir, Pt) metal complexes are much slower in comparison with those for 3d and 4f metal complexes.81,82 Platinum group metal complexes are kinetically very inert and thermodynamically more stable. In addition, they have low isomerization rate constants. The two ruthenium isomers 1 and 2 and two related osmium isomers 3 and 4 presented in this work are in accord with these general rules. High resolution NMR spectroscopy is an appropriate technique to characterize isomers in solution and to monitor their mutual transformations.

The assignment of NMR signals of the coordinated 1H-indazole has been performed based on 2D NMR spectroscopy (see Supporting Information, Figures S2–S4) and was correlated with the spectra of the noncoordinated 1H-indazole.83 A marked difference in the chemical shifts of NH and CH protons of the coordinated 1H-indazole ligand in cis and trans isomers (Figure 2) allows for the determination of population rates and an investigation of the kinetics of isomerization.

Figure 2.

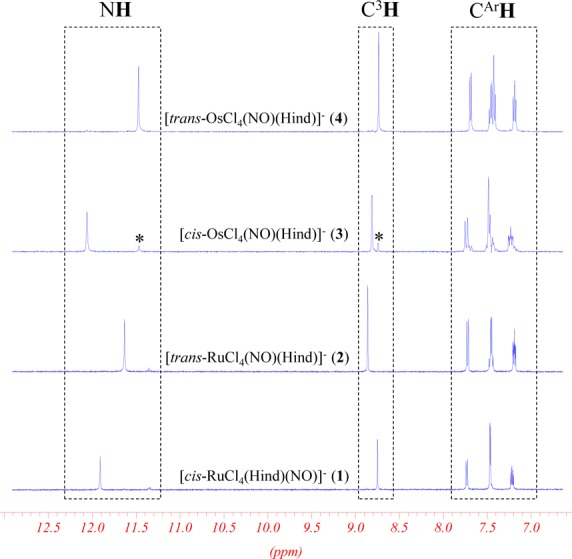
Figure 2

Open in a new tab

Selected region of 1H NMR (500 MHz; 25 °C) spectra of (n-Bu4N)[cis-MCl4(NO)(Hind)] (M = Ru (1), Os (3)) and (n-Bu4N)[trans-MCl4(NO)(Hind)] (M = Ru (2), Os (4)) in C2D2Cl4.

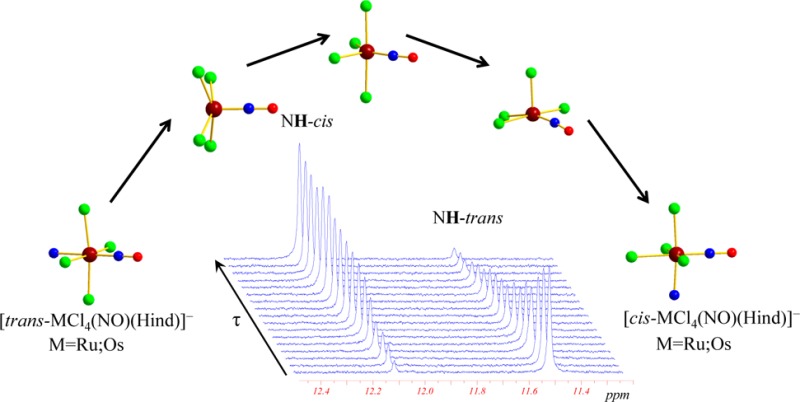
A typical series of time-dependent 1H NMR spectra upon isomerization of [trans-RuCl4(NO)(Hind)]− to [cis-RuCl4(NO)(Hind)]− ([t–c]) and [cis-RuCl4(NO)(Hind)]− to [trans-RuCl4(NO)(Hind)]− ([c–t]) is shown in Figure 3, while that of [trans-OsCl4(NO)(Hind)]− conversion into [cis-OsCl4(NO)(Hind)]− and vice versa is displayed in Figure 4. From Figures 3a and 4, a progressive decrease of the NH signal intensity with time, corresponding to the trans isomer, and an increase of the signal corresponding to the cis isomer is seen. After 72 h of heating at 100 °C, [trans-RuCl4(NO)(Hind)]− is partially converted into [cis-RuCl4(NO)(Hind)]−, and the trans–cis equilibrium is reached. Similarly, starting from the [cis-RuCl4(NO)(Hind)]− isomer, the same equilibrium ratio between the cis and trans isomers is reached after 72 h of heating the solution at 100 °C. These time-dependent NMR spectra and the same equilibrium ratios between cis and trans isomers indicate the reversibility of the isomerization process.

Figure 3.

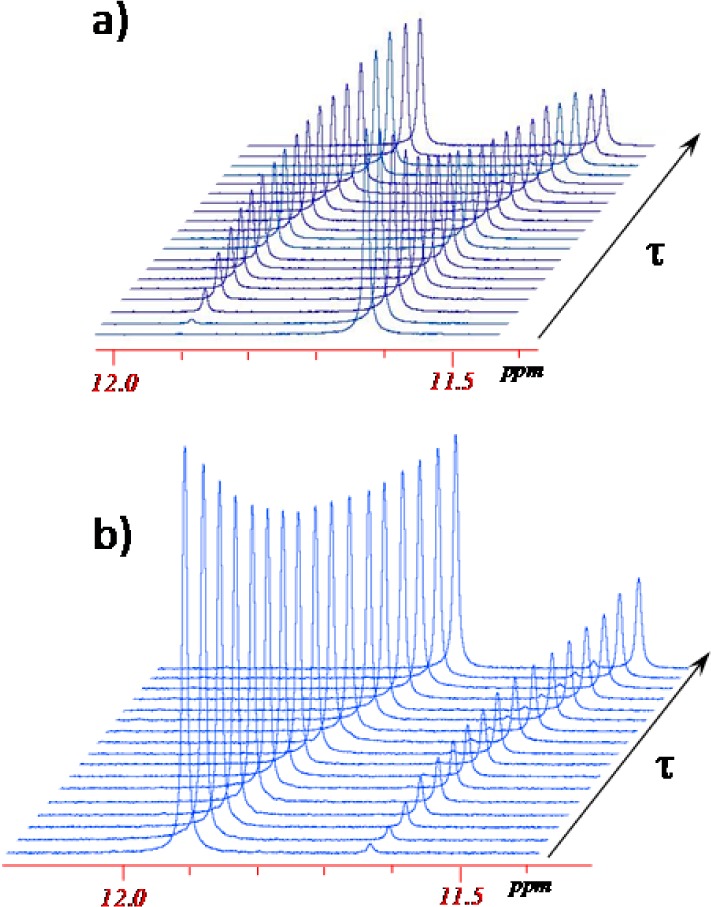
Figure 3

Open in a new tab

Evolution of 1H NMR spectra (500 MHz) in the NH region of the [trans-RuCl4(NO)(Hind)]− (a) and [cis-RuCl4(NO)(Hind)]− (b) isomers as a function of time (τ = [0–3] × 105 s) at 100 °C in C2D2Cl4 (C0(trans) = 14.5 mmol/L; C0(cis) = 13.7 mmol/L) showing the formation of the cis and trans isomers, respectively.

Figure 4.

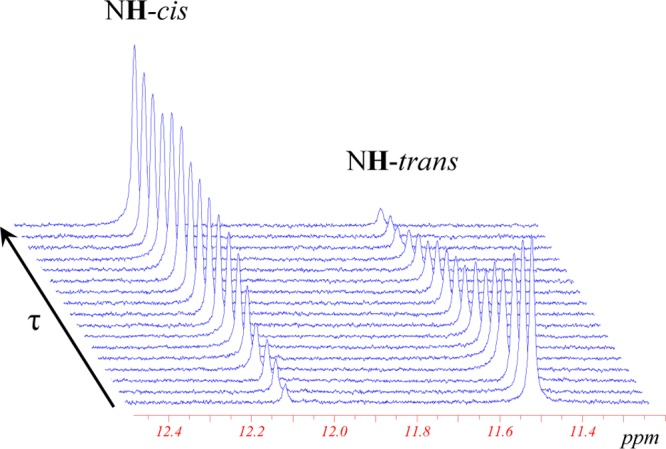
Figure 4

Open in a new tab

Evolution of 1H NMR spectra (300 MHz) of the [trans-OsCl4(NO)(Hind)]− isomer in the NH region as a function of time (τ = [0–3] × 105 s) at 120 °C in C2D2Cl4 (C0 = 15.26 mmol/L) showing the formation of the cis isomer (for complete aromatic region spectrum, see Supporting Information Figure S5).

The trans to cis conversion is also detected in the case of the [trans-OsCl4(NO)(Hind)]− anion. However, the isomerization occurs slower and can be efficiently monitored only upon heating at temperatures higher than 100 °C. As can be seen from Figure 4, heating at 120 °C for 96 h leads to an almost complete conversion of the trans isomer into the cis one. According to the kinetic analysis (see below), the conversion of the cis isomer into the trans isomer in the case of osmium complexes also takes place, but only trans to cis transformation was experimentally investigated because of the very low conversion rate of cis species into trans.

Plots of population evolution of cis and trans isomeric species of ruthenium and osmium complexes versus heating times at different temperatures are shown in Figures 5, 6, and S6–S9.

Figure 5.

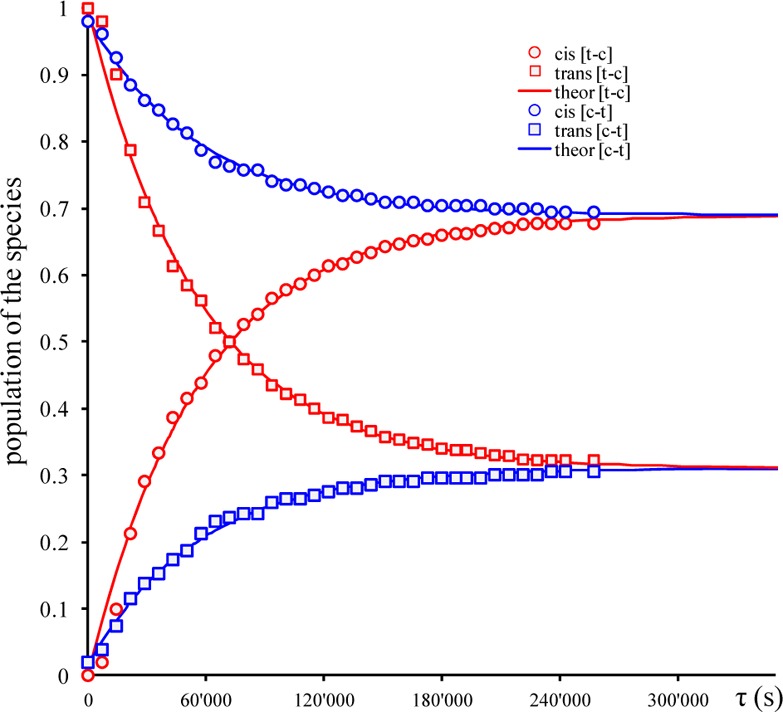
Figure 5

Open in a new tab

Time evolution of populations for [cis-RuCl4(NO)(Hind)]− (○) and [trans-RuCl4(NO)(Hind)]− (□) isomers at 100 °C in C2D2Cl4 for cis to trans [c–t] (blue) and trans to cis [t–c] (red) isomerization processes. The solid lines are the best fits with activation parameters indicated in the text (for fitted plots at 90, 105, and 110 °C, see Supporting Information Figures S6 and S7).

Figure 6.

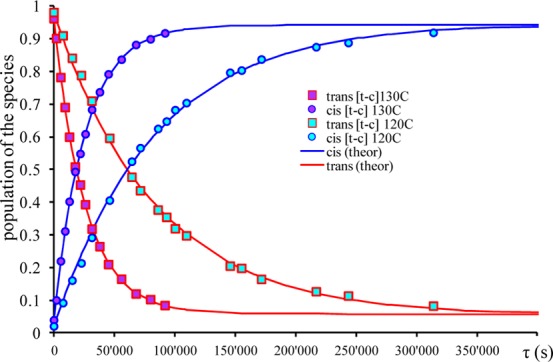
Figure 6

Open in a new tab

Time evolution of populations for [cis-OsCl4(NO)(Hind)]− (○) and [trans-OsCl4(NO)(Hind)]− (□) isomers at 120 and 130 °C in C2D2Cl4 for trans to cis [t–c] isomerization processes. The solid lines are the best fits with activation parameters indicated in the text (see also Figure S8 in the Supporting Information).

For the estimation of population rates upon isomerization, the NH and C3H signals of coordinated 1H-indazole in cis and trans complexes from NMR spectra were used. Analogously to other isomerization processes,73,74,84−86 the reversible first order kinetics are assumed for ruthenium and osmium complexes (see eqs 1 and 2).

graphic file with name ic-2013-004824_m001.jpg 1
graphic file with name ic-2013-004824_m002.jpg 2

In eqs 1 and 2, A is trans and B is cis isomer. Concentration evolution of trans (AτT) and cis (Bτ) isomers as functions of time (τ) at different temperatures (T) were analyzed (by nonlinear least-squares fits) according to a reversible first order model via the eqs 3 and 4:87,88

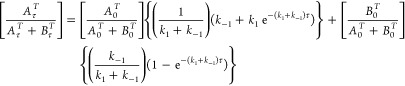graphic file with name ic-2013-004824_m003.jpg 3
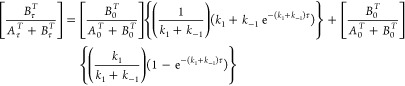graphic file with name ic-2013-004824_m004.jpg 4

Appropriate temperature values 80–110 °C for 1 and 2 and 105–130 °C for 3 and 4 were used in this analysis. The best fits of experimental data were obtained by using eqs 3 and 4 (Table 3). Initially, the conversion of [trans-OsCl4(NO)(Hind)]− into [cis-OsCl4(NO)(Hind)]− was analyzed as a first order irreversible process. The deviation of experimental data from the theoretical ones at high temperatures (120 and 130 °C) at longer time intervals (see Figure S9) suggested applying the reversible first order isomerization law. The activation parameters (ΔH# and ΔS#) have been estimated using two methods (Table 4). In the first one (method I), the corresponding values of k1 and k–1 at different temperatures have been obtained after fitting the experimental population rates with those calculated via eqs 3 and 4 and analysis by the logarithmic Eyring eq 5:

graphic file with name ic-2013-004824_m005.jpg 5

In the second method (method II), the experimental population ratios at different temperatures were fitted simultaneously by using the reversible first order model (eqs 4 and 5) with constraining eq 5. In this case, two enthalpies of activation (ΔHcis–trans‡ and ΔHtrans–cis) and two entropies of activation (ΔScis–trans‡ and ΔStrans–cis) were used as variable parameters (Table 4). The results obtained from both methods are similar. The second method was not applied in the case of osmium complexes because of the absence of experimental data for cis to trans transformation.

Table 3. Rate Constants k (s–1) with Standard Deviations in Parentheses and Equilibrium Constant K at Different Temperatures for the Isomerization Reactions of [cis-MCl4(NO)(Hind)]− (M = Ru (1), Os (3)) and [trans-MCl4(NO)(Hind)]− (M = Ru (2), Os(4)) in C2D2Cl4.

  process k(80 °C) × 10–6 k(90 °C) × 10–6 k(100 °C) × 10–6 k(105 °C) × 10–6 k(110 °C) × 10–6 k(120 °C) × 10–6 k(130 °C) × 10–6
[ cis-RuCl4(NO)(Hind)]− (1) cis → trans 0.58(8) 1.78(2) 5.51(6) 8.3(1) 20.1(7)    
[trans-RuCl4(NO)(Hind)]− (2) trans → cis 1.05(6) 2.66(3) 12.2(1) 19.5(2) 50.1(5)    
[RuCl4(NO)(Hind)]− K = (kc–t)(kt–c) 0.55 0.57 0.45 0.42 0.40    
cis-[OsCl4(NO)(Hind)]− (3) cis → transa       0.04(1) 0.08(1) 0.6(1) 2.3(2)
trans-[OsCl4(NO)(Hind)]− (4) trans → cis       1.26(1) 2.68(2) 11.4(1) 36.6(7)
[OsCl4(NO)(Hind)]− K = (kc–t)(kt–c)       0.03 0.03 0.05 0.06
Open in a new tab
a

The kinetic parameters were obtained from reversible first order law analysis of trans to cis conversion data of trans-[OsCl4(NO)(Hind)]− (4).

Table 4. Activation Parameters (ΔH‡, ΔS‡, ΔG‡) for the isomerization of [cis-MCl4(NO)(Hind)]− (M = Ru (1), Os(3)) and [trans-MCl4(NO)(Hind)]− (M = Ru (2), Os(4)) in C2D2Cl4a.

    ΔH‡ (kJ/mol)
 ΔS‡ (J/(mol·K))
 ΔG‡(25 °C) (kJ/mol) ΔG‡(110 °C) (kJ/mol)
compound process method I method II method I method II method I method I
[cis-RuCl4(NO)(Hind)]− (1) cis → trans 124.1 ± 0.3 122.8 ± 1.3 –14.9 ± 0.7 –18.7 ± 3.6 128.5 129.8
[trans-RuCl4(NO)(Hind)]− (2) trans → cis 143.7 ± 0.5 138.8 ± 1.0 28.5 ± 1.4 31.0 ± 2.7 135.2 132.8
[cis-OsCl4(NO)(Hind)]− (3) cis → transb 200.7 ± 0.7   142.7 ± 8.9   161.7 146.0
[trans-OsCl4(NO)(Hind)]− (4) trans → cis 168.2 ± 0.6   85.4 ± 3.9   144.9 135.5
Open in a new tab
a

Estimation from method I by fitting k1 and k–1 by Eyring equation (eq 5) and by method II, simultaneously fitting the all population ratios at different temperatures via eqs 3 and 4 with constraining eq 5.

b

The kinetic parameters were obtained from reversible first order law analysis of trans to cis conversion data of 4.

The best fit for activation parameters (ΔH‡, ΔS‡) and calculated Gibbs energy (ΔG‡) for the isomerization reactions of [cis-MCl4(NO)(Hind)]− (M = Ru (1), Os (3)) and [trans-MCl4(NO)(Hind)]− (M = Ru (2), Os (4)) in C2D2Cl4 are quoted in Table 4 (see also Figure 7). The obtained enthalpies of isomerization is approximately two times as high as that reported for trans to cis isomerization of [Os(tpy)Cl2(N)]+, where tpy = terpyridine (ΔH#= 78 ± 8 kJ/mol ΔS#= 79 ± 10 J/mol·K),84 while the entropy factors are similar.84

Figure 7.

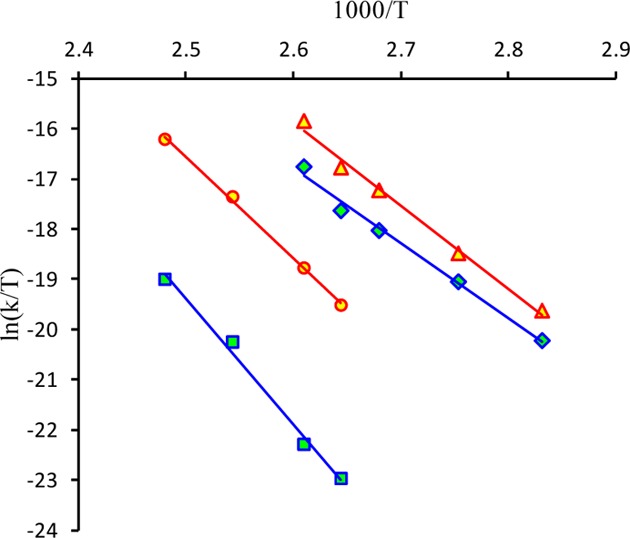
Figure 7

Open in a new tab

Eyring plots for the isomerization reactions of [MCl4(NO)(Hind)]−trans to cis (in red) (M = Ru (2) (Δ), Os (4) (○)) and cis to trans (in blue) (M = Ru (1) (◊), Os (3) (□)) in C2D2Cl4. The solid lines are the best fits with activation parameters quoted in Table 4.

The equilibrium constants at different temperatures were obtained as a ratio between the rate constant for trans→cis and cis→trans isomerizations (Table 3). The equilibrium constants (Ki) for isomerization of [RuCl4(NO)(Hind)]− are not changing much with temperature and vary slightly between 0.57 and 0.40, indicating the low thermodynamic differences between cis and trans isomers.

The thermodynamic parameters (ΔH° = 13.5 ± 1.5 kJ/mol; ΔS° = −5.2 ± 3.4 J/(mol·K)) for [RuCl4(NO)(Hind)]− isomerization have been obtained by fitting the experimental data with eq 6 (see van’t Hoff plot in Figure S10 of Supporting Information):

graphic file with name ic-2013-004824_m006.jpg 6

The enthalpy of isomerization reaction obtained from van’t Hoff plot is close to value obtained from difference between two enthalpy of activation (ΔH° = ΔHtrans–cis‡ – ΔHcis–trans) ΔH° = 16 kJ/mol (method I) and 19.6 kJ/mol (method II). For osmium complexes, the equilibrium constants have low values (0.03–0.06) and suggest the dominant stability of the cis isomer. This result is in accordance with the evolution of NMR spectra for [trans-OsCl4(NO)(Hind)]− (Figure 4), which was almost completely transformed into the cis isomer upon heating.

Note that the isomerization also occurs in DMSO-d6 (see Figure S11). However, the isomerization in DMSO is accompanied by the ligand substitution process (DMSO/indazole). Detailed investigation of isomerization in different solvents and of exchange/substitution reactions will be part of a separate work.

Electrochemistry

The cyclic voltammograms of ruthenium and osmium complexes 1–4 in CH3CN containing 0.10 M TBAPF6 as the supporting electrolyte using a glassy carbon working electrode and a saturated calomel electrode (SCE) as a reference electrode are shown in Figures S12 and 8, respectively. The redox processes occur exclusively on the complex anions [MCl4(NO)(Hind)]−, where M = Ru or Os. The cyclic voltammograms of 1 and 2 showed a large irreversible reduction wave at −1.0 V and an irreversible oxidation wave at 1.77 V vs SCE (Figure S12). The multiscan cyclic voltammetry on the oxidation peak at 0.1 V/s is characterized by a dramatic decrease of the peak intensity, presumably due to nonconductor deposit generation. The peak intensities (normalized vs concentration) are similar for 1 and 2, and one-electron processes were determined by calibration with the Fc/Fc+ couple. In the isomeric mixture, 1 and 2 cannot be distinguished by cyclic voltammetry since the phenomenon of deposit was encountered again during the coulometry with a fast and abnormal decrease of the current intensity. The ruthenium complexes are generally more reactive than the related osmium compounds. This seems to affect their redox processes, in which, both the oxidized and reduced species generated are unstable.

Figure 8.

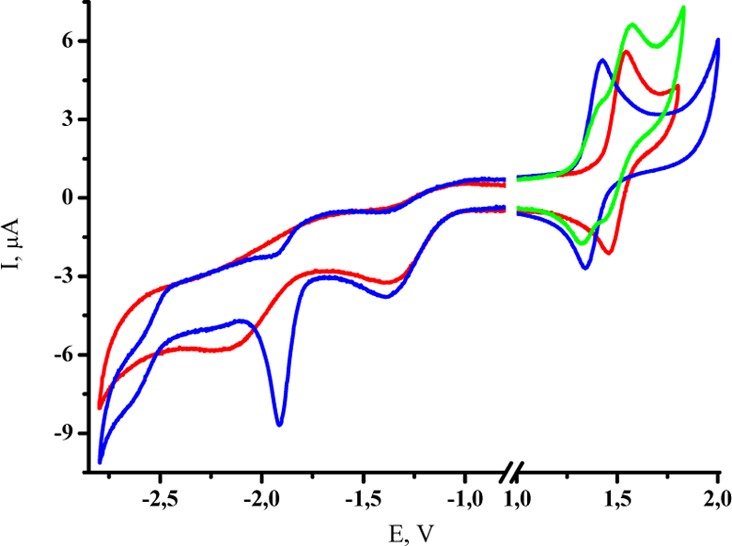
Figure 8

Open in a new tab

Cyclic voltammetry of [cis-OsCl4(NO)(Hind)]− (red), [trans-OsCl4(NO)(Hind)]− (blue), and their mixture (green) at 100 mV/s on GC electrode (3 mm) in 0.1 M TBAPF6 in CH3CN (see also Figure S17).

The cyclic voltammograms of the osmium complexes 3 and 4 display two irreversible reductions and a reversible oxidation wave (Figure 8) with E1/2 = 1.40 and 1.52 V vs SCE for trans3 and cis4 complexes, respectively (Figure 8). The difference in redox potentials indicates that the two isomers can be identified by standard cyclic voltammetry measurement (see Experimental Section and Figure 8). The linear dependence of the oxidation peak current Ip versus the square-root of the scan rate potential between 0.025 and 0.3 V/s for 3 and 4 is indicative of a diffusion-controlled process. Moreover, the oxidation peak intensities (at the same concentration) of 3 and 4 are similar (Figure 8). The exhaustive electrolysis of 4 performed at 2.00 V exhibited a one-electron oxidation accompanied by development of a new visible absorption band with λmax at 519 nm (Figures S13 and S14). The cyclic voltammetry followed after electrolysis showed the same reversible wave, indicating the stability of the oxidized state of 4 under an inert atmosphere. Similar electrochemical behavior was reported for [OsCl5(NO)]2–.89−91

Thus, we can assign a reversible one-electron oxidation for these two isomers as follows:

graphic file with name ic-2013-004824_0014.jpg

An exhaustive electrolysis of 3 at 2.00 V resulted in the appearance of a new visible band with λmax at 502 nm (Figures S15 and S16). Unexpectedly, the determined electron apparent number value was napp = 2 (Figure S18). The voltammograms recorded immediately after coulometry showed the disappearance of all the initial redox processes. So, the oxidized form of 3 appeared to be stable at the time scale of the cyclic voltammetry but unstable at the time scale of the coulometry. From the NMR experiment at room temperature, cis isomer 3 undergoes a slow isomerization into 4. By association with the electrochemical results, a general mechanism can be proposed as summarized in Scheme 2:

Scheme 2. cis–trans Isomerization Reactions (Red Outline) Associated with the Redox Processes (Black Outline).

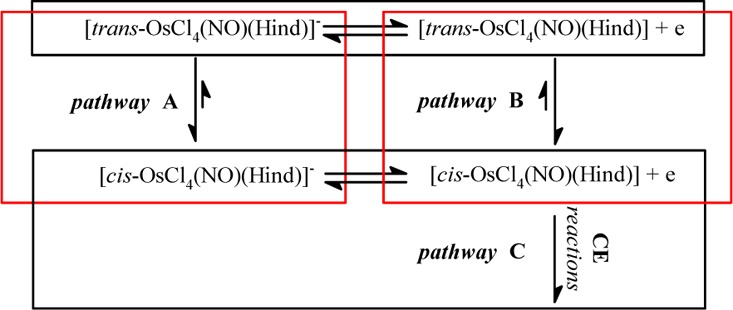
Scheme 2

Open in a new tab

The same isomerization reaction can be envisaged from the one-electron oxidized form of 4 in agreement with the mechanism presented in Scheme 2. Some examples of a redox-induced cis–trans isomerization of metal complexes are well-documented in the literature.92 In order to prove whether pathway B in Scheme 2 is indeed operative in our case, the multiscan cyclic voltammetry of 4 at a slow scan rate of potential was performed to generate the 1e oxidized species of 4 at the electrode, which could hypothetically convert into the corresponding isomer (1e oxidized form of 3). However, no mixture of one-electron oxidized species of 4 and 3 was observed in the diffusion layer during the experiment. This result indicates that (i) pathway B is not operative or (ii) the rate of the transformation of 1e oxidized species of 4 into the corresponding oxidized form of 3 is very slow, and we cannot observe it on the time scale of our experiments. Finally, on the time scale of the coulometry, we observed a more complex mechanism which led to the degradation of the oxidized form of 3 after two electrons transfer according to pathway C. We can suggest a CE mechanism in which the chemical reaction C can be considered slow on the time scale of the cyclic voltammetry.93 Indeed, the system 3/1e oxidized 4 is reversible in cyclic voltammetry, even at a slow scan rate of the potential. On the coulometry time scale, the process is irreversible because a chemical reaction occurs followed by an irreversible 1e oxidation reaction in accord with a general ECE mechanism with a global apparent electron number value napp = 2.

Computational Study

The theoretical analysis starts with a brief comparison of the calculated NO stretching vibrational frequencies of 1–4 to their experimental values. This allows for verifying the experimental distinguishability of the cis and trans isomers by the ν(NO) wavenumber in the IR spectrum, that is the most prominent peak in the IR spectra of all investigated compounds. It deserved particular attention for two reasons: first, it is the peak with the highest intensity, and second, its vibrational frequency differs for the cis and trans isomers due to different trans effects of the chlorido and indazole ligands.

Table 5 shows calculated and experimental wavenumber values for the NO vibrational frequency. The trans isomers (2 and 4) show an NO absorption frequency which is larger by ca. 30 cm–1 than that of the corresponding cis isomers. Although calculations overestimate the NO absorption frequency by ca. 20 cm–1 on average, the error is systematic; i.e., the difference between the NO frequencies in trans and cis compounds is almost the same. Thus, the calculations support the distinguishability of the cis and trans isomers by their NO vibrational frequencies. The good agreement between the experimental and the B3LYP/6-31G* geometries validates the employed method for the calculation of equilibrium geometries.

Table 5. Experimental and Scaled NO Stretching Vibrations (in cm–1) at the B3LYP/6-31G* Level of Theory.
complex 1 2 3 4
calculated 1863 1892 1829 1860
experimental 1846 1875 1805 1838
Open in a new tab

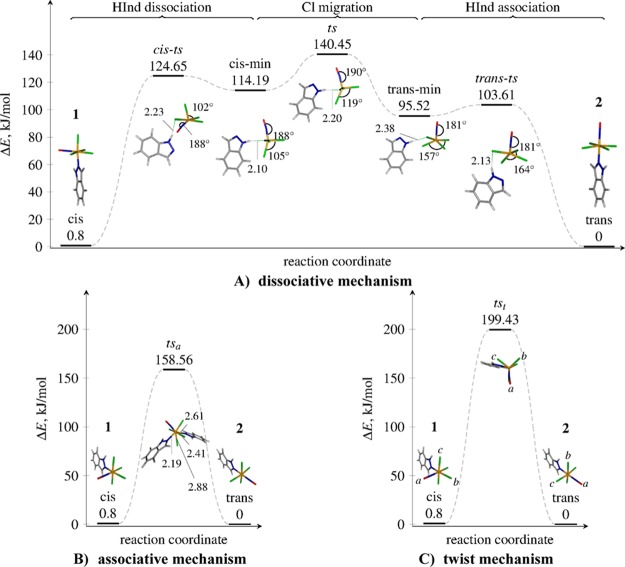
In the following, we discuss the cis↔trans isomerization mechanism of the [RuCl4(NO)(Hind)]− complex. We present and compare activation energies for three different isomerization pathways: the dissociative mechanism with intermediates, the associative mechanism, and the twist mechanism. The outlines for the three mechanisms showing the involved transition states and intermediates are given in Figure 9, showing the most relevant geometrical parameters. All the optimized values can be found in the Supporting Information (Tables S1–S9). Although the mechanisms are described only in the cis → trans direction, they are thermodynamically reversible, and hence the described reaction paths are also valid for the reverse reaction.

Figure 9.

Figure 9

Open in a new tab

Schematic representation of three cis–trans isomerization mechanisms investigated for [RuCl4(NO)(Hind)]−: dissociative (A), associative (B), and twist (C). The involved transition states and the reaction intermediates are shown, together with the most relevant geometrical parameters (in Å and degrees) obtained at the B3LYP/6-31G* level of theory in the gas phase. The relative energies are calculated at the PCM-B2GP-PLYP/6-311G*//B3LYP/6-31G* level of theory. The labels cis-ts, ts, and trans-ts refer to transition states, while cis-min and trans-min are intermediates. For a better illustration of the twist mechanism (c), the letters a, b, and c mark the NO–Cl–Cl triangle. Upon the isomerization, the triangle rotates around the ruthenium atom, as shown in the figure.

The Dissociative Mechanism

Starting from the cis structure, the dissociative mechanism (Figure 9A) is found to consist of three key steps: (i) the dissociation of the indazole ligand, (ii) migration of a Cl– ligand around the metal center from the axial to the equatorial position, and (iii) reassociation of the indazole ligand. Each of the three substeps shows a transition state and metastable intermediates. After the ligand dissociation (step i), the system is found in a metastable intermediate (a local minimum along the reaction coordinate, labeled cis-min) showing a distorted square-pyramidal coordination geometry around Ru. This minimum presents a hydrogen bond-like interaction of the NH group of the indazole with one of the Cl ligands. The H–Cl bond length in cis-min is 2.10 Å and remains in the range of 2.10–2.38 Å throughout all intermediates and transition states. The Cl–Ru–Cl angle increases from 90° in the cis compound to 102° in the cis-min structure.

The ligand dissociation from the cis complex is immediately accompanied with an NO bending up to 9° out of the Ru–Cl–N plane: this is most likely due to the noninnocent character of the NO ligand, i.e. the ability of NO to donate another electron pair to ruthenium after the indazole ligand has dissociated. Upon conversion to the trans structure, NO becomes linear again during step ii. In step ii, the cis-min structure is easily converted to another, more stable trans-min intermediate via the transition state ts, which shows a trigonal-bipyramidal coordination geometry around Ru. Both the cis-min and the trans-min structures show a square-pyramidal coordination geometry with the Ru atom coming out from the basal plane. In the cis-min structure, one of the Cl– ligands is bound apically, while in the trans-min structure, all four Cl– ligands are equatorially bound. The Cl– migrates from the apical position in cis-min to the equatorial position in trans-min, while the rest of the coordination sphere remains almost unchanged—only the Cl–Ru–Cl angle changes from 105° in cis-min via 119° in ts to 158° in trans-min. Step iii, the final step, is the reversion of the step i, where an indazole ligand reassociates to the square-pyramidal coordination polyhedron and completes the isomerization process. The dissociative mechanism described herein is similar to that of Berry pseudorotation in PF5.94−97 In our case, the square-pyramidal transition states (cis-ts and trans-ts) are more stable than the trigonal-bipyramidal intermediate (ts). This can be explained by a large crystal field splitting of 4d orbitals of ruthenium.

The Associative and the Twist Mechanisms

The associative mechanism involves coordination of a second indazole ligand to ruthenium, resulting in a pentagonal–bipyramidal coordination geometry around ruthenium in the transition state (Figure 9B). The transition state (labeled tsa) is asymmetric: the Ru–indazole bond lengths for the indazoles attached cis and trans relatively to the NO are 2.19 and 2.41 Å, respectively. The Ru–Cl bond lengths are not identical either. One of them involving the chlorido ligand between the two indazole ligands is of 2.88 Å, while the other Ru–Cl bonds are shorter at 2.41 Å. Inspection of the vibrational normal mode associated with the imaginary frequency shows that tsa is also a transition state for the indazole vs chlorido ligand substitution reaction: while in a direct cis↔trans isomerization one would expect a transition state with an imaginary frequency associated with an asymmetric indazole–indazole stretch, the found saddle point normal mode is a linear combination of the indazole–indazole and indazole–chlorido asymmetric stretches.

The twist mechanism (Figure 9C) is likewise mediated by one transition state (tst), where the NO–Cl–Cl triangle (marked with a, b, and c in Figure 9C) rotates on top of the central atom and the three remaining ligands. This transition state shows a trigonal-prismatic coordination geometry around ruthenium. Along with the NO–Cl–Cl rotation, the indazole ligand rotates slightly around the Ru–N bond, so that the two H atoms of the indazole close to other chlorido ligands can maintain hydrogen bond-like interactions with them. The vibrational normal-mode analysis of the transition state shows a low frequency corresponding to the Ru–indazole stretching normal mode. A relaxed potential energy surface scan at the B3LYP/6-31G* level of theory along with the normal modethe Ru-indazole stretching coordinate has revealed that at slightly longer Ru–indazole distances (2.481 Å) this coordinate becomes dissociative; in other words, an indazole ligand dissociates very easily from the twist transition state.

Relative Thermodynamic Stabilities and Activation Energies

Table 6 quotes the relative energies of 1 and 2 and all the transition state species involved in the isomerization reaction. The enthalpy ΔH° for the isomerization reaction is taken from Table 4, and it is equal to the difference between activation enthalpy obtained from kinetic study ΔH‡ for the trans → cis and cis → trans reactions. This value corresponds to the rate limiting step transition state (ts in Figure 9A). The experimental enthalpy for the cis compound is calculated as the difference of the experimental activation enthalpies ΔH‡ for the cis → trans and trans → cis isomerization, also taken from Table 4 (method II):

graphic file with name ic-2013-004824_m007.jpg

Table 6. Electronic Energies (in kJ/mol, Relative to the trans Compound 2 for cis (1) and trans (2) Minima), Transition States and Associated Intermediates Calculated at Different Levels of Theory.

  (A) dissociative mechanism
 (B) associative (C) twist
method cis (1) cis-ts cis-min ts trans-min trans-ts trans (2) tsa tst
B3LYPgasa 15.28 96.03 91.29 92.12 72.85 86.6 0 139.19 193
B3LYPsolb –3.94 111.99 107.65 125.3 90.56 94.82 0 140.47 189.09
B2GP-PLYPgasc 27.61 118.38 109.04 112.08 87.02 105.99 0 163.68 192.58
B2GP-LYPsold 0.8 124.65 114.19 140.45 95.52 103.61 0 158.56 199.43
ΔH0 16.0     138.8e     0 138.8e 138.8e
Open in a new tab
a

B3LYP/6-31G*.

b

PCM-B3LYP/6-311G*//B3LYP/6-31G*.

c

B2GP-PLYP/6-311G*//B3LYP/6-31G*.

d

PCM-B2GP-PLYP/6-311G*//B3LYP/6-31G*.

e

Activation enthalpy is obtained without explicit considerations of a particular transition state.

All calculated energies are relative to the trans compound 2. Moreover, electronic energies are used instead of calculated enthalpies: B3LYP/6-31G* enthalpies at 298 K show that the deviations of electronic energies from enthalpies are under 1 kJ/mol. A comparison of calculated electronic energies with experimental activation enthalpy as performed here introduces errors which are negligible in comparison to the intrinsic error of the method.

As can be clearly seen, the thermodynamic values obtained with B3LYP and B2GP-PLYP functionals are substantially different, confirming the need of a highly accurate functional for estimating energetics. However, the inclusion of the solvent with the PCM method is reflected in a similar manner for both B3LYP and B2GP-PLYP functionals. For instance, in the dissociative mechanism, the cis isomer is stabilized by ca. 19 kJ/mol and ca. 27 kJ/mol, respectively, as compared to the trans, while the limiting step transition state (ts) is destabilized (by 33 and 28 kJ/mol), increasing the total activation energy for the reaction. The increase of the activation energy for the dissociative mechanism is consistent with the fact that it is harder for the ligand to escape the metal coordination sphere to initiate a reaction when the molecule is trapped in a solvent cage. This is not relevant for the twist mechanism, where no dissociation is required to initiate the reaction. Accordingly, the solvent effect on the activation barrier is much smaller (less than 10 kJ/mol).

Conspicuously, the B3LYP/6-31G* gas phase result for the relative cis–trans thermodynamic stability (15.3 kJ/mol) is very close to the experimental value (13.5 kJ/mol). However, the inclusion of the solvent effects changes the value down to −3.9 kJ/mol, leading to the cis isomer being thermodynamically more stable than the trans, in contrast to the experiment. This evidences the importance of including solvent effects. Both the gas phase and PCM values obtained with the B2GP-PLYP functional are in line with the experiment, although the solvated value predicts both cis and trans isomers as almost degenerate. We attribute the discrepancy between the experimental and B2GP-PLYP calculated value at least in part to the fit errors in the Eyring plots.

The best value for the activation energy in the dissociative mechanism is given by the PCM-B2GP-PLYP/6-311G* (140.45 kJ/mol, see ts energy in Table 6), remarkably close to the experimental activation enthalpy (138.8 kJ/mol). At the same level of theory, the corresponding energies for the associative and twist mechanisms are higher in energy, i.e. ca. 159 and 200 kJ/mol, respectively. It is important to note that regardless of the functional and the exact comparison with the experimental value, the activation energy for the dissociative mechanism is the lowest. Therefore, we propose the dissociative mechanism as the primary mechanism for the cis↔trans isomerization of the ruthenium complexes.

Conclusion

In this work, we report on the synthesis and crystal structures of ruthenium and osmium compounds of the general formula (Bu4N)[MCl4(NO)(Hind)], where M = Ru or Os and Hind = 1H-indazole. All compounds have an octahedral {MCl4N2} structure and have been isolated as cis and trans isomers. The negative charge of each complex is counterbalanced by one tetrabutylammonium (Bu4N+) cation. A good solubility of the compounds in aprotic solvents assured by the presence of the (Bu4N+) cation allowed for the investigation of these compounds in solution by electrochemistry and NMR spectroscopy.

NMR spectroscopy showed that the cis and trans complexes are stable in DMSO and C2D2Cl4 solutions at room temperature. In the case of ruthenium complexes, the cis↔trans isomerization in C2D2Cl4 solution is discovered at temperatures above 80 °C. For osmium complexes, the isomerization process occurs at temperatures above 100 °C in accord with higher inertness of osmium complexes as compared to ruthenium counterparts. A kinetic investigation by NMR spectroscopy revealed that the isomerization reaction corresponds to a reversible first order process. The rates of isomerization reaction even at 110 °C are very low at 10–5 s–1 in the case of ruthenium and 10–6 s–1 in the case of osmium. The activation parameters, which have been obtained from fitting the reaction rates at different temperatures to the Eyring equation, are also in line with the inertness of these systems. The entropy of activation for the isomerization process of the osmium compounds is highly positive and suggests the dissociative mechanism of isomerization. In the case of ruthenium, the activation entropy for the cis to trans isomerization is negative (−18.6 J/(mol·K)), but positive for the trans to cis isomerization reaction (31.0 J/(mol·K)). The thermodynamic parameters for cis/trans isomerization of [RuCl4(NO)(Hind)]−, viz., ΔH° = 13.5 ± 1.5 kJ/mol and ΔS° = −5.2 ± 3.4 J/(mol·K), indicate the low difference between the energy of cis and trans isomers. The obtained thermodynamic parameters are consistent with kinetic results. Estimation of rates of the isomerization reactions at room temperature is on the order of 10–10 s–1, representing one of the slowest isomerization processes reported so far.

The theoretical calculation of possible isomerization mechanisms has been carried out on ruthenium complexes with DFT methods. The dissociative, associative, and intramolecular twist isomerization mechanisms have been considered. The best value for the activation energy is given for the dissociative mechanism by the PCM-B2GP-PLYP/6-311G* method (140.5 kJ/mol), close to the experimental activation enthalpy (138.8 kJ/mol). At the same level of theory, the corresponding energies for the associative and twist mechanisms are higher in energy, i.e., ca. 159 and 200 kJ/mol, respectively. Electrochemical investigation confirmed higher reactivity of ruthenium complexes compared to those of osmium and showed that intramolecular electron transfer reactions do not affect the isomerization process. On the basis of the results above and also taking into account the high temperature of reactions, we propose the dissociative mechanism as the primary mechanism for the cis↔trans isomerization of both the ruthenium and osmium complexes.

Acknowledgments

We thank Dr. Jozef Kožišek and Alexander Roller for collection of X-ray data sets for complexes 3 and 4, respectively. The authors also thank Professor André E. Merbach from École Polytechnique Fédérale de Lausanne (EPFL) and Dr. S. Shova from The State University of Moldova for useful discussions and suggestions. This work was done in the frame of an Austrian–French joint project supported in France by ANR (Agence Nationale de la Recherche) through project ANR-09-BLAN-0420-01 (VILYGRu) and in Austria by FWF (Fonds zur Förderung der Wissenschaftlichen Forschung) through the project I 374-N19. The PHC Amadeus is also greatly acknowledged for his support.

Supporting Information Available

Crystallographic refinement details, NMR spectra, and results of kinetic analysis for 1–4; results of theoretical calculation for 1 and 2; and calculated structures (in xyz format) for 1, 2, and all transition states and intermediates for the theoretically investigated mechanism. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Supplementary Material

ic4004824_si_001.cif (158.8KB, cif)
ic4004824_si_002.pdf (2.1MB, pdf)

References

  1. Baumann F.; Kaim W.; Baraldo L. M.; Slep L. D.; Olabe J. A.; Fiedler J. Inorg. Chim. Acta 1999, 285, 129–133. [Google Scholar]
  2. Ferlay S.; Schmalle H. W.; Francese G.; Stoeckli-Evans H.; Imlau M.; Schaniel D.; Woike T. Inorg. Chem. 2004, 43, 3500–3506. [DOI] [PubMed] [Google Scholar]
  3. Schaniel D.; Woike T. Phys. Chem. Chem. Phys. 2009, 11, 4391–4395. [DOI] [PubMed] [Google Scholar]
  4. Schaniel D.; Woike T.; Behrnd N. R.; Hauser J.; Kramer K. W.; Todorova T.; Delley B. Inorg. Chem. 2009, 48, 11399–11406. [DOI] [PubMed] [Google Scholar]
  5. Zangl A.; Klufers P.; Schaniel D.; Woike T. Dalton Trans. 2009, 1034–1045. [DOI] [PubMed] [Google Scholar]
  6. Singh P.; Sarkar B.; Sieger M.; Niemeyer M.; Fiedler J.; Zalis S.; Kaim W. Inorg. Chem. 2006, 45, 4602–4609. [DOI] [PubMed] [Google Scholar]
  7. Cormary B.; Ladeira S.; Jacob K.; Lacroix P. G.; Woike T.; Schaniel D.; Malfant I. Inorg. Chem. 2012, 51, 7492–7501. [DOI] [PubMed] [Google Scholar]
  8. Zuech E. A.; Hughes W. B.; Kubicek D. H.; Kittleman E. T. J. Am. Chem. Soc. 1970, 92, 528–531. [Google Scholar]
  9. Wilson S. T.; Osborn J. A. J. Am. Chem. Soc. 1971, 93, 3068–3070. [Google Scholar]
  10. Videla M.; Jacinto J. S.; Baggio R.; Garland M. T.; Singh P.; Kaim W.; Slep L. D.; Olabe J. A. Inorg. Chem. 2006, 45, 8608–8617. [DOI] [PubMed] [Google Scholar]
  11. Roncaroli F.; Videla M.; Slep L. D.; Olabe J. A. Coord. Chem. Rev. 2007, 251, 1903–1930. [Google Scholar]
  12. Montenegro A. C.; Amorebieta V. T.; Slep L. D.; Martin D. F.; Roncaroli F.; Murgida D. H.; Bari S. E.; Olabe J. A. Angew. Chem., Int. Ed. 2009, 48, 4213–4216. [DOI] [PubMed] [Google Scholar]
  13. Serres R. G.; Grapperhaus C. A.; Bothe E.; Bill E.; Weyhermuller T.; Neese F.; Wieghardt K. J. Am. Chem. Soc. 2004, 126, 5138–5153. [DOI] [PubMed] [Google Scholar]
  14. Radon M.; Broclawik E.; Pierloot K. J. Phys. Chem. B 2010, 114, 1518–1528. [DOI] [PubMed] [Google Scholar]
  15. Hayton T. W.; Legzdins P.; Sharp W. B. Chem. Rev. 2002, 102, 935–991. [DOI] [PubMed] [Google Scholar]
  16. Baraldo L. M.; Forlano P.; Parise A. R.; Slep L. D.; Olabe J. A. Coord. Chem. Rev. 2001, 219, 881–921. [Google Scholar]
  17. Sinitsyn N. M.; Svetlov A. A.; Bobrova L. V. Zh. Neorg. Khim. 1980, 25, 780–783. [Google Scholar]
  18. McCleverty J. A. Chem. Rev. 2004, 104, 403–418. [DOI] [PubMed] [Google Scholar]
  19. Siladke N. A.; Meihaus K. R.; Ziller J. W.; Fang M.; Furche F.; Long J. R.; Evans W. J. J. Am. Chem. Soc. 2012, 134, 1243–1249. [DOI] [PubMed] [Google Scholar]
  20. Rose M. J.; Mascharak P. K. Curr. Opin. Chem. Biol. 2008, 12, 238–244. [DOI] [PubMed] [Google Scholar]
  21. Tfouni E.; Truzzi D. R.; Tavares A.; Gomes A. J.; Figueiredo L. E.; Franco D. W. Nitric Oxide-Biol. Chem. 2012, 26, 38–53. [DOI] [PubMed] [Google Scholar]
  22. Butler A. R.; Megson I. L. Chem. Rev. 2002, 102, 1155–1165. [DOI] [PubMed] [Google Scholar]
  23. Ignarro L. J.; Byrns R. E.; Wood K. S. Circulation 1986, 74, 287–287. [Google Scholar]
  24. Carducci M. D.; Pressprich M. R.; Coppens P. J. Am. Chem. Soc. 1997, 119, 2669–2678. [Google Scholar]
  25. Khot U. N.; Novaro G. M.; Popovic Z. B.; Mills R. M.; Thomas J. D.; Tuzcu E. M.; Hammer D.; Nissen S. E.; Francis G. S. New Engl. J. Med. 2003, 348, 1756–1763. [DOI] [PubMed] [Google Scholar]
  26. Serli B.; Zangrando E.; Gianfeffara T.; Yellowlees L.; Alessio E. Coord. Chem. Rev. 2003, 245, 73–83. [Google Scholar]
  27. Rosenberg B.; Van Camp L.; Trosko J. E.; Mansour V. H. Nature 1969, 222, 385–386. [DOI] [PubMed] [Google Scholar]
  28. Metal Complexes in Cancer Chemotherapy; Keppler B. K., Ed.; Wiley-VCH: Weinheim, Germany, 1993. [Google Scholar]
  29. Cleare M. J.; Höschele J. D. Plat. Met. Rev. 1973, 17, 2–13. [Google Scholar]
  30. Cleare M. J.; Höschele J. D. Bioinorg. Chem. 1973, 2, 187–210. [Google Scholar]
  31. Scaffidi-Domianello Y. Y.; Meelich K.; Jakupec M. A.; Arion V. B.; Kukushkin V. Y.; Galanski M.; Keppler B. K. Inorg. Chem. 2010, 49, 5669–5678 (and references therein). [DOI] [PubMed] [Google Scholar]
  32. Coluccia M.; Nassi A.; Boccarelli A.; Giordano D.; Cardellicchio N.; Locker D.; Leng M.; Sivo M.; Intini F. P.; Natile G. J. Inorg. Biochem. 1999, 77, 31–35. [DOI] [PubMed] [Google Scholar]
  33. Bartel C.; Bytzek A. K.; Scaffidi-Domianello Y. Y.; Grabmann G.; Jakupec M. A.; Hartinger C. G.; Galanski M.; Keppler B. K. J. Biol. Inorg. Chem. 2012, 17, 465–474. [DOI] [PubMed] [Google Scholar]
  34. Arion V. B.; Reisner E.; Fremuth M.; Jakupec M. A.; Keppler B. K.; Kukushkin V. Y.; Pombeiro A. J. L. Inorg. Chem. 2003, 42, 6024–6031. [DOI] [PubMed] [Google Scholar]
  35. Stepanenko I. N.; Cebrian-Losantos B.; Arion V. B.; Krokhin A. A.; Nazarov A. A.; Keppler B. K. Eur. J. Inorg. Chem. 2007, 400–411. [DOI] [PubMed] [Google Scholar]
  36. Kolf S.; Preetz W. Z. Anorg. Allg. Chem. 1999, 625, 411–416. [Google Scholar]
  37. Ni W. X.; Man W. L.; Yiu S. M.; Ho M.; Cheung M. T. W.; Ko C. C.; Che C. M.; Lam Y. W.; Lau T. C. Chem. Sci. 2012, 3, 1582–1588. [Google Scholar]
  38. Bučinský L.; Büchel G. E.; Ponec P.; Breza M.; Kožíšek J.; Gall M.; Biskupič S.; Fronc M.; Schiessl K.; Cuzan O.; Prodius D.; Turta C.; Shova S.; Zajac D. A.; Arion V. B. Eur. J. Inorg. Chem. 2013, 2505–2519. [Google Scholar]
  39. Bhattacharyya R.; Saha A. M.; Ghosh P. N.; Mukherjee M.; Mukherjee A. K. J. Chem. Soc., Dalton Trans. 1991, 501–510. [Google Scholar]
  40. Fritz H. P.; Keller H. J.; Schwarzhans K. E.. J. Organomet. Chem. 1967, 7, 105. [Google Scholar]
  41. Helm L.NMRICMA 3.0; Institut des Sciences et Ingénierie Chimiques, EPFL: Lausanne, Switzerland, 2003. [Google Scholar]
  42. Yerly F.VISUALIZEUR-OPTIMISEUR; EPFL: Lausanne, Switzerland, 2001. [Google Scholar]
  43. SAINT-Plus, version 7.06a; APEX2; Bruker-Nonius AXS Inc.: Madison, WI, 2004. [Google Scholar]
  44. CrysAlisPro; Oxford Diffraction Ltd.: Abingdon, England, 2009. [Google Scholar]
  45. Clark R. C.; Reid J. S. Acta Crystallogr. 1995, A51, 887–897. [Google Scholar]
  46. Sheldrick G. Acta Crystallogr., Sect. A 2008, 64, 112–122. [DOI] [PubMed] [Google Scholar]
  47. Johnson G. K.Report ORNL-5138; OAK Ridge National Laboratory: Oak Ridge, TN, 1976. [Google Scholar]
  48. Becke A. D. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar]
  49. Lee C. T.; Yang W. T.; Parr R. G. Phys. Rev. B 1988, 37, 785–789. [DOI] [PubMed] [Google Scholar]
  50. Andrae D.; Haussermann U.; Dolg M.; Stoll H.; Preuss H. Theor. Chim. Acta 1990, 77, 123–141. [Google Scholar]
  51. Scott A. P.; Radom L. J. Phys. Chem. 1996, 100, 16502–16513. [Google Scholar]
  52. Karton A.; Tarnopolsky A.; Lamere J. F.; Schatz G. C.; Martin J. M. L. J. Phys. Chem. A 2008, 112, 12868–12886. [DOI] [PubMed] [Google Scholar]
  53. Escudero D.; Weisheit T.; Weigand W.; González L. Dalton Trans. 2010, 39, 9505–9513. [DOI] [PubMed] [Google Scholar]
  54. Cances E.; Mennucci B. J. Math. Chem. 1998, 23, 309–326. [Google Scholar]
  55. Mennucci B.; Cances E.; Tomasi J. J. Phys. Chem. B 1997, 101, 10506–10517. [Google Scholar]
  56. Miertus S.; Scrocco E.; Tomasi J. Chem. Phys. 1981, 55, 117–129. [Google Scholar]
  57. Cammi R.; Tomasi J. J. Comput. Math. 1995, 16, 1449–1458. [Google Scholar]
  58. Scalmani G.; Frisch M. J. J. Chem. Phys. 2010, 132, 114110. [DOI] [PubMed] [Google Scholar]
  59. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X.; Hratchian H. P.; Izmaylov A. F.; Bloino J.; Zheng G.; Sonnenberg J. L.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Rega N.; Millam J. M.; Klene M.; Knox J. E.; Cross J. B.; Bakken V.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Martin R. L.; Morokuma K.; Zakrzewski V. G.; Voth G. A.; Salvador P.; Dannenberg J. J.; Dapprich S.; Daniels A. D.; Farkas Ö.; Foresman J. B.; Ortiz J. V.; Cioslowski J.; Fox D. J.. Gaussian 09; Gaussian, Inc.: Wallingford, CT, 2009. [Google Scholar]
  60. Krause R. A.; Krause K. Inorg. Chem. 1980, 19, 2600–2603. [Google Scholar]
  61. Ferreira V.; Krause R. A.; Larsen S. Inorg. Chim. Acta 1988, 145, 29–38. [Google Scholar]
  62. Breher F.; Ruegger H.; Mlakar M.; Rudolph M.; Deblon S.; Schonberg H.; Boulmaaz S.; Thomaier J.; Grutzmacher H. Chem.—Eur. J. 2004, 10, 641–653. [DOI] [PubMed] [Google Scholar]
  63. Mebi C. A.; Frost B. J. Inorg. Chem. 2007, 46, 7115–7120. [DOI] [PubMed] [Google Scholar]
  64. Kakoti M.; Chaudhury S.; Deb A. K.; Goswami S. Polyhedron 1993, 12, 783–789. [Google Scholar]
  65. Dovletoglou A.; Meyer T. J. J. Am. Chem. Soc. 1994, 116, 215–223. [Google Scholar]
  66. Bakhmutov V. I.; Bertran J.; Esteruelas M. A.; Lledos A.; Maseras F.; Modrego J.; Oro L. A.; Sola E. Chem.—Eur. J. 1996, 2, 815–825. [Google Scholar]
  67. Bakhmutov V. I.; Visseaux M.; Baudry D.; Dormond A.; Richard P. Inorg. Chem. 1996, 35, 7316–7324. [DOI] [PubMed] [Google Scholar]
  68. Guido E.; D’Amico G.; Russo N.; Sicilia E.; Rizzato S.; Albinati A.; Romeo A.; Plutino M. R.; Romeo R. Inorg. Chem. 2011, 50, 2224–2239. [DOI] [PubMed] [Google Scholar]
  69. Hughes R. P.; Meyer M. A.; Tawa M. D.; Ward A. J.; Williamson A.; Rheingold A. L.; Zakharov L. N. Inorg. Chem. 2004, 43, 747–756. [DOI] [PubMed] [Google Scholar]
  70. Alibrandi G.; Scolaro L. M.; Romeo R. Inorg. Chem. 1991, 30, 4007–4013. [Google Scholar]
  71. Shafaatian B.; Akbari A.; Nabavizadeh S. M.; Heinemann F. W.; Rashidi M. Dalton Trans. 2007, 4715–4725. [DOI] [PubMed] [Google Scholar]
  72. Ashby M. T. J. Am. Chem. Soc. 1995, 117, 2000–2007. [Google Scholar]
  73. Lu K. L.; Lo H. U.; Lin Y. C.; Wang Y. Inorg. Chem. 1992, 31, 4499–4502. [Google Scholar]
  74. Haynes A.; McNish J.; Pearson J. M. J. Organomet. Chem. 1998, 551, 339–347. [Google Scholar]
  75. Yang F. Z.; Wang Y. H.; Chang M. C.; Yu K. H.; Huang S. L.; Liu Y. H.; Wang Y.; Liu S. T.; Chen J. T. Inorg. Chem. 2009, 48, 7639–7644. [DOI] [PubMed] [Google Scholar]
  76. Smith D. C.; Gray G. M. J. Chem. Soc., Dalton Trans. 2000, 677–683. [Google Scholar]
  77. Rapaport I.; Helm L.; Merbach A. E.; Bernhard P.; Ludi A. Inorg. Chem. 1988, 27, 873–879. [Google Scholar]
  78. Steblerrothlisberger M.; Hummel W.; Pittet P. A.; Burgi H. B.; Ludi A.; Merbach A. E. Inorg. Chem. 1988, 27, 1358–1363. [Google Scholar]
  79. Helm L.; Nicolle G. M.; Merbach A. E. Adv. Inorg. Chem. 2005, 57, 327–379. [Google Scholar]
  80. Helm L.; Merbach A. E. Chem. Rev. 2005, 105, 1923–1959. [DOI] [PubMed] [Google Scholar]
  81. Riblet F.; Novitchi G.; Scopelliti R.; Helm L.; Gulea A.; Merbach A. E. Inorg. Chem. 2010, 49, 4194–4211. [DOI] [PubMed] [Google Scholar]
  82. Novitchi G.; Riblet F.; Helm L.; Scopelliti R.; Gulea A.; Merbach A. E. Magn. Reson. Chem. 2004, 42, 801–806. [DOI] [PubMed] [Google Scholar]
  83. Elguero J.; Fruchier A.; Tjiou E. M.; Trofimenko S. Khim. Geterotsikl. Soedin. 1995, 1159–1179. [Google Scholar]
  84. Williams D. S.; Coia G. M.; Meyer T. J. Inorg. Chem. 1995, 34, 586–592. [Google Scholar]
  85. Bae B. J.; Park J. E.; Kim Y.; Park J. T.; Suh I. H. Organometallics 1999, 18, 2513–2518. [Google Scholar]
  86. Cotton F. A.; Dikarev E. V.; Wong W. Y. Inorg. Chem. 1997, 36, 3268–3276. [DOI] [PubMed] [Google Scholar]
  87. Atwood J. D.Inorganic and Organometallic Reaction Mechanisms; Wiley-VCH: Weinheim, Germany, 1997. [Google Scholar]
  88. Bielski B. H. J.; Capellos C.. Kinetic Systems; Mathematical Description of Chemical Kinetics in Solution; RE Krieger: New York, 1980. [Google Scholar]
  89. Ooyama D.; Nagao N.; Nagao H.; Sugimoto Y.; Howell F. S.; Mukaida M. Inorg. Chim. Acta 1997, 261, 45–52. [Google Scholar]
  90. Svetlov A. A.; Sinitsyn N. M. Zh. Neorg. Khim. 1986, 31, 2902–2914. [Google Scholar]
  91. Svetlov A. A.; Sinitsyn N. M.; Kravchenko V. V. Zh. Neorg. Khim. 1990, 35, 336–343. [Google Scholar]
  92. Pombeiro A. J. L.; da Silva M.; Lemos M. Coord. Chem. Rev. 2001, 219, 53–80. [Google Scholar]
  93. Amatore C.; Azzabi M.; Calas P.; Jutand A.; Lefrou C.; Rollin Y. J. Electroanal. Chem. 1990, 288, 45–63. [Google Scholar]
  94. Berry R. S. J. Chem. Phys. 1960, 32, 933–938. [Google Scholar]
  95. Tobe M. L.Inorganic Reaction Mechanisms; Nelson: London, 1972. [Google Scholar]
  96. Ugi I.; Marquard. D.; Klusacek H.; Gillespi. P.; Ramirez F. Acc. Chem. Res. 1971, 4, 288–296. [Google Scholar]
  97. Koga N.; Morokuma K. Chem. Rev. 1991, 91, 823–842. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ic4004824_si_001.cif (158.8KB, cif)
ic4004824_si_002.pdf (2.1MB, pdf)

Articles from Inorganic Chemistry are provided here courtesy of American Chemical Society

RESOURCES