Abstract
Neutrophil polarity relies on local, mutual inhibition to segregate incompatible signaling circuits to the leading and trailing edges. Mutual inhibition alone should lead to cells having strong fronts and weak backs or vice versa. However, analysis of cell-to-cell variation in human neutrophils revealed that back polarity remains consistent despite changes in front strength. How is this buffering achieved? Pharmacological perturbations and mathematical modeling revealed a new functional role for microtubules to buffer back polarity by mediating positive, long-range crosstalk from front to back; loss of microtubules inhibits buffering and results in anti-correlation between front and back signaling. Further, a systematic, computational search of network topologies found that a long-range, positive front-to-back link is necessary for back buffering. Our studies suggest a design principle that can be employed by polarity networks: short-range mutual inhibition establishes distinct signaling regions, after which directed long-range activation insulates one region from variations in the other.
INTRODUCTION
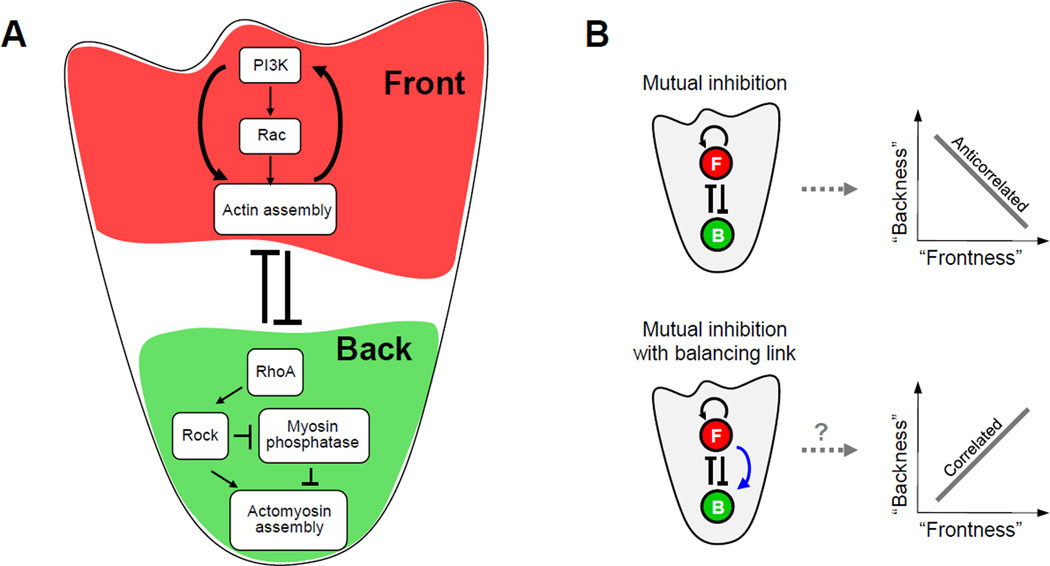
Neutrophils are fast-moving first responders of the immune system that are essential for the innate response against invading pathogens. Upon stimulation with chemoattractant, neutrophils adopt a polarized morphology by forming a protrusive F-actin enriched leading edge (front) and a contractile myosin-enriched trailing edge (back). A large body of work has identified many biochemical components and interactions within the neutrophil polarity network and placed them into distinct front and back signaling modules (Figure 1A) (Stephens et al., 2008; Xu et al., 2003) whose activities regulate the behaviors of the morphological front and back. Current studies suggest a core network motif in which local mutual inhibition between front and back establishes spatially segregated domains, while front positive feedback is a driving force in maintaining polarity.
Figure 1. Core neutrophil polarity network.
A. Simplified schema of the core neutrophil network motif of mutual inhibition between the front (red shaded region) and back (green shaded region) signaling modules together with positive feedback at the front. B. Cartoon illustration of potential relationships between front and back signaling for the core network motif without (top) or with (bottom) a long-range positive link from front to back (blue arrow).
How might this core motif of mutual front-back inhibition and positive front feedback affect the relation between front and back signaling? On the one hand, the positive feedback loop in the front should permit front signals to overpower and strongly diminish back signals in their inhibitory “tug of war” within the cell (Van Keymeulen et al., 2006; Wong et al., 2006); this suggests an anti-correlated trend between the back and front (Figure 1B, top), (Van Keymeulen et al., 2006). On the other hand, a long-range positive link from the front module to the back module has been observed (Kumar et al., 2012; Van Keymeulen et al., 2006) and has been proposed to promote front-back balancing by creating a proportionately stronger back following activations in the front (Van Keymeulen et al., 2006); this suggests a positively correlated trend between the front and back (Figure 1B, bottom).
Here, we explored these possibilities by studying the natural variation of downstream readouts of the front (F-actin) and back (p-MLC2) modules in populations of polarized primary human neutrophils. We performed quantitative image analysis to extract measures of signaling phenotypes (activity and localization) of each of these readouts. We found that the relation between front and back signaling is surprisingly different than originally postulated. Rather than being anti-correlated or positively correlated, back signaling is surprisingly constant across a wide range of front signaling levels (Figures 2 and S1). That is, the back is “buffered” from the front.
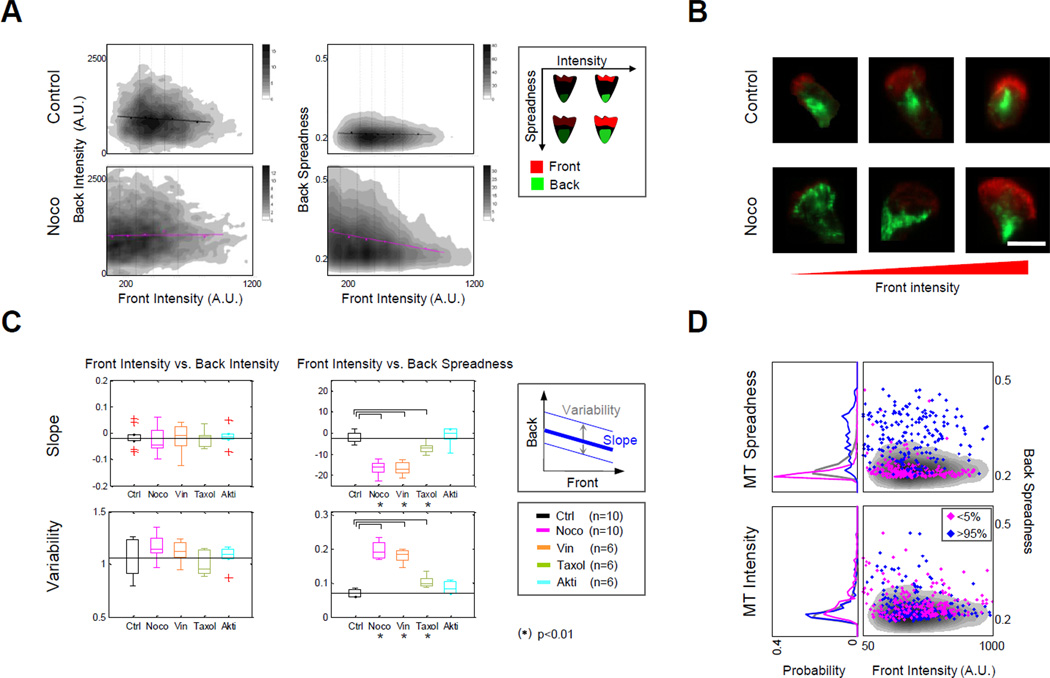
Figure 2. Microtubules buffer back polarity against varying front strength in polarized human neutrophils.
A. Density plots suggest that depolymerization of microtubules with nocodazole reduces the ability of back spreadness to be buffered from changes in front intensity in fMLP-stimulated human neutrophils. (Density plots were derived from pooled data (n=10) with the top and bottom 1% trimmed; replicates are analyzed individually in D.) Regression lines: computed as described in Experimental Procedures. Legend: illustration of polarized neutrophils with varying degrees of intensity or spreadness for front and back signaling markers. B. Representative images of neutrophils treated with or without nocodazole (left to right: low to high F-actin intensity). Colors: red (F-actin); green (p-MLC2). Scale bar: 10µm. C. Summary of regression slope (top) and variability (bottom) between front intensity and back spreadness in replicates of control and drug-treated cells. Slope and variability: shown schematically in box at right and described in Supplemental Information. Box plots: median values (center lines) and 25th and 75th percentiles (box edges) across replicate experiments. The vertical lines extend to the most extreme data points not considered outliers (minima and maxima whiskers). Outliers are plotted individually (red “+”). The back spreadness slope values were expressed in percentages of their theoretical maximum (Supplemental Information). (*): Wilcoxon’s two-sided rank sum test with p-value < 0.01. D. Density plots (right column) of non-drug treated control cells (as in A, top right) overlaid with scatter plot of cells ranked in the bottom 5% (magenta points) or top 5% (blue points) based on intensity (bottom) or spreadness (top) of microtubule staining. Probability plots (left column) reflect densities of scatterplots at right. Gray curve reflects overall population density. See also Figures S1–3 and Table S1.
How is this buffering achieved? Past experimental studies have uncovered evidence that microtubules could act as an intermediate for long-range communication between the front and the back of polarized neutrophils (Kumar et al., 2012; Pestonjamasp et al., 2006). We analyzed neutrophils with pharmacologically disrupted microtubules and found that microtubules additionally play a strong role in buffering back signaling. However, they appear to do so predominantly via their effect on the localization but not the activity of p-MLC2. Experimental disruption of microtubules uncovered an anti-correlated trend between front activity and back localization. These data suggest that buffering depends on the role of microtubules in positively-regulating transport (Van Keymeulen et al., 2006; Xu et al., 2005) rather than the inhibitory sequestration (Xu et al., 2005) of back activators. Thus, although the importance of microtubules in front back communication has been established, we demonstrate here an unanticipated role of microtubules in buffering the localization of back signaling.
To computationally test whether microtubule-based regulation is sufficient to create buffering of back localization, we developed a conceptual mathematical model of the core neutrophil network motif of front positive feedback coupled with front-back mutual inhibition. We found that our model of this core motif recapitulated the anti-correlated trend between front and back observed in microtubule-disrupted neutrophils, and that the addition of a microtubule-mediated positive link from front to back helped to restore buffering. Finally, because the core motif of front positive feedback and front-back mutual inhibition is a conserved topology among various types of migrating cells (Chau et al., 2012; Swaney et al., 2010), we asked what additional links to the core motif could buffer back signaling. We systematically searched over network topologies (Chau et al., 2012; Ma et al., 2009) containing the core motif and found within this collection that all topologies that recapitulated buffering necessarily contained a positive long-range link from front to back. Together, our work demonstrates that: (i) back signaling in neutrophils is surprisingly buffered from variations in front signaling, (ii) microtubules play an essential role in buffering the localization of back signaling and achieve this buffering primarily via back activation, and (iii) a long-range positive link might be a general design principle for insulating spatially segregated signaling domains created via mutual inhibition.
RESULTS
Front and back signaling phenotypes in polarized neutrophils
Previous studies have shown that analysis of cell-to-cell variability can reveal topological properties of signaling networks (Cagatay et al., 2009; Janes et al., 2010; Kollmann et al., 2005; Kuchina et al., 2011; Raj and van Oudenaarden, 2008). Here, we used this approach to examine how back phenotypes vary over a range of observed front phenotypes within populations of polarized neutrophils. To reduce experimentally-induced variability, we made use of primary human neutrophils, which exhibit a higher synchrony of chemotactic responses than cell lines like neutrophil-like HL-60s, and we studied natural fluctuations rather than using genetic or pharmacological disruptions (Van Keymeulen et al., 2006; Xu et al., 2003) to the front or back modules.
Freshly harvested human neutrophils were seeded onto 96-well plates and stimulated with uniform chemoattractant N-formyl-methionyl-leucyl-phenylalanine (fMLP, 10nM). Cell signaling states were assayed at 2 and 3 minutes after stimulation. At these time points, nearly all neutrophils were morphologically polarized (Figure S2A). Cells were fixed and co-stained for F-actin and monophosphorylated myosin light chain 2 (p-MLC2); these readouts provided downstream, integrated readouts of the front and back cytoskeletal signaling modules in each neutrophil (Ku et al., 2012) (Supplemental Information).
Recent work has indicated that network interactions governing polarization of human neutrophils can be phenotype dependent: both the strength and the spatial localization of front and back signaling components–important phenotypes of polarizing neutrophils– were seen to be regulated by different patterns of interactions (Ku et al., 2012). Thus, we measured cell-averaged intensities of F-actin and p-MLC2 (Figure 2A, horizontal axis), and also quantified the spatial localization patterns of F-actin and p-MLC2 by computing their “spreadness”, defined as the degree to which the brightest pixels for each marker were close together (low spreadness value) or far apart (high spreadness value) within each cell (Figure 2A, vertical axis; Supplemental Information) (Ku et al., 2010). In general, a measurement of low spreadness indicates a more polarized state while a measurement of high spreadness indicates a less polarized state. Together, measurement of intensity and spread provided readouts of activity and polarity phenotypes for front and back modules.
Neutrophils produce and retract transient, actin-rich pseudopods as they explore their environments (Zigmond et al., 1981). How does the back respond to these constant changes in the front? From our thousands of individually measured cells, we created density plots for simultaneously measured intensity and spreadness measures for both the p-MLC2 and F-actin readouts. To assess front influence on the back, we calculated and plotted regression lines (Figure 2A, top; Figures S1A–B, black lines). Inspection of one of the four phenotype pairs, namely front spreadness vs. back spreadness, showed a positive correlation. However, for the other three phenotype pairs, p-MLC2 signaling appeared remarkably constant across the natural range of F-actin signaling. This observation raised the question of what network interactions within chemotaxing neutrophils enable this buffering of back signaling from variations in front signaling.
A functional role for microtubules to buffer back polarity from changes in front
Previous studies have demonstrated crosstalk between microtubules and the front and back modules (Ku et al., 2012; Kumar et al., 2012; Pestonjamasp et al., 2006; Van Keymeulen et al., 2006; Xu et al., 2005). We therefore wondered whether microtubules play a role in creating the buffering we observed in the back module. To investigate this possibility, we pretreated neutrophils with nocodazole, a microtubule depolymerizing drug, for 30 minutes before fMLP stimulation and searched for front/back relations that showed significant changes upon drug treatment (Figures 2A–B). To only partially disrupt microtubule functions, we chose a nocodazole concentration (9µM) that is lower than typical treatment conditions previously used in the literature (Xu et al., 2005) and only partially reduces tubulin staining intensity (Ku et al., 2012).
We quantified the effects of microtubule disruption in two ways. First, we compared the regression slopes between back and front signaling in control and nocodazole-treated cells. We found that disruption of microtubules via nocodazole significantly altered the correlation between front intensity and back spreadness (Figure 2C), but not for the other three pairs of front/back phenotypes (Figure S1C, top). Specifically, for nocodazole-treated cells we observed a significant change in anti-correlation (5.7-fold change to slope) between F-actin intensity and p-MLC2 spreadness. Second, we measured variability based on the scatter of back phenotypes for given values of front phenotype (i.e. the dispersion of back phenotypes along the regression line; Figure 2C, gray vertical arrow). Variability increased significantly in the nocodazole-treated condition for both F-actin intensity and F-actin spreadness vs. p-MLC2 spreadness (2.72-fold and 2.64-fold changes respectively) (Figure 2C, bottom; Figure S1C, bottom). We noted that these trends were not due to increased variability in fMLP response times (Figure S2A; in fact, nocodazole-treated cells had a tighter distribution of peak response times than control cells), non-uniform drug effects (Figure S2B), morphological changes or the number of bins used in computing slope (data not shown). Taken together, our measurements of slope and variability suggest that microtubules play a role in keeping the localization of back signaling consistent across the physiological range of F-actin signaling variations.
An intriguing and unresolved question posed by previous work is whether microtubules predominantly act positively or negatively on the back module (Xu et al., 2005), particularly in physiological conditions. In the case of an activating role, microtubules were speculated to direct the transport of GEFs to the back; while in the case of an inhibiting role, microtubules were speculated to sequester these GEFs. In the latter case, a loss of microtubule mass would be expected to cause an increase in p-MLC2 intensity by releasing GEFs throughout the cell. However, our mild nocodazole treatment did not significantly alter the average p-MLC2 intensity; instead, it created a severe disruption in p-MLC2 localization. This suggests a positive role for a microtubule-mediated link in regulating back localization, likely due to transport of back-activating factors.
We sought to investigate the role of microtubules in buffering with two other microtubule inhibitors, vinblastine and taxol (n = 6 replicates each; Figure S3, Table S1). Both vinblastine and taxol inhibit microtubule dynamics while maintaining the mass of polymerized tubulin, but vinblastine additionally blocks microtubule based-transport (Kwan and Kirschner, 2005) while taxol does not. As with nocodazole, neither vinblastine nor taxol affected the buffering of back intensity (vs. either front phenotype) (Figure 2C; Figure S1C). Additionally, the loss of buffering (as measured by slope and/or variation) to back localization observed in nocodazole-treated cells was also observed in vinblastine-treated cells; however, in taxol-treated cells the loss of buffering, though statistically significant, was greatly diminished (Figure 2C; Figure S1C). Reassuringly, no apparent loss of buffering was observed for cells treated with Akt1/2 inhibitor (Akti), a drug that does not target microtubule machinery (Figure 2C; Figure S1C).
Next, we examined our control (non-drug-treated) cells to see whether natural variation in microtubule properties could reveal similar trends. We reanalyzed our images of nondrug treated cells, ranked the control cells by the intensity or spreadness of microtubule staining, and studied the buffering of the top and bottom 5% of the cells in these categories. Cells in the top and bottom 5% of microtubule intensity showed similar abilities to buffer (Figure 2D, bottom). However, the 5% of cells with the lowest microtubule spreadness showed remarkably consistent back localization, while the 5% of cells with the most microtubule spreadness showed dramatically increased variability (Figure 2D, top). Taken together, our analysis of both natural and drug-induced perturbations of microtubules was consistent with the conclusion that the localization of microtubules is more important than the total mass of microtubules for creating back buffering.
A conceptual mathematical model for investigating the role of microtubules in buffering back polarity
Is the network topology suggested by the experimental findings (mutual inhibition between front and back, a positive feedback loop in the front, and microtubules acting positively in a spatially dependent manner on the back) sufficient to produce the experimentally observed buffering of back polarity against front intensity? On one hand, one may see intuitively that microtubule-mediated activation of the back (implicated above) may counter mutual inhibition between the front and back. On the other hand, it is not clear whether the addition of this positive long-range link is sufficient to explain the observed buffering effect. Therefore, we made use of mathematical modeling to investigate the behavior that emerges from links between the front, back, and microtubules.
We chose a phenomenological rather than a mechanistic approach for modeling network interactions as many detailed network parameters are still unknown and our primary goal was to understand the fundamental behaviors emerging from our identified network interactions (Rodrigue and Philippe, 2010). Our mathematical model of polarity was designed in two steps: the first step captured the core motif of front and back interactions; and the second step captured microtubule-mediated communication between front and back. We note that this modeling effort is not intended to build an “end-to-end” model of neutrophil chemotaxis that predicts the entire process from chemoattractant sensing to symmetry breaking to motility. Rather, we focused on how neutrophils stabilize their asymmetry once asymmetry is established. As previously noted, breaking symmetry is not enough to maintain stable polarity (Van Keymeulen et al., 2006; Wong et al., 2006), and there is a need for a quantitative model of how polarity is not only initiated but stabilized (Van Keymeulen et al., 2006).
Step 1: Modeling the core motif
Many mathematical models have been proposed to investigate potential mechanisms underlying the initial symmetry breaking that establishes polarity in a cell (Gamba et al., 2005; Irimia et al., 2009; Jilkine et al., 2007; Keren et al., 2008; Levchenko and Iglesias, 2002; Meinhardt, 1999; Narang, 2006; Neilson et al., 2011; Onsum and Rao, 2007; Otsuji et al., 2007; Weiner et al., 2007; Xiong et al., 2010). To model the core motif, we chose as our starting point a previously developed model for neutrophils in which front and back distributions evolve via a system of mass-conserved, reaction-diffusion equations (Figure 3A, top left, gray shaded background) (Supplemental Information) (Otsuji et al., 2007). This model captured the establishment of polarization for front and back signaling domains on a cell membrane represented as a 1-D interval, with stimulant presented in a spatial gradient. We modified this model as follows (Supplemental Information, Table S2)). First, we simplified the model to capture interactions between a single front and a single back component. Second, we extended the model so that the spatial distributions of front and back were simulated on a 1-D circular (rather than an interval) cell membrane. Third, to mimic the conditions of our experiments conducted on human neutrophils, we allowed cells to spontaneously polarize in a uniform but noisy stimulation field rather than a gradient.
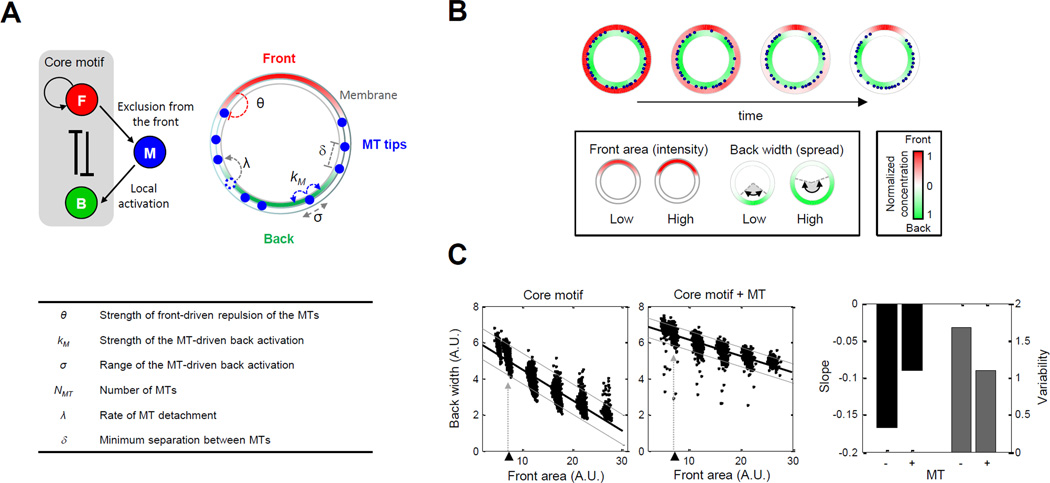
Figure 3. Mathematical model of microtubule interactions with front and back reveals a role for buffering back polarity.
A. Illustration of the neutrophil polarity model featuring interactions among front (red), back (green) and microtubules (blue). (Top left) Two additional interactions were added to the “core” motif accounting for the exclusion of microtubules from the front and microtubule-mediated activation of the back. (Top right and table) Parameters used to model microtubule-mediated front-to-back interaction (Supplemental Information). See also Figure S4A and Table S2. B. Sample outcome of polarization from simulated model. Cell membrane is visualized with an annulus; blue dots represent the location of microtubule tips on the membrane. Red/green color map: spatial distribution of active front/back components. For visualization, the maximum values of front and back concentrations are both normalized to one. For each polarized cell, the front area and back width were measured as proxies of the front intensity and back spreadness (Supplemental Information). C. Scatter plots of back width versus front area obtained by sampling parameters. Top left/middle panels: without/with microtubules. Thick black lines: regression lines. Lower and upper gray lines: spreadness around regression line (Supplemental Information). Triangles and dotted lines refer to data points obtained by varying the front amount around its nominal value. Bar graph: regression slope and variability of back width versus front area.
To simulate naturally occurring variability, we generated populations of “virtual” cells by randomly sampling parameters of the core motif within a small (1.5-fold) range of their nominal values (Otsuji et al., 2007) (see Supplemental Information for justification of nominal parameter values; Table S2). We additionally varied the total concentration of the front module over a larger (4-fold) concentration range to mimic variation to front signaling (Supplemental Information). In total, we generated 6,000 cells (1,000 per each of 6 front concentrations). As proxies for front intensity and back polarity, we computed the area under the front concentration curves (front area) and the width at half-maximal range of the back concentration curves (back width), respectively (Supplemental Information). Based on these simulations, we found that increased front concentrations resulted in decreased back widths, which led to a pronounced anti-correlation between front and back (Figure 3C). These results were consistent with our experimental observations of cells with disrupted microtubules (Figure 2B, bottom right; Figure 2D, right).
Step 2: adding microtubule interactions
A large body of computational work has also proposed detailed mathematical models of microtubules (Ebbinghaus and Santen, 2011; Flyvbjerg et al., 1994; Mishra et al., 2005; VanBuren et al., 2005) and examined their functions in different contexts, such as chromosomal spindle organization (Gay et al., 2012; Loughlin et al., 2010) and the establishment of polarity in leukocytes (Baratt et al., 2008; Irimia et al., 2009). For our phenomenological model, we focused on experimental findings related to the distribution of microtubules and the role of microtubules in transporting back activators. First, in unstimulated primary human neutrophils microtubules are uniformly distributed, but, after neutrophils are stimulated with chemoattractant, microtubules are rapidly excluded from the front and reorient to the sides and backs of cells (Eddy et al., 2002). Second, microtubules are involved in the activation and spatial distribution of back signaling components. As mentioned previously, microtubules locally deliver GEFs, some of which regulate localization of RhoA signaling activity (Bement et al., 2005; Rogers et al., 2004; Wong et al., 2007). Based on these experimental findings, we modeled two interactions between microtubules and the core polarity motif: exclusion of microtubules from the front and microtubule-based activation of the back (Figure 3A; Figure S4A). Together, these two interactions constituted a long-range, positive link from front to back.
Our inclusion of microtubule interactions required an additional six parameters: (exclusion) the strength of front-driven exclusion of the microtubules, θ; (activation) the strength, kM, and the spatial range, σ, of microtubule-based back activation; and (microtubule distribution) the total number of microtubule cables, NMT, the rate of microtubule repositioning, λ, and the minimum separation between individual microtubules, δ. In our model, the locations of microtubule cables were represented simply by the positions of their tips on the cell membrane (Figure 3A, top right; blue circles).
Could our extended model with microtubule interactions recapitulate the experimentally observed buffering of back (Figure 2B)? In our simulations, we started with uniform distributions for front and back, and uniformly randomly chosen microtubule tip positions. During the simulation, cells rapidly underwent random symmetry breaking: front and back components self-organized into distinct signaling domains on the cell membrane, while microtubule tips also broke their uniform distributions to reorganize themselves towards the back (Figure 3B, top). We found that in the presence of microtubules the slope decreased by ~46% and variability decreased by ~35%. (In general, decreasing model parameters that helped deliver or spread back activation decreased buffering (data not shown).) Thus, consistent with our experimental findings, our numerical studies suggested that the addition of a positive, long-range link mediated by microtubules could help to buffer back localization from front intensity variations within a cell and reduce variability of back signaling localization from cell to cell.
Systematic search for network topologies that buffer back from front
An intriguing question is whether the ability to buffer the back could be obtained by adding different links, or combinations of links, to this motif. The segregation of polarity network proteins to opposite poles in various migratory cells is regulated by a circuit containing positive feedback and mutual inhibition (Chau et al., 2012; Swaney et al., 2010). We performed a systematic computational search of network topologies (Chau et al., 2012; Kollmann et al., 2005; Ma et al., 2009) to gain insight into how combinatorial additions of links to the core motif could buffer back polarity (Figure 4A; Figure S4B).
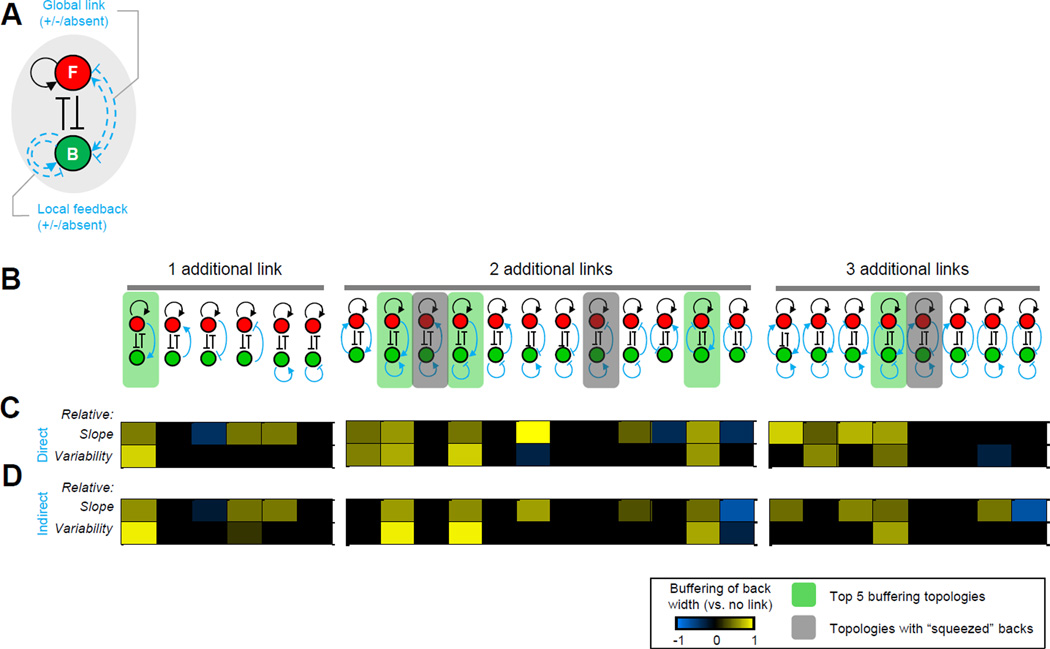
Figure 4. Systematic assessment of the performance of different polarity network topologies in buffering back polarity.
A. Set of possible additional links (blue dashed lines) to the core topology (black lines). B. Schema of additions: one, two, or three positive or negative links. C–D. Heat map of changes to the buffering performance upon addition of direct (C) or indirect (D) links. Heat map color scale: change to the buffering between the new and the original topologies (i.e. link vs. no link). Color bar: cyan or yellow indicates decreased or increased (respectively) buffering capability compared to the core topology. Green shaded background: topologies with best overall buffering performance for both direct and indirect model implementations. Gray shaded background: topologies where the back was excessively “squeezed” into a narrow region. See also Figure S4B–C and Table S3.
To identify general principles (and to make this search computationally tractable), we simplified and abstracted mechanisms of feedback and crosstalk. We again began with our modified model of the core motif. We implemented both positive and negative long-range interactions between front and back. We additionally considered local positive or negative feedback at the back. We excluded network topologies that would have simply altered the strength of any existing link within the core circuit such as combining negative and positive links at the front. The set of all possible non-redundant additions to the core topology contained 6 topologies with one additional link, 12 topologies with two additional links and 8 topologies with three additional links (Figure 4B; Figure S4C). We chose interaction strengths for these additional links that were large enough to have a noticeable effect compared with the reference model yet not so large as to eliminate polarization or overpower the original core topology (Supplemental Information; Table S3).
As before, we randomly generated “virtual” cells (n = 1000) and measured the width of back signaling in polarized cells (Supplemental Information). To compare buffering performance, we again extracted the regression slope of front area versus back width from the scatter plots and the variability of back width along the regression line (Supplemental Information). We then computed the relative regression slopes or variabilities as measured by the logarithm of the ratio between these values for an extended model and the core motif (Supplemental Information). A value of zero meant that the model offered no change to regression slope or variability, while a positive (negative) value indicated increased (diminished) buffering capabilities. Interestingly, we found that only the topology containing a long-range front-to-back positive interaction improved back buffering based on both metrics (Figure 4B, topologies with green shaded background). In several topologies, the back component was constantly squeezed into a narrow region on the membrane (Figure 4B, topologies with grey shaded background). While such configurations of front and back polarization could seemingly lead to high values of buffering, they consistently resulted in unbalanced polarity (strong front and weak back) and were hence discarded from our analysis.
Our study also revealed that the directionality of the additional long-range link is important: the addition of a reversed long-range positive link from back to front did not buffer back width. This was due to pre-existing asymmetries in the core motif, namely: positive feedback at the front, and a greater total amount of front than back components (based on existing literature (Michaelson et al., 2001); Table S2, u2 versus u4). As a consequence, models with symmetric topologies (with respect to front and back) need not have similar buffering performance in our simulations. We further observed that the network with an additional back negative feedback link resulted in a significant loss of polarization. In this case, an inhibitory strength that was relatively weak (compared with the positive feedback link) was required to achieve a reasonable polarization rate; hence, the buffering performance of this topology was similar to that of the reference model. Finally, we observed that similar results were obtained regardless of whether we modeled the long-range links as direct (Figure 4C) or indirect (Figure 4D) connections between front and back (Supplemental Information). Taken together, all topologies in our computational search that recapitulated buffering necessarily contained a positive long-range link from front to back. Thus, short-range negative cross-talk establishes spatially segregated front and back signaling domains, while long-range positive crosstalk insulates the back from changes in front signaling.
DISCUSSION
While mutual inhibition has been established as a front-back signaling network motif responsible for symmetry breaking, several unexplored questions remain, including how the front and back modules vary with respect to one another and how cellular asymmetry is maintained despite those variations. To investigate these questions, we analyzed naturally occurring variation in the relations between downstream readouts of front (F-actin) and back (p-MLC2) signaling observed within tens of thousands of individually polarized primary human neutrophils. We found (for three out of our four phenotype pairs) that back signaling is buffered across a wide range of naturally varying front signaling levels. However, disruption of microtubules by nocodazole revealed significant increases in anti-correlation and/or variability of back signaling localization with respect to front signaling. This result shows that front/back mutual inhibition operates as a core motif in microtubule-disrupted cells and that the presence of microtubules is required to buffer back polarity.
Microtubules are known to be essential for proper regulation of the back module. However, it has been unclear what signaling behaviors of the front and back module emerge from microtubule regulation of the back–or even whether this regulation is primarily activating (Pestonjamasp et al., 2006; Van Keymeulen et al., 2006; Xu et al., 2005) through mechanisms such as spatially localized microtubule delivery of GEFs (Odell and Foe, 2008), or whether this regulation is suppressing (Xu et al., 2005) through polymerized tubulin acting as a passive, global sink for GEFs. Our studies of natural variation in polarizing primary human neutrophils show that microtubules buffer the localization but not the global intensity of p-MLC2 signaling, with microtubules primarily activating rather than suppressing the back. Computational studies of a conceptual polarity circuit, in which microtubules are excluded by the front and transport Rho activators to the back recapitulate the buffering behavior that we experimentally observed. Together, these studies provide a model for how microtubules could mediate a positive, long-range link from front to back.
How does this specific role of microtubules fit in with previous reports of neutrophil chemotaxis after microtubule disruption? We note that, in our nocodazole-treated cells, we did not observe a global change in p-MLC2 intensity after 3 minutes of fMLP exposure, whereas an increase was previously reported for RhoA-GTP after 1 minute of fMLP exposure (Xu et al., 2005). This may be due to our choice of a further downstream readout (p-MLC2 vs. RhoA-GTP), or our lower dose of nocodazole (9µM) compared to higher doses previously used (25µM or 20mM) (Wong et al., 2007; Xu et al., 2005). Depolymerization of microtubules with a high dose of nocodazole could release a global “cloud” of activating GEFs, altering both the intensity and localization of front and back readouts. Such an alteration could produce a dramatic phenotype, but the cause of the phenotype may be hard to dissect, as both sequestration and delivery would be simultaneously lost.
Does the addition of a positive, long-range front-to-back link to the neutrophil core polarity motif provide a general solution to buffer back signaling? Could other combinations of links provide similar buffering? Previous systematic searches through network topologies have provided a powerful approach for identifying network design principles and guiding future experimental searches (Geva-Zatorsky et al., 2006; Ma et al., 2009; von Dassow et al., 2000). Our computational studies predicted that the addition of a long-range front-to-back link buffers back localization from variation of front activity and that other topologies that buffer back signaling also contain this link. Importantly, in the absence of a long-range front-to-back link, back signaling was predicted to be anti-correlated with front signaling, which is not experimentally observed in control neutrophils, but is observed in microtubule-disrupted neutrophils. Since we are reporting the first observation of back localization buffering, the complete set of signaling components and measured parameters responsible for this phenomenon are not yet fully known. Thus, the modeling approach we took was conceptual. More refined models, incorporating larger numbers of components and measured parameters, can be used in the future to guide experimental investigations of mechanism in neutrophils as well as in other cell types that create spatially segregated signaling domains through mutual inhibition.
The design of a molecular network constrains signaling behaviors. Here, in polarized human neutrophils, we have taken a reverse-engineering approach: we inferred network topology by observing cell-to-cell variation and asking which networks permit observed ranges of behavioral variability. Such analysis may reveal trends that may not be visible by studying one component alone, one phenotype alone, or population averages. Similar reverse-engineering analyses will be useful for identifying core network motifs operating in other biological systems and understanding their behavioral consequences.
EXPERIMENTAL PROCEDURES
Isolation of primary neutrophils from human blood
Human neutrophils were isolated as described in (Boyum, 1968). In brief, neutrophils from venous blood of a single healthy donor were purified by dextran sedimentation and density-gradient centrifugation with Ficoll (GE health care, #17-5442-02). Contaminating red blood cells were removed by hypotonic lysis.
Chemotactic assay for drug-treated cells
Purified human neutrophils were plated into 96-well Nunc glass plate (Fisher, #12-566-35), precoated with fibronectin (BD Bioscience, #354008), at a density of ~10,000 cells per well. Cells were incubated at 37oC with 5% CO2 for 20 minutes before adding drugs. The concentrations for each drug were as follows: 9µM for Nocodazole (Sigma, M1404), 5µM for Taxol (Sigma, T1912), 20µM for Vinblastine (Sigma, V1377), and 10uM for Akti (Fisher, #124018). All experiments had multiple repeats (Nocodazole n = 10; Taxol n = 6; Vinblastine n = 6; Akti n = 6) that were performed on at least three different days, including 4 repeats on a single day for each condition. Each replicate experiment had two replicate wells (that were pooled for subsequent analysis). After incubation with drugs for 30 minutes at room temperature (RT), cells were uniformly stimulated with 10nM fMLP for 2 or 3 minutes at 37°C before formaldehyde fixation.
Immunofluorescence assay
Human neutrophils were fixed and permeabilized after fMLP stimulation. The primary antibodies, anti-p-MLC2 (Cell signaling technology, #3675) and anti-alpha tubulin (Cell signaling technology, #2144), were added to each well for overnight incubation at 4°C. After three washes, cells were incubated with secondary antibodies conjugated with Alexa 488 (Invitrogen, A11055) and Alexa 546 (Invitrogen, A10040) for 2 hrs at RT to fluorescently label p-MLC2 and alpha tubulin, respectively. To label F-actin and DNA, cells were incubated with Alexa 647-conjugated phalloidin (Invitrogen, A22287) and Hoechst 33342 (Invitrogen, H1399), respectively, for 30 minutes at RT followed by three washes.
Image acquisition for fixed cells assay
All fluorescence images were acquired using a BD Pathway 855 Bioimager (BD Biosciences) equipped with laser auto-focus system, Olympus 40x objective lens and high resolution Hamamatsu ORCA ER CCD camera using 1×1 camera binning. Image acquisition was controlled by AttoVision v1.5 (BD Biosciences).
Data Analysis
Image quality control
We manually inspected all fluorescence images and discarded those presenting obvious anomalies (e.g. focus issues and abnormal fluorescence staining). Images with poorly segmented cells were re-segmented with manually optimized segmentation parameters.
Identification of cellular regions
Image background correction was done using the National Institute of Health ImageJ software (Rasband et al., 1997–2008). Cellular regions were determined using a watershed-based segmentation algorithm that first retrieved nuclear regions using DNA staining then combined multiple cytosolic region markers to identify cellular boundaries. To account for the polymorphonuclear nature of neutrophil DNA, we used a segmentation algorithm that automatically merged multiple segmented regions into one cell to avoid oversegmentation (Ku et al., 2010). Cellular regions located at the edge of an image or sharing long boundaries with neighbor cells were also discarded to avoid erroneous characterization of polarization patterns.
Cellular feature extraction
For each segmented cellular region and readout for front (F-actin) or back (p-MLC2), we extracted the average intensity and the spreadness (see Supplemental Information for details).
Computing slope and variability of back vs. front phenotypes
Given a pair of front and back phenotypes, (pF, pB), cells were sorted by increasing values of pF and partitioned into Q (=5) bins with equal numbers of cells. Slope. The mean value of pB in each bin was computed, and the Matlab built-in function regress.m was then used to compute a regression line through these means. Variability. We estimated the variability by: 1) sorting all values of pB by their height difference to the regression line; 2) shifting the height of the best-fitting regression line up or down to coincide with the two data points at the 90th or 10th percentiles of this height measure, respectively; then 3) reporting the height difference between the two shifted lines. See Supplemental Information for details.
Mathematical Models
The mathematical models were modified from a mass-conserved reaction-diffusion mechanism originally proposed by Otsuji and colleagues (Otsuji et al., 2007) that described the qualitative model proposed by Bourne and colleagues (Xu et al., 2003). Details of the mathematical model and general network topology search may be found in Supplemental Information.
Supplementary Material
Highlights.
Back signaling in neutrophils is remarkably buffered from variations in front signaling.
Microtubules play an essential role in buffering the localization of back signaling.
Microtubules achieve this buffering via positive and spatially localized activation.
A long-range positive link is a network design principle for implementing buffering.
ACKNOWLEDGEMENTS
We thank Neal Alto, Henry Bourne, Min Chen, Gaudenz Danuser, Alexandra Jilkine, Luke Rice, Michael Rosen, Hongtao Yu, and members of the Altschuler, Weiner, and Wu labs for critical feedback. ODW was supported by NIH GM084040. LFW and SJA were supported by the NIH (R01CA133253, R01 GM071794) and the Welch Foundation (I-1644, I-1619).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- Baratt Arkhipov, et al. An experimental and computational study of effects of microtubule stabilization on T-cell polarity. PLoS One. 2008;3:e3861. doi: 10.1371/journal.pone.0003861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bement Benink, et al. A microtubule-dependent zone of active RhoA during cleavage plane specification. J Cell Biol. 2005;170:91–101. doi: 10.1083/jcb.200501131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyum Isolation of mononuclear cells and granulocytes from human blood. Isolation of monuclear cells by one centrifugation, and of granulocytes by combining centrifugation and sedimentation at 1 g. Scand J Clin Lab Invest Suppl. 1968;97:77–89. [PubMed] [Google Scholar]
- Cagatay Turcotte, et al. Architecture-dependent noise discriminates functionally analogous differentiation circuits. Cell. 2009;139:512–522. doi: 10.1016/j.cell.2009.07.046. [DOI] [PubMed] [Google Scholar]
- Chau Walter, et al. Designing synthetic regulatory networks capable of self-organizing cell polarization. Cell. 2012;151:320–332. doi: 10.1016/j.cell.2012.08.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ebbinghaus, Santen Theoretical modeling of aging effects in microtubule dynamics. Biophys J. 2011;100:832–838. doi: 10.1016/j.bpj.2010.11.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eddy Pierini, et al. Microtubule asymmetry during neutrophil polarization and migration. Mol Biol Cell. 2002;13:4470–4483. doi: 10.1091/mbc.E02-04-0241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flyvbjerg Holy, et al. Stochastic dynamics of microtubules: A model for caps and catastrophes. Phys Rev Lett. 1994;73:2372–2375. doi: 10.1103/PhysRevLett.73.2372. [DOI] [PubMed] [Google Scholar]
- Gamba de Candia, et al. Diffusion-limited phase separation in eukaryotic chemotaxis. Proc Natl Acad Sci U S A. 2005;102:16927–16932. doi: 10.1073/pnas.0503974102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gay Courtheoux, et al. A stochastic model of kinetochore-microtubule attachment accurately describes fission yeast chromosome segregation. J Cell Biol. 2012;196:757–774. doi: 10.1083/jcb.201107124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geva-Zatorsky Rosenfeld, et al. Oscillations and variability in the p53 system. Molecular systems biology. 2006;2:2006 0033. doi: 10.1038/msb4100068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irimia Balazsi, et al. Adaptive-control model for neutrophil orientation in the direction of chemical gradients. Biophys J. 2009;96:3897–3916. doi: 10.1016/j.bpj.2008.12.3967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janes Wang, et al. Identifying single-cell molecular programs by stochastic profiling. Nat Methods. 2010;7:311–317. doi: 10.1038/nmeth.1442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jilkine Maree, et al. Mathematical model for spatial segregation of the Rho-family GTPases based on inhibitory crosstalk. Philosophical Transactions of the Royal Society (part B) 2007;69:1943–1978. doi: 10.1007/s11538-007-9200-6. [DOI] [PubMed] [Google Scholar]
- Keren Pincus, et al. Mechanism of shape determination in motile cells. Nature. 2008;453:475–480. doi: 10.1038/nature06952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kollmann Lovdok, et al. Design principles of a bacterial signalling network. Nature. 2005;438:504–507. doi: 10.1038/nature04228. [DOI] [PubMed] [Google Scholar]
- Ku Wang, et al. On Identifying Information from Image-Based Spatial Polarity Phenotypes in Neutrophils. Proc IEEE Int Symp Biomed Imaging. 2010;14–17:1029–1032. doi: 10.1109/ISBI.2010.5490165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ku Wang, et al. Network crosstalk dynamically changes during neutrophil polarization. Cell. 2012;149:1073–1083. doi: 10.1016/j.cell.2012.03.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuchina Espinar, et al. Temporal competition between differentiation programs determines cell fate choice. Mol Syst Biol. 2011;7:557. doi: 10.1038/msb.2011.88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar Xu, et al. Cdc42 regulates neutrophil migration via crosstalk between WASp, CD11b, and microtubules. Blood. 2012;120:3563–3574. doi: 10.1182/blood-2012-04-426981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwan, Kirschner A microtubule-binding Rho-GEF controls cell morphology during convergent extension of Xenopus laevis. Development. 2005;132:4599–4610. doi: 10.1242/dev.02041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levchenko, Iglesias Models of eukaryotic gradient sensing: application to chemotaxis of amoebae and neutrophils. Biophys J. 2002;82:50–63. doi: 10.1016/S0006-3495(02)75373-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loughlin Heald, et al. A computational model predicts Xenopus meiotic spindle organization. J Cell Biol. 2010;191:1239–1249. doi: 10.1083/jcb.201006076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma Trusina, et al. Defining network topologies that can achieve biochemical adaptation. Cell. 2009;138:760–773. doi: 10.1016/j.cell.2009.06.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meinhardt Orientation of chemotactic cells and growth cones: models and mechanisms. Journal of cell science. 1999;112(Pt 17):2867–2874. doi: 10.1242/jcs.112.17.2867. [DOI] [PubMed] [Google Scholar]
- Michaelson Silletti, et al. Differential localization of Rho GTPases in live cells: regulation by hypervariable regions and RhoGDI binding. J Cell Biol. 2001;152:111–126. doi: 10.1083/jcb.152.1.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mishra Kunwar, et al. Dynamic instability of microtubules: effect of catastrophe-suppressing drugs. Phys Rev E Stat Nonlin Soft Matter Phys. 2005;72 doi: 10.1103/PhysRevE.72.051914. 051914. [DOI] [PubMed] [Google Scholar]
- Narang Spontaneous polarization in eukaryotic gradient sensing: a mathematical model based on mutual inhibition of frontness and backness pathways. J Theor Biol. 2006;240:538–553. doi: 10.1016/j.jtbi.2005.10.022. [DOI] [PubMed] [Google Scholar]
- Neilson Veltman, et al. Chemotaxis: a feedback-based computational model robustly predicts multiple aspects of real cell behaviour. PLoS biology. 2011;9:e1000618. doi: 10.1371/journal.pbio.1000618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Odell, Foe An agent-based model contrasts opposite effects of dynamic and stable microtubules on cleavage furrow positioning. J Cell Biol. 2008;183:471–483. doi: 10.1083/jcb.200807129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Onsum, Rao A mathematical model for neutrophil gradient sensing and polarization. PLoS Comput Biol. 2007;3:e36. doi: 10.1371/journal.pcbi.0030036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otsuji Ishihara, et al. A mass conserved reaction-diffusion system captures properties of cell polarity. PLoS Comput Biol. 2007;3:e108. doi: 10.1371/journal.pcbi.0030108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pestonjamasp Forster, et al. Rac1 links leading edge and uropod events through Rho and myosin activation during chemotaxis. Blood. 2006;108:2814–2820. doi: 10.1182/blood-2006-01-010363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raj, van Oudenaarden Nature, nurture, or chance: stochastic gene expression and its consequences. Cell. 2008;135:216–226. doi: 10.1016/j.cell.2008.09.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodrigue, Philippe Mechanistic revisions of phenomenological modeling strategies in molecular evolution. Trends Genet. 2010;26:248–252. doi: 10.1016/j.tig.2010.04.001. [DOI] [PubMed] [Google Scholar]
- Rogers Wiedemann, et al. Drosophila RhoGEF2 associates with microtubule plus ends in an EB1-dependent manner. Curr Biol. 2004;14:1827–1833. doi: 10.1016/j.cub.2004.09.078. [DOI] [PubMed] [Google Scholar]
- Stephens Milne, et al. Moving towards a better understanding of chemotaxis. Curr Biol. 2008;18:R485–R494. doi: 10.1016/j.cub.2008.04.048. [DOI] [PubMed] [Google Scholar]
- Swaney Huang, et al. Eukaryotic chemotaxis: a network of signaling pathways controls motility, directional sensing, and polarity. Annual review of biophysics. 2010;39:265–289. doi: 10.1146/annurev.biophys.093008.131228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Keymeulen Wong, et al. To stabilize neutrophil polarity, PIP3 and Cdc42 augment RhoA activity at the back as well as signals at the front. Journal of Cell Biology. 2006;174:437–445. doi: 10.1083/jcb.200604113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanBuren Cassimeris, et al. Mechanochemical model of microtubule structure and self-assembly kinetics. Biophys J. 2005;89:2911–2926. doi: 10.1529/biophysj.105.060913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- von Dassow Meir, et al. The segment polarity network is a robust developmental module. Nature. 2000;406:188–192. doi: 10.1038/35018085. [DOI] [PubMed] [Google Scholar]
- Weiner Marganski, et al. An actin-based wave generator organizes cell motility. PLoS Biol. 2007;5:e221. doi: 10.1371/journal.pbio.0050221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wong Pertz, et al. Neutrophil polarization: spatiotemporal dynamics of RhoA activity support a self-organizing mechanism. Proc Natl Acad Sci U S A. 2006;103:3639–3644. doi: 10.1073/pnas.0600092103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wong Van Keymeulen, et al. PDZRhoGEF and myosin II localize RhoA activity to the back of polarizing neutrophil-like cells. J Cell Biol. 2007;179:1141–1148. doi: 10.1083/jcb.200706167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiong Huang, et al. Cells navigate with a local-excitation, global-inhibition-biased excitable network. Proceedings of the National Academy of Sciences of the United States of America. 2010;107:17079–17086. doi: 10.1073/pnas.1011271107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu Wang, et al. Divergent signals and cytoskeletal assemblies regulate self-organizing polarity in neutrophils. Cell. 2003;114:201–214. doi: 10.1016/s0092-8674(03)00555-5. [DOI] [PubMed] [Google Scholar]
- Xu Wang, et al. Neutrophil microtubules suppress polarity and enhance directional migration. Proceedings of the National Academy of Sciences of the United States of America. 2005;102:6884–6889. doi: 10.1073/pnas.0502106102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zigmond Levitsky, et al. Cell polarity: an examination of its behavioral expression and its consequences for polymorphonuclear leukocyte chemotaxis. J Cell Biol. 1981;89:585–592. doi: 10.1083/jcb.89.3.585. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.