TherMos: Estimating protein–DNA binding energies from in vivo binding profiles

Abstract

Accurately characterizing transcription factor (TF)-DNA affinity is a central goal of regulatory genomics. Although thermodynamics provides the most natural language for describing the continuous range of TF-DNA affinity, traditional motif discovery algorithms focus instead on classification paradigms that aim to discriminate ‘bound’ and ‘unbound’ sequences. Moreover, these algorithms do not directly model the distribution of tags in ChIP-seq data. Here, we present a new algorithm named Thermodynamic Modeling of ChIP-seq (TherMos), which directly estimates a position-specific binding energy matrix (PSEM) from ChIP-seq/exo tag profiles. In cross-validation tests on seven genome-wide TF-DNA binding profiles, one of which we generated via ChIP-seq on a complex developing tissue, TherMos predicted quantitative TF-DNA binding with greater accuracy than five well-known algorithms. We experimentally validated TherMos binding energy models for Klf4 and Esrrb, using a novel protocol to measure PSEMs in vitro. Strikingly, our measurements revealed strong non-additivity at multiple positions within the two PSEMs. Among the algorithms tested, only TherMos was able to model the entire binding energy landscape of Klf4 and Esrrb. Our study reveals new insights into the energetics of TF-DNA binding in vivo and provides an accurate first-principles approach to binding energy inference from ChIP-seq and ChIP-exo data.

INTRODUCTION

One of the central goals of functional genomics is to understand how transcription factors (TFs) bind to specific functional elements in the genome to regulate gene expression. This specificity is conferred primarily by the intrinsic sequence preference, i.e. the binding energy landscape, of the DNA-binding TF. If a TF binds nucleotide sequences of length n, this landscape is defined by the TF-DNA binding free energy of each of the 4ⁿ possible DNA n-mers. However, it is common to assume that each nucleotide contributes independently to the binding energy, and that the total interaction energy is, therefore, merely the sum of the n individual contributions. This is the so-called ‘additive’ model of TF-DNA binding energy (1). Although deviations from this additive model have long been noted (2,3), it is still the most widely used paradigm because of its simplicity. More general algorithms that attempt to fit non-additive models to experimental data could be susceptible to overfitting because of the large number of free parameters in such models. This is particularly true when the training data are subject to modulation by in vivo factors, such as chromatin state. Thus, in practice, even when non-additivity is a known or suspected feature of TF-DNA binding energy, it is important to define the best possible additive approximation to the non-additive landscape. All widely used algorithms for in vivo motif discovery adopt this additive strategy, and so do we.

With the aforementioned assumption, the binding energy landscape can be represented by a position-specific energy matrix (PSEM) with n columns and four rows—one for each of the four possible nucleotides. However, for historical reasons, PSEMs have rarely been used to represent TF-DNA binding energy. Traditionally, TF-DNA binding energy models have been inferred from limited data sets comprising a small number of experimentally validated binding sites, either in the genome or in vitro oligomer binding assays (4). Such data sets are usually insufficient for quantitative estimation, and the DNA sequences are, therefore, merely classified as ‘bound’ or ‘unbound’. The binding energy landscape is modeled by a ‘position weight matrix’ (PWM), which is most commonly defined as the log-likelihood (or log-odds relative to background DNA sequences) of observing a specific nucleotide at a specific position in the bound n-mers. Many algorithms have been developed to infer PWM motifs from TF-DNA binding data using the traditional bound–unbound paradigm, including the widely used MEME (5) and Weeder (6).

It has been shown that, when the PWM is derived from sites bound at low TF concentrations in vitro, it is approximately equivalent to the PSEM (7,8). However, the proportionality of PWMs to binding energies is only approximate, as there is some arbitrariness in the classification of DNA sequences as bound or unbound. In reality, the occupancy (binding probability) of a TF at any DNA site varies continuously between zero and one. The bound–unbound approach requires selection of an arbitrary threshold for discretizing this continuously variable binding level. Consequently, different thresholds for defining bound sites would yield different PWMs for the same TF (8).

With the advent of high-throughput microarray technology, it became possible to quantify TF-DNA binding on a genomic scale using chromatin immunoprecipitation followed by array hybridization (ChIP-chip). The MatrixREDUCE algorithm (9) was developed to exploit the quantitative binding information in ChIP-chip by directly fitting a thermodynamic position-specific affinity matrix (PSAM) to the range of binding intensities observed in the probed genomic regions. The logarithm of the PSAM is equal to the negative of the PSEM (9). This algorithm explicitly accounts for the continuous nature of binding levels. However, as it was designed for ChIP-chip data, which typically has low resolution (hundreds of base pairs), the algorithm only makes use of the aggregate binding intensity within an entire genomic segment.

Recently, ChIP-chip has been supplanted by ChIP-seq, which uses massively parallel sequencing instead of array hybridization to identify TF-bound regions genome wide (10). ChIP-seq provides higher resolution (tens of base pairs) and more comprehensive genome-wide profiling of binding sites than ChIP-chip. Moreover, ChIP-seq peak height is well correlated with quantitative binding levels (11). Although MatrixREDUCE applies equally well to ChIP-seq data, its aggregate-intensity approach cannot fully exploit the rich information content of the ChIP-seq tag distribution. Zhao et al. (12) have recently developed an algorithm for inferring binding energy models from high-throughput sequencing-based data on TF-DNA binding. However, this method (BEEML) is only applicable to data on in vitro binding of TFs to short DNA fragments. We are not aware of any equivalent algorithms for binding energy inference from in vivo ChIP-seq data. To fully exploit the information contained in the shape of the ChIP-seq tag profile, we developed a PSEM estimation method named Thermodynamic Modeling of ChIP-seq (TherMos). TherMos can also be used on ChIP-exo data, which provide even higher spatial resolution than ChIP-seq (13).

Through cross-validation on five ChIP-seq data sets from mouse embryonic stem (mES) cells (14), one newly generated ChIP-seq data set from mouse embryonic spinal cord (GEO accession number GSE43159), and one ChIP-exo data set from Saccharomyces cerevisiae (13), we found that the TherMos binding energy model has higher accuracy than other widely used algorithms. We further confirmed the high accuracy of TherMos by performing systematic in vitro measurements of quantitative TF-DNA affinity. In the course of in vitro validation, we discovered that both of the TFs analyzed in this manner showed striking deviations from the additive binding energy model. As a result of this non-additivity, the in vivo motifs detected by the traditional PWM-based algorithms were accurate only on high-affinity sequences. In contrast, the TherMos in vivo PSEM was predictive of in vitro binding affinity over the entire range of sequences tested.

MATERIALS AND METHODS

Biophysical model

The interaction between a TF and a DNA sequence can be written as

where TF is the TF, D is the DNA sequence and TF·D is the complex of the TF and the DNA sequence. The dissociation equilibrium constant of the reaction K_d can be written as

(1)

where [ ] represents concentration, ΔG is Gibbs free energy change of the reaction, R is gas constant and T is temperature.

The occupancy O(D) of any DNA sequence D by the TF is defined as the probability of binding or fraction bound for that sequence, and it can be written as (8,9,12)

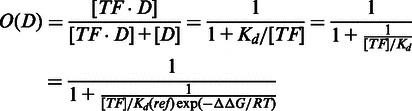(2)

where 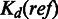is the dissociation equilibrium constant for the reaction between the TF and the reference sequence. Hence,

(3)

Position-specific energy matrix

For an n-mer motif, a PSEM is defined as a 4 × n matrix with the rows 1–4 correspond to A, T, G, C, respectively. Each element of the PSEM contains relative DNA–protein binding free energy change to the reference sequence (in unit of RT), 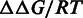[Equation (3)], directly related to the actual discrimination energies in physical units. Therefore, only three elements in each column of the PSEM are independent (15,16). For convenience, the elements in the last row of the PSEM are set to zeros. Smaller 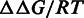means stronger binding affinity compared with the reference sequence. The independence among the positions in the target sequence is assumed (17). Consequently, 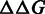is additive across positions in the binding site.

ChIP-seq data sets

The in vivo ChIP-seq data were derived from chromatin extracted from the dorsal domain of the dissected spinal cords of embryonic day 12.5 (E12.5) mouse embryos. Immunoprecipitation was performed using a monoclonal Mash1/Ascl1 antibody as described in Castro et al. (18). ChIP-seq data for the five mES cell TFs (Esrrb, Klf4, Stat3, Zfx and n-Myc) are from Chen et al. (14). Yeast Reb1 ChIP-exo data are from Rhee and Pugh (13).

Peak calling

TherMos takes a set of externally generated peak calls as input. Here, we used the MACS algorithm with default settings and a P-value threshold of 1 × 10⁻¹⁰ to call peaks (19). The control library from Chen et al. (14) for ChIP-seq data set in mES cells is used. No control library is available for Mash1 and Reb1 data set. The numbers of peak calls are 31 621, 7508, 1380, 9678, 5320 and 2521 for Esrrb, Klf4, Stat3, Zfx, n-Myc and Mash1, respectively. For ChIP-exo of Reb1, 1776 peaks called in Rhee and Pugh (13) were used. To save computational time, one-third of the Esrrb peak calls (10 540) were randomly chosen as input for TherMos and other algorithms.

TherMos implementation

In TherMos, we assume that binding affinities are only determined by the interaction between TFs and DNA sequences. Effects of chromatin status, competing nucleosomes and cooperative or competing TFs are neglected. The free parameters optimized in TherMos are the 3 × n elements in the PSEM for an n-mer motif (n is user-specified), plus the scaled TF concentration parameter [TF]/K_d(ref) [Equation (2)] (15). Input of TherMos include a set of ChIP-seq tag coordinates, a set of control-library tag coordinates and a set of externally generated peak calls. TherMos is designed to exploit the information from ChIP-seq peak shape within peak calls.

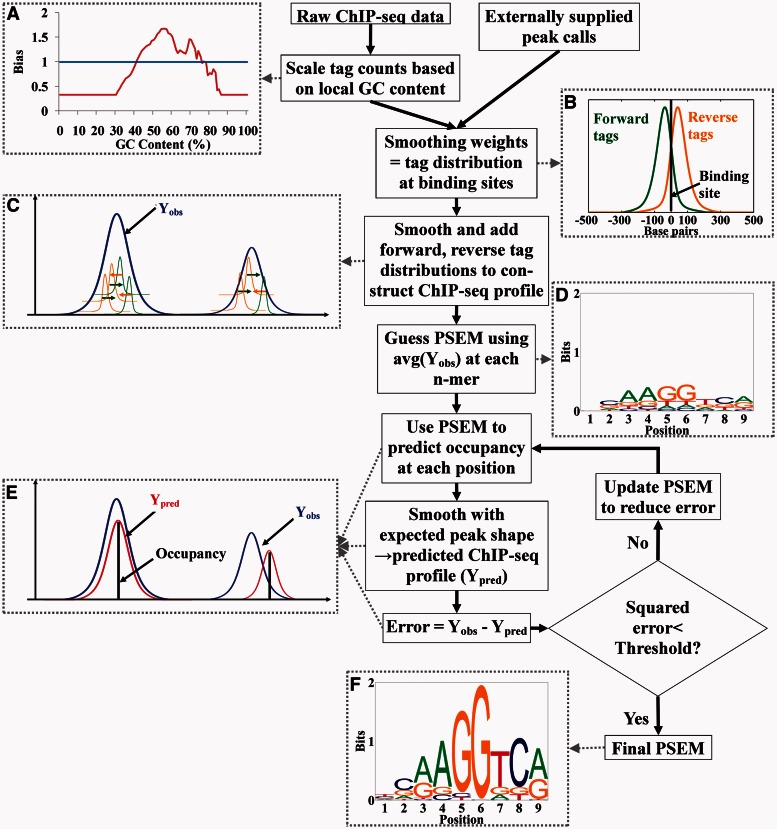
Based on the GC content of the control library, TherMos first performs GC bias correction on the ChIP-seq tag counts (Figure 1A and Supplementary Information). Second, a smoothing weight, i.e. the average shape of the tag distribution at binding sites, is derived for the forward and reverse GC-corrected tags (Figure 1B and Supplementary Information). Within 1-kb regions centered on peak calls, the reverse or forward GC-corrected tag counts are smoothed using the forward or reverse smoothing weights and added to generate a ChIP-seq profile (Y_obs) (Figure 1C).

Figure 1.

Workflow of the TherMos algorithm. (A) Enrichment of tags in the control library as a function of local GC content. (B) Forward and reverse smoothing weights (tag distribution at binding sites) estimated using an iterative peak refinement procedure. Most tag fragments are <100 bp from the binding site. (C) Construction of ChIP-seq profile (Y_obs) from per base pair tag profile. (D) Initial guess of PSEM. (E) Theoretically predicted ChIP-seq profile (Y_pred), based on PSEM and inferred average peak shape. (F) PSEM that best fits the Y_obs.

Y_obs shows some background noise because of randomly generated tags regardless of the specific antibody. A noise level is estimated as the average tag counts of the ChIP-seq library in the whole genome and subtracted from Y_obs. High ChIP-seq peaks are observed because of the low complexity DNA (20) both in the ChIP-seq library and the control library. To eliminate these false-positive peaks, tag densities of the control library within 1-kb region centered on the peak calls are calculated and regions with tag densities >6× inter quartile range are removed.

Next, TherMos generates an initial guess of PSEM as a starting point of the optimization routine (Figure 1D). Each possible n-mer is given a score according to the average height of Y_obs where the n-mer occurs. The n-mer, which has the highest z-score, is chosen as the consensus sequence. The initial guess of PSEM is then constructed from the consensus sequence and its all singly mutated variants based on their average Y_obs.

Then TherMos starts the optimization routine by scanning the PSEM along the genomic sequence to calculate thermodynamic occupancy estimates at each position within 1 kb regions centered on peak calls [Figure 1E and Equation (2)]. An expected peak shape is obtained by convolving the forward and reverse smoothing weights. A predicted ChIP-seq profile (Y_pred) is generated by smoothing the estimated occupancy profile using the expected peak shape. Smoothing the occupancy of each n-mer with the expected peak shape is equivalent to two-step smoothing. The occupancy is firstly smoothed with the reverse smoothing weight to generate positions of the reverse tags relative to the position of the occupancy (position of the n-mer). Second, equivalent to the construction of Y_obs, smoothing the aforementioned predicted reverse tags profiles with the forward smoothing weight to generate the Y_pred. Both forward and reverse strands are taken into account in the occupancy calculation. To allow for comparison, Y_pred in each 1-kb binding region is scaled according to Y_obs in the same region. Then the Levenberg–Marquardt algorithm (21,22) is used to minimize the squared prediction error ||Y_obs − Y_pred||² (SPE) covering all the 1-kb binding regions by iteratively updating the PSEM. Finally, TherMos outputs a PSEM when the SPE is smaller than a threshold (Figure 1F). The TherMos program can be downloaded from http://collaborations.gis.a-star.edu.sg/∼cmb6/TherMos.

Cross-validation

To evaluate the performance of TherMos, a 10-fold cross-validation test was performed for TherMos and other five motif discovery algorithms. Settings and details of running these five algorithms can be found in the Supplementary Information. PWMs predicted by Weeder, MEME, DREME (23) and ChIPMunk (24) were converted to PSEMs as described previously (7). In each round of the test, 90% of the ChIP-seq data were randomly chosen as the training set and the remaining 10% were used as the test set. Another parameter [TF]/K_d(ref) [Equation (2)] was optimized using the training set for the algorithms except TherMos, respectively. The SPE (||Y_obs − Y_pred||²) and the rank correlation coefficient between the total occupancy and the total tag counts within 1-kb region centered on the peak calls in the test set were calculated. To compare the cross-validation results for each algorithm, the average SPE and rank correlation coefficient from all of the folds for each TF were calculated, respectively.

Model for deriving K_d and PSEM from competitive electrophoretic mobility shift assays

In an competitive electrophoretic mobility shift assay (EMSA), labeled and unlabeled DNA sequences compete with each other to bind TFs.

where D_L and D_U are labeled and unlabeled DNAs, respectively. The dissociation equilibrium constants for the two reactions are

(4)

(5)

The total concentrations of labeled DNAs, unlabeled DNAs and TFs, i.e. [D_L]_t, [D_U]_t and [TF]_t are known.

(6)

(7)

(8)

The fraction bound f measured from the competition assay is defined as

(9)

Based on Equations (4–7),

(10)

If the unlabeled competitor DNA sequence is the same as the labeled consensus DNA sequence, we assume that K_d1 = K_d2. Then,

(11)

The quantities with prime are used here to indicate this special case. From Equation (11), we get

(12)

Combine Equations (7–9) and (12), we get

(13)

Then from Equations (4, 6, 9 and 13), K_d1 can be written as

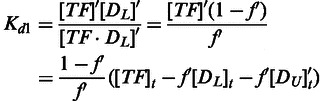(14)

As not all the proteins are active in the solution, the active total protein concentration needs to be determined before K_d1 and K_d2 can be calculated. The lower limit of the active total protein concentration can be determined from Equation (14) and K_d1 > 0. That is,

(15)

If K_d1 ≠ K_d2, based on Equations (6, 7) and (9, 10),

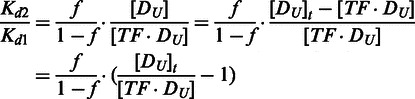(16)

From Equations (4, 8 and 9),

(17)

Combine Equations (14, 16 and 17),

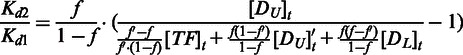(18)

As K_d2/K_d1 > 0, so

(19)

For those unlabeled competitors with f > f', the upper limit of the active total protein concentration can be determined as

(20)

Once the upper and lower limits of the active total protein concentration are determined, we take the mean of the limits as the active total protein concentration. Then K_d1 and K_d2 can be calculated using Equations (14 and 18) accordingly. Finally, the PSEM can be obtained based on the relationship

(21)

RESULTS

Overview of the TherMos approach

TherMos infers an additive binding energy model (PSEM) using least-squares fitting to the ChIP-seq tag profile (Figure 1 and ‘Materials and Methods’ section). The algorithm takes as input a set of ChIP-seq tag coordinates, a set of control-library tag coordinates and a set of externally generated peak calls. First, TherMos performs GC bias correction on the ChIP-seq tag counts and infers the average shape of the tag distribution at binding sites (1-kb regions centered on peak calls, Supplementary Information). The GC-corrected per base pair (un-binned) tag counts are then smoothed using the tag distribution to generate the ChIP-seq profile (Y_obs). TherMos starts the optimization routine by using a heuristic to generate an approximate PSEM from Y_obs. This PSEM is scanned along the genomic sequence to calculate thermodynamic occupancy estimates at each position within 1-kb regions centered on peak calls (‘Materials and Methods’ section). The estimated occupancy profile is converted into a predicted ChIP-seq profile (Y_pred) using the appropriate tag-distribution-based peak shape (‘Materials and Methods’ section). The squared prediction error ||Y_obs − Y_pred||² is then minimized by iteratively updating the PSEM in successive rounds of optimization. The output of the TherMos algorithm is a PSEM that models the free energy of TF-DNA binding and can readily be expressed as a sequence logo (1,25).

TherMos outperforms other algorithms in cross-validation tests

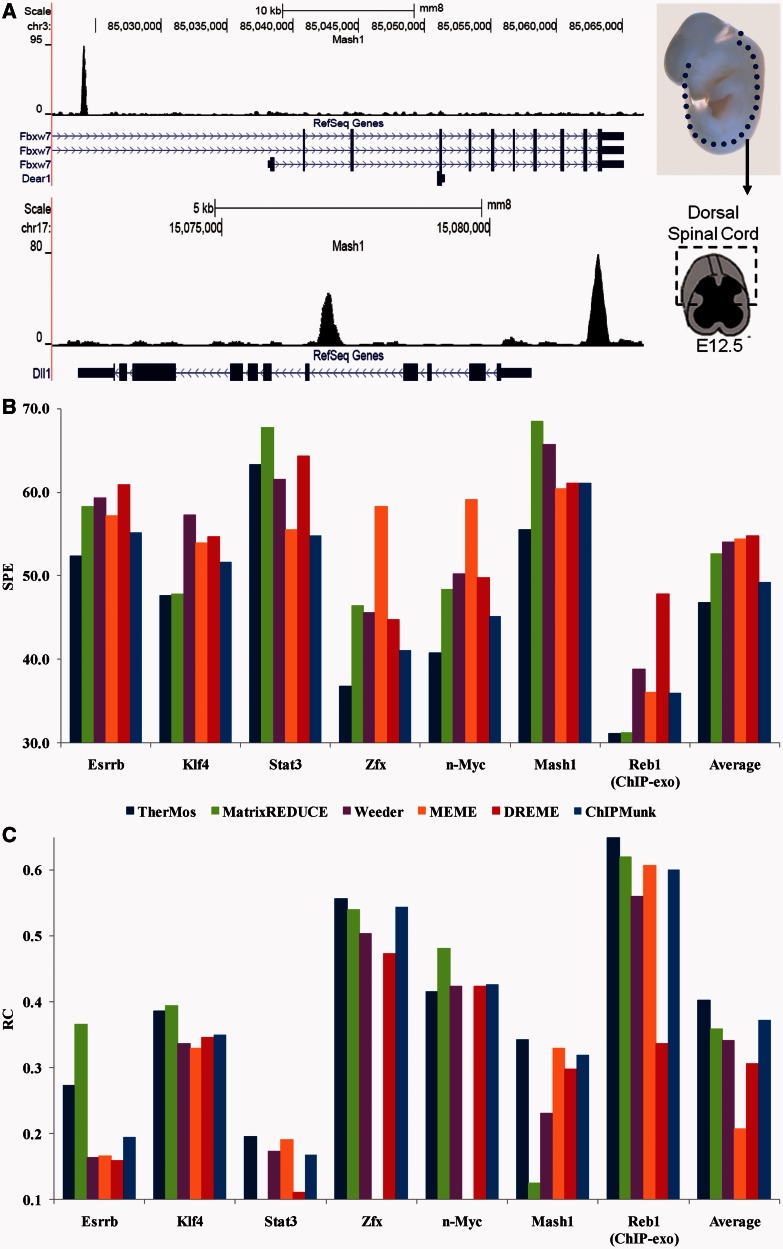
We used TherMos to derive PSEMs for six TFs spanning a broad range of DNA-binding domains, based on ChIP-seq data from mES cells (Esrrb, Klf4, Stat3, Zfx and n-Myc) (14) and ChIP-exo data from S. cerevisiae (Reb1) (13). In addition, to evaluate TherMos on data from a heterogeneous tissue, we generated and analyzed Mash1 ChIP-seq data from mouse spinal cord at embryonic day 12.5 (‘Materials and Methods’ section). Only the dorsal region of the spinal cord was analyzed, as Mash1 expression is restricted to the dorsal domain at this time point (26). As seen in Figure 2A, the Mash1 ChIP-seq profile showed strong peaks at Fbxw7 and Dll1, two known targets of the TF (18).

Figure 2.

(A) Mash1 in vivo ChIP-seq profile (E12.5 mouse spinal cord) shows strong peaks at known targets of Mash1. (B, C) Performance of TherMos and other algorithms in 10-fold cross-validation testing on the seven whole-genome TF binding profiles. For each algorithm and each TF, the bar height indicates the average SPE or rank correlation coefficient across the 10 test sets. The summary bars at the end indicate average performance across all seven TFs. (B) SPE is calculated between predicted (motif) and observed (experimental data) ChIP-seq binding profile. Smaller SPE indicates higher accuracy. (C) Rank correlation coefficient is calculated between predicted (motif) and observed (experimental data) ChIP-seq tag counts. Average rank correlation coefficients below zero for some of the algorithms are not shown.

To visualize the results, the seven PSEMs were converted into sequence logos (Supplementary Figure S1). Reassuringly, the motifs discovered by TherMos qualitatively match the known motifs for corresponding factors (TRANSFAC database) (27). For comparison, we also inferred binding affinity matrices using MatrixREDUCE, and PWMs using four well-known algorithms: Weeder, MEME, DREME and ChIPMunk. The accuracy of the inferred PSEMs, PSAMs and PWMs was quantified through 10-fold cross-validation analysis using two different performance metrics. The objective was to determine whether the methods, when trained on 90% of the ChIP-seq peaks, could predict the ChIP-seq profile in 1-kb regions centered on the remaining 10% (test set). We first measured accuracy as the SPE between the predicted and measured ChIP-seq profiles in the test set (Figure 2B and ‘Materials and Methods’ section). A smaller SPE indicates higher accuracy. By this metric, TherMos ranked first on all but one of the seven data sets, and it had the smallest average SPE. ChIPMunk had the second-lowest average SPE, and the remaining four had similar average SPE to each other.

As a second method to evaluate the performance of TherMos, we computed the rank correlation coefficient between the total predicted TF occupancy and the total tag count in the test set of 1-kb peak regions (Figure 2C). Note that the rank correlation metric is precisely the quality measure optimized by MatrixREDUCE, and this could potentially give the algorithm an advantage in this particular comparison. However, TherMos was once again the most accurate overall, and ChIPMunk again ranked second (though by a narrower margin). Sequence logos and box-plots illustrating the range of SPE and rank correlation values for each TF and each algorithm are presented in Supplementary Figures S2–S7. In summary, the PSEMs inferred by TherMos show the highest overall accuracy in predicting ChIP-seq and ChIP-exo profiles.

TherMos accurately predicts Esrrb in vitro binding energy

To experimentally benchmark the performance of TherMos in predicting the intrinsic binding energy of TFs, we developed a competitive EMSA protocol that can measure PSEMs in vitro (‘Materials and Methods’ section and Supplementary Information). We first applied this validation approach to the nuclear receptor Esrrb. As in the standard EMSA competition assay, we mixed a labeled high-affinity DNA fragment with the purified Esrrb DNA-binding domain and multiple unlabeled competitor DNA fragments, and then quantified the fraction of labeled DNA fragments that bound Esrrb. The bound fractions were then used to infer the dissociation constants of TF binding to the competitor fragments (‘Materials and Methods’ section). Using the 9-bp Esrrb ‘consensus’ element CCAAGGTCA as the core of the labeled fragment, we tested 28 competitors: the consensus sequence itself, plus all 27 (3 × 9) singly mutated variants of the consensus (Figure 3B). From the resulting bound-fraction data, we estimated an additive in vitro PSEM for Esrrb. The equivalent sequence logo is shown in Figure 3C.

Figure 3.

In vitro binding energy model for Esrrb and comparison with algorithmic predictions from ChIP-seq. (A) Sequence logos of Esrrb motifs predicted by TherMos, MatrixREDUCE, Weeder, MEME, DREME and ChIPMunk. (B) Results of the EMSA competition assays. (C) The sequence logo of the Esrrb affinity model measured in vitro by EMSA competition assays. (D) Euclidean distance between in vitro motif and the motifs predicted by various algorithms.

To use the EMSA-generated in vitro PSEM for Esrrb as a benchmark, we require a measure of how different the benchmark PSEM is from the PSEMs and log-odds PWMs predicted by the six algorithms. For this purpose, we transformed all binding energy and affinity models into their equivalent nucleotide frequency matrix, and then we used Euclidean distance between the experimentally and computationally derived matrices as a measure of prediction error (Supplementary Information). We adopted this approach because Euclidean distance was found to be the best performer in a systematic assessment of seven different distance measures for TF-binding motifs (28). By this measure, the binding energy model measured in vitro for Esrrb was closest to the ChIPMunk prediction (Figure 3D). TherMos ranked second in prediction accuracy, followed by MEME, DREME, Weeder and MatrixREDUCE.

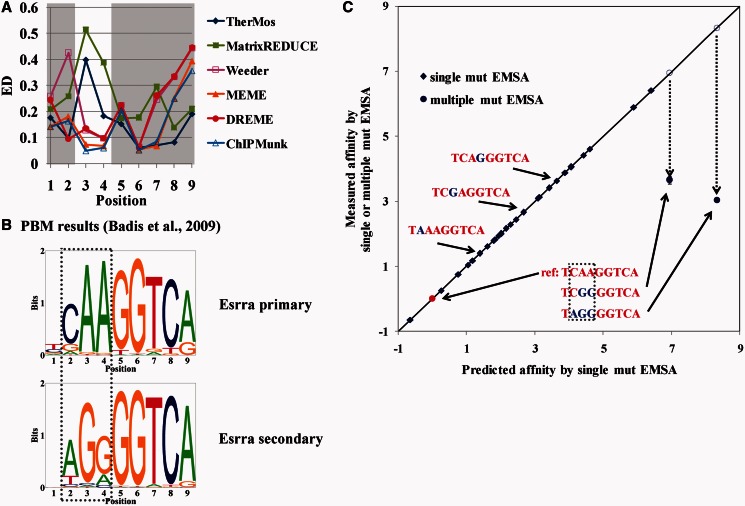
On visual inspection, we noticed systematic differences between the thermodynamic methods (TherMos and MatrixREDUCE) and the dichotomous ‘bound–unbound’ methods (Weeder, MEME, DREME and ChIPMunk). The dichotomous algorithms predicted a strict ‘AA’ sequence at positions 3 and 4 in the Esrrb-bound n-mer (Figure 3A), whereas the two thermodynamic methods were relatively tolerant of mismatches at those two positions. To quantify this effect, we examined the per position Euclidean distance of the six algorithms (Figure 4A). In comparison with the dichotomous methods, the biophysical methods deviated strongly from the in vitro PSEM at positions 3 and 4.

Figure 4.

Position interdependence in Esrrb binding. (A) Euclidean distance at each nucleotide position between in vitro motif and the motifs predicted by various algorithms. (B) Esrra primary and secondary motifs measured using PBM (29). The nucleotides showing positional interdependence are highlighted in the box. (C) The measured affinity by single or multiple mutation EMSA (i.e. the measured log ratio of the K_d of the mutant sequences to K_d of the reference sequence) versus the predicted affinity (i.e. the corresponding predicted log ratio) by single mutation EMSA. Twenty-seven single mutant (diamond) and two multiple mutant (circle) sequences were tested in EMSA competition assays. The consensus (reference) sequence is highlighted in red with the mutated nucleotides highlighted in blue. Error bars for the two multiple-mutant sequences are too small to be visible in this plot.

The local discrepancy in Esrrb binding energy models has an intriguing parallel in protein-binding microarray (PBM) measurements of TF-DNA binding energy (29). According to the PBM data, the binding energy landscape of Esrra, a close paralog of Esrrb, could not be modeled by a single additive PWM. A better fit was obtained by combining two PWMs that differed strongly at positions 2–4 but were almost identical elsewhere (Figure 4B) (29). Thus, Esrra (and presumably also Esrrb) DNA-binding energy shows position interdependence at precisely the location where TherMos and MatrixREDUCE differed from enrichment-based PWM models. The primary Esrra motif strongly resembled the in vitro EMSA binding energy model for Esrrb and also the models of the four enrichment-based algorithms. In contrast, the TherMos model presumably represents an additive approximation to the non-additive binding energy contributions of positions 2–4. The same could be said for MatrixREDUCE, except for a scaling of the information content relative to TherMos.

The non-additive Esrra/b binding energy model inferred by Badis et al. (29) from PBMs provides a qualitative explanation for the observations noted earlier in the text. First, the similarity of the in vitro EMSA binding energy model to the ‘primary motif’ of Badis et al. is not surprising when one considers that both were inferred from single mutations relative to the consensus n-mer. As double mutations were not considered, these two motifs represent the additive binding energy landscape in the immediate vicinity of the consensus binding n-mer. The EMSA model and the PBM-derived primary motif are, by definition, ‘blind’ to non-additivity. In contrast, TherMos and MatrixREDUCE fit quantitative binding models to a large array of genomic binding sites, many of which contain multiple mutations relative to the consensus. We would, therefore, expect these two algorithms to estimate binding energy models that represent an additive approximation to the entire binding energy landscape. As the primary and secondary PBM motifs differ mainly at positions 2–4, it is thus not surprising that TherMos and MatrixREDUCE show higher tolerance for sequence variability at those motif positions. The behavior of the statistical algorithms (Weeder, MEME, DREME and ChIPMunk) was not predictable a priori, but it is possible that the bound–unbound paradigm used by such methods might cause them to systematically converge on the higher-affinity primary motif.

Esrrb multi-mutations deviate from additive model: confirmation using EMSA

To independently confirm the prediction that position-interdependence affects Esrrb–DNA binding energy, we used EMSA to measure the affinity of two multiply mutated versions of the Esrrb consensus binding site. These two oligomers were designed to match the secondary Esrra motif inferred by Badis et al. (29) from PBM data. Our hypothesis was, therefore, that they would bind Esrrb with significantly greater affinity than predicted from the single-mutation EMSA measurements (Figure 4C). Indeed, we found that both sequences bound Esrrb more strongly than expected. The sequence TAGGGGTCA, which exactly matched the secondary Esrra motif from PBM measurements, showed the most dramatic deviation; it bound Esrrb with 100-fold greater affinity than predicted from the single mutations. In general, non-specific binding at the extreme low end of the affinity spectrum could be one potential cause of deviations from the additive binding energy model. However, this is an unlikely explanation for our results, as the two multi-mutated oligomers are well within the affinity range of singly mutated sequences. In fact, the affinity of the TAGGGGTCA sequence was 29-fold higher than that of the weakest measured binder (CCAAGCTCA), indicating that non-specific binding is not likely to be a factor. Thus, these results validate our hypothesis that the relatively low specificity of the TherMos binding energy model and MatrixREDUCE affinity model for Esrrb at positions 2–4 are a consequence of non-additive binding energy contributions at those positions.

TherMos accurately predicts Klf4 in vitro binding energy

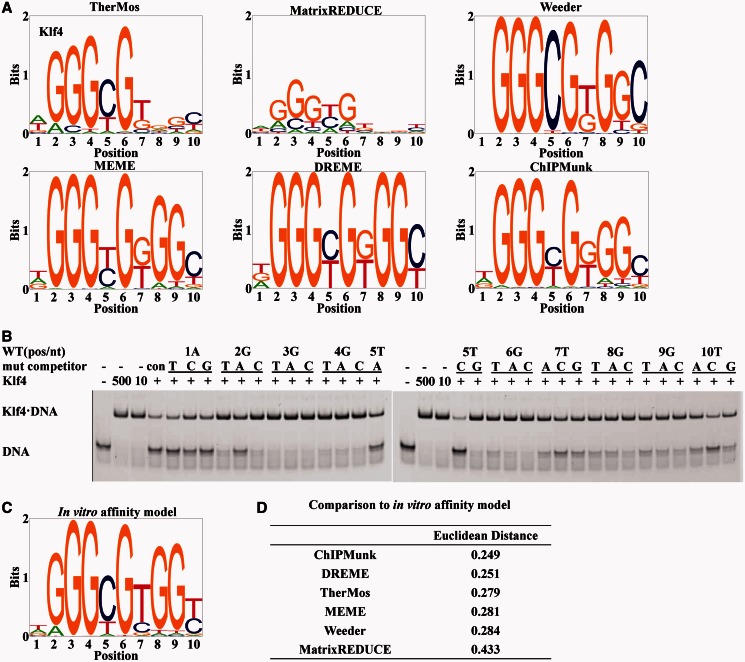
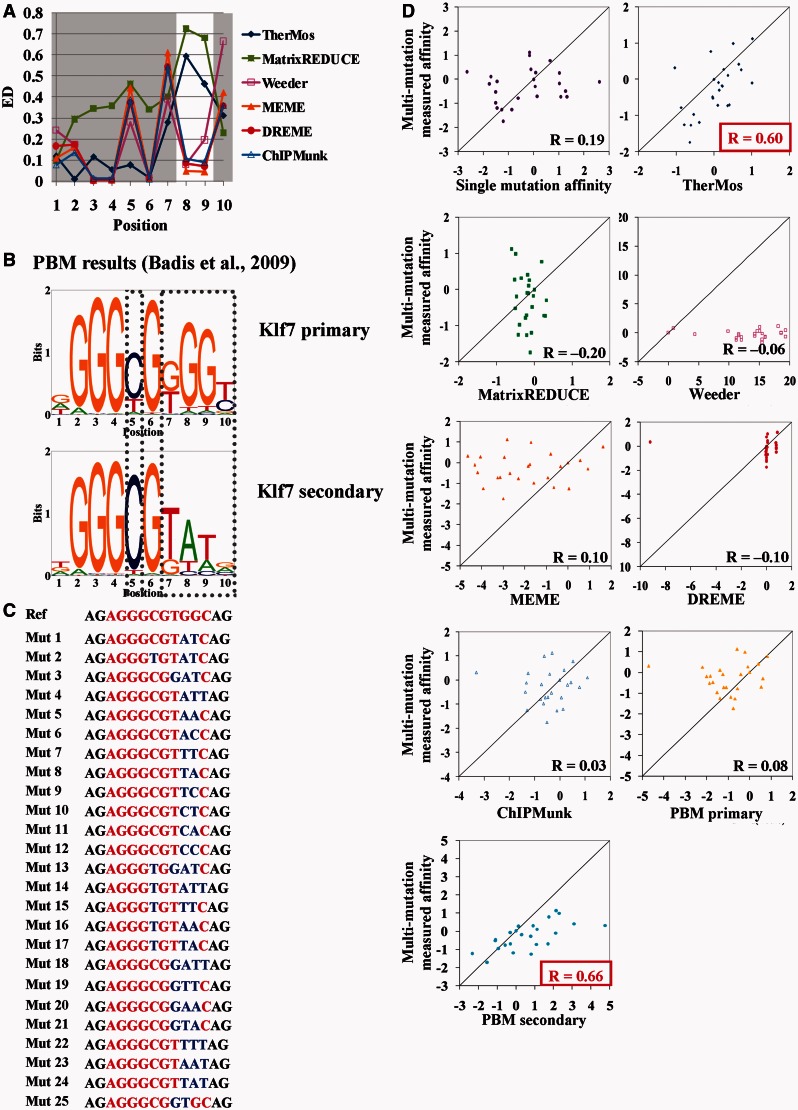
For further validation of the performance of TherMos in predicting the intrinsic binding energy of TFs, we performed a similar analysis of the C₂H₂ zinc-finger protein Klf4 binding energy (Figure 5). In this case, the motif inferred from ChIP-seq data by ChIPMunk showed the closest overall resemblance to the in vitro EMSA PSEM, and TherMos ranked third. Interestingly, we again found that the binding site contained a sub-region (positions 8 and 9) where the biophysical methods (TherMos and MatrixREDUCE) tolerated mismatches to the consensus, whereas the statistical methods inferred a fairly strict requirement for the consensus dinucleotide (GG) (Figure 5A). This dichotomy was again quantitatively supported by examining the Euclidean distance at each nucleotide position (Figure 6A). The discrepancy between TherMos and EMSA was also highest in this region (positions 7–10). Encouragingly, we again found a parallel in the PBM data, which support two different binding energy matrices for Klf7, a close paralog of Klf4 (Figure 6B). As before, the two Klf7 PBM motifs differed most noticeably at exactly the positions where TherMos differed from EMSA (positions 7–10). Given the consistent localized discrepancies between the biophysical algorithms and our in vitro EMSA models, we hypothesized as before that the EMSA approach of measuring only singly mutated DNA sequences had failed to capture the full breadth of the binding energy landscape of Klf4.

Figure 5.

In vitro binding energy model for Klf4 and comparison with the algorithmic predictions from ChIP-seq. (A) Sequence logos of Klf4 motifs predicted by TherMos, MatrixREDUCE, Weeder, MEME, DREME and ChIPMunk. (B) Results of the EMSA competition assays. (C) The sequence logo of the Klf4 affinity model measured in vitro by EMSA competition assays. (D) Euclidean distance between the in vitro motif and the motifs predicted by various algorithms.

Figure 6.

Position interdependence in Klf4 binding. (A) Euclidean distance at each nucleotide position between the in vitro motif and the motifs predicted by various algorithms from ChIP-seq data. (B) Klf7 primary and secondary motifs measured using PBM (29). The nucleotides showing positional interdependence are highlighted in the box. (C) Twenty-five mutant sequences were tested in multiple mutations EMSA competition assays. The 10-bp consensus sequence is highlighted in red with two flanking nucleotides (in black) at both ends. The mutated nucleotides are highlighted in blue. (D) The multi-mutation measured affinity (i.e. the observed log ratio of the K_d of the 25 mutant sequences to K_d of the Mut 10) versus the corresponding log ratio predicted by single mutation affinity model, TherMos, MatrixREDUCE, Weeder, MEME, DREME, ChIPMunk, PBM primary motif and PBM secondary motif (29). The Pearson correlation coefficient is also shown in the plot.

TherMos in vivo PSEM predicts binding energy landscape of Klf4 multi-mutations in vitro

To independently confirm the non-additivity of nucleotide interaction energies in the Klf4 binding site, we designed a second round of in vitro affinity measurements focused on multiple mutations at interdependent positions within the Klf4 binding site. We also hypothesized that, in this test, TherMos would outperform the binding energy models that resembled the primary Klf7/4 PBM motif. Combinatorial mutations at positions 5, 7, 8, 9 and 10 were designed based on significant differences between the two PBM models at these positions (Figure 6). We used EMSA as before to measure the in vitro affinity of 25 multiply mutated DNA fragments (Figure 6C).

Strikingly, the additive binding energy model based on single-mutation in vitro measurements failed almost completely in predicting the binding energy of multiply mutated Klf4 binding sites (Pearson correlation coefficient: R = 0.19) (Figure 6D). This result strongly supports binding energy interdependence at positions 5, 7, 8, 9 and 10 and highlights the inadequacy of the binding energy model inferred from the single-mutation in vitro assay. Given the poor performance of the single-mutation in vitro motif for Klf4, we hypothesized that the primary PBM-derived motif would also perform poorly in this multi-mutation binding energy prediction test. Indeed, we found that this was the case (R = 0.08). In contrast, the secondary PBM-derived motif displayed good predictive power (R = 0.66), indicating that it represents a reasonable additive approximation to the binding energy landscape far from the consensus binding n-mer.

We evaluated the ability of the various in vivo Klf4 binding models inferred from ChIP-seq data to predict the in vitro binding energy of the multi-mutated DNA sequences. In this test, TherMos was the only algorithm that provided accurate binding energy predictions (R = 0.6). The other five algorithms were mostly unable to predict multi-mutation affinities (R ≤ 0.1), despite their accuracy in the previous single-mutation benchmark. Thus, the other algorithms fail to capture the binding energies of sites that deviate significantly from the high-affinity consensus at interdependent positions. As the TherMos model is based on the entire binding energy landscape of in vivo binding sites, it is able to provide a more accurate additive approximation to the in vitro binding energy even in the presence of position interdependence.

DISCUSSION

The occupancy of a TF at any given genomic binding site is related to its intrinsic binding energy, which can most naturally be described using the language of thermodynamics. Viewed from a thermodynamic perspective, every DNA n-mer has some non-zero likelihood of being bound by a given TF, with this likelihood (i.e. occupancy) being a continuous function of the binding free energy of the n-mer. However, before the advent of high-throughput methods, this continuum of TF-DNA binding energy was commonly discretized into two categories: bound and unbound. The bound–unbound dichotomy is artificial, and also somewhat arbitrary, as it reflects the detection limits of specific biochemical binding assays, rather than any inherent bimodality in TF-DNA binding levels. Nevertheless, it was unavoidable in most cases because of the limitations of traditional forms of the training data. Consequently, bioinformatic methods typically eschewed explicit thermodynamic modeling and instead favored a machine-learning approach based on motif enrichment in bound sequences relative to unbound sequences.

Now that multiple high-throughput methods exist for generating quantitative binding profiles, it is possible to adopt a more natural thermodynamic formalism for motif detection, based on a continuum of free energy and occupancy. Continuous-occupancy binding energy models are already incorporated in some modern motif detection algorithms (9,12). However, using a thermodynamic approach in conjunction with ChIP-seq data on in vivo TF binding requires additional effort. Most importantly, TherMos has the ability to predict the precise shape of the ChIP-seq profile implied by any particular binding energy model. This feature is key to the ability of TherMos to exploit the rich information content of the ChIP-seq tag distribution, and likely contributes to the robustness of the algorithm.

Uniquely, TherMos fits to the peak shape in binding regions, rather than to absolute peak height (see ‘Materials and Methods’ section). This largely insulates the algorithm from locus-specific scaling of TF binding levels by the local chromatin state. As MatrixREDUCE in effect predicts peak height rather than peak shape, it is more susceptible to distortions from chromatin state variation; therefore, it infers binding energy models of relatively low information content (Figures 3 and 5). When the locus-specific scaling feature is disabled, TherMos similarly produces PSEMs with low information content, although the effect is not as pronounced (data not shown).

In this study, we used a two-pronged approach to comprehensively validate the TF-DNA binding energy and affinity models inferred from ChIP-seq and ChIP-exo data by TherMos and other algorithms. The validation strategy included both in vivo cross-validation and in vitro EMSA assays for quantifying dissociation constants. Overall, these analyses indicated that the binding energy models estimated by TherMos provided the most accurate representation of the entire binding energy landscape. This was particularly true when the non-additivity of interaction energies across neighboring nucleotides in Esrrb and Klf4 binding sites was taken into account.

Recent studies based on high-throughput in vitro TF-DNA affinity measurements suggest that additive models of TF-DNA binding energy are generally effective, and only occasionally violated (30–32). In particular, it was found that non-additivity was prevalent in vitro among TFs from the zinc-finger and zipper classes (31). Our experiments were performed before publication of these studies. However, coincidentally, the two TFs we selected for non-additive binding energy analysis happen belong to the zinc-finger class.

For both Esrrb and Klf4, our in vitro dissociation constant measurements provide strong evidence for non-additivity in the binding energy landscape. Strikingly, the TAGGGGTCA DNA oligomer, which was predicted to have negligible affinity for Esrrb based on the additive model, displayed 100-fold greater affinity than expected. This is highly consistent with the PBM-based prediction of Badis et al. that Esrra, a close paralog, can bind a secondary DNA motif whose consensus sequence is AGGGGTCA. We performed a more systematic survey of non-additivity for Klf4, by measuring the in vitro affinity of 25 multiply mutated versions of the consensus binding site. We designed these mutations to coincide with positions that differed between the primary and secondary Klf7 motifs inferred by Badis et al. from PBM data. Remarkably, the binding energy of Klf4 for the multiply mutated sequences bore almost no resemblance to the additive PSEM inferred from our single-mutation EMSA assays. Rather, they closely matched the secondary Klf7 PBM motif. Thus, our EMSA measurements independently confirm the PBM-based predictions of non-additive binding for Klf4/Klf7 and Esrra/Esrrb.

Little is known about the in vivo significance of non-additive binding. It is conceivable that the non-additivity observed in vitro may only affect DNA sequences whose affinity is too low to have any effect on genomic binding. However, the TAGGGGTCA Esrrb-binding sequence does not fit this pattern; its affinity is within a factor of 50 of the consensus n-mer, and in fact higher than that of nine singly mutated versions of the consensus. The TherMos PSEMs inferred from ChIP-seq data provide even more direct evidence for the in vivo importance of non-additivity. Consider a hypothetical scenario in which the additive model is dominant in vivo and sufficient to explain genomic TF binding. In such a scenario, the TherMos PSEM would correlate with the primary PBM motif of Badis et al., but not with the secondary motif. However, we see that the TherMos PSEM diverges significantly from the primary motif, and this divergence occurs precisely at the nucleotide positions where the two PBM models diverge. Similarly, if additive binding were dominant in vivo, the TherMos PSEM would fail to predict the binding energy of Klf4 binding sites that violated the additive model in vitro. However, TherMos can indeed predict the binding energy of such sequences (Figure 6D). Thus, our results consistently reflect the influence of non-additivity on TF binding in vivo.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online: Supplementary Figures 1–7, Supplementary Methods and Supplementary References [33–37].

FUNDING

Joint Council Office of the Agency for Science, Technology and Research, Singapore [JCOAG03_FG02_2009]; Funding for open access charge: The Agency for Science, Technology and Research, Singapore.

Conflict of interest statement. None declared.