Automatic cone photoreceptor segmentation using graph theory and dynamic programming

Abstract

Geometrical analysis of the photoreceptor mosaic can reveal subclinical ocular pathologies. In this paper, we describe a fully automatic algorithm to identify and segment photoreceptors in adaptive optics ophthalmoscope images of the photoreceptor mosaic. This method is an extension of our previously described closed contour segmentation framework based on graph theory and dynamic programming (GTDP). We validated the performance of the proposed algorithm by comparing it to the state-of-the-art technique on a large data set consisting of over 200,000 cones and posted the results online. We found that the GTDP method achieved a higher detection rate, decreasing the cone miss rate by over a factor of five.

1. Introduction

Diagnosis, prognosis, and treatment of many ocular and neurodegenerative diseases require visualization of microscopic structures in the eye. Integration of adaptive optics (AO) into ocular imaging systems has made the visualization of living human photoreceptors possible [1–14]. More specifically, the AO scanning light ophthalmoscope (AOSLO) [2] has been a key instrument for analyzing the photoreceptor mosaic and revealing subclinical ocular pathologies missed by other modern ophthalmic imaging modalities [15]. Studies have been conducted on the photoreceptor mosaic to gather normative data on photoreceptor distribution [16,17], density [18–20], spacing [8,21,22], directionality [23], and temporal changes [24,25]. Characterization of irregular mosaics in the presence of various retinal diseases such as cone-rod dystrophy has also been achieved [22,26–38].

To generate quantitative metrics of the photoreceptor mosaic, identification of individual photoreceptors is often a required step. Since manual identification is extremely time-consuming, many groups have utilized some form of automation when studying the photoreceptor mosaic [9,12,14,17,18,27]. Cone identification algorithms have also been developed and validated for accuracy [39–43]; the Garrioch et al. 2012 algorithm [44], for example, is a modified version of the Li & Roorda 2007 algorithm [39] and was thoroughly validated for repeatability on a large cone mosaic data set. Even so, manual correction was still necessary to identify missed photoreceptors [20,34].

In this work, we propose the use of graph theory and dynamic programming (GTDP), a framework we previously developed to segment layered [45–47] and closed contour structures [48], to both identify and segment cone photoreceptors in AO ophthalmoscopy images (Section 2.3). We then validate our algorithm’s performance for cone identification (Section 3.2) and evaluate its reproducibility in cone density and spacing estimation (Section 3.3). Finally, the proposed algorithm is extended to segment an image containing both rod and cone photoreceptors (Section 3.4).

2. Methods

The methods for image acquisition, photoreceptor segmentation, and result validation are discussed in the following sections. Section 2.1 explains the image capture and pre-processing steps, while Section 2.2 describes the gold standard (target) for cone identification. Section 2.3 describes our method for cone segmentation, and Section 2.4 outlines the method for validation. Lastly, Section 2.5 introduces the preliminary rod-cone segmentation algorithm.

2.1 Image data set

We validated our algorithm on 840 images (150 × 150 pixels) from the Garrioch et al. study [44], where the methods for image acquisition and pre-processing are described in detail. To summarize, the right eye of 21 subjects (25.9 ± 6.5 years in age, 1 subject with deuteranopia) was imaged using a previously described AOSLO system [13,17] with a 775 nm super luminescent diode and a 0.96 × 0.96° field of view. Four locations 0.65° from the center of fixation (bottom left, bottom right, top left, and top right) were imaged, capturing 150 frames at each site. This process was repeated 10 times for each subject. Axial length measurements were also acquired with an IOL Master (Carl Zeiss Meditec, Dublin, CA) to determine the lateral resolution of the captured images.

Following image acquisition, pre-processing steps were taken in the Garrioch et al. study to generate a single registered image from each 150 image sequence. To do this, first any sinusoidal distortions from the resonant scanner were removed from individual frames. The frames from each sequence were then registered to a reference frame [49], and the top 40 frames with the highest normalized cross correlation to the reference were averaged together. This procedure was performed for all 21 subjects at each of the 4 locations and repeated 10 times over, resulting in a total of 840 images in the image data set. Finally, to ensure that each set of 10 repeated images captured the same patch of retina, the images were aligned using strip registration.

Since the image data set was used strictly for algorithm validation, we obtained a separate set of images to tune the algorithm. These training images were captured using the same imaging protocol, and patients from the test and validation data sets did not overlap.

2.2 Gold standard for cone identification

We defined the gold standard as the semi-automatically identified cone locations reported in the Garrioch et al. study, since the cone locations on all 840 images had been carefully reviewed and corrected by an expert grader. As described in the study, the initial cone coordinates were first automatically generated using the Garrioch et al. 2012 algorithm, a modified version of the Li & Roorda 2007 cone identification algorithm [39]. Any missed cones were then added manually. Automatically segmented cones were not removed or adjusted, as the Garrioch et al. 2012 algorithm exhibited a tendency towards false negatives rather than false positives.

2.3 GTDP cone segmentation algorithm

We developed a customized implementation of our generalized GTDP framework for closed contour structures [48] to segment cone photoreceptors in AOSLO images. In brief, we used maxima operators to obtain pilot estimates of prominent cones. We then used the quasi-polar transform [48] to map the closed contour cone estimates from the Cartesian domain into layers in the quasi-polar domain. The layered structures were then segmented utilizing our classic GTDP method [45]. By applying the inverse quasi-polar transform, the segmentation lines were carried back into the Cartesian space. Finally, we performed additional iterations to find any missed cones. These steps are described in details in the following.

We first brightened dim photoreceptors by applying Eq. (1) to the 150 × 150 pixel image $I_c^{orig}$ (subscript c denotes the Cartesian domain), where $normalize(X,y,z)$ indicates a linear normalization of the elements in matrix X to range from y to z.

$$I_c^{all}=normalize(log(normalize(I_c^{orig},0.1,0.9)),0,1)$$ (1)

The range 0.1 to 0.9 was chosen to increase the contrast between the dimmest and brightest pixels, as well as to avoid the log(0) and log(1) computations. The superscript all means all pixels were present in the image.

We then determined pilot estimates of the cones by finding local maxima using the $imregionalmax(I_c^{all},4)$ function in MATLAB, The MathWorks, Natick, MA. This resulted in the binary image $B_c^{all},$ where values of 1 corresponded to pilot estimates of cones. Individual cones were then analyzed by order of decreasing intensity, where $I_c^{all}$ and $B_c^{all}$ were cropped about the centroid of the cone’s pilot estimate to generate the 21 × 21 pixel images $I_c$ and $B_c;$ cropping the images enabled a faster computation time, and the ten pixel buffer on all sides of the centroid ensured that the target cone was not cropped out of $I_c.$ Pilot estimates for other cones contained within $B_c$ were removed, and the remaining cone estimate in $B_c$ was refined using thresholding. The new pilot estimate consisted of connected pixels in $I_c$ ranging from $0.95T_{\max }$ to $T_{\max }$ in intensity, where $T_{\max }$ was the maximum intensity in $I_c$ that coincided with $B_c=1,$ and $0.95T_{\max }$ was determined empirically to avoid thresholding adjacent cones.

To segment each cone, we first used our previously described quasi-polar transform [48] to transform $I_c$ to $I_q$ (q denotes the quasi-polar domain). To do this, we first transformed $I_c$ and $B_c$ (Figs. 1(a) and 1(b)) into the polar domain to create $I_p$ and $B_p$ (Figs. 1(c) and 1(d)). Next, we column-wise shifted $I_p$ until the pilot estimate in $B_p$ was flat, resulting in the quasi-polar images $I_q$ and $B_q$ (Figs. 1(e) and 1(f)). After obtaining $I_q,$ we removed regions containing other pilot estimates and already-segmented cones from the search space, and used GTDP to find the shortest path across $I_q$ with the following weight scheme:

$$\begin{array}{l}{w}_{ab}=normalize(-(g_a^{LD}+g_b^{LD}),1,2)+\\ normalize(-(g_a^{DL}+g_b^{DL}),0,0.1)+\\ normalize(d_{ab},0,0.05)+w_{\min },\end{array}$$ (2)

where $w_{ab}$ is the edge weight connecting nodes a and b, $g_n^{LD}$ and $g_n^{DL}$ are the vertical light-to-dark and dark-to-light gradients [45] of the image at node n, respectively, $d_{ab}$ is the Euclidian distance from node a to b, and $w_{\min }=\mathrm{0.00001.}$ The vertical light-dark gradient comprised the majority of the weight, since it was the primary indicator for the boundary of the central cone. A smaller weight was given to the dark-light gradient to segment boundaries of dimmer cones adjacent to brighter cones (Fig. 1(c), left). Finally, a vertical distance penalty was added to discourage the segmented line from including adjacent cones. Specific values for weight ranges were determined empirically.

Fig. 1.

Cone photoreceptor segmentation using the quasi-polar transform. (a) Cartesian image containing the cone to segment. (b) Pilot estimate of the cone in (a). (c,d) Polar transformation of (a) and (b), respectively. The black regions in (c) are invalid points that lie outside the image in the Cartesian domain. (e,f) Images (c) and (d) column-wise shifted until the pilot estimate in (d) was flat. (g) Segmentation of (e) using GTDP (magenta). (h) Transformation of the segmentation in (g) back into the Cartesian domain (magenta).

We then transformed the shortest path from the quasi-polar domain (Fig. 1(g)) back into the Cartesian domain to obtain the final segmentation of the cone (Fig. 1(h)), keeping it only if the mean radius was greater than one pixel. This entire process was then repeated for all subsequent cone estimates.

At this stage of the algorithm, the cones identified and segmented by the GTDP method (Fig. 2(b), black) may be similar to those detected by previous methods, since local maxima were used to initialize the cone locations. To further identify any missed cones, we obtained pilot estimates of the cones using a second method: image deblurring using maximum likelihood blind deconvolution [50–52] (deconvblind function in MATLAB) with a Gaussian point spread function of half the mean radius of already segmented cones, followed by locating all regional maxima with a pixel connectivity of eight. Any pilot estimates lying outside already-segmented cone locations (Figs. 2(a) and 2(b), white) were segmented using the same quasi-polar GTDP technique, with the modification to the weighting matrix as shown in Eq. (3). In this weighting scheme, the vertical dark-light gradient was assigned a higher weight since cones detected during this section iteration were typically dimmer and adjacent to brighter cones. The vertical distance penalty was also removed since adjacent cones were already segmented and thus removed from the search region.

Fig. 2.

Identification of cones missed by local maxima. (a) AOSLO image in log scale with missed cones shown inside the white boxes. (b) Cone photoreceptors segmented using local maxima initialization in black, and pilot estimates of missed cones found using deconvolution and local maxima are shown in white asterisks.

$$\begin{array}{l}{w}_{ab}=normalize(-(g_a^{LD}+g_b^{LD}),1,2)+\\ normalize(-(g_a^{DL}+g_b^{DL}),1,1.5)+w_{\min }\end{array}$$ (3)

2.4 Statistical validation

We validated our GTDP algorithm by comparing its performance to the Garrioch et al. 2012 algorithm and to the gold standard generated by the Garrioch et al. paper [44]. To perfectly replicate the Garrioch et al. study, all images were cropped to a 55 µm × 55 µm region about the image center to remove any boundary effects.

To evaluate the performance in cone identification, we compared both fully automatic methods (GTDP and Garrioch et al. 2012) to the gold standard using two metrics: # of true positives, those detected by both the fully automatic and gold standard techniques, and # of false positives, those detected by the fully automatic method but not by the gold standard. A cone was considered to be a true positive if it was within a 1.75 µm Euclidian distance from a gold standard cone. This value was chosen since the mean cone spacing reported in the Garrioch et al. study was approximately 3.50 µm; half this value was therefore a reasonable estimate for the cone radius. If an automatically identified cone did not have any gold standard cones within the 1.75 µm distance, then it was tagged as a false positive. Furthermore, more than one automatically identified cone could not be matched to a single gold standard cone, thus yielding the following relationships:

$$\begin{array}{l}{N}_{\text{automatic cones identified}}=N_{\text{true positive}}+N_{\text{false positive}}and\\ N_{\text{gold standard cones identified}}=N_{\text{true positive}}+N_{\text{false negative}},\end{array}$$ (4)

where $N_{\text{false negative}}$ was the number of cones detected by the gold standard but not by the fully automatic method. The proportion of true and false positives were then estimated with 95% confidence intervals (CI) across all patients and all quadrants using a generalized estimating equation (GEE) model with log link [53].

The reproducibility of each method was assessed by the comparing cone density (number of cones per mm²) and cone spacing (mean distance from each cone to its nearest neighbor) measurements output by each method at each quadrant. The variability in cone density and spacing measurements (characterized by the variance $V_{\text{total}})$ stemmed from two sources: 1) variability in measurements taken on the same subject, resulting from the method used (within-subject variability; variance $V_{\text{within}}),$ and 2) variability in true values between subjects, resulting from biological variation between subjects (between-subjects variability; variance $V_{\text{between}}).$ Thus, $V_{\text{total}}=V_{\text{within}}+V_{\text{between}}.$ The reproducibility was characterized using two components: 1) within-subject coefficient of variation (CV), and 2) intra-class (intra-subject) correlation coefficient (ICC). The within-subject CV was defined as the ratio of the square root of $V_{\text{within}}$ to the overall mean measurement, where a lower CV indicates a better the method. ICC was defined as the ratio of $V_{\text{between}}$ to $V_{\text{total}},$ thus a ratio closer to 1 indicates a better method.

2.5 Preliminary GTDP rod-cone segmentation algorithm

To illustrate the potential of this algorithm to segment images containing both rods and cones, we modified the cone segmentation algorithm described in Section 2.3 to segment a rod and cone photoreceptor image (originally 250 × 250 pixels, scaled to 578 × 578 pixels at 0.186 µm/pixel) captured using the new generation of AOSLO systems [17,54]. In this modified version of the algorithm, photoreceptors were segmented with weights determined by Eq. (5), where $i_n$ is the intensity of the image at node n, and $r_n$ is the distance of node n from the top of the image $I_q.$ These additional weights were included to target the location of minimum intensity rather than maximum gradient, and to penalize peripheral photoreceptors from being segmented.

$$\begin{array}{l}{w}_{ab}=normalize(-(g_a^{LD}+g_b^{LD}),1,2)+\\ normalize(i_a+i_b,0.1,0.2)+\\ normalize(r_a+r_b,0,0.05)+\\ normalize(d_{ab},2,2.1)+w_{\min }\end{array}$$ (5)

Segmentations with radii less than 3.72 µm were considered to isolate rods, and the rest were re-segmented with the weighting scheme in Eq. (6) to isolate cones. The $r_n$ distance penalty was removed since cones have larger radii than rods, and the $g_n^{LD}$ weights were removed to delineate the prominent hypo-reflective region surrounding cones on AOSLO rather than the high gradient boundary.

$$\begin{array}{l}{w}_{ab}=normalize(i_a+i_b,0.2,1)+\\ normalize(d_{ab},0,0.1)+w_{\min }\end{array}$$ (6)

3. Results

Section 3.1 discusses the segmentation results of our method, while Sections 3.2 and 3.3 show quantitative results comparing the performance of our method against the state-of-the-art for cone identification and cone density and spacing reproducibility, respectively. Finally, Section 3.4 shows a preliminary segmentation result for an image containing both rod and cone photoreceptors.

3.1 Cone segmentation result

Figure 3(b) (top) is a representative segmentation result generated by our GTDP algorithm to segment cone photoreceptors in AOSLO images, and Fig. 3(c) (top) shows the centroid of each segmented cell. While the GTDP algorithm delineated the perceived cone boundaries, we used the result in Fig. 3(c) to validate our algorithm against other cone identification techniques. Figure 3 (bottom) shows the segmentation result for an image of lower quality.

Fig. 3.

Qualitative GTDP segmentation result. Top row: (a) Higher quality AOSLO image of cone photoreceptors in log scale, (b) fully automatic segmentation result of (a) using GTDP for closed contour structures, and (c) centroid of each fully automatically segmented cone from (b). Bottom row: Lower quality AOSLO image (a) and its segmentation (b) and centroid (c) result.

The entire validation data set and the corresponding GTDP, Garrioch et al. 2012, and gold standard segmentation results are available at http://www.duke.edu/~sf59/Chiu_BOE_2013_dataset.htm. The fully automated algorithm was coded in MATLAB (The MathWorks, Natick, MA) and had an average computation time of 1.56 seconds per image (150 × 150 pixels, an average of 300 cones per uncropped image) using 8-thread parallel processing on a laptop computer with a 64-bit operating system, Core i7-820QM CPU at 1.73 GHz (Intel, Mountain View, CA), 7200 rpm hard drive, and 16 GB of RAM. This time included the overhead required for reading and writing operations.

3.2 Cone identification performance

The performance in cone identification for each of the methods is shown in Table 1. This table shows that after taking into consideration all correlated data, our GTDP method correctly detected 99.0% of the cones, compared to the Garrioch et al. 2012 method which detected 94.5% of the gold standard cones; this difference was found to be significant (Z = 15.0, p<0.0001). In addition, 1.5% of the cones found by the GTDP method were not in the gold standard. False positive cones could not be detected by the Garrioch et al. 2012 method since the gold standard was based off of the Garrioch et al. 2012 algorithm (see Section 2.2). Lastly, the mean distance error from the true positive GTDP cones to the gold standard cones was 0.20 ± 0.26 µm.

Table 1. Cone Identification Performance of Fully Automatic Methods Compared to the Gold Standard Across All 840 Images.

Method	% True Positive (95% CI)*	% False positive (95% CI)
Garrioch et al. 2012	94.5 (93.7, 95.2)	–
GTDP	99.0 (98.8, 99.2)	1.5 (1.2, 1.9)

*Statistically significant

Figure 4 is an illustrative example of the cone identification results, where the middle row shows the mean cone identification performance for both automatic algorithms, while the top and bottom rows show the performance approximately one standard deviation above and below the mean. The middle column displays the Garrioch algorithm et al. 2012 results, with true positives in yellow and false negatives in green. The right column shows the GTDP results, with true positives in magenta, false negatives in green, and false positives in blue. The performance (% true positive by Garrioch et al. 2012; % true positive by GTDP; % false positive by GTDP) for the top, middle, and bottom rows of Fig. 4 were (100; 98.4; 0), (99.1; 94.4; 2.1), and (97.5; 90.4; 3), respectively.

Fig. 4.

Variable performance of the fully automatic cone identification algorithms. Left column: AOSLO image of the cone mosaic in log scale. Middle column: Garrioch et al. 2012 algorithm results (yellow: true positives; green: false negatives). Right column: GTDP algorithm results (magenta: true positives; green: false negatives; blue: false positives). Middle row: Typical (mean) performance by both algorithms. Top and bottom rows: Performance one standard deviation above and below the mean for both algorithms, respectively.

Finally, Fig. 5 takes a closer look at the results from Fig. 4(b) (right). The black box highlights a “false positive” cone added by the GTDP algorithm per the gold standard, however inspection of the original image in Fig. 5(a) indicates that a cone is indeed present at that location. In contrast, the white boxes in Fig. 5 highlight “false negative” cones missed by the algorithm per the gold standard. By inspecting Fig. 5(a), however, these locations do not seem to exhibit hyper reflectivity.

Fig. 5.

A closer look at the performance of the GTDP algorithm. (a) AOSLO image corresponding to Fig. 4(b) (left), and (b) automatic GTDP segmentation result (magenta: true positives; green: false negatives; blue: false positives). White boxes: locations where the algorithm “missed” a cone, even though there appears to be no cone present. Black box: location where the algorithm “erroneously added” a cone, although the original image seems to contain an added cone not identified by the gold standard.

3.3 Reproducibility results

Table 2 shows the mean, ICC, and within-subject CV values for the cone density and spacing metrics as measured by the Garrioch, GTDP, and gold standard methods separated by image quadrant. The average GTDP cone density ICC of 0.989 indicates that on average, 98.9% of the total variability in the measurements was due to the variability between subjects, while only 1.1% was due to the GTDP algorithm. The average GTDP within-subject CV of 0.0146 indicates that the error in reproducing the same measurement for the same subject was within 1.46% of the mean.

Table 2. Reproducibility Comparison of Cone Density and Spacing Measurements.

	Cone Density				Cone Spacing
Fixation Location	Mean (cones/mm2)	ICC	Within-subject CV		Mean (µm)	ICC	Within-subject CV
Garrioch
Bottom left	67,207	0.979	0.0217		3.50	0.989	0.0074
Bottom right	66,812	0.972	0.0253		3.50	0.983	0.0087
Top left	70,928	0.950	0.0272		3.37	0.975	0.0090
Top right	69,192	0.970	0.0273		3.39	0.984	0.0093
Average	68,534	0.968	0.0254		3.44	0.983	0.0086
GTDP
Bottom left	70,796	0.993	0.0121		3.42	0.978	0.0110
Bottom right	70,783	0.989	0.0149		3.40	0.964	0.0131
Top left	75,485	0.988	0.0133		3.28	0.960	0.0124
Top right	74,216	0.985	0.0181		3.29	0.957	0.0154
Average	72,820	0.989	0.0146		3.35	0.965	0.0130
Gold standard
Bottom left	70,577	0.995	0.0101		3.45	0.981	0.0097
Bottom right	70,204	0.994	0.0111		3.44	0.975	0.0106
Top left	75,416	0.994	0.0103		3.31	0.968	0.0113
Top right	73,914	0.995	0.0109		3.32	0.985	0.0090
Average	72,528	0.994	0.0106		3.38	0.977	0.0101

3.4 Preliminary rod and cone segmentation result

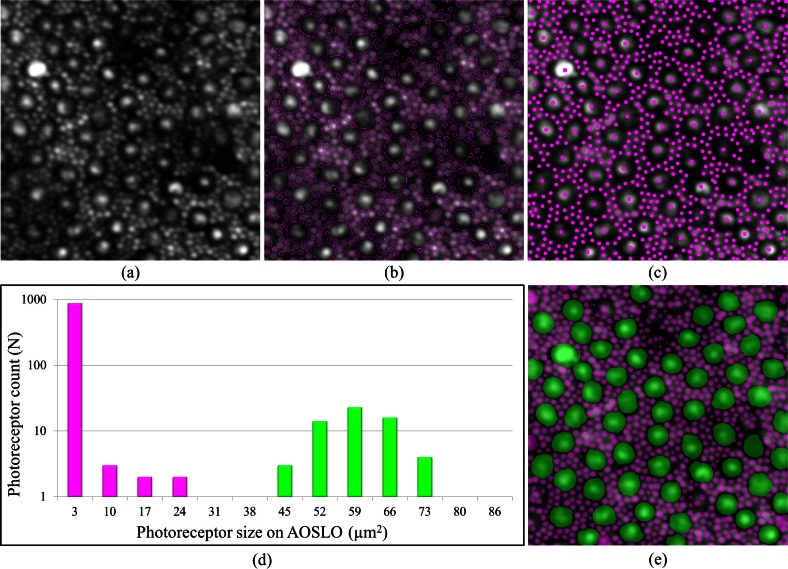
Figure 6(a) shows an example rod and cone photoreceptor image [17,54] accompanied by the GTDP segmentation result in Fig. 6(b) and its associated centroids in Fig. 6(c). Figure 6(d) shows a histogram of the number of photoreceptors at various sizes based on the segmentation from Fig. 6(b), and Fig. 6(e) demonstrates a simple classification of rod and cone photoreceptors using a size threshold of 27.7 µm².

Fig. 6.

Fully automatic identification of rods and cone photoreceptors. (a) AOSLO image of rods and cone photoreceptors in log scale (image taken from [54]). (b,c) Fully automatic segmentation (b) and identification (c) of rods and cones using GTDP for closed contour structures. (d) Histogram of the segmentations from (b). (e) Threshold of 27.7 µm² used to classify the photoreceptors from (d) into rods (magenta) and cones (green).

4. Discussion and conclusion

We developed a fully automatic algorithm using graph theory and dynamic programming to segment cone photoreceptors in AOSLO images of the retina and validated its performance. We were able to achieve a higher cone detection rate, more accurate cone density and spacing measurements, and comparable reproducibility compared to the Garrioch et al. 2012 algorithm. Furthermore, the segmentation-based approach enabled identification and classification of rods and cones within a single image. This is highly encouraging for large-scale ophthalmic studies requiring an efficient and accurate analysis of the photoreceptor mosaic.

We obtained the data set from the Garrioch et al. study [44] to validate the performance of our algorithm on a large untrained data set. We compared the performance of our fully automatic cone segmentation algorithm to the state-of-the-art technique, and found that our GTDP method decreased the Garrioch et al. 2012 cone miss rate by a factor of 5.5 (Table 1, 1.0% vs. 5.5% false positives). One point five percent of the cones not identified by the gold standard were also found using our technique. While this implies that our algorithm falsely identified these cones, Fig. 5 shows that in some cases, our GTDP method was able to identify cones not found by the gold standard; such observations, while not the norm, are likely due to the resource intensive nature of semi-automatic cone identification.

The mean results in Table 2 indicate that the cone density and spacing metrics extracted by the GTDP method were more accurate on average than the Garrioch et al. 2012 algorithm, despite the bias where the Garrioch et al. results were used as the starting point for generating the gold standard. While an unbiased comparison could have been conducted, this would have required a fully manual identification of nearly 256,000 cones. Table 2 also shows that the GTDP method generated more reproducible cone density measurements (mean 0.0146 CV) than the other automated method (mean 0.0254 CV). To be consistent with previous publications, we also compared reproducibility in cone spacing, which showed that the Garrioch et al. 2012 method produced more reproducible results (mean 0.0086 CV) compared to both the GTDP method (mean 0.0130 CV) and the gold standard. This is because both the GTDP method as well as the gold standard detected more cones; these were typically the harder and more irregularly spaced cones, and thus resulted in more variable cone spacing. As a result, cone spacing reproducibility might not be the most reliable quantitative measure of performance. Nevertheless, all three methods had a very good within-subject CV, showing that the within-subject standard error (error due to method) ranged by only 0.74% to 2.73% from the mean. Furthermore, all three methods had a very good ICC, showing that 95% to 99.5% of the total variability in the measurements was due to variability between subjects, while only 0.5% to 5% was due to the method. This high ICC was a result of the pre-processing image alignment performed in the Garrioch et al. study (Section 2.1) to ensure that the same patch of retina was imaged.

A notable difference and novelty of the GTDP algorithm as compared to existing en face cone segmentation algorithms, is its use of segmentation to identify cones. While the most common technique for cone identification is to locate points of maximal intensity, such a method only locates cone centers. In contrast, our technique delineates cone boundaries, resulting in added information about the size and shape of the segmented object. This information may be helpful for applications such as studying how the multimodal structure of larger cones changes with time or wavelength. However, it is of importance to note that in the context of AO photoreceptor imaging, cone sizes may be near the resolution limit, especially towards the foveal center. Furthermore, estimation of photoreceptor size depends on the wavelength of the imaging modality (e.g. fundus camera, SLO, OCT) and even varies over time based on intensity fluctuations. As a result, extracting size and shape information about the cones, while helpful, may not be an accurate indication of its true morphologic state.

Another advantage of using segmentation is that it enables a higher cone detection rate. By keeping track of the entire area of a cone rather than only its centroid, we can look for added cones in regions where cones have not yet been found (Fig. 2(b)). Our technique also provides an advantage for isolating rods and cones within a single image (Fig. 6(e)), as we can readily distinguish between the two types of photoreceptors based on their segmented area in normal retinae. Since accurate photoreceptor classification depends on correctly segmented photoreceptors, however, the rods improperly segmented as cones in Fig. 6(b) resulted in misclassification. A more accurate and robust rod-cone segmentation algorithm moving forward will be essential to improving this preliminary classification result.

A limitation of this study is its rather optimistic validation on higher quality images of normal retina. The AO images taken from diseased retinae, however, are often low in quality and plagued with diverse pathological features. This paper is the first step in introducing a conceptually simple yet robust framework adaptable to incorporating the mathematical and algorithmic innovations necessary for segmenting the more challenging real-world, clinical AOSLO images. Future steps include validation of our rod and cone segmentation algorithm, as well as extension and application of our framework to segment more complicated images of photoreceptors in disease states.