Pressure-induced superconductivity in CaC₂

Abstract

Carbon can exist as isolated dumbbell, 1D chain, 2D plane, and 3D network in carbon solids or carbon-based compounds, which attributes to its rich chemical binding way, including sp-, sp²-, and sp³-hybridized bonds. sp²-hybridizing carbon always captures special attention due to its unique physical and chemical property. Here, using an evolutionary algorithm in conjunction with ab initio method, we found that, under compression, dumbbell carbon in CaC₂ can be polymerized first into 1D chain and then into ribbon and further into 2D graphite sheet at higher pressure. The C2/m structure transforms into an orthorhombic Cmcm phase at 0.5 GPa, followed by another orthorhombic Immm phase, which is stabilized in a wide pressure range of 15.2–105.8 GPa and then forced into MgB₂-type phase with wide range stability up to at least 1 TPa. Strong electron–phonon coupling λ in compressed CaC₂ is found, in particular for Immm phase, which has the highest λ value (0.562–0.564) among them, leading to its high superconducting critical temperature T_c (7.9∼9.8 K), which is comparable with the 11.5 K value of CaC₆. Our results show that calcium not only can stabilize carbon sp² hybridization at a larger range of pressure but also can contribute in superconducting behavior, which would further ignite experimental and theoretical interest in alkaline–earth metal carbides to uncover their peculiar physical properties under extreme conditions.

High pressure, as a crucial thermodynamic parameter, has been emerging as a powerful tool to investigate physical and chemical behavior of materials, especially to explore the evolution of planets, and synthesize or design materials with peculiar properties such as superhardness and superconductivity (1–5). Recently, Ca and C, as ordinary elemental solids, have been studied extensively in physical, chemical, and material science fields due to their interesting structural properties when pressure is applied (6–10). These peculiar physical properties of compressed Ca and C solids have motivated our attention on Ca-based dicarbide CaC₂. In CaC₂ (11, 12) at ambient pressure, experimentally, four temperature-induced modifications were reported, which are the well-known tetragonal room temperature modification CaC₂ I (space group I4/mmm, Z = 2), two low-temperature monoclinic modifications CaC₂ II (C2/c, Z = 4), and CaC₂ III (C2/m, Z = 4), and cubic high-temperature modification CaC₂ IV (Fm-3m, Z = 4) (12). Theoretically, orthorhombic CaC₂ Immm (Z = 2, referred to as Immm-1 below) structure, monoclinic CaC₂ C2/m (Z = 2, referred to as C2/m-1 below) structure, and trigonal CaC₂ R-3m (Z = 1) structure, were predicted by Kulkarni et al. (13) using a global exploration method based on simulated annealing scheme. In all structures reported above, carbon atoms form isolated dumbbells. Because both Ca and C solids tend to form C-atom network structures at ambient and high pressure (6–10), it is reasonable and interesting to investigate pressure-induced possibility of polymerization of isolated C₂ dumbbells in CaC₂. To our knowledge, there are few studies on compressed CaC₂ so far. Kulkarni et al. (13) observed that C2/m-1 structure transforms into R-3m structure at about 24 GPa using local density approximation or 34 GPa using B3LYP. Srepusharawoot et al. (14) studied pressure-induced carbon network formation for five alkaline–earth metal dicarbides (AEMDs) using ab initio random-searching method. Very recently, structural and vibrational properties of AEMD BaC₂ at ambient temperature and high pressure up to 40 GPa were reported experimentally (15). Amorphous states were observed, which can be viewed as a precursor for the formation of carbon networks embedded in a metal framework.

Covalent bonding and ionic bonding coexist in AEMDs. There is a strong covalent bonding in C₂ units, but ionic in between Ca and C. Up to now, there have been many open questions for compressed AEMD: (i) How did C₂ dumbbell evolve after applying pressure? (ii) Could it be metalized under reasonable pressure? (iii) Is the metallic high-pressure phase a superconductor? Here, we select CaC₂ as an example to address these problems.

The structural properties of CaC₂ at high pressure were investigated by using global structural searching scheme based on an evolutionary algorithm (EA) (16, 17) in combination of first-principles total energy calculations. At high pressure, it was found that CaC₂ adopt the layered structures, in which carbon atoms first form chains and then ribbons or graphene sheets separated by Ca atomic layers. Of the three of the predicted high-pressure phases, two have orthorhombic symmetry (Cmcm and Immm) and the third one is a well-known MgB₂-type structure with P6/mmm symmetry. Calculated vibrational properties are similar to those observed in CaC₆ (18). The electronic structure calculations show that all of the three predicted high pressure phases are metallic. Finally, phonon-mediated superconducting behavior of three new high-pressure phases of CaC₂ was revealed by exploring electron–phonon coupling.

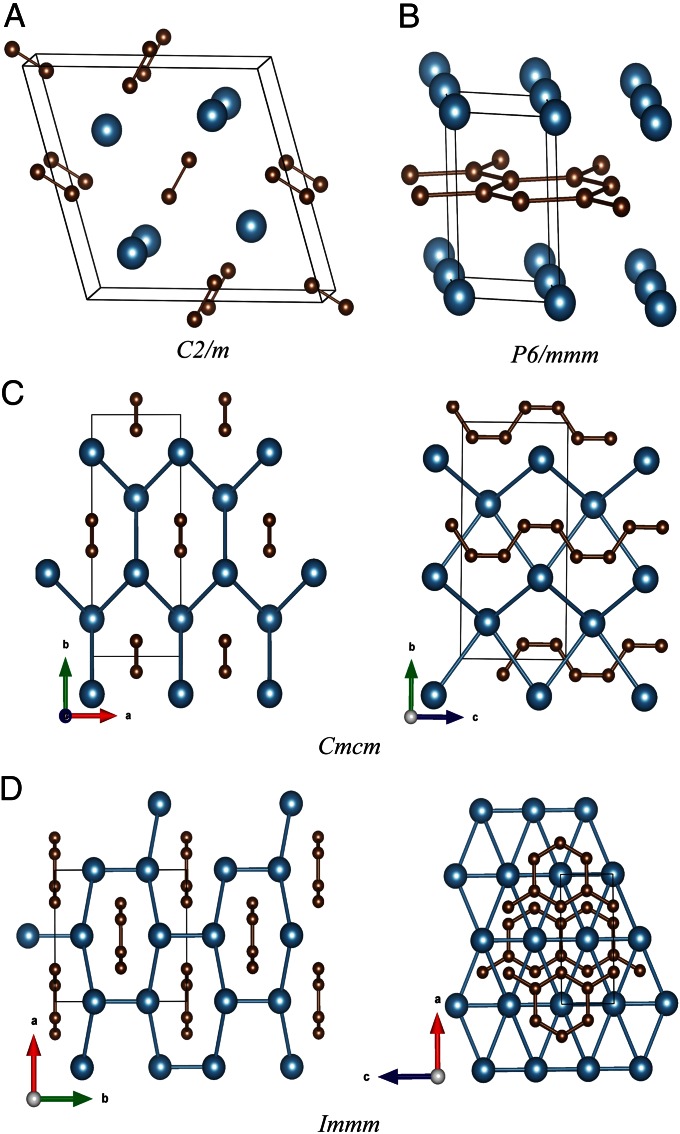
Knowledge of the structural information is the first step toward understanding the physical properties of any material. To get the most stable structure of CaC₂, we searched for its lower enthalpy’s phase based on EA in combined with Vienna ab initio simulation package (VASP) package. We performed variable-cell structure prediction simulations using USPEX code for CaC₂ containing two, three, and four molecules in the simulation cell at 5, 20, 40, 80, 120, 200, 300, 500, and 700 GPa, and 1 TPa, respectively. During the evaluation, the total energy was calculated via the VASP package. For comparison, the structures discussed in BeC₂, MgC₂, and BaC₂ experimentally and theoretically, are also considered in our calculations. The enthalpies per chemical formula unit vs. pressure curves of selected structures are plotted in Fig. 1. Considering that I4/mmm, C2/m, C2/c, C2/m-1, and Immm-1 structures hold very close enthalpy, their enthalpies vs. pressure curves are specially given in Fig. 1B, in which I4/mmm, C2/c, and C2/m refer to three modifications determined at different temperature by experiments, whereas C2/m-1 and Immm-1 represent lower enthalpy structures suggested by a global exploration method based on simulated annealing (13). From Fig. 1, one can see that, for compressed CaC₂, the monoclinic C2/m structure (referred as phase I) is the most stable structure below 0.5 GPa. An orthorhombic Cmcm phase (referred as phase II) takes over the pressure range from 0.5 to 15.2 GPa. Another orthorhombic Immm structure (referred to as phase III) is the most stable structure over the wide pressure range of 15.2–105.8 GPa, followed by a MgB₂-type structure (space group P6/mmm, referred to as phase IV) at 105.8 GPa above. Among these, phases II, III, and IV are metallic. Our total energy calculations rule out other competitive low-enthalpy structures that exist in MgC₂, CaC₂, and BaC₂, including I4₁/amd (16), P4₂/mnm (19), P4₃32 (20), I4/mmm, C2/m-1, Immm-1, P6₃/mmc, and R-3m (13). Our calculations show that the previous R-3m structure of CaC₂ suggested theoretically (13) is not a favorable one (Fig. 1). In addition, Cmmm structure, a metastable phase, has comparative enthalpy with phases III and IV at large pressure range due to their similar structural properties (atomic layered arrangement). The optimized structural parameters at different pressure are listed in Table S1. For phase II, the equilibrium lattice constants at 4 GPa are a = 3.6822 Å, b = 8.6324 Å, and c = 4.7360 Å. In this structure, four calcium atoms lie in the Wyckoff 4c site and eight carbon atoms occupy the 8f site, in which calcium atoms construct cylinder with hexagon cross-section, centered by one-dimensional (1D) armchair carbon chain along z direction (Fig. 2C). The equilibrium lattice constants of phase III at 15.2 GPa are a = 7.0623 Å, b = 2.6317 Å, and c = 6.2697 Å. Four calcium atoms hold the Wyckoff 4e sites and eight C atoms occupy two in-equivalent Wyckoff 4i (referred as C1) and 4j (referred as C2) sites. It is worthwhile to note that phase III suggested here differs clearly from the Immm-1 phase predicted by simulated annealing (13). The Immm-1 phase includes two molecules per unit cell, in which carbon atoms form isolated dumbbells, whereas our stable phase III contains four molecules per unit cell, in which carbon atoms were polymerized into nanoribbon with a six-membered ring. From Fig. 2D, one can see that a carbon nanoribbon, forming quasi-1D carbon ribbons, lies in the center of cylinder constructed by calcium atoms. For phase IV, a MgB₂-type structure, including only one molecule per unit cell, the equilibrium lattice parameters at 105.8 GPa are a = 2.5412 Å and c = 3.6864 Å. One calcium atom exists in 1a site and two carbon atoms lie in 2d sites. Structurally, phase IV of CaC₂ consists of hexagonal honeycombed layers (referred as graphene sheet) of carbon atoms separated by planes of Ca atoms, with the calcium atoms centered above and below the carbon hexagons (Fig. 2B). Also, we have noticed that pressure-induced phase transition in CaC₂ is first-order phase transition because of an obvious change in volume at the phase transition point. Under chemical precompression and external compression, dumbbell-type carbon is polymerized first into ordered armchair chain and further into quasi-1D well-ordered nanoribbon and eventually into 2D graphite sheets (graphene). Besides this, we did explore possibility of 3D network carbon under higher pressure until 1 TPa based on EA. Surprisingly, all performed calculations always point to a MgB₂-type (P6/mmm) structure. Phonon calculation further confirms its dynamical stability.

Fig. 1.

The relative enthalpy per chemical formula molecule as a function of pressure for competing structures. The phase transition series monoclinic C2/m phase to orthorhombic Cmcm phase (0.5 GPa) to another orthorhombic Immm phase (15.2 GPa) to hexagonal P6/mmm phase (105.8 GPa) obtained. Further calculations determined the stability of hexagonal phase up to 1 TPa.

Fig. 2.

Phase C2/m and three new phases of CaC₂. The big and small balls represent calcium and carbon atoms, respectively. One-dimensional armchair carbon chains along c-axis direction observed in Cmcm. One-dimensional carbon ribbons and 2D graphene sheets observed in Immm and P6/mmm phases, respectively. In Immm, calcium atoms construct cylinder with hexagon cross-section, which is arranged periodically, centered by 1D carbon ribbon (Left of D).

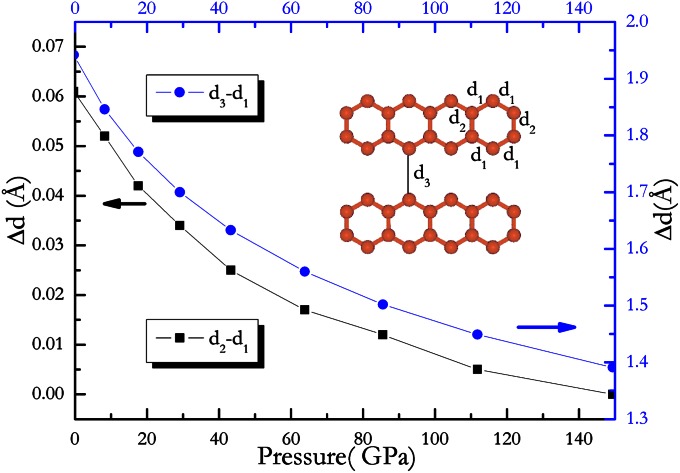
It will be constructive to look at the change of carbon–carbon bonding with increasing pressure to study the structural phase transformation mechanism. From low-pressure phase to high-pressure phase, C–C bonding behavior reveals obvious change due to external pressure and internal chemical precompression. Applying pressure to CaC₂, I4/mmm structure with isolated dumbbell space orientation along the z axis, which is stable at room temperature observed experimentally, is not energetically favorable compared with those (such as C2/m, C2/c, C2m-1, and Immm-1; Fig. 1) that possess isolated dumbbell space orientation keeping an angle with z axis. With increasing pressure, the distance between isolated dumbbell decreases, resulting in carbon atomic chain formed at lower pressure (see Cmcm structure). Upon further pressure, carbon atomic chain tends to well-organized arrangement, making orthorhombic phase II being transformed into an orthorhombic phase III. In phase III, there are two different bonding lengths (referred as d₁ and d₂) in ribbon with six-membered carbon ring (Fig. 3). At the pressure of 10 GPa, two among the six C–C bondings (d₁) hold a length of 1.4747 Å, and four of them (d₂) have a length of 1.5246 Å. Under further compression, the difference (Δd) between d₁ and d₂ begins to decrease smoothly (Fig. 3). At the same time, the distance (d₃) between neighbor ribbons begins to decrease (Fig. 3). In other words, for phase III, the difference of carbon–carbon bond length gradually decreases with increasing pressure until it disappears at 150 GPa, which results in a formation of a regular hexagonal ring. This kind of pressure-induced structural modification indicates the feasibility of graphite sheet (i.e., graphene sheet) formed in compressed CaC₂, as is observed in phase IV.

Fig. 3.

Change of structural property for ribbon formed by carbon atoms in Immm phase with increasing pressure. Upon compression, the lengths of two kinds of C–C bonds in ribbon tend to be uniform.

Due to the occurrence of graphite sheet between neighbor Ca atomic layers, phase IV could be one of graphite intercalation compounds (GICs). The properties of the GIC family have been studied extensively using a variety of different experimental techniques (21–25). Especially, the discovery of superconductivity in CaC₆ at the enhanced transition temperature (11.5 K) (26, 27) excited intense research interest in GICs experimentally (28, 29). The C–C bond length in phase IV is 1.4672 Å at 105.8 GPa, which is slightly longer than that (1.42 Å) in graphite. Also, we can see that phase III has a similar structural property as CaC₆ (all of the calcium atoms lie above and below of the center of carbon six-membered ring). This peculiar structural behavior indicates that compressed CaC₂ would present similar physical properties as CaC₆, such as superconductivity.

It is essential to check mechanical and dynamical stability of low enthalpy phases by means of elastic constants and phonon spectrum. There are 13, 9, and 5 independent elastic constants for monoclinic, orthorhombic, and hexagonal structures, respectively. The calculated elastic constants for four low enthalpy phases of CaC₂ are presented in Table 1. For hexagonal symmetry, c₆₆ is equal to (c₁₁ − c₁₂)/2. From Table 1, it is obvious that elastic constants satisfy mechanical stable criterion, implying their stability mechanically. Additionally, bulk modulus B, shear modulus G, and Young’s modulus E were obtained using Voigt’s formulas. For phase I, the calculated B, G, and E are 55, 24, and 63 GPa. Small B value indicates its strong compressibility. We have noticed that volume collapse 19.3% at phase transition point from phase I to phase II. Strong compressibility attributes to highly ionic bonding in between calcium and carbon. For hexagonal phase IV, high elastic moduli originate from strong covalent bonding between carbon atoms.

Table 1.

Independent elastic constants, bulk, shear, and Young’s moduli (all in GPa) of stable phases of CaC₂

Space group	P	c11	c22	c33	c44	c55	c66	c12	c13	c23	c15	c25	c35	c46	B	G	E
C2/m	0	86	98	91	13	47	6	29	58	22	7	9	−21	5	55	24	63
Cmcm	4	158	188	317	70	72	48	43	68	78					115	70	174
Immm	15.2	338	650	397	162	79	86	64	59	71					197	145	349
P6/mmm	105.8	1,056		824	373		458	141	238						463	396	924

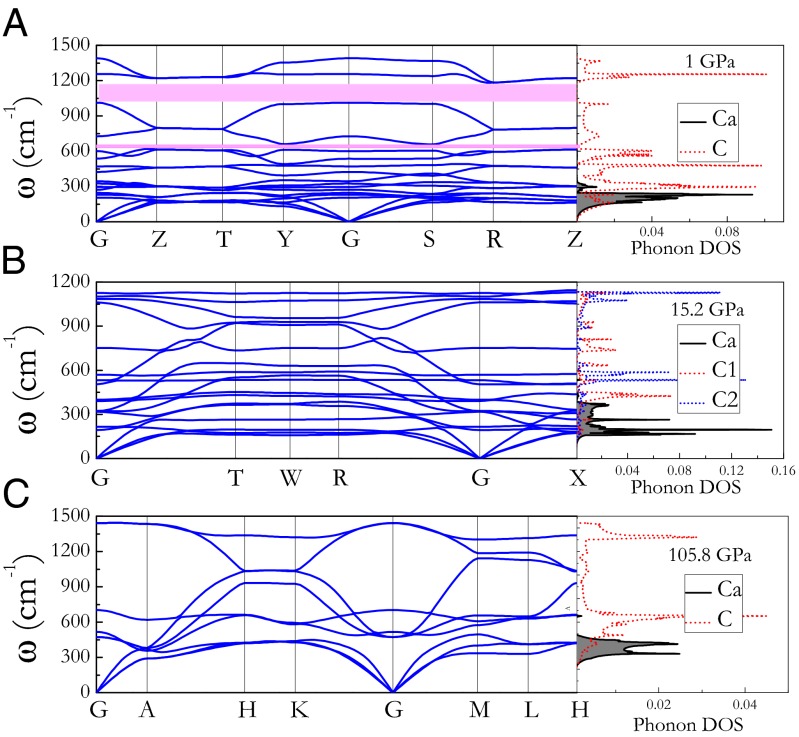
Phonon calculations show that phases II, III, and IV are stable dynamically at their stable pressure ranges. Phonon dispersions and partial phonon density of states (PPHDOS) of phases II, III, and IV are shown in Fig. 4. The maximum optical branch frequencies are 1,390.4 cm⁻¹ for phase II at 1 GPa, 1,129.7 cm⁻¹ for phase III at 15.2 GPa, and 1,443.9 cm⁻¹ for phase IV at 105.8 GPa, which are lower than the value 1,860 cm⁻¹ (30) of room temperature phase I4/mmm due to an obvious structural difference. From PPHDOS, one can conclude that calcium atom dominates the low-frequency region, whereas carbon atoms contribute to the high-frequency region. In Fig. 4, flat bands along peculiar direction in Brillouin zone (BZ) indicate layered structural property for three new phases. For phase II, the phonon dispersions possess two frequency gaps (48.4 and 171.6 cm⁻¹, see Fig. 4A), which originate from the stiffening of the carbon chains.

Fig. 4.

Phonon spectrum and partial atomic phonon density of states of three new phases for cold compressed CaC₂. Soft phonon modes are observed in them, in particular, for Immm phase.

Phase IV contains interesting graphene sheets, so we only discuss its phonon behavior in the following. For phase IV, PPHDOS calculation shows that the Ca-related phonons occur at the lower frequencies typically below 491 cm⁻¹ because the Ca atoms are much heavier and more weakly bonded than the C atoms (Fig. 4). In detail, for phase IV, Ca_y modes mainly occupy in below 400.3 cm⁻¹, whereas Ca_x and Ca_z modes dominate the spectrum range from 400.3 to 700.6 cm⁻¹. The graphene sheets in phase IV have strong planer bonding, indicating that the out-of-plane C_z modes fall between 300.2 and 667.2 cm⁻¹, whereas the in-plane C_xy modes are mainly in higher frequency and dominate the frequencies above 700.6 cm⁻¹ (Fig. 4C). So there is strong coupling between Ca_xz phonons and C_z phonons. The observed carbon atomic vibration behavior here has been determined in well-known Ca-based carbide CaC₆ experimentally. The most important issue is that the calculated phonon frequency windows of C_z modes and C_xy modes in CaC₂ are very similar to that observed in CaC₆, implying that phase IV of CaC₂ has similar phonon-related property as CaC₆. The partial atomic phonon distribution of phase III is similar to that of phase IV. All three phases possess soft phonon modes at peculiar high-symmetry point direction in BZ. In particular, phase III has more soft modes at the low-frequency region along the G-R, G-X, and G-T directions in BZ (Fig.4B), which serves as evidence of strong electron–phonon coupling in phase III (discussed below).

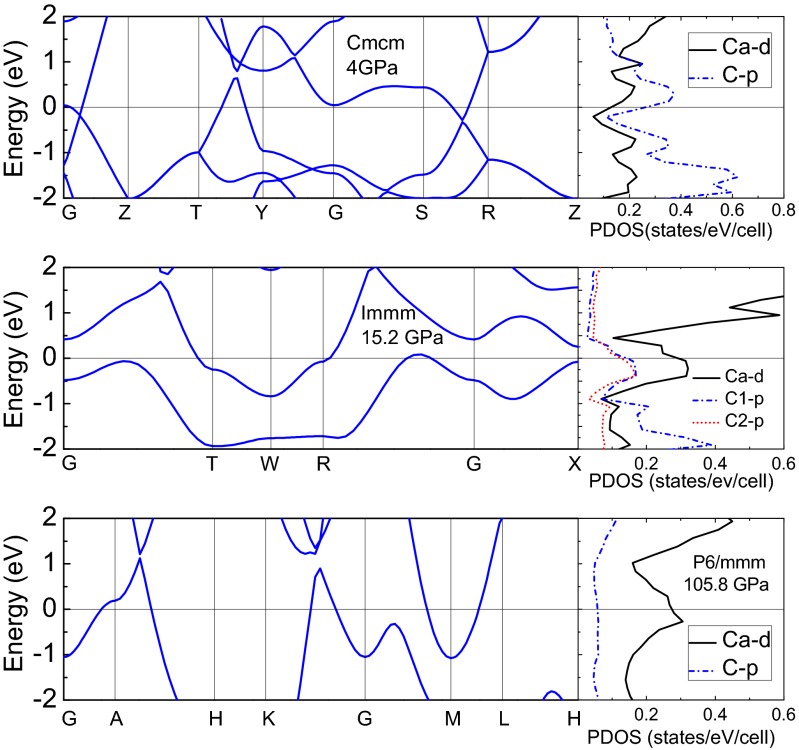
Electronic structure calculations show that phase I is a semiconductor (Fig. S1), whereas phases II, III, and IV are metallic. From projected density of states (PDOS) given in Fig. 5, one can see that three metallic phases have consistent electronic distributions. C-p electrons dominate in the wide energy range of covalence bands and strongly hybridize with Ca-d electrons near the Fermi level (i.e., Ca-d electrons and C-p electrons dominate Fermi level). However, there are few C-s electrons and Ca-s electrons near the Fermi level, denoting a pressure-driven charge transfer from s electrons to p or d electrons, which is confirmed by the atomic Mulliken population analysis shown in Table S2. According to this, one can conclude that the majority of Ca-4s electrons transform to Ca-d orbital, while the remaining, into C atom. For C atom, charge transfer is clearly from 2s orbital to 2p orbitals. The pressure-driven s-d charge transfer makes newly predicted phases being favorable ones energetically. In addition, we considered pressure effect by taking phase III as an example. From Fig. S2, it is obvious that pressure broaden the bands, making conduction band shift to higher level and covalence band shift to lower level. Additionally, PDOS calculations show that, near the Fermi level, the hybridization between C-p states and Ca-d states is enhanced with increasing pressure.

Fig. 5.

Energy band and projected density of states (PDOS) of Cmcm at 4GPa, Immm at 15.2 GPa, and P6/mmm at 105.8 GPa. The Fermi level was taken as the energetic reference point.

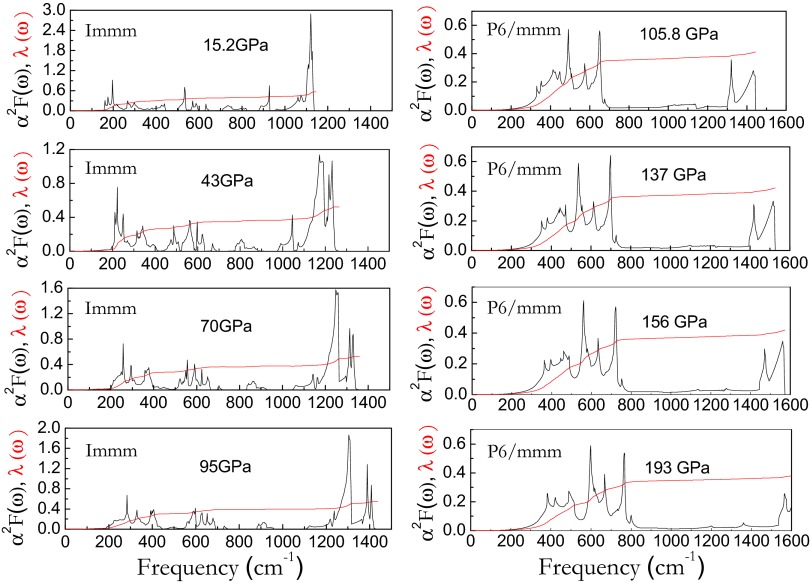
Observed soft phonon modes, similar vibrational properties as CaC₆, and flat energy bands near Fermi level in phase III arouse our interest to explore its superconducting behavior. The calculated spectral function α²F(ω) and integrated λ(ω) of phases III and IV of CaC₂ at different pressure were plotted in Fig. 6 (for the case of phase II, see Fig. S3). For phase III, at 17 GPa, the vibrations below 587.2 cm⁻¹ provide the major contribution to λ, accounting for 66.7% of total λ value (about 0.565). The phonons below 150.1 cm⁻¹, which are mostly attributed to the Ca atom, contribute only 2.9% of total λ value. The phonons between 150.1 and 280.2 cm⁻¹, which originates mostly from Ca-yz modes (along Ca-C1 bonding direction) as well as a small quantity of C1-yz modes (along Ca-C1 bonding direction), contribute 39.6% of the total λ. The phonons between 280.2 and 383.6 cm⁻¹, which originates mostly from Ca-x modes (parallel to carbon ribbon plane) as well as a small quantity of C1-yz modes (along Ca-C1 bonding direction), contribute 10.1% of the total λ. The phonons between 383.6 and 587.2 cm⁻¹, which originates mostly from C2-yz modes (along Ca-C2 bonding direction), contribute 8.7% of the total λ. To summarize, strong electron–phonon coupling, which is necessary for superconductivity in phase III of compressed CaC₂, is due to the phonons from Ca and C1 atoms together with electrons from the Ca-d and C-p states. From Fig. 6, one can see that there is obvious difference between phase III and phase IV in mechanism of electron–phonon coupling. For phase IV, at 105.8 GPa, the vibrations below 700.6 cm⁻¹ provide the major contribution to λ (about 0.47). The low-frequency phonons (below 300.2 cm⁻¹), which mostly involve the Ca atoms yield only 6.6% of total λ value. The phonons between 300.2 and 700.6 cm⁻¹ contribute 75.4% of the total λ. The frequencies at 700.6 cm⁻¹ above, that is, the in-plane vibration modes from carbon atoms, only contribute 18% of the total λ. These results combined with PPHDOS indicate that out-of-plane C_z modes in phase IV dominate superconductivity in phase IV of CaC₂, due to the prominent contributions to the electron–phonon interaction. Phonons from out-of-plane C_z modes together with the electrons from the Ca-d and C-p states provide the strong electron–phonon coupling necessary for superconductivity in phase IV of compressed CaC₂. Most interesting is that phase IV can dominate wide pressure range (see Figs. S4–S6).

Fig. 6.

The Eliashberg phonon spectral function α²F(ω) (blank line) and integrated λ(ω) (red line) for Immm and P6/mmm at four pressure points.

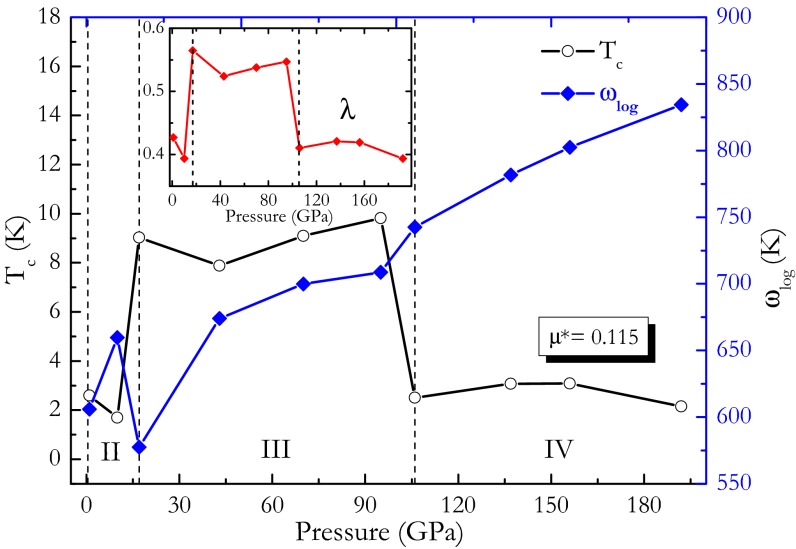
The Allen and Dynes modified equation (31) was used to estimate the superconducting transition temperature T_c from the value of λ determined above. Taking a typical value of 0.115 for the effective Coulomb repulsion parameter μ*, [which is thought to be able to get T_c in agreement with 11.5 K (26, 27) of experiment in CaC₆ (32)], we calculated T_c of three phases for CaC₂ and T_c’s dependence on pressure. Calculated T_c values and logarithmic phonon momentum ω_log vs. pressure curves are presented in Fig. 7. Logarithmic phonon momentum ω_log increases with pressure increase. Among three phases, phase III has the strongest electron–phonon coupling (0.564; Fig. 7, Inset) and so have the highest T_c. At wide range of pressure, phase III of CaC₂ has comparative superconducting critical temperatures (from 7.9 K at 43 GPa to 9.8 K at 95 GPa) with 11.5 K value (26, 27) of CaC₆.

Fig. 7.

Calculated T_c values and logarithmic phonon momentum ω_log vs. pressure. Inset shows the integrated electron–phonon coupling λ as a function of pressure.

The structural, dynamical, and electronic properties of compressed CaC₂ were systemically investigated up to 1 TPa. Three stable high-pressure phases, Cmcm (phase II), Immm (phase III), and MgB₂-type (phase IV) structures, were predicted by using ab initio EA. The carbon atomic arrangement form from “isolated” dumbbell to 1D chain to quasi-1D ribbon to 2D plane is observed. Phonon calculations have shown their dynamical stability at the dominating pressure range. Strong electron–phonon coupling between Ca-d and C-p electrons and Ca-yz and C1-yz phonons (vibration along Ca-C1 bonding direction) dominates superconductivity of phase III, whereas strong electron–phonon coupling between Ca-d electrons and carbon out-of-plane phonons is responsible for superconductivity of phase IV. The predicted evolution of carbon from “local” dumbbell to 2D graphene sheet and high superconducting critical temperature in compressed CaC₂ would stimulate further experimental and theoretical studies on alkaline–earth metal carbides.

Methods

Ab initio EA, designed to search for the structure possessing the lowest free energy at given pressure and temperature conditions, has been used, using USPEX code (16, 17). The structural and electronic properties of CaC₂ over a wide range of the pressure were performed using density functional theory as implemented in VASP (33), using the projected augmented wave (PAW) pseudopotential included in the released pseudopotential library (34, 35) where 2s²2p² and 3s²3p⁶4s² are treated as valence electrons for C and Ca atoms, respectively. Under the PAW approach, Perdew, Burke, and Ernzerhof’s exchange correlation functional (36) was chosen for both Ca and C. For the C atom, we select hard pseudopotential to carry out our calculations because hard pseudopotential was thought to be more suitable for high pressure research. When searching the stable structures, we performed calculations with relaxation of cell volume, cell shape, and ionic positions. Forces on the ions were calculated through derivatives of the free energy with respect to the atomic positions, including the Harris–Foulkes-like correction. All possible structures were optimized using conjugate gradient scheme. For the searches, we used a plane-wave basis set cutoff of 700 eV and performed the Brillouin zone integrations using a coarse k-point grid. The most interesting structures were further relaxed at a higher level of accuracy with a basis set cutoff of 1,000 eV and a k-point grid of spacing 2π × 0.018 Å⁻¹. Iterative relaxation of atomic positions was stopped when all forces were smaller than 0.001 eV/ Å.

The dynamical and superconducting properties were calculated in terms of the Quantum Espresso package (37) using Vanderbilt-type ultrasoft pseudopotentials (38) with cutoff energies of 50 and 500 Ry for the wave functions and the charge density, respectively. The electronic BZ integration in the phonon calculation was based on a 15 × 15 × 12, 15 × 15 × 15, and 32 × 32 × 24 of Monkhorst–Pack k-point meshes for phases II, III, and IV, respectively. The electron–phonon coupling was convergent with a finer grid of 64 × 64 × 64 k points and a Gaussian smearing of 0.01 Ry. The dynamic matrix was computed based on a 4 × 4 × 4 mesh of phonon wave vectors for phases II and IV and on a 3 × 3 × 3 mesh of phonon wave vectors for phase III. All calculations were carried out using a primitive cell, which can largely reduce the amounts of computation in comparison with using a unit cell.