Consistent Group Identification and Variable Selection in Regression with Correlated Predictors

Abstract

Statistical procedures for variable selection have become integral elements in any analysis. Successful procedures are characterized by high predictive accuracy, yielding interpretable models while retaining computational efficiency. Penalized methods that perform coefficient shrinkage have been shown to be successful in many cases. Models with correlated predictors are particularly challenging to tackle. We propose a penalization procedure that performs variable selection while clustering groups of predictors automatically. The oracle properties of this procedure including consistency in group identification are also studied. The proposed method compares favorably with existing selection approaches in both prediction accuracy and model discovery, while retaining its computational efficiency. Supplemental material are available online.

1 Introduction

The collection of large quantities of data is becoming increasingly common with advances in technical research. These changes have opened up many new statistical challenges; the availability of high dimensional data often brings with it large quantities of noise and redundant information. Separating the noise from the meaningful signal has led to the development of new statistical techniques for variable selection.

Consider the usual linear regression model setup with n observations and p predictors given by y = X β + ∊, where ∊ is a random vector with E(∊) = 0 and Var(∊) = σ²I. Let the response vector be y= (y₁, …, y_n)^T, the j^th predictor of the design matrix X be x_j=(x_1j, …, x_nj)^T for j=1,…,p and the vector of coefficients be β = (β₁,…, β_p)^T. Assume the data is centered and the predictors are standardized to have unit L₂ norm, so that $\sum _{i=1}^n{y}_i=0$, $\sum _{i=1}^n{x}_{\mathit{\text{ij}}}=0$ and $\sum _{i=1}^n{x}_{\mathit{\text{ij}}}^2=1$ for all j=1,…,p. This allows the predictors to be put on a comparative scale, and the intercept may be omitted.

In a high dimensional environment this model could include many predictors that do not contribute to the response or have an indistinguishable effect on the response, making variable selection and the identification of the true underlying model an important and necessary step in the statistical analysis. To this end, consider the true underlying linear regression model structure given by y = X_oβ* + ∊, where X_o is the n × p_o true design matrix obtained by removing unimportant predictors and combining columns of predictors with indistinguishable coefficients and β* is the corresponding true coefficient vector of length p_o. For example, if the coefficients of two predictors are truly equal in magnitude, we would combine these two columns of the design matrix by their sum and if a coefficient were truly zero, we would exclude the corresponding predictor. In practice, the discovery of the true model raises two issues; the exclusion of unimportant predictors and the combination of predictors with indistinguishable coefficients. Most existing variable selection approaches can exclude unimportant predictors but fail to combine predictors with indistinguishable coefficients. In this paper we explore a variable selection approach that achieves both goals.

Penalization schemes for regression such as ridge regression (Hoerl and Kennard, 1970) are commonly used in coefficient estimation. Suppose P_λ(·) is a penalty on the coefficient vector and λ is its corresponding non-negative penalization parameter. From a loss and penalty setup, estimates from a penalization scheme for the least squares model are given as the minimizers of $\Vert \mathbf{\text{y}}-\sum _{j=1}^p{\mathbf{\text{x}}}_j{\beta }_j{\Vert }^2+P_{\lambda }(\beta )$. Penalization techniques for variable selection in regression models have become increasingly popular, as they perform variable selection while simultaneous estimating the coefficients in the model. Examples include nonnegative garrote (Breiman, 1995), least absolute shrinkage and selection operator (LASSO, Tibshirani, 1996), smoothly clipped absolute deviation (SCAD, Fan and Li, 2001), elastic-net (Zou and Hastie, 2005), fused LASSO (Tibshirani et al., 2005), adaptive LASSO (Zou, 2006), group LASSO (Yuan and Lin, 2006) and adaptive elastic-net (Zou and Zhang, 2009).

Although these approaches are popular, they fail to combine predictors with indistinguishable coefficients. In some cases, there may be a smoothness structure, or at least an approximate smoothness structure, that is unknown. For example there have been many proposals for gene expression data that are based on averaging groups of genes to use in prediction called a ‘super gene’ by Park et al. (2007). To accomplish this task, Hastie et al. (2001) and Park et al. (2007)), among others, first perform hierarchical clustering on the predictors, and, for each level of the hierarchy, take the cluster averages as the new set of potential predictors for the regression. Note that setting coefficients equal is exactly equivalent to averaging the corresponding predictors. However, as discussed in Bondell and Reich (2008), the clustering step in previous approaches does not use the response information. ‘Supervised clustering’ uses the response information to form clusters of predictors. Supervised clustering aims to identify meaningful groups of predictors that form predictive clusters; such as a group of highly correlated predictors that have a unified effect on the response. Octagonal shrinkage and clustering algorithm for regression (OSCAR, Bondell and Reich, 2008) and collapsing and shrinkage in analysis of variance (CAS-ANOVA, Bondell and Reich, 2009) are penalized techniques that studied supervised clustering in the linear regression and ANOVA context respectively. The OSCAR identifies a predictive cluster by assigning identical coefficients to each element in the group up to a change in sign, while simultaneously eliminating extraneous predictors. The OSCAR estimates can be defined as the solution to

$$\Vert \mathbf{\text{y}}-\sum _{j=1}^p{\mathbf{x}}_j{\beta }_j{\Vert }^2+{\lambda }_1\sum _{j=1}^p|{\beta }_j|+{\lambda }_2\sum _{1\le j<k\le p}\text{max}\{|{\beta }_j|,|{\beta }_k|\}.$$ (1)

The OSCAR penalty contains two penalization parameters λ₁ and λ₂, for λ₁, λ₂ ≥ 0. The first, λ₁, penalizes the L₁ norm of the coefficients and encourages sparseness. The second, λ₂, penalizes the pair-wise L_∞ norm of the coefficients encouraging equality of coefficients.

Although the OSCAR performs effectively in practice, we note that the procedure has certain limitations. The method defined in (1) is implemented via quadratic programming of order p², which becomes increasingly expensive as p increases. Another limitation of the OSCAR is that it is not an oracle procedure. An oracle procedure (Fan and Li, 2001) is one that should consistently identify the correct model and achieve the optimal estimation accuracy. That is, asymptotically, the procedure performs as well as performing standard least-squares analysis on the correct model, were it known beforehand.

Adaptive weighting is a successful technique to constructing oracle procedures. Zou (2006) showed oracle properties for the adaptive LASSO in linear models and generalized linear models (GLMs) by incorporating data dependent in the penalty. Oracle properties for adaptive LASSO was separately studied in other contexts including survival models by Zhang and Lu (2007) and least absolute deviation (LAD) models by Wang et al. (2007). Oracle properties for adaptive elastic-net were studied by Zou and Zhang (2009). The reasoning behind these weights is to ensure that estimates of larger coefficients are penalized less while those that are truly zero have unbounded penalization. Note that all of these procedures define an oracle procedure solely based on selecting variables, not the full selection and grouping structure. Furthermore, an oracle procedure for grouping must also consistently identify the the group of indistinguishable coefficients.

Bondell and Reich (2009) showed oracle properties for the full selection and grouping structure of the CAS-ANOVA procedure in the ANOVA context, using similar arguments of adaptive weighting. In this paper, we show that the OSCAR penalty does not lend itself intuitively to data adaptive weighting. Weighting the pairwise L_∞ norm by an initial estimate, as is the typical case, fails in the following simple scenario. Suppose two coefficients in the pair-wise term are small but should be grouped, then an initial estimate of this quantity would shrink both to zero instead of setting them as equal.

These limitations are the main motivations of this paper. Our goal in this paper is to find an oracle procedure for simultaneous group identification and variable selection, and to address the limitations of existing methods, including the computational burden. The remainder of this paper proceeds as follows. Section 2 proposes a penalization procedure for simultaneous grouping and variable selection along with an algorithm efficient for computation. Section 3 studies theoretical properties of the procedure. Section 4 discusses extensions of the method to GLMs. Section 5 contains a simulation study and the analysis of real examples. A discussion concludes in Section 6.

2 Pairwise Absolute Clustering and Sparsity

2.1 Methodology

In this section, we consider a new penalization scheme for simultaneous group identification and variable selection. We introduce an alternative to the pairwise L_∞ norm in Bondell and Reich (2008) for setting coefficients as equal in magnitude. Note that coefficients with opposite signs are desired to be grouped together in the presence of high negative correlation, leaving the problem equivalent to a sign change of the predictors.

In our setup, the equality of coefficients is achieved by penalizing the pairwise differences and pairwise sums of coefficients. In particular, we propose a penalization scheme with non-negative weights, w, whose estimates are the minimizers of

$$\Vert \mathbf{\text{y}}-\sum _{j=1}^p{\mathbf{\text{x}}}_j{\beta }_j{\Vert }^2+\lambda \{\sum _{\text{j}=\text{1}}^{\text{p}}{w}_j|{\beta }_j|+\sum _{1\le j<k\le p}{w}_{jk(-)}|{\beta }_k-{\beta }_j|+\sum _{1\le j<k\le p}{w}_{jk(+)}|{\beta }_j+{\beta }_k|\}.$$ (2)

The penalty in (2) consists of a weighted L₁ norm of the coefficients that encourages sparseness and a penalty on the differences and sums of pairs of coefficients that encourages equality of coefficients. The weighted penalty on the differences of pairs of coefficients encourages coefficients with the same sign to be set as equal, while the weighted penalty on the sums of pairs of coefficients encourages coefficients with opposite sign to be set as equal in magnitude. The weights are pre-specified non-negative numbers, and their choices will be studied in Section 2.3. We call this penalty Pairwise Absolute Clustering and Sparsity (PACS) penalty and for the remainder of this article we will refer to the PACS procedure in the form given in (2). The PACS objective function is a convex function since it is a sum of convex functions; in particular, if X^T X is full rank then it is strictly convex.

We note here that a specific case of the PACS turns out to be an equivalent representation for the OSCAR. It can be shown that max $\{|{\beta }_j|,|{\beta }_k|\}=\frac{1}{2}\{|{\beta }_k-{\beta }_j|+|{\beta }_j+{\beta }_k|\}$. Suppose 0 ≤ c ≤ 1, then the OSCAR estimates can be equivalently expressed as the minimizers of ${\Vert \mathbf{\text{y}}-\sum _{\text{j}=1}^{\text{p}}{\mathbf{\text{x}}}_j{\beta }_j\Vert }^2+\lambda \{\sum _{j=1}^{p}c|{\beta }_j|+\sum _{1\le j<k\le p}0.5(1-c)|{\beta }_j-{\beta }_k|+\sum _{1\le j<k\le p}0.5(1-c)|{\beta }_j+{\beta }_k|\}$. Hence the OSCAR can be regarded as a special case of the PACS.

The PACS formulation enjoys certain advantages over the original formulation of the OSCAR as given in (1). Like the OSCAR it can be computed via quadratic programming. However, it can also be computed using a local quadratic approximation of the penalty, which is not directly applicable to the original formulation of the OSCAR. The latter strategy is superior to quadratic programming in that quadratic programming becomes expensive in computation and is not feasible for large and even moderate numbers of parameters, while the latter strategy continues to be feasible in these cases, and can be conveniently implemented in standard software.

Furthermore the choice of weighting scheme in the penalty offers the possibility of subjectivity. With a proper reformulation, we show later that it needs only one tuning parameter. The OSCAR has two tuning parameters and this reduction in tuning parameters vastly improves on the cost of computation. This flexibility in choice of weights allows us to explore data adaptive weighting. This is explored in Section 3 where we show that a data adaptive PACS has the oracle property for variable selection and group identification.

We also note here that ridge regression (Hoerl and Kennard (1970)) can be expressed as $2(p-1)\sum _{j=1}^p{\beta }_j^2=\sum _{1\le j\ne k\le p}\{{({\beta }_j-{\beta }_k)}^2+{({\beta }_j+{\beta }_k)}^2\}$, and thus can be viewed as penalizing both pairwise differences and sums. In this manner, the proposed PACS approach can be viewed as a natural generalization of the L₂ penalty to an L₁ version while allowing for different degrees of smoothing on the sum versus the difference for each pair. So including the regular L₁ penalty on the coefficients along with the sums and differences can also be seen as a generalization of the elastic-net (Zou and Hastie (2005)).

2.2 Geometric Interpretation of PACS Penalty

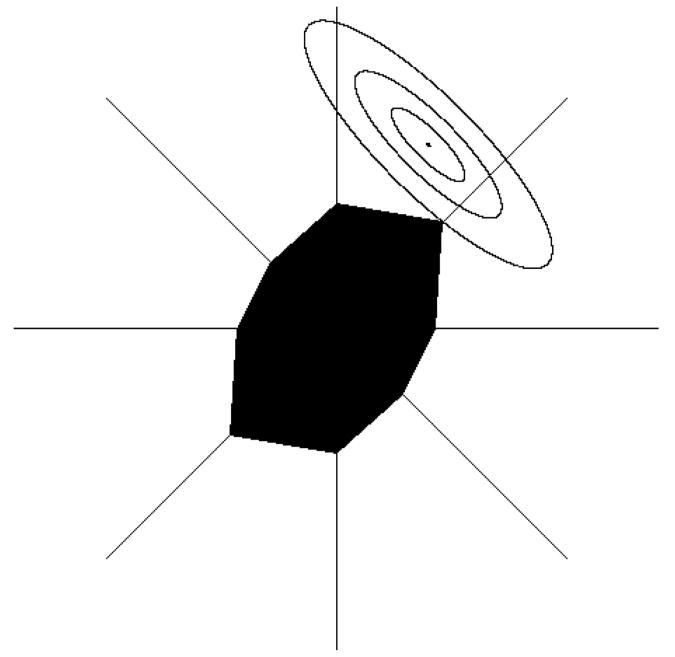
The geometric interpretation of the constrained least squares solutions illustrate the flexibility of the PACS penalty over the OSCAR penalty in accurately selecting the estimates. Aside from a constant, the contours of the least squares loss function are given by ${(\beta -{\hat{\beta }}_{\mathit{\text{OLS}}})}^T{X}^{T}X(\beta -{\hat{\beta }}_{\mathit{\text{OLS}}})=K$. These contours are ellipses centered at the OLS solution. Since the predictors are standardized, when p=2 the principal axis of the contours are at ±45° to the horizontal. As the contours are in terms of X^TX, as opposed to (X^TX)⁻¹, positive correlation would yield contours that are at −45° whereas negative correlation give the reverse. In the (β₁, β₂) plane, intuitively, the solution is the first time the contours of the loss function hit the constraint region.

Figure 1 illustrates the flexibility of the PACS approach over the OSCAR approach in terms of the constraint region in the (β₁, β₂) plane for a specific high correlation (ρ = 0.85) setup. In figures 1 (a) and 1 (b), we see that when the OLS solutions for β₁ and β₂ are close to each other, a specific case of the OSCAR penalty sets the OSCAR solutions as equal, ${\hat{\beta }}_1={\hat{\beta }}_2$, while a specific case of the PACS penalty also sets ${\hat{\beta }}_1={\hat{\beta }}_2$. In figures 1 (c) and 1 (d) we see the same OSCAR and PACS penalty functions find different solutions when the OLS solution for β₁ is close to 0 and not close to that of β₂. Here the OSCAR solutions remain equal to each other while the PACS sets ${\hat{\beta }}_1=0$. Also note that for the OSCAR, although the shape varies with c in 0 ≤ c ≤ 1, it always remains symmetric across the four axes of symmetry. Thus the OSCAR solution is more dependent on the correlation of the predictors, and does not easily adapt to the different least squares solutions.

Figure 1.

Graphical representation to represent the flexibility of the PACS approach over the OSCAR approach in the (β₁, β₂) plane. All figures represent correlation of ρ = 0.85. The top panel has OLS solution βˆ_OLS = (1,2) while the bottom panel has βˆ_OLS = (0.1,2) The solution is the first time the contours of the loss function hits the constraint region.

(a) When the OLS solutions of (β₁, β₂) are close to each other, OSCAR sets βˆ₁ = βˆ₂.

(b) When the OLS solutions of (β₁, β₂) are close to each other, PACS sets βˆ₁ = βˆ₂.

(c) When the OLS solutions of (β₁, β₂) are not close to each other and the OLS solution of β₁ is close to 0, OSCAR sets βˆ₁ = βˆ₂.

(d) When the OLS solutions of (β₁,β₂) are not close to each other and the OLS solution of β₁ is close to 0, PACS sets βˆ₁ = 0.

2.3 Choosing the Weights

In this section we study different strategies for choosing the weights. The choice of weights offers the possibility of subjectivity which come in various forms. Four choices will be examined in detail: weights determined by a predictor scaling scheme, data adaptive weights for oracle properties, an approach to incorporate variable correlation into the weights and an approach to incorporate correlation into the weights with a threshold.

2.3.1 Scaling of the PACS Penalty

The weights for the PACS could be determined via standardization. For any penalization scheme, it is important that the predictors are on the same scale so that penalization is done equally. In penalized regression this is done by standardization, for example, each of the columns of the design matrix has unit L₂ norm. In a penalization scheme such as the LASSO, upon standardization, each column of the design matrix contributes equally to the penalty. When the penalty is based on a norm, rescaling a column of the design matrix is equivalent to weighting coefficients by the inverse of this scaling factor (Bondell and Reich, 2009). We will now determine the weights in (2) via a standardization scheme.

Standardization for the PACS is not a trivial matter since it must incorporate the pairwise differences and sums of coefficients. In fact one needs to consider an over-parameterized design matrix that includes the pairwise coefficient differences and sums. Let the vector of pairwise coefficient differences of length d = p(p−1)/2 be given by τ = {τ_jk : 1 ≤ j < k ≤ p}, where τ_jk = β_k − β_j. Similarly, let the vector of pairwise coefficient sums of length d be given by γ = {γ_jk: 1 ≤ j < k ≤ p}, where γ_jk = β_k + β_j. Let θ = [β^T τ^T γ^T]^T be the coefficient vector of length q = p² for this over-parameterized model. We have θ = Mβ, where M is a matrix of dimension q × p given by $\text{M}={[I_p{D}_{(-)}^T{D}_{(+)}^T]}^T$, with D₍₋₎ being a d × p matrix of ±1 that creates η from β and D₍₊₎ being a d × p matrix of +1 that creates γ from β. The corresponding design matrix for this over-parameterized design is an n × q matrix such that Zθ = Xβ for all β, i.e. ZM = X.

Note that Z is not uniquely defined; possible choices include Z = [X 0_n×2d] and Z = XM*, where M* is any left inverse of M. In particular, choose Z = XM⁻, where M⁻denotes the Moore-Penrose generalized inverse of M.

Proposition 1. The Moore-Penrose generalized inverse of M is $M^{-}=\frac{1}{(2p-1)}[I_p{D}_{(-)}^T{D}_{(+)}^T]$.

Proof of Proposition 1 is given in the appendix. The above proposition allows the determination of the weights via the standardization in the over-parameterized design space. The resulting matrix Z determined using the Moore-Penrose generalized inverse of M is an appropriate design matrix for the over-parametrization. We propose to use the L₂ norm of the corresponding column of Z for standardization as the weights in (2). In particular, these weights are w_j = 1, $w_{\mathit{\text{jk}}(-)}=\sqrt{2(1-r_{\mathit{\text{jk}}})}$ and $w_{\mathit{\text{jk}}(+)}=\sqrt{2(1+r_{jk})}$ for 1 ≤ j < k ≤ p, where r_jk is the correlation between the (j, k)^th pair of predictors of the standardized design matrix.

2.3.2 Data Adaptive Weights

PACS with appropriately chosen data adaptive weights will be shown to be an oracle procedure. Suppose β̃ is a √n-consistent estimator of β, such as the ordinary least squares (OLS) estimates. Adaptive weights for the PACS penalty are given by w_j = |β̃_j|^−α, w_jk(−) = |β̃_k − β̃_j|^−α and w_jk(+) = |β̃_k − β̃_j|^−α for 1 ≤ j < k ≤ p and α > 0. Such weights allow for less penalization when the coefficients, their pairwise differences, or their pairwise sums are larger in magnitude and penalized in an unbounded manner when they are truly zero.

We note that for α = 1, the adaptive weights belong to a class of scale equivariant weights, as long as the initial estimator β̃ is scale equivariant. When the weights are scale equivariant, the resulting solution to the optimization problem is also scale equivariant. In such cases the design matrix does not need to be standardized beforehand, since the resulting solution obtained after transforming back is the same as the solution obtained when the design matrix is not standardized. Due to this simplicity, for the remainder of this paper we set α = 1.

In practice, the initial estimates can be obtained using OLS or other shrinkage estimates like ridge regression estimates. In studies with collinear predictors, we notice that using ridge estimates for the adaptive weights perform better than those given by OLS estimates. The choice of ridge estimate controls the collinearity by smoothing the coefficients. Ridge estimates selected by AIC are used for adaptive weights in all applications in this paper. Ridge estimates chosen by AIC provide slight regularization while not over shrinking, as opposed to BIC. Note that, since the original data are standardized, the ridge estimates are equivariant. Any other choice would require using the scaling in Section 2.3.1 along with the adaptive weights.

2.3.3 Incorporating Correlation

The choice of weights is subjective and in particular, one may wish to assist the grouping of predictors based on the correlation between predictors. This approach is explored in Tutz and Ulbricht (2009) in the ridge regression context. To this end, consider incorporating correlation in the weighting scheme scheme such as those given by w_j = 1, w_jk(−) = (1 − r_jk)⁻¹ and w_jk(+) = (1 + r_jk)⁻¹ for 1 ≤ j < k ≤ p. Intuitively, these weights more heavily penalize the differences in coefficients when they are highly positively correlated and heavily penalize their sums when they are highly negatively correlated. Though such weighting will not discourage uncorrelated predictors to have equal coefficients, they will encourage pairs of highly correlated predictors to have equal coefficients. Adaptive weights that incorporate these correlations terms are then given by w_j(−) = |β̃_j|⁻¹, w_jk(−) = (1 − r_jk)⁻¹ |β̃_k − β̃_j|⁻¹ and w_jk(+) = (1 + r_jk)⁻¹ |β̃_k + β̃_j|⁻¹ for 1 ≤ j < k ≤ p.

2.3.4 Correlation Thresholding

An additional choice of weights incorporates correlation between predictors where pairs of predictors are penalized for their differences or sums only if their pairwise correlation is over a certain threshold. This approach is motivated by Kim et al. (2009), which uses a similar weighting scheme to smooth coefficients for a single predictor in a multiple response regression, in the network analysis context. To this end, we consider incorporating correlation in the weighting scheme with a correlation threshold value, say 0 ≤ c ≤ 1, as follows; w_j = 1, w_jk(−) = I[r_jk > c] and w_jk(+) = I[r_jk < −c] for 1 ≤ j < k ≤ p, where I[·] is the indicator function. This scheme discourages predictors whose pairwise correlation is below the threshold from having equal coefficients, unlike the weighting scheme from Section 2.3.3. In this scheme, the threshold value, 0 ≤ c ≤ 1, can also act as an additional tuning parameter, where sliding the threshold between 0 and 1, would yield different models. The threshold can also be incorporate with either from of adaptive weights from Sections 2.3.2 and 2.3.3, for an adaptive threshold weights.

2.4 Computation

The PACS estimates of (2) can be computed via quadratic programming with (p²+p) parameters and 2p(p − 1) + 1 linear constraints. As the number of predictors increases, quadratic programming becomes more computationally expensive and hence is not feasible for large, and even moderate p. In the following, we suggest an alternative computation technique that is more cost efficient. The algorithm is based on a local quadratic approximation of the penalty similar to that used in Fan and Li (2001). The penalty of the PACS in (2) can be locally approximated by a quadratic function. Suppose for a given value of λ, P(|β_j|) is the penalty on the |β_j| term of the penalty for j = 1,…, p and β_0j is a given initial value that is close to the minimizer of (2). If β_0j is not 0, using the first order expansion with respect to ${\beta }_j^2$, we have $P(|{\beta }_j|)=P({({\beta }_j^2)}^{\frac{1}{2}})\approx P(|{\beta }_{0j}|)+P^{\prime }(|{\beta }_{0j}|)\frac{1}{2}{({\beta }_{0j}^2)}^{-\frac{1}{2}}({\beta }_j^2-{\beta }_{0j}^2)$. Thus $P(|{\beta }_j|)\approx P(|{\beta }_{0j}|)+\frac{1}{2}\frac{P^{\prime }(|{\beta }_{0j}|)}{|{\beta }_{0j}|}({\beta }_j^2-{\beta }_{0j}^2)$ for j = 1, …, p and in the case of the PACS $|{\beta }_j|\approx \frac{{\beta }_j^2}{2|{\beta }_{0j}|}+K$, where K is a term not involving β_j and thus does not play a role in the optimization. We approximate the penalty terms on the differences and sums of the coefficients in a similar manner. Thus both the loss function and penalty are quadratically expressed, and hence there is a closed form solution.

An iterative algorithm with closed form updating expressions follows from these local quadratic approximations. Suppose, at step (t) of the algorithm, the current value, β^(t), close the minimizer of (2) is used to construct the following diagonal matrices; $I_w^{(t)}=\mathit{\text{diag}}(\frac{w_j}{|{\beta }_j^{(t)}|})$, $I_{w(-)}^{(t)}=\mathit{\text{diag}}(\frac{w_{\mathit{\text{jk}}(-)}}{|{\beta }_k^{(t)}-{\beta }_j^{(t)}|})$ and $I_{w(+)}^{(t)}=\mathit{\text{diag}}(\frac{w_{\mathit{\text{jk}}(+)}}{|{\beta }_j^{(t)}+{\beta }_k^{(t)}|})$. The value of the solution at step (t+1) using these constructed matrices is given as ${\hat{\beta }}^{(t+1)}={(X^{T}X+\frac{\lambda }{2}(I_w^{(t)}+D_{(-)}^T{I}_{w(-)}^{(t)}{D}_{(-)}+D_{(+)}^T{I}_{w(+)}^{(t)}{D}_{(+)}))}^{-}{X}^T\mathbf{\text{y}}$.

The algorithm follows as:

1. Specify an initial starting value, ${\beta }^{(0)}={\hat{\beta }}^{(0)}$ close to the minimizer of (2).

2. For step (t+1), construct $I_w^{(t)}$, $I_{w(-)}^{(t)}$ and $I_{w(+)}^{(t)}$ and compute ${\hat{\beta }}^{(t+1)}$.

3. Let t = t + 1. Go to step 2 until convergence.

We note in the algorithm, that at the current step t, we check each ${\hat{\beta }}_j^{(t)}$, as well as the differences and the sums, and any that are smaller (in absolute value) than a chosen ε, say 10⁻⁷, are set to zero. This means that we either remove a column from the design completely, or collapse two (or more) columns together by taking the sum (or difference). One drawback of this approach is that if a column is removed, it will continue to be removed, or that once the columns of the design are collapsed, they will continue to remain collapsed until the algorithm converges.

Proposition 2. Assume X^TX is full rank, then the optimization problem in (2) is strictly convex, and the proposed algorithm is guaranteed to converge to the unique minimizer. Note that if X^TX is not full rank, then the problem is not strictly convex, and in that case it is guaranteed to converge to a local minimizer.

The proof of Proposition 2 is due to the fact that it is an MM algorithm (see Hunter and Li, 2005).

Once the estimates are computed for a given λ, the next step is to select λ that corresponds to the best model. Cross-validation or an information criterion like AIC or BIC could be used for model selection. When using an information criterion, we need an estimate of the degrees of freedom. The degrees of freedom for the PACS is given as the number of unique absolute nonzero estimates as in the case of the OSCAR (see Bondell and Reich, 2008). This notion of degrees of freedom is similar to that given for the fused LASSO (see Tibshirani et al., 2005).

3 Oracle Properties

The use of data adaptive weights in penalization assist in obtaining oracle properties for structure identification. This is complicated when we are interested in group identification; the oracle properties for the adaptive LASSO as in Zou (2006) only applies to the exclusion of unimportant variables. Additional considerations need to be discussed for group identification as in the case of the PACS. Suppose β̃ is a √n-consistent estimator of β. Consider weights for this data adaptive PACS given by w*, where w* incorporates the weighting scheme from Section 2.3.2, so that w* is given by $w_j^{\ast }={\upsilon }_j{|{\stackrel{\sim }{\beta }}_j|}^{-1},w_{\mathit{\text{jk}}(-)}^{\ast }={\upsilon }_{\mathit{\text{jk}}(-)}{|{\stackrel{\sim }{\beta }}_k-{\stackrel{\sim }{\beta }}_j|}^{-1}$ and $w_{\mathit{\text{jk}}(+)}^{\ast }={\upsilon }_{\mathit{\text{jk}}(+)}{|{\stackrel{\sim }{\beta }}_k+{\stackrel{\sim }{\beta }}_j|}^{-1}$ for 1 ≤ j < k ≤ p. The choice of the constants υ is flexible; one could use the correlation terms of Section 2.3.3 or any other choice satisfying the condition that υ_j → c_j, υ_jk(−) → c_jk(−) and υ_jk(+) → c_jk(+) with 0 < c_j, c_jk(−), c_jk(+) < ∞ for all 1 ≤ j < k ≤ p. The adaptive PACS estimates are given as the minimizers of

$$\Vert \mathbf{\text{y}}-\sum _{j=1}^p{\mathbf{\text{x}}}_j{\beta }_j{\Vert }^2+{\lambda }_n\{\sum _{j=1}^p{w}_j^{\ast }|{\beta }_j|+\sum _{1\le j<k\le p}{w}_{\mathit{\text{jk}}(-)}^{\ast }|{\beta }_k-{\beta }_j|+\sum _{1\le j<k\le p}{w}_{\mathit{\text{jk}}(+)}^{\ast }|{\beta }_k+{\beta }_j|\}.$$ (3)

We now show that the adaptive PACS has the oracle property of variable selection and group identification. Consider the overparameterization, θ = Mβ from Section 2.3.1. Let A = {i : θ_i ≠ 0, i = 1,…, q}, q = p², denote the set of indices for which θ is truly non-zero. Let A _n denote the set of indices that are estimated to be non-zero.

Consider β*, a vector of length p_o ≤ p that denotes the oracle parameter vector derived from A. Let A* be the p_o × p full rank matrix such that β* = A*β. For example, suppose the first two coefficients of β are truly equal in magnitude, then the first two elements of the first row of A* would be equal to 0.5 and the remaining elements in the first row would equal 0. If a coefficient in β is not in the true model, then every element of the column of A* corresponding to it would equal 0. We assume the regression model, y = X_oβ* + ε, where ε is a random vector with E(ε) = 0 and Var(ε) = σ²I. Further assume that $\frac{1}{n}{X}_o^T{X}_o\to C$, where X_o is the design matrix collapsed to the correct oracle structure determined by A, and C is a positive definite matrix. The following theorem shows that the adaptive PACS has the oracle property.

Theorem 1. (Oracle properties). Suppose λ_n → ∞ and $\frac{{\lambda }_n}{\sqrt{n}}\to 0$, then the adaptive PACS estimates must satisfy the following:

1. Consistency in structure identification: lim_nP(A_n = A) = 1.

2. Asymptotic normality: $\sqrt{n}(A\ast \hat{\beta }-A\ast \beta ){\to }_{d}N(0,{\sigma }^2{C}^{-1})$.

Remark 1. We note here a correction to Theorem 1 in Bondell and Reich (2009). The proof of that theorem is also under the assumption that λ_n → ∞ and $\frac{{\lambda }_n}{\sqrt{n}}\to 0$. The condition is stated incorrectly in the statement of the theorem.

4 Extension to Generalized Linear Models

We now study an extension of the PACS to GLMs and present a framework to show that an adaptive PACS is an oracle procedure. We consider estimation of penalized log likelihoods using an adaptive PACS penalty, where the likelihood belongs to the exponential family whose density is of the form f(y|x,β) = h(y) exp(y(x^Tβ − φ(x^Tβ))) (see McCullagh and Nelder, 1989). Suppose β̃ is the maximum likelihood estimate (MLE) in the GLM, then the adaptive PACS estimates are given as the minimizers of

$$\sum _{i=1}^n(-y_i({\mathbf{\text{x}}}_i^T\beta )+\phi ({\mathbf{\text{x}}}_i^T\beta ))+{\lambda }_n\{\sum _{j=1}^p{w}_j^{\ast }|{\beta }_j|+\sum _{1\le j<k\le p}{w}_{\mathit{\text{jk}}(-)}^{\ast }|{\beta }_k-{\beta }_j|+\sum _{1\le j<k\le p}{w}_{\mathit{\text{jk}}(+)}^{\ast }|{\beta }_k+{\beta }_j|\},$$

where the weights are given as in Section 3. We assume the following regularity conditions:

1. The Fisher information matrix for β*, $I({\beta }^{\ast })=E[{\phi }^{″}({\mathbf{\text{x}}}_o^T{\beta }^{\ast }){\mathbf{\text{x}}}_o{\mathbf{\text{x}}}_o^T]$, is positive definite.

1. There is a sufficiently large open set O that contains β* such that for all vectors of length p_o contained in O, $|{\phi }^{‴}({\mathbf{\text{x}}}_o^T{\beta }^{\ast })|\le M({\mathbf{\text{x}}}_o)<\infty$ and E[M(x_o) | x_ojx_okx_ol] < ∞ for all 1 ≤ j, k, l ≤ p.

Theorem 2. (Oracle properties for GLMs). Assume conditions (A) and (B) and suppose λ_n → ∞ and $\frac{{\lambda }_n}{\sqrt{n}}\to 0$, then the adaptive PACS estimates must satisfy the following:

1. Consistency in structure identification: lim_n P(A_n = A) = 1.

2. Asymptotic normality: $\sqrt{n}(A\ast \hat{\beta }-A\ast \beta ){\to }_{d}N(0,I{({\beta }^{\ast })}^{-1})$.

The proof of Theorem 2 follows the proof of Theorem 1 after a Taylor expansion of the objective function as done in the proof of Theorem 4 of Zou (2006).

4.1 Computation using Least Squares Approximation

The PACS estimates for GLMs can be computed via a Newton-Raphson type iterative algorithm. These algorithms are often computationally expensive and alternative methods if available are preferred. Recently, a novel method of computing an asymptotically equivalent solution was proposed by Wang and Leng (2007) where a least squares approximation (LSA) was applied to the negative log likelihood function, given by $-\frac{1}{n}{\ell }_n(\beta )$, and transforms the problem to its asymptotically equivalent Wald-statistic form. In particular, suppose the MLE, β̃ is √n-consistent, asymptotically normal with (β̃) = Γ, then the minimization of $-\frac{1}{n}{\ell }_n(\beta )$ is asymptotically equivalent to the minimization of (β̃ − β)^TΓˆ⁻¹(β̃ − β), where Γˆ is a consistent estimate of Γ. Consider the specific case that Γˆ⁻¹ is symmetric and positive definite, then by the Cholesky decomposition we get Γˆ⁻¹ L^T L, where L is an upper triangular matrix. So β)^TΓˆ⁻¹(β̃ − β) = β)^TL^TL(β̃ − β) = ║L(β̃ − β)║². Then the minimization of $-\frac{1}{n}{\ell }_n(\beta )$ is asymptotically equivalent to the minimization of ║L(β̃ − β)║². Thus the asymptotic equivalent PACS estimates computed via the LSA are given as the minimizers of

$${\Vert L(\stackrel{\sim }{\beta }-\beta )\Vert }^2+\lambda \{\sum _{j=1}^p{w}_j|{\beta }_j|+\sum _{1\le j<k\le p}{w}_{\mathit{\text{jk}}(-)}|{\beta }_k-{\beta }_j|+\sum _{1\le j<k\le p}{w}_{\mathit{\text{jk}}(+)}|{\beta }_j+{\beta }_k|\}.$$

The PACS estimates can now be computed using the algorithm for the least squares model from Section 2.4. In this paper we suggest using the LSA technique to solve for the PACS estimates for GLMs.

5 Numerical Examples

5.1 Simulation Study

A simulation study compares the PACS approach with existing selection approaches in both prediction accuracy and model discovery. We present 6 illustrative examples, each containing 100 simulated data sets. The true models were simulated from a regression model given by y = Xβ + ε, ε ∼ N(0, σ²I). In all illustrations, predictors are standard normal and standardized before model fitting.

We compare three versions of the PACS approach with ridge regression, LASSO, adaptive LASSO, elastic-net and adaptive elastic-net. The first PACS approach is the adaptive PACS (Adapt PACS) with the weights given in Section 2.3.2 as w_j = |β̃_j|⁻¹, w_jk(−) = |β̃_k − β̃_j|⁻¹ and w_jk(+) = |β̃_k + β̃_j|⁻¹ for 1 ≤ j < k ≤ p. The second PACS approach is the adaptive PACS that incorporates correlations (AdCorr PACS) with the weights given in Section 2.3.3 as w_j = |β̃_j|⁻¹, w_jk(−) = (1 − r_jk)⁻¹|β̃_k − β̃_j|⁻¹ and w_jk(+) = (1 + r_jk)⁻¹|β̃_k + β̃_j|⁻¹ for 1 ≤ j < k ≤ p. The third PACS approach is a combination of the correlation threshold weights in Section 2.3.4, with c=0, 0.25, 0.5 and 0.75 and the weights proposed above, being the Adapt PACS. In this version (ThAdapt PACS), the weights are given as w_j = |β̃_j|⁻¹, w_jk(−) = |β̃_k − β̃_j|⁻¹ and w_jk(+) = |β̃_k + β̃_j|⁻¹ for 1 ≤ j < k ≤ p. For Example 1, we also compare the results from the OSCAR approach. Models were selected by BIC, where the degrees of freedom for the PACS approaches are the number of unique absolute nonzero estimates as in the case of the degrees of freedom for the OSCAR estimates.

All methods were compared in terms of model error (ME) for prediction accuracy and the resulting model complexity for model discovery. We report (median) ME = (βˆ − β)^TV(β̃ − β), where V is the population covariance matrix of X and its bootstrap standard error. We report average degrees of freedom (DF), selection accuracy (SA, the percentage of correct models identified), grouping accuracy (GA, the percentage of correct groups identified) and the percentage of both selection and grouping accuracy (SGA). Note that none of the other methods perform grouping, so that their grouping accuracy will always be zero. Also, for a few of our more complex illustrations with additional clusters of variables and with no clusters of variables, we include other measures of model complexity which we explain in context of the illustrations. Other choices of thresholds combined with correlation-based weights were investigated and the results were similar, hence omitted.

Example 1 is an illustration of a group of 3 important highly correlated predictors whose coefficients are equal in magnitude. We simulate n=50 and 100 observations with p=8 predictors. The true parameters are β = (2, 2, 2, $0_5^T$)T and σ² = 1, where $0_5^T$ denotes a vector of 5 zeros. The first 3 predictors have pairwise correlation of 0.7 while the remainder are uncorrelated. Table 1 summarizes the results. The PACS approaches have the lowest ME for all sample sizes. In model complexity, the PACS approaches have the lowest DF estimates. Although the elastic-net and the adaptive elastic-net have the highest SA, we note that the elastic-net approaches do not perform grouping. We also note that the OSCAR which performs grouping, has poor ME as well as lower percentages of selection and grouping. The PACS approaches successfully identify and group the cluster of predictors as seen in the GA and SGA columns. Here we also see that AdCorr PACS, which incorporates the pairwise correlation in the weighting scheme has lower ME and a higher rate of grouping than Adaptive PACS. Of the four ThAdapt PACS approaches, when c = 0.0 the results are very similar to those of the Adapt PACS approach. When the threshold increases the grouping accuracy improves, although when c = 0.75, at a level above the pairwise correlation in the group, the grouping accuracy goes down. We also note that due to the fact that tuning for the OSCAR is over 2 parameters which increases the cost of computation, we do not include it in the remainder of the examples, as the additional burden does not lead to a gain in performance.

Table 1. Results of Example 1.

Method	ME (s.e)	D.F	SA	GA	SGA
n=50
Ridge	0.1703(0.0083)	8.00	0	0	0
LASSO	0.1094(0.0090)	3.63	60	0	0
Adapt LASSO	0.0840(0.0087)	3.36	74	0	0
Elastic-net	0.0759(0.0088)	3.32	78	0	0
Adapt elastic-net	0.0726(0.0119)	3.26	77	0	0
OSCAR	0.1194(0.0067)	3.07	43	19	10
Adapt PACS	0.0574(0.0091)	1.73	68	67	49
AdCorr PACS	0.0477(0.0118)	1.65	63	80	56
ThAdapt PACS (c = 0.0)	0.0493(0.0093)	1.57	74	76	60
ThAdapt PACS (c = 0.25)	0.0448(0.0133)	1.74	53	86	47
ThAdapt PACS (c = 0.5)	0.0407(0.0119)	1.82	46	89	42
ThAdapt PACS (c = 0.75)	0.0834(0.0078)	3.20	51	8	3
n=100
Ridge	0.0762(0.0051)	8.00	0	0	0
LASSO	0.0454(0.0061)	3.43	68	0	0
Adapt LASSO	0.0361(0.0047)	3.19	85	0	0
Elastic-net	0.0334(0.0039)	3.09	92	0	0
Adapt elastic-net	0.0318(0.0038)	3.13	89	0	0
OSCAR	0.0635(0.0065)	2.78	49	31	23
Adapt PACS	0.0120(0.0034)	1.39	88	78	73
AdCorr PACS	0.0073(0.0017)	1.30	82	91	77
ThAdapt PACS (c = 0.0)	0.0082(0.0017)	1.30	89	84	78
ThAdapt PACS (c = 0.25)	0.0146(0.0032)	1.63	58	90	53
ThAdapt PACS (c = 0.5)	0.0144(0.0036)	1.65	57	89	52
ThAdapt PACS (c = 0.75)	0.0363(0.0070)	3.19	56	9	6

Example 2 is an illustration of a situation where there is high pairwise correlation among the important predictors while their coefficients differ in magnitude. We simulate n=50 and 100 observations with p=8 predictors. The true parameters are β = (0.5, 1, 2, $0_5^T$)T and σ² = 1. The first three predictors have pairwise correlation of 0.7 while the remainder are uncorrelated. We report a column for percentage of no-grouping (NG, no groups found) instead of GA and percentage of selection and no-grouping (SNG). Table 2 summarizes the results. We notice that the PACS approaches do not perform as well in prediction and selection as the existing selection approaches and that the elastic-net approaches perform the best in terms of and selection. All approaches perform well in terms of not identifying the group. Thus, the PACS approaches would not be an advisable approach when there is high correlation but where the important coefficients do not form a group.

Table 2. Results of Example 2.

Method	ME (s.e)	D.F	SA	NG	SNG
n=50
Ridge	0.1717(0.0086)	8.00	0	100	0
LASSO	0.1126(0.0091)	3.60	58	100	58
Adapt LASSO	0.1147(0.0128)	3.09	47	100	58
Elastic-net	0.0941(0.0122)	3.10	59	100	59
Adapt elastic-net	0.0870(0.0150)	3.21	68	100	68
Adapt PACS	0.1262(0.0098)	3.04	39	100	39
AdCorr PACS	0.1384(0.0087)	2.89	46	96	45
ThAdapt PACS (c = 0.0)	0.1267(0.0095)	3.03	45	100	45
ThAdapt PACS (c = 0.25)	0.1372(0.0103)	4.02	17	99	17
ThAdapt PACS (c = 0.5)	0.1413(0.0115)	4.16	16	99	16
ThAdapt PACS (c = 0.75)	0.1312(0.0111)	4.35	15	99	15
n=100
Ridge	0.0788(0.0076)	8.00	0	100	0
LASSO	0.0454(0.0059)	3.43	68	100	68
Adapt LASSO	0.0413(0.0059)	3.13	69	100	69
Elastic-net	0.0346(0.0030)	3.00	83	100	83
Adapt elastic-net	0.0359(0.0059)	3.13	86	100	86
Adapt PACS	0.0536(0.0066)	3.09	64	100	64
AdCorr PACS	0.0573(0.0037)	2.91	68	100	68
ThAdapt PACS (c = 0.0)	0.0516(0.0057)	3.06	64	100	64
ThAdapt PACS (c = 0.25)	0.0612(0.0062)	4.33	14	100	14
ThAdapt PACS (c = 0.5)	0.0612(0.0067)	4.32	13	100	13
ThAdapt PACS (c = 0.75)	0.0544(0.0064)	4.54	13	100	13

Example 3 is an illustration of a group of 3 highly correlated important predictors whose coefficients are equal in magnitude and 3 additional important predictors with lower correlation and different magnitudes. We simulate n=50 and 100 observations with p=10 predictors. The true parameters are β = (1, 1, 1, 0.5, 1, 2, $0_4^T$)T and σ² = 1. The first 3 predictors have pairwise correlation of 0.7, the next 3 have pairwise correlation of 0.3 while the remainder are uncorrelated. Table 3 summarizes the results. We notice that the two elastic-net approaches have the best selection accuracy, however, the PACS approach, particularly with the thresholding weights performs better in terms of model error. Adapt PACS and AdCorr PACS have good grouping accuracy with the ThAdapt PACS approaches having improved grouping accuracy with increases in thresholding. When c = 0.0, c = 0.25 and c = 0.5, the results are improved for grouping and model error, although then c = 0.75, there is no improvement in results. In this setting, we notice that all PACS approaches continue to identify the important group with high GA and SGA, suggesting the use of the PACS approach particularly with the correlation threshold, in such settings.

Table 3. Results of Example 3.

Method	ME (s.e)	D.F	SA	GA	SGA
n=50
Ridge	0.1982(0.0123)	10.00	0	0	0
LASSO	0.1834(0.0178)	6.82	46	0	0
Adapt LASSO	0.1736(0.0093)	6.18	68	0	0
Elastic-net	0.1598(0.0114)	6.20	72	0	0
Adapt elastic-net	0.1541(0.0143)	6.23	76	0	0
Adapt PACS	0.1762(0.0133)	4.32	54	28	15
AdCorr PACS	0.1684(0.0196)	3.98	54	54	33
ThAdapt PACS (c = 0.0)	0.1725(0.0199)	4.01	61	51	35
ThAdapt PACS (c = 0.25)	0.1302(0.0168)	4.60	52	77	46
ThAdapt PACS (c = 0.5)	0.1242(0.0114)	4.72	55	80	48
ThAdapt PACS (c = 0.75)	0.1602(0.0090)	6.02	50	9	6
n=100
Ridge	0.0998(0.0070)	10.00	0	0	0
LASSO	0.0882(0.0062)	6.94	41	0	0
Adapt LASSO	0.0656(0.0045)	6.23	79	0	0
Elastic-net	0.0721(0.0043)	6.21	85	0	0
Adapt elastic-net	0.0614(0.0042)	6.15	86	0	0
Adapt PACS	0.0620(0.0050)	4.03	73	47	38
AdCorr PACS	0.0550(0.0066)	3.72	71	79	57
ThAdapt PACS (c = 0.0)	0.0555(0.0059)	4.03	73	68	51
ThAdapt PACS (c = 0.25)	0.0526(0.0044)	4.75	44	87	37
ThAdapt PACS (c = 0.5)	0.0524(0.0054)	4.81	46	87	39
ThAdapt PACS (c = 0.75)	0.0684(0.0034)	6.27	47	11	2

Example 4 is similar to Example 3 and is an illustration of a group of 3 correlated important predictors whose coefficients are equal in magnitude and 3 additional important predictors with higher correlation and different magnitudes. We simulate n=50 and 100 observations with p=10 predictors. The true parameters are β = (1, 1, 1, 0.5, 1, 2, $0_4^T$)T and σ² = 1. The first 3 predictors have pairwise correlation of 0.3, the next 3 have pairwise correlation of 0.7 while the remainder are uncorrelated. Table 4 summarizes the results. The two elastic-net approaches have the best selection accuracy, but comparable ME to the PACS approaches and that ThAdapt PACS with c = 0.0 has better results than the other PACS approaches. When the threshold is above the value of the pairwise correlation of the group, no groups were formed. In such settings, the PACS approaches, particularly with the thresholding at or below the level of the pairwise correlation of the group would be appropriate.

Table 4. Results of Example 4.

Method	ME (s.e)	D.F	SA	GA	SGA
n=50
Ridge	0.2120(0.0126)	10.00	0	0	0
LASSO	0.1878(0.0170)	6.83	41	0	0
Adapt LASSO	0.1807(0.0105)	6.00	53	0	0
Elastic-net	0.1762(0.0161)	6.23	68	0	0
Adapt elastic-net	0.1812(0.0128)	6.09	69	0	0
Adapt PACS	0.1705(0.0150)	3.93	57	35	22
AdCorr PACS	0.1792(0.0149)	3.86	56	43	29
ThAdapt PACS (c = 0.0)	0.1804(0.0135)	3.74	49	55	28
ThAdapt PACS (c = 0.25)	0.1578(0.0120)	4.54	47	46	27
ThAdapt PACS (c = 0.5)	0.1907(0.0162)	5.71	48	0	0
ThAdapt PACS (c = 0.75)	0.1772(0.0088)	6.16	47	0	0
n=100
Ridge	0.1027(0.0068)	10.00	0	0	0
LASSO	0.0855(0.0062)	6.94	39	0	0
Adapt LASSO	0.0685(0.00470	6.15	72	0	0
Elastic-net	0.0651(0.0054)	6.22	80	0	0
Adapt elastic-net	0.0620(0.0041)	6.15	82	0	0
Adapt PACS	0.0621(0.0057)	3.78	73	56	44
AdCorr PACS	0.0755(0.0080)	3.64	72	65	47
ThAdapt PACS (c = 0.0)	0.0610(0.0070)	3.71	73	72	53
ThAdapt PACS (c = 0.25)	0.0653(0.0039)	4.79	43	65	27
ThAdapt PACS (c = 0.5)	0.0839(0.0061)	6.34	42	0	0
ThAdapt PACS (c = 0.75)	0.0704(0.0045)	6.50	44	0	0

Example 5 is an illustration of 2 groups of 3 and 2 important highly correlated predictors (respectively) whose coefficients are equal in magnitude. We simulate n=50 and 100 observations with p=10 predictors. The true parameters are β = (2, 2, 2, 1, 1, $0_5^T$)T and σ² = 1. The first 3 predictors have pairwise correlation of 0.7, the next 2 predictors have pairwise correlation of 0.7, while the remainder are uncorrelated. Here we report in addition, GA1 and GA2, being the % of grouping accuracy for each of the 2 groups. Table 5 summarizes the results. We notice that the adaptive elastic-net approach has the best selection accuracy. The PACS approaches have excellent grouping accuracy, with results improving with the thresholding, although when c = 0.75, the PACS approach does not do well in grouping. In this setting, we notice that all PACS approaches successfully identify the groups of predictors as seen in the GA1, GA2, GA and SGA columns, suggesting the use of the PACS approach particularly with the correlation threshold, in such settings.

Table 5. Results of Example 5.

Method	ME (s.e)	D.F	SA	GA1	GA2	GA	SGA
n=50
Ridge	0.1816(0.0146)	10.00	0	0	0	0	0
LASSO	0.1677(0.0143)	5.87	40	0	0	0	0
Adapt LASSO	0.1316(0.0105)	5.32	70	0	2	0	0
Elastic-net	0.1360(0.0119)	5.42	65	0	1	0	0
Adapt elastic-net	0.1208(0.0113)	5.24	80	0	0	0	0
Adapt PACS	0.1236(0.0109)	3.32	73	49	53	30	21
AdCorr PACS	0.0870(0.0105)	2.86	71	77	72	57	45
ThAdapt PACS (c = 0.0)	0.0956(0.0080)	2.91	76	70	63	45	36
ThAdapt PACS (c = 0.25)	0.0546(0.0094)	2.62	72	84	87	75	59
ThAdapt PACS (c = 0.5)	0.0561(0.0081)	2.46	75	87	93	82	67
ThAdapt PACS (c = 0.75)	0.1084(0.0104)	4.61	72	9	23	1	1
n=100
Ridge	0.0970(0.00028)	10.00	0	0	0	0	0
LASSO	0.0810(0.0068)	5.69	57	0	0	0	0
Adapt LASSO	0.0514(0.0042)	5.23	83	0	0	0	0
Elastic-net	0.0646(0.0054)	5.25	83	0	0	0	0
Adapt elastic-net	0.0485(0.0040)	5.13	88	0	0	0	0
Adapt PACS	0.0390(0.0039)	2.82	86	72	65	45	43
AdCorr PACS	0.0308(0.0044)	2.49	80	87	88	78	65
ThAdapt PACS (c = 0.0)	0.0321(0.0057)	2.57	87	82	77	64	60
ThAdapt PACS (c = 0.25)	0.0214(0.0036)	2.32	82	95	96	92	77
ThAdapt PACS (c = 0.5)	0.0192(0.0032)	2.31	83	95	96	92	78
ThAdapt PACS (c = 0.75)	0.0446(0.0049)	4.54	80	14	24	6	6

Example 6 is an illustration of a situation of a p > n example with a group of 3 important highly correlated predictors whose coefficients are equal in magnitude and more than n predictors. We simulate n=50 with p=103 predictors. The true parameters are β = (2, 2, 2, $0_{100}^T$)T and σ² = 0.5. The first three predictors have pairwise correlation of 0.7 while the remainder are uncorrelated. Table 6 summarizes the results. The PACS approaches continue to have excellent model, selection and grouping accuracy with the threshold approach, ThAdapt PACS with c = 0.25 having the lowest ME as well as the best grouping accuracy. When c = 0.5 and c = 0.75, the model size is increased and the selection and grouping accuracy is decreased. This suggests that the PACS approach, particularly with the correlation threshold, is a successful approach for the p > n setting as well.

Table 6. Results of Example 6.

Method	ME (s.e)	D.F	SA	GA	SGA
Ridge	5.8974(0.0945)	103.00	0	0	0
LASSO	0.1007(0.0089)	4.76	44	0	0
Adapt LASSO	0.0370(0.0031)	3.77	73	0	0
Elastic-net	0.0706(0.0045)	3.65	84	0	0
Adapt elastic-net	0.0260(0.00028)	3.14	87	0	0
Adapt PACS	0.0297(0.0033)	2.47	85	18	18
AdCorr PACS	0.0220(0.0030)	1.84	91	44	44
ThAdapt PACS (c = 0.0)	0.0308(0.0050)	2.07	92	36	36
ThAdapt PACS (c = 0.25)	0.0219(0.0035)	1.30	79	95	76
ThAdapt PACS (c = 0.5)	0.0226(0.0102)	16.44	55	94	55
ThAdapt PACS (c = 0.75)	0.0892(0.1870)	23.50	28	10	4

5.2 Analysis of Real Data Examples

In this section we illustrate the performance of the PACS approach with existing selection approaches in the analysis of examples of real data. Two data sets are studied, being the NCAA sports data from Mangold et al. (2003) and the pollution data from McDonald and Schwing (1973). OLS, LASSO, adaptive LASSO, elastic-net, adaptive elastic-net, Adapt PACS, AdCorr PACS and ThAdapt PACS, as given in Section 5.1 were applied to the data. The predictors were standardized and the response was centered before performing analysis. Ridge regression estimates selected by AIC was used as adaptive weights for all data-adaptive approaches.

Each data set was randomly split into a training and testing set, with 20% of the data used for testing, and models were fit on the training set using BIC. For the ThAdapt PACS approach, we also tuned over a grid of the threshold parameter and test error was calculated after tuning on the threshold parameter. The data sets were randomly split 100 times each to allow for more stable comparisons. We report the ratio of test error over OLS (RTE, average and s.e) of all methods, the estimates of the coefficients and the effective model size after accounting for equality of absolute coefficient estimates. OLS variables that are significant at a level of 0.05 are reported with an asterisk.

The NCAA sports data are taken from the 1996-99 editions of the US News ”Best Colleges in America” and from the US Department of Education data which includes 97 NCAA Division 1A schools. The study aimed to show that successful sports programs raise graduation rates. The response is average 6 year graduation rate for 1996 through 1998 and the predictors are sociodemographic indicators and various sports indicators. The data contains n=94 observations and p=19 predictors where 20% of the pairwise (absolute) correlations are greater than 0.5. For the ThAdapt PACS approach, the threshold was set at c = 0.5. In Table 7, we see that two of the three PACS methods do significantly better than the existing selection approaches in test error, with the ThAdapt PACS not doing better than the other approaches. In fact, all the existing selection approaches perform worse than the OLS in test error. The effective model sizes are 6 for Adaptive PACS and 5 for AdCorr PACS, although they include all variables in the models, and the effective size for ThAdapt PACS was 10 with the exclusion of 3 variables.

Table 7. Results for NCAA Data Analysis.

Variable	OLS	LASSO	Adapt LASSO	Elastic-net	Adapt elastic-net	Adapt PACS	AdCorr PACS	ThAdapt PACS
Top 10 high school	0.700	0	0	0	0.643	0.787	0.849	1.051
ACT Composite 25%	7.164*	7.911	9.459	10.405	7.295	6.430	5.356	5.510
% Living on campus	4.450*	3.264	4.121	4.416	4.392	4.045	4.171	3.699
% First time grad	4.050*	1.360	2.389	0	4.050	3.014	3.312	3.699
Total enrollment / 1000	3.124*	0	1.687	0	3.052	2.279	2.530	3.262
% Course TA taught	1.327	0	0	0	1.316	0.787	0.849	1.390
Basketball Ranking	-2.390*	0	-0	0	-2.344	-0.787	-0.849	-1.426
Instate tuition/1000	-3.246	0	0	0	-3.106	-0.787	-0.849	0
Room and board/1000	2.694*	0	0	0	2.715	0.787	0.849	1.051
Basketball (mean) attend	-1.095	0	0	0	-1.061	-0.787	-0.849	-1.368
Full professor salary	1.437	1.328	0	0	1.302	0.787	0.849	1.051
Student to faculty ratio	-1.617	0	0	0	-1.624	-0.787	-0.849	-1.051
% White	1.394	0	0	0	1.412	0.787	0.849	1.604
Asst. professor salary	-0.652	0	0	0	-0.432	0.509	0.849	1.051
City population	-0.773	0	0	0	-0.806	-0.787	-0.849	-1.109
% Faculty with Ph.D	0.116	0	0	0	0	0.509	0.849	0
Acceptance rate	-1.275	0	0	0	-1.256	-0.787	-0.849	-1.051
% Receiving loans	-0.859	0	0	0	-0.857	-0.787	-0.849	-0.934
% Out of state	0.239	0	0	0	0	0.509	0.849	0
Model Size	19	4	5	2	17	6	5	10
Ratio Test Error (s.e)	1 (0.0)	1.124 (0.030)	1.059 (0.026)	1.127 (0.032)	1.000 (0.002)	0.935 (0.015)	0.928 (0.015)	1.005 (0.021)

The pollution data is from a study of the effects of various air pollution indicators and socio-demographic factors on mortality. The data contains n=60 observations and p=15 predictors where 5% of the pairwise (absolute) correlations are greater than 0.6. For the ThAdapr PACS, the threshold was set at c = 0.6. In Table 8, we see that LASSO has the lowest test error followed by the four PACS approaches. Although the Adapt PACS includes all the variables in the model, it has an effective model size of 4, while the AdCorr PACS includes 11 variables with an effective model size of 5. The ThAdapt PACS includes 8 variables without forming any group.

Table 8. Results for Pollution Data Analysis.

Variable	OLS	LASSO	Adapt LASSO	Elastic-net	Adapt elastic-net	Adapt PACS	AdCorr PACS	ThAdapt PACS
Annual precipitation (mean)	19.025*	11.779	14.761	14.003	13.042	16.03	16.276	18.69
January temperature (mean)	-19.703	-8.807	-12.856	-10.100	0	-16.03	-14.969	-14.683
July temperature (mean)	-14.768	0	0	0	0	-5.349	-6.036	-4.372
% Older than 65 years	-13.277	0	0	0	0	-2.672	0	0
Household population	-14.448	0	0	0	6.747	-2.672	0	0
Years of school (median)	-14.503	-9.988	-5.767	-12.004	-10.101	-5.349	-6.036	-4.156
% Houses with facilities	-3.348	0	0	0	-7.889	-2.672	-0.883	0
Population density	5.235	2.625	0	3.001	8.836	5.349	6.036	4.945
% Non-white	39.785*	30.044	34.424	35.564	18.933	36.006	38.332	36.669
% White collar	-0.863	0	0	0	0	-2.672	-0.883	-1.235
% Poor	-0.697	0	0	0	3.948	2.672	0.883	0
Hydrocarbons	-61.822	0	0	0	0	-2.672	0	0
Nitrogen oxides	62.091	0	0	0	0	2.672	0	0
Sulphur dioxide	5.468	13.659	16.613	16.287	15.500	16.030	14.969	16.541
Relative humidity	0.574	0	0	0	0	2.672	0.883	0
Model Size	15	6	5	6	8	4	5	8
Ratio Test Error (s.e)	1 (0.0)	0.758 (0.035)	0.790 (0.033)	0.839 (0.040)	0.809 (0.035)	0.775 (0.032)	0.789 (0.032)	0.779 (0.031)

6 Discussion

In this paper we have proposed the PACS, a consistent group identification and variable selection procedure. The PACS produces a sparse model that clusters groups of predictive variables by setting their coefficients as equal, and in the process identifies these groups. Computationally, the PACS is shown to be easily implemented with an efficient computational strategy. Theoretical properties of the PACS are also studied and a data adaptive PACS is an oracle procedure for variable selection and group identification. The PACS is shown to have favorable predictive accuracy while identifying relevant groups in simulation studies and has favorable predictive accuracy in the analysis of real data.