Specificity in Transition State Binding: The Pauling Model Revisited

Abstract

Linus Pauling proposed that the large rate accelerations for enzymes are due to the high specificity of the protein catalyst for binding the reaction transition state. The observation that stable analogs of the transition states for enzymatic reactions often act as tight-binding binding inhibitors provided early support for this simple and elegant proposal. We review experimental results which support the proposal that Pauling’s model provides a satisfactory explanation for the rate accelerations for many heterolytic enzymatic reactions through high energy reaction intermediates, such as proton transfer and decarboxylation. Specificity in transition state binding is obtained when the total intrinsic binding energy of the substrate is significantly larger than the binding energy observed at the Michaelis complex. The results of recent studies to characterize the specificity in binding of the enolate oxygen at the transition state for the 1,3-isomerization reaction catalyzed by ketosteroid isomerase are reviewed. Interactions between pig heart succinyl-CoA:3-oxoacid coenzyme A transferase (SCOT) and the nonreacting portions of CoA are responsible for a rate increase of 3 × 10¹²-fold, which is close to the estimated total 5 × 10¹³-fold enzymatic rate acceleration. Studies that partition the interactions between SCOT and CoA into their contributing parts are reviewed. Interactions of the protein with the substrate phosphodianion group provide a ca. 12 kcal/mol stabilization of the transition state for the reactions catalyzed by triosephosphate isomerase, orotidine 5′-monophosphate decarboxylase and α-glycerol phosphate dehydrogenase. The interactions of these enzymes with the substrate piece phosphite dianion provide a 6 – 8 kcal/mol stabilization of the transition state for reaction of the appropriate truncated substrate. Enzyme activation by phosphite dianion reflects the higher dianion affinity for binding to the enzyme-transition state complex compared with the free enzyme. Evidence is presented that supports a model in which the binding energy of the phosphite dianion piece, or the phosphodianion group of the whole substrate, is utilized to drive an enzyme conformational change from an inactive open form E_O to an active closed form E_C, by closure of a phosphodianion gripper loop. Members of the enolase and haloalkanoic acid dehalogenase superfamilies use variable capping domains to interact with nonreacting portions of the substrate and sequester the substrate from interaction with bulk solvent. Interactions of this capping domain with the phenyl group of mandelate have been shown to activate mandelate racemase for catalysis of deprotonation of α-carbonyl carbon. We propose that an important function of these capping domains is to utilize the binding interactions with nonreacting portions of the substrate to activate the enzyme for catalysis.

Linus Pauling proposed that the large rate accelerations for enzymatic reactions arise from the high specificity of the protein catalyst for binding the reaction “activated complex”, or transition state, as it is now known.^1,2 There is abundant evidence to support this proposal. Stable analogs of the transition states for the reactions catalyzed by triosephosphate isomerase,^3–5 proline racemase,^6,7 adenosine deaminase,⁸ and many other enzymes, are tight-binding enzyme inhibitors.^9–11 X-ray crystal structures show that enzyme-ligand complexes are stabilized by elaborate networks of protein-ligand interactions that appear sufficiently strong to rationalize enzymatic rate accelerations. Enzymes that operate on small substrates such as ethanol, acetaldehyde or the acetyl group have evolved effective strategies to increase the total substrate binding energy. For example, by recruiting a high molecular weight cofactor such as TPP, NAD/H or PLP, or by attaching a large molecular weight moiety such as coenzyme A, or a charged moiety such as a phosphodianion or pyrophosphotranion group, to the substrate.

The Pauling formalism provides a framework for the development of detailed models for enzyme catalysis that can be tested in experimental and computational studies. It is less useful when transition state theory fails,^12,13 but there are no well-documented examples of this for enzyme catalysis. Modern theory has been used to support alternative models that rationalize enzyme catalysis, such as the proposals that interactions between the protein and substrate lower the reaction barrier by modifying the reaction potential energy surface,¹⁴ or that enzymatic reactions are accelerated by coupling motion at the protein catalyst to motion along a vibrational mode on the reaction coordinate from substrate to product.^14,15 This review highlights experimental results from our laboratory which show that transition state stabilization is central to enzyme catalysis. We do not discuss other models, because the Pauling model provides a satisfactory framework for the rationalization of our experimental observations.

Specificity in Transition State Binding

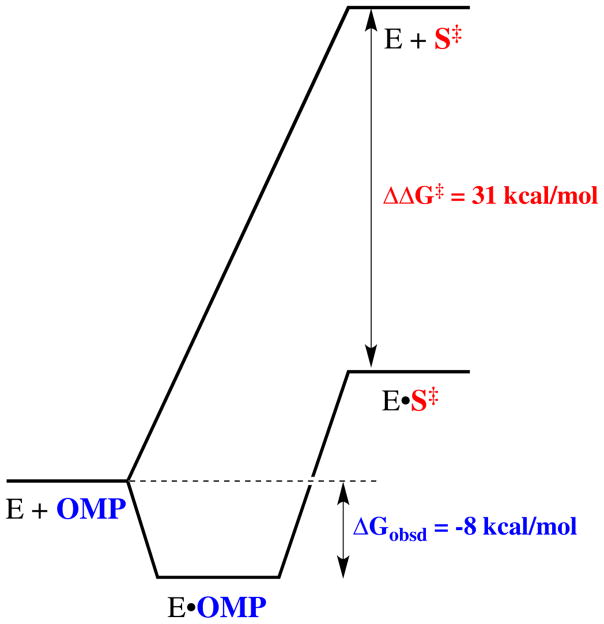
X-ray crystal structures of liganded enzymes would seem to place in plain view everything that is needed to understand the catalytic rate acceleration. These complexes reveal most, or all, of the important protein-ligand interactions, but this information is less useful than it appears at first glance. The ligand binding energy required to account for an enzymatic rate acceleration is generally so large that it cannot be expressed entirely at the ground state Michaelis complex, because this would result in effectively irreversible ligand binding.¹⁶ Consider the decarboxylation of orotidine 5′-monophosphate (OMP) to form uridine 5′-monophosphate (UMP) catalyzed by orotidine 5′-monophosphate decarboxylase (OMPDC, Scheme 1). This enzyme provides a ~31 kcal/mol stabilization of the transition state for the decarboxylation of OMP through a vinyl carbanion intermediate (Figure 1),^17,18 which corresponds to K_S^‡ ≈ 10⁻²³ M for release of the transition state to water.¹⁹ If the second-order rate constant for ligand binding is close to the encounter-controlled limit of k_d = 10⁸ M⁻¹ s⁻¹,²⁰ then the absolute rate constant for release from OMPDC of a ligand with the same affinity as the transition state would be k_−d = K_Sk_d ≈ (10⁻²³ M)(10⁸ M⁻¹ s⁻¹) ≈ 10⁻¹⁵ s⁻¹, and the halftime for ligand release would be on the order of 20 million years! In fact, OMPDC provides a much smaller 8 kcal/mol stabilization of the Michaelis complex with OMP (K_S ≈ 1 μM),²¹ which is formed rapidly and reversibly, so that more than 70% of the intrinsic substrate binding energy is expressed only on moving from the ground state to the transition state (Figure 1).

Scheme 1.

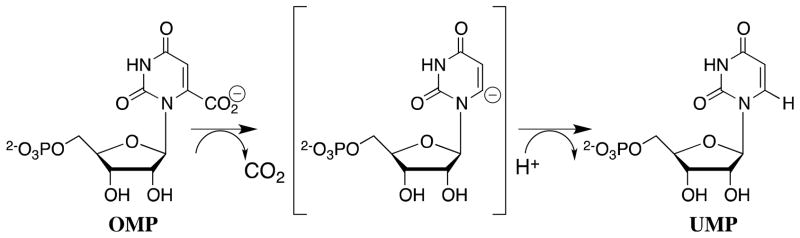
Figure 1.

Reaction coordinate profiles for the nonenzymatic and the OMPDC-catalyzed decarboxylation of OMP to form UMP through a vinyl carbanion-like transition state. The total stabilization of the transition state by interactions with the protein catalyst is estimated to be 31 kcal/mol,¹⁹ which is much larger than the observed binding energy for OMP in the ground state Michaelis complex of 8 kcal/mol.

There are no X-ray crystal structures of the short-lived transition state complexes for enzymatic reactions for comparison with the structure of the corresponding Michaelis complex. The structures of complexes with stable ligands, including transition state analogs, provide limited insight into the explanation for the large differences in the enzymatic stabilization of ground state and transition state complexes. For example, structures of OMPDC complexed with the product UMP or tight-binding inhibitors reveal an extensive network of enzyme-ligand interactions that may be sufficient to account for the 31 kcal/mol transition state binding energy.^22–30 These structures have generated a great deal of discussion, but they were not sufficient to define the mechanism for the decarboxylation reaction, or to explain the specificity of OMPDC in transition state binding.³¹

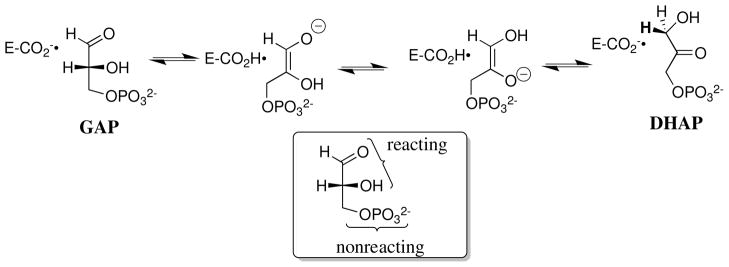
Our discussion of specificity in transition state binding is divided into two sections, as can be illustrated for the isomerization of glyceraldehyde 3-phosphate (GAP) to form dihydroxyacetone phosphate (DHAP) through a pair of enediolate reaction intermediates,^32,33 catalyzed by triosephosphate isomerase (TIM, Scheme 2).^34,35 The first section describes experiments that characterize the specificity in transition state binding resulting from interactions of the enzyme with the reacting portion of the substrate that undergoes substantial changes in charge, geometry or polarity on moving from the reactant to transition state. For example, the unit increase in negative charge at GAP upon conversion of the substrate to the high-energy enediolate intermediate at TIM (Scheme 2).^34,36 The second section discusses experiments that characterize the specificity in transition state binding resulting from interactions of the enzyme with nonreacting substrate fragments, such as the phosphodianion group of GAP (Scheme 2).

Scheme 2.

Specificity in Transition State Binding: Interactions with the Reacting Center

Heterolytic bond cleavage/formation results in a redistribution of charge at the reactant on proceeding to the transition state. Large catalytic rate accelerations for both nonenzymatic and enzymatic reactions are obtained by the placement of groups that provide stabilizing electrostatic, hydrogen bonding or other polar interactions at the site of changing charge.³⁷ For example, Zn²⁺ provides modest catalysis of the deprotonation of α-carbonyl carbon, by stabilizing the negative change that develops at the enolate oxygen of the delocalized carbanion product.³⁸ Transition state stabilization is largest, and most easily characterized, when the interacting centers carry multiple charges, such as for a metal dication and a phosphodianion group.³⁷

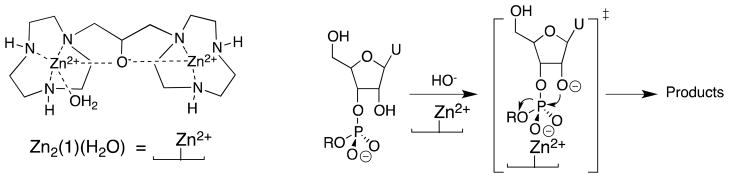
The enzyme-like 9.3 kcal/mol stabilization of the anionic transition state for the base-catalyzed cleavage of the dinucleotide uridylyl-(3′-5′)-uridine and related phosphate diesters by interactions with the cationic dinuclear Zn²⁺ catalyst Zn₂(1)(H₂O) (Scheme 3) corresponds to an impressive 10⁷-fold catalytic rate acceleration.^39–41 The large 10⁵-fold effect of the K12G mutation at yeast TIM on k_cat/K_m for the isomerization of GAP shows that interactions between an amine monocation and the transition state for formation of the enediolate phosphate trianion intermediate (Scheme 2) makes a large contribution to the overall enzymatic rate acceleration.^42,43

Scheme 3.

It is difficult to characterize the smaller transition state stabilization from hydrogen bonding interactions between enzymes and a carbonyl oxygen that is transformed to an oxyanion by nucleophilic addition to the carbonyl group, or by deprotonation of α-carbonyl carbon. The X-ray crystal structures of enzyme-ligand complexes of trypsin and chymotrypsin suggest that two backbone amide NH groups form hydrogen bonds that stabilize a tetrahedral oxyanion intermediate.^44,45 This arrangement of hydrogen bond donors, commonly known as an oxyanion hole, has been observed for enzymes that catalyze the hydrolysis of amides⁴⁶ and esters,⁴⁷ and also the deprotonation of α-carbonyl carbon.^48–50 There is no simple protocol for the excision of interactions between a protein backbone amide NH and the transition state for these enzyme-catalyzed reactions. However, the amide side chain of Asn-155 provides one of the hydrogen-bonding groups for the oxyanion intermediate of the reaction catalyzed by subtilisin, and this side chain has been varied by site directed mutagenesis.^51,52

Oxyanion holes might appear to provide little stabilization of the transition state for an uncatalyzed reaction in water, because hydrogen bonds to the weakly acidic backbone amide NH groups are not expected to be stronger than hydrogen bonds to water. However, Jencks argued that there is a substantial entropic advantage to oxyanion formation at preorganized enzyme active sites, because this eliminates the loss in the translational and rotational entropy of three solvent molecules that occurs when the oxyanion is generated in aqueous solution.¹⁶ Warshel emphasized that the water dipoles, which stabilize the developing oxyanion at a transition state for reaction in water, are randomly oriented compared with the preorganized dipoles at an oxyanion hole.⁵³ He has proposed that the lower barrier for the enzymatic reaction represents the elimination of the energetic cost for dipole reorganization that is needed for the nonenzymatic reaction.^53,54

3-Oxo-Δ⁵-steroid isomerase (KSI) catalyzes the reaction shown in Scheme 4, proceeding through a dienolate intermediate that is stabilized by hydrogen bonding to the phenolic side chain of Tyr-16 and the carboxylic acid side chain of Asp-103 (numbering for the enzyme from Pseudomonas putida).⁵⁵ This hydrogen-bonding network resembles the oxyanion hole of proteases and esterases, but the overall stabilizing interactions should be larger, because of the greater acidity of the amino acid side chains at KSI compared with that of a backbone amide NH group.

Scheme 4.

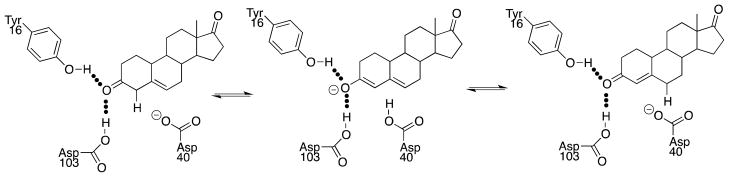
The intramolecular proton transfer catalyzed by KSI is mediated by the carboxylate side chain of Asp-40. The second-order rate constant k_cat/K_m = 3 × 10⁸ M⁻¹ s⁻¹ for KSI-catalyzed isomerization (Scheme 4)⁵⁶ is 5 × 10¹¹-fold larger than k_AcO = 6 × 10⁻⁴ M⁻¹ s⁻¹ for the corresponding deprotonation of the substrate by acetate ion in aqueous solution.⁵⁷ This shows that the catalytic base at KSI is strongly activated for catalysis by interactions between the substrate and enzyme. The binding interactions of the nonreacting rings of the steroid substrate contribute 3 × 10⁴-fold to this total effect.⁵⁸ The remaining rate acceleration of ca. 2 × 10⁷-fold is presumably due to either the enhancement of Brønsted base catalysis by Asp-40,⁵⁹ or to the stabilization of negative charge at the enolate oxygen anion by interactions with the amino acid side chains at the oxyanion hole.

The contribution of the hydrogen bonding in the oxyanion hole to the catalytic rate acceleration for KSI has been probed by site directed mutagenesis. The 50,000-fold falloff in k_cat for the Y16F mutant of KSI from Pseudomonas putida is reduced to 200-fold for the Y16G, Y16A, Y16S and Y16T mutants.⁶⁰ It was concluded that the elimination of the hydrogen bond by the Y16F mutation results in a destabilizing interaction between the intermediate oxyanion and the hydrophobic phenyl ring of phenylalanine, and that this destabilization is attenuated for the Y16G, Y16A, Y16S and Y16T mutants.⁶⁰ The Y16F/D103L double mutation at KSI from P. putida and the Y16F/D103A double mutation at the enzyme from Comamonas testosteroni result in 10⁵- and 10⁸-fold decreases, respectively, in k_cat/K_m for enzyme-catalyzed isomerization.^61,62 These large effects overestimate the magnitude of the stabilizing hydrogen-bonding interactions at KSI compared to those in water, because of the minimal hydrogen-bonding stabilization of the oxyanion at the active site of the mutant enzyme compared with an aqueous solvent. Additional mutations at double mutants of KSI from P. putida and C. testosteroni were made to carve out a ca. 650 ų cavity at the enzyme active site that is sufficiently large to hold 15 – 17 water molecules.⁴⁹ One of these mutant enzymes exhibited only a 1000-fold falloff in k_cat/K_m compared with wildtype KSI.⁴⁹ This 1000-fold effect is the best available estimate of the contribution of the oxyanion hole at KSI to the overall enzymatic rate acceleration.

Specificity in Transition State Binding: Interactions with Nonreacting Substrate Fragments

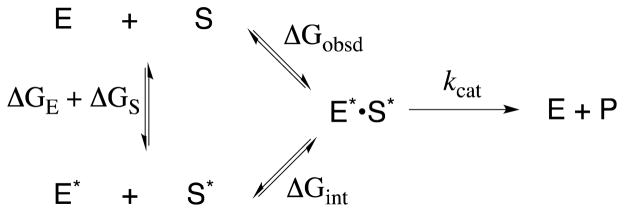
In a classic review published in 1975,¹⁶ Bill Jencks considered the possibility that “the intrinsic binding energy that results from the noncovalent interaction of a specific substrate with the active site of the enzyme is considerably larger than is generally believed. An important part of this binding energy may be utilized to provide the driving force for catalysis, so that the observed binding energy represents only what is left over after this utilization.” He went on to propose that “the availability of this energy from binding interactions with nonreacting portions of specific substrates provides a critical difference between enzymic and most nonenzymic catalysis.”¹⁶ Specificity in the expression of binding interactions with nonreacting portions of the substrate at an enzymatic transition state results when these interactions drive thermodynamically unfavorable changes in the conformation of the enzyme or substrate that result in an increase in k_cat for conversion of the enzyme-substrate complex to product. This is shown in Scheme 5,¹⁶ where ΔG_E and ΔG_S are the unfavorable energetic prices paid to move the enzyme and substrate, respectively, into a conformation with an increased chemical reactivity, ΔG_obsd is the observed substrate binding energy, and ΔG_int is the total or intrinsic substrate binding energy. The intrinsic substrate binding energy is larger than the observed binding energy by the amount of binding energy that is specifically utilized to drive unfavorable changes in the conformation of the enzyme and/or the substrate, resulting in the conversion of E to E^* and S to S^* (ΔG_E + ΔG_S, eq 1). The binding interactions that are utilized in this manner are not expressed as tighter overall binding and a decrease in the experimental Michaelis constant (for simplicity we treat the binding constant K_S as being equal to the Michaelis constant K_m), but, rather, result in an increase in the chemical reactivity of the E^*•S^* complex and in the kinetic parameter k_cat, compared with that for the unactivated enzyme-catalyzed reaction.

Scheme 5.

$$-(\mathrm{\Delta }{\text{G}}_{int}-\mathrm{\Delta }{\text{G}}_{\text{obsd}})=\mathrm{\Delta }{\text{G}}_{\text{E}}+\mathrm{\Delta }{\text{G}}_{\text{S}}$$ (1)

Jencks’ review discussed: (1) The utilization of substrate binding energy to induce electrostatic stress, torsional strain or other types of strain into the substrate (S^*, Scheme 5), which is then relieved at the transition state for the catalyzed reaction. (2) The utilization of substrate binding energy to induce electrostatic stress, torsional strain or other types of strain into the enzyme (E^*, Scheme 5), which is then relieved at the transition state for the catalyzed reaction. He noted that “the induction of a geometric destabilization requires the application of a force and since neither the enzyme nor the substrate have available irresistible forces or substituent groups that are immovable objects, the induction of strain will cause at least a small change in the conformation of both the substrate and the enzyme to give the structures S^* and E^*, respectively.” (3) The utilization of substrate binding energy to drive thermodynamically unfavorable desolvation of the enzyme and substrate to give E^* and S^* that are activated at the E^*•S^* complex for conversion to reaction product.¹⁶

Since 2000, our work has focused on defining the mechanisms by which the binding interactions of the nonreacting substrate phosphodianion group are utilized to activate enzymes for catalysis.⁶³ We review here this work, along with that of Jencks and coworkers that was completed after publication of his 1975 review.

Coenzyme A Binding Interactions

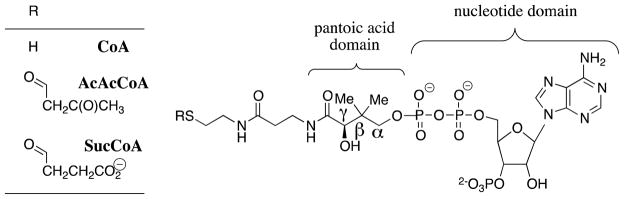
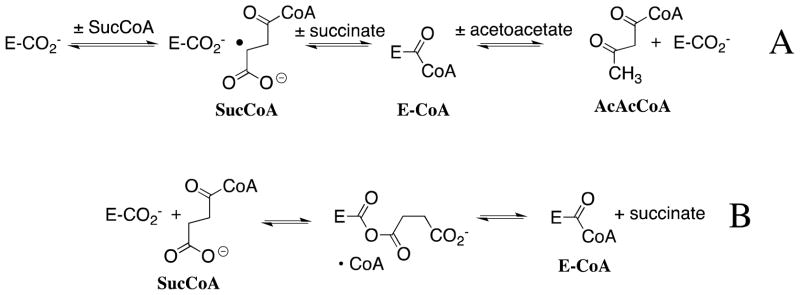
Coenzyme A (CoA, Scheme 6, R = H) functions as an acyl group carrier and is an essential cofactor for all organisms. It serves to activate the carbonyl group for nucleophilic addition and deprotonation at α-carbonyl carbon.^64,65 This coenzyme is central to many biochemical transformations and is utilized by an estimated 4% of all known enzymes.⁶⁶ Succinyl-CoA:3-oxoacid coenzyme A transferase (SCOT) catalyzes the reversible reaction of succinyl-CoA (SucCoA) with acetoacetate to give acetoacetyl-CoA (AcAcCoA) and succinate through a covalent enzyme thiol ester intermediate, E-CoA (Scheme 7A). The CoA transfer reaction catalyzed by class I SCOT from pig heart proceeds by the chemically difficult nucleophilic displacement of a basic thiolate anion by an enzyme carboxylate anion to form an anhydride that partitions between addition of CoA to the substrate-derived carbonyl group to reform substrate and to the enzyme-derived carbonyl group to give the enzyme-based thiol ester intermediate E-CoA (Scheme 7B).^67–71

Scheme 6.

Scheme 7.

A comparison of k_cat/K_m = 9 × 10⁵ M⁻¹ s⁻¹ for transfer of CoA from SucCoA to SCOT to give E-CoA (Scheme 7) and k_cat/K_m = 3 × 10⁻⁷ M⁻¹ s⁻¹ for transfer of the minimal thiol from succinyl-SCH₂CH₂C(O)OMe shows that interactions between SCOT and the nonreacting nucleotide and pantotheine and nucleotide “domains” of CoA are responsible for a rate acceleration of 3 × 10¹²-fold,⁶⁹ which is close to the estimated 5 × 10¹³-fold total enzymatic rate acceleration. This corresponds to a 17 kcal/mol stabilization of the transition state by binding interactions of SCOT with the nonreacting CoA fragment of SucCoA. By contrast, the large K_i of 1 mM for competitive inhibition of SCOT by CoA, and the small 2-fold difference in the Michaelis constants for the SCOT-catalyzed reactions of acetoacetate and AcAcCoA, show that the observed binding interactions between CoA and the enzyme at the ground state Michaelis complex are weak,^72,73 so that these binding interactions are utilized specifically in transition state stabilization.

The strengths of the following specific interactions between SCOT and CoA have been determined:^74,75 (1) The interactions between SCOT and the complete CoA fragment that are expressed at the initial Michaelis complex, at the transition state(s) for formation of the E-CoA intermediate, and at the covalent intermediate E-CoA. (2) The interactions between SCOT and the individual nucleotide and pantoic acid domains of CoA that are expressed at the initial Michaelis complex, at the transition state(s) for formation of the E-CoA intermediate, and at the covalent intermediate E-CoA (Scheme 6). The binding interactions with the pantoic acid domain involve only the small region of the CoA molecule that contains the α-β- and γ-carbon atoms of the longer pantotheine moiety (Scheme 6).⁷⁴

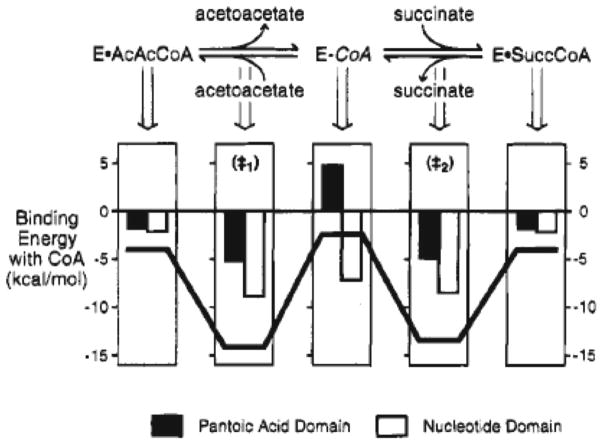
The nucleotide and pantoic acid domains of CoA each provide a small ca. 2 kcal/mol stabilization of the Michaelis complex. However, the nucleotide domain of CoA stabilizes the E-CoA intermediate by 7 kcal/mol, while the pantoic acid domain destabilizes this intermediate by 5 kcal/mol (Figure 2). The strongest stabilizing interactions are observed at the transition states (‡₁) and (‡₂) for SCOT-catalyzed CoA transfer (Figure 2). Interactions with the nucleotide domain provide a similar 7 – 8 kcal/mol stabilization of both E-CoA and the transition states (‡₁) and (‡₂) for the half reactions of AcAcCoA and SucCoA. However, the interactions with the pantoic acid domain are stabilizing at these transition states, but destabilizing (!) at the E-CoA covalent intermediate (Figure 2).

Figure 2.

Diagram illustrating the expression of noncovalent binding energy from interaction of SCOT with domains of the CoA moiety at key points along the reaction coordinate, using the free enzyme and substrate as the ground state at a relative free energy of zero (reproduced with permission from: Role of binding energy with coenzyme A in catalysis by 3-oxoacid coenzyme A transferase, Biochemistry 34, 11678 – 11689 (1995), American Chemical Society). The histograms indicate the binding energies derived from interactions with the pantoic acid domain (black bars) and the terminal nucleotide domain of CoA (white bars). The bold black line illustrates the total noncovalent binding energy derived from interaction of the entire nonreacting CoA moiety.

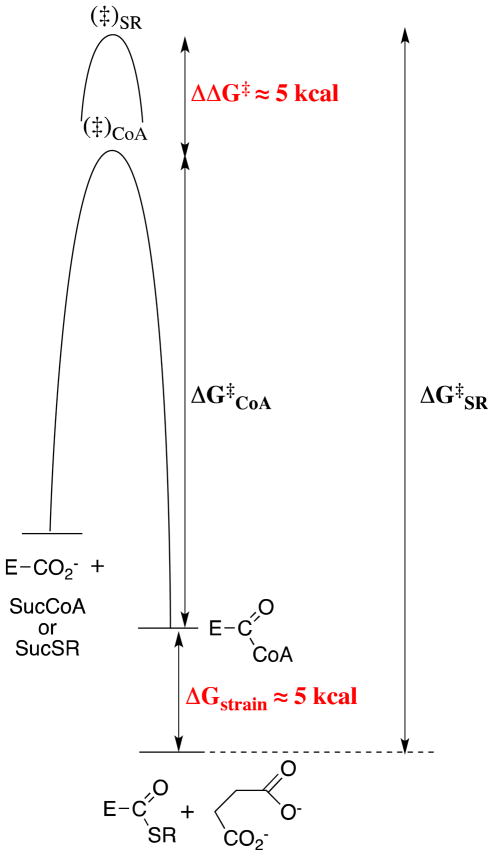
Figure 3 compares the free energy profile for the SCOT-catalyzed transfer of CoA from SucCoA to SCOT to form E-CoA with that for transfer of a hypothetical thiol from SucSR, for which the binding interactions with only the pantoic acid domain have been eliminated. Figure 3 shows that a portion of the binding energy of the pantoic acid domain is used to destabilize the E-CoA intermediate relative to E-SR by 5 kcal/mol (ΔG_strain = (ΔG_E + ΔG_S), eq 1), while a portion is used to stabilize the transition state for CoA transfer relative to that for SR transfer by ca. 5 kcal/mol (ΔΔG^‡). The result is a 10 kcal/mol smaller barrier for the reaction of E-CoA with succinate than for the reaction of E-SR (ΔG^‡_SR − ΔG^‡_CoA = 10 kcal/mol, Figure 3). This corresponds to a 10⁷-fold contribution of the small nonreacting pantoic acid domain of CoA to the rate acceleration for SCOT.^74,75

Figure 3.

Free energy profiles for the SCOT-catalyzed transfer of CoA from SucCoA to form the E-CoA covalent intermediate (through transition state (‡)_CoA), and for the transfer of a hypothetical thiol from SucSR to give E-SR, for which the binding interactions with only the pantoic acid domain have been eliminated (through transition state (‡)_SR). The binding interactions between SCOT and the pantoic acid domain stabilize the transition state for transfer of CoA to SCOT by 5 kcal/mol but destabilize the resulting E-CoA intermediate by 5 kcal/mol. The net effect is a 10 kcal/mol smaller barrier for the reverse transfer to succinate of CoA from E-CoA than for the transfer of SR from E-SR.

These differences in the expression of binding interactions at different enzyme complexes require multiple modes for the binding of CoA to SCOT, in which interactions between the nucleotide and pantoic acid domains are expressed differently. For example, the stabilizing interactions between SCOT and the pantoic acid domain of CoA might be expressed first at the rate-determining transition state for formation of the short-lived and thermodynamically unstable anhydride reaction intermediate (Scheme 7B),^67–71 while the destabilizing interactions are expressed only after thermodynamically favorable collapse of this complex to form E-CoA. The destabilizing interactions of the pantoic acid domain at E-CoA then serve to attenuate the large driving force for breakdown of the high energy anhydride, preventing E-CoA from lying in a deep thermodynamic well. X-ray structures of crystals of pig heart SCOT grown in the presence of AcAcCoA show subunits of the dimeric protein as both the free enzyme and as the covalently-linked E-CoA intermediate, in a conformation substantially different from that of the free enzyme.⁷⁶ This change in enzyme conformation affects interactions between SCOT and both the nucleotide and pantoic acid domains of CoA. Molecular mechanics calculations on X-ray crystal structures of wildtype and mutants of SCOT from Acetobactor aceti provide evidence that the thiol ester functional group of substrate is compressed against the catalytic glutamate.⁷⁷ The results are consistent with the use of the intrinsic CoA binding energy to induce strain into the reactant complex, that is relieved at the transition for formation of the acyl anhydride intermediate.⁷²

Enzymes that catalyze the deprotonation of the α-carbonyl carbon of CoA thiol esters have solved the baffling catalytic challenge of stabilizing the enolate-like transition state and intermediate.⁷⁸ The acetyl group is too small to provide the large transition state binding energy required to rationalize the rate acceleration for enzyme-catalyzed deprotonation of the α-carbonyl carbon of these carbon acids.^79,80 It is expected that the binding interactions between these enzymes and the CoA moiety of the substrate are utilized to stabilize the transition state for carbon deprotonation. However, X-ray crystal structures of these enzymes provide limited insight into the mechanism for transition state stabilization,^48,81,82 and we are not aware of studies to determine the mechanism for enzyme activation by interactions with CoA.

Phosphodianion Binding Interactions

We targeted the small charged phosphodianion group as a stable substrate fragment that should show specificity in transition state binding for the following reasons: (1) This group often provides a substantial fraction of the total transition state binding energy needed to account for the enzymatic rate acceleration.^63,83 (2) The closure of phosphodianion “gripper loops” of enzymes over the bound substrate provides a starting point for the development of mechanisms to rationalize the utilization of phosphodianion binding energy in enzyme activation. (3) The wide distribution of phosphate gripper loops,^84,85 and of phosphate cups,⁸⁶ suggests a common function for these structural elements, so that it should be possible to generalize the results of studies of representative enzymes to a broad range of catalysts. We have used the following protocols to quantify the stabilization of the transition states for the reactions catalyzed by TIM,^63,87 OMPDC⁸³ and α-glycerol phosphate dehydrogenase (α-GPDH)⁸⁸ by interactions with the substrate phosphodianion group.

1. The second-order rate constants for the enzyme-catalyzed reaction of the whole substrates were determined to be ca. 10⁸-fold larger than the corresponding rate constants for the enzyme-catalyzed reactions of truncated substrates that lack a phosphodianion group.^63,83,88 This shows that the interactions of the enzyme with the substrate phosphodianion stabilize the respective transition states by 11 – 12 kcal/mol. This phosphodianion binding energy may be utilized to anchor the Michaelis complex to the enzyme so that it is expressed in the binding constant, or to activate the enzyme for catalysis, in which case it is expressed specifically at the transition state for the catalyzed reaction, as an increase in k_cat.

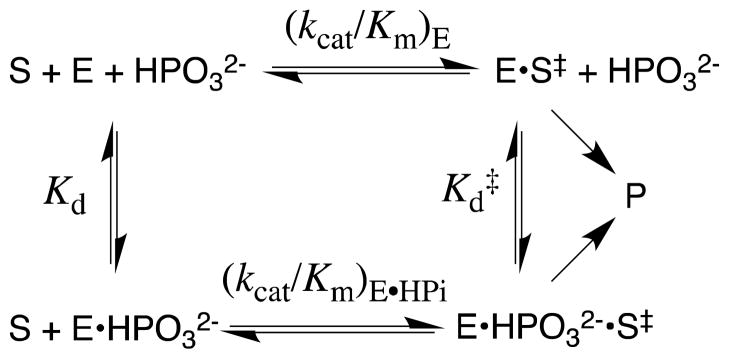
2. The activation of the enzyme-catalyzed reactions of truncated substrates by added phosphite dianion (HPO₃²⁻) was characterized for the reactions catalyzed by TIM, α-GPDH and OMPDC (Scheme 8).^83,87,88 Despite the absence of an anchoring covalent connection to the substrate, in each case the binding of HPO₃²⁻ to the enzyme results in large increases in the observed second-order rate constant (k_cat/K_m)_obsd for the enzyme-catalyzed reaction of the truncated substrate piece. The dependence of (k_cat/K_m)_obsd on [HPO₃²⁻] is accounted for by the model in Scheme 9, and the data were used to give values of (k_cat/K_m)_E for the unactivated reaction, K_d for dissociation of phosphite from the E•HPO₃²⁻ complex, and (k_cat/K_m)_E•HPi for the reaction of the second truncated substrate piece catalyzed by this complex.^83,87,88

Scheme 8.

Scheme 9.

$$\frac{{(k_{\text{cat}}/K_{\text{m}})}_{\text{E}•\text{HPi}}}{{(k_{\text{cat}}/K_{\text{m}})}_{\text{E}}}=\frac{K_{\text{d}}}{K_{\text{d}}^{‡}}$$ (2)

Rate constant ratios of (k_cat/K_m)_E•HPi/(k_cat/K_m)_E ≥ 10³ were determined for the three enzyme-catalyzed reactions of the “two-part substrates” (Scheme 8A – 8C), which shows that there is a similar strong activation of each enzyme for turnover of the second truncated substrate piece by the binding of phosphite dianion to form the phosphite-liganded enzyme E•HPO₃²⁻. This activation reflects the weak binding of HPO₃²⁻ to the free enzyme (K_d ≥ 0.01 M), but the much higher specificity for binding to the transition state complex (K_d ≫ K_d^‡, eq 2).88 The values of K_d^‡ were used to calculate total intrinsic phosphite binding energies in the transition state of 6 – 8 kcal/mol, which are 4 – 6 kcal/mol stronger than the binding energies of phosphite dianion at the ground-state Michaelis complex. In other words, the strong interactions between these enzymes and phosphite dianion are utilized specifically to stabilize the respective transition states.^83,87–89

Scheme 10 shows the TIM-catalyzed reactions of the whole substrate GAP and the two-part substrate glycolaldehyde (GA) + phosphite. Our results strongly suggest that the reactivities of the binary TIM•GAP complex and the ternary TIM•GA•HPO₃²⁻ complex are similar [(k_cat)_GAP ≈ (k_cat)_GA•HPi], but much higher than that of the binary TIM•GA complex [(k_cat)_GA]. The 12 kcal/mol total intrinsic phosphodianion binding energy for the whole substrate GAP is larger than the 6 kcal/mol intrinsic phosphite binding energy for the reaction of the substrate pieces.^87,88 This difference is due mainly, or entirely, to the entropic advantage provided by the covalent attachment of the pieces at the whole substrate, which undergoes binding to the enzyme with the loss of the translational and rotational entropy of a single molecule, compared with the larger loss in entropy associated with the binding and reaction of two separate pieces.⁹⁰

Scheme 10.

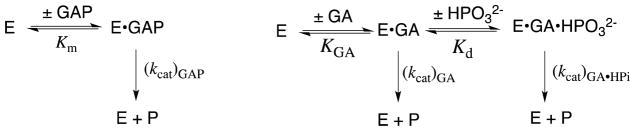
Enzyme Activation by Phosphite Dianion

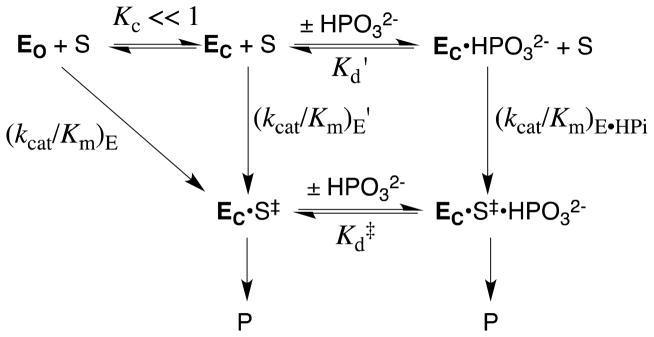
In developing a physical model to rationalize phosphite activation of three radically different enzyme-catalyzed reactions, we decided to emphasize the common catalytic features of OMPDC,^23,26,91 TIM,^92,93 and α-GPDH.^88,94,95 Each enzyme utilizes a flexible loop that interacts with the phosphodianion group of bound substrate, and in each case loop closure over the substrate sequesters the ligand from interaction with bulk solvent. These observations guided our proposal of a minimal general model in which the binding of phosphite dianion drives this loop closure and converts an inactive open enzyme E_O to an active closed form E_C (Scheme 11).

Scheme 11.

$$\mathrm{\Delta }{\text{G}}_{int}=-\mathit{RT}ln\left[\frac{{(k_{\text{cat}}/K_{\text{m}})}_{\text{E}•\text{HPi}}/K_{\text{d}}}{{(k_{\text{cat}}/K_{\text{m}})}_{\text{E}}}\right]$$ (3)

$$\mathrm{\Delta }{\text{G}}_{\text{C}}=\mathit{RT}ln{K}_{\text{c}}=\mathit{RT}ln\left[\frac{{(k_{\text{cat}}/K_{\text{m}})}_{\text{E}•\text{HPi}}}{{(k_{\text{cat}}/K_{\text{m}})}_{\text{E}}}\right]$$ (4)

The observed binding of HPO₃²⁻ to E_O to give E_C•HPO₃²⁻ (Scheme 11) is weak (K_d = K_d′/K_c), because much of the ligand binding energy is used to drive the unfavorable enzyme conformational change that converts E_O to E_C (K_c ≪ 1). Once the cost for the conformational change has been paid, the full intrinsic binding energy of the second ligand is observed in the formation of E_C•S^‡•HPO₃²⁻ from E_C•HPO₃²⁻ [barrier for (k_cat/K_m)_E•HPi, Scheme 11], or from E_C•S^‡ (K_d^‡, Scheme 11). This model may be supplanted by enzyme-specific models that consider the energetic cost for moving both the enzyme and the substrate into a reactive conformation (Scheme 5). Such models have been considered in detail for the catalysis of decarboxylation of OMP catalyzed by OMPDC.^23,96,97

Enzyme Activation: TIM

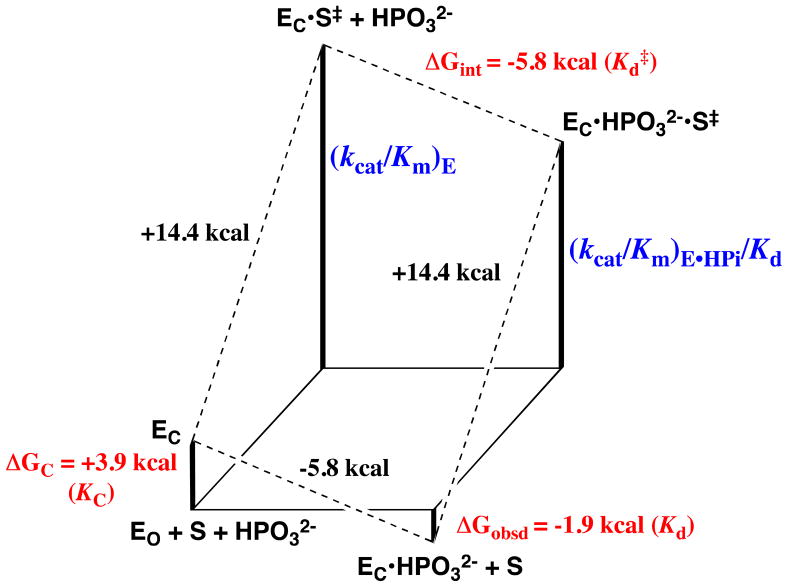
Figure 4 shows a free energy diagram that was constructed for Scheme 11 using the kinetic parameters for the unactivated and phosphite-activated TIM-catalyzed reactions of the truncated substrate glycolaldehyde (GA).⁸⁷ The intrinsic binding energy for association of HPO₃²⁻ with the transition state complex E_C•S^‡ to give E_C•S^‡• HPO₃²⁻, ΔG_int = −5.8 kcal/mol, is obtained as the difference in the barriers to the activated reaction (defined by (k_cat/K_m)_E•HPi/K_d) and the unactivated reaction (defined by (k_cat/K_m)_E), according to eq 3. The difference between this intrinsic phosphite binding energy and the observed binding energy of phosphite dianion in the ground state of −1.9 kcal/mol (K_d ≈ 40 mM), is then the binding energy that is utilized to drive the conversion of E_O to E_C, ΔG_C = 3.9 kcal/mol, as shown by eq 4.⁸⁷ Phosphite is proposed to act as a “spectator” in holding the enzyme in the active E_C conformation and it does not affect the second-order rate constant for the enzyme-catalyzed reaction of GA catalyzed by the closed form of the enzyme, so that (k_cat/K_m)_E′ = (k_cat/K_m)_E•HPi (Scheme 11). Essentially, the barrier for conversion of E_O to E_C (ΔG_C) is included in the observed barrier for the reaction of GA catalyzed by the free enzyme E_O [(k_cat/K_m)_E = K_c(k_cat/K_m)_E′], but not in the barrier for the reaction catalyzed by E_C•HPO₃²⁻ [(k_cat/K_m)_E•HPi, Figure 4].⁸⁷

Figure 4.

Free energy diagram for the turnover of the truncated substrate glycolaldehyde (S) by free TIM (E_O) and by TIM that is saturated with phosphite dianion (E_C•HPO₃²⁻, Scheme 11) constructed using data from Ref. 87. The observed tighter binding of phosphite dianion to the transition state complex E_C•S^‡ to give E_C•HPO₃²⁻•S^‡ (ΔG_int = −5.8 kcal/mol, eq 3) than to the free enzyme E_O to give E_C•HPO₃²⁻ (ΔG_obsd = −1.9 kcal/mol) represents the “interaction energy” of 3.9 kcal/mol.⁹⁰ This can be attributed to ΔG_C = +3.9 kcal/mol for the unfavorable conformational change that converts the inactive open ground state enzyme E_O to the active closed enzyme E_C (eq 4). The observed value of ΔG^‡ = +18.3 kcal/mol for turnover of glycolaldehyde with second order rate constant (k_cat/K_m)_E can be partitioned into ΔG^‡ = +14.4 kcal/mol for proton transfer from glycolaldehyde to E_C and ΔG_C = +3.9 kcal/mol for the unfavorable conformational change that converts E_O to E_C.

The conversion of E_O to E_C in Scheme 11 and Figure 4 is formally equivalent to the conversion of E to E^* shown in Scheme 5.¹⁶ We emphasize, for the sake of simplicity, a minimal model where the dianion binding energy is utilized entirely to drive an unfavorable change in the enzyme conformation, but the intrinsic substrate binding energy might also be utilized to drive the unfavorable change from S to S^* (Scheme 5). The thermodynamic barrier to the E_O to E_C conformational change might represent strain induced in E_C by loop closure, or an entropic price for loop closure arising from the requirement to obtain optimal alignment of the catalytic side chains relative to the bound substrate.^98,99 However, the report that the thermodynamic barrier to loop closure at unliganded TIM is only ca. 1.4 kcal/mol, suggests that the protein conformational strain induced by loop closure is small.¹⁰⁰ Enzyme active sites must be open to the bulk solvent, in order for the substrate to bind. However, catalysis of polar reactions is favored at desolvated active sites of low effective dielectric constant (D), because the magnitude of stabilizing polar/electrostatic interactions between the enzyme and the reaction transition state increases with 1/D.^34,101,102 Therefore, we propose that a large fraction of the free energy barrier for the conversion of E_O to E_C is the barrier to desolvation of the enzyme active site that accompanies ligand binding and loop closure.³⁴

The displacement of water from the active site of TIM that is driven by the binding of phosphite dianion will result in a decrease in the effective local dielectric constant of the enzyme active site that will enhance all stabilizing polar interactions between the enzyme and bound ligand. We have proposed that desolvation of the active site of TIM results in a large 8 kcal/mol stabilizing interaction between the cationic alkyl ammonium side chain of Lys-12 and the transition state for formation of the trianionic enediolate-phosphate reaction intermediate of the isomerization of GAP.^42,43 The specific desolvation of the carboxylate side chain of the catalytic base Glu-167 at TIM should lead to an increase in the basicity of this side chain and enhance its reactivity in the deprotonation of bound carbon acids. Our studies of the effects of the I172A and L232A mutations at TIM from Trypanosoma brucei brucei on the kinetic parameters for the enzyme-catalyzed reactions of the whole substrates GAP and DHAP and the substrate pieces GA + phosphite provided direct evidence for the activation of the side chain of Glu-167 by loop closure at TIM.^103,104 These results were summarized in a recent review.³⁴

Enzyme Activation: Amino Acid Racemases

When the protein catalyst is relatively rigid, enzyme activation may be due entirely to ligand driven desolvation of the substrate and the enzyme active site that occurs on formation of the Michaelis complex. In this case, E_sol and E_desol could be substituted for E_O and E_C in Scheme 11, in order to emphasize the importance of desolvation. Deprotonation of the α-amino carbon of an N-protonated amino acid to form a zwitterionic amino acid carbanion is the first step in the reactions catalyzed by proline racemase (Scheme 12),¹⁰⁵ glutamate racemase,^106,107 and diaminopimelate epimerase.¹⁰⁸

Scheme 12.

Proline racemase provides a ca. 19 kcal/mol stabilization of the transition state for deprotonation of bound proline to form the zwitterionic carbanion reaction intermediate (Scheme 12).¹⁰⁹ However, the complete desolvation of N-protonated proline by transfer from aqueous solution to the gas phase is expected to result in a much larger 100 kcal/mol increase in the thermodynamic driving force for this proton transfer.¹¹⁰ Proline racemase,¹⁰⁵ glutamate racemase,^106,107 and diaminopimelate epimerase¹⁰⁸ each bind their substrate at the bottom of a deep hydrophobic cavity, so that partial desolvation of the amino acid is expected to accompany substrate binding from water.^111–113 A 19 kcal/mol reduction in the barrier for deprotonation of partly desolvated proline at such a water-free enzyme active site is much smaller than the limiting 100 kcal/mol difference in the driving force for proton transfer in the gas phase compared to water, and it could account for most or all of the rate acceleration for enzyme-catalyzed deprotonation.^{102,109,110,114} We propose that binding interactions between amino acid racemases and their amino acid substrates are utilized to drive the desolvation of the enzyme active site and the substrate, so that proton transfer occurs at an active site of low effective dielectric constant.^109,110 This proposal is supported by the results of a QM/MM study about the “importance of being zwitterionic” for the amino acid racemization catalyzed by glutamate racemase.¹¹⁴

Enzyme Activation: OMPDC

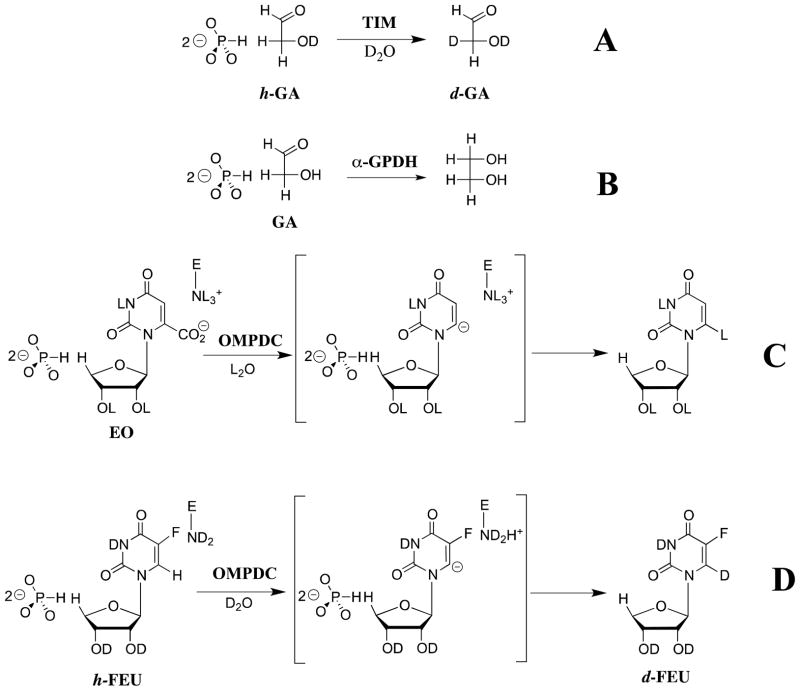
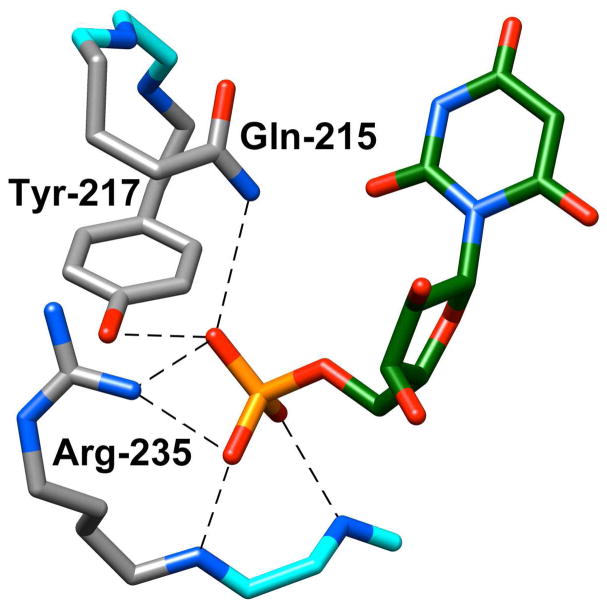
We have proposed: (1) That the closed conformation of OMPDC (E_C) exercises the enzyme’s full catalytic power for catalysis of decarboxylation and C-6 deuterium exchange reactions (Scheme 8C and 8D).¹¹⁵ (2) That the turnover of the truncated substrates 1-(β-D-erythrofuranosyl)orotic acid (EO, Scheme 8C) and 1-(β-D-erythrofuranosyl)-5-fluorouracil (FEU, Scheme 8D) is slow in the absence of HPO₃², because the fraction of the enzyme in the active form E_C is low (K_c ≪ 1, Scheme 11).¹¹⁵ (3) That the function of the three amino acid side chains of OMPDC that interact with the phosphodianion group of OMP, Gln-215, Tyr-217, and Arg-235 (Figure 5) is to drive the conversion of OMPDC from E_O to the active form E_C•OMP or E_C•HPO₃^2−.116

Figure 5.

X-ray crystal structure of yeast OMPDC liganded with 6-hydroxyuridine 5′-monophosphate (Protein Data Bank entry 1DQX),²⁶ showing interactions of side chains of the protein with the bound phosphodianion group of the ligand.

These proposals were tested by preparing all possible of yeast OMPDCs containing the single (Q215A, Y217F, R235A), double (Q215A/Y217F, Q215A/R235A, Y217F/R235A) and triple (Q215A/Y217F/R235A) substitutions for alanine of the side chains of Gln-215, Tyr-217 and Arg-235.¹¹⁶ The single mutations result in up to a 20,000-fold decrease in k_cat/K_m for decarboxylation of the whole substrate OMP, but only very small < 3-fold decreases in (k_cat/K_m)_E (Scheme 9) for decarboxylation of the truncated substrate EO that lacks a phosphodianion group. Essentially the entire effect of these mutations is expressed as up to a 3 × 10⁵-fold decrease in the third-order rate constant (k_cat/K_m)_E•HPi/K_d for the phosphite-activated reaction of EO (Scheme 9). The small effect of these mutations on (k_cat/K_m)_E for the unactivated decarboxylation of EO shows that there is no significant direct stabilization of the transition state for decarboxylation by long-range interactions of the side chains of Gln-215, Tyr-217 and Arg-235 with the remote pyrimidine ring of EO.¹¹⁶

We concluded that the activation of OMPDC by phosphite dianion is the result of the development of loop-dianion interactions that drive loop closure over OMP or EO. This provides direct evidence that the conversion of unliganded enzyme E_O to E_C•HPO₃²⁻ activates OMPDC for catalysis of decarboxylation (Scheme 11). We find a clean separation of the functions of the pyrimidine and phosphodianion binding sites of OMPDC. The pyrimidine binding site has the potential to provide effective catalysis of the decarboxylation of EO (Scheme 8C) and of C-6 carbon deprotonation of FEU (Scheme 8D), but the observed catalysis is weak because the fraction of the enzyme in the active form E_C is low. The phosphodianion binding site functions to enable the pyrimidine site to reach its full catalytic potential, by using stabilizing interactions between the protein and a bound phosphodianion to drive the conversion of E_O to E_C•HPO₃²⁻ or E_C•OMP, resulting in an increase in the fraction of the enzyme in the active form E_C.¹¹⁶

Part of the intrinsic binding energy of the phosphodianion group of the natural substrate OMP might be used to induce destabilizing “electrostatic stress” between the substrate carboxylate group and the carboxylate group of the side chain of Asp-91 at the E•OMP Michaelis complex, and which is then relieved at the transition state for decarboxylation.²³ However, we have shown that the phosphodianion groups of OMP and 5-fluorouridine 5′-monophosphate (FUMP) both provide a similar stabilization of the transition state for the OMPDC-catalyzed decarboxylation of OMP and the C-6 deuterium exchange reaction of FUMP of ca. 11 and 9 kcal/mol, respectively.¹¹⁵ There are recoveries of 8 and 6 kcal/mol of this intrinsic phosphodianion binding energy as phosphite dianion activation of the OMPDC-catalyzed decarboxylation and deuterium exchange reactions of the corresponding truncated substrates EO (Scheme 8C) and FEU (Scheme 8D), respectively.¹¹⁵ The binding energy of HPO₃²⁻ is utilized mainly to stabilize features of the transition state that are common to the OMPDC-catalyzed decarboxylation and deuterium exchange reactions, rather than to introduce electrostatic stress into complexes between OMPDC and EO or OMP.²³ Part of the intrinsic binding energy of the phosphodianion group of OMP may also be utilized to induce destabilizing strain into the protein catalyst that is relieved at the transition state for the enzyme-catalyzed decarboxylation and deuterium exchange reactions.^96,97

Enzyme Activation: Reaction of the Whole Substrate

The reactions of truncated substrates catalyzed by TIM, OMPDC and α-GPDH are activated by phosphite dianion.^83,87,88 These results uncover dianion activation for the reactions of the whole phosphorylated substrates, which was not detected in direct kinetic studies using the natural substrates, or in analyses of X-ray crystal structures. In fact, earlier intense mechanistic studies on these enzymes uniformly failed to suggest the possibility of such enzyme activation in the reaction of the whole phosphodianion substrate. However, it is necessary to extend the model shown in Scheme 11, developed to rationalize the results of our studies on catalysis of the reaction of substrates in pieces, to enzymatic catalysis of the reaction of the whole substrate.

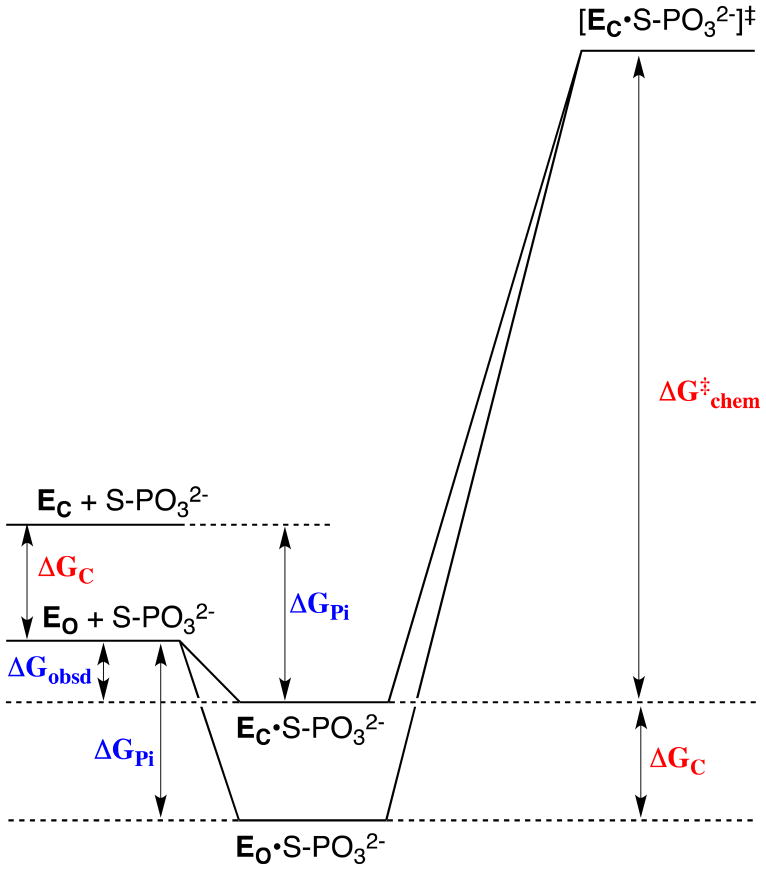
Figure 6 shows the free energy profile for the enzymatic reaction of a whole phosphorylated substrate S-PO₃²⁻. For simplicity, the Figure shows only the binding energy of the phosphodianion portion of the substrate, ΔG_Pi. Once again, part of this available binding energy is utilized to drive the conversion of the inactive open enzyme E_O to the active loop-closed form E_C that occurs on the binding of S-PO₃²⁻ to give the reactive E_C•S-PO₃²⁻ ground state Michaelis complex, so that the observed substrate binding energy, ΔG_obsd, differs from ΔG_Pi by an amount ΔG_C. Therefore, this portion of the available phosphodianion binding energy is not expressed in the Michaelis constant K_m, but is manifested at the transition state for catalysis by the “activated” enzyme E_C, as a lowered barrier to the reaction of the bound substrate, ΔG^‡_chem, and hence an increase in k_cat for conversion of the Michaelis complex to product (Figure 6). Now, if this phosphodianion binding energy were not used to drive the unfavorable enzyme conformational change, but rather was fully expressed as tight binding of the substrate in the Michaelis complex with the open enzyme, E_O•S-PO₃²⁻, then the barrier for reaction of the bound substrate through the transition state complex containing the active closed enzyme would be increased by an amount ΔG_C, resulting in a smaller value of k_cat (Figure 6). In other words, coupling of the thermodynamically unfavorable loop closure and conformational change to the development of interactions between the catalyst and substrate phosphodianion group provides a mechanism to circumvent tight and irreversible substrate binding, by providing a high specificity for binding of the reaction transition state.

Figure 6.

Free energy profile for the reaction of a whole phosphorylated substrate S-PO₃²⁻ catalyzed by an enzyme that exists predominantly in a stable inactive open form E_O. For simplicity, the Figure shows only the binding energy of the phosphodianion portion of the substrate, ΔG_Pi. The relative small observed binding energy of the phosphodianion group (ΔG_obsd) is the sum of the much larger total available binding energy of this group (ΔG_Pi) and the binding energy that is utilized to drive the unfavorable enzyme conformational change (ΔG_C). Catalysis occurs at a higher energy active closed form E_C, which is stabilized by interactions with the phosphodianion group of substrate at the E_C•S-PO₃²⁻ Michaelis complex (upper profile). In the case that the phosphodianion binding energy is not used to drive the unfavorable conformational change at the ground state Michaelis complex (lower profile), the activation barrier ΔG^‡_chem for turnover of the enzyme-bound substrate will increase by an amount ΔG_C (see text).

At first glance, it might appear inefficient for a catalyst to exist mainly in an inactive form ([E_O] ≫ [E_C], Figure 6). However, the utilization of substrate binding energy to drive an uphill enzyme conformational change will not result in a large decrease in k_cat/K_m, provided the reaction is close to the diffusion-controlled limit, as is the case for OMPDC and TIM.^20,21,117 The binding of substrate to E_O to form E_C•S-PO₃²⁻ (Scheme 13) will occur at the diffusion limit, so long as the initial encounter complex E_O•S-PO₃²⁻ undergoes loop closure to form the reactive Michaelis complex E_C•S-PO₃²⁻ faster than release of substrate back to solution. It is not clear that natural selection would favor the evolution of a predominantly inactive enzyme (K_c ≪ 1) over an enzyme for which K_c ≈ 1 for the activating conformational change (Scheme 11). However, we note the requirement that enzyme active sites be solvent-exposed and presumably well solvated, in order to allow access for the substrate, and that there are clear catalytic advantages (see above) to desolvation of the substrate and active site. This serves as an imperative for the utilization of substrate binding energy to drive the necessary desolvation of enzymes and substrates. In the case of TIM, we have proposed that desolvation is driven by an enzyme conformational change that results in solvent being swept out of the enzyme active site, and that the barrier for this active site desolvation makes a large contribution to ΔG_C (Figure 6).^{34,101,103,104}

Scheme 13.

Enolase and Other Superfamilies

The many members of the enolase superfamily catalyze a common half-reaction in which an active site base abstracts a proton from an α-carboxylate carbon to generate an enolate dianion intermediate stabilized by coordination to one or two essential Mg^2+.118,119 The reaction may be completed by reprotonation of the carbanion intermediate to give the product of a racemization or epimerization reaction, or by the loss of an oxygen- or nitrogen-based leaving group from the β-carbon to give an alkene (Figure 7). This catalytic diversity is provided by a two-domain structure. A modified TIM barrel domain [(β/α)₇β barrel], for which the active site lies at the C-terminal end of the β-strands that provide the functionalities that carry out the reaction chemistry. These include a Mg²⁺ [or two Mg²⁺ for enolase]¹²⁰ which stabilizes the developing negative charge at the enolate intermediate, and one or more amino acid side chains that function as Brønsted acid/base catalysts. Variations in the acid/base functional groups located at the ends of the second, third, fifth, sixth, and seventh β-strands of the catalytic domain contribute to the enormous range of reactions catalyzed by the enolase superfamily members. A second variable capping domain, composed of segments at the N- and C-termini of the polypeptide, plays a role similar to that of phosphodianion gripper loops. This capping domain interacts with nonreacting portions of the substrate and acts to sequester the substrate from interaction with bulk solvent.^119,121 Specificity for the nonreacting portions of the substrate is provided by variations in the capping domain. An important question is whether or not interactions with the capping domain of the enolase superfamily provide specificity for formation of the Michaelis complex, or if a part of the available substrate binding energy is expressed specifically at the transition state. This would result if ligand-driven closure of the capping domain activates these enzymes for catalysis of proton transfer, in a manner similar to that observed for the activation of TIM for deprotonation of GAP by phosphodianion-driven closure of loop 6 over the substrate.³⁴

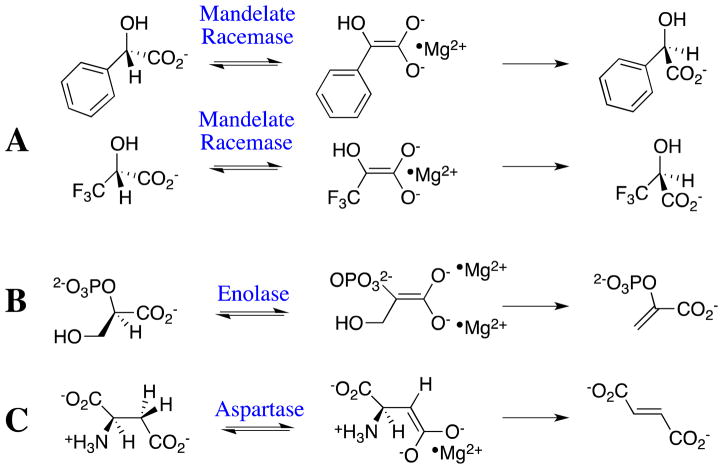
Figure 7.

Reactions catalyzed by members of the enolase superfamily, for which an active site base abstracts an α-carboxylate proton to generate an enolate dianion stabilized by coordination with one or two essential Mg²⁺ ions. (A) Deprotonation of mandelate and trifluorolactate, the first step in racemization catalyzed by mandelate racemase. (B) Deprotonation of 2-phosphoglycerate, the first step in the elimination reaction catalyzed by enolase. (C) Deprotonation of aspartate, the first step in the elimination reaction catalyzed by aspartate ammonia-lyase.

The capping domain of mandelate racemase (MR) interacts with the phenyl group of mandelate. The specificity of this interaction for stabilization of the Michaelis complex is low, as shown by the small effect of mutations at the capping domain on substrate binding affinity,¹²² and by the similar values of K_m ≈ K_S for the MR-catalyzed racemization of mandelate and trifluorolactate (Figure 7A).¹²³ By contrast, the same α-CF₃ for α-phenyl substitution results in a 400-fold decrease in k_cat for racemization of (R)-mandelate. A detailed comparison of the free energy profiles for the nonenzymatic and MR-catalyzed racemizations of mandelate and trifluorolactate shows that the enzyme provides a 6 kcal/mol greater stabilization of the transition state for racemization of mandelate, the physiological substrate.¹²³ These results show that there is a large specific stabilization of the transition state for the reaction catalyzed by MR, from interactions of the capping domain with the phenyl group of mandelate. They are consistent with the conclusion that closure of this domain, which is driven by stabilizing interactions with the phenyl group, activates the enzyme for catalysis of racemization of the physiological substrate. It is likely that closure of the capping domain provides a similar activation of other members of the enolase superfamily.

Members of the haloalkanoic acid dehalogenase superfamily (>19,000 unique sequences) function mainly to catalyze the hydrolysis of adenosine triphosphate and phosphate monesters.¹²⁴ These enzymes bind phosphate monoesters with the phosphoryl group oriented toward the Rossmann-fold core, and with the leaving group projected towards a “capping” domain that sequesters the bound substrate from bulk solvent and also provides substrate specificity. It would be informative to carry out experiments to test the proposal that interactions between this capping domain and the substrate leaving group activate members of this superfamily for catalysis.

Concluding Remarks

We show in this review that a significant fraction of the enzymatic rate accelerations for polar reactions of substrates which contain a phosphodianion moiety may be rationalized by Pauling’s simple model,^1,2 and consider the mechanism for the utilization of binding interactions of the nonreacting substrate phosphodianion group in enzyme activation. The possibility of enzyme activation by the substrate phosphodianion was not suggested by X-ray crystallographic analysis, computational studies, or by the other tools of mechanistic enzymology. Rather, this possibility arose from an intuitive sense of the power of the Pauling model to rationalize the rate acceleration for enzymatic reactions. We expect that the catalytic rate acceleration for many other enzymatic reactions will eventually be rationalized by experiments that characterize enzyme activation by interactions with nonreacting substrate fragments. Such activation is one important function of enzyme loops, capping domains, and other structural elements that function to sequester the substrate from interaction with bulk solvent at the interior of the protein catalyst.¹⁰¹

Debates about the origins of the catalytic rate acceleration for enzymes should focus on distinguishing the effects that make essential contributions to the rate acceleration, from those that are incidental. X-ray crystal structures of enzymes that catalyze polar reactions show extensive networks of interactions between the protein and ligand; and, the free energy profiles for these reactions show that the enzymes provide a much larger stabilization of the transition state than of the ground state Michaelis complex. Understanding of the role of protein-ligand interactions in transition state stabilization, and of the mechanism for their differential expression in the binding of ground and transition state is essential to understanding the enzymatic rate acceleration. These relatively simple issues have not yet been resolved for most enzymes that catalyze polar reactions. Their resolution may not provide us with a complete understanding of enzymatic catalysis, but it would represent a significant step forward.

Abbreviations

TPP

thiamine pyrophosphate

NAD

nicotinamide adenine dinucleotide

PLP

pyridoxal 5′-phosphate

OMPDC

orotidine 5′-monophosphate decarboxylase

OMP

orotidine 5′-monophosphate

UMP

uridine 5′-monophosphate

TIM

triosephosphate isomerase

GAP

glyceraldehyde 3-phosphate

DHAP

dihydroxyacetone phosphate

KSI

3-Oxo-Δ⁵-steroid isomerase (ketosteroid isomerase)

CoA

coenzyme A

SucCoA

succinyl-CoA

AcAcCoA

acetoacetyl-CoA

SCOT

succinyl-CoA:3-oxoacid coenzyme A transferase

α-GPDH

α-glycerol phosphate dehydrogenase

GA

glycolaldehyde

EO

1-(β-D-erythrofuranosyl)orotic acid

FEU

1-(β-D-erythrofuranosyl)-5-fluorouracil

FUMP

5-fluorouridine 5′-monophosphate

MR

mandelate racemase