Seven benzimidazole pesticides combined at sub-threshold levels induce micronuclei in vitro

Abstract

Benzimidazoles act by disrupting microtubule polymerisation and are capable of inducing the formation of micronuclei. Considering the similarities in their mechanisms of action (inhibition of microtubule assembly by binding to the colchicine-binding site on tubulin monomers), combination effects according to the principles of concentration addition might occur. If so, it is to be expected that several benzimidazoles contribute to micronucleus formation even when each single one is present at or below threshold levels. This would have profound implications for risk assessment, but the idea has never been tested rigorously. To fill this gap, we analysed micronucleus frequencies for seven benzimidazoles, including the fungicide benomyl, its metabolite carbendazim, the anthelmintics albendazole, albendazole oxide, flubendazole, mebendazole and oxibendazole. Thiabendazole was also tested but was inactive. We used the cytochalasin-blocked micronucleus assay with CHO-K1 cells according to OECD guidelines, and employed an automated micronucleus scoring system based on image analysis to establish quantitative concentration–response relationships for the seven active benzimidazoles. Based on this information, we predicted additive combination effects for a mixture of the seven benzimidazoles by using the concepts of concentration addition and independent action. The observed effects of the mixture agreed very well with those predicted by concentration addition. Independent action underestimated the observed combined effects by a large margin. With a mixture that combined all benzimidazoles at their estimated threshold concentrations for micronucleus induction, micronucleus frequencies of ~15.5% were observed, correctly anticipated by concentration addition. On the basis of independent action, this mixture was expected to produce no effects. Our data provide convincing evidence that concentration addition is applicable to combinations of benzimidazoles that form micronuclei by disrupting microtubule polymerisation. They present a rationale for grouping these chemicals together for the purpose of cumulative risk assessment.

Introduction

Benzimidazoles, commonly used as veterinary medicines (anthelmintics) and pesticides, act by inhibiting microtubule formation by binding to free β-tubulin monomers at the colchicine-binding site (1). In target organisms, the intended effect is cytotoxicity, which occurs through disruption of microtubuli (2,3). At lower, non-cytotoxic concentrations, the impairment of the microtubuli of the spindle apparatus can disturb the alignment of chromosomes during mitosis and lead to the formation of micronuclei (MN). In cultured mammalian cells from a variety of species, MN have been observed after exposure to albendazole and albendazole oxide (4,5), benomyl (6,7), carbendazim (8), mebendazole (9–11) and thiabendazole (12,13). Negative results for thiabendazole were also reported (9,14).

Through residual levels in food, human populations are exposed to a combination of different pesticides and veterinary medicines and, thus, may become exposed to more than one benzimidazole simultaneously (15). Although the use of benzimidazoles is regulated and therefore the potential risks from exposure to single benzimidazoles could be regarded as negligible, possible aneugenic combination effects from co-exposure to several benzimidazoles have not yet been considered in risk assessment. Because of the commonalities in their mechanism of action, the United Kingdom Committee on Mutagenicity of Chemicals in Food, Consumer Products and the Environment (COM) considered it plausible that these substances might produce combination effects according to the principles of concentration addition (CA), but data to support this conjecture are missing altogether. From the few experimental studies with mixtures of pesticides that have investigated genotoxic effects (7,16,17), it is difficult to derive any information about the nature of the observed combination effects. This is partly because clear additivity expectations were not specified, and partly because the tested mixtures included pesticides with undefined genotoxicity. If it could be shown experimentally that benzimidazoles act together in a concentration additive fashion, their risk assessment together as a group would merit serious consideration (18). In this study, we describe experiments specifically designed to address this issue.

The assessment of combination effects of chemicals after simultaneous exposure relies on two different concepts: CA and independent action (IA). Both concepts can be used to calculate the additive effects of a mixture from the toxicity of its components. This is possible when all components produce their effects without influencing each other’s action (non-interaction). Deviations from this so-called additivity assumption are then identified as synergisms or antagonisms.

CA (sometimes also referred to as dose addition) is based on the idea that all components in a mixture behave as if they were dilutions of one another (19). If they all interact with the same molecular target, it is thought that one chemical can be replaced by an equal fraction of an equieffective concentration (e.g. an EC₅₀) of another, without diminishing the overall combined effect. CA implies that every toxicant in the mixture contributes to the combination effect in proportion to its concentration and individual potency. Whether the individual doses are also effective on their own does not matter. Thus, if CA applies, combination effects are expected when toxicants are present at levels below effect thresholds (zero-effect levels), but only if the number of components sums up to a total mixture dose sufficiently large to produce effects. For example, two chemicals combined at one-tenth of their threshold concentration are not expected to produce a combination effect according to CA.

IA (sometimes also termed response addition, effect multiplication or Abbotts Rule) conceptualises mixture effects in a different way. It assumes that a combination effect can be calculated from the responses of the individual mixture components by following the statistical concept of independent random events (20). Unlike CA, IA utilises the individual effects of each mixture component as input values for calculating the expected mixture effect. Components present at doses below thresholds and thus associated with zero effects will not contribute to the joint effect of the mixture. If this condition is fulfilled for all mixture components, combination effects are not expected under IA. In the case of simultaneous exposure to several chemicals, the principles of independence of action are thought to be met only by substances with strictly dissimilar mechanisms of action. The validity of IA under such conditions has been shown in algae (21) and in bacteria (22).

The aim of this study was to test the hypothesis that benzimidazoles act together according to CA. However, despite their differing conceptual origins, CA and IA frequently produce very similar predictions of the combined effects of one and the same mixture. Thus, the following factors that can influence differences in the mixture effect predictions derived from CA and IA have to be taken into account: the mixture ratio, the effect magnitude considered for analysis, the steepness of the concentration–response curves of the individual components and the number of components included in the mixture (23). Inconclusive results would be obtained with combinations of benzimidazoles whose joint effects are described equally well by CA and IA. To avoid such ambiguities, we had to define conditions where CA and IA yielded mixture effect predictions that differed sufficiently, so that they could be distinguished experimentally. To maximise the prediction differences, we chose the mixture ratio in proportion to the potency of benzimidazoles and based the analysis on effect magnitudes of MN frequencies that could be measured reliably. For obvious reasons, the steepness of the individual concentration–response curves for MN formation was not open to experimental manipulation. This left only the number of benzimidazoles to be included in the mixture as a factor that could be varied to achieve sufficient discrimination between CA and IA predictions. Simulation studies based on concentration–response relationships of individual benzimidazoles indicated that CA and IA produced almost identical predictions for combinations of only two benzimidazoles. However, with seven or more of these chemicals, the additive effects predicted by CA and IA differed by margins large enough to become distinguishable experimentally.

Due to the benzimidazoles’ mechanism of aneugenicity by interaction with β-tubulin, the induction of MN is associated with concentration thresholds below which the effects are not different from background MN frequencies (24,25). These findings offered the opportunity to test the applicability of CA and IA also in terms of an additional aspect: If it can be shown that mixture effects occur when all benzimidazoles are combined at their threshold levels and below, IA can be ruled out as a valid prediction concept for these chemicals.

We analysed MN frequencies in an in vitro MN assay employing the well-established Chinese hamster ovary cell line CHO-K1. We used a protocol that included a cytokinesis block with cytochalasin B to ensure that the cells had undergone one round of mitosis, as suggested by OECD guideline 487 (26). To be able to generate concentration–response data for all the individual benzimidazoles and their mixture with sufficient accuracy, we implemented an automated MN scoring system based on image analysis, the Pathfinder™ Cellscan μN platform (IMSTAR, France). Altogether, we tested eight benzimidazoles that comprised the fungicides benomyl and its metabolite carbendazim, the anthelmintics albendazole, its metabolite albendazole oxide, flubendazole, mebendazole and oxibendazole, all of which were capable of inducing MN in our assay (‘CBMN positive’). Thiabendazole, which is used as both an anthelmintic and a fungicide, was also tested but was omitted from mixture testing as it did not induce MN in our assay system. For the first time, we conducted detailed concentration–response analyses for the seven remaining benzimidazole pesticides and used these data for predicting and testing their combined effects in the cytokinesis-blocked micronucleus (CBMN) assay with CHO-K1 cells. This strategy allowed us to resolve decisively the question whether aneugenic benzimidazoles act in combination in a concentration additive fashion.

Materials and methods

Chemicals and reagents

Albendazole (methyl [6-(propylthio)-1H-benzoimidazol-2-yl]carbamate, CAS 54965-21-8), albendazole oxide (methyl [5-(propane-1-sulfinyl)-1H-benzoimidazol-2-yl]-carbamate, CAS 54029-12-8), benomyl (methyl [1-[(butylamino)carbonyl]-1H-benzimidazol-2-yl]carbamate, CAS 17804-35-2), carbendazim (methyl 1H-benzimidazol-2-ylcarbamate, CAS 10605-21-7), flubendazole (methyl N-[6-(4-fluorobenzoyl)-1H-benzimidazol-2-yl]carbamate, CAS 31430-15-6), mebendazole (methyl (5-benzoyl-1H-benzimidazol-2-yl)carbamate, CAS 31431-39-7), oxibendazole (methyl N-(6-propoxy-1H-benzimidazol-2-yl)carbamate, CAS 20559-55-1) and thiabendazole (4-(1H-1,3-benzodiazol-2-yl)-1,3-thiazole, CAS 148-79-8) were purchased from Sigma–Aldrich (Dorset, UK) at the highest purity available. MTT (3-(4,5-dimethylthiazol-2-yl)-2,5-diphenyltetrazolium bromide), acridine orange and cytochalasin B (10mg/ml) were also obtained from Sigma. Paraformaldehyde (PFA) was provided by Avocado chemicals (Lancashire, UK), and dimethyl sulphoxide (DMSO, cell culture grade) and Triton X-100 by VWR (Lutterworth, UK). F-12K cell culture medium and Hanks’ balanced salt solution (HBSS) buffer were purchased from Invitrogen (Paisley, UK).

Routine cell culture of CHO-K1 cells

CHO-K1 cells are a Chinese hamster ovary cell line and were purchased from the American Type Culture Collection (ATCC No CCL-61, LGC standards, Teddington, UK). They were routinely grown in 75-cm² canted neck tissue culture flasks in F-12K medium (Invitrogen) supplemented with 10% foetal calf serum (FCS; Invitrogen) in a humidified incubator at 37°C with 5% CO₂. Cells were sub-cultured when confluent over a maximum of 10 passages and were tested routinely for Mycoplasma infections.

CBMN assay

Treatment of CHO-K1 cells.

The CBMN assay (27) was performed in 24-well plates. CHO-K1 cells were seeded in F-12K medium (10% FCS) at a density of 1.2 × 10⁴ cells/well in 24-well plates and allowed to attach for 24h. After this period, the medium was changed to F-12K medium containing the test compounds or mixture. Chemicals were dissolved in DMSO and serial dilutions of the chemical or mixture stocks were prepared in assay medium, the DMSO concentration never exceeding 0.5%. We tested eight different concentrations for each benzimidazole or the mixture in each experiment. The control cultures were treated in duplicate with DMSO (0.5%, solvent control). DMSO on its own did not have any genotoxic or cytotoxic effects.

Cytokinesis block.

After treatment with the test compounds for 24h, the cells were washed once with F-12K medium. F-12K medium (10% FCS) supplemented with 3 µg/ml cytochalasin B was added to block cytokinesis for 18–20h. After this period, the medium was changed to F-12K medium (10% FCS) and the cells left to recover for 1–2h.

Slide preparation and staining.

The cells were harvested by trypsinisation, counted and centrifuged onto glass slides using a cyto-centrifuge for 10min at 1200rpm. The final cell density per slide was kept between 50 000 and 100 000 cells. The cells were immediately fixed in 4% PFA [in phosphate buffered saline (PBS)] for 10min at room temperature. The fixed slides were washed for 2 × 5min in PBS on a shaker, before staining with 10 µg/ml acridine orange (in ddH₂O) for 20min at room temperature. The slides were washed for 2 × 5min in ddH₂O on a shaker, then dipped into ddH₂O, allowed to air dry and mounted with Vectashield HardSet mounting medium containing 4′,6-diamidino-2-phenylindole (DAPI) (1.5 µg/ml; Vector Laboratories, Peterborough, UK).

Automated image acquisition and micronucleus scoring

For automated image acquisition and MN scoring, a Pathfinder™ Cellscan μN platform for automated micronucleus assay scoring (IMSTAR, Paris, France) was used. It was equipped with an Olympus BX41 fluorescence microscope with an automated stage and employed the IMSTAR Pathfinder™ software for image acquisition and analysis. It could process up to four slides in one round of imaging. For each slide, a mosaic of images were captured using an ×20 objective. Images were acquired in the DAPI channel for the nuclei and the rhodamine (red) channel for the cytoplasm. Automated image analysis was started after scanning of the first slide. The algorithm used for image analysis was based on an existing algorithm for detection of cells, nuclei and MN (28), which was optimised for fluorescence stained cells. In brief, the cytoplasm regions were first identified in the red channel. Next, the nuclei were detected within these cytoplasm regions using the images in the DAPI channel. Last, the MNs were detected within cells that were first identified as valid in terms of cytoplasm and nuclei in the previous detection steps. Data output contained the total number of mono- and binucleated cells and the number of mono- and binucleated cells that contained MNs. For each slide >1000 binucleated cells were analysed. Comparison with manual counts showed that the automated system persistently underestimated the MN score. This was, however, consistent for different compounds and at different effect concentrations. The reasons for the underscoring were due to the more conservative setting of the scoring algorithm towards avoiding false-positive MNs. Most importantly, the system produced data with sufficiently low inter-experimental variability and high data reproducibility to be employed in mixture experimentation.

MTT assay for detection of cytotoxicity

A modified version of the MTT assay (29) was carried out as described in reference (30). CHO-K1 cells were seeded at a density of 5000 cells/well in F-12K medium (10% FCS) in clear plastic 96-well plates. Cells were allowed to attach for 24h before being treated with the test compounds. Chemicals were dissolved in DMSO and diluted in assay medium, the DMSO concentration never exceeding 0.5%. Samples were tested in duplicate. Controls were treated with DMSO only (solvent control) or with 1% Triton X-100 (positive control). After treatment for 24h, the cells were washed once with F-12K medium; subsequently F-12K medium (10% FCS) containing 3 µg/ml cytochalasin B was added and the cells were incubated for a further 18–20h. After this period, the medium was changed to F-12K medium (10% FCS) and the cells left to recover for 1–2h before the medium was removed and replaced with F-12K medium (10% FCS) containing 250 µg/ml MTT. Cells were incubated for 1h with the MTT solution, allowing viable cells to reduce the yellow MTT to dark blue crystals of formazan. Next, the cells were washed once with HBSS buffer before adding DMSO to dissolve the formed formazan crystals for 30min on a shaker. The optical density of solubilised formazan product was photometrically quantitated by reading the absorbance at 570nm and 620nm using a plate reader. The 570nm readings were corrected for background by subtracting the 620nm readings. Data were normalised by subtracting the average values of positive (Triton X-100) controls from sample values and the average of solvent control and then by dividing the such corrected sample values by the negative controls.

Biostatistical analysis of the CBMN assay

The induction of MNs in the CBMN assay is measured as the number of binucleated (bn) cells with at least one MN (N _MN≥1) in relation to all bn cells (N _total), and expressed as ratio r:

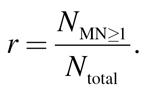(1)

If all cells with at least one MN count as ‘success’, this ‘success’ is a binary outcome. Because the number of successes from a definite sample size N _total is of interest, the success rate is estimated statistically by the binomial distribution. Consequently, treatment effects were analysed by quantal concentration–response analysis assuming binomially distributed data, and expressed as success probability P, e.g. a value of P = 0.1 means that 10% of all bn cells are most likely to have at least one MN. In some cases, we observed a greater variability (statistical dispersion) in our data than was expected based on the binomial distribution, i.e. an extra binomial variation. In such cases, we included an overdispersion parameter in data analysis.

As expected for this assay endpoint, a low baseline rate of MNs was observed, even when the cells had not been exposed. This low response in ‘control cultures’ is called baseline or spontaneous response. A common assumption is that this baseline rate is independent of treatment effects, i.e. a baseline rate higher than normal does not necessarily imply that all treatment-related MN rates are increased in the same (proportional) way. Baseline rates might vary from experiment to experiment (‘inter-experimental variability’), and thus we estimated them on a chemical-to-chemical basis.

A further complication for the concentration–response analysis was that for the studied assay endpoint, a concentration threshold concept is assumed, i.e. the existence of a threshold concentration, at and below which the response is assumed to be constant and not different from the baseline rate of the controls. To achieve an accurate estimation of low concentration–responses, which is essential for the analysis and assessment of mixture effects, concentration–response models must be able to describe this threshold concentration, and data analysis should provide an accurate estimate of a threshold concentration from this model.

Together with the problem of baseline or spontaneous responses, the estimation of a threshold concentration defines a complex data and modelling situation, which cannot be solved with classical concentration–response models. One possibility would have been to use the so-called ‘hockey stick’ model of Lutz and Lutz (31), which assumes a linear dose–response relationship at concentrations above the threshold. However, our data suggested a non-linear pattern and as the most accurate description of the concentration–response data was considered essential for an unbiased mixture assessment, we focused on more flexible models. In the following, we present various threshold concentration–response models that we used for our data analysis, how these models were fitted to the data and how standard mixture models were adopted to our specific data situation.

Threshold dose–response models

The general equation of a threshold model with an implicit baseline response rate is given for a response likelihood P at concentration c by

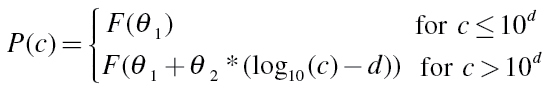(2)

Here F(c) is a non-linear concentration–response regression model from a family of continuous distributions, where θ ₁ and θ ₂ are location and scale model parameters. The threshold model parameter d defines the threshold concentration c _threshold = 10^d, and the baseline rate of response is defined as F(θ ₁).

We selected three potential models—logit, probit and weibull—all capable of accurately describing concentration–response data from the CBMN assay. The corresponding functions are

Logit:

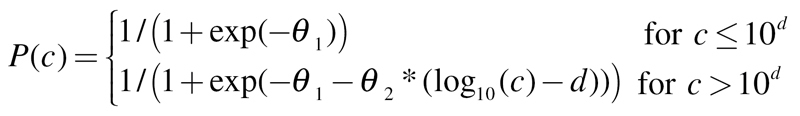(3)

Probit:

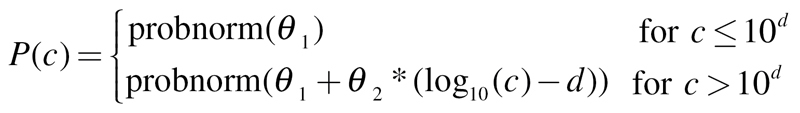(4)

Weibull:

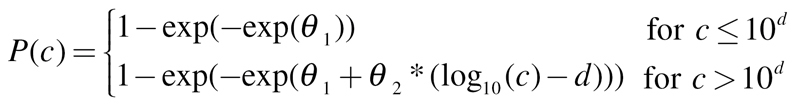(5)

Here, probnorm(x) is the function that returns the probability that an observation from the standard normal distribution is less than or equal to x (inverse of the probit function).

All models were separately fitted to each data set, and then the best-fitting model was selected for each chemical according to a statistical goodness-of-fit criterion (Akaike information) and used for the subsequent mixture modelling (32). Only data from concentrations associated with cytotoxicity of <40% were included in data analysis, and the EC₄₀ derived earlier from the MTT assay was used as guidance for an upper limit above which data sets were excluded from regression analysis because above this concentration cytotoxicity was deemed to have a negative impact on data quality. Data analyses were always performed on pooled data sets from at least three independent experiments, and model parameters were estimated by (restricted) maximum likelihood. Overdispersion was modelled by including a dispersion parameter into the variance function (multiplicative dispersion) and estimated by Pearson chi-square statistic divided by its degrees of freedom. All statistical analyses were performed using SAS statistical software version 9.2 (SAS Institute Inc., Cary, NC, USA).

Mixture predictions

For the prediction of mixture effects according to CA (33) and IA (21), we adapted the two models to the use of threshold concentration–response relationships as described below.

Calculation of concentration addition.

For a binary mixture of substances 1 and 2, the concept of CA is usually defined by the equation

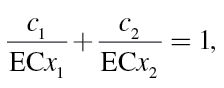(6)

but can be extended to any number of n components by

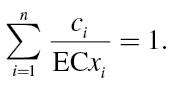(7)

In these equations, c _i are the individual concentrations of the substances 1 to n, which are present in a mixture that produces the definite effect x, and ECx _i denotes the equivalent effect concentrations (ECs) of the single substances, i.e. those concentrations that alone would produce the same quantitative effect x as the mixture. The individual concentrations c _i sum up to a total concentration c _mix that causes the joint effect E(c _mix) = x. This is defined as the effect concentration ECx _mix. Hence, c _i in (7) can be substituted for the expression p _i · ECx _mix, where p _i is the prevalence of a mixture component in the mixture, i.e. the ratio of its concentration to the total mixture concentration (p _i = c _i/c _mix). By rearrangement we obtain:

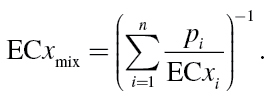(8)

The individual effect concentrations ECx _i are derived from individual concentration–response functions F _i. For that purpose, the inverse functions F _i ^–1 are used, which give the concentrations c of the ith substances that produce an individual effect x, i.e. ECx _i = F _i ^–1(x). Thus, we can write:

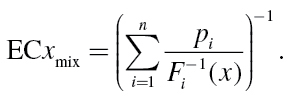(9)

An EC derived from the threshold concentration–response model can only be estimated for effect levels above the baseline response and is defined for the functions from (3–5) as

Logit:

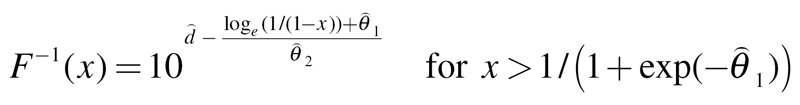(10)

Probit:

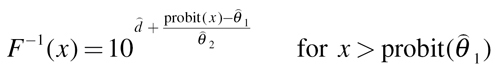(11)

Weibull:

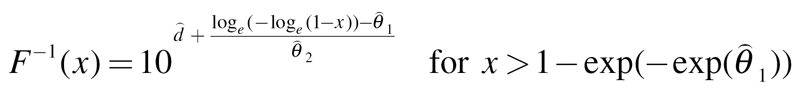(12)

Here, 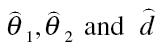are estimates of the unknown model parameters θ ₁, θ ₂ and d, derived from the best-fitting approach.

Equation (9) allows the prediction of any EC of a mixture under the hypothesis of CA. However, this is possible only for effect levels x that are greater than the highest individual baseline rate from the individual compounds. Only under such conditions it is possible to calculate ECs for all the compounds in the mixture. The baseline response for the mixture experiment cannot be predicted according to this equation, but might be below the lowest predictable effect level, and in this case we suggest ignoring the effect restrictions in (10–12), which then allows the estimation of concentrations for effect levels even below the baseline rate.

Calculation of independent action.

The basic version of IA has been formulated under the simple assumption that the susceptibilities of the individuals of an at-risk-population to different dissimilarly acting mixture components are not correlated with each other (20). For a binary mixture, this is commonly defined by the equation

(13)

E(c ₁) and E(c ₂) denote the effects produced by the individual compounds c ₁ and c ₂, and E(c _mixture) is the total effect of the mixture. This equation can be extended to any number of mixture components, resulting in

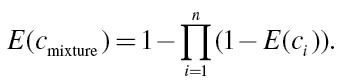(14)

The individual effects of mixture compounds E(c _i) are calculated from concentration–response functions F _i determined for single substances, i.e. E(c _i) = F _i (c _i). For concentration–response models with a baseline effect, the single effects have to be first corrected by their individual background baseline estimates (baseline_i), and in the end the total mixture effect should be corrected by an estimate for the expected baseline for the mixture, i.e.

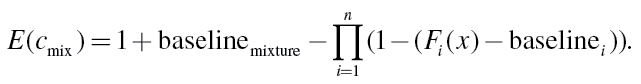(15)

Ideally, all baseline estimates would be identical and thus work as a common reference. It is, therefore, important that the variation between the individual baseline estimates is reasonably small, which demands a good reproducibility of the test system and an experimental design that ensures accurate and precise estimations of all background baselines. If this is not the case, the estimation of a common baseline from all data must be implemented in the concentration–response data analysis of the compounds. There is no common consensus about how to estimate the baseline response for the mixture experiment. We used the smallest and highest baselines from all compounds and calculated for each mixture concentration two effect predictions, spanning a range of IA predictions.

Mixture experiment design and testing

The mixture to be tested in the CBMN assay was designed using the concentration–response relationships of the CBMN-positive benzimidazoles (Table II). A fixed mixture ratio approach (34) was used with mixture ratios proportional to equieffective levels. The chosen effect levels were the estimated threshold concentrations of all the individual benzimidazoles present in the mixture. The mixture ratio, i.e. the fractions of the individual benzimidazoles within the mixture, is presented in Table I. Mixture stock solutions with a mixture ratio as described were prepared and serially diluted to cover the effective concentration ranges predicted by CA and IA. This meant also testing concentrations in the cytotoxic range. We also ensured that the sum of the estimated threshold was tested. Finally, the mixture effects were assessed experimentally in the CBMN assay and compared with the predictions.

Table II.

Threshold concentration–response models for individual benzimidazoles and their mixture in the CBMN assay

Compound	Model	Model parameter			Baseline ratea	Threshold concentration
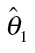
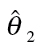
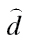
					% (95% CI)	(95%CI) [M]
Individual benzimidazoles
Albendazole	Logit	−4.399	2.588	−6.807	1.21 (1.09–1.34)	1.56E-07 (1.25E-07–1.96E-07)
Benomyl	Logit	−4.272	2.626	−5.644	1.38 (1.27–1.49)	2.27E-06 (1.79E-06–2.88E-06)
Carbendazim	Logit	−4.213	2.085	−5.743	1.46 (1.31–1.61)	1.81E-06 (1.40E-06–2.34E-06)
Flubendazole	Weibull	−4.358	3.134	−7.035	1.27 (1.14–1.41)	9.22E-08 (7.29E-08–1.16E-07)
Mebendazole	Logit	−4.321	2.918	−6.950	1.31 (1.18–1.44)	1.12E-07 (9.31E-08–1.35E-07)
Oxibendazole	Weibull	−4.378	5.004	−6.883	1.25 (1.14–1.35)	1.31E-07 (1.31E-07–1.32E-07)
Albendazole oxide	Logit	−4.168	2.543	−5.217	1.52 (1.42–1.63)	6.07E-06 (5.24E-06–7.04E-06)
Mixture
Seven benzimidazoles	Weibull	−3.861	2.813	−5.726	2.08 (1.92–2.25)	1.88E-06 (1.66E-06–2.13E-06)

^aBaseline rate is expressed as percentage; 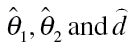are estimates of the unknown model parameter θ ₁, θ ₂ and d.

Table I.

Composition of the benzimidazole mixture tested in the CBMN assay

Compound	Fraction in the mixture (%)
Albendazole	1.09
Albendazole oxide	61.46
Benomyl	19.17
Carbendazim	15.26
Flubendazole	0.78
Mebendazole	0.99
Oxibendazole	1.25

Percentages show the fraction of the individual compounds in the mixture.

Mixture assessment

The statistical uncertainty for the predicted mixture effects and EC was determined using the bootstrap method (35) and expressed as 95% confidence limits for the predicted mean estimate. Differences between predicted and observed effect doses were deemed statistically significant when the 95% confidence belts of the prediction did not overlap with those of the experimentally observed mixture effects.

Results

Concentration–response analysis of individual benzimidazoles in the CBMN assay

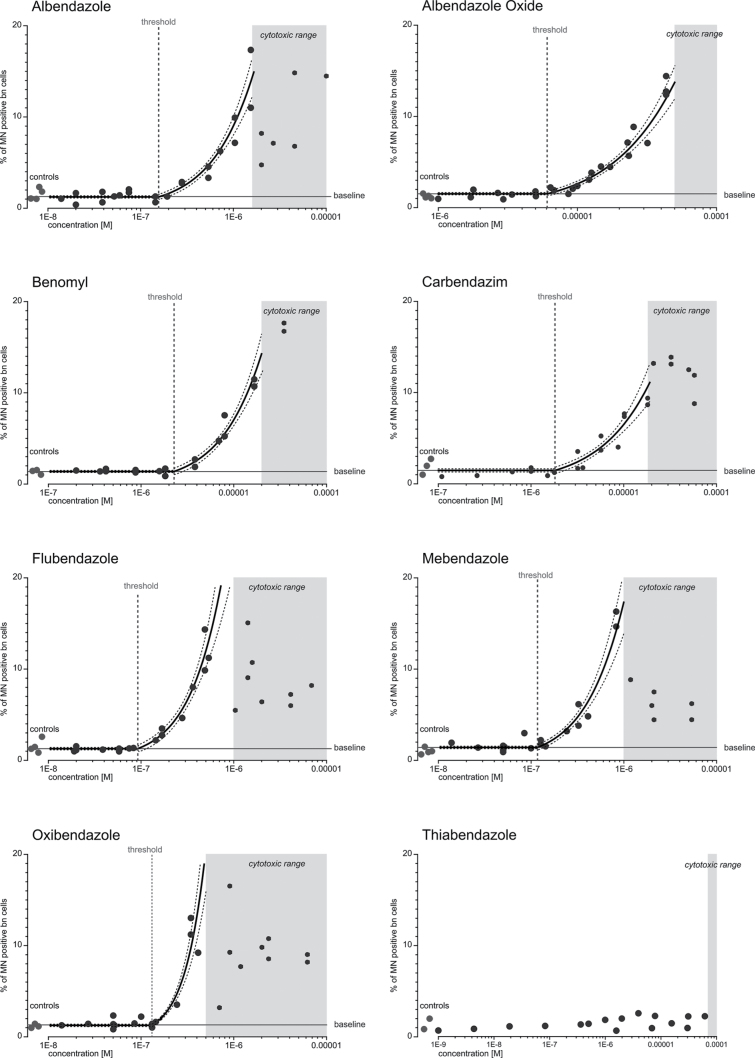
For this study, eight benzimidazoles were tested for their ability to induce MNs in the CBMN assay using CHO-K1 cells. Albendazole, albendazole oxide, benomyl, carbendazim, flubendazole, mebendazole and oxibendazole-induced MNs in a concentration-dependent manner, whereas no increased formation of MNs was observed after treatment with thiabendazole (Figure 1). The seven MN-positive benzimidazoles were, therefore, subjected to detailed concentration–response analyses in the CBMN assay. Each compound was tested in at least three independent experiments and eight different concentrations to obtain sufficiently reproducible concentration–response data for the subsequent mixture testing. All positive benzimidazoles exhibited concentration–responses that were best described by regression models comprising a threshold parameter. As shown by the best-fitting models for the seven active benzimidazoles in Figure 1, there were concentration ranges where the cells showed a baseline percentage of MNs that did not change with increases in concentrations until a certain threshold concentration (marked by the dashed vertical line) was reached. Above this concentration, concentration dependent increases in MNs were seen that could be modelled by non-linear regression models. The model parameters, including the threshold parameters as well as the baseline rates of MNs and the threshold concentrations for each benzimidazole, are listed in Table II. The baseline rates of MN in CHO-K1 cells were between 1.21 and 1.52%.

Fig. 1.

Concentration–response data for individual benzimidazoles in the CBMN assay. Induction of MN by eight benzimidazoles (as indicated) was analysed in the CBMN assay using CHO-K1 cells. MN induction is shown as percentage of MN-positive bn cells. The graphs show the experimental data of at least three independent experiments (black dots). Solvent controls are displayed on the left as indicated. The regression curves (thick black curves) are shown with their respective 95% CIs (thick dashed lines). The vertical dashed line indicates the estimated threshold concentration for aneugenic effects, and the horizontal line shows the mean baseline levels of MN present in the cells. The grey areas show the cytotoxic concentrations for each benzimidazole as determined in the MTT assay (MTT-EC₄₀).

Flubendazole was the most potent benzimidazole, with an estimated threshold concentration of 92.2nM, followed by mebendazole, oxibendazole, albendazole, carbendazim, benomyl and albendazole oxide, which was the least potent, with a threshold concentration of 6.07 µM.

To define a suitable concentration range within which cytotoxicity did not have a major impact on data quality and assay reproducibility, we also determined the cytotoxicity of the individual benzimidazoles. Although the cytotoxicity block proliferation index (CBPI) is recommended to be used for measurement of cytotoxicity in the CBMN assay (26), there is a debate whether this parameter is applicable to aneugens (36). The CBPI did not provide a good measure for cytotoxicity in our hands, and we therefore tested all benzimidazoles in the MTT assay (Table III, see Supplementary material, available at Mutagenesis Online, for a comparison between MTT and CBPI). We used the MTT-EC₄₀, i.e. the concentration that produced a reduction in viable cells by 40%, as a guidance concentration above which the data variability in the CBMN assay increased due to cytotoxicity. The impact of cytotoxicity was recognisable in terms of a reduction of bn cells. In some cases, the effect of cytotoxicity was less pronounced and concentrations above the MTT-EC₄₀ could be included in the analysis. The grey shaded areas in the graphs in Figure 1 indicate the concentration ranges above which cytotoxicity caused undue data variability in each individual case. Below these concentrations, the intra- and inter-experimental data variability was acceptable and the assay exhibited good data reproducibility. Therefore, only data below the grey shaded areas were included in the regression modelling of CBMN concentration–response data and the consecutive mixture modelling.

Table III.

Cytotoxicity of the individual benzimidazoles and their mixture in the MTT assay

Compound	Concentration–response function					EC10	EC20	EC40
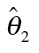
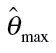
	RM					M [CI]	M [CI]	M [CI]
Individual benzimidazoles
Albendazole	Logit	−28.39	−4.28	0.54	1	1.19E-7 [9.29E-8−1.52E-7]	2.06E-7 [1.74E-7−2.43E-7]	6.63E-7 [4.76E-7−9.25E-7]
Benomyl	Logit	−18.01	−3.75	0a	1	4.06E-6 [2.87E-6−5.76E-6]	6.69E-6 [5.27E-6−8.48E-6]	1.22E-5 [1.04E-5−1.43E-5]
Carbendazim	Logit	−17.96	−3.78	0a	1	4.58E-6 [2.54E-6−8.26E-6]	7.51E-6 [5.05E-6−1.12E-5]	1.37E-5 [9.89E-6−1.89E-5]
Flubendazole	Logit	−37.62	−5.59	0.57	1	1.15E-7 [8.03E-8−1.64E-7]	1.77E-7 [1.38E-7−2.28E-7]	5.44E-7 [3.03E-7−9.77E-7]
Mebendazole	Logit	−35.89	−5.36	0.59	1	1.24E-7 [7.62E-8−2.03E-7]	1.98E-7 [1.42E-7−2.75E-7]	9.88E-7 [1.29E-7−7.54E-6]
Oxibendazole	Logit	−49.89	−7.27	0.58	1	9.09E-8 [3.66E-8−2.26E-7]	1.63E-7 [9.67E-8−2.75E-7]	3.55E-7 [1.22E-7−1.03E-6]
Thiabendazole	-					>7E-5	>7E-5	>7E-5
Albendazole oxide	Logit	−13.60	−2.75	0.41	1	3.03E-6 [1.78E-6−5.15E-6]	6.56E-6 [5.39E-6−7.98E-6]	2.16E-5 [1.75E-5−2.66E-5]
Mixture
Seven benzimidazoles	Logit	−30.58	−5.65	0.55	1	2.31E-6 [1.83E-6−2.92E-6]	3.53E-6 [2.99E-06−4.17E-6]	9.32E-6 [6.46E-6−1.35E-5]

EC₁₀, EC₂₀, EC₄₀: concentrations provoking 10, 20 and 40% lower optical density readings to the negative controls, respectively. Values in brackets denote the upper and lower limits of the ~95% confidence interval; the column ‘RM’ indicates the mathematical regression function as defined at [28]: 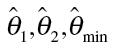estimated model parameters, given for concentrations expressed in M (rounded values), 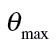were not estimated, but set to 1 relating to the mean value of the negative controls.

^ahold fixed; ‘>’ indicates highest test concentration

Prediction and testing of mixture effects

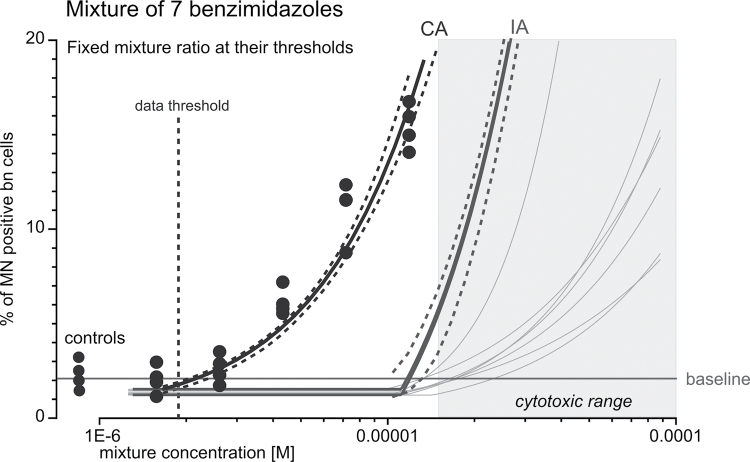
Using the concentration–response data of the seven individual CBMN active benzimidazoles, albendazole, albendazole oxide, benomyl, carbendazim, flubendazole, mebendazole and oxibendazole (Table II), we next predicted their combined effect according to the competing models of CA and IA. First, it was important to decide on a suitable mixture ratio to be able to distinguish between the two prediction models and to ensure that all of the mixture components contributed to the mixture effect. To achieve this, we chose a fixed mixture ratio approach (34), with mixture ratios proportional to the estimated threshold concentrations of all mixture components. Simulation studies were conducted to decide which common effect level would be the most suitable to attain the best discrimination between CA and IA (data not shown). A nearly optimal solution, based on these studies, was a combination of the seven benzimidazoles at their estimated threshold levels. This had the additional advantage of investigating a combination of ‘zero’-ECs to assess whether combination effects would occur, as expected under CA. Thus, we designed a mixture at a mixture ratio reflecting the benzimidazoles’ estimated threshold levels (the fractions of the individual benzimidazoles are presented in Table I) and calculated their effects according to CA and IA (black and dark grey curves, respectively, as labelled; Figure 2). The two models yielded prediction curves that were clearly distinguishable (Figure 2). The 95% confidence intervals (CI) for both predictions (dashed lines in the respective colours) did not overlap. Minor experimental variations between experiments led to slight differences in the baseline levels of MN for the individual benzimidazoles. Taking these variations into account for the calculation of the IA prediction, we obtained two IA prediction curves. One was based on the highest and the other on the lowest observed estimated baselines for the single compounds, but these curves differed only marginally (Figure 2). The CA prediction curve covered the entire range of estimated baseline rates. The concentration–effect curves of the individual benzimidazoles at their actual concentrations present in the mixture are shown in light grey (Figure 2). Under the assumption that the estimated threshold concentration approximated the compounds’ true ‘zero’-ECs, no mixture effects were expected according to IA at and below the mixture concentration that corresponded to the sum of the estimated individual threshold concentrations. In contrast, CA predicted clear additive effects at and even below this mixture concentration.

Fig. 2.

Predicted and observed MN induction by a benzimidazole mixture in the CBMN assay. The mixture of seven MN-inducing benzimidazoles was designed at a fixed mixture ratio, using the estimated threshold concentrations of the individual compounds. The mixture effects were predicted according to CA (thick black curve, as indicated) and IA (thick dark grey curve, as indicated). The dashed curves show the respective 95% CIs for the predictions. The thin grey curves indicate the effects of the individual benzimidazoles at the concentrations present within the mixture. Experimental concentration–response data were pooled data from at least three independent experiments (black dots). The vertical dashed line indicates the estimated threshold concentration, and the horizontal line shows the mean baseline levels of MN for the experimental data. The grey area shows the cytotoxic mixture concentrations as determined in the MTT assay (MTT-EC₄₀).

Next, we tested the mixture experimentally in the CBMN assay (black dots in Figure 2). The mixture induced MN in a concentration-dependent manner, and its effects were accurately predicted by CA over the entire tested (sub-cytotoxic) concentration range. IA, on the other hand, underestimated the observed effects over this concentration range. Most notably, as predicted by CA, clear combination effects of 15.5% induction of MN were observed at total mixture concentrations that corresponded to the sum of the estimated threshold concentrations of the single benzimidazoles. MN frequencies of ~5% were observed at a mixture concentration ~50% lower than the sum of the thresholds of the single chemicals. The threshold concentration estimated for the experimental mixture effects (Table II) was almost one order of magnitude lower than the mixture threshold predicted by IA, but again in good agreement with CA. A comparison of the statistical uncertainty of the two prediction models and the experimental data for 5% and 10% effects are provided in Table IV.

Table IV.

Statistical uncertainty of predicted and observed ECs of the mixture

Induction of MN	Effect concentration ECx mix [M]
	Observed		Predicted by CA		Predicted by IA
	Mean	95% CI	Mean	95% CI	Meana	95% CI
5%	3.94E-6	[3.68E-6–4.22E-6]	4.46E-6	[4.31E-6–4.73E-6]	1.36E-5–1.39E-5	[1.27E-5–1.58E-5]
10%	7.35E-6	[6.90E-6–7.84E-6]	7.86E-6	[7.47E-6–8.31E-6]	1.77E-5–1.79E-5	[1.68E-5–1.98E-5]

^aPredictions are calculated assuming lowest or highest observed baseline.

The grey shaded area in Figure 2 again indicates the concentrations above which the CBMN data were omitted from regression analysis due to increased data variability caused by cytotoxicity. The cytotoxicity of the mixture was also tested in the MTT assay (Table III) to confirm that cytotoxicity did not overly interfere with the mixture results in the CBMN assay. Notably, the benzimidazole mixture acted also according to CA in the cytotoxicity endpoint. The experimentally determined MTT-EC₄₀ of the mixture (9.32 µM with a 95% CI of 6.46–13.5 µM) was in good agreement with CA, which estimated an MTT-EC₄₀ of 7.62 µM, whereas IA underestimated the combined cytotoxic effects (50 µM).

Discussion

Our analysis of the joint aneugenic effects of the seven selected benzimidazoles shows decisively that these chemicals act together according to the principles of CA. This conclusion is based on two findings.

First, the observed combination effects agreed excellently with the MN frequencies that were expected from the concentration–response curves of the individual chemicals. IA predicted mixture effects that were significantly smaller than the experimentally observed effects. Secondly, at a total mixture concentration equivalent to the sum of the estimated threshold concentrations of the individual benzimidazoles, MN frequencies well above background levels were observed. Had IA been applicable, the observed combination effect should have been similar to background levels.

These results strongly suggest that the benzimidazoles in our mixture behaved like dilutions of one another, such that a fraction of an equieffective concentration of one benzimidazole could be replaced by another. An explanation can be sought in the mechanism of action of the selected benzimidazoles at the molecular level. They all disrupt microtubule polymerisation by binding to the colchicine-binding site of tubulin monomers.

The validity of CA as an assessment concept has been demonstrated with numerous experimental systems and endpoints involving a wide range of chemical mixtures (see the review by Kortenkamp et al. (37)), but evidence with endpoints relevant to genotoxicity is scarce. The only study showing agreement with CA is an Ames test with various polycyclic hydrocarbons (38). In that same article, larger effects than predicted by CA were observed for induction of MN by ionising radiation combined with ethyl methanesulphonate; however, this synergism was cell line dependent. Other cell lines showed induction of MN in agreement with CA. To our knowledge, our study is the first to show that CA is valid for the prediction of MN induction with multi-component mixtures of chemicals that exhibit strictly similar modes of action, such as benzimidazoles.

Our results could not have been achieved without implementing an assay system that produced concentration–response data of high quality and reproducibility. To realise this, we used the Chinese hamster ovary cell line CHO-K1, a well-established cell line for MN scoring (26,39). Unlike primary human lymphocytes, these cells are not subject to donor variability and do not require mitogenic stimulation for growth, are easy to maintain and are well characterised. Considering the large number of experiments required for establishing concentration–response relationships for the individual benzimidazoles and the mixture, manual counting of MN was not feasible. We, therefore, implemented an automated image acquisition and MN scoring system based on image analysis using an existing MN scoring algorithm (28). We previously validated the system by comparison with results obtained by manual MN counting. The automated system persistently underestimated the MN score and detected on average ~56% of MN compared with visual counts. This was, however, consistent for different compounds and at different concentrations and is well within the range of other automated MN scoring systems, with reported detection rates of ~35 (40), ~51 (41) and ~69% (28). This lower MN detection rate has been explained earlier by the strict scoring criteria used in the scoring algorithm. For ambiguous MN, the algorithm was set to reject the signal, where a manual scorer could decide to include or reject (28). However, these stringent settings were chosen in order to avoid false-positive scores. Most importantly, this set-up allowed us to produce MN data with sufficiently low inter-experimental variability and good reproducibility to be employed in mixture experimentation.

In our hands, automated scoring produced MN baseline levels that agreed very well with earlier reports for CHO cells (36,39,42,43). The potencies we measured for benomyl and mebendazole were comparable to the data reported from assays with mouse fibroblast and human lymphocytes (6,7,9–11). In the case of albendazole and albendazole oxide, our system was slightly more sensitive when compared with primary human lymphocytes (4,5). For carbendazim, we obtained potency estimates that fell between the data reported for mouse lymphoma cells (8) and those for human lymphocytes (9–11,28,44). We could not find any peer-reviewed publications that corroborated our observations of MN with flubendazole and oxibendazole. However, the Committee for Veterinary Medicinal Products (EU) listed oxibendazole as causing polyploidy in CHO cells and as inactive in an in vivo MN test with mice (45). In another publication, they reported flubendazole to be inactive in MN assays with rats and mice (46). Thiabendazole was found to induce MN in some systems (12,13) but was negative in others (9,14) or produced ambiguous results (43,47). In our system, thiabendazole, tested in the absence of metabolic activation, was inactive, and was therefore not included in our mixture experiments. The reasons for the absence of increased MN after treatment with thiabendazole could be due to differences in the cell lines or assay protocols as well as the solubility limit of thiabendazole, which was lower in our assay set-up compared with reported MN-inducing concentrations (13,48). Other explanations might be found in the narrow effective concentration range due to the very steep toxic profile of thiabendazole, which might be overlooked by the experimenter (49) or the possibility that thiabendazole may cause acytokinesis, thus not resulting in MN (43).

Variability in MN frequencies increased as the concentrations of benzimidazoles exceeded a certain level. This was particularly noticeable with albendazole, carbendazim, flubendazole, mebendazole and oxibendazole and was generally associated with a downturn in MN frequencies (Figure 1) and a decrease in the number of analysable bn cells. These levels correlated with and were most likely caused by the increased cytotoxicity. This made it necessary to establish criteria for selecting concentrations beyond which cytotoxicity was deemed to be unacceptable. Initially, we determined the CBPI index, which is recommended as a useful measure for cytotoxicity in the CBMN assay (26,50), but in the light of reports that the index is not suitable for aneugenic agents (36) we considered the MTT assay as an alternative. We found that benzimidazole concentrations associated with more than ~40% cytotoxicity had a negative impact on data reproducibility. In contrast, the CBPI index produced data with high variability that did not correspond to the downturn in MN frequencies as benzimidazole concentrations increased (for a comparison of MTT and CBPI data, see Supplementary material, available at Mutagenesis Online). Therefore, we chose the MTT-EC₄₀ as a cut-off criterion; concentrations that produced cytotoxicity >40% were not considered for concentration–response analysis in the CBMN assay. With this exclusion criterion, the data produced for the individual benzimidazoles in the CBMN assay was of a quality suitable for regression analysis. With accepting data from concentrations up to 40% cytotoxicity, we were also well within the range of up to maximal 55±5% cytotoxicity as suggested by OECD guideline 487 (26).

Our results have profound implications for risk assessment and regulation. They provide a rationale for grouping benzimidazoles capable of inducing MN together for the purpose of cumulative risk assessment. This will safeguard against the possibility that joint effects might occur, despite each individual agent being present at levels not associated with observable effects.

Supplementary data

Supplementary material is available at Mutagenesis Online.

Funding

This work was supported by the United Kingdom Food Standards Agency (T10022) and is gratefully acknowledged.

Conflict of interest statement: None declared.