Abstract
Controlling the coupling between localized spins and itinerant electrons can lead to exotic magnetic states. A novel system featuring local magnetic moments and extended 2D electrons is the interface between LaAlO3 and SrTiO3. The magnetism of the interface, however, was observed to be insensitive to the presence of these electrons and is believed to arise solely from extrinsic sources like oxygen vacancies and strain. Here we show the existence of unconventional electronic phases in the LaAlO3/SrTiO3 system pointing to an underlying tunable coupling between itinerant electrons and localized moments. Using anisotropic magnetoresistance and anomalous Hall effect measurements in a unique in-plane configuration, we identify two distinct phases in the space of carrier density and magnetic field. At high densities and fields, the electronic system is strongly polarized and shows a response, which is highly anisotropic along the crystalline directions. Surprisingly, below a density-dependent critical field, the polarization and anisotropy vanish whereas the resistivity sharply rises. The unprecedented vanishing of the easy axes below a critical field is in sharp contrast with other coupled magnetic systems and indicates strong coupling with the moments that depends on the symmetry of the itinerant electrons. The observed interplay between the two phases indicates the nature of magnetism at the LaAlO3/SrTiO3 interface as both having an intrinsic origin and being tunable.
Keywords: oxide interfaces, local moments, magnetotransport, Kondo effect, multi-orbital physics
The electronic system at the LaAlO3/SrTiO3 (LAO/STO) interface (1) has shown an intriguing combination of superconductivity (2, 3), spin–orbit coupling (4, 5), and most recently, magnetism (6–13). An especially fascinating feature of this system is the existence of localized magnetic moments (14, 15) in proximity with itinerant d electrons (16–21) resulting in interesting coexistence phenomena (7–10). An unresolved issue central to a microscopic understanding of these properties is whether the electrons and moments interact with each other. It was shown that the itinerant electrons can be gate-tuned through a Lifshitz transition (22), where they change from populating light 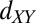 bands with a circular Fermi surface to occupying also heavy
bands with a circular Fermi surface to occupying also heavy 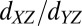 bands with highly elongated elliptical Fermi surfaces oriented along crystalline axes. The latter bands can have preferred axes for anisotropy along crystalline directions (21). Preferred crystalline directionality may also arise due to the localized magnetic moments, because they too originate from d orbitals localized on individual Ti atoms. Therefore, signatures of if and how the moments couple to the electrons will be embedded in the spatial character of the ground states of the LAO/STO system.
bands with highly elongated elliptical Fermi surfaces oriented along crystalline axes. The latter bands can have preferred axes for anisotropy along crystalline directions (21). Preferred crystalline directionality may also arise due to the localized magnetic moments, because they too originate from d orbitals localized on individual Ti atoms. Therefore, signatures of if and how the moments couple to the electrons will be embedded in the spatial character of the ground states of the LAO/STO system.
Measurements of anisotropic magnetoresistance (23) (AMR) in a rotating in-plane magnetic field are a powerful tool to determine these symmetries. Previous AMR measurements in this system have addressed the effects of surface terraces (24), possible magnetic ordering (25), and prominent Rashba spin–orbit interactions (26). Magnetic ordering in STO-based systems is also inferred from the anomalous Hall effect (AHE) in a perpendicular field (27). The interpretation of both AMR and AHE measurements at the LAO/STO interface, however, is complicated by a competing effect. On one hand, AMR measurements can be overwhelmed by orbital effects due to the slightest perpendicular field (25). Moreover, the multiband nature of conduction at the LAO/STO interface induces a nonlinear Hall effect, thus mimicking the AHE even without any magnetization present (22, 28). On the other hand, direct scanning superconducting quantum interference device (29) and torque magnetometry (10) measurements show that the magnetization lies in-plane, suggesting one probe for signatures of the interaction between the moments and the electrons in this specific geometry. In this work we use AMR with a high degree of alignment of the field to lie purely in the interfacial plane, in conjunction with measurements of AHE in the unconventional planar configuration, to probe the symmetries and polarization in this system. In the space of magnetic field and electron density we observe two distinct phases: The first is characterized by a weak noncrystalline AMR (where the AMR induced by the field does not depend on its direction with respect to the crystal axes), a normal Hall behavior, and a large longitudinal resistivity. The second region shows strong crystalline AMR (where the AMR depends on the orientation of the field with respect to the crystal axes), large AHE indicative of strong polarization, and a huge drop in longitudinal resistivity (4, 25). The transition between these regions occurs at a density-dependent critical field that diverges at the Lifshitz transition (where the shape of the Fermi surface changes from circular to elliptical as the chemical potential crosses into the 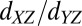 bands), demonstrating the crucial role played by itinerant electrons in the observed phases. This unusual behavior cannot be explained by considering only the intrinsic energy bands or scattering by magnetic moments, but is shown to naturally follow from a model wherein both these components are correlated via strong coupling between them that changes sign depending on whether the electrons are of
bands), demonstrating the crucial role played by itinerant electrons in the observed phases. This unusual behavior cannot be explained by considering only the intrinsic energy bands or scattering by magnetic moments, but is shown to naturally follow from a model wherein both these components are correlated via strong coupling between them that changes sign depending on whether the electrons are of 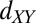 or
or 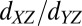 character.
character.
We observed similar behavior in two independent samples with 6 and 10 unit cells (uc) of LAO. Data from the first sample is presented in detail below (see SI Text, section 6 for sample growth and processing details). The longitudinal and transverse resistivities (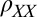 and
and 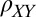 ) were measured using Hall bars while rotating the sample in a magnetic field applied in the plane of the interface (Fig. 1A) at temperatures of T = 2 K. Special care has been taken to minimize the wobble in our rotation apparatus, because the small wobble of standard cryogenic rotators
) were measured using Hall bars while rotating the sample in a magnetic field applied in the plane of the interface (Fig. 1A) at temperatures of T = 2 K. Special care has been taken to minimize the wobble in our rotation apparatus, because the small wobble of standard cryogenic rotators  produces a spurious perpendicular field component that oscillates in sync with the angle of the field in the plane. With
produces a spurious perpendicular field component that oscillates in sync with the angle of the field in the plane. With 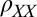 in LAO/STO being extremely sensitive to even small perpendicular fields (25), such wobble induces spurious
in LAO/STO being extremely sensitive to even small perpendicular fields (25), such wobble induces spurious 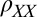 modulations that overwhelm the intrinsic in-plane field modulations that we wish to measure. To eliminate this artifact we constructed an especially low-wobble rotator apparatus (
modulations that overwhelm the intrinsic in-plane field modulations that we wish to measure. To eliminate this artifact we constructed an especially low-wobble rotator apparatus ( ) based on an Attocube piezo rotator (ANR200), and have taken special care to mount the sample on it with parallelism
) based on an Attocube piezo rotator (ANR200), and have taken special care to mount the sample on it with parallelism . The results reported in this paper are therefore free of the spurious artifacts due to perpendicular fields.
. The results reported in this paper are therefore free of the spurious artifacts due to perpendicular fields.
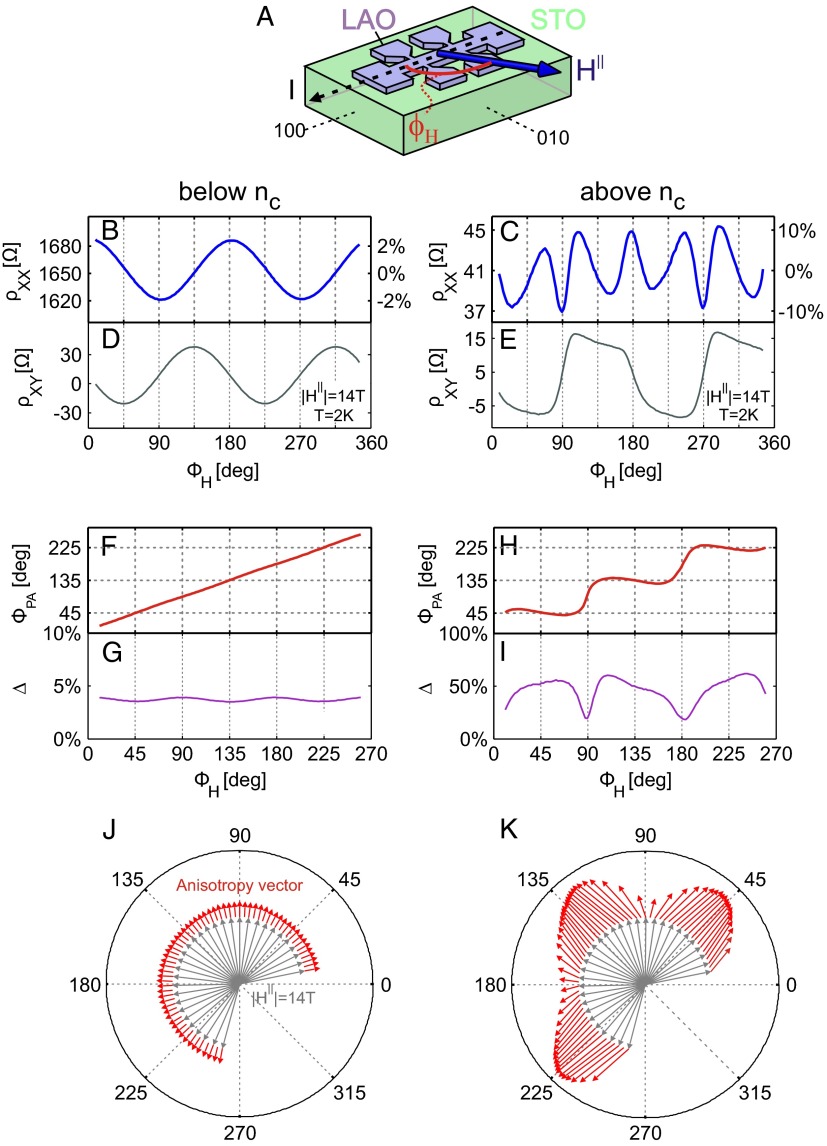
Fig. 1.
AMR measurements below and above the Lifshitz critical density, 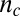 . (A) Hall bar along the (100) crystallographic direction in LAO/STO used for measuring the transport with in-plane magnetic field
. (A) Hall bar along the (100) crystallographic direction in LAO/STO used for measuring the transport with in-plane magnetic field 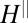 , oriented at various angles
, oriented at various angles 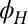 , with respect to the current direction. (B and D) Measured longitudinal resistivity
, with respect to the current direction. (B and D) Measured longitudinal resistivity 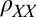 and transverse resistivity
and transverse resistivity 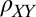 for
for 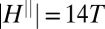 as a function of
as a function of 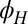 , at a gate voltage of
, at a gate voltage of 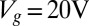 , corresponding to a total carrier density
, corresponding to a total carrier density 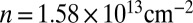 , just below the Lifshitz transition density in this sample (22),
, just below the Lifshitz transition density in this sample (22), 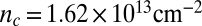 . (C and E) Similar measurements for
. (C and E) Similar measurements for 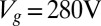 , corresponding to a total density
, corresponding to a total density 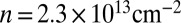 , which is above
, which is above 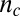 . The relative change in
. The relative change in 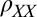 is indicated on the right y axes. (F and G) Direction of the principal axes of the anisotropy with respect to the current
is indicated on the right y axes. (F and G) Direction of the principal axes of the anisotropy with respect to the current 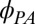 and its magnitude
and its magnitude 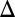 , extracted by diagonalizing the resistivity tensor from the data below
, extracted by diagonalizing the resistivity tensor from the data below 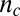 shown in B and D (text). (H and I) Similar results for the data above
shown in B and D (text). (H and I) Similar results for the data above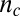 , shown in C and in E. A small offset of
, shown in C and in E. A small offset of 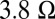 was removed from
was removed from 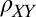 and
and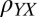 to make them symmetric around zero. Similar analysis without the offset removed also gives pinning of the anisotropy along diagonal directions (as in H) but further breaks the symmetry between the
to make them symmetric around zero. Similar analysis without the offset removed also gives pinning of the anisotropy along diagonal directions (as in H) but further breaks the symmetry between the 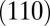 and
and 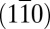 directions. (J) Anisotropy vector (red arrows) below
directions. (J) Anisotropy vector (red arrows) below 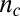 determined by
determined by 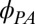 and
and 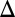 , for various in-plane angles
, for various in-plane angles 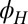 of
of 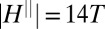 (gray arrows). Note that for clarity the magnitude of the anisotropy vector has been scaled up by a factor of 4 compared with K showing the corresponding results above
(gray arrows). Note that for clarity the magnitude of the anisotropy vector has been scaled up by a factor of 4 compared with K showing the corresponding results above 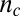 .
.
When we measure the AMR at large magnetic fields we observe a fundamental difference below and above the Lifshitz point. Fig. 1B shows the longitudinal resistivity 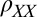 measured at a large magnetic field (
measured at a large magnetic field (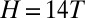 ) as a function of the angle of the field in the plane
) as a function of the angle of the field in the plane 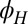 at a carrier density below the sample’s Lifshitz critical density,
at a carrier density below the sample’s Lifshitz critical density, 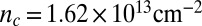 (Fig. 1B legend). At this density,
(Fig. 1B legend). At this density, 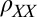 has a small modulation as a function of
has a small modulation as a function of 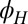 (∼4%) that accurately follows a simple
(∼4%) that accurately follows a simple 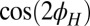 dependence (see also ref. 26). The situation is quite different above
dependence (see also ref. 26). The situation is quite different above 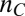 (Fig. 1C), where the modulation is much larger (∼20%), and has a complex angular dependence (25), which peaks and dips along special angular directions (
(Fig. 1C), where the modulation is much larger (∼20%), and has a complex angular dependence (25), which peaks and dips along special angular directions (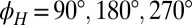 ), besides subsidiary features at intermediate angles.
), besides subsidiary features at intermediate angles.
We also measure a surprisingly large off-diagonal resistivity, 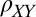 . Below
. Below 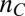 ,
, 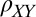 shows a simple dependence on
shows a simple dependence on 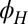 (Fig. 1D), similar to
(Fig. 1D), similar to 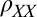 , but shifted by 45° [
, but shifted by 45° [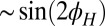 ] with almost identical peak-to-peak modulation (∼60 Ω). Above
] with almost identical peak-to-peak modulation (∼60 Ω). Above 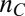 (Fig. 1E),
(Fig. 1E), 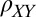 modulations become square-wave–like with values comparable even to the average value of
modulations become square-wave–like with values comparable even to the average value of 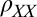 , suggesting that these two quantities should be considered on equal footing. Note that
, suggesting that these two quantities should be considered on equal footing. Note that 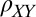 shown here is not related to a Hall effect: First, it is measured with precisely in-plane field and second, whereas the Hall effect
shown here is not related to a Hall effect: First, it is measured with precisely in-plane field and second, whereas the Hall effect 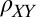 must be antisymmetric in magnetic field and under exchange of the spatial coordinates
must be antisymmetric in magnetic field and under exchange of the spatial coordinates 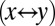 , the measured
, the measured 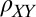 is symmetric in both.
is symmetric in both.
The observed symmetric 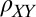 is in fact a direct signature of the anisotropy in this system. A 2D anisotropic system is fully characterized by a 2 × 2 resistivity tensor with principal axes along two orthogonal directions in the plane, along which the resistivity assumes its highest
is in fact a direct signature of the anisotropy in this system. A 2D anisotropic system is fully characterized by a 2 × 2 resistivity tensor with principal axes along two orthogonal directions in the plane, along which the resistivity assumes its highest 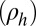 and lowest
and lowest 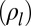 values (23). For a general angle between the direction of the current and that of the principal axis
values (23). For a general angle between the direction of the current and that of the principal axis 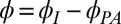 , the full resistivity tensor reads
, the full resistivity tensor reads
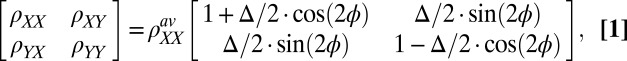 |
where 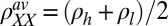 is the angle-averaged longitudinal resistivity, and
is the angle-averaged longitudinal resistivity, and 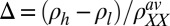 is the relative magnitude of the anisotropy. Clearly,
is the relative magnitude of the anisotropy. Clearly, 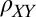 is nonzero only if there is anisotropy present, i.e.,
is nonzero only if there is anisotropy present, i.e., 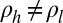 .
.
Below 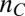 , the data (Fig. 1 B and D) correspond to an anisotropy whose principal axis is determined solely by the direction of
, the data (Fig. 1 B and D) correspond to an anisotropy whose principal axis is determined solely by the direction of 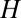 (i.e.,
(i.e., 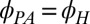 ), hence we term this a noncrystalline anisotropy. In this case, Eq. 1 reduces to simple cosine and sine dependencies:
), hence we term this a noncrystalline anisotropy. In this case, Eq. 1 reduces to simple cosine and sine dependencies:
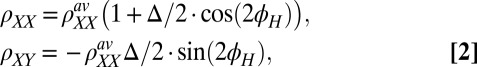 |
accurately capturing the 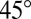 phase shift between
phase shift between 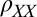 and
and 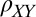 , and their identical peak-to-peak amplitudes, as seen in our data below
, and their identical peak-to-peak amplitudes, as seen in our data below 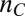 . Any angular dependence that deviates from these two simple relations (Eq. 2) necessarily implies the existence of an additional direction which, together with the direction of
. Any angular dependence that deviates from these two simple relations (Eq. 2) necessarily implies the existence of an additional direction which, together with the direction of 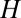 , determines the principal axis. The most natural direction is given by the underlying crystal. The
, determines the principal axis. The most natural direction is given by the underlying crystal. The 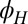 -dependence above
-dependence above 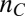 therefore corresponds to crystalline anisotropy, namely, one in which the electronic system is affected by the existence of preferred crystalline directions.
therefore corresponds to crystalline anisotropy, namely, one in which the electronic system is affected by the existence of preferred crystalline directions.
In our experiments the direction of the current is fixed along the crystal axis, but we can still determine the directionality and magnitude of the anisotropy for each 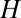 by knowing the corresponding four components of the resistivity tensor. We measure
by knowing the corresponding four components of the resistivity tensor. We measure 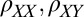 , and
, and 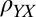 for every
for every 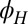 and derive
and derive 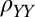 by assuming that the system has square symmetry in the plane and thus is invariant under reflection about, say
by assuming that the system has square symmetry in the plane and thus is invariant under reflection about, say 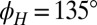 , yielding
, yielding 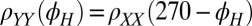 . By determining the eigenvectors and eigenvalues of the full resistivity tensor, after removing a small constant offset in
. By determining the eigenvectors and eigenvalues of the full resistivity tensor, after removing a small constant offset in 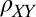 and
and 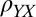 (Fig. 1 legend), we extract for every
(Fig. 1 legend), we extract for every 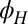 the direction of the principal axis of the anisotropy
the direction of the principal axis of the anisotropy 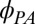 and its magnitude
and its magnitude 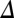 . Below
. Below 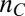 , we find that the anisotropy is along
, we find that the anisotropy is along 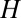 (
(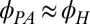 , Fig. 1F), and its magnitude is almost independent of
, Fig. 1F), and its magnitude is almost independent of 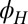 (Fig. 1G), consistent with noncrystalline symmetry. Above
(Fig. 1G), consistent with noncrystalline symmetry. Above 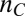 ,
, 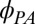 does not simply follow
does not simply follow 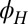 , but rather gets pinned along diagonal crystalline directions (Fig. 1H). The overall magnitude of the anisotropy (∼50%) is also 10-fold larger and depends on
, but rather gets pinned along diagonal crystalline directions (Fig. 1H). The overall magnitude of the anisotropy (∼50%) is also 10-fold larger and depends on 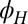 , being enhanced when the field is away from the crystalline axes (Fig. 1I). This striking change in the nature of the anisotropy across the Lifshitz point is summarized in Fig. 1 J and K.
, being enhanced when the field is away from the crystalline axes (Fig. 1I). This striking change in the nature of the anisotropy across the Lifshitz point is summarized in Fig. 1 J and K.
The change from noncrystalline to crystalline symmetry might be assigned to a change between 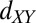 band occupation with an isotropic Fermi surface, to the population of
band occupation with an isotropic Fermi surface, to the population of 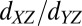 orbitals with elliptical Fermi surfaces oriented along crystalline axes. On the other hand, the large square-wave–like angular dependence of
orbitals with elliptical Fermi surfaces oriented along crystalline axes. On the other hand, the large square-wave–like angular dependence of 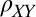 strongly resembles the anisotropy observed in semiconductors doped with magnetic impurities (30, 31). However, there are fundamental differences between the LAO/STO system and magnetic semiconductors. These materials are intentionally doped with magnetic impurities whereas the local magnetic moments in LAO/STO are uncontrolled and their nature is still poorly understood. Compared with magnetic semiconductors (32), the itinerant d electrons in the LAO/STO system have a much more anisotropic bandstructure than the itinerant holes in magnetic semiconductors which are derived from p bands, and the d electrons can have an order of magnitude larger effective mass (33) than the holes, leading to enhanced correlation effects in the LAO/STO system. Furthermore, spin–orbit splitting in the bandstructure of LAO/STO is an order of magnitude smaller than that of the magnetic semiconductors. To better understand the possible interplay of magnetic moments and conduction electrons in the LAO/STO system we measured the field dependence of its AMR. Surprisingly, for densities well above
strongly resembles the anisotropy observed in semiconductors doped with magnetic impurities (30, 31). However, there are fundamental differences between the LAO/STO system and magnetic semiconductors. These materials are intentionally doped with magnetic impurities whereas the local magnetic moments in LAO/STO are uncontrolled and their nature is still poorly understood. Compared with magnetic semiconductors (32), the itinerant d electrons in the LAO/STO system have a much more anisotropic bandstructure than the itinerant holes in magnetic semiconductors which are derived from p bands, and the d electrons can have an order of magnitude larger effective mass (33) than the holes, leading to enhanced correlation effects in the LAO/STO system. Furthermore, spin–orbit splitting in the bandstructure of LAO/STO is an order of magnitude smaller than that of the magnetic semiconductors. To better understand the possible interplay of magnetic moments and conduction electrons in the LAO/STO system we measured the field dependence of its AMR. Surprisingly, for densities well above 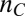 , where the
, where the 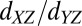 bands are expected to be populated, the AMR at a small magnetic field is perfectly sinusoidal, namely, noncrystalline. Plotting the
bands are expected to be populated, the AMR at a small magnetic field is perfectly sinusoidal, namely, noncrystalline. Plotting the 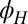 -dependence of
-dependence of 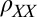 (Fig. 2A) and
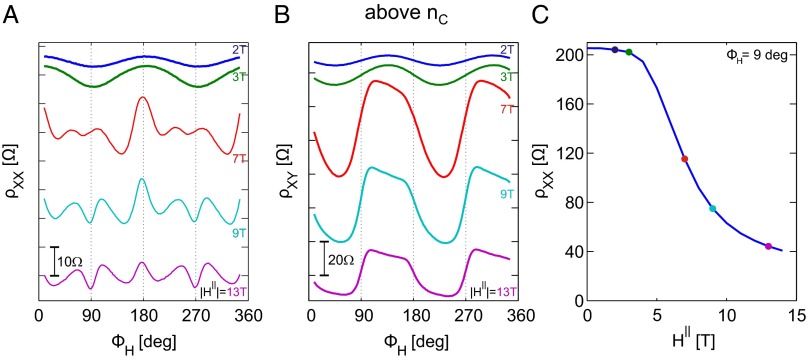
(Fig. 2A) and 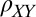 (Fig. 2B) for different magnetic fields, we see a clear transition from noncrystalline to crystalline AMR, occurring at a critical field (
(Fig. 2B) for different magnetic fields, we see a clear transition from noncrystalline to crystalline AMR, occurring at a critical field (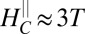 , for the carrier density in Fig. 2). Furthermore, this change in AMR is concomitant with a huge fall (25) in
, for the carrier density in Fig. 2). Furthermore, this change in AMR is concomitant with a huge fall (25) in 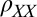 also commencing at
also commencing at 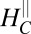 (Fig. 2C). The existence of a critical field cannot be explained by a single-particle band interpretation. It is also completely opposite to the trend seen in magnetic semiconductors where the AMR switches from crystalline to noncrystalline with increasing field (30, 31). Finally, in contrast with magnetic semiconductors where hysteresis is observed in
(Fig. 2C). The existence of a critical field cannot be explained by a single-particle band interpretation. It is also completely opposite to the trend seen in magnetic semiconductors where the AMR switches from crystalline to noncrystalline with increasing field (30, 31). Finally, in contrast with magnetic semiconductors where hysteresis is observed in 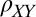 vs.
vs. 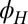 due to switching of the easy axis (30, 31), we do not observe any such hysteresis.
due to switching of the easy axis (30, 31), we do not observe any such hysteresis.
Fig. 2.
Observation of a critical field in the AMR. (A) Longitudinal resistivity 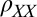 measured as a function of the angle of the field in the plane
measured as a function of the angle of the field in the plane 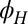 at various field strengths (indicated). The curves were shifted along the y axis for clarity (resistance scale is indicated on the bottom left). (B) Corresponding
at various field strengths (indicated). The curves were shifted along the y axis for clarity (resistance scale is indicated on the bottom left). (B) Corresponding 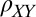 measurements. (C)
measurements. (C) 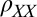 as a function of the field strength for
as a function of the field strength for 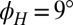 . Colored dots mark the fields corresponding to the traces in A and B.
. Colored dots mark the fields corresponding to the traces in A and B.
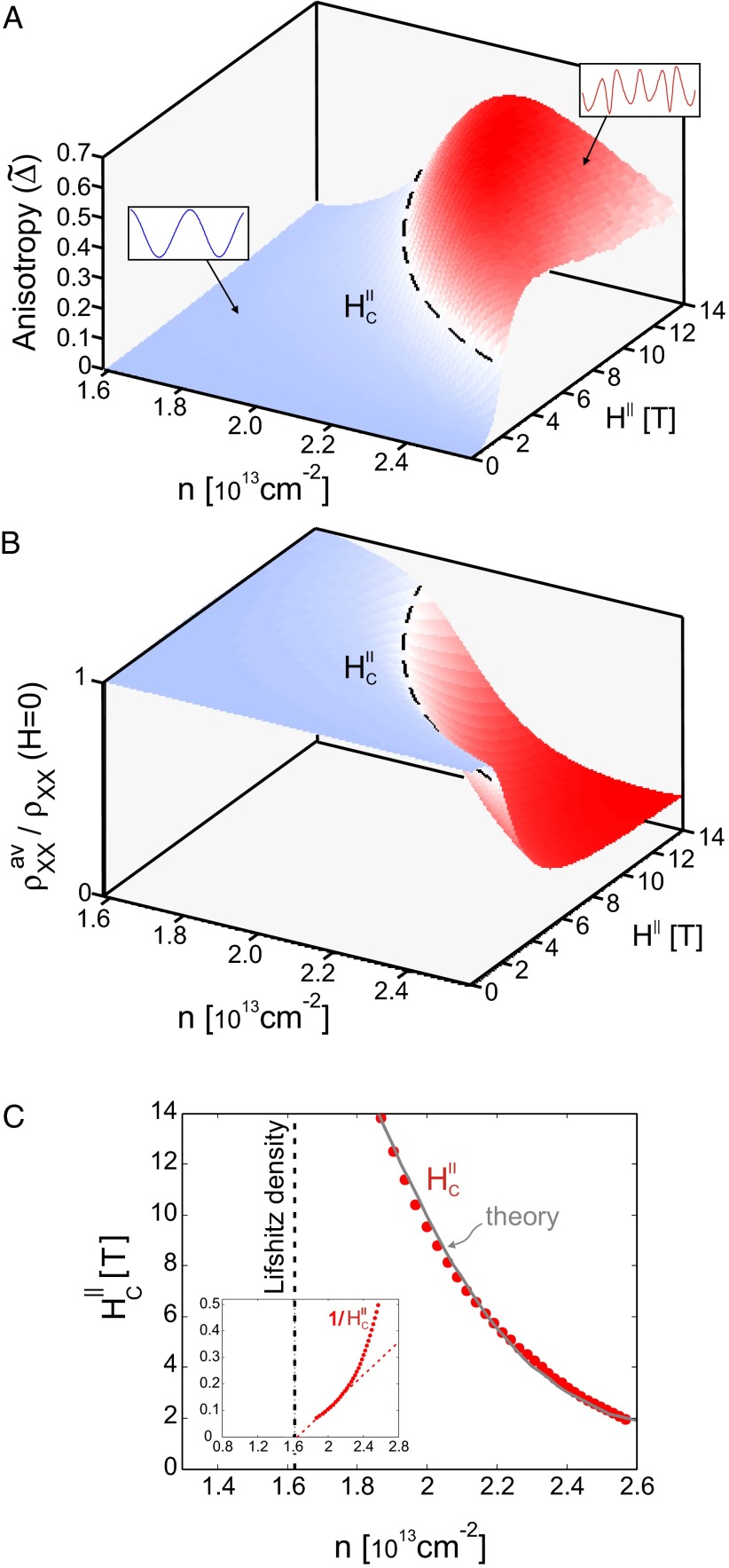
Fig. 3A maps out the magnitude of anisotropy in the space of electron density and in-plane magnetic field using the peak-to-peak modulation of 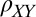 (see Fig. 3A legend for details). Two distinct regions are clearly visible in the phase diagram: one with a small anisotropy (
(see Fig. 3A legend for details). Two distinct regions are clearly visible in the phase diagram: one with a small anisotropy (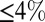 , blue) and another with a large one (∼50%, red). Within these regions, the magnitude of the anisotropy varies very little but at their boundary (dashed black line) it changes sharply. Interestingly, the
, blue) and another with a large one (∼50%, red). Within these regions, the magnitude of the anisotropy varies very little but at their boundary (dashed black line) it changes sharply. Interestingly, the 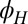 -averaged value of
-averaged value of 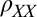 changes throughout this phase diagram in perfect synchrony with the AMR (Fig. 3B):
changes throughout this phase diagram in perfect synchrony with the AMR (Fig. 3B): 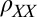 is large in the region of small anisotropy and it drops to an asymptotic value about sixfold smaller in the region of large anisotropy.
is large in the region of small anisotropy and it drops to an asymptotic value about sixfold smaller in the region of large anisotropy.
Fig. 3.
Phase diagram in the density–field plane. (A) Magnitude of the anisotropy plotted as a function of the total carrier density and magnitude of the in-plane field. Anisotropy 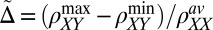 was determined by measuring for each density and field the modulation of
was determined by measuring for each density and field the modulation of 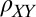 with
with 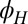 , extracting its peak-to-peak amplitude,
, extracting its peak-to-peak amplitude, 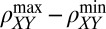 , and normalizing it by the average of
, and normalizing it by the average of 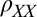 over the angle
over the angle 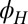 ,
, 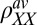 . A density-dependent critical field
. A density-dependent critical field 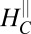 (dashed line) separates two regions of substantially different anisotropy magnitude and angular dependencies (Insets). (B) The
(dashed line) separates two regions of substantially different anisotropy magnitude and angular dependencies (Insets). (B) The 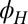 -averaged
-averaged 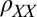 normalized to its value at
normalized to its value at 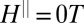 , plotted in the same density–field plane. The indicated
, plotted in the same density–field plane. The indicated 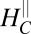 (dashed line) is taken from A. (C) Field
(dashed line) is taken from A. (C) Field 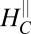 extracted from A or B plotted vs. density (solid red circles). The gray line is a fit to
extracted from A or B plotted vs. density (solid red circles). The gray line is a fit to 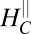 based on the theoretical model (SI Text, section 2). The vertical dashed line is the Lifshitz critical density of the sample determined from perpendicular field measurements (22). (Inset) Density dependence of
based on the theoretical model (SI Text, section 2). The vertical dashed line is the Lifshitz critical density of the sample determined from perpendicular field measurements (22). (Inset) Density dependence of 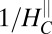 .
.
The most striking feature in the phase diagram is that the critical field 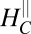 continuously rises with decreasing density (dashed black line) and appears to diverge at the Lifshitz density (Fig. 3C, Inset, see also data from more samples in Fig. S1). Indeed, below this critical density we do not observe crystalline AMR at all. Curiously, both the trend and the magnitude of
continuously rises with decreasing density (dashed black line) and appears to diverge at the Lifshitz density (Fig. 3C, Inset, see also data from more samples in Fig. S1). Indeed, below this critical density we do not observe crystalline AMR at all. Curiously, both the trend and the magnitude of 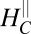 are very similar to the scaling perpendicular field we reported elsewhere (22) (Fig. S2). This empirical observation suggests that the effect of the magnetic field on transport, even in perpendicular fields, must involve spin–orbit interactions (SI Text, section 1).
are very similar to the scaling perpendicular field we reported elsewhere (22) (Fig. S2). This empirical observation suggests that the effect of the magnetic field on transport, even in perpendicular fields, must involve spin–orbit interactions (SI Text, section 1).
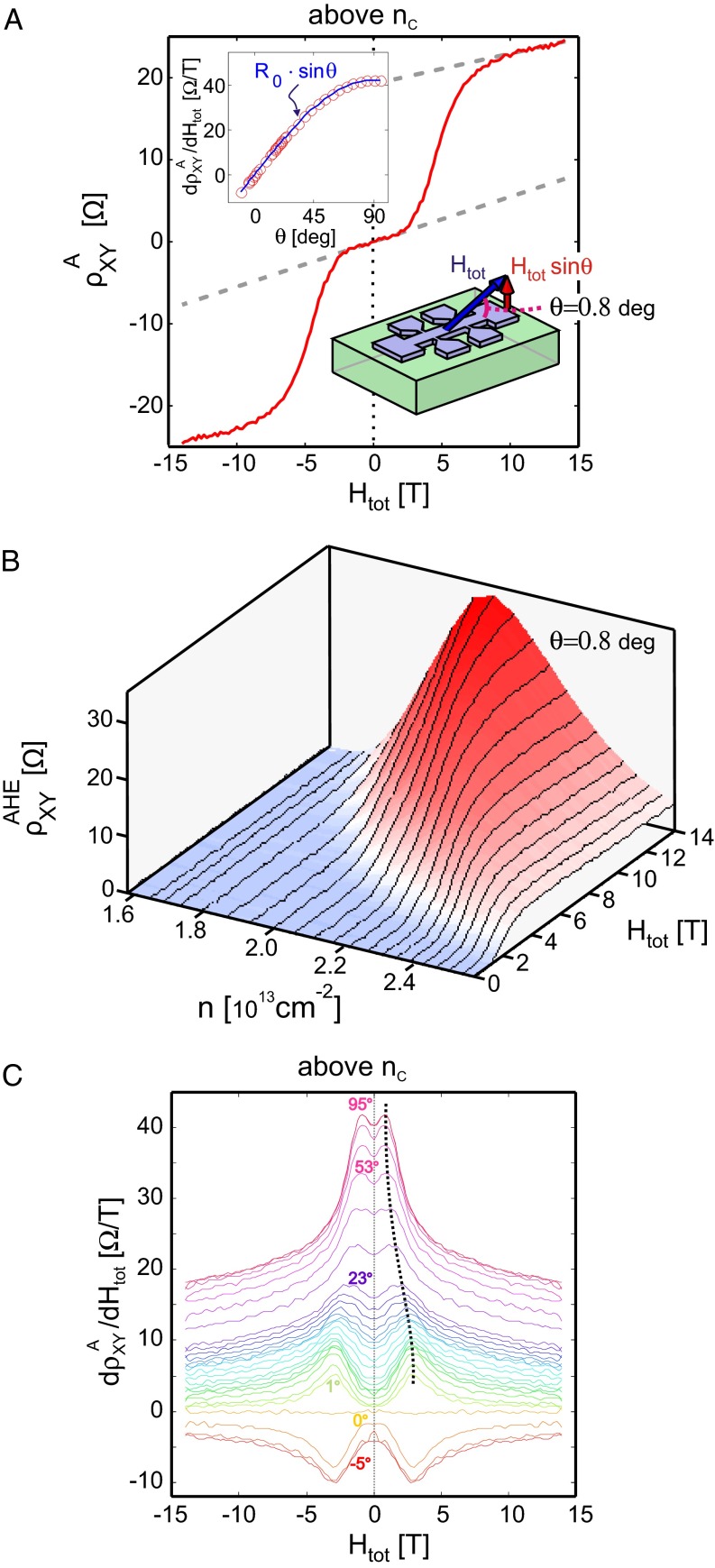
An important insight into the large-anisotropy phase is gained by tilting the field slightly out of plane (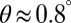 ). This is an unusual configuration to measure transport wherein along with the symmetric component we also measure an antisymmetric (Hall) component of the transverse resistivity,
). This is an unusual configuration to measure transport wherein along with the symmetric component we also measure an antisymmetric (Hall) component of the transverse resistivity, 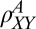 (Fig. 4A), which is strongly influenced by the dominant in-plane field. This antisymmetric component is linear at low values of the total field
(Fig. 4A), which is strongly influenced by the dominant in-plane field. This antisymmetric component is linear at low values of the total field 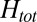 ; around
; around 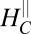 it unexpectedly rises and then finally settles, at higher fields, on a slope comparable yet slightly smaller than that at low fields. As a function of the tilt angle, the low-field slope
it unexpectedly rises and then finally settles, at higher fields, on a slope comparable yet slightly smaller than that at low fields. As a function of the tilt angle, the low-field slope 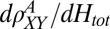 scales perfectly as
scales perfectly as 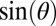 all of the way from in-plane to perpendicular field (Fig. 4A, Inset). Thus, for
all of the way from in-plane to perpendicular field (Fig. 4A, Inset). Thus, for 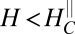 , the linear dependence of
, the linear dependence of 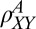 is simply due to the normal Hall effect induced by the perpendicular field component.
is simply due to the normal Hall effect induced by the perpendicular field component.
Fig. 4.
Observation of an unusual AHE above the Lifshitz transition. (A) Antisymmetric component of the transverse resistivity 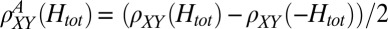 vs. the magnetic field
vs. the magnetic field 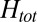 , applied at
, applied at 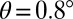 with respect to the plane of the interface. Dashed lines are guides to the eye to indicate the linear behavior at small and large fields. The low-field slope of the transverse resistance
with respect to the plane of the interface. Dashed lines are guides to the eye to indicate the linear behavior at small and large fields. The low-field slope of the transverse resistance 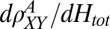 (shown by the lower dashed line in A), as a function of
(shown by the lower dashed line in A), as a function of 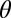 (red circles, Inset), is simply proportional to the component of the field out of the plane,
(red circles, Inset), is simply proportional to the component of the field out of the plane, 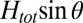 , with a coefficient
, with a coefficient 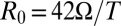 (fit shown by blue line, Inset). (B) AHE component which develops at nonzero fields vs. density and field, obtained by subtracting out the low-field normal Hall slope
(fit shown by blue line, Inset). (B) AHE component which develops at nonzero fields vs. density and field, obtained by subtracting out the low-field normal Hall slope 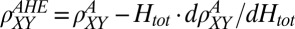 . (C) Derivative
. (C) Derivative 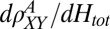 vs.
vs. 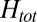 and
and 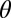 . The step in
. The step in 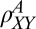 due to the AHE at
due to the AHE at 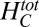 shows up as a peak in
shows up as a peak in 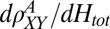 , prominent for nearly in-plane fields (
, prominent for nearly in-plane fields (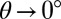 ) but surviving even when the field is applied out-of-plane (
) but surviving even when the field is applied out-of-plane (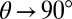 ). The dashed line follows the evolution of this peak.
). The dashed line follows the evolution of this peak.
The surprising feature in the above measurement is the sharp rise of 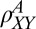 near
near 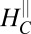 . If this was due to a normal Hall effect it would imply a rapid decrease in carrier density. However, judging from slopes of the linear regions below and above
. If this was due to a normal Hall effect it would imply a rapid decrease in carrier density. However, judging from slopes of the linear regions below and above 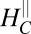 it seems that the opposite happens, the density in fact slightly increases above
it seems that the opposite happens, the density in fact slightly increases above 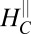 . A more plausible origin of the sharp increase in
. A more plausible origin of the sharp increase in 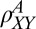 is an AHE due to the emergence of magnetization in the system. This unusual AHE is distinct from the “usual” AHE in the perpendicular configuration reported in the literature (27, 34). Compared with the usual AHE where the magnetization increase commences around zero field (35), here the effect appears suddenly around
is an AHE due to the emergence of magnetization in the system. This unusual AHE is distinct from the “usual” AHE in the perpendicular configuration reported in the literature (27, 34). Compared with the usual AHE where the magnetization increase commences around zero field (35), here the effect appears suddenly around 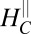 behaving as a metamagnetic transition. We note that this transition shows no evidence of a first-order discontinuity that characterizes conventional metamagnetic transitions. Furthermore, this metamagnetic AHE is revealed only by suppressing the strong orbital effects present in the perpendicular configuration which cause a nonlinear HE unrelated to magnetization in the LAO/STO system (22, 28).
behaving as a metamagnetic transition. We note that this transition shows no evidence of a first-order discontinuity that characterizes conventional metamagnetic transitions. Furthermore, this metamagnetic AHE is revealed only by suppressing the strong orbital effects present in the perpendicular configuration which cause a nonlinear HE unrelated to magnetization in the LAO/STO system (22, 28).
In Fig. 4B we isolate the metamagnetic AHE component (see Fig. 4B legend for details and Fig. S3 for the raw data) and plot it over the entire field–density phase diagram. Interestingly, this AHE appears in perfect correlation with the large crystalline anisotropy (Fig. 3A) and the huge drop in resistivity (Fig. 3B). The appearance of the metamagnetic AHE suggests that an internal spin polarization develops for 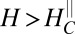 , which is converted to an anomalous Hall component through spin–orbit coupling. The magnitude of this AHE increases together with
, which is converted to an anomalous Hall component through spin–orbit coupling. The magnitude of this AHE increases together with 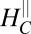 as the density is lowered toward
as the density is lowered toward 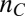 . This observation is consistent with increased spin–orbit coupling seen upon lowering the density (4), which we attributed to the orbital degeneracy at the Lifshitz transition (22).
. This observation is consistent with increased spin–orbit coupling seen upon lowering the density (4), which we attributed to the orbital degeneracy at the Lifshitz transition (22).
Finally, we show that signatures of the metamagnetic AHE exist even for perpendicular fields. In perpendicular fields, the strong normal Hall signal masks this AHE, making it harder to detect. However, this AHE is clearly visible in the derivative 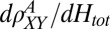 (Fig. 4C), where the step in
(Fig. 4C), where the step in 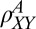 shows up as a peak that is seen for the full range of angles
shows up as a peak that is seen for the full range of angles 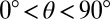 . In our previous work, we consistently observed this peak at small perpendicular fields and noted that it could not be explained by two-band physics. The data shown here identify this peak with the metamagnetic AHE, which indeed goes beyond the simple band picture.
. In our previous work, we consistently observed this peak at small perpendicular fields and noted that it could not be explained by two-band physics. The data shown here identify this peak with the metamagnetic AHE, which indeed goes beyond the simple band picture.
We now turn to discuss the nature of the two regimes observed in transport. It is tempting to associate the change in symmetry and magnitude of the AMR around 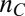 solely to the onset of the occupation of the anisotropic
solely to the onset of the occupation of the anisotropic 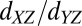 bands. However, such a single-particle picture cannot account for the pinning of AMR along diagonal directions, the square-wave behavior of
bands. However, such a single-particle picture cannot account for the pinning of AMR along diagonal directions, the square-wave behavior of 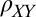 , and the existence of a critical field at which the AMR, AHE, and
, and the existence of a critical field at which the AMR, AHE, and 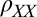 sharply change. A more plausible scenario involves also local magnetic moments whose easy axes and scattering of itinerant electrons lead to crystalline AMR. However, in such a “magnetic semiconductor picture” the crystalline AMR appears at low fields and is suppressed for fields exceeding the scale of the anisotropic magnetic couplings responsible for their easy axes (32, 36, 37), whereas we see that crystalline AMR set in only above a critical field. Thus, this model does not explain why spin polarization appears only above a critical field and why the drop of resistivity is so large.
sharply change. A more plausible scenario involves also local magnetic moments whose easy axes and scattering of itinerant electrons lead to crystalline AMR. However, in such a “magnetic semiconductor picture” the crystalline AMR appears at low fields and is suppressed for fields exceeding the scale of the anisotropic magnetic couplings responsible for their easy axes (32, 36, 37), whereas we see that crystalline AMR set in only above a critical field. Thus, this model does not explain why spin polarization appears only above a critical field and why the drop of resistivity is so large.
A possible explanation is that compared with magnetic semiconductors, here the local moments freeze into a glassy phase, resulting in a critical field for their polarization. Random spin orientation which generates strong scattering in the magnetic channel is eliminated when the moments are polarized, possibly accounting for the observed large resistivity drop. On the other hand, within this picture we cannot easily understand the strong density dependence of the critical field. In fact, magnetic domains observed in the LAO/STO system (9, 10) are density-independent (11), in contrast with the tunable polarization we find, and also vanish in patterned samples (9) such as are used in our experiments. In addition, a spin glass is expected to give rise to a hysteretic behavior in magnetic field, which we do not observe. Another appealing explanation may involve a spin-spiral phase (38), whose axis may be aligned with the magnetic field giving rise to AMR. This model too cannot, however, naturally explain the striking density dependence of the critical field.
Having excluded alternative scenarios, we show below that the best explanation for the counterintuitive behavior of the data has to involve the 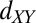 and
and 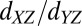 itinerant electrons having competing couplings to the local moments. The moments themselves can be considered to have
itinerant electrons having competing couplings to the local moments. The moments themselves can be considered to have 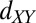 character, as suggested by current theories of their origin based on charge ordering (14) or oxygen vacancy mechanisms (39). From symmetry arguments we show (Fig. 5) that these moments couple antiferromagnetically to the
character, as suggested by current theories of their origin based on charge ordering (14) or oxygen vacancy mechanisms (39). From symmetry arguments we show (Fig. 5) that these moments couple antiferromagnetically to the 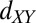 electrons and ferromagnetically to the
electrons and ferromagnetically to the 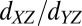 electrons (SI Text, section 3, and Fig. S4). Such couplings lead to a competition between two phases: Below
electrons (SI Text, section 3, and Fig. S4). Such couplings lead to a competition between two phases: Below 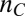 , when only the
, when only the 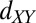 band is occupied, the moments are screened by their Kondo coupling to these electrons. Within this picture involving strong Kondo correlations between the itinerant electrons and the local moments (see also ref. 40), exceeding the critical field is responsible for breaking the Kondo singlets (41) and for the polarization of the moments. Above
band is occupied, the moments are screened by their Kondo coupling to these electrons. Within this picture involving strong Kondo correlations between the itinerant electrons and the local moments (see also ref. 40), exceeding the critical field is responsible for breaking the Kondo singlets (41) and for the polarization of the moments. Above 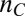 the increasing occupation of the
the increasing occupation of the 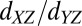 bands results in a competing ferromagnetic Hund’s coupling that leads to a continuous drop of the critical field. Comparison of the critical field computed based on this model with the measured value reproduces well the density dependence of the critical in-plane field observed in the experiment and is shown in Fig. 3C (details in SI Text, section 2, and Fig. S5). This picture provides a unified explanation for the concurrent changes observed in various transport properties across
bands results in a competing ferromagnetic Hund’s coupling that leads to a continuous drop of the critical field. Comparison of the critical field computed based on this model with the measured value reproduces well the density dependence of the critical in-plane field observed in the experiment and is shown in Fig. 3C (details in SI Text, section 2, and Fig. S5). This picture provides a unified explanation for the concurrent changes observed in various transport properties across 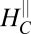 : Below
: Below 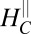 , the moments are screened and thus act as unitary scatterers leading to high resistivity, no polarization, and simple anisotropy. Above
, the moments are screened and thus act as unitary scatterers leading to high resistivity, no polarization, and simple anisotropy. Above 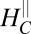 the moments get polarized and their scattering cross-section drops sharply, leading to a low resistivity polarized state with crystalline anisotropy. The easy axes of this polarized state, reflecting the anisotropy in the g factor for the coupling of the field to the moments, will eventually be overridden by intense enough fields yielding once again the original noncrystalline AMR. We note that a possible criticism of the Kondo picture is that it requires the concentration of impurities to be smaller or equal to the itinerant electron density, whereas a large concentration of paramagnetic moments was observed (9). However, the measured 1/T dependence of their susceptibility (9) suggests that the majority of moments are in fact free, and only a small fraction is coupled to the itinerant electrons. Indeed, recent experiments (42, 43) estimate them to have a significantly smaller density than that of the itinerant electrons. This lends further support to the Kondo model.
the moments get polarized and their scattering cross-section drops sharply, leading to a low resistivity polarized state with crystalline anisotropy. The easy axes of this polarized state, reflecting the anisotropy in the g factor for the coupling of the field to the moments, will eventually be overridden by intense enough fields yielding once again the original noncrystalline AMR. We note that a possible criticism of the Kondo picture is that it requires the concentration of impurities to be smaller or equal to the itinerant electron density, whereas a large concentration of paramagnetic moments was observed (9). However, the measured 1/T dependence of their susceptibility (9) suggests that the majority of moments are in fact free, and only a small fraction is coupled to the itinerant electrons. Indeed, recent experiments (42, 43) estimate them to have a significantly smaller density than that of the itinerant electrons. This lends further support to the Kondo model.
Fig. 5.
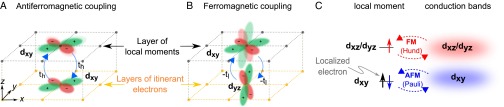
Competing magnetic couplings between t2g conduction electrons and Ti3+ local moments. In our model Ti3+ ions close to the interface form local magnetic moments of 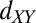 symmetry. Subsequent TiO2 layers, further away from the interface, harbor the itinerant electrons of either
symmetry. Subsequent TiO2 layers, further away from the interface, harbor the itinerant electrons of either 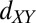 ,
, 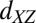 or
or 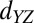 symmetry. (A) The
symmetry. (A) The 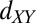 itinerant spin hops into the occupied
itinerant spin hops into the occupied 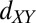 state on the local moment and back. Here the conduction and local spins must be anti-aligned due to Pauli exclusion, resulting in an overall antiferromagnetic coupling. (B) On the other hand, for the
state on the local moment and back. Here the conduction and local spins must be anti-aligned due to Pauli exclusion, resulting in an overall antiferromagnetic coupling. (B) On the other hand, for the 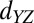 itinerant spin which hops into the unoccupied
itinerant spin which hops into the unoccupied 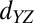 state on the moment site, a parallel alignment of spins is favored due to Hund’s coupling on the local moment site. A similar ferromagnetic coupling is also favored for the
state on the moment site, a parallel alignment of spins is favored due to Hund’s coupling on the local moment site. A similar ferromagnetic coupling is also favored for the 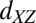 itinerant electrons. (C) A schematic diagram of the energy spectrum on the local moment site including the virtual processes giving rise to the competing magnetic couplings.
itinerant electrons. (C) A schematic diagram of the energy spectrum on the local moment site including the virtual processes giving rise to the competing magnetic couplings.
In summary, AMR and AHE measurements in a planar field configuration show that the electronic system at the LAO/STO interface transitions at a critical magnetic field between two regimes with dramatically different anisotropy, polarization, and longitudinal resistivity. The clear density dependence of the critical field means that the itinerant electrons play an important role in the formation of these phases. This is surprising because the magnetic signatures of the LAO/STO system have so far been supposed to arise only from the local moments (whose origin is still debated). Our results not only provide compelling evidence for strong coupling between the itinerant electrons and moments, modeled to be localized in 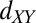 orbitals at the interface (14, 15, 39), but also shed light on the symmetry-dependent nature of this coupling. This sets the stage for studying novel effects in the interacting system of moments and electrons at the LAO/STO interface where the polarization and easy axes develop only at high fields in contrast with conventional magnetic systems. The interplay between competing magnetic couplings studied here opens prospects for tunability by a gate of magnetism at the LAO/STO interface.
orbitals at the interface (14, 15, 39), but also shed light on the symmetry-dependent nature of this coupling. This sets the stage for studying novel effects in the interacting system of moments and electrons at the LAO/STO interface where the polarization and easy axes develop only at high fields in contrast with conventional magnetic systems. The interplay between competing magnetic couplings studied here opens prospects for tunability by a gate of magnetism at the LAO/STO interface.
Supplementary Material
Acknowledgments
We acknowledge A.D. Caviglia, S. Gariglio, A. Fete, and J.-M. Triscone for samples and fruitful discussions. We benefited greatly also from discussions with E. Berg, Y. Dagan, S. Finkelstein, D. Goldhaber-Gordon, Y. Meir, Y. Oreg, D. Shahar, A. Stern, V. Venkataraman, and A. Yacoby. S.I. acknowledges the financial support from the Israel Science Foundation (ISF) Legacy Heritage, the Minerva Foundation, the European Commission Marie Curie International Reintegration Grant, and an Alon fellowship. S.I. is the incumbent of the William Z. and Eda Bess Novick Career Development Chair. E.A. acknowledges financial support from the ISF. E.A. is the incumbent of the Louis and Ida Rich Career Development Chair.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1221453110/-/DCSupplemental.
References
- 1.Ohtomo A, Hwang HY. A high-mobility electron gas at the LaAlO3/SrTiO3 heterointerface. Nature. 2004;427:423–426. doi: 10.1038/nature02308. [DOI] [PubMed] [Google Scholar]
- 2.Reyren N, et al. Superconducting interfaces between insulating oxides. Science. 2007;317:1196–1199. doi: 10.1126/science.1146006. [DOI] [PubMed] [Google Scholar]
- 3.Caviglia AD, et al. Electric field control of the LaAlO3/SrTiO3 interface ground state. Nature. 2008;456:624–627. doi: 10.1038/nature07576. [DOI] [PubMed] [Google Scholar]
- 4.Ben Shalom M, Sachs M, Rakhmilevitch D, Palevski A, Dagan Y. Tuning spin-orbit coupling and superconductivity at the SrTiO3/LaAlO3 interface: A magnetotransport study. Phys Rev Lett. 2010;104(12):126802. doi: 10.1103/PhysRevLett.104.126802. [DOI] [PubMed] [Google Scholar]
- 5.Caviglia AD, et al. Tunable Rashba spin-orbit interaction at oxide interfaces. Phys Rev Lett. 2010;104(12):126803. doi: 10.1103/PhysRevLett.104.126803. [DOI] [PubMed] [Google Scholar]
- 6.Brinkman A, et al. Magnetic effects at the interface between non-magnetic oxides. Nat Mater. 2007;6:493–496. doi: 10.1038/nmat1931. [DOI] [PubMed] [Google Scholar]
- 7.Ariando , et al. Electronic phase separation at the LaAlO₃/SrTiO₃ interface. Nat Commun. 2011;2:188. doi: 10.1038/ncomms1192. [DOI] [PubMed] [Google Scholar]
- 8.Dikin DA, et al. Coexistence of superconductivity and ferromagnetism in two dimensions. Phys Rev Lett. 2011;107(5):056802. doi: 10.1103/PhysRevLett.107.056802. [DOI] [PubMed] [Google Scholar]
- 9.Bert JA, et al. Direct imaging of the coexistence of ferromagnetism and superconductivity at the LaAlO3/SrTiO3 interface. Nat Phys. 2011;7:767–771. [Google Scholar]
- 10.Li L, Richter C, Mannhart J, Ashoori RC. Coexistence of magnetic order and two-dimensional superconductivity at LaAlO3/SrTiO3 interfaces. Nat Phys. 2011;7:762–766. [Google Scholar]
- 11.Kalisky B, et al. Critical thickness for ferromagnetism in LaAlO₃/SrTiO₃ heterostructures. Nat Commun. 2012;3:922. doi: 10.1038/ncomms1931. [DOI] [PubMed] [Google Scholar]
- 12.Pavlenko N, Kopp T, Tsymbal EY, Sawatzky GA, Mannhart J. Magnetic and superconducting phases at the LaAlO3/SrTiO3 interface: The role of interfacial Ti 3d electrons. Phys Rev B. 2012;85(2):020407(R). [Google Scholar]
- 13.Moetakef P, et al. Carrier-controlled ferromagnetism in SrTiO3. Phys Rev X. 2012;2(2):021014. [Google Scholar]
- 14.Pentcheva R, Pickett WE. Charge localization or itineracy at LaAlO3/SrTiO3 interfaces: Hole polarons, oxygen vacancies, and mobile electrons. Phys Rev B. 2006;74(3):035112. [Google Scholar]
- 15.Michaeli K, Potter AC, Lee PA. Superconducting and ferromagnetic phases in SrTiO3/LaAlO3 oxide interface structures: Possibility of finite momentum pairing. Phys Rev Lett. 2012;108(11):117003. doi: 10.1103/PhysRevLett.108.117003. [DOI] [PubMed] [Google Scholar]
- 16.Popović ZS, Satpathy S, Martin RM. Origin of the two-dimensional electron gas carrier density at the LaAlO3 on SrTiO3 interface. Phys Rev Lett. 2008;101(25):256801. doi: 10.1103/PhysRevLett.101.256801. [DOI] [PubMed] [Google Scholar]
- 17.Cen C, et al. Nanoscale control of an interfacial metal-insulator transition at room temperature. Nat Mater. 2008;7:298–302. doi: 10.1038/nmat2136. [DOI] [PubMed] [Google Scholar]
- 18.Delugas P, et al. Spontaneous 2-dimensional carrier confinement at the n-type SrTiO3/LaAlO3 interface. Phys Rev Lett. 2011;106(16):166807. doi: 10.1103/PhysRevLett.106.166807. [DOI] [PubMed] [Google Scholar]
- 19.Liao YC, Kopp T, Richter C, Rosch A, Mannhart J. Metal-insulator transition of the LaAlO3-SrTiO3 interface electron system. Phys Rev B. 2011;83(7):075402. [Google Scholar]
- 20.Khalsa G, MacDonald AH. Theory of the SrTiO3 surface state two-dimensional electron gas. Phys Rev B. 2012;86(12):125121. [Google Scholar]
- 21.Fischer MH, Raghu S, Kim E. Spin-orbit coupling in LaAlO3/SrTiO3 interfaces: magnetism and orbital ordering. New J Phys. 2013;15(2):023022. [Google Scholar]
- 22.Joshua A, Pecker S, Ruhman J, Altman E, Ilani S. A universal critical density underlying the physics of electrons at the LaAlO₃/SrTiO₃ interface. Nat Commun. 2012;3:1129. doi: 10.1038/ncomms2116. [DOI] [PubMed] [Google Scholar]
- 23.Rushforth AW, et al. Anisotropic magnetoresistance components in (Ga,Mn)As. Phys Rev Lett. 2007;99(14):147207. doi: 10.1103/PhysRevLett.99.147207. [DOI] [PubMed] [Google Scholar]
- 24.van Zalk M, Brinkman A, Hilgenkamp H. Conductance anisotropy and linear magnetoresistance in La(2 - x)Sr(x)CuO4 thin films. J Phys Condens Matter. 2011;23(20):205602. doi: 10.1088/0953-8984/23/20/205602. [DOI] [PubMed] [Google Scholar]
- 25.Ben Shalom M, et al. Anisotropic magnetotransport at the SrTiO3/LaAlO3 interface. Phys Rev B. 2009;80(14):140403(R). [Google Scholar]
- 26.Fête A, Gariglio S, Caviglia AD, Triscone J-M, Gabay M. Rashba induced magnetoconductance oscillations in the LaAlO3-SrTiO3 heterostructure. Phys Rev B. 2012;86(20):201105(R). [Google Scholar]
- 27.Lee Y, et al. Phase diagram of electrostatically doped SrTiO3. Phys Rev Lett. 2011;106(13):136809. doi: 10.1103/PhysRevLett.106.136809. [DOI] [PubMed] [Google Scholar]
- 28.Lerer S, Ben Shalom M, Deutscher G, Dagan Y. Low-temperature dependence of the thermomagnetic transport properties of the SrTiO3/LaAlO3 interface. Phys Rev B. 2011;84(7):075423. [Google Scholar]
- 29.Bert JA, et al. Gate-tuned superfluid density at the superconducting LaAlO3/SrTiO3 interface. Phys Rev B. 2012;86(6):060503(R). [Google Scholar]
- 30.Tang HX, Kawakami RK, Awschalom DD, Roukes ML. Giant planar Hall effect in epitaxial (Ga,Mn)as devices. Phys Rev Lett. 2003;90(10):107201. doi: 10.1103/PhysRevLett.90.107201. [DOI] [PubMed] [Google Scholar]
- 31.Bason Y, Klein L, Yau J-B, Hong X, Ahn CH. Giant planar Hall effect in colossal magnetoresistive La0.84Sr0.16MnO3 thin films. Appl Phys Lett. 2004;84(14):2593. [Google Scholar]
- 32.Dietl T, Ohno H, Matsukura F, Cibert J, Ferrand D. Zener model description of ferromagnetism in zinc-blende magnetic semiconductors. Science. 2000;287:1019–1022. doi: 10.1126/science.287.5455.1019. [DOI] [PubMed] [Google Scholar]
- 33.Santander-Syro AF, et al. Two-dimensional electron gas with universal subbands at the surface of SrTiO3. Nature. 2011;469:189–193. doi: 10.1038/nature09720. [DOI] [PubMed] [Google Scholar]
- 34.Seri S, Klein L. Antisymmetric magnetoresistance of the SrTiO3/LaAlO3 interface. Phys Rev B. 2009;80(18):180410(R). [Google Scholar]
- 35.Nagaosa N, Onoda S, MacDonald AH, Ong NP. Anomalous Hall effect. Rev Mod Phys. 2010;82(2):1539–1592. [Google Scholar]
- 36.Trushin M, et al. Anisotropic magnetoresistance of spin-orbit coupled carriers scattered from polarized magnetic impurities. Phys Rev B. 2009;80(13):134405. [Google Scholar]
- 37.Timm C, MacDonald A. Anisotropic exchange interactions in III-V diluted magnetic semiconductors. Phys Rev B. 2005;71(15):155206. [Google Scholar]
- 38.Banerjee S, Erten O, Randeria M. 2013. Ferromagnetic exchange, spin-orbit coupling and spiral magnetism at the LaAlO3/SrTiO3 interface. arXiv:13033275v2.
- 39.Pavlenko N, Kopp T, Tsymbal EY, Mannhart J, Sawatzky GA. Oxygen vacancies at titanate interfaces: Two-dimensional magnetism and orbital reconstruction. Phys Rev B. 2012;86(6):064431. [Google Scholar]
- 40.Fidkowski L, Jiang H, Lutchyn RM, Nayak C. Magnetic and superconducting ordering at LaAlO3/SrTiO3 interfaces. Phys Rev B. 2013;87(1):014436. [Google Scholar]
- 41.Lee M, Williams JR, Zhang S, Frisbie CD, Goldhaber-Gordon D. Electrolyte gate-controlled Kondo effect in SrTiO3. Phys Rev Lett. 2011;107(25):256601. doi: 10.1103/PhysRevLett.107.256601. [DOI] [PubMed] [Google Scholar]
- 42.Fitzsimmons MR, et al. Upper limit to magnetism in LaAlO3/SrTiO3 heterostructures. Phys Rev Lett. 2011;107(21):217201. doi: 10.1103/PhysRevLett.107.217201. [DOI] [PubMed] [Google Scholar]
- 43.Salman Z, et al. Nature of weak magnetism in SrTiO3/LaAlO3 multilayers. Phys Rev Lett. 2012;109(25):257207. doi: 10.1103/PhysRevLett.109.257207. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.