Driven Metadynamics: Reconstructing Equilibrium Free Energies from Driven Adaptive-Bias Simulations

Abstract

We present a novel free-energy calculation method that constructively integrates two distinct classes of nonequilibrium sampling techniques, namely, driven (e.g., steered molecular dynamics) and adaptive-bias (e.g., metadynamics) methods. By employing nonequilibrium work relations, we design a biasing protocol with an explicitly time- and history-dependent bias that uses on-the-fly work measurements to gradually flatten the free-energy surface. The asymptotic convergence of the method is discussed, and several relations are derived for free-energy reconstruction and error estimation. Isomerization reaction of an atomistic polyproline peptide model is used to numerically illustrate the superior efficiency and faster convergence of the method compared with its adaptive-bias and driven components in isolation.

Computational investigation of complex systems such as biological macromolecules is often hampered by the need to sample rare events, that is, crossing high free-energy barriers, which cannot be accomplished by standard sampling techniques such as conventional room-temperature molecular dynamics (MD) simulations. To enhance the sampling of such rare barrier-crossing events, one may use a biasing potential. Using a time-independent bias (e.g., umbrella sampling technique¹) has the advantage of keeping the system in equilibrium; however, designing a “practical” biasing potential may require a priori knowledge of the free-energy landscape, particularly when this landscape is rugged. On the other hand, simulations generated by time-dependent biasing protocols require a nonequilibrium treatment. In the context of MD simulations using (i) a history-dependent “adaptive-bias” force/potential and (ii) an external (explicitly time-dependent) “driving” force/potential are two well-known²⁻⁶ nonequilibrium schemes to enhance the sampling and estimate the free energies.

In adaptive-bias methods, for example, local elevation,² coarse MD,⁷ adaptively biased MD,⁸ adaptive accelerated MD,⁹ metadynamics,^3,4 and λ-metadynamics,¹⁰ the simulation history is used to enhance the sampling by discouraging the system to return to the already visited regions of the phase space. Potential is adaptively biased until converged and used to reconstruct the free energy landscape. A nonequilibrium driven scheme (e.g., steered MD¹¹) can be used to induce a transition by steering the system along a reaction coordinate that otherwise may not be sampled in an unbiased simulation. By measuring the work along these nonequilibrium trajectories, one may estimate the free-energy differences or reconstruct the free-energy profiles using nonequilibrium work relations.^5,6,12 These relations can be also used to estimate relative reaction rates¹³ and generally any equilibrium path-ensemble averages.¹⁴

Adaptive-bias and driven MD schemes are powerful methods whose applications have been extended to biomolecular simulations;¹⁵⁻¹⁹ however, both methods have practical limitations. Steered MD is often associated with a slow convergence if used for free-energy calculations (because the dissipative work is often large and many iterations may be needed to capture a small one, that is, the dominant term in work-based free energy estimators⁵) but it can be used to explore the transition paths, at least qualitatively, an advantage over metadynamics, in which the system starting from one end of the configuration space (the reactant) may take a long time to visit the other end (the product). One cannot estimate the free-energy difference of the two end states until both states have been sufficiently sampled.

By incorporating an explicitly time-dependent scheme into a history-dependent scheme, we introduce a novel driven adaptive-bias scheme, termed driven metadynamics (d-MetaD), that takes advantage of both its driven and adaptive-bias components and is advantageous over both components in isolation. d-MetaD has an advantage over conventional metadynamics in that it ensures the exploration of the transition pathway (from one end to the other) in the early stages of the simulation and gradually improves the estimate of the free energies almost uniformly along the reaction coordinate. d-MetaD also has an advantage over the conventional steered MD in that the effective free-energy surface gradually becomes smooth and flat such that the system can move along the reaction coordinate with progressively less amount of work.

We use nonequilibrium work relations not only in analyzing the trajectories but also more importantly in constructing the biasing protocol that is per se a novel use of nonequilibrium work relations. The approach presented here expands the scope of nonequilibrium work relations into a new realm, namely, designing work-based biasing protocols. We introduce a general framework to combine an adaptive-bias scheme with a nonequilibrium driven scheme by reweighting the kernel memory (used in most adaptive-bias schemes) using on-the-fly nonequilibrium work measurements. Although, for the sake of clarity, we discuss a particular algorithm here, this approach can be easily generalized to combine any methods from the adaptive-bias class with any from the nonequilibrium driven class, resulting in “hybrid” protocols that could be more efficient than their adaptive-bias and driven components in isolation.

Consider a system described by coordinates r and momenta p and governed by the Hamiltonian H(r,p) with a canonical equilibrium distribution at temperature 1/β. Suppose that x(r) is a holonomic coordinate (e.g., representing a slow mode) and F(x) is the free energy associated with x; that is, p(x) = e^–βF(x) describes the distribution of x in equilibrium:

1

In the adaptive-bias scheme, one adds a history-dependent biasing potential to the system such as:

2

in which K(Δx) is a kernel function (e.g., (1/((2π)^1/2σ))exp(−(1/2)(Δx/σ)²) and σ is the kernel width), U⁰(x) is an arbitrary function, and ω(x, t) is an energy rate that is ω₀e^{–β′U_a(x,t)} in the well-tempered metadynamics²⁰ (1/β′ is an arbitrary temperature) that reduces to a constant ω₀ in the β′ → 0 limit (i.e., conventional metadynamics³). Kernel K(Δx) approximates a smooth δ function, and ⟨K(x – x^t)⟩_acan be thought of as an approximation of the probability density p(x, t) (⟨.⟩_a is the average over an ensemble of adaptive-bias trajectories). It has been shown^21,20 that ⟨U_a(x,t → ∞)⟩_a ≈ U_a^s(x) + u(t) (u(t) is an additive constant at each t) in which U_a(x) equals −F(x) and −(1 + (β′/β))⁻¹F(x) in the conventional²¹ and well-tempered²⁰ metadynamics, respectively. The steady-state distribution of x can be described by p^s(x) ∝ e^{–β(F(x)+U_as(x))}. U⁰(x) could be a flat function or an initial guess for U_a^s(x) to speed up the convergence process, but U_a(x) does not depend on it. Here we focus only on these variations, although the generalization of our method to other variations of the adaptive-bias scheme is straightforward.

In the nonequilibrium driven scheme, one adds a driving potential U_d(x, t) to the system that is often harmonic, U_d(x, t) = (1/2)k(x – X(t))², in which X(t) is a protocol controlling the target (e.g., X(t) = x₀ + (x₁ – x₀)(t/T); x₀ and x₁ may represent the reactant and product or the two ends of the x space to be explored). Although the system might remain far from equilibrium, one can reconstruct the unbiased distribution⁶ according to:

3

in which Δw^t = w^t – U_d(x^t,t), w^t = ∫₀^t dt′(∂/∂t′)U_d(x^t′,t′) is the total work up to time t, and ⟨.⟩_d denotes an average over the ensemble of driven trajectories (driven ensemble). The initial configurations are prepared in an equilibrium state perturbed by the biasing potential U_d(x,0). The e^–βΔwt term can be thought of as a weighting factor to connect the driven ensemble to the equilibrium ensemble.²²

To combine the two schemes described above, here we introduce a driven adaptive-bias scheme that adds an adaptive (U_a(x, t)) and a driving (U_d(x, t)) potential to the Hamiltonian. We use an iterative approach in which an independent simulation is performed from time t = 0 to T in the nth iteration (n = 1, 2, ...), biased by the potential U_d(x, t) + U_aⁿ(x, t) in which U_d(x, t) = (k/2)(x – X(t))² for all n and:

4

in which Δw^t = w^t – U_d(x, t) similar to relation 3 and Uⁿ(x) = U_aⁿ(x, T) for n > 0 and U⁰(x) is an initial guess. ω(x, t) is the same as its nondriven (conventional or well-tempered) counterpart. Note that the “weighted” average ⟨K(x – x^t)e^–βΔwt⟩_da approximates ⟨δ(x – x^t)e^–βΔwt⟩_da (⟨.⟩_da denotes an average over the driven adaptive-bias ensemble). We also note that for practical reasons the e^–βΔwt factor in relation 4 can be also reweighted using “weight functions” similar to those used for the free-energy estimation from conventional pulling experiments. (See ref (23).) To simplify the discussions we leave the e^–βΔwt factor as is (i.e., using the “constant weight” protocol²³). However, the “pulling potential” or “occupancy” weights are generally more appropriate for practical/numerical reasons.²³

In general, the initial configuration for iteration n needs to be equilibrated under the biasing potential U_aⁿ(x,0) + U_d(x,0). However, preparing the initial configurations can be simplified if we assume that the driven term is considerably greater than the adaptive term, (guaranteed in the stiff-spring limit²⁴) such that the equilibrium distribution for the perturbed system is more or less independent of the adaptive term. Because the driven potential is the same for all n, the initial configurations for all iterations can be also prepared simply by using the U_d(x,0) bias.

If we iterate the protocol described above until the adaptive term of the biasing potential converges to U_a^s(x), the system can be considered as a nonequilibrium driven system governed by the Hamiltonian H(r,p) + U_a(x) + U_d(x, t). One can show that U_a^s(x) of a driven metadynamics protocol is the same as that of its nondriven counterpart (see Supporting Information), for example, U_a(x) = −(1 + (β′/β))⁻¹F(x) for the well-tempered variation and U_a^s(x) = −F(x) for the β′ → 0 limit.

Although U_a^s(x) can be used directly to estimate the free energy of the system, one might alternatively measure work along the trajectories once the U_a(x, t) has nearly converged (i.e., U_a(x, t) ≈ U_a(x) + u(t)). If the driving process at time t = 0 starts from the state X(0), governed by the Hamiltonian H(r,p) + U_a(x, t) + U_d(x,0), then the distribution of states associated with x in the steady state, governed by H(r,p) + U_a(x, t), may be represented by p^s(x) ∝ exp(−βF^s(x)), and F^s(x) = F(x) + U_a^s(x) may be estimated from the nonequilibrium work relation:

5

In principle, this estimator will result in an accurate description of free energy along x by using the work measurements at any given t, assuming enough sampling for all x. In practice, one might combine multiple time slices (by storing x^t and w^t at different t) to estimate the free energy, for instance, by employing the Hummer–Szabo estimator method:⁶

6

that can be solved self-consistently along with f(t):

7

Ideally, in the case of conventional variation of metadynamics, F^s(x) is flat because U_a^s(x) = −F(x). In practice, F^s(x) estimated from the relation above is not flat and can be used to correct the free energy estimated from biasing potential F_U(x) = −U_a(x) via F_W = F_U(x) + F^s(x); F_W is the corrected free energy, and ε(x) = |F_W(x) – F_U(x)| = |F^s(x)| is an error estimate associated with it. This can be thought of as the driven counterpart of “umbrella corrections”⁸ in conventional adaptive-bias simulations. In the case of well-tempered metadynamics, F^s(x) = −(β′/β)F(x), so the above work-based estimate of F^s(x) can be used as an alternative method for estimating F(x) as −(β/β′)F^s(x). However, choosing a β′ considerably smaller than β may result in a larger error than direct use of U_a^s(x). In this case, F^s(x) can be used to correct F_U(x) = −(1 + (β/β′))U_a(x) and estimate the error similar to the case of β′ = 0 discussed above. The corrected free energy would be F_W(x) = −U_a^s(x) + F^s(x), associated with an error ε(x) = |F_W(x) – F_U(x)| = |F^s(x) + (β′/β)U_a(x)|. One can estimate F^s(x) and U_a^s(x) from work measurements and converged potential, respectively.

We note that one may derive other work-based free-energy estimators for driven adaptive-bias trajectories similar to those used in nonadaptive variations of nonequilibrium driven systems. More importantly, a bidirectional driving protocol is known to result in a faster convergence than a unidirectional one by combining the forward and reverse driven ensembles. d-MetaD as introduced here can be used in a bidirectional scheme such that the forward direction X_F(t) varies from X_F(0) to X_F(T) and in the reverse direction X_R(t) = X_F(T – t). One can iteratively run the forward and reverse simulations in an alternating manner with an initial equilibration for each simulation. Note that the two protocols (forward and reverse) are associated with the same U_a^s(x). Deriving bidirectional free-energy estimators¹² is also straightforward.

d-MetaD in ω₀ → 0 and k → 0 limits describes the nonadaptive driven MD and nondriven metadynamics, respectively. Interestingly, because of its iterative nature, at the end of any iteration n, d-MetaD can be easily turned into metadynamics or steered MD by removing its driven or adaptive component, respectively. The biasing potential Uⁿ(x) will be the initial guess for the metadynamics simulations and a time-independent bias for the steered MD simulations. By removing both driven and adaptive components and using Uⁿ(x) as a time-independent bias, d-MetaD can be turned into a conventional biased equilibrium simulation.

Finally, our method can be generalized to reconstruct multidimensional free-energy surfaces. While this generalization is straightforward in adaptive-bias simulations, the driving protocol is easier to implement using a 1-D reaction coordinate, x. One can use the driving potential U_d(x, t) and construct a multidimensional adaptive potential U_aⁿ(x,y,t) described by:

8

in which y represents collective variables other than x and K′ is a multidimensional kernel function.

To test the d-MetaD method and compare its performance to that of metadynamics and steered MD, we carried out several sets of MD simulations, investigating the cis–trans isomerization reaction in polyproline peptides. Proline is unique among the common amino acids in that its side chain is cyclized onto the backbone nitrogen atom, restricting its conformational space to a narrow region in the Ramachandran map.²⁵ However, of the 20 common amino acids, only proline is “comfortable” in both cis- and trans-isomer conformations. Polyproline is known to form helical structures with two well-characterized conformations: (i) a right-handed polyproline type-I helix (PPI) with all residues in the cis-isomer conformation (all-cis conformer) and (ii) a left-handed polyproline type II helix (PPII) with all residues in the trans-isomer conformation (all-trans conformer) (see Figure 1). Traditionally, an oligomeric proline peptide in aqueous solution is seen as a “rigid rod”; however, recent experimental²⁶ and computational¹⁶ studies suggest a considerable heterogeneity in the conformational space of polyproline with subpopulations of distinct end-to-end distances due to the existence of distinct cis–trans patterns.

Figure 1.

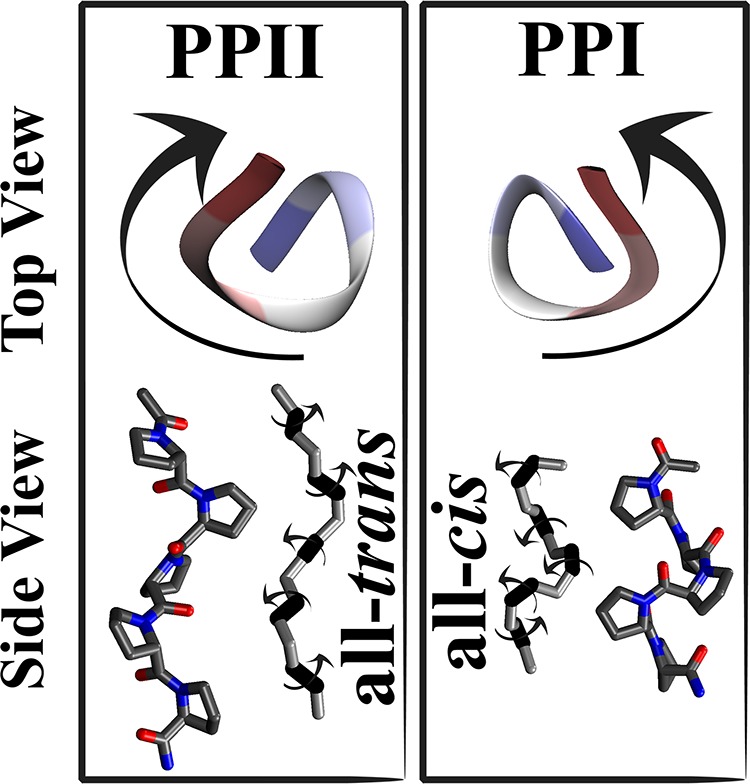
Top (ribbon representation) and side (licorice representation) views of the right-handed PPI and the left-handed PPII conformations of a pentameric polyproline peptide. The backbone atoms involved in the definition of ω dihedral angles are shown; the prolyl peptide bonds are highlighted.

From a computational point of view, the characterization of proline-rich peptides is rather difficult because the cis–trans isomerization reaction is an extremely slow process (i.e., tens to hundreds of seconds at room temperature²⁷). This reaction has recently been studied using conventional adaptive-bias and driven MD schemes both on pure polyproline^16,28 and on other proline-containing peptides.²⁹⁻³¹ Free-energy landscapes of polyproline peptides in different environments including water, propanol, and hexane, obtained using a variation of conventional metadynamics (i.e., adaptively biased MD⁸) reveal that water and hexane favor PPII while propanol favors PPI.^16,28 Here we investigate the PPII ↔ PPI reaction of polyproline peptides (Ac-(Pro)_n-NH₂) of various length (1 ≤ n ≤ 5) in an implicit water environment (using the Generalized Born model³²). NAMD 2.8³³ simulation package was used to perform the simulations using the CHARMM27 force field³⁴ with a 1 fs time step at a constant temperature of 300 K (using a Langevin thermostat with a damping coefficient of 1/ps) with no cutoff for nonbonded interactions.

To study the cis–trans isomerization, we define a collective variable Ω = ∑_i=1ⁿcos²(ω_i/2) based on the backbone dihedral angles {ω_i} that roughly measures the number of cis-prolyl bonds in an n-mer peptide; ω_i is around 0 (±180) for cis (trans) isomers, and thus cos²(ω_i/2) falls around 1 (0). Ω ranges between 0 and n (representing all-trans PPII and all-cis PPI conformers, respectively) and is associated with a free energy F(Ω) with n + 1 minima and n maxima centered around integer and half-integer values of Ω, respectively.^16,28 We note that generally designing a 1D collective variable (e.g., Ω) that reflects all of the slow conformational changes of the system (e.g., cis/trans isomerization of all prolyl bonds) is a key factor in free-energy calculation methods such as metadynamics, steered MD, and inherently d-MetaD.

A bidirectional steered MD (SMD) scheme was used to steer the system along Ω between 0 and n with a constant speed of Ω̇ = 10/ns and a harmonic constant of 100 kcal/mol, iterated 10 000 times in each direction with a total simulation time of 2, 4, 6, 8, and 10 μs for monomeric, dimeric, trimeric, tetrameric, and pentameric polyproline peptides, respectively. A metadynamics MD (MetaD) scheme described by a Gaussian kernel of width σ = 0.2 and a well-tempered rate of (ω₀ = 0.1 (kcal/mol) ps^–1, (β/β′) = 10), and a flat initial bias U⁰(Ω) = 0 was used to reconstruct F(Ω) using a total simulation time matching that of the SMD runs for each peptide. Finally, a d-MetaD scheme combining the SMD and MetaD methods with the exact same parameters described above was used to reconstruct F(Ω). The e^–βΔwt factor was simplified to e^–βwt, mimicking the pulling potential weight protocol²³ (i.e., e^–βΔwt was multiplied by the unnormalized pulling potential weight e^{–βU_d(Ω,t)}).

In the SMD and d-MetaD simulations, Ω and work values were stored every 1 ps and used at the end of each bidirectional iteration to reconstruct the free-energy profiles F(Ω) and F^s(Ω) (for SMD and d-MetaD, respectively) using the self-consistent bidirectional implementation¹² of the Hummer–Szabo method.⁶ For the MetaD and d-MetaD simulations, the instantaneous adaptive potential U_a(Ω,t) was used as an estimate for U_a^s(Ω) to reconstruct F_U(Ω) at time t. The corrected d-MetaD free energy F_W(Ω) was constructed using U_a(Ω) and F^s(Ω), as approximated from U_a(Ω,t) and work measurements, respectively.

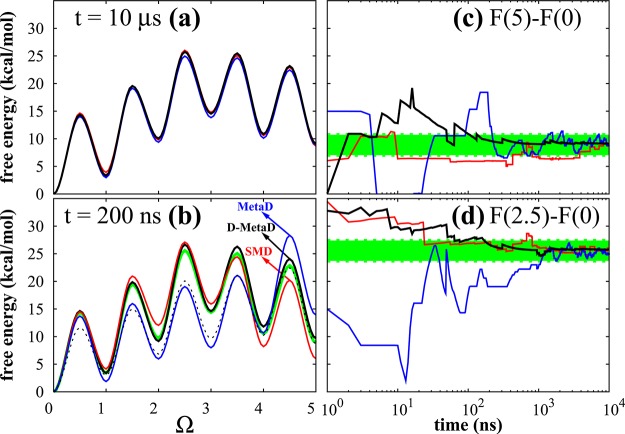
Figure 2 summarizes our results for the pentameric peptide; SMD, MetaD, and d-MetaD methods give very similar estimates for F(Ω) eventually (Figure 2a), but the d-MetaD simulations converge considerably faster than the others (see Figure 2b). To illustrate the convergence behavior, we plot two physically relevant quantities in Figure 2c,d: the free-energy difference between the PPI and the PPII conformers, F(5) – F(0), and between the transition state and the global minimum, F(2.5) – F(0). Figure 2 generally reveals that d-MetaD constructively combines both MetaD and SMD methods to speed up the convergence time. To quantify the convergence time associated with a method m (SMD, MetadD, or d-MetaD), we define it as the smallest time τ_c in which |F_t^m(Ω) – F_c(Ω)| < ε for all Ω and for all t > τ_c; F_t(Ω) is the free energy estimated from the method m at time t, F_c(Ω) is our final free-energy estimate averaged over the results of all three methods, and ε is an error parameter adjusted to ensure the meaningfulness of the analysis statistically. Figure 3 shows τ_c associated with all three methods for all of the peptides studied using ε = 2 kcal/mol. τ_c is expected to grow exponentially by the peptide length n (that somewhat represents the complexity of the problem) due to the exponential growth of the number of states; considering the cis-trans isomerization only, we precisely have 2ⁿ conformers for an n-mer peptide. Interestingly, the τ_c growth constant of d-MetaD method is considerably smaller than that of MetaD and SMD such that at least in this particular case and within this range (1 ≤ n ≤ 5) τ_c grows almost linearly by n.

Figure 2.

(a,b) Free-energy profile F(Ω) (offset by F(0)) of a pentameric polyproline peptide obtained from SMD (red), MetaD (blue), and d-MetaD (black) simulations at t = 10 000 and 200 ns, respectively. In panel b, the dashed curve is the d-MetaD results without the work-based corrections (i.e., F_U(Ω)) and the green curve is the average of the three converged curves in (a) (i.e., F_c(Ω)). (c,d) Evolution of ΔF = F(5) – F(0) and ΔF = F(2.5) – F(0) by time as estimated from SMD (red), MetaD (blue), and d-MetaD (black). The green regions represent F_c(Ω) ± ε with ε = 2 kcal/mol.

Figure 3.

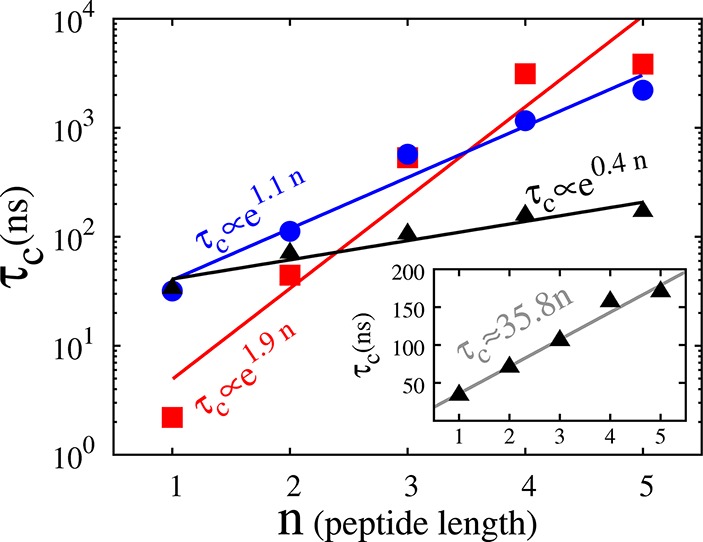
Convergence time τ_c associated with SMD (red squares), MetaD (blue circles), and d-MetaD (black triangles) simulations performed on polyproline peptides of length n = 1, ..., 5. The data were fitted using a τ_c = re^αn function (linear fitting in the (log τ_c,n) space). Inset: τ_c associated with the d-MetaD method fitted using a linear function τ_c = an.

In summary, we have introduced a nonequilibrium free-energy method with an explicitly time- and history-dependent biasing protocol. d-MetaD is a novel scheme that takes advantage of both driven and adaptive-bias schemes. Unlike the nondriven metadynamics, d-MetaD samples the reaction path almost uniformly from the very beginning, and unlike the nonadaptive driven MD, the amount of work along the reaction path decreases gradually. The history-dependent term of the potential on average behaves similarly to that of conventional adaptive-bias systems and once converged can be used to reconstruct the free-energy profile whose error can be estimated using nonequilibrium work measurements.

Supporting Information Available

Discussion on the asymptotic convergence of d-MetaD method is provided. The converged free-energy profiles of n-meric polyproline peptides (n = 1,...,4) are shown in Figure S1 (similar to Figure 2a). These profiles estimated at in earlier stage are given in Figure S2 (similar to Figure 2b). This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States