Discrete - Continuous Duality of Protein Structure Space

Summary

Recently, the nature of protein structure space has been widely discussed in the literature. The traditional discrete view of protein universe as a set of separate folds has been criticized in the light of growing evidence that almost any arrangement of secondary structures is possible and the whole protein space can be traversed through a path of similar structures. Here we argue that the discrete and continuous descriptions are not mutually exclusive, but complementary: the space is largely discrete in evolutionary sense, but continuous geometrically when purely structural similarities are quantified. Evolutionary connections are mainly confined to separate structural prototypes corresponding to folds as islands of structural stability, with few remaining traceable links between the islands. However, for a geometric similarity measure, it is usually possible to find a reasonable cutoff that yields paths connecting any two structures through intermediates.

Introduction

In the history of every branch of science, the duality of concepts emerges when two seemingly contradicting descriptions appear to be applicable to the same object. The most prominent example is the wave-particle duality, which stems from the 17th century debate about the nature of light. Is light transferred by particles or waves? In the 20^th century, the wave-particle duality became a foundation of quantum mechanics [1], leading to multiple practical applications, e.g. electron microscopy. In protein science, similar, but maybe less fundamental dualities have been a matter of debate for years. Does folding proceed along a pathway [2,3] or down a funnel [4]? After quite heated arguments at the end of the last century, the consensus view is that within a funnel, there typically are several semi-discrete preferred pathways of folding towards native structure [5,6].

Presently, the question about the nature of protein structure space is being widely discussed in the literature. Is protein world a set of discrete structure groups or a continuum? The traditional picture of distinct structural folds is being criticized and evidence is emerging in support of the continuous view. According to this view, almost any arrangement of secondary structures is possible and the whole protein space can be traversed through a path of similar structures. Here we would like to argue that the apparent contradiction between these two views represents yet another duality, and each of these views has its place in the context of protein evolution and structural properties.

Protein folds as discrete entities

An essential point lacking in most discussions about the discreteness of the structure space is the actual space definition. The properties of any space are mathematically defined by the way of measuring distance between objects. It is quite possible that under some metrics the structures are distributed continuously, whereas other metrics produce discrete grouping. The "old" discrete view was originally developed regardless of any metric, under the influence of amazing structural similarities revealed by earliest structures determined by X-ray crystallography. Myoglobin [7] and hemoglobin [8], the first solved protein structures, were unexpectedly similar in spite of differences in their sequence (Fig 1A). This similarity was later followed by chymotrypsin [9] and trypsin [10], as well as an array of TIM beta/alpha barrels, doubly-wound Rossmann folds and immunoglobulin-like beta sandwiches [11] (Fig 1). These structures were unique and recognizable, thus even in the absence of quantitative measure it was easy to attribute a new structure to one of these types, called "folds". The concept of fold was introduced largely to mark this discreteness, so that a newly determined structure could either be assigned to one of these clearly defined types or be used to establish a "new" fold and serve as a prototype for many more structures to come. While the number of available protein structures was not large, this concept was holding up very well, as most structures easily matched these commonly observed prototypes.

Figure 1. Abundant structural folds and their evolution.

(A) Top left: globin-like fold (PDB ID 3SDH); top right: Rossmann-like fold (PDB ID 2JFG); bottom left: trypsin-like fold (PDB ID 1AQ7); bottom right: immunoglobulin-like fold (PDB ID 1VCA). All structures are rainbow colored from blue (N-terminus) to red (C-terminus), except for the protein of Rossmann-like fold where N-terminal and C-terminal halves are colored orange and green, respectively, with the connecting helix in red. (B) TIM-barrel homologs with deviations from canonical (βα)₈ fold. Top left: canonical TIM-barrel (PDB ID 7TIM); top right: enolase (PDB ID 1P43); bottom left: phosphoesterase or PHP domain (PDB ID 1M65); bottom right: luciferase (PDB ID 1NFP). N-terminal and C-terminal halves are shown in light orange and light green, respectively. β-Strands are sequentially numbered from 1 to 8, with asterisks denoting incomplete barrels. In enolase (top right) and luciferase (bottom right), β-hairpins deviating from the canonical parallel topology are colored red.

As an example of such prototype, a significant fraction of metabolic enzymes belong to the TIM-barrel fold [12,13]. Most of these families did not show significant sequence similarity to each other and thus surprised X-ray crystallographers who were finding TIM-barrels among various enzyme families. For some time, the abundance and sequence divergence of TIM-barrels convinced researchers that these families originated independently and thus represented evolutionary convergence to a stable protein structure [14]. Today, with the recent availability of a plethora of genomic sequences and the development of powerful profile-based methods for sequence similarity search [15–17], many researchers argue for a different scenario: most of these TIM-barrel families originated as a result of gene duplications and build-up of metabolic pathways [12,13,18,19]. Interesting experimental examples that received extensive attention [20,21] suggest the origin of a TIM-barrel family as an internal duplication of a 4-beta-alpha-unit.

Another prominent structural prototype is the doubly-wound fold discovered by Michael Rossmann [22] and present in approximately a quarter of all protein structures (Fig1A). This easily recognizable motif minimally consists of two right-handed βαβ units that are placed centrosymmetrically to form hydrogen bonds between the first strands of the units. An alpha-helix typically connects the units together. Most of these Rossmann-like proteins develop active site at the same location between the two units, and have a detectable sequence profile similarity [16,23–27], suggesting evolutionary relationship. TIM-barrel and Rossmann-like proteins exemplify discrete and identifiable folds that are likely the products of extensive divergent evolution of sequences locked within a certain structure type that is not easy to change.

Fold evolution

However, with more structures being determined, different research groups discovered proteins that exhibited features of a certain well-known fold but were still quite different from the prototype in other features. Not stepping far from the TIM-barrel example, nonfluorescent flavoprotein from Photobacterium [28] is a notable case of a clear TIM-barrel homolog with incomplete structure, missing a couple of elements compared to the symmetric (βα)₈ prototype core (Fig 1B). Among other interesting evolutionary changes of TIM-barrels are anti-parallel βα unit in the otherwise parallel (βα)₈ structure of enolase [29], and further examples of barrel deterioration, such as the loss of one (βα) unit in the PHP domain forming a closed (βα)7 barrel [30,31]. By geometric criteria, all these deviant structures are clearly different from the (βα)₈ prototype and thus deserve to be placed in a fold of their own; however, for most of them there is a solid evidence of homology to the complete (βα)8 barrel. This evidence suggests that the deviant proteins originated from the prototype through various degrees of deterioration. These and other examples lead to several important observations. First, "discreteness" and "uniqueness" of a structural fold are not always clear-cut concepts. Second, discreteness holds at the evolutionary level: in spite of the structural divergence, these proteins are most likely related to each other, and none of the structures cross into a completely different well-populated fold, e.g. Rossmann fold. Finally, although these deviants might be viewed as representatives of unique folds of their own, they constitute a very small fraction of families: the majority of TIM-barrel families are complete (βα)₈ structures.

The ultimate discreteness of the protein space stems from evolutionary process constrained by thermodynamic stability of the structure. According to Lupas et al. [32], protein folds are islands of stability in the ocean of the overwhelming majority of unstable conformations. Only a miniscule fraction of possible amino acid sequences can achieve stability of the folded chain. The majority of mutations move conformation away from the island and drown the protein in the ocean, being therefore eliminated by selection. This stabilizing selection enforces evolution within folds and makes movements between folds very uncommon [32,33]. We agree that in the evolutionary sense, structure space is largely discrete, with only a handful of examples of structural changes between well-defined folds populated by many sequences [34–37]. Perhaps the most prominent case of such change observed in nature is the remarkable "jump" from the all-beta SH3-like fold to an alpha-helical hairpin in the two homologous domains of NusG protein [38]. Protein design experiments suggest that such jumps are possible even after a handful of point mutations (introduced simultaneously, not in an evolutionarily meaningful step-wise way): Orban and coworkers [39] were recently able to achieve as high as 95% sequence identity between two small domains of clearly different alpha/beta and three-helical bundle folds. However, such transformations between two well-populated folds are rare [34,36]: the majority of observed fold connections represent the emergence of a unique, single-family fold from an abundant major fold. Although these "tunnels" between folds are not particularly common, it does not mean that they are evolutionarily unimportant. As in paleontological records, intermediate forms, quite rarely found, shed light on evolutionary mechanisms of protein structure change. It is quite possible to imagine that present-day proteins evolved by combination of marginally stable smaller supersecondary structural elements [40,41]. Duplications, insertions and deletions of these elements likely dominated early events in fold evolution, when fold islands were being formed in a shallow ocean of marginally stable early proteins [42], possibly stabilized by RNA. Fold changes we observe today are likely to be particularly well-preserved remnants of these processes.

Continuous space of structural similarity

A growing number of publications [43–48] suggests that the structure space is continuous, with many paths from one fold to another. In fact, using certain similarity metrics, such as TM-score [49], it is possible to find a relatively stringent cutoff that provides the connection between virtually any two structures through no more than 7 steps [48]. Skolnick and coworkers [48] used the particular cutoff value of 0.4, which corresponds to ~40% alignment coverage between the two structures. Thus some of the intermediate steps involve partial alignments with just 40% coverage of the protein core in otherwise quite different structures: for example, an alignment covering two helices in a sandwich of four strands and two helices. The existence of partial similarity between many different folds, termed "gregariousness", has been known for quite some time [43].

Interesting in silico experiments with artificial structures by Skolnick and colleagues [48] suggest that such continuity is not a consequence of evolution, as it could be reproduced in a set of randomly generated structures with simple requirements for hydrogen bonding and compactness. Thus the observed continuity of the structure space is likely to be caused not by evolutionary divergence but by folding rules involving hydrogen-bond formation, parallel or antiparallel arrangement of secondary structural elements to form stable packing, etc.

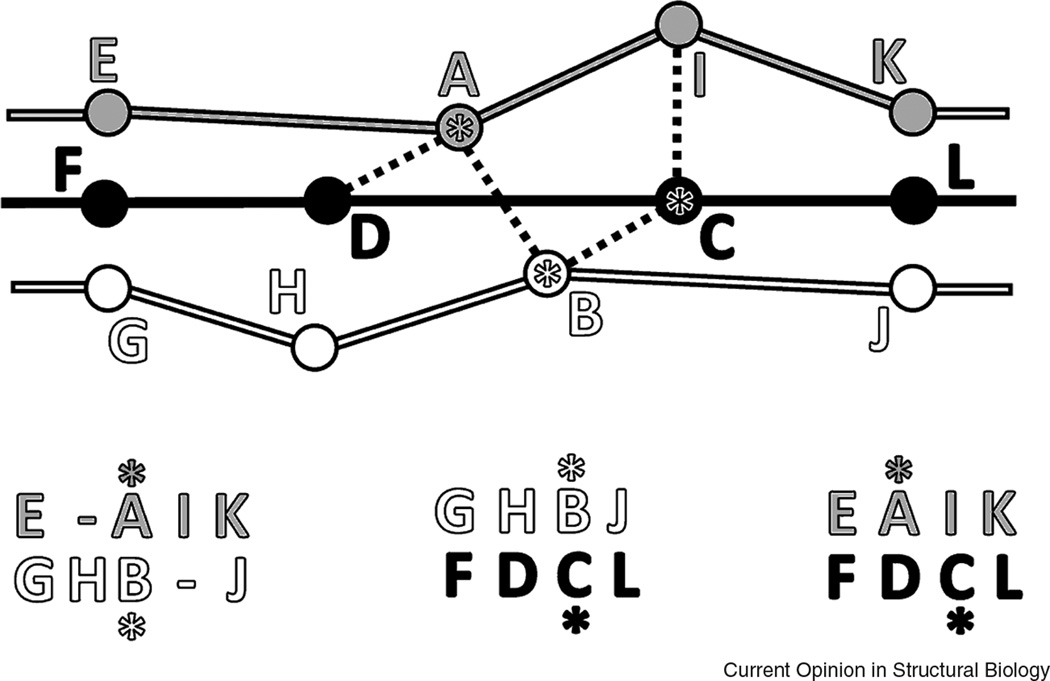
Correspondingly, a continuous path of intermediate structural similarities does not necessarily involve transitivity, an essential property of homology connections. Homology is transitive: if protein A is homologous to B and protein B is homologous to C, then proteins A and C are also homologous, i.e. originated from a common ancestor. This property provides a very powerful method of deducing remote protein relationships and is widely used both in sequence and structure analysis [50–52]. Indeed, if the similarity between proteins A and C is low and homology cannot be directly inferred, the presence of an intermediate protein B with clear similarity to both suggests that A and C are likely homologs. In contrast, geometry is not transitive: if protein B shows local geometric similarities to proteins to A and C, this does not necessarily mean the similarity between A and C: these proteins could be very different and might not pass the structural score cutoff. The geometric structure-based alignments are not transitive either. As illustrated on Fig 2, if residue A is aligned to residue B in structures 1 and 2, and residue B is aligned to C in structures 2 and 3, it does not imply that a structure-based alignment of 1 and 3 should align residues A and C. Evolutionarily meaningful alignment is transitive, however.

Figure 2. Non-transitivity of structure-based alignments.

Unlike homology-based alignments, alignments guided purely by structure geometry do not necessarily have the property of transitivity. Structure-based alignment of fragments of three protein chains (colored white, black, and gray, with circles representing C-alpha atoms) is schematically shown. Residues are aligned based on the criterion of minimal distance (marked by dotted lines). In this example, pairwise alignments between residues A, B, and C (marked with asterisks both in the schema and in the alignments below) are not transitive: A is aligned to B and B to C, yet A and C are not aligned.

Regardless of the exact metric defining protein structure space, it seems that the distribution of individual structures in this space has a highly uneven probability density function: there are “mountains” with higher density of points and “valleys” with low density (Fig 3). When only a small sample of protein structures was solved, these structures (assuming semi-random sampling) were more likely to concentrate around mountains, thus creating an apparently discrete picture. With more structures determined, points from the valleys are sampled, thus connecting the mountains [50] and making the distribution look more continuous. This recent extension of structure sample leads researchers to quite rightful reassessment of the nature of protein space. It is equally important to note, however, that even with the refined sampling mountains remain mountains: the majority of structures still concentrates around the originally discovered high-density regions. Taking an analogy with the space of dipeptide conformations, the organization of protein structure space is somewhat similar to Ramachandran plot, which clearly represents a continuous space but has a few discrete maxima of preferred conformations.

Figure 3. Distribution of protein structures in a space based on geometric similarities.

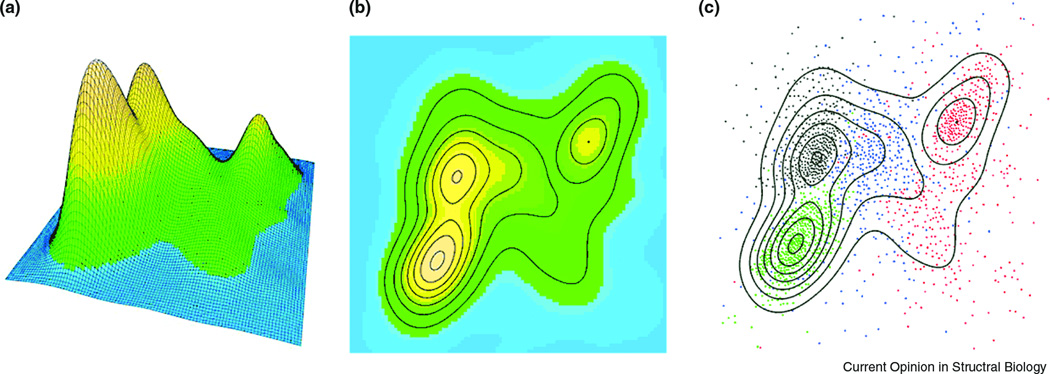
2000 SCOP domains [56] are selected (428 all α, 546 all β, 561 α+β, and 465 α/β) and clustered by CLANS [71] according to structure similarity measured by DALI Z-scores [54]. The probability density is estimated with the kernel method by MASS R statistical package and shown as (A) 3D perspective and (B) contour plot, color-coded from blue to orange. In panel (C), the actual points for SCOP domains are overlaid on the plot, with all α, all β, α+β, and α/β classes marked black, red, blue and green, respectively. Density peaks correspond to α/β, all α, and all β classes, with domains of α+β class scattered more diffusely.

The value of discrete and continuous descriptions

A few recent publications [45,46,48] have questioned the value of the term ”fold”, suggesting that grouping structures into non-overlapping folds might miss important functional connections between different folds. Such connections are easily revealed in "overlapping" classification, where structural neighbors for each query are found by an automatic method and ordered according to a certain statistic [44–46,48,53]. We suggest that both approaches can be useful, consistent with the discreteness-continuum duality.

Since many commonly seen structures have very distinct core geometry, grouping them according to this evolutionary conserved substructure is very instructive at least for categorization and visualization. For instance, such categories as “TIM-barrel”, “Rossmann fold”, “OB-fold” “IG beta sandwich” are extremely useful for both structure and function prediction regardless of evolutionary connections [54–57]. Other “folds” may be more obscure, unique to a particular evolutionary group, and lack a clear-cut definition. As a major particular example, proteins of different alpha-helical folds are often distinguished by gradual changes in the angles of helix packing, rather than discrete topological differences. For these cases continuous description may be more appropriate. For the purposes of function prediction, it is certainly important to study the ranked lists of structure similarities regardless of fold assignments [44,53,58–60], since placement and conformation of functional sites can be shared by structures of different folds [46,61]. For instance, despite the discretely distinct geometries of TIM-barrels and Rossmann folds (circular roll vs. doubly-wound), their active sites develop in similar locations between beta-strands and alpha-helices and can be frequently aligned, with alignments showing predictive power.

The term fold, as being applied today, is intrinsic to the SCOP classification [56]. SCOP is a widely recognized resource and a manual standard for remote evolutionary connections between proteins. According to SCOP, proteins are classified within the same fold if they have the same major secondary structural elements in the same mutual orientation and with the same connectivity (topology). For most proteins, a thorough comparative analysis can identify recurrent structural units representing one of the major folds. However, application of fold definition can occasionally cause confusion due to subjectivity in deciding which secondary structure elements are major [62]. In many cases fold definition remains an empirical approximate "art", and even experts disagree on fold assignments for many proteins [47,62,63]. The additional classification criteria are often rather loose and are frequently based not only on structural data, but also on evolutionary and functional considerations. In attempt to alleviate the major differences between main classification systems, the term “metafold” was suggested by Dagget and coworkers [62] and recently elaborated by Lupas and coworkers [64].

Since SCOP is often used as standard of fold definition, its subjectivity and the use of non-structural criteria may be, at least in part, a source of recent argument about the applicability of the term fold. For instance, whereas all TIM-barrels are assembled in one SCOP fold, doubly-wound Rossmann-like structures are dispersed among at least 77 folds, mostly annotated by protein function. Direct application of automatic methods to SCOP will easily reveal such inconsistency [47,62,63,65] and cause criticism of such fold arrangement [45].

The current heavy use of the term “New fold” by experimentalists deserves a special comment. Most structural biologists prefer their newly determined protein structures to be “new”, with the ultimate novelty being frequently perceived as having a “new fold”. Taking this approach, it is easy to overlook functionally and evolutionarily meaningful connections to known protein structures. We think that finding such remote connections is more valuable and biologically interesting than declaring a "new fold", as more information is revealed about a protein through comparisons. Moreover, recent and quite instructive analysis [66] has shown that the current sample of solved protein structures present in PDB [67] appears to be almost complete at the level of single domain structures (with the exception of membrane proteins), and thus discovering a truly new fold now is not a common feat.

As a final point, although discussions about the nature of the protein structure space are fundamentally important, there is a question of their immediate practical value. We would like to point out at least two important areas where the notion of discreteness/continuity can be directly applied. First, in the field of structure prediction, geometric continuity of the structure space implies that all structures are currently predictable if connections to relevant 40% overlapping structures are found [43,48]. It also implies that structures can be piece-wise assembled from several such overlapping templates. Apparently, many prediction methods [68–70] are already quite successful in the practical usage of multiple templates. Another important area of application is the prediction of functional properties, such as active site placement [44,53,58–60]. As part of the power in prediction comes from evolutionary considerations, both discrete and continuous views are helpful for function prediction. Fold classification may point to connections between geometrically different proteins that are not found by automated structure similarity searches, but are nevertheless of the same fold. At the same time, a long list of significant hits produced by a database search program may point to a functionally relevant connection to a protein that does not belong to the same fold [44,53,58–60]. Thus, both views have their place in practical applications and neither should be neglected or unnecessarily criticized.

Conclusions

As a summary, we suggest that there is an intrinsic duality to the nature of the protein structure space. Evolutionarily, it is largely discrete, with certain islands of stability corresponding to protein folds, and few remaining traceable evolutionary connections between the islands. Geometrically, the space is continuous, in the sense that almost any relative arrangements of secondary structures are allowable, and almost any two structures can be connected through a path of intermediate locally similar structures. It is important to note that while the notion of homology is transitive, structure similarity is not.