Abiotic Production of Methane in Terrestrial Planets

Abstract

On Earth, methane is produced mainly by life, and it has been proposed that, under certain conditions, methane detected in an exoplanetary spectrum may be considered a biosignature. Here, we estimate how much methane may be produced in hydrothermal vent systems by serpentinization, its main geological source, using the kinetic properties of the main reactions involved in methane production by serpentinization. Hydrogen production by serpentinization was calculated as a function of the available FeO in the crust, given the current spreading rates. Carbon dioxide is the limiting reactant for methane formation because it is highly depleted in aqueous form in hydrothermal vent systems. We estimated maximum CH₄ surface fluxes of 6.8×10⁸ and 1.3×10⁹ molecules cm⁻² s⁻¹ for rocky planets with 1 and 5 M_⊕, respectively. Using a 1-D photochemical model, we simulated atmospheres with volume mixing ratios of 0.03 and 0.1 CO₂ to calculate atmospheric methane concentrations for the maximum production of this compound by serpentinization. The resulting abundances were 2.5 and 2.1 ppmv for 1 M_⊕ planets and 4.1 and 3.7 ppmv for 5 M_⊕ planets. Therefore, low atmospheric concentrations of methane may be produced by serpentinization. For habitable planets around Sun-like stars with N₂-CO₂ atmospheres, methane concentrations larger than 10 ppmv may indicate the presence of life. Key Words: Serpentinization—Exoplanets—Biosignatures—Planetary atmospheres. Astrobiology 13, 550–559.

1. Introduction

Missions such as EChO (Tessenyi et al., 2012) and the James Webb Space Telescope (Deming et al., 2009) may be able to detect atmospheric compounds from potentially habitable planets around other stars. With Earth as the only known habitable planet, the ongoing question is how to distinguish a habitable planet from an inhabited one, having a single template, Earth, for establishing the characteristics of habitable exoplanets. In the present paper, we will call habitable planets those which meet the general conditions of being rocky, with water, massive enough to retain their atmospheres, and with an average surface temperature above the freezing point of water (e.g., Kasting and Catling, 2003; Segura and Kaltenegger, 2010). Our analysis is constrained to anoxic atmospheres because the most stable bulk atmospheric composition of an abiotic rocky planet is CO₂ and N₂, as is the case of early Earth (e.g., Zahnle et al., 2010), Mars, and Venus.

To detect life on a planet, global changes to the planetary surface or atmosphere must have occurred due to the presence of a biota. For example, chemical compounds produced by life may be abundant enough to produce a signature in the planetary spectrum. The spectral features of this type of molecule are called biological signatures or biosignatures (Des Marais et al., 2002; Kaltenegger et al., 2002; Meadows, 2006).

Oxygen (O₂) and ozone (O₃) are signals of life in Earth's atmosphere; O₂ is produced by photosynthesis, while O₃ is generated by O₂ photolysis. On habitable planets around Sun-like stars, high CO₂ atmospheres do not produce high-enough abiotic O₂ or O₃ to be detected in the planetary spectrum (Segura et al., 2007). Consequently, they are usable biosignatures for terrestrial planets (Des Marais et al., 2002).

Methane (CH₄) has also been proposed as another possible biosignature (Des Marais et al., 2002). Nevertheless, CH₄ can be produced by both biological and geological sources. Biological CH₄ is generated by methanogenic bacteria from

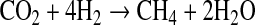(R1)

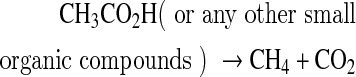Experimental simulations of hydrothermal vent environments have shown that methane forms abiotically in these systems (e.g., McCollom and Seewald, 2001; Oze et al., 2012). These results agree with the detection of methane on peridotite-dominated hydrothermal vents in which methanogens are not present (e.g., Proskurowski et al., 2006; Fiebig et al., 2007). Abiotic production of methane is usually explained by a reaction of Fischer-Tropsch synthesis (e.g., McCollom et al., 1999; Charlou et al., 2002; Fiebig et al., 2007), where H₂ molecules reduce CO₂, forming CH₄, as in Reaction R1. Hydrogen for this reaction comes from the process known as serpentinization, which will be detailed in the next section.

There are no atmospheric processes that yield CH₄ in CO₂- or O₂-rich atmospheres. The sinks for atmospheric CH₄ are (1) in O₂-poor atmospheres, CH₄ is broken by photolysis below 145 nm, which leads to the production of CH₃, CH₂, and CH radicals (Atreya et al., 2006); (2) in O₂-rich atmospheres, CH₄ reacts quickly with the hydroxyl radical (OH) through the following reactions:

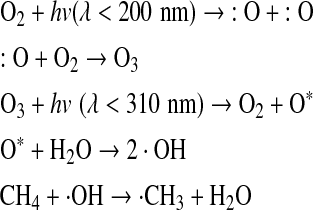The removal of atmospheric CH₄ from O₂-rich atmospheres is faster and more efficient than the geological production rate, so these atmospheres need a biological source to maintain high CH₄ concentrations. For this reason, some authors such as Lovelock (1965), Sagan et al. (1993), and Des Marais et al. (2002) have suggested that CH₄ detection, together with O₂ (or O₃), would be good evidence of life. However, this rule may not apply for planets with high O₂ atmospheres around M dwarfs, where methane can build up because of the particular UV emission from these stars (Segura et al., 2005). In abiotic, CO₂-rich atmospheres, CH₄ may be detectable in the planetary spectrum even if its source is solely geological (Segura et al., 2007). With the aim to evaluate the relevance of methane as a biosignature in terrestrial planets, we estimated possible production rates of methane from serpentinization processes. Then we used the production rates to evaluate CH₄ fluxes and the atmospheric abundances in terrestrial CO₂-rich atmospheres, using a 1-D photochemical model coupled to a 1-D climate model.

2. Abiotic Methane Production

Methane can be produced by serpentinization. Through this process, Fe- and Mg-rich ultramafic rocks, like olivine, are transformed to serpentine (Mg₃Si₂O₅(OH)₄) by hydrolysis. Other products are brucite (Mg(OH)₂), magnetite (Fe₃O₄), and H₂. Serpentinization occurs in hydrothermal vent systems at mid-ocean ridges (e.g., Proskurowski et al., 2006) and subduction zones (e.g., Hyndman and Peacock, 2003). It is a complex process that may be described by the following reaction sequence (Bach et al., 2006):

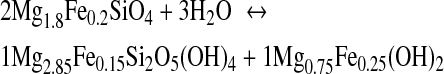(R2)

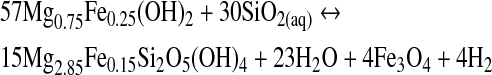(R3)

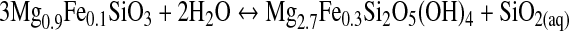(R4)

During serpentinization, H₂ is formed at the mineral surface as a result of the Fe²⁺ oxidation. This reaction needs aqueous silica that is likely to be provided by the breakdown of orthopyroxene to serpentine (Bach et al., 2006). Indeed, serpentinization has been proposed as an abundant H₂ source (McCollom and Seewald, 2001; Sleep et al., 2004). In environments with abundant CO₂, CH₄ is formed from rising H_2(aq) generated by serpentinization (Reaction R1). This occurs at ridges in the seafloor associated with hydrothermal vent flows (pH 9–11).

2.1. Abundance of reactants for CH₄ abiotic production in terrestrial planets

2.1.1. Iron abundance

Iron (FeO) is consumed during serpentinization, and the renewal of the crust by plate tectonics provides new Fe²⁺ that can be used in the serpentinization process. The oceanic crust composition is nearly homogeneous, with FeO content between 6 and 10 wt % (Taylor and McLennan, 1985; Condie, 1997) and a density of 3×10⁶ g m⁻³. Then the FeO abundance in the oceanic crust is 2.5×10³ and 4.2×10⁶ mol m⁻³, for 6 and 10 wt %, respectively. FeO is supplied as new crust forms, with a production rate that can be expressed as

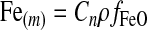(1)

where ρ is the crust density, f_FeO is the iron mass fraction in the crust, and C_n is the crust formation rate calculated as C_n=l×d×S_c, with l the total length of the ridges, d the average thickness of the crust, and S_c the crust spreading rate. Table 1 shows the values used for the 1 M_⊕ planet and those estimated for the 5 M_⊕ planet. The values for the 5 M_⊕ planet were scaled from Earth by using the power law M_m=bm^x, with M_m a given variable (e.g., crust thickness, ridge length) for a planet with m Earth masses, b Earth's value for that variable, and x the exponent calculated by Valencia et al. (2007a). The crust density and the iron fraction were assumed to be equal to Earth's values.

Table 1.

Planet Parameters for Calculating FeO Formation Rates

Variable	Exponent	1 M⊕a	5 M⊕b
Ridge length (l)	0.28	7×107 m	1.1×108 m
Crust thickness (d)	−0.45	2600 m	1260.2 m
Spreading rate (Sc)	1.19	2 cm yr−1	13.6 cm yr−1

^aTotal length of the ridges and average crustal thickness from Macdonald (2001), average spreading rate sustained on Earth during the last ∼150 million years (Cogné and Humler, 2004, and references therein).

^bCalculated from Valencia et al. (2007a); see text.

The iron supply rate is then calculated to be between 9.1×10¹² and 1.5×10¹³ mol yr⁻¹ for 1 M_⊕ planets and between 4.7×10¹³ and 7.8×10¹³ for 5 M_⊕ planets. The minimum and maximum supply rates correspond to crust FeO mass fraction contents of 0.06 and 0.1, respectively.

2.1.2. Hydrogen production

In a strict sense, serpentinization is described by Reactions R2 to R4, although it is usually expressed from its redox state, controlled by the quartz-fayalite-magnetite buffer, represented by equilibrium in the aqueous fluid for the reaction (Basaltic Volcanism Study Project, 1981)

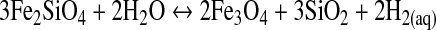(R5)

From this, we can assume a simple reaction between a solid A and a liquid phase B, where the reaction velocity is v_r=κ[A]^x, where κ is the kinetic rate constant, A is the fayalite concentration, and x is the reaction order (Rudge et al., 2010). Here, we assume that R5 is a first-order reaction for fayalite, so that v_r=κ[Fe₂SiO₄]. From the R5 stoichiometry, the H₂ reaction velocity vf(H₂)=2v_r, so that vf(H₂)=2κ[Fe₂SiO₄]. To use the FeO values calculated before, we will express the fayalite abundance by its FeO equivalent content (2[Fe₂SiO₄]=[FeO]), so that vf(H₂)=κ[FeO].

The rate constant κ has not been experimentally evaluated for R5 but was parameterized by Kelemen and Matter (2008) from volumetric studies of peridotite hydrolysis (Martin and Fyfe, 1970) as

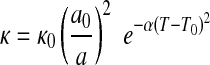(2)

where a is the fayalite grain size, T is the reaction temperature, and κ₀, a₀, α, and T₀ are the constants given in Table 2. The H₂ formation rate [vf(H₂)] can then be calculated from the FeO abundance, temperature, and grain size. Maximum H₂ formation rate is reached at 260°C. Such a temperature is possible if we consider that serpentinization occurs in hydrothermal vent systems where the temperature varies from 40°C to 400°C (e.g., Kelley et al., 2005; Haase et al., 2009).

Table 2.

Values for Calculation of the Parameterization of the Serpentinization Constant Rate

Constant	Value
κ0	1×10−6 s−1
a0	70 μm
α	2.09×10−4 °C−2
T0	260°C

The contact area between the mineral surface and the liquid phase depends on the grain size a. For this parameter, the optimum value for maximizing vf(H₂) is 70 μm. As we mentioned in Section 2.1.1, the FeO supply (Fe_(m)) depends on the creation of new crust that has rates of 9.1×10¹² and 4.7×10¹³ FeO mol yr⁻¹, for 1 and 5 M_⊕ planets, respectively.

To verify the balance between the generated and consumed FeO, we consider the reaction

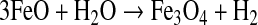(R6)

From the Reaction R6 stoichiometry, we can establish a relationship between the formation rates of FeO (Fe_(m)) and H₂. If 3vf(H₂)>Fe_(m), all the FeO will be consumed, and the reaction would happen only during a given period of time. If 3vf(H₂)<Fe_(m), the reaction could continue indefinitely. When 3vf(H₂)=Fe_(m), the H₂ formation is in equilibrium with the generation of FeO, and the reaction is at a sustainable limit. Because vf(H₂)=κ[FeO], then 3κ[FeO]=Fe_(m). Then, using the values for the grain size and temperature that optimize κ and the maximum rates for FeO production, we obtain [FeO]=26.4 mol m⁻³. This FeO abundance is available under the conditions assumed here (see Section 2.1.1). Then the maximum production of H₂ is 3.0×10¹² mol yr⁻¹ (1.1×10¹⁰ molecules cm⁻² s⁻¹) for a 1 M_⊕ planet and 1.6×10¹³ mol yr⁻¹ (2.2×10¹⁰ molecules cm⁻² s⁻¹) for a 5 M_⊕ planet.

2.1.3. Carbon dioxide abundance

On Earth, CO₂ is recycled in the atmosphere-crust system by tectonic activity. It is estimated that the preindustrial ocean intake was ∼6.2×10¹⁵ mol CO₂ yr⁻¹, from which only 1.7×10¹³ mol CO₂ yr⁻¹ form carbonates (Siegenthaler and Sarmiento, 1993). Sedimentary carbon is estimated to be 7.1×10²¹ mol (Holser et al 1988) to 7.75×10²¹ mol (Hirschmann and Dasgupta, 2009), equivalent to ∼62–68 bar of atmospheric CO₂, respectively. Of this volume, 15–20% by mole is organic carbon, and the remaining 80–85% is carbonate (Holser et al., 1988). A review by Hirschmann and Dasgupta (2009) of CO₂ estimations in the mantle gives a range of ∼9.75±4.2×10²¹ mol with the mid value equivalent to ∼85 bar of atmospheric CO₂. The CO₂ production in the mid-ocean ridge was calculated to be 2.2×10¹² mol yr⁻¹ (Marty and Tolstikhin, 1998) and more recently 9.3±2.8×10¹¹ mol yr⁻¹ (Fischer, 2008).

Two possible sources of CO₂ may then be available for reacting with H₂ to form methane (R1) in the hydrothermal vent systems. One source comes directly from the mantle and may be the most likely for oceanic crust spreading centers; the other source is the decarboxylation of carbonates in sediments. Carbonates, mainly in the form of calcite, release CO₂ at temperatures above 500°C (Morse et al., 2007). This means that they can be a relevant source of CO₂ only if they are deep enough in the crust to reach those temperatures. Therefore, carbonate decarboxylation may be an important source of CO₂ for hydrothermal vent systems associated with subduction zones, like back-arc systems. Regardless of the high amount of carbon in the mantle and crust, aqueous CO₂ is quantitatively depleted in hydrothermal vent systems. The largest CO₂ concentrations measured in hydrothermal vents are 3×10³ mol m⁻³ in the Mariana Arc (Sakai et al., 1990). This concentration is 100 times larger than those measured on most of the hydrothermal vent systems located in the mid-ocean ridge (Lupton et al., 2006). The aqueous CO₂ supersaturation found in the Mariana Arc is only explained if there is a source of liquid CO₂ (Brewer et al., 1999, 2000, 2002) leaking into the hydrothermal vent flux (Lupton et al., 2006). Lupton et al. (2006, 2008) concluded that, for hydrothermal vent systems, the maximum concentration of CO₂ in aqueous phase is 50 mol m⁻³. This is derived from the water/rock ratio that usually ranges from 1 to 5 for hydrothermal vent systems but can be as large as 12 (Kawahata and Scott, 1990). Aqueous CO₂ concentrations larger than 50 mol m⁻³ require water/rock ratios significantly less than 1, which is both physically and chemically unreasonable for hydrothermal vents.

Even if larger amounts of CO₂ were available in hydrothermal vent systems, recent experiments show that the addition of large amounts of inorganic carbon into hydrothermal serpentinization systems does not enhance abiotic CH₄ production. This is because of the competition of Fe²⁺ incorporation into carbonate solid phases versus oxidative magnetite formation, which plays an important role in governing the H₂ and CH₄ production (Jones et al., 2010).

3. Methane Production by Serpentinization

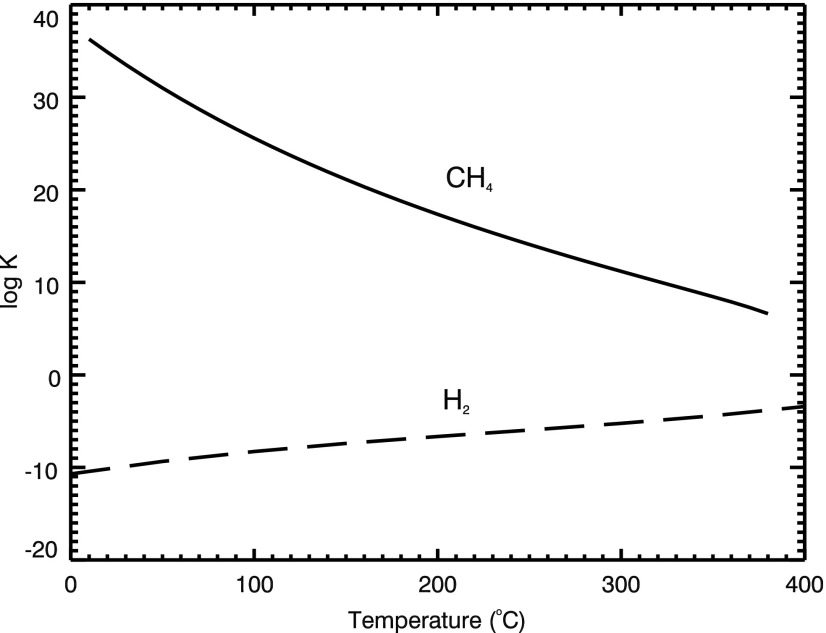
Using the program SUPCRT92 (Johnson et al., 1992), we calculated the equilibrium constants (K) for the reactions that produce methane (R1) and H₂ (R5) as a function of temperature (Fig. 1). The equilibrium constant (K) is a measure of the conversion of reactants to products. The equilibrium constants in Fig. 1 show that the formation of H₂ is more efficient at high temperatures, while methane formation is more efficient at low temperatures.

FIG. 1.

Equilibrium constant for the production of methane (solid line) and for the production of H₂ (dashed line) as a function of temperature.

The equilibrium constant can be expressed as a function of the chemical species that participate in the reaction. For R1,

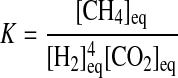(3)

Because we assume that the reaction occurs in water, its concentration is not modified during the reaction, and it is therefore omitted in Eq. 3.

The amounts of the chemical species involved in the reaction change from their initial concentrations [H₂]₀, [CO₂]₀, and [CH₄]₀ to the equilibrium concentrations [H₂]_eq, [CO₂]_eq, and [CH₄]_eq depending on the limiting reactant in the following form:

• (1) If H₂ is the limiting reactant, the initial conditions are [CO₂]₀>0.25[H₂]₀ and [CH₄]₀=0. When equilibrium is achieved, the amounts of H₂ and CO₂ consumed are x[H₂]₀ and 0.25x[H₂]₀, respectively, and methane is 0.25x[H₂]₀, where x is the reaction yield. Then, for each reactant, the equilibrium concentration is equal to the initial concentration minus the consumed amount, and by using the appropriate stoichiometry the product is equal to what was consumed. Then, for this case, [H₂]_eq=[H₂]₀−x[H₂]₀, [CO₂]_eq=[CO₂]₀−0.25x[H₂]₀, and [CH₄]_eq=0.25x[H₂]₀.

• (2) If CO₂ is the limiting reactant, then [CO₂]₀<0.25[H₂]₀ and [CH₄]₀=0. Consumed H₂ and CO₂ are 4x[CO₂]₀ and x[CO₂]₀, respectively, and the produced methane is x[CO₂]₀. At equilibrium, [H₂]_eq=[H₂]₀−4x[CO₂]₀, [CO₂]_eq=[CO₂]₀−x[CO₂]₀, and [CH₄]_eq=x[CO₂]₀.

Substituting the equilibrium quantities on Eq. 3 for both cases:

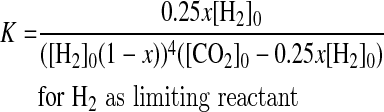(4)

4

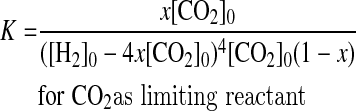(5)

In these equations, K is known, as well as the initial conditions for the reactants, so that the reaction yield x can be calculated as a function of temperature. For H₂, the initial concentration is 3.0×10¹² mol yr⁻¹ for 1 M_⊕ planets and 1.6×10¹³ mol yr⁻¹ for 5 M_⊕ planets (see Section 2.1.2). For CO₂, the maximum value is 50 mol m⁻³ (see Section 2.1.3), and assuming a water/rock ratio equal to 1, the amount of rock will be equal to the generated crust volume, that is, 3.6×10⁹ m³ yr⁻¹ and 1.9×10¹⁰ m³ yr⁻¹ for 1 and 5 M_⊕ planets, respectively. The CO₂ available to produce methane then is 1.8×10¹¹ mol yr⁻¹ for 1 M_⊕ planets and 9.5×10¹¹ mol yr⁻¹ for 5 M_⊕ planets. For these amounts of H₂ and CO₂, the limiting reactant is CO₂; then we use Eq. 5 to estimate that x ∼ 1.

Finally, we obtain that for a 1 M_⊕ planet the maximum CH₄ flux is 6.8×10⁸ molecules cm^−l2 s⁻¹ (1.8×10¹¹ mol yr⁻¹), the H₂ flux is 8.6×10⁹ molecules cm⁻² s⁻¹ (2.3×10¹² mol yr⁻¹), and the CO₂ flux is 0.7 molecules cm⁻² s⁻¹ (182 mol yr⁻¹). For the 5 M_⊕ planet, the maximum CH₄ flux is 1.3×10⁹ molecules cm⁻² s⁻¹ (9.4×10¹¹ mol yr⁻¹), the H₂ flux is 1.7×10¹⁰ molecules cm⁻² s⁻¹ (1.2×10¹³ mol yr⁻¹), and the CO₂ flux is 1.3 molecules cm⁻² s⁻¹ (939.8 mol yr⁻¹).

Because of the low solubility of methane, we assume that it is released into the atmosphere after it is generated in the hydrothermal vents. Methane could in principle undergo other chemical processes in the ocean, like the formation of methane clathrates, but it is beyond the scope of this work to make a detailed model of the fate of methane in an anoxic ocean. Our assumption is consistent with finding an upper limit for the amount of abiotic methane that may be present in the anoxic atmosphere of a habitable planet.

4. Atmospheric Models

We used two atmospheric models, a 1-D photochemical model (1D-Pm) originally developed by Pavlov and Kasting (2002) that was later modified by Kharecha et al. (2005) and Segura et al. (2007), and a 1-D radiative/convective model (R-Cm) (Haqq-Misra et al., 2008). The R-Cm produces a temperature profile for an atmosphere with a given bulk atmospheric composition (CO₂, CH₄, and H₂O), and this temperature profile is used as an input for the 1D-Pm.

4.1. Photochemical model

The 1D-Pm computes the chemical equilibrium for 38 chemical species involved in 162 reactions. The atmosphere is divided into 100 layers with a fixed vertical extent of 1 km each. The long-lived chemical species are O, O₂, O₃, H₂O, H, OH, HO₂, H₂O₂, H₂, CO, CO₂, HCO, H₂CO, CH₄, CH₃, C₂H₆, NO, NO₂, HNO, SO, SO₂, and H₂SO₄; N₂ is also included with a constant mixing ratio. The 1D-Pm solves the flux (Eq. 6) and continuity (Eq. 7) equations at each height for each long-lived species, including transport by eddy and molecular diffusion:

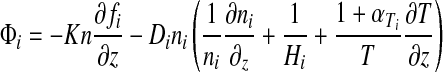(6)

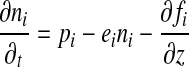(7)

where f_i=flux of the i^th species, n_i=number density of the i^th species (cm⁻³), Φ_i=mixing ratio of the i^th species, n=total number density of the atmosphere (cm⁻³), z=altitude (cm), p_i=chemical production rate (cm⁻³ s⁻¹), e_i=chemical loss rate (s⁻¹), and K=eddy diffusion coefficient (cm⁻² s⁻¹), D_i=diffusion coefficient between species i and the background atmosphere, H_i (=kT/m_ig) is the scale height of species i, and α_Ti is the thermal diffusion coefficient of species i with respect to the background atmosphere. In these definitions, k=Boltzmann's constant, m_i=molecular mass of species i, and m=molecular mass of the atmosphere.

Boundary conditions for each chemical species were applied at the top and bottom of the model atmosphere, and the resulting set of coupled differential equations was integrated in time to reach a steady state by using the reverse Euler method. The model simulates the Sun's influence over terrestrial anoxic atmospheres, with a fixed solar zenith angle of 50°. A key feature of the 1D-Pm is its ability to keep track of the atmospheric hydrogen (or redox) budget. This is done by considering that when one species is oxidized, another one must be reduced, and vice versa. Following the Kasting and Brown (1998) strategy, “redox-neutral” species are defined as H₂O (for H), N₂ (for N), CO₂ (for C), and SO₂ (for S). All other species are assigned redox coefficients relative to these gases by determining how much H₂ is produced or consumed during their formation from redox neutral species (Appendix 1 in Kharecha et al., 2005). For example, the redox coefficients of CH₄ and NO are calculated from the reactions that would convert them to their corresponding neutral constituents, CO₂ and N₂, respectively:

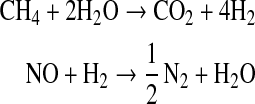Then, 1 mol of CH₄ produces 4 mol of H₂, and 1 mol of NO consumes 1 mol of H₂, so that the redox coefficients of CH₄ and NO are +4 and −1, respectively. The contribution of each chemical species i to the hydrogen budget is calculated as [Φ_rain(i)−Φ_surf(i)] H_coeff(i), where Φ_rain(i) is the loss of species i for rain removal, Φ_surf(i) is the flux from (positive) or into (negative) the ocean of species i, and H_coeff(i) is the redox coefficient of that chemical species. The total contributions for loss and production of H₂ are

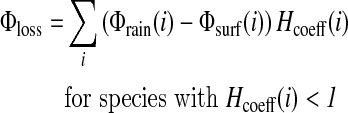(8)

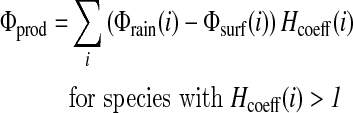(9)

The total hydrogen outgassing contribution to the redox budget is expressed as

(10)

For our case, Φ(H₂) and F(CH₄)=4Φ(CH₄) are the fluxes calculated from serpentinization. Then, the hydrogen budget is calculated as

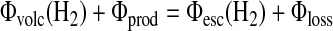(11)

where Φ_esc(H₂) is limited by the H₂ diffusion rate through the homopause. The diffusion-limited escape flux at the top of the atmosphere is calculated using the formulation of Walker (1977) as

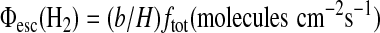(12)

where b is an average binary diffusion coefficient for the diffusion of H, H₂, and CH₄ in nitrogen; H is the atmospheric scale height; and f_tot is the sum of the mixing ratios at 100 km of all the hydrogen-bearing species abundant in the stratosphere, weighted by the number of hydrogen atoms contained by each of the species (Segura et al., 2007):

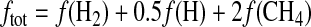The redox balance in Eq. 11 is diagnostic, not prognostic; hence, it provides a good check both on the redox balance and on the photochemical scheme.

The upper boundary conditions are constant effusion velocity (v_eff) or constant flux (Φ_up), and for most of the species v_eff=0. The flux at the top is expressed as Φ_up=v_eff n_i, where n_i is the number density of the compound i at the top of the atmosphere. For H and H₂, v_eff is set equal to the diffusion-limited value, v_eff=D_i/H. Species such as O₂ that can be photodissociated above the model grid are given upward velocities that balance the column-integrated loss above this level, that is, v_eff=J(O₂)H, where J(O₂) is the O₂ photolysis rate. Atomic O is then given a fixed downward flux equal to twice the upward flux of O₂. Likewise, photolysis of CO₂ above the model grid leads to downward fluxes of CO and O.

The code has three options for lower (surface) boundary conditions: fixed surface flux, fixed surface mixing ratio, and fixed deposition velocity. Soluble species are removed by direct deposition at the lower boundary to account for the uptake by the ocean. This is done by calculating the flux into the ocean of the chemical species i as n_iv_dep(i), with n_i the number density of species i and v_dep(i) its deposition velocity. The upper limit on v_dep is set by diffusion through the turbulent atmospheric boundary layer, assuming that molecules are absorbed by the surface each time they collide with it (Kharecha et al., 2005).

4.2. Radiative/Convective model

The R-Cm code is a 1-D cloud-free model with a (log pressure) grid extended from the assumed surface pressure down to a pressure that was set depending on the planetary atmosphere. The program subdivides this range into 101 levels. The time-stepping procedure and the solar (visible/near-IR) portion of the radiation code are from the model of Pavlov et al. (2000). The solar code incorporates a δ two-stream scattering algorithm (Toon et al., 1989) to calculate the net absorbed visible and mid IR solar radiation by using four-term, correlated-k coefficients to parameterize absorption by O₃, CO₂, H₂O, O₂, and CH₄ in each of 38 spectral intervals (Kasting and Ackerman, 1986). Fluxes in the mid IR are calculated with the hemispheric mean two-stream approximation (Toon et al., 1989). Absorption coefficients in the mid and far IR for methane are those derived by Haqq-Misra et al. (2008). All gases other than H₂O are considered to be well mixed in the model atmosphere. A moist adiabatic lapse rate is assumed in the model troposphere with a fixed relative humidity following Manabe and Wetherald (1967).

4.3. Simulated atmospheres

We simulated anoxic atmospheres of lifeless, habitable planets with mixing ratios of 0.03 and 0.1 CO₂. Two planet sizes were tested: 1 M_⊕ and 5 M_⊕; a radius of 1.6 R_⊕ for the 5 M_⊕ planet was calculated by using the mass-radius relationship of Valencia et al. (2007b) for a rocky planet (with a similar Fe/Si ratio to Earth) with a 10% water content. The atmospheric surface pressure was scaled with the planet's gravity; therefore, the surface pressures were 1 and 2 bar for the 1 M_⊕ and 5 M_⊕ planets, respectively.

The planets were located at 1.15 AU from the Sun, where the solar flux is 0.75 S₀, with S₀ the solar constant (the flux that is received at the top of the present Earth atmosphere). We choose these atmospheres as illustrative examples of how much methane would exist in the planetary atmosphere given the calculated fluxes of this compound produced by serpentinization. Our choice of stellar distance is the result of considering that (1) closer distances between the planet and the star will mean higher surface temperatures and higher UV stellar fluxes, which are both detrimental to the methane abundance; (2) being near the outer limit of the habitable zone (0.53 S₀, 1.37 AU, Table III in Kasting et al., 1993) requires the inclusion of CO₂ cloud condensation in the R-Cm, a process which is presently not included in the model.

The climate model uses a pressure grid that is “translated” to an altitude grid to transfer the calculated temperature profile to the photochemical model. For the minimum pressures (∼10⁻⁶ bar) that the R-Cm code is able to manage, the atmosphere altitudes are ∼70 km for planets with 1 M_⊕ and ∼35 km for planets with 5 M_⊕. The temperatures above those altitudes were considered constant and equal to the last upper value calculated by the R-Cm. Temperature profiles were calculated by using the Manabe-Wetherald relative humidity profile (Manabe and Wetherald, 1967), with an O₂ mixing ratio of 10⁻¹⁵ and no O₃. Carbon dioxide was included by using the selected mixing ratios of 0.03 and 0.1. The first temperature profile was created with a guess value for the CH₄ mixing ratio, and after running the 1D-Pm code to equilibrium, a new temperature profile was calculated with the CH₄ mixing ratio computed by the 1D-Pm code. This process was not repeated unless the change for the methane mixing ratio was larger than a factor of 2.

Boundary surface conditions in the photochemical model were as follows: a fixed deposition velocity for CO, v_dep(CO)=1×10⁻⁸ cm s⁻¹, and a fixed velocity deposition for H₂ equal to zero; both values are consistent with calculations for an abiotic planet (Kharecha et al., 2005). The methane lower boundary condition was set as a fixed surface flux with the values calculated for maximum production by serpentinization. Table 3 presents the relevant parameters for the modeled atmospheres.

Table 3.

Parameters for Atmospheric Simulations

			Surface flux (cm−2 s−1)		Surface mixing ratio
Planet mass	CO2 mixing ratio	Tsurf(K)	CH4	H2	CH4	H2
1 M⊕	0.03	303.5	6.8×108	8.6×109	2.5×10−6	4.7×10−4
	0.1	308.3			2.1×10−6	4.5×10−4
5 M⊕	0.03	314.2	1.3×109	1.7×1010	4.1×10−6	4.5×10−4
	0.1	320.5			3.7×10−6	4.6×10−4

4.4. Abundance of atmospheric methane

Table 3 presents the atmospheric methane abundance obtained for the simulated atmospheres. Mixing ratios obtained by the photochemical model for the most important chemical species are presented in Fig. 2. For all cases, methane was lower than 5 ppmv. The redox budget was conserved in all cases as shown in Table 4.

FIG. 2.

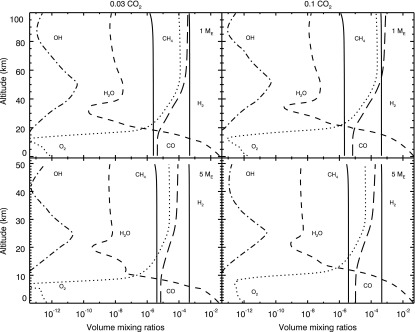
Mixing ratios of the most relevant chemical species for the simulated atmospheres.

Table 4.

Redox Budget for the Simulated Atmospheres (see Text Eqs. 8–12)

		1 M⊕		5 M⊕
Compound	Hcoeff	0.03 CO2	0.1 CO2	0.03 CO2	0.1 CO2
H2 production
H	0.5	5.208×105	4.762×105	1.398×105	1.491×105
CO	1.0	−2.389×102	1.426×102	−2.169×101	−8.026×101
HCO	1.5	3.663×106	5.996×106	6.843×106	1.372×107
H2CO	2.0	2.760×107	6.595×107	8.302×107	4.980×108
CH3	3.5	2.642×106	1.573×106	5.067×106	2.380×106
C2H6	7.0	−1.009	6.819×10−2	−2.734×10−2	−9.842×10−2
SO	1.0	5.647×106	4.956×106	5.537×106	4.271×106
Φprod		4.007×107	7.895×107	1.006×108	5.185×108
Reduced volcanic species
H2	1.0	4.477×101	−5.501	−8.141	9.493
F(CH4)	4.0	2.270×109	2.720×109	5.200×109	5.200×109
Φ(H2)		8.600×109	8.600×109	1.700×1010	1.700×1010
Φvolc		1.132×1010	1.132×1010	2.220×1010	2.220×1010
Total H2 production		1.136×1010	1.140×1010	2.230×1010	2.272×1010
H2 loss
O	−1.0	−3.699×103	−6.927×103	−8.931×102	−2.201×103
O2	−2.0	−5.196×103	−1.103×104	−6.057×103	−1.073×104
OH	−0.5	−1.977×103	−1.452×103	−1.366×103	−1.203×103
HO2	−1.5	−1.173×103	−4.673×103	−2.513×103	−1.217×104
H2O2	−1.0	−2.273	−2.483×103	−2.026	−6.825
O3	−3.0	−6.048×10−4	−2.404×10−3	−2.998×10−4	−1.353×10−3
NO	−1.0	−3.798×102	−7.982×102	−1.200×102	−3.769×102
NO2	−2.0	−3.734×10−4	−4.720×10−3	−9.372×10−5	−5.896×10−2
HNO	−0.5	−1.408×108	−2.457×108	−1.929×108	−4.368×108
H2SO4	−1.0	−1.099×105	−1.656×105	−8.891×104	−6.232×105
SO4AER	−1.0	−1.116×108	−7.708×107	−1.934×108	−1.167×108
Φloss		−2.525×108	−3.230×108	−3.863×108	−5.541×108
Φesc(H2)		1.144×1010	1.153×1010	2.216×1010	2.217×1010
Total H2 loss		1.170×1010	1.186×1010	2.255×1010	2.272×1010
H2 balance		2.875×10−2	3.850×10−2	1.087×10−2	1.748×10−4

5. Discussion

Oze et al. (2012) proposed that H₂/CH₄ ratios larger than 40 indicate the absence of biological sources of methane based on serpentinization experiments with a water/rock ratio of 2.5 and an analysis of several hydrothermal vent systems with and without methanogens. In our model (H₂/CH₄) ∼ 13, and in order to achieve the ratio proposed by these authors, we need to assume that CO₂ is limited to 18.75 mol m⁻³ instead of 50 mol m⁻³. This is consistent with the scenario we have proposed, in which CO₂ is the limiting reactant for methane formation, regardless of its abundance in the planetary crust and mantle.

We tested our model by comparing the calculated production of CO₂, H₂, and CH₄ with those measured in hydrothermal vent systems. We used a CO₂ concentration of 18.75 mol m⁻³ given that 50 mol m⁻³ is a maximum that is not usually achieved in Earth's hydrothermal vent systems (see Section 2.1.3). Table 5 shows a comparison between the measured values and our model for CO₂, H₂, and CH₄ in four hydrothermal vent systems. The measured temperature in Table 4 was used as an input for our model. The other parameters used in our model were as follows: 6 wt % FeO in the crust, crust density of 3×10⁶ g m⁻³, grain size of 70 μm, and 26.4 mol m⁻³ available to participate in serpentinization.

Table 5.

Abundances of Principal Constituents in Hydrothermal Vent Fluxes (Tivey, 2007), Compared with Abundances Calculated by Our Model

	Mid-ocean ridge		Back-arc basin		Rainbow		Lost City
	Observed	Our model	Observed	Our model	Observed	Our model	Observed	Our model
T (°C)	≤405	405	278–334	306	365	365	≤91	91
H2 (mol m−3)	5×10−4 to 38	1.3×10−2	0.035–0.5	460	13	8.1	<1–15	1×10−7
CO2 (mol m−3)	3.56–39.9	16.1	14.4–200	1.8×10−8	—	1.9×10−8	—	18.2
CH4 (mol m−3)	7×10−3 to 2.58	2.56	5×10− 10−2	18.8	0.13–2.2	18.7	1–2	0.5

The hydrothermal vent systems that are best reproduced by our model are those in the mid-ocean ridge. This is something we expect because we used the average iron abundance measured in those systems. Insular arc systems are mainly found in the west margin of the Pacific Ocean, and they are associated with subduction zones (Pearce and Stern, 2006; Martínez et al., 2007), in which the ocean crust is mainly composed of Si- and Al-rich felsic rocks (Martínez et al., 2007) with low Fe (Le Maitre et al., 2002). The lower Fe content explains the smaller concentration of H₂ in those systems, compared to the ones calculated by the model. The Rainbow system is located at the Southeast of the Azores Islands, over the mid-Atlantic Ridge. This system is lying on an ultramafic rock substratum (Douville et al., 2002) that has more Fe than the average mid-ocean ridge systems. Therefore, larger amounts of H₂ are expected to be produced in these systems.

Previous work has estimated abiotic methane production rates of 10¹² mol yr⁻¹ (∼4×10⁹ molecules cm⁻² s⁻¹) (Kasting and Catling, 2003; Segura et al., 2007). According to our model, the FeO needed to achieve those methane fluxes is 1.4×10¹³ mol yr⁻¹, while Earth only generates 9.1×10¹² mol yr⁻¹. This means that a methane flux of 10¹² mol yr⁻¹ may not be sustained with the current crust spreading rates.

The results obtained here for the atmospheric abundance of methane may not apply to habitable planets around main sequence M stars (M dwarfs), where the sinks of methane are perturbed due to the particular UV radiation emitted by these stars (Segura et al., 2005). Simulations by Domagal-Goldman et al. (2011) for atmospheres with 0.3 CO₂ showed that, for a surface methane flux of 7×10¹⁰ molecules cm⁻² s⁻¹, methane atmospheric abundances were ∼3 times larger for planets around M dwarfs than for a planet irradiated by the Sun.

6. Conclusions

The methane production for terrestrial planets was estimated by considering geological processes that occur within hydrothermal vent systems, linked to crust spreading centers, and estimating the kinetic properties of the main reactions involved in CH₄ production by serpentinization. Hydrogen production by serpentinization was calculated as a function of the available FeO in the crust, given the present spreading rates. Carbon dioxide is the limiting reactant for methane formation because it is highly depleted in aqueous form in hydrothermal vent systems. We estimated maximum surface CH₄ fluxes of 6.8×10⁸ and 1.3×10⁹ molecules cm⁻² s⁻¹ for rocky planets with 1 M_⊕ and 5 M_⊕, respectively. Using a 1-D photochemical model, we simulated poor- and rich-CO₂ atmospheres to calculate atmospheric CH₄ mixing ratios. The resulting abundances were 2.5×10⁻⁶ and 2.1×10⁻⁶ for 1 M_⊕ planets and 4.1×10⁻⁶ and 3.7×10⁻⁶ for 5 M_⊕ planets.

We have shown that low atmospheric concentrations of methane may be produced by serpentinization. For habitable planets with N₂-CO₂ atmospheres, concentrations of methane larger than 10 ppmv may indicate the presence of life.

Acknowledgments

We thank Norman Sleep and an anonymous referee for their constructive suggestions that greatly improved this work. We acknowledge support from the Universidad Nacional Autónoma de México grant DGAPA PAPIIT IN119709-3. This work was also performed as part of the NASA Astrobiology Institute's Virtual Planetary Laboratory Lead Team, supported by the NASA Astrobiology Institute under Cooperative Agreement Notice NNH05ZDA001C.

Author Disclosure Statement

No competing financial interests exist.

Abbreviations

1D-Pm, 1-D photochemical model; R-Cm, 1-D radiative/convective model.