Mathematical Model Approach to Describe Tumour Response in Mice After Vaccine Administration and its Applicability to Immune-Stimulatory Cytokine-Based Strategies

Abstract

Immunotherapy is a growing therapeutic strategy in oncology based on the stimulation of innate and adaptive immune systems to induce the death of tumour cells. In this paper, we have developed a population semi-mechanistic model able to characterize the mechanisms implied in tumour growth dynamic after the administration of CyaA-E7, a vaccine able to target antigen to dendritic cells, thus triggering a potent immune response. The mathematical model developed presented the following main components: (1) tumour progression in the animals without treatment was described with a linear model, (2) vaccine effects were modelled assuming that vaccine triggers a non-instantaneous immune response inducing cell death. Delayed response was described with a series of two transit compartments, (3) a resistance effect decreasing vaccine efficiency was also incorporated through a regulator compartment dependent upon tumour size, and (4) a mixture model at the level of the elimination of the induced signal vaccine (k₂) to model tumour relapse after treatment, observed in a small percentage of animals (15.6%). The proposed model structure was successfully applied to describe antitumor effect of IL-12, suggesting its applicability to different immune-stimulatory therapies. In addition, a simulation exercise to evaluate in silico the impact on tumour size of possible combination therapies has been shown. This type of mathematical approaches may be helpful to maximize the information obtained from experiments in mice, reducing the number of animals and the cost of developing new antitumor immunotherapies.

Electronic supplementary material

The online version of this article (doi:10.1208/s12248-013-9483-5) contains supplementary material, which is available to authorized users.

INTRODUCTION

Immunotherapy is one of the different strategies that are being pursued to improve cancer therapy. The goal of immunotherapy is to eliminate tumour cells by enhancing the effector mechanisms and/or neutralizing the inhibitory pathways of the immune system (1). Dendritic cells (DCs) are key organizers of the immune system due to their ability to initiate T cell responses. Antigens are captured, processed and presented to naïve T cells by dendritic cells. The maturation status of the DCs defines the outcome of interaction of the DC and the naïve T cells. If the DC presents the antigen while receiving a danger signal that induces its maturation, then the antigen presentation will be accompanied by co-stimulatory signals and cytokines such as interleukin 12 (IL-12) or interferon alpha. In this case, the T lymphocytes will initiate an effector immune response that might destroy tumour cells (2).

Anticancer therapeutic vaccines and treatments with immune-stimulatory cytokines such as IL-12 are designed to promote this process of antigen presentation to naïve T cells (2–4), which is corrupted by tumours, leading to antigen tolerance rather than antitumor immune responses (5,6). The most promising anticancer vaccines combines the targeting of the tumour antigen to the DCs, interacting with a specific receptor expressed on the surface of the DC, with a maturation signal. An example of this strategy is the fusion of the adenylate cyclase of Bordetella pertussis to the human papillomavirus E7 protein (CyaA-E7). The adenylate cyclase is able to interact with the CD11b present in many DCs, leading to the internalization of the vaccine and to the antigen presentation by class I and class II major histocompatibility molecules (7). CyaA-E7 vaccine proved to trigger a potent immune response able to induce full tumour shrinkage; however, a therapeutic efficacy loss was detected when large tumours were treated (8). This antitumor therapeutic vaccine is now being tested in phase I clinical trial with good results in term of safety and induction of immune responses (http://www.genticel.com).

The intense preclinical and clinical research in immunotherapy is starting to translate into new approved drugs with a clear benefit on the overall survival of patients with advanced cancers (9). However, most of the immunotherapies that are tested in clinical trials fail to replicate the successful results obtained in preclinical animal models, indicating that a change in animal experimentation paradigm in cancer immunotherapy is needed in order to better predict the outcome in humans (10,11).

Mathematical models are useful tools to better understand complex systems, such as the interaction between immune and tumour cells, and identify plausible mechanisms that can explain the observed clinical or preclinical outputs (12). A variety of mathematical models have been proposed to describe the interaction between the different immune cell populations and the tumours (13–21). Among others, we can highlight the works of de Pillis et al. (15) or Cappuccio et al. (16) where the interaction between natural killer, CD8⁺ T and tumour cells was described combining literature and experimental parameters and latter used to successfully propose more effective dosing regimens (22). A more recent work was published in 2010 by Kronik et al. (19), where a model able to predict response based on partial data collected during early phases of the treatment was developed and applied to real-time treatment personalization (23).

On these bases, the objectives of this work were (1) to develop a minimal mathematical model integrating the different key mechanisms implied in tumour response to characterize the observed outcomes after the administration of the previously described CyaA-E7 vaccine to mice, (2) to evaluate its general applicability by describing anti-tumour activity of a different immune-stimulatory agent, and (3) to show its potential as in silico evaluation tool for potential combination therapies.

MATERIALS AND METHODS

Experimental Data

1. Berraondo et al. (8) published data were used to build the mathematical model. In their experiments, 5 × 10⁵ tumour cells expressing human papillomavirus E7 protein were injected into the shaved back of 5-week-old female C57BL/6 mice (day 0). Mice were treated with PBS on day 4 (control group, n = 19) or with 50 μg of the CyaA-E7 vaccine based on the fusion of the adenylate cyclase enzyme of Bordetella pertussis to the oncogenic protein E7 expressed by human papillomavirus. In C57BL/6 mice, the antigen target CD11b, is expressed in around 75% of dendritic cells (CD11c⁺) in the spleen (24). Six different groups of mice received a single dose of CyaA-E7 vaccine administered intravenously either on day 4 (n = 15), 7 (n = 16), 11 (n = 14), 18 (n = 15), 25 (n = 14) or 30 (n = 15) after the injection of the tumour cells (training dataset). Two independent studies where PBS on day 4 (n = 23) or a single dose of 50 μg of CyaA-E7 on day 25 (n = 11) were saved to validate the model externally (validation dataset).

2. Medina-Echeverz et al. (25) published data were used to test the applicability of the model developed in a different immune-stimulatory scenario. In their experimental setting, 5 × 10⁵ MC38 cells were subcutaneously injected to 5-week-old female C57BL/6 mice. Subsequently, mice were treated with either PBS (control group, n = 12) or with 10 μg of a plasmid codifying for murine IL-12 administered by hydrodynamic injection on day 23 (n = 21).

In both publications, tumour size measurements were reported as the average of two perpendiculars diameters and 2 mm was considered as the minimum tumour size that could be properly measure with the calliper. Mice with a tumour size higher than 20 mm were sacrificed according to the institutional guidelines for animal care.

Model Building and Selection

During the analysis, average of two perpendiculars diameters as reported in the original publications, instead of the tumour volume, was used to enable a better comparison of small tumour sizes and to avoid formulating any assumptions regarding tumour shape. Data were logarithmically transformed and NONMEM VII software using the Laplacian numerical estimation method was used (26). Inter-animal variability (IAV) was modelled exponentially and residual variability was modelled considering an additive error in the logarithmic domain of the transformed data.

Measurements of tumour size lower or equal to 2 mm represented a considerable percentage of the reported values (61.6%). Therefore, below limit of quantification (BQL) data were not removed from the dataset neither assigned to an arbitrary value (i.e., 0 or 2), they were considered during the analysis instead and treated as censored information, therefore maximizing the likelihood that the observation is indeed a BQL data (27).

Selection between models was based on the evaluation of different statistical and graphical criteria: precision of parameter estimates obtained from the analysis of 1000 bootstrap datasets using the software Perl-speaks-NONMEM (PsN) (28), goodness-of-fit plots, and minimum value of the objective function value provided by NONMEM (MVOF) and approximately equal to −2×log (likelihood) (−2LL). Differences between two hierarchical (nested) models were compared with a χ² distribution in which a decrease of 6.63 points in −2LL was considered significant at the 1% level for one extra parameter in the model (26). Non-nested models were compared using the Akaike information criteria (AIC). The model with the lowest value of AIC, given the precision of model parameters and an adequate description of the data, was selected (29).

Data Evaluation, Biological Assumptions and Mathematical Model

Exploratory analysis of the tumour size data used to build the model (CyaA-E7 data) (Fig. 1) revealed four main aspects to be considered during model building process:

1. Tumour growth: in absence of vaccine administration, tumours grew almost linearly without reaching a plateau (Fig. 1a).

2. CyaA-E7 effect: the vaccine was able to induce a strong therapeutic response, delayed in time, against tumours expressing the protein and enabling a complete tumour regression under favourable environment conditions in most of the animals (Fig. 1b–d).

3. Resistance: an abrogated response to the vaccine efficacy was observed as tumour size at the time of vaccine administration increased. That phenomenon is particularly apparent in those groups receiving the vaccine at times greater than day 11 after cell inoculation (Fig. 1e–g). In fact, when vaccine was injected 30 days after the start of the experiment, tumour size profiles were very similar to those obtained from the control group.

4. Relapse: although complete tumour regression was expected in those mice sensitive to the treatment, tumour re-growth was observed in a small percentage of animals (Fig. 1b–d).

Fig. 1.

Individual raw data profiles. a–g C57BL/6 mice were injected with 5 × 10⁵ TC1 cells (n = 13–19 mice per group) on day 0. A unique dose of PBS or of 50 μg of CyaA-E7 was intravenously administered on day 4, 7, 11, 18, 25 or 30 (yellow line) (8). h–i C57BL/6 mice were injected with 5 × 10⁵ MC38 cells (n = 12–21 mice per group) on day 0. A unique dose of PBS or a hydrodynamic injection of 10 μg of a plasmid codifying for murine IL-12 was administered on day 23 (yellow line) (25). Tumour size, computed as the mean of two perpendicular diameters, over time is represented for each mouse and each dosing group included in the study; 2 mm was considered as the limit of quantification (dashed line)

Taking into account previous knowledge of the system and the observed tumour size profiles, the following assumptions were made:

1. Tumour growth was considered to be independent of tumour size.

2. Given the absence of pharmacokinetic data of the vaccine, and to describe its fate, a K-PD type of approach (30) where the kinetics of the antigen is inferred from the dynamics of the response observed was used, assuming in this case that once the antigen enters into the systemic circulation, it distributes fast and it is eliminated following a first-order rate process. Equation 1 (see below) represents the K-PD model used.

3. CyaA-E7 vaccine (VAC) was considered to trigger, through an intermediate transit compartment (TRAN), a vaccine signal (SVAC) able to reduce tumour size by a term proportional to both the vaccine signal and the tumour size (Ts). SVAC was assumed to remain constant over time (parameter k₂ in Eq. 3 set to 0; see below), thus avoiding tumour re-growth after vaccine clearance.

4. A vaccine resistance explaining the decrease in vaccine response was included in the model by incorporating a regulator (REG) compartment controlled by tumour size, and able to inhibit vaccine efficacy.

5. And finally, the existence of a sub-population of mice able to trigger only a temporal tumour response was postulated to describe the relapse observed in a few mice. To account for the two sub-populations, a mixture model (31) was implemented at the vaccine signal level by allowing the estimation of different degradation constant rates for each sub-population (k₂ in Eq. 3; see below) and the probability of belonging to each sub-population 1 [P(1)] or 2 [1 − P(1)].

Figure 2 depicts schematically the final selected model which is mathematically represented by the following set of ordinary differential equations (1–5):

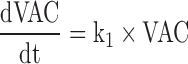1

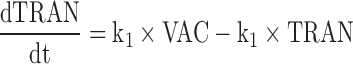2

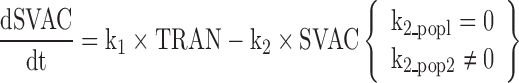3

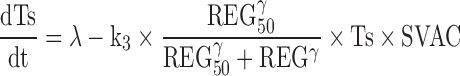4

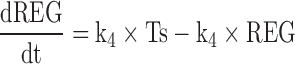5

Fig. 2.

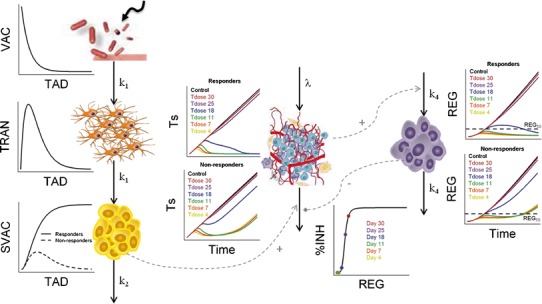
Schematic representation and population performance of the mathematical model selected. After VAC administration and through a transit compartment (TRAN), the vaccine triggers a signal (SVAC) able to decrease tumour size (Ts). Two different populations (responders and non-responders) at the level of the SVAC elimination were identified. An inhibition of vaccine efficacy induced by a regulator compartment (REG) controlled by tumour size was detected. The behaviour of the different model compartment over time for both populations, along with the percentage of inhibition (%INH) induced by REG over k₃ versus the amount in the regulator compartment under no vaccine administration, and highlighting the REG amount at relevant time points, are presented. k ₁ first-order rate constant controlling vaccine elimination and transit between compartments; k ₂ first-order rate constant accounting for SVAC degradation; λ zero-order rate constant of tumour growth; k ₃ the vaccine efficacy second-order rate constant; k ₄ the first-order rate constant controlling the regulator compartment dynamics; REG ₅₀ amount in the regulator compartment needed to inhibit vaccine activity by a half; γ the shape of that inhibitory process. TAD time after dose (vaccine) administration. Tdose day of vaccine administration

Where λ is the zero-order rate constant of tumour growth, k₁ represents the first-order rate constant controlling vaccine elimination and transit between compartments, k₂ is first-order rate constant accounting for SVAC degradation, k₃ is the vaccine efficacy second-order rate constant, and k₄ is the first-order rate constant controlling the regulator compartment dynamics. REG₅₀ represents the amount in the regulator compartment needed to inhibit vaccine activity by a half, and γ the steepness of the k₃versus REG relationship.

The system described by Eqs. 1, 2, 3, 4, and 5 showed the following initial conditions at the time of cell inoculation: Ts₀, tumour size at baseline (a parameter to be estimated); the rest of initial conditions VAC₀, TRAN₀, SVAC₀, and REG₀ were equal to 0. At the time of vaccine injection, VAC₀ was set to an arbitrary value of 1 due to the absence of pharmacokinetic data.

Note that due to the fact that the proposed model has been developed based on tumour size data only, and to preserve model parameter identifiability, the processes reflecting vaccine elimination and turnover of the vaccine elicited inhibitory signal (SVAC) share the same parameter (k₁).

Model Evaluation and Validation

A total of 1,000 datasets with the same study design characteristics as the original one were simulated using the inter-animal and residual variability of the model for each animal group. Performance of the selected model was graphically evaluated by exploring the simulated tumour size time course, percentage of BQL over time and probability of cure at the end of the study. Since data were pooled from independent experiments and measurements were not performed at the same times, observations were finally grouped in eight bins obtaining a similar number of observations per bin to facilitate model evaluation.

• Visual predictive checks: The 50^th percentile of the simulated observations in each dataset were computed for the different time intervals. Then, the 90% confidence interval of the 50^th percentile was obtained and plotted against the 50^th percentile of raw tumour size data.

• Numerical Predictive Checks: for each simulated dataset and group of treatment, (1) the probability of cure—calculated as the ratio between the number of mice which predicted tumour size was below the limit of quantification at the end of the study and the total number of simulated mice— and (2) the percentage of BQL data—obtained as the ratio between the number of simulated BQL data over the total number of measurements at different time intervals—were obtained and compared with the corresponding values derived from raw data.

Applicability of the Mathematical Model

To describe tumour size dynamics from Medina-Echeverz et al. (25) (Fig. 1h–i), the same set of equations was used, now considering IL-12 as immune-stimulatory agent, and estimating those parameters dependent upon the tumour cell line (Ts₀, λ and REG₅₀) or upon the immunotherapeutic agent (k₁) together with the corresponding inter-animal variability.

The results were evaluated and graphically inspected as previously described for the CyaA-E7 vaccine data.

Sensitivity Analysis

The relevance of the different model parameters on the system was evaluated by increasing or decreasing a 10% one parameter at a time and evaluating the impact on the predicted tumour size on day 40 after CyaA-E7 vaccine administration on day 25.

Generalization of the Model: Combination Therapy

Berkeley-Madonna software was used to evaluate the effects on tumour size of administering CyaA-E7 vaccine in combination with a theoretical drug. Different mechanism of action and a range of efficacy or potency constant rate values were evaluated (see Supplementary materials for a detailed description of the simulated scenarios).

RESULTS

Mathematical Model

In a first step, a model describing unperturbed (i.e., absence of the therapeutic agent) tumour growth was developed using data from the control group only. A linear growth governed by the λ parameter and independent of Ts described data well. The exponential model (which is dependent on Ts) provided also proper model performance but the typical estimate of Ts₀ was 2.4 mm, an unrealistic value given that the limit of tumour detection was set to 2 mm. Other models frequently used in the analysis of xenograft mice (32,33) were also tested in the current analysis, but a worse model performance was observed.

Parameter estimates of the selected model are summarized in Table I. IAV was found significant for λ (p < 0.01) but not for TS₀ (p > 0.01).

Table I.

Parameters of the Mathematical Model Developed

Parameter	CyaA-E7		IL-12
	Mean value	IAV (%)	Mean value	IAV (%)
	[2.5th–97.5th]	[2.5th–97.5th]	[2.5th–97.5th]	[2.5th–97.5th]
Ts0 (mm)	0.324 [0.0796–0.572]	–	1.16 × 10−6 [5.57 × 10−7–2.35 × 10−6]	–
λ (mm · day−1)	0.354 [0.325–0.381]	10.1 [4.9–13.4]	0.335 [0.306–0.362]	19.3 [11.3–24.4]
k 1 (day−1)	0.0907 [0.0842–0.118]	–	0.189 [0.101–0.615]	–
P(1)	0.844 FIX	–	0.844 FIX	–
k 2_pop1 (day−1)	0 FIX	–	0 FIX	–
k 2_pop2 (day−1)	0.0907 [0.0842–0.118]	–	0.189 [0.101–0.615]	–
k 3 (au · day−1)	1.08 [0.870–1.378]	–	1.08 FIX	–
k 4 (day−1)	0.0390 [0.0193–0.0771]	–	0.0390 FIX	–
REG50 (mm)	3.18 [1.767–4.422]	33.8 [25.4–53.2]	2.08 [1.387–2.966]	36.1 [6.4–60.2]
γ	5.24 [3.673–6.781]	–	5.24 FIX	–
Residual error [Log (mm)]	0.206 [0.184–0.228]	–	0.168 [0.128–0.215]	–

Once the unperturbed tumour growth was characterized, the effect of the CyaA-E7 vaccine over tumour growth was introduced into the model integrating the information gathered from the exploratory analysis of the observed profiles (training dataset, see “Materials and Methods” section), and the previous knowledge of the system.

To account for the observed delay in the response to the CyaA-E7, a transit compartmental model, originally proposed to describe drug absorption process and where the optimal number of transit compartments can be estimated as a model parameter (34), was tested. The model described the data adequately, but number of transit compartments could not be estimated with precision. Therefore, intermediate (transit) compartments were included one at a time, and the AIC and model performance of the models with the different number of compartments was compared. Two transit compartments, where the signal in the second would be responsible for inducing tumour shrinkage (SVAC), proved to be enough to describe the data successfully (ΔAIC of −1097, −96 and −3 points compared with no delay, one or three transit compartments, respectively). A simpler model describing the delayed effect incorporating a lag time was also evaluated, but model description was worse (ΔAIC = 109 points compared with two transit compartments).

The introduction of a mixture model at the level of SVAC disappearance allowed us to describe the relapse process and its frequency within the studied population (15.6% when considering only dosing at 4, 7, 11 days where resistance can be neglected). It was assumed the existence of two sub-populations, one with a permanent (k₂ = 0) vaccine signal, while in the other, the treatment would elicit a transient (k₂ ≠ 0) vaccine signal. Considering a “tumour size threshold” below which permanent cure would be achieved or simple variability in drug efficacy or drug elimination parameters were also evaluated to describe tumour relapses; however, those assumptions presented convergence problems.

Regarding the reduced treatment efficiency observed when vaccine administration was delayed, an inhibition of the vaccine efficiency rate (k₃) as a function of the current tumour size was introduced. Inhibition of the constant rate controlling the appearance of the signal vaccine (k₁) or a simple drug efficacy decay with time were also explored but a worse fit was obtained in both cases (ΔAIC of 268 or 1436, respectively). Different models were tested to account for the inhibitory effect, observing the lowest AIC and overall better model performance when the Hill function was implemented (Eq. 4). Finally, inclusion of a regulator compartment to delay the inhibitory effect of the tumour further improved the description of the data (ΔAIC = −101 points compared with no delay).

With regard to random effects, our data supported the inclusion of inter-animal variability in λ and REG₅₀ (ΔAIC = −356 points compared with no IAV). Table I summarizes the estimates of parameters that characterize the final selected model schematically represented in Fig. 2. Note that in Fig. 2 the dynamics of the components of the model developed corresponding to the typical mice in each of the two sub-populations are shown.

Observed and model predicted tumour size profiles for selected mice (training dataset, see “Materials and Methods”) showing complete remission or relapse for each of the groups used to develop the model can be seen in Fig. 3 (Supplementary Figure 1 shows additional plots for individual predictions).

Fig. 3.

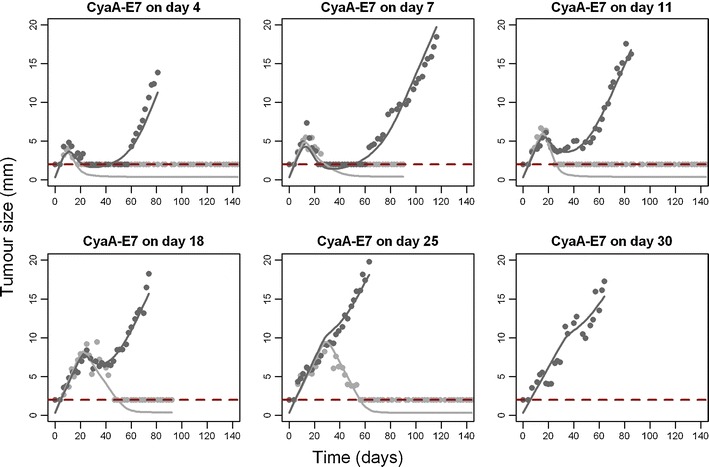
Individual model predictions. Tumour size observations (points) and individual model predictions of a mouse that respond (light grey) or do not respond (dark grey) to the vaccine are presented for the different CyaA-E7 dosing groups. 2 mm was considered as the limit of quantification (dashed line)

Visual predictive checks were performed for tumour size data above the quantification limit, along with the predicted percentage of BQL over time for the different vaccine administration protocols (training dataset, see “Materials and Methods”) (Fig. 4). Despite some discrepancies observed, especially at early vaccine administration protocols due to the low number and variability of the relapsing mice, globally, the selected model was able to successfully describe tumour size data, not only of those experiments from the training dataset, but also of two independent studies not used during the model building process (validation dataset) (Supplementary Figure 2) increasing model robustness. In addition, a good agreement between the observed and the model predicted probabilities of cure of each studied group was obtained (Fig. 5) in both training and validation datasets.

Fig. 4.

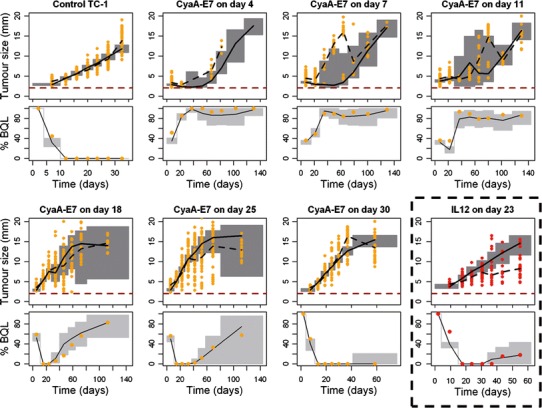
Visual and numerical predictive check to evaluate final model performance. Simulated tumour size measurements above the limit of quantification (upper panels) and percentage of data below the limit of quantification (lower panel) versus raw data (points) are plotted over time for CyaA-E7 (orange) or IL-12 (red) dosing groups. Grey areas in the upper panels represent the 90% prediction interval of the simulated median. Grey areas in the lower panels represent the 90% prediction interval of the simulated percentage of data below the limit of quantification. Solid and dashed black lines are the simulated and raw median respectively. 2 mm was considered as the limit of quantification (red dashed line)

Fig. 5.

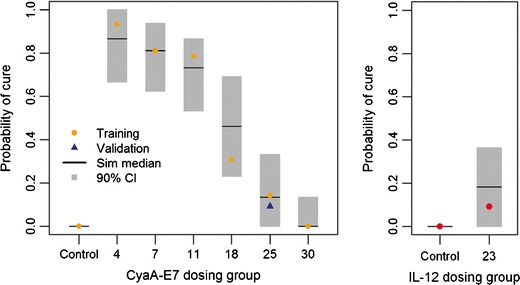
Vaccine efficacy evaluation. Probability of cure at the end of the experiment was estimated for 1000 simulated studies for both tested therapies CyaA-E7 (left panel) and IL-12 (right panel). Simulated median was plotted against raw probability of cure for each dosing group in the training dataset (points). Grey shadow represents 90% prediction interval of the simulated data. Blue triangle represents probability of cure of an independent study not included in the analysis (external evaluation with the validation dataset)

Applicability of the Mathematical Model

To study if the proposed model structure for tumour size response after CyaA-E7 vaccine administration could be extrapolated to other immunotherapy protocols, data from the work of Medina-Echeverz et al. (25) were used. In their experimental setting, hydrodynamic administration of IL-12, a cytokine known to activate effector cells, was performed in tumour-bearing mice. Pharmacokinetic data were not available and therefore, an instantaneous expression of the plasmid followed by an exponential decay of the drug, as did for the CyaA-E7 vaccine, was assumed.

The same set of model equations was used to fit the data, allowing the estimation of those parameters either related to the tumour cell line (REG₅₀, λ and Ts₀) or to the drug kinetic (k₁). The model was able to fairly capture the data, both above and below the limit of quantification (Fig. 4), and successfully estimate the probability of cure observed in each dosing group after vaccine administration (Fig. 5).

This result provides a further validation of the mathematical model developed and its biological assumptions suggesting that this structure could be used as a general approach to model other drugs with similar mechanisms of action.

Generalization of the Model: Combination Therapy

Combining two or more therapeutic agents is a common strategy to increase the rate of success in cancer therapy. Simulation exercises can be undertaken to gain some insight on the impact that diverse theoretical treatments could have on tumour size when administered along with the CyaA-E7 vaccine once the reliability of a model has been proven.

To evaluate which components of the system had a greater impact on tumour size response when vaccine efficiency was impaired (i.e., CyaA-E7 administered on day 25), a sensitivity analysis was performed as in (15). Sensitivity was assessed by increasing or decreasing one model parameter at a time and quantifying the induced change on tumour size at the end of the simulation (day 40). For the exercise, sub-population developing a permanent response to the treatment (k₂ = 0), and therefore susceptible to cure, was only considered.

The results of the analysis are shown in Fig. 6a. The system showed to be more sensitive to those parameters controlling tumour growth (λ) and the appearance (k₄) or potency (REG₅₀ and γ) of the inhibitory response triggered by tumour size than to those parameters related to vaccine kinetics (k₁) or efficacy (k₃). These results suggested that in order to increase treatment efficiency, drugs able to impair the inhibitory response triggered by tumour size or to act on tumour growth should be considered.

Fig. 6.

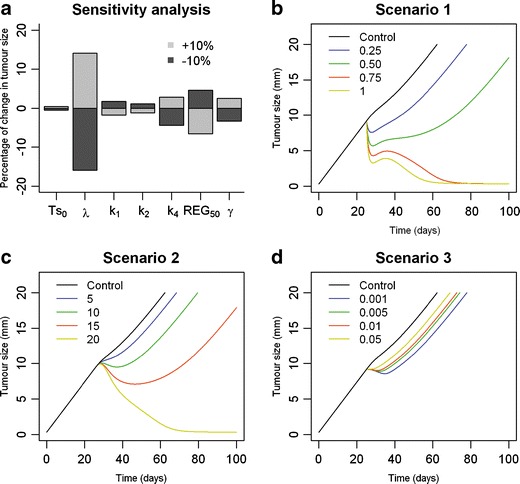
Generalization of the model. a Sensitivity analysis of the model representing the percentage of change in tumour size when one model parameter at a time is modified. b–d Predicted tumour response over time for different theoretical drugs when administered in combination with CyaA-E7 vaccine on day 25 after tumour cell inoculation. A range of efficacy parameters is explored for each simulated scenario (see Supplementary material)

Taking into account the results from the sensibility analysis and plausible drugs mechanisms of action, three different combination therapy scenarios where a drug able to either induce tumour cell death (scenario 1), increase clearance of regulator compartment (therefore reducing the inhibitory effect exerted over vaccine efficiency, scenario 2), or inhibit tumour growth (scenario 3) were evaluated (the structure of the combination therapy models used for the discussed simulations are shown as supplementary material).

Results from the simulation exercise showed that a complete tumour regression could be achieved in scenarios 1 or 2 if drugs potent enough were used (Fig. 6b–c) or if more multiple dosing regimens were followed (data not shown). On the other hand, decreasing tumour growth rate, apparently the most sensitive parameter, only had a small impact on tumour growth, even when highly potent drugs were simulated (Fig. 6d).

DISCUSSION

Applications of modelling and simulation concepts to describe the outcome from pre-clinical studies and clinical trials have been reported in many occasions and during several decades. More specifically, in the arena of cancer, Norton et al. published in 1976 a general application of the Gompertz model to describe tumour growth (35). More recently several authors have developed models that incorporate important characteristics of the anticancer drugs (i.e., pharmacokinetics or pharmacodynamics). Simeoni and co-workers proposed a model including pharmacokinetics, drug effects, signal transduction, and tumour dynamics (33,36). This pioneer work was followed by others in which biomarker contribution was also considered (37–39).

In the field of immunotherapy, different mathematical models have been proposed to describe the interaction between immune response and tumour growth (13,18,20,40). However, only a few of them have been successfully applied to real data (15–17,19), mainly due to the complexity and high number of model parameters of the proposed models. Therefore, the current work represents a reduction in the description of the biological complexity in which cellular and molecular components are not individually modelled but empirically incorporated into the model (i.e., using a series of transit compartments to account for maturation processes).

The main objective of this work was to develop a mathematical model to describe tumour size dynamics and its interaction with the immune system after the administration of a previously developed vaccine consisting on the fusion of the E7 human papillomavirus protein to the adenylate cyclase of Bordetella pertussis (7). This vaccine increases antigen presentation to dendritic cells, which will then activate a potent and specific Th1 and cytotoxic T-lymphocyte response (effector cells) against tumours in a murine model of cervical cancer.

In agreement with the described CyaA-E7 vaccine mechanism of action, where intermediate cell populations are needed before effector cells proliferate, two transit compartments were needed to describe the observed delay in tumour shrinkage after vaccine administration, where the last compartment (here called SVAC) could be associated to the effector cells activated by the vaccine. Given the lack of drug or effector T cells measurements a common parameter (k₁) had to be used to describe the different processes.

In the proposed model, two important features, usually present in datasets from antitumor therapies in mice, were considered during the analysis: values of tumour size that fall below the detection limit (BQL data) and information about individual tumour behaviour, which normally is treated as pool data assuming that all the animals from an experimental group react uniformly to the drug.

Inclusion of BQL data as censored observations (27) proved to be relevant not only after drug treatment to capture relapse, but also at early times after tumour cell inoculation, to characterize the unperturbed tumour model. Ignoring BQL data, an exponential model would have been selected (rendering an estimate of tumour size at baseline higher than the detection limit and inclusion of variability in that parameter). Including the censored information, first, tumour size at baseline had a realistic estimate, and its inter-animal variability was not supported by the data (an expected result), and second, data after relapse could be described better since they appeared to follow a linear increase with time. A similar relevance of BQL inclusion was reported very recently for the case of the testosterone levels in cancer patients, in which for most of the time period of the study some patients were mainly below the detection limit (41).

Another feature that has been incorporated in the model, and which to the best of our knowledge has not been applied in this type of analysis yet, has been the possibility to identify different subject populations with regard to the response to the treatment, by including mixture models (31), successfully applied in clinical studies (42,43). Apart from the estimation of different parameters across the various sup-populations, the percentage of subjects belonging to each of them is also estimated [P(1)]. This result, in addition to the parameters reflecting drug efficacy, is worth to be taken into account when comparing different treatments.

A challenge when using a mixture model is to relate the presence of more than one population to a particular mechanism. In our case, no statistical differences on tumour size at the moment of vaccine administration were found between both populations (p > 0.05). In addition, different parameters for vaccine induce signal (k₁), or signal efficacy (k₂) rate constants would not have been able to explain relapse after full tumour shrinkage. Consequently, the mixture model was applied to the rate of disappearance of the vaccine induced signal (k₃). This result suggests that the vaccine is able to trigger a permanent immune response (probably mediated by memory T cells) in the cured mouse population, but no in all the mice. A well-known phenomenon in immunotherapy (not all the subjects respond equally to vaccination protocols) (44,45). Since only tumour size information was available, a fixed value of 0 had to be assigned to those animals that did not show relapse. Other cure mechanisms, such as considering a “cure threshold” as in (46), were also tested, but failed in predicting individual profiles.

The final feature included into the model was vaccine resistance. A decrease in the number of cured mice as the time between tumour inoculation and vaccine administration increased could be clearly observed in the raw data (Fig. 1). Lu et al. (47) found a similar decrease in tumour response when multiple dosing regimens were followed. They modelled that phenomenon as a time-dependent exponential decay of drug efficacy. In our model, a more mechanistic approach was followed. It has been described that the observed resistance phenomenon is caused by tumour recruitment and expansion of an immune-regulatory cell population (regulatory T cells) able to suppress anti-tumour immune response (48,49). This mechanism was mathematically implemented by considering that tumour size inhibited vaccine efficiency through a regulator compartment that could be interpreted as the immune-regulatory cell compartment.

Given the complexity of the different phenomena controlling tumour growth, probability of cure and resistance related parameters could not be simultaneously obtained. We attribute this result to the fact that the tumour size induced resistance shown in later groups was masking the real proportion of non-cured mice. Therefore, P(1) was fixed to a value obtained when only dose on day 4,7 or 11 groups (where the resistance term was not yet needed) were analysed.

Proper evaluation of model performance is always required, but it is even more important in cases as the one we show here in which different type of measurements (censored and non-censored), and different populations are considered. In that respect, our work provides additional novelties. For example, Fig. 4 shows how the model behaves for the data that were reported as below the detection limit. In addition, Fig. 5 provides an alternative to judge model performance and efficacy of the treatment based on the percentage of cured animals.

Ideally, a model should be (1) capable to describe response outcomes for a series of different experimental scenarios, (2) validated with additional set of data, and (3) applicable to different therapeutic strategies. Results from the model evaluation, model validation, and model applicability exercises undertaken during the current investigation confirm that the proposed model fulfilled main goals in mathematical modelling of in vivo response.

Despite the semi-mechanistic nature of the model here developed, it has been proven that the model can be applied to describe drugs that might apparently have different mechanisms of action, but in last term induce an adaptive immune response. Nevertheless, drugs acting on different levels at the same time or with complex pharmacokinetics or pharmacodynamics interaction would probably require of extra biological information to properly characterize the different biological processes.

A natural expansion of the current work will be its generalization to handle combination with other anticancer therapies, a widely accepted strategy to improve efficacy of cancer immunotherapy (50). Raw data of tumour size after combination therapy were also shown in the work by Berraondo et al. (8). Data showed increment in vaccine response after combination. Despite in the current work initial exploration of potential response outcome based on different assumptions about possible mechanisms of action of the drugs to be combined has been performed (Fig. 6b–d), the analysis of those data, which corresponds to an ongoing project, are beyond the scope of this study.

CONCLUSION

This work presents a novel mathematical model where different modelling strategies within the population approach such as censored data or mixture model have been integrated to successfully describe the different outcomes obtained after CyaA-E7 vaccine administration. Moreover, the model structure here proposed can be extrapolated to describe tumour growth response to different immunotherapeutic strategies with a similar mechanism of action, such as IL-12. This model can be used to maximize the information obtained from preclinical cancer immunotherapy experiments and therefore, can be useful for the design of better clinical trials of immune modulating drugs.

Electronic Supplementary Material

Below is the link to the electronic supplementary material.