Abstract
The Constraint Network Analysis (CNA) web server provides a user-friendly interface to the CNA approach developed in our laboratory for linking results from rigidity analyses to biologically relevant characteristics of a biomolecular structure. The CNA web server provides a refined modeling of thermal unfolding simulations that considers the temperature dependence of hydrophobic tethers and computes a set of global and local indices for quantifying biomacromolecular stability. From the global indices, phase transition points are identified where the structure switches from a rigid to a floppy state; these phase transition points can be related to a protein’s (thermo-)stability. Structural weak spots (unfolding nuclei) are automatically identified, too; this knowledge can be exploited in data-driven protein engineering. The local indices are useful in linking flexibility and function and to understand the impact of ligand binding on protein flexibility. The CNA web server robustly handles small-molecule ligands in general. To overcome issues of sensitivity with respect to the input structure, the CNA web server allows performing two ensemble-based variants of thermal unfolding simulations. The web server output is provided as raw data, plots and/or Jmol representations. The CNA web server, accessible at http://cpclab.uni-duesseldorf.de/cna or http://www.cnanalysis.de, is free and open to all users with no login requirement.
INTRODUCTION
Proteins carry out their biological functions by interacting with other biomacromolecules or small molecules (1). These interactions require a certain degree of conformational adaptation to better complement the binding partners. That way, structural flexibility of proteins is linked to molecular recognition and catalysis (2). Additionally, flexibility (and its opposite, rigidity) also plays a central role for a protein’s structural stability (3). Particularly, thermophilic proteins are in general more rigid than their mesophilic homologues to retain their fold at higher temperatures (4). Hence, knowing what can move in a protein is important for linking a protein’s structure to its function and (thermo-)stability. Finally, information on protein flexibility is increasingly incorporated in computer-aided drug discovery and design projects (5).
X-ray crystallography, cryo-electron microscopy, single molecule fluorescence and nuclear magnetic resonance spectroscopy are experimental means from which the flexibility of a protein can be inferred (6–9). As an alternative, computational methods such as molecular dynamics (MD) simulations (10) and normal mode analysis are used to probe protein flexibility and dynamics (11). As yet another computational approach, a computationally highly efficient graph theory-based rigidity analysis for probing protein flexibility has been implemented in the Floppy Inclusions and Rigid Substructure Topography (FIRST) software (12). FIRST builds a constraint network from a biomolecular structure and then decomposes this network into rigid clusters and flexible regions by using the pebble game algorithm (13,14). In the constraint network, atoms are represented as bodies, and covalent bonds and non-covalent interactions (including hydrogen bonds, salt bridges, stacked rings, and hydrophobic tethers) are represented as bars (constraints) between them. Building on the ideas of Rader et al. (15) on diluting non-covalent constraints in a constraint network, our group has developed the Constraint Network Analysis (CNA) approach that performs thermal unfolding simulations of proteins (16). CNA goes beyond the mere identification of rigid clusters and flexible regions in a biomolecule in that it (i) provides a refined modeling of thermal unfolding simulations that also considers the temperature dependence of hydrophobic tethers; (ii) allows performing rigidity analyses on ensembles of network topologies, either generated from structural ensembles or by using the concept of fuzzy non-covalent constraints; and (iii) computes a set of global and local indices for quantifying biomacromolecular stability (17). Furthermore, CNA robustly handles small-molecule ligands in general. CNA has been successfully used for investigating protein thermostability, identifying unfolding nuclei (‘structural weak spots’), and linking protein flexibility and function (18–20).
In this study, we present the CNA web server that allows (i) setting up a variety of constraint network representations of proteins from either single structures or ensembles of structures; (ii) performing rigidity analyses and thermal unfolding simulations on these networks; and (iii) processing the results. For that, the CNA web server provides a layer of user-friendly input and output interfaces around the CNA software. As input, the web server only requires a Protein Data Bank (PDB) code or user-provided PDB file(s) of the input structure(s), and choosing the simulation type. Results are presented in the browser in an interactive manner. For global indices, plots are provided; for local indices, plots and mappings onto the 3D structure [via a JmolApplet (http://jmol.sourceforge.net)] are provided. Weak spots predicted for a protein structure are also mapped onto the 3D structure. To the best of our knowledge, there are no other web servers that allow performing and analyzing thermal unfolding simulations of proteins in as much detail as the CNA web server does. Of the two most closely related web servers, KINARI (http://kinari.cs.umass.edu/Site/kinariWeb.html) (21) only performs rigid cluster decompositions, but no thermal unfolding simulations. Flexweb (http://flexweb.asu.edu/software/first/) does allow performing thermal unfolding simulations; however, it neither supports the use of ensembles of structures (which leads to more robust results from rigidity analyses) nor does it automatically determine phase transition points (‘melting points’) and unfolding nuclei (which extends the application domain of rigidity analysis to data-driven protein engineering). Thus, in addition to characterizing the distribution of flexible and rigid regions in a protein, the CNA web server can be used for probing changes in the flexibility/(thermo-)stability of a protein due to mutations or on ligand binding, and it aids in identifying structural weak spots in a protein that, when mutated, may improve the protein’s (thermo-)stability. Note that the CNA web server solely characterizes what can move in a protein but does not simulate actual protein movements. To do the latter, the user is referred to the NMSim web server (http://cpclab.uni-duesseldorf.de/nmsim/ or http://www.nmsim.de) developed by us (22).
MATERIALS AND METHODS
Constructing a constraint network
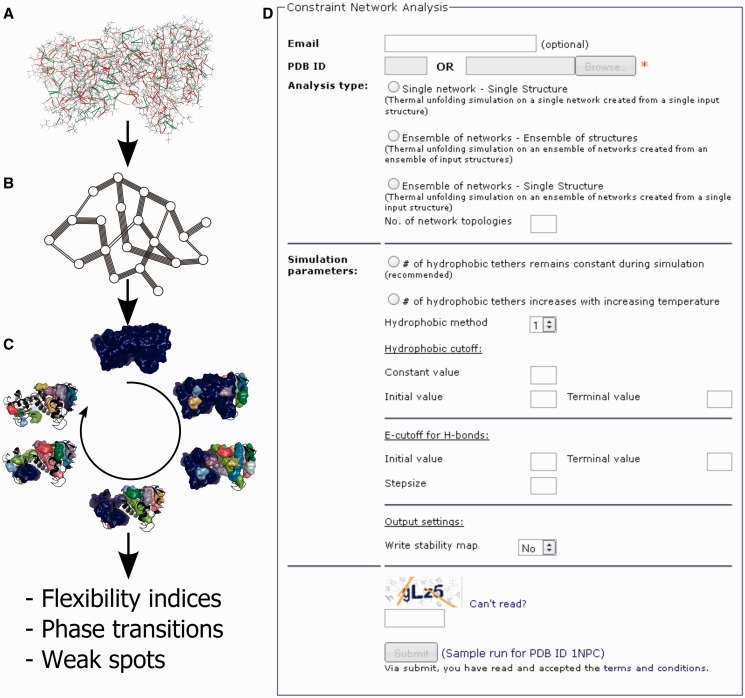
Proteins are modeled as body-and-bar networks where each atom is represented as a body with six degrees of freedom (23). Interactions between the atoms (covalent and non-covalent bonds) are modeled as a set of bars that restrict internal motion between the atoms. A covalent single bond is modeled with five bars allowing for the dihedral rotation about it; peptide and double bonds are modeled with six bars, disallowing any bond rotation. For example, a diatomic molecule with a single bond, owing to the five constraints, has seven degrees of freedom (6 × 2 − 5), six of which represent the trivial overall rotations and translations and one of which represents the internal rotation around the single bond. Non-covalent interactions, which contribute significantly to protein stability, are also modeled as bars. As such, hydrogen bonds (and salt bridges) are modeled with five bars, whereas hydrophobic and ring stacking interactions are modeled with two and three bars, respectively (24). Figure 1A shows the structure of thermolysin-like protease (TLP; PDB code: 1NPC) from which a body-and-bar network is then generated (Figure 1B).
Figure 1.
Covalent and non-covalent interactions in a protein structure (A) are modeled as bars in a body-and-bar network (B). A rigid cluster decomposition is carried out for all network states during a thermal unfolding simulation (C) and then post-processed to calculate flexibility indices, phase transitions, and weak spots. (D) Submission page to the CNA web server.
Performing a rigid cluster decomposition
Once the constraint network of a protein is built, the pebble game algorithm (13,14) as implemented in the FIRST software (12) decomposes the network into rigid clusters and flexible regions (Figure 1C). The pebble game algorithm then computes the rigidity of the protein network at a bond level by determining whether a bond is part of a rigid cluster or a flexible region. As such, a rigid cluster is a set of atoms for which no internal motions are allowed and that move together in a collective manner.
Simulating thermal unfolding
By successively removing non-covalent constraints from a biomolecular constraint network, new network representations at elevated temperatures are constructed. To do so, for a given network state s = f(T), hydrogen bonds (including salt bridges) with an energy Ehb > Ecut,hb are removed from the network (25). This follows the idea that stronger hydrogen bonds will break at higher temperatures than weaker ones. The hydrogen bond energy scale Ehb (25) is converted into a temperature scale T, using a linear equation proposed by Radestock and Gohlke (19). By default, the number of hydrophobic tethers is kept constant during the thermal unfolding simulation. However, as the strength of hydrophobic interactions increases with increasing temperature (26,27), hydrophobic tethers can also be treated in a temperature-dependent manner on request (20). Finally, a rigid cluster decomposition is performed on each constraint network state s to compute global and local flexibility indices (Figure 1C).
Computing global and local flexibility indices
The CNA web server computes in total six global and three local flexibility indices. Detailed definitions of the global and local flexibility indices are given elsewhere (17). In short, the global indices represent the macroscopic network flexibility (and rigidity) of each network state s: (i) The floppy mode density Φ refers to the number of internal independent degrees of freedom that are associated with dihedral rotations, normalized by the number of overall internal degrees of freedom associated with the total number of bodies in the network; (ii) the mean rigid cluster size S is computed with the size of the largest rigid cluster always being excluded; (iii) & (iv) the rigidity order parameter P∞ denotes the fraction of the network belonging to the giant percolating cluster (type 1) or the actual largest rigid cluster (type 2). The giant percolating cluster is the largest rigid cluster in the network state at the lowest temperature, i.e. with all constraints in place. During the thermal unfolding simulation, the melting of the giant percolating cluster is monitored, and the largest rigid subcluster of the previous giant percolating cluster becomes the new giant percolating cluster of the present network state s. In contrast, the actual largest rigid cluster is the largest cluster present at a network state s, irrespective of its evolutionary history during the thermal unfolding simulation; (v) & (vi) the cluster configuration entropy H (type 1 and type 2) is a measure of the degree of disorder in the realization of a given network state.
Local indices characterize the flexibility of network at the bond level by monitoring the change in the flexibility for each bond during the thermal unfolding simulation: (i) the percolation index pi is determined for each covalent bond by the Ecut,hb value during the thermal unfolding simulation at which the bond segregates from the giant percolating cluster; (ii) the rigidity index ri is determined for each covalent bond by the Ecut,hb value during the thermal unfolding simulation at which the bond changes from rigid to flexible. For a Cα atom-based representation of a protein structure, the lower of the pi values (the average of the ri values) of the two backbone bonds is taken; (iii) a stability map rcij is a 2D itemization of the rigidity index ri and is derived by identifying the Ecut,hb value during the thermal unfolding simulation at which a rigid contact between a pair of residues represented by their Cα atoms is lost. Two residues are in rigid contact if they are part of the same rigid cluster.
Identifying phase transitions and unfolding nuclei
The global flexibility indices are used for identifying phase transitions during the thermal unfolding simulation when the network switches from being largely rigid to flexible. Such transitions (‘melting points’) can be related to the (thermo-)stability of proteins (18–20). The CNA web server provides phase transition points for four of the global indices: P∞, type 1 and 2 and Htype 1 and 2. A smoothed spline fitted to the global indices is used to identify the phase transition points except for Htype2, for which a double sigmoid curve is fitted. The phase transition points are identified as the maximum in the first derivative in the case of the smoothed spline and the maximum of the differences in the asymptote pairs in the case of the double sigmoid curve. The phase transition points can be further exploited to identify structural weak spots in the network from where an unfolding begins: these are residues that are part of the largest rigid cluster before the phase transition and become flexible afterwards. Weak spots provide hints as to where introducing mutations in a structure may improve a protein’s (thermo-)stability.
Simulating thermal unfolding of a network ensemble
Results from rigidity analyses are in general sensitive to the input structure in that small changes in the conformation can lead to a different rigid cluster decomposition (28,29). To overcome this drawback, an ensemble-based variant of CNA has been developed that makes use of an ensemble of structures derived from MD simulations (20,28). Structural ensembles from any other sources can be used as input, too. As yet another alternative, the CNA web server provides an option to create an ensemble of networks from a single input structure by using fuzzy non-covalent constraints (Pfleger, C., Gohlke, H., unpublished data). Here, the number and distribution of non-covalent constraints are modulated by random components within certain ranges, that way simulating thermal fluctuations of a biomolecule without actually moving atoms. This approach avoids the use of computationally expensive MD simulations. For ensemble-based CNA, averages are computed over the entire ensemble for phase transition points and local indices. In the case of weak spots, the frequencies of occurrence across the entire ensemble are reported.
DESCRIPTION OF THE WEB SERVER
Input
The submission page to the CNA web server is shown in Figure 1D. The CNA web server requires either a single structure of a protein provided as a PDB file or a PDB-ID (in which case the PDB file will be downloaded from the Research Collaboratory for Structural Bioinformatics repository), or multiple protein structures provided as PDB files in a compressed folder (allowed file formats are *.tgz, *.tar.gz or *.zip) or as a ‘multi-PDB file’ using MODEL/ENDMDL cards. Furthermore, the web server requires selection of an analysis type and input of a given security code to prevent misuse. Analyses can be performed on a single constraint network derived from a single structure, on an ensemble of networks derived from a single structure or on an ensemble of networks derived from a structural ensemble. According to the selected analysis type, default parameters will be provided that have been successfully used in previous studies (17–20). In addition, the user can request the time-consuming computation of a stability map. An email address can be provided in which case a link to the results will be sent to that address. In either case, a link to a results page is provided after job submission for monitoring the progress of the computations and viewing the results in the web browser. The results will also be stored on the server for 10 days and can be accessed via the provided link.
If the user provides a PDB ID, missing sidechain and hydrogen atoms will be automatically added by the leap program of the AMBER suite (30). For amino acid sidechains, a standard protonation state is assumed, i.e. Asp and Glu are treated as deprotonated, and Arg and Lys as protonated. By default, His is singly protonated with the hydrogen on the epsilon nitrogen. Alternate sidechain conformations are allowed, but only the first conformation is considered. Water molecules and ligands will be removed.
To have complete control on the input structure(s), a user can upload a/multiple PDB file(s). In that case, water molecules and ligands are considered, and correct bond orders for ligands are identified automatically using the Open Babel wrapper (Pybel) for Python (31,32). The correct identification of ligand bond orders is important to accurately set up covalent constraints for the network. In this case (i) hydrogen atoms must have been added already, (ii) alternate side-chain conformations are not allowed; and (iii) the protein structure must be complete, i.e. no missing sidechains are allowed. Finally, if the analysis is based on an ensemble of structures, all protein structures must be identical except for the coordinates. Otherwise, an error message will be issued.
Output and representation of results
A typical analysis run of the CNA web server for a constraint network of a single structure takes a few minutes; for the analysis of an ensemble, several hours of computing time may be required. After the start, the progression of the analysis is reported on the results page. On completion of a job, the results are presented in the web browser and, if an address is provided by the user, an email is sent with a link to the results, too.
The first part of the results page contains a summary of input parameters that were provided by the user and a download link to the modified input file. The modified input file contains all changes made during preparation of the uploaded structure.
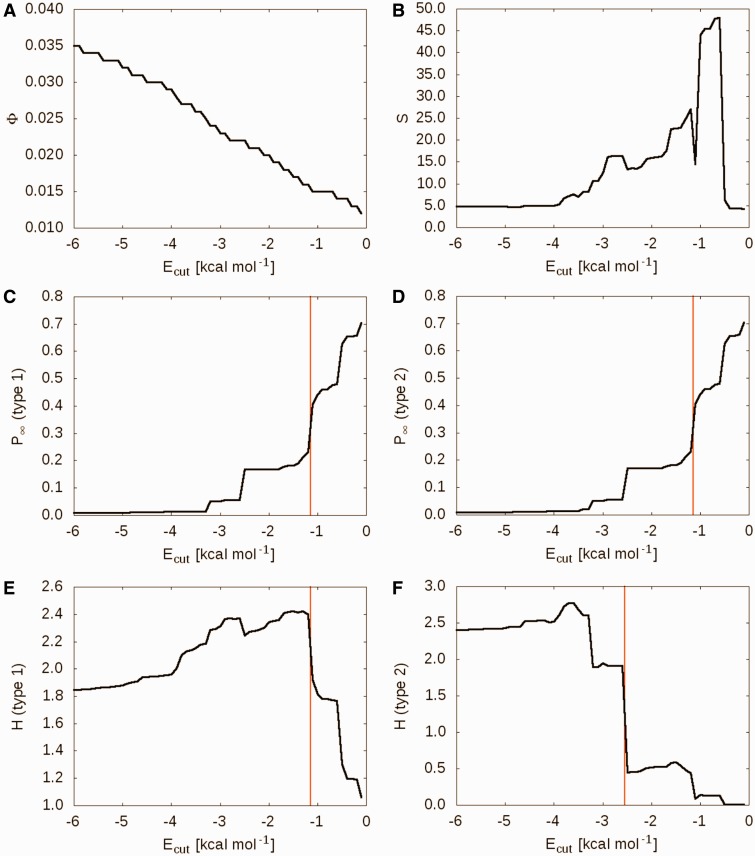
The second part of the results page contains a table that provides information about identified phase transition points. In the case of a single-network analysis, six plots of the global flexibility indices are depicted: floppy mode density Φ (Figure 2A), mean rigid cluster size S (Figure 2B), rigidity order parameter P∞, type 1 and 2 (Figure 2C and D) and cluster configuration entropy Htype 1 and 2 (Figure 2E and F). Identified phase transition points are marked by red vertical lines. In the case of an ensemble-based analysis, a summary of the identified phase transition points is presented instead. In any case, a file with the raw data can be downloaded by a link given next to the headline of the chapter for further evaluation.
Figure 2.
Global indices for the thermal unfolding of TLP as a function of the hydrogen bonding energy cutoff Ecut,hb: (A) floppy mode density Φ; (B) mean rigid cluster size S; rigidity order parameter P∞ (C) type 1 and (D) type 2; cluster configuration entropy H (E) type 1 and (F) type 2. The red vertical lines (C–F) correspond to the identified phase transitions.
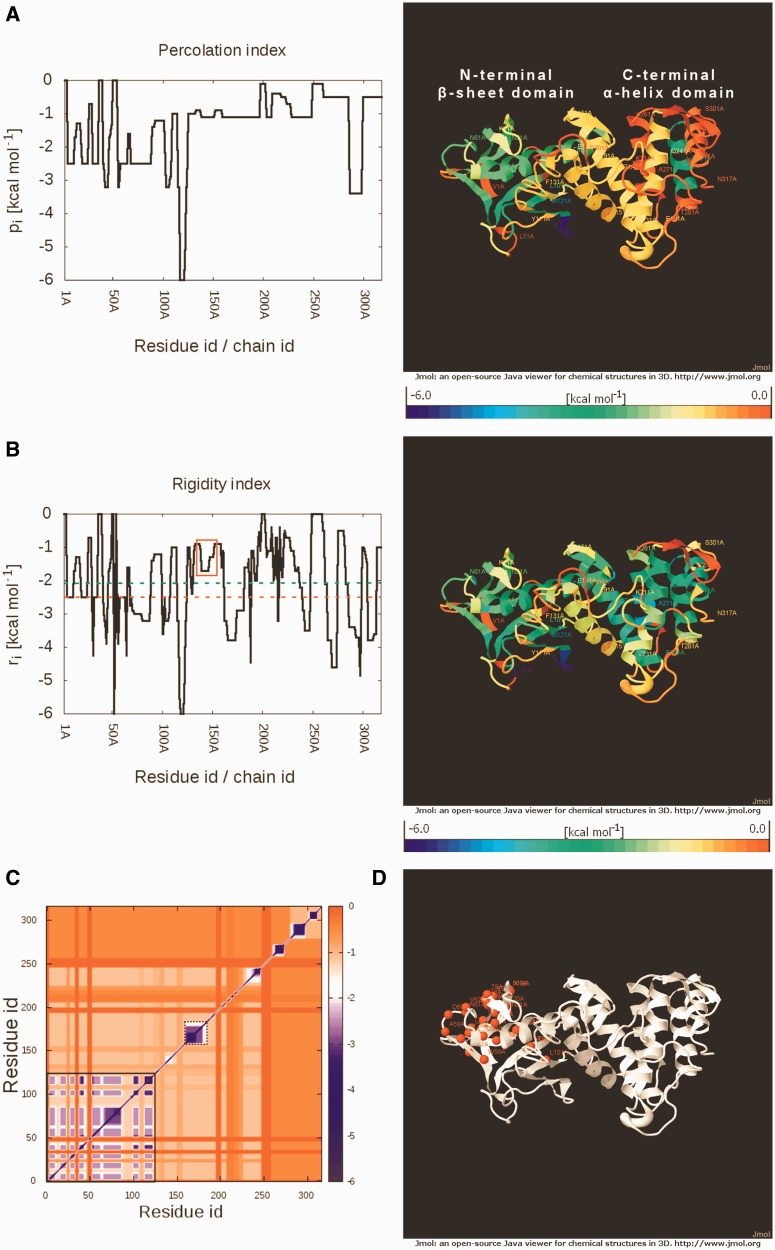
The third part contains two plots of the local flexibility indices for each residue: percolation index pi (Figure 3A) and rigidity index ri (Figure 3B). In the case of an ensemble-based analysis, the standard errors are depicted in gray in addition to the mean values. Furthermore, both indices are mapped onto the input structure in a color-coded fashion and shown in JmolApplets. A file with the raw data can be downloaded by a link given next to the headline of the chapter for further evaluation as can be two PDB files. These PDB files contain the modified input structure of the protein with the respective index values of Cα atoms in the B-factor column.
Figure 3.
(A) Percolation index pi for TLP. The lower pi the longer is a residue part of the giant percolating cluster during the thermal unfolding simulation. (B) Rigidity index ri for TLP. The lower the ri, the longer is a residue part of a rigid cluster during the thermal unfolding simulation. Red- and green-dashed horizontal lines represent the identified phase transition point and the working temperature of TLP, respectively. The central α-helix and two preceding Gly residues (residues 136–154) residues are enclosed in a red rectangle. On the right, the respective indices are mapped onto the input structure in a color-coded manner. (C) Stability map rcij for TLP. Red colors indicate pairs of residues where no or only a weak rigid contact exists. In contrast, blue colors indicate strong rigid contacts. The black box with a continuous line covers the N-terminal giant rigid cluster, whereas the box with the broken line indicates a rigid cluster in the C-terminal domain. (D) Weak spots in the TLP structure are represented by red spheres.
The fourth part contains a stability map rcij (Figure 3C) (if requested) and information about weak spots identified in the protein (Figure 3D). For rcij, the color code reveals for each residue pair if the rigid contact is weak (red) or strong (blue). Information about weak spots is mapped onto the input structure and displayed in a JmolApplet: in the case of a single-network analysis, identified weak spots are marked by red spheres; in the case of an ensemble-based analysis, the frequency of a residue for being identifed as a weak spot across the entire ensemble is depicted. This information is provided as a plot, too. Again, two files can be downloaded by links given next to the headline of the chapter for further evaluation: a file with the raw data and a PDB file containing the modified input structure of the protein with the respective frequency values in the B-factor column.
Implementation
The CNA web server has been implemented in Python, as have been the underlying CNA routines (16). All plots are generated with Gnuplot. Given the low computational demand of our approach, up to 10 submitted jobs can be run in parallel at present.
APPLICATION TO TLP AS A TEST CASE
In a previous study from our group, the CNA approach has been shown to link protein rigidity and thermostability by correctly predicting which one of two proteins is more thermostable for two thirds of a data set of 19 pairs of proteins from mesophilic and thermophilic organisms (18). In the same study, we showed that structural weak spots identified by CNA agreed with the positions of thermostabilizing mutations for two systems investigated. Extending the application domain of CNA one step further, the local flexibility and rigidity distributions in the active sites of 3-isopropylmalate dehydrogenase and TLP were then linked to enzymatic activity at different temperatures (19). Recently, using CNA on citrate synthases with distinct thermostabilities, we showed that thermostabilizing mutations preferentially occur at structural weak spots with a high mutation ratio (14).
Here, we demonstrate the application of the CNA web server to TLP from Bacillus cereus (PDB code: 1NPC) using a single-network approach with default settings. These results are also available as a sample run on the web server. Plots for global indices are shown in Figure 2. The decrease in network rigidity of TLP with increasing temperature (equivalent to a decreasing Ecut,hb) is evident from the plots of all six global indices. Interestingly, the decay of the giant rigid cluster occurs in a hierarchical fashion as reflected by the presence of multiple steps in the P∞ and H profiles (Figure 2C–F). The reason for this percolation behavior is that the TLP structure is composed of multiple sub-domains (N-terminal β-sheet domain and C-terminal α-helical domain connected by a central helix) that segregate from the giant cluster independently from each other. Phase transition points at which the TLP structure sharply loses rigidity on thermal unfolding are then identified: an early phase transition point at Ecut,hb = −1.14 kcal mol−1 is identified from the P∞ and Htype1 profiles when the C-terminal α-helical domain segregates from the giant cluster; in contrast, Htype 2 fosters the identification of a late transition at Ecut,hb = −2.55 kcal mol−1 [or, equivalently, 351 K (19)], which represents the final substantial decay of the rigid core. Such late transitions have been found to best relate to the melting of a protein. The temperatures of the transition points should be considered relative values only because the absolute values may depend on the size and architecture of the analyzed protein (19). Still, the temperatures are helpful, e.g. when it comes to comparing the thermostability of two or more homologous proteins or the stability of a wild-type with its mutant (18–20). Accordingly, the Htype 2 phase transition point for a thermophilic homologue of TLP, thermolysin from Bacillus thermoproteolyticus, was found at 373 K (24), ∼20 K higher than for the mesophilic homologue investigated here.
The percolation index plot depicts the percolation behavior of TLP at a residue level (Figure 3A). The C-terminal α-helical domain segregates from the giant cluster early during the thermal unfolding simulation at Ecut,hb ≈ −1.1 kcal mol−1. The giant percolating cluster, which then consists of mainly the β-sheet region and an α-helix in the N-terminal domain, disintegrates into smaller clusters at the later phase transition point (Ecut,hb = −2.55 kcal mol−1). Unsurprisingly, the rigidity index, which monitors the flexibility at a residue level, shows secondary structure elements to be more rigid than loops. As an exception, residues 117–120 forming a loop in the N-terminal domain are always part of a rigid cluster throughout the thermal unfolding simulation owing to a network of hydrophobic tethers. For TLPs, the central α-helix (residues 139–154) and the preceding Gly136 and Gly137 are important with respect to a postulated hinge bending motion (33,34), suggesting that these residues should be flexible at the working temperature of TLP [342 K, equivalent to Ecut,HB = −2.1 kcal mol−1 (19)]. This is also found in the rigidity index profile (Figure 3B). Furthermore, contacts of these residues with other residues of TLP are less stable than contacts between residues of the giant cluster (black box with continuous line) and contacts between residues of a large rigid cluster in the C-terminal domain (black box with broken line) as identified by the stability map (Figure 3C). This is again in line with the hinge character of the central α-helix. Finally, several of the weak spots identified by CNA in the N-terminal β-sheet domain of TLP (Figure 3D) have been shown to improve the protein’s thermostability on mutation in previous studies (35–38).
CONCLUSIONS
Increasing evidence of the importance of protein flexibility has warranted the development of efficient and accurate computational tools for characterizing protein flexibility at global and local levels. To this end, the CNA approach has been developed for deriving maximal advantage from information on biomolecular flexibility and rigidity by linking results from rigidity analyses to biologically relevant characteristics of a structure, such as (thermo-)stability and function (16). In particular, CNA provides a refined modeling of thermal unfolding simulations that also considers the temperature dependence of hydrophobic tethers, allows performing rigidity analyses on ensembles of network topologies and computes a set of global and local indices for quantifying biomacromolecular stability. Furthermore, CNA robustly handles small-molecule ligands in general. To make these computations available for users even with only minimal or no prior knowledge of structural bioinformatics techniques, we developed the CNA web server. It provides a user-friendly interface, requires minimal input and displays the results intuitively both as plots and mappings onto the protein structure via JmolApplets. As a typical analysis run of the CNA web server for a constraint network of a single structure only takes a few minutes, we strongly believe that the CNA web server will be a valuable (interactive) tool for data-driven protein engineering and estimating the influence of ligand molecules on biomolecular stability.
FUNDING
Ministry of Innovation, Science, and Research of North Rhine-Westphalia and Heinrich Heine University, Düsseldorf, via a scholarship to P.C.R. within the CLIB-Graduate Cluster Industrial Biotechnology. Funding for open access charge: Institutional funding from Heinrich-Heine-University.
Conflict of interest statement. None declared.
ACKNOWLEDGEMENTS
The authors are grateful to Prof. Michael F. Thorpe (Arizona State University) for granting a FIRST license. They thank Daniel B. Ciupka, Doris L. Klein, Tobias Kröger and Giulia Pagani (Heinrich Heine University, Düsseldorf) for testing the web server and helpful suggestions.
REFERENCES
- 1.Schellman JA. Macromolecular binding. Biopolymers. 1975;14:999–1018. [Google Scholar]
- 2.Daniel RM, Dunn RV, Finney JL, Smith JC. The role of dynamics in enzyme activity. Annu. Rev. Biophys. Biomol. Struct. 2003;32:69–92. doi: 10.1146/annurev.biophys.32.110601.142445. [DOI] [PubMed] [Google Scholar]
- 3.Vihinen M. Relationship of protein flexibility to thermostability. Protein Eng. 1987;1:477–480. doi: 10.1093/protein/1.6.477. [DOI] [PubMed] [Google Scholar]
- 4.Závodszky P, Kardos J, Svingor Á, Petsko GA. Adjustment of conformational flexibility is a key event in the thermal adaptation of proteins. Proc. Natl Acad. Sci. U.S.A. 1998;95:7406–7411. doi: 10.1073/pnas.95.13.7406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cozzini P, Kellogg GE, Spyrakis F, Abraham DJ, Costantino G, Emerson A, Fanelli F, Gohlke H, Kuhn LA, Morris GM, et al. Target flexibility: an emerging consideration in drug discovery and design. J. Med. Chem. 2008;51:6237–6255. doi: 10.1021/jm800562d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Frank J, Agrawal RK. A ratchet-like inter-subunit reorganization of the ribosome during translocation. Nature. 2000;406:318–322. doi: 10.1038/35018597. [DOI] [PubMed] [Google Scholar]
- 7.Ishima R, Torchia DA. Protein dynamics from NMR. Nat. Struct. Mol. Biol. 2000;7:740–743. doi: 10.1038/78963. [DOI] [PubMed] [Google Scholar]
- 8.Weiss S. Fluorescence spectroscopy of single biomolecules. Science. 1999;283:1676–1683. doi: 10.1126/science.283.5408.1676. [DOI] [PubMed] [Google Scholar]
- 9.Zhang XJ, Wozniak JA, Matthews BW. Protein flexibility and adaptability seen in 25 crystal forms of T4 lysozymes. J. Mol. Biol. 1995;250:527–552. doi: 10.1006/jmbi.1995.0396. [DOI] [PubMed] [Google Scholar]
- 10.Karplus M, McCammon JA. Molecular dynamics simulations of biomolecules. Nat. Struct. Mol. Biol. 2002;9:646–652. doi: 10.1038/nsb0902-646. [DOI] [PubMed] [Google Scholar]
- 11.Case DA. Normal mode analysis of protein dynamics. Curr. Opin. Struct. Biol. 1994;4:285–290. [Google Scholar]
- 12.Jacobs DJ, Rader AJ, Kuhn LA, Thorpe MF. Protein flexibility predictions using graph theory. Proteins. 2001;44:150–165. doi: 10.1002/prot.1081. [DOI] [PubMed] [Google Scholar]
- 13.Jacobs DJ, Hendrickson B. An algorithm for two-dimensional rigidity percolation: the pebble game. J. Comp. Phys. 1997;137:346–365. [Google Scholar]
- 14.Jacobs DJ, Thorpe MF. Generic rigidity percolation: the pebble game. Phys. Rev. Lett. 1995;75:4051–4054. doi: 10.1103/PhysRevLett.75.4051. [DOI] [PubMed] [Google Scholar]
- 15.Rader AJ, Hespenheide BM, Kuhn LA, Thorpe MF. Protein unfolding: rigidity lost. Proc. Natl Acad. Sci. U.S.A. 2002;99:3540–3545. doi: 10.1073/pnas.062492699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Pfleger C, Rathi PC, Klein DL, Radestock S, Gohlke H. Constraint Network Analysis (CNA): A Python software package for efficiently linking biomacromolecular structure, flexibility, (thermo-)stability, and function. J. Chem. Inf. Model. 2013;53:1007–1015. doi: 10.1021/ci400044m. [DOI] [PubMed] [Google Scholar]
- 17.Pfleger C, Radestock S, Schmidt E, Gohlke H. Global and local indices for characterizing biomolecular flexibility and rigidity. J. Comp. Chem. 2013;34:220–233. doi: 10.1002/jcc.23122. [DOI] [PubMed] [Google Scholar]
- 18.Radestock S, Gohlke H. Exploiting the link between protein rigidity and thermostability for data-driven protein engineering. Eng. Life Sci. 2008;8:507–522. [Google Scholar]
- 19.Radestock S, Gohlke H. Protein rigidity and thermophilic adaptation. Proteins. 2011;79:1089–1108. doi: 10.1002/prot.22946. [DOI] [PubMed] [Google Scholar]
- 20.Rathi PC, Radestock S, Gohlke H. Thermostabilizing mutations preferentially occur at structural weak spots with a high mutation ratio. J. Biotechnol. 2012;159:135–144. doi: 10.1016/j.jbiotec.2012.01.027. [DOI] [PubMed] [Google Scholar]
- 21.Fox N, Jagodzinski F, Li Y, Streinu I. KINARI-Web: a server for protein rigidity analysis. Nucleic Acids Res. 2011;39:W177–W183. doi: 10.1093/nar/gkr482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Krüger DM, Ahmed A, Gohlke H. NMSim web server: integrated approach for normal mode-based geometric simulations of biologically relevant conformational transitions in proteins. Nucleic Acids Res. 2012;40:W310–W316. doi: 10.1093/nar/gks478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Whiteley W. Counting out to the flexibility of molecules. Phys. Biol. 2005;2:S116–S126. doi: 10.1088/1478-3975/2/4/S06. [DOI] [PubMed] [Google Scholar]
- 24.Hespenheide BM, Jacobs DJ, Thorpe MF. Structural rigidity in the capsid assembly of cowpea chlorotic mottle virus. J. Phys. Condens. Matter. 2004;16:S5055–S5064. [Google Scholar]
- 25.Dahiyat BI, Gordon DB, Mayo SL. Automated design of the surface positions of protein helices. Protein Sci. 1997;6:1333–1337. doi: 10.1002/pro.5560060622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Privalov PL, Gill SJ. Stability of protein structure and hydrophobic interaction. Adv. Protein Chem. 1988;39:191–234. doi: 10.1016/s0065-3233(08)60377-0. [DOI] [PubMed] [Google Scholar]
- 27.Schellman JA. Temperature, stability, and the hydrophobic interaction. Biophys. J. 1997;73:2960–2964. doi: 10.1016/S0006-3495(97)78324-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Gohlke H, Kuhn LA, Case DA. Change in protein flexibility upon complex formation: analysis of Ras-Raf using molecular dynamics and a molecular framework approach. Proteins. 2004;56:322–337. doi: 10.1002/prot.20116. [DOI] [PubMed] [Google Scholar]
- 29.Mamonova T, Hespenheide B, Straub R, Thorpe MF, Kurnikova M. Protein flexibility using constraints from molecular dynamics simulations. Phys. Biol. 2005;2:S137–S147. doi: 10.1088/1478-3975/2/4/S08. [DOI] [PubMed] [Google Scholar]
- 30.Case DA, Cheatham TE, III, Darden T, Gohlke H, Luo R, Merz KM, Jr, Onufriev A, Simmerling C, Wang B, Woods RJ. The Amber biomolecular simulation programs. J. Comp. Chem. 2005;26:1668–1688. doi: 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.O'Boyle NM, Banck M, James CA, Morley C, Vandermeersch T, Hutchison GR. Open Babel: an open chemical toolbox. J. Cheminform. 2011;3:33. doi: 10.1186/1758-2946-3-33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.O'Boyle NM, Morley C, Hutchison GR. Pybel: a Python wrapper for the OpenBabel cheminformatics toolkit. Chem. Cent. J. 2008;2:5. doi: 10.1186/1752-153X-2-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.van Aalten DM, Amadei A, Linssen AB, Eijsink VG, Vriend G, Berendsen HJ. The essential dynamics of thermolysin: confirmation of the hinge-bending motion and comparison of simulations in vacuum and water. Proteins. 1995;22:45–54. doi: 10.1002/prot.340220107. [DOI] [PubMed] [Google Scholar]
- 34.Veltman OR, Eijsink VG, Vriend G, de Kreij A, Venema G, Van den Burg B. Probing catalytic hinge bending motions in thermolysin-like proteases by glycine –> alanine mutations. Biochemistry. 1998;37:5305–5311. doi: 10.1021/bi972374j. [DOI] [PubMed] [Google Scholar]
- 35.Imanaka T, Shibazaki M, Takagi M. A new way of enhancing the thermostability of proteases. Nature. 1986;324:695–697. doi: 10.1038/324695a0. [DOI] [PubMed] [Google Scholar]
- 36.Van den Burg B, Dijkstra BW, Vriend G, Vandervinne B, Venema G, Eijsink VGH. Protein stabilization by hydrophobic interactions at the surface. Eur. J. Biochem. 1994;220:981–985. doi: 10.1111/j.1432-1033.1994.tb18702.x. [DOI] [PubMed] [Google Scholar]
- 37.Van den Burg B, Vriend G, Veltman OR, Venema G, Eijsink VG. Engineering an enzyme to resist boiling. Proc. Natl Acad. Sci. U.S.A. 1998;95:2056–2060. doi: 10.1073/pnas.95.5.2056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Veltman OR, Vriend G, Middelhoven PJ, van den Burg B, Venema G, Eijsink VG. Analysis of structural determinants of the stability of thermolysin-like proteases by molecular modelling and site-directed mutagenesis. Protein Eng. 1996;9:1181–1189. doi: 10.1093/protein/9.12.1181. [DOI] [PubMed] [Google Scholar]