Effects of Pharmacokinetic Processes and Varied Dosing Schedules on the Dynamics of Acquired Resistance to Erlotinib in EGFR-Mutant Lung Cancer

Abstract

Introduction

Erlotinib (Tarceva) is an epidermal growth factor receptor (EGFR) tyrosine kinase inhibitor, which effectively targets EGFR-mutant driven non–small-cell lung cancer. However, the evolution of acquired resistance because of a second-site mutation (T790M) within EGFR remains an obstacle to successful treatment.

Methods

We used mathematical modeling and available clinical trial data to predict how different pharmacokinetic parameters (fast versus slow metabolism) and dosing schedules (low dose versus high dose; missed doses with and without make-up doses) might affect the evolution of T790M-mediated resistance in mixed populations of tumor cells.

Results

We found that high-dose pulses with low-dose continuous therapy impede the development of resistance to the maximum extent, both pre- and post-emergence of resistance. The probability of resistance is greater in fast versus slow drug metabolizers, suggesting a potential mechanism, unappreciated to date, influencing acquired resistance in patients. In case of required dose modifications because of toxicity, little difference is observed in terms of efficacy and resistance dynamics between the standard daily dose (150 mg/d) and 150 mg/d alternating with 100 mg/d. Missed doses are expected to lead to resistance faster, even if make-up doses are attempted.

Conclusions

For existing and new kinase inhibitors, this novel framework can be used to rationally and rapidly design optimal dosing strategies to minimize the development of acquired resistance.

Erlotinib (Tarceva; OSI Pharmaceuticals, Farmingdale, NY) is an orally active selective inhibitor of the epidermal growth factor receptor (EGFR) tyrosine kinase.¹ More than 70% of patients with non–small-cell lung cancer (NSCLC) harboring specific mutations in the EGFR kinase domain exhibit a radiographic response to erlotinib as defined by Response Evaluation Criteria In Solid Tumors (RECIST) standards on tumor reduction.^2–5 However, the evolution of acquired resistance remains a significant obstacle to successful treatment, with most patients usually progressing within 10 to 16 months.^6–9 In more than 50% of these patients, acquired resistance to erlotinib or the related drug, gefitinib, is mediated by a second-site mutation (T790M) within EGFR.^6,7,9

A major assumption for achieving clinical successes using small-molecule tyrosine kinase inhibitors (TKIs) in cancer therapy is that prolonged target inhibition is essential. Thus, TKIs usually have long half-lives and are administered on a clinically tolerable schedule that results in continuous target suppression. For example, the oral kinase inhibitor imatinib, used in frontline therapy for chronic myeloid leukemia (CML), causes prolonged inhibition of the breakpoint cluster region-Abelson tyrosine kinase 1 (BCR-ABL) kinase 24 hours after a single dose; the drug has a half-life of 18 hours and a long-acting metabolite with a half-life of 40 hours.^10,11 Other approved TKIs have similarly long half-lives in patients, including erlotinib (36 hours), gefitinib (48 hours), lapatinib (24 hours), sunitinib (40–60 hours), and sorafenib (25–48 hours). However, investigators recently demonstrated that intermittent target inhibition by another ABL TKI, dasatinib, was sufficient for activity in CML,¹² suggesting that TKIs can be dosed alternatively and remain clinically effective. These findings have prompted us to investigate optimal dosing strategies for EGFR TKIs in EGFR-mutant lung cancer.

In our previous work, we developed isogenic TKI-sensitive and TKI-resistant pairs of cell lines that mimic the behavior of human EGFR-mutant tumors.¹³ We determined that the drug-sensitive and drug-resistant EGFR-mutant cells exhibited differential growth kinetics, with the drug-resistant cells showing slower growth. We then used evolutionary cancer modeling to elucidate novel dosing strategies that prevent or delay progression of EGFR-mutant lung cancer caused by acquired resistance.

Here, we studied how patient-specific pharmacokinetic processes and therapeutic dosing strategies might alter the dynamics of resistance in heterogeneous cell populations. Using our previous cell-line measurements¹³ and additional clinical data,¹⁴ we modeled the pharmacokinetic processes under various dosing schedules to obtain an accurate description of the temporal plasma concentration of erlotinib over time. We then constructed a hybrid approach combining models of these pharmacokinetic processes with evolutionary models of the dynamics of resistance in the cell population, enabling us to study detailed time-dependent features of pharmacokinetic processes such as the speed of drug elimination and its impact on the emergence of resistance. We also determined how patient noncompliance (e.g., missed doses) and treatment withdrawal upon progression of disease affect the risk of developing resistance. This mathematical framework allowed us to generate novel predictive theoretical models of EGFR-mutant lung cancer, which could be used to improve treatment of patients with the disease.

MATERIALS AND METHODS

Evolutionary Modeling of EGFR-Mutant Cancer Cells

The population of EGFR-mutant cells was modeled as a multitype, inhomogeneous, continuous-time birth–death process. The numbers of sensitive and resistant cells at any particular time t are given by X(t) and Y(t), respectively. We considered a population that initially consists of M(1-s) sensitive and Ms resistant cells, where s varies between 0 and 1; thus the case when s = 0 corresponds to a fully sensitive initial population of size M. Sensitive cells proliferate and die with rates λ_X(t) and μ_X(t), whereas resistant cells proliferate and die with rates λ_Y(t) and μ_Y(t). These time-dependent rates reflect the effect of treatment on the population and thus depend on how the drug concentration in the body varies over time. Note that in our model, the parameters describing cell death, denoted by the rates μ_X(t) and μ_Y(t), take into account both apoptosis and any other potential forms of cell death that cells might undergo.

During each replication of a sensitive cell, the EGFR T790M mutation may arise with probability μ, giving rise to a new resistant cell. The joint process X(t) = (X(t), Y(t)) represents the combined state of the sensitive and resistant populations at time t. We obtained analytical formulae for the probability of resistance and estimates of the mean and variance of sensitive and resistant cells under general time-dependent dosing schedules. The derivation of the analytical approximations is outlined elsewhere.^15,16

Pharmacokinetics refers to the processes by which a drug is absorbed, distributed, metabolized, and eliminated by the body.¹⁷ Because these processes directly impact the concentration of drugs in different organs over time, any mathematical model describing the effects of treatment schedules on the evolution of resistance should incorporate pharmacokinetic considerations.^18,19 We thus used clinical data in conjunction with a pharmacokinetic model to describe the drug concentration as a function of time for a given treatment schedule.

To study the dynamics of resistance emerging during a particular dosing schedule, we coupled the pharmacokinetic model with our stochastic evolutionary model of the cancer cell population. This combined mathematical framework was then used to investigate the effects of pharmacokinetic processes on the risk of resistance. In particular, for a given treatment schedule defined by a dose intensity over time, the pharmacokinetic model was used to obtain the drug concentration, C(t), in the body as a function of time. We subsequently used experimentally determined relationships between the drug concentration and the birth and death rates of sensitive and resistant individuals to obtain the parameters of the stochastic model, λ_X(t) and μ_X(t) as well as λ_Y(t) and μ_Y(t). The stochastic model was then used to investigate the dynamics of resistance emerging during pharmacological interventions directed at cancer cells. This hybrid methodology can be extended to include arbitrarily complex pharmacokinetic models with multiple compartments describing many different pharmacokinetic processes.^20,21 However, here we used a simple exponential drug-elimination model as dictated by the clinical pharmokinetic data on erlotinib.

Determining Growth- and Death-Rate Parameters

Sensitive and resistant cells may have distinct growth and death rates, which vary depending on the drug concentration. These evolutionary model parameters were experimentally determined as previously described,¹³ using a pair of isogenic PC-9 human EGFR-mutant cell lines with and without the T790M point mutation. Measurements were performed at erlotinib concentrations of 0, 1, 3, 10, and 20 μM.

Note that we considered pharmacokinetic data and models of dosing schedules in human patients. However, when comparing the dynamics of resistance among these schedules, we used the available in vitro growth kinetic data from our model system. This limitation prevented us from making predictions about the actual temporal dynamics of resistance evolution in human patients because in vitro growth kinetics occur on a different time scale than the in vivo kinetics do. However, even though in vivo growth kinetic data are unavailable, we were able to gain valuable insights from this model system about the relative comparison of various dosing schedules because the relative differences in growth kinetics in vitro are likely preserved in patients.

Estimating Pharmacokinetic Parameters for Erlotinib

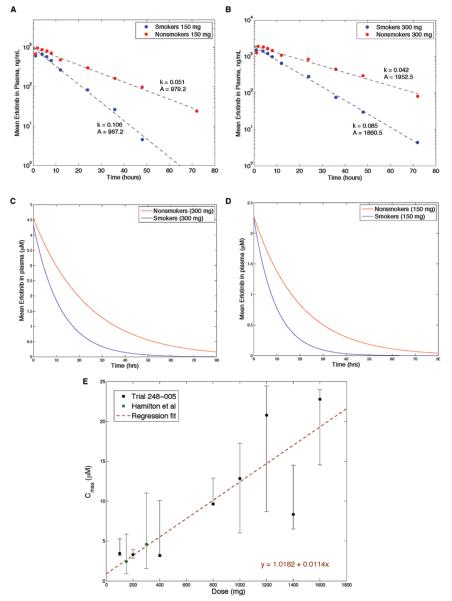
Detailed measurements of erlotinib plasma concentrations have been recorded over time for current smokers and nonsmokers.¹⁴ Healthy subjects were given single doses of 150 mg and 300 mg of erlotinib, and the erlotinib concentration of plasma was sampled 11 times over the course of 72 hours. This approach showed that the metabolic clearance of erlotinib occurs faster in smokers at both concentrations. We used data collected in this study to estimate the pharmacokinetic rate of erlotinib elimination from the body. We considered a function governing the erlotinib plasma concentration over time after each dose d of the form C(t) = A e^−kt. The parameter k represents the elimination rate of the drug and the parameter A approximates the maximum concentration usually known as the C_max; both parameters depend on the initial dose and may vary between patients, such as between groups of smokers and nonsmokers. Note that we used data on smokers and nonsmokers to obtain an understanding of the diversity of pharmacokinetic rates within a patient population. Even though the majority of lung cancer patients with EGFR-mutant tumors have a history of not smoking, these rates serve as the extreme ends of the distribution of rates within a heterogeneous patient population.

Figure 1A and B displays the erlotinib plasma concentration¹⁴ over time after a single dose of 150 mg (Fig. 1A) and 300 mg (Fig. 1B). For each dose and test group, we performed least squares regression to infer the two parameters, A and k, which are displayed in the panels. Our choice of the functional form implies that C_max is achieved immediately after each dose; as shown by the panels, this functional form approximates the exponential decay indicated in the data very well. Although the data points show that the erlotinib concentration peaks approximately 2 to 3 hours after administration, the exponential form used is appropriate because we considered dosing strategies changing on the time scale of days, not hours; this modeling choice has the advantage of a smaller number of parameters to fit. This assumption was made for all dose levels.

FIGURE 1.

Pharmacokinetics of NSCLC cells. Plasma concentration over time for smokers and nonsmokers after (A) a 150 mg dose and (B) a 300 mg dose, both shown on a log-linear plot. Fitted plasma concentration over time for smokers and nonsmokers after (C) a 150 mg dose and (D) a 300 mg dose, both on a linear plot. E, The mean C_max of erlotinib as a function of the oral dose administered, with error bars reflecting the minimum and maximum values observed. The average time of C_max varied between 2 and 9 hours. Data were obtained from the Tarceva Investigators Brochure and Hamilton et al.¹⁴

The fitted curves of concentration versus time with erlotinib shown in micromolar units (μM) are provided in Figure 1C and D. These units are used in the remainder of the article. The molecular weight of erlotinib, used in this conversion, is 429.9 g/mol.

We then extrapolated this data to understand the pharmacokinetic processes at a spectrum of doses between 0 and 1600 mg erlotinib. Because our studies focused on patients whose tumors harbored EGFR mutations, and because this patient population was enriched for nonsmokers, we used pharmacokinetic data from the nonsmoker cohort of Hamilton et al.¹⁴ We observe a linear relationship between the C_max and the oral dose (Fig. 1E). We therefore used this fitted relationship as an estimate for A (in μM units) in our model: A (d) = 1.0182 + 0.0114 d, where d is the oral dose.

We then investigated the rate k and its dependence on the administered dose. We obtained values of k at doses 150 mg and 300 mg for nonsmokers and smokers.¹⁴ However, data for other doses were not available. Because the rate of elimination at 300 mg was slightly lower than at 150 mg for both smokers and nonsmokers, we set k as the mean of the observed k at 150 and 300 mg (k[d] = 0.0465 hours⁻¹ for nonsmokers). A nonconstant relationship between d and k may exist, but in the absence of additional data points, we used the simplest assumption.

RESULTS

Dosing Schedules Affect the Dynamics of Resistance

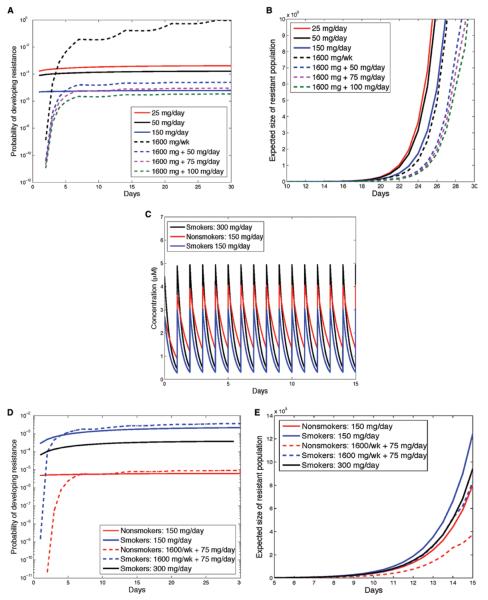
Erlotinib was approved for the treatment of unselected NSCLC at 150 mg/d. However, doses of erlotinib 25 mg/d still lead to characteristic response rates and progression-free survival in EGFR-mutant lung cancer.²² To date, no prospective randomized trials have been performed in patients with EGFR-mutant lung cancer to determine which dosing strategy leads to superior clinical outcomes. Here, we explored the effects of altering the dosing schedule on the dynamics of resistance. In addition to the Food and Drug Administration-approved schedule of 150 mg/d, we investigated doses of 25 mg/day and 50 mg/day as well as schedules involving a high-dose pulse of 1600 mg/week with and without additional daily low doses throughout the remainder of the week (Fig. 2). Variation in the number of sensitive cells when changing from one schedule to the next is minimal. To determine the probability of resistance over time for a variety of dosing schedules (Fig. 3A), we assumed that initially, the tumor contains 1 million cells and has a mutation rate generating resistant cells of 10⁻⁸ per cell division. Although a modification of these estimates would alter the outcomes slightly, it would not affect the relative comparison between dosing schedules.

FIGURE 2.

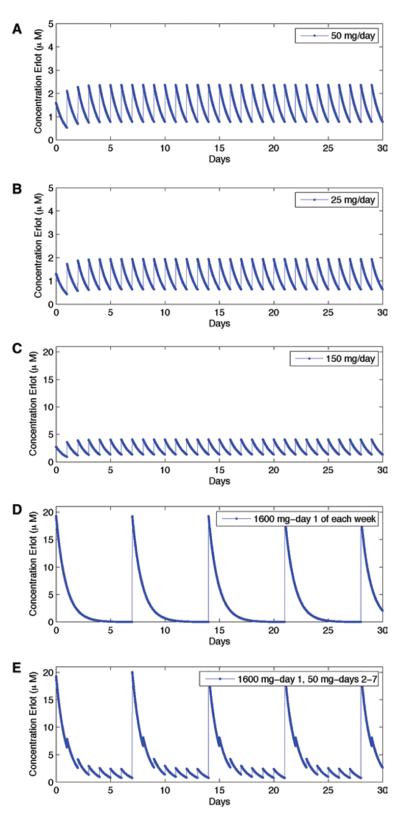
The choice of treatment schedule influences the plasma concentrations of erlotinib. Erlotinib plasma concentration as a function of time during several dosing schedules (50 mg/d, 25 mg/d, 150 mg/d, and 1600 mg/week, and 1600 mg/week with 50 mg on remaining days.

FIGURE 3.

The choice of treatment schedule influences the probability of resistance and expected number of resistant cells. Probability of resistance as a function of time under various dosing schedules with no preexisting resistance. A, Initial population size: M = 10⁶ cells with no preexisting resistance. Expected size of resistant population as a function of time during various dosing schedules. B, Initial population size: M = 10⁶ cells containing 100 resistant cells. C, Plasma concentration over time in smokers and nonsmokers for the standard 150 mg/d dose, and for smokers on the 300 mg/d schedule. D, Probability of resistance as a function of time for smokers and nonsmokers with no preexisting resistance. Expected size of resistant population as a function of time, under various dosing schedules for smokers and nonsmokers with preexisting resistance. E, Initial population size: M = 10⁶ cells with 100 resistant cells. For all panels, the mutation rate is μ = 10⁻⁸ per cell division.

We first performed modeling under the assumption that cell populations contain no preexisting resistance. A schedule including a once-weekly pulse of 1600 mg/week with a break for the remainder of the week resulted in the highest probability of developing resistance. This outcome occurs because during treatment breaks cells resume proliferation; note that the rates of apoptosis are not significantly changed by the concentration of the drug. By contrast, schedules combining a once-weekly pulse with low doses during the remainder of the week were comparable with the 150 mg/d schedule. In both cases, sensitive cell division is inhibited continuously.

We next evaluated these treatment schedules for the scenario that preexisting resistant cells are present at a small frequency in the cancer cell population at diagnosis. For instance, consider that 100 out of the initially present 1 million cells harbor the T790M point mutation conferring resistance to erlotinib. In all cases, pulsed schedules were favorable to daily schedules, because the use of high doses decelerates the overall growth of the resistant population (Fig. 3B). In this scenario, the 1600 mg/week schedule outperformed the 150 mg/d schedule, and continuing low doses during the remainder of the week further enhanced this benefit. Collectively, these data show that the use of high-dose pulses with low-dose continuing therapy impedes the development of resistance to the maximum extent. This combination would also be optimal for situations in which the presence of preexisting resistance is unknown.

Pharmacokinetic Effects Alter the Dynamics of Resistance

We next sought to understand the effects of interpatient pharmacokinetic variability on the dynamics of resistance. Specifically, we aimed to determine how variability in the rate of drug elimination (fast metabolism versus slow metabolism) affects the probability of developing resistance and the size of the resistant cell population among patients. To study plausible human ranges of variability in the rate of drug elimination, we used detailed pharmacokinetic studies with 150 mg/d and 300 mg/d demonstrating that smokers have a faster rate of drug elimination compared with nonsmokers.¹⁴ For these investigations, we did not consider the effects of the metabolites OSI-413 and OSI-420 against EGFR; generally, these metabolites arise at 5% to 10% of the levels of erlotinib in the plasma and have similar activity against EGFR as erlotinib does.

In the case of no preexisting resistant cells, the probability of developing resistance in fast metabolizers was approximately two orders of magnitude higher than that for slow metabolizers, for both a standard dose of 150 mg/d or a double dose of 300 mg/d (Figs. 3C and D). Note that the plasma concentration for 300 mg/d in the fast metabolizers closely matches that of the slow metabolizers receiving 150 mg/d (Fig. 3C). When the dose was doubled for fast metabolizers, the probability of resistance decreased but remained an order of magnitude larger than that for slow metabolizers on the 150 mg/d schedule. The differences between the two cohorts were preserved for other dosing schedules such as the 1600/week plus 75 mg/d schedule (Fig. 3D).

If resistant cells existed prior to treatment (Fig. 3E), fast metabolizers had a higher expected resistant clone size for any therapy schedule, because of faster elimination of the drug. In particular, fast metabolizers receiving a high-dose pulse plus continuing low doses still had a higher expected resistant cell population size than nonsmokers receiving the standard 150 mg/d dose. By taking a double dose of 300 mg/d, fast metabolizers could effectively reduce the growth of the resistant population; however, the benefit conferred was not sufficient to overcome the faster rate of drug metabolism.

Missed Doses, Make-Up Doses, and Alternating Doses

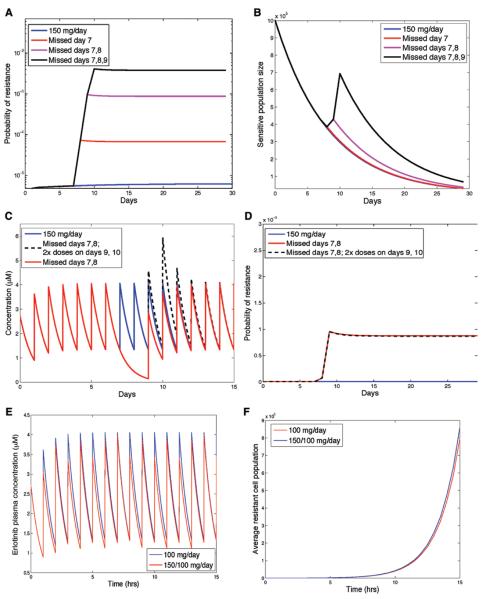
Despite a recommended daily dosing schedule, patients will miss, not infrequently, one or several doses of drug. We used our predictive models to evaluate the effects of such noncompliance (i.e., missed doses) on the dynamics of sensitive and resistant cancer cells. Specifically, we considered the effects of missing 1, 2, and 3 days in succession, as compared with the standard 150 mg/d dose, on the overall probability of developing resistance in the case of no preexisting resistance (Fig. 4A and B). The probability of resistance was affected by missing several days of treatment by several orders of magnitude (10-fold–100-fold). Interestingly, noncompliance had little effect on the sensitive-cell population (i.e., the bulk of the tumor). However, the effects of noncompliance on the dynamics of resistance were significant.

FIGURE 4.

The effect of patient noncompliance on the risk of resistance. A, Effect of missing doses on the probability of resistance as a function of time, for nonsmoking patients with no preexisting resistance. B, Dynamics of the number of sensitive cells for compliant and noncompliant dosing schedules (missing 1, 2, and 3 days starting with day 7). C, Drug concentration in plasma over time (in μM) for compliant schedule of 150 mg/d, a noncompliant schedule missing days 7/8 and taking twice the dose on days 8/9, and a noncompliant schedule missing days 7/8 with no make-up doses. D, Probability of resistance for each of these schedules. E, Drug concentration in plasma over time (in μM) for schedule taking 150 mg and 100 mg on alternate days, and the standard schedule of 150 mg/d. F, Expected size of the resistant clone as a function of time for the schedules shown in (E), assuming 100 preexisting resistant cells. For all panels, the mutation rate is μ =10⁻⁸ per cell division and the initial population size is M = 10⁶ cells with no preexisting resistance.

We next investigated the effects of make-up doses after missed drug on the dynamics of resistance (Fig. 4C and D). For a nonsmoker with no preexisting resistant cells, we compared the probability of resistance on a compliant schedule, a schedule with missed but no make-up doses, and a schedule with missed drug on 2 consecutive days followed by doubled doses on 2 subsequent days. Interestingly, make-up doses did not reverse the effects of missed doses.

We also modeled the effects of a schedule in which alternating doses of 150 mg and 100 mg were administered on successive days. This schedule is sometimes prescribed for patients who have dose-limiting toxicity at the 150 mg/d dose. There was little difference between these two schedules in terms of efficacy and resistance dynamics (Fig. 4E and F).

Treatment Withdrawal and Treatment beyond Progression

Finally, we used our methodology to study treatment strategies after the development of T790M-mediated progression of the disease on a standard 150 mg/d schedule. We assumed that initially, the population contains 100 resistant and 10⁶ sensitive cells. On day 12 of treatment in vitro, the resistant population size grows sufficiently large so that the total population size begins to increase again after the initial decline. This time point marks the time of progression on therapy (Fig. 5A). Three scenarios were then examined (Fig. 5B and C): (1) treatment withdrawal, (2) continuing therapy with 150 mg/d, and (3) change of the treatment strategy to a high-dose pulse (1600 mg for 1 day) followed by 6 days on low dose (75 mg/d). For each of these schedules, Figure 5B shows the total population size and the number of sensitive cancer cells whereas Figure 5C displays the plasma concentration of erlotinib over time. Treatment withdrawal (strategy 1) led to a rapid rebound of the numbers of sensitive cells, therefore, the total population size increased rapidly. Continuation of 150 mg/d (strategy 2) led to a less-rapid rebound and the sensitive cells were kept in check. Weekly high-dose pulses followed by low daily doses (strategy 3) provided a further modest benefit. Thus, our mathematical modeling predicted that treatment beyond progression was superior to drug withdrawal, and a schedule with high-dose pulses and low-dose maintenance seemed modestly better than the use of 150 mg/d.

FIGURE 5.

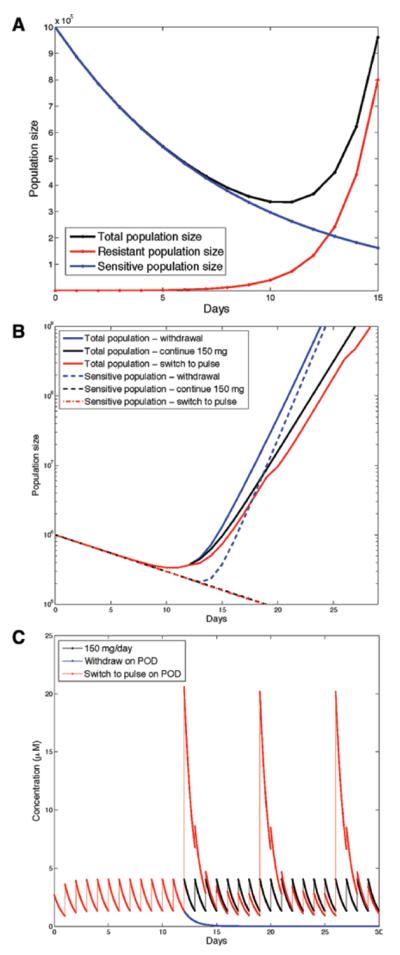
Effect of various treatment strategies in in vitro models of acquired resistance. Erlotinib discontinuation after progression of disease is detrimental to patient survival. A, Dynamics of the total population size (black), the number of sensitive cells (blue), and the number of resistant cells (red) after the total tumor size begins to increase. B, The effects of various strategies on the total population size and sensitive population size in response to (1) treatment withdrawal, (2) continuing therapy with 150 mg/d, and (3) treatment alteration to a high-dose pulse (1600 mg) followed by 6 days on low dose (75 mg/d). C, Drug concentration in plasma over time (in μM) during various strategies, (1–3).

DISCUSSION

In this article, we outlined the use of a combined evolutionary and pharmacokinetic modeling approach to study the emergence and dynamics of T790M-mediated resistance to erlotinib in patients with EGFR-mutant lung cancers. We used a pharmacokinetic modeling perspective informed by human subject data to model the concentration of erlotinib over time in patient plasma for diverse dosing schedules. To study the evolution of drug-sensitive and drug-resistant populations during these schedules, we used growth kinetic data from an isogenic pair of NSCLC cell lines with and without the T790M mutation.¹³ Combining these types of data through a novel hybrid modeling approach, we were able to investigate the relative benefits of various treatment strategies and pharmacokinetic parameters.

We considered the evolution of resistance during administration of daily oral doses of 25, 50, and 150 mg as well as pulsed doses of 1600 mg weekly, with and without additional low-dose continuations of 50 mg to 100 mg on the remaining 6 days. We found that when preexisting resistant cells are present, all schedules containing pulsed doses are superior in delaying the time to progression of disease (POD) by impeding the growth of resistant cells. However, when preexisting resistance is not present, a schedule with a once-weekly 1600 mg pulse is an unfavorable choice as the probability of developing resistance increases because of treatment breaks; during treatment breaks, sensitive cells resume proliferation, potentially leading to the development of resistance. In contrast, the schedule of 1600 mg weekly pulses plus continuation doses on the remaining 6 days achieves a probability of resistance similar to that of the 150 mg/d standard dose. Therefore, we conclude that independent of whether preexisting resistance is present, patients administered high-dose pulsed therapy once a week plus low doses during the remaining 6 days would derive the most benefit in terms of preventing or delaying progression of disease because of resistance. We recommend that this regimen be tested in clinical trials for its safety, tolerability, and efficacy.

Anecdotally, some patients are unable to tolerate the 150 mg/d regime and are administered 150 mg on alternate days with 100 mg, or a lower daily dose. We demonstrated that this type of change has little effect on the dynamics of resistance because the resistant cell clones are not substantially inhibited by erlotinib at levels below 150 mg. As long as the administered dose is sufficiently high to largely inhibit sensitive-cell reproduction, the probability of developing resistance and the expected size of the resistant cell clones are not significantly affected.

We further investigated the impact of variation in pharmacokinetic processes on the emergence of resistance. Previously, investigators showed that smokers eliminate erlotinib significantly faster than nonsmokers.¹⁴ We predicted that when administered the same daily dose of 150 mg/d, smokers would have an approximately 100-times higher chance of developing resistance than nonsmokers, when no preexisting resistance is assumed. We then considered the effects on smokers who were administered a double dose of 300 mg/d instead of 150 mg. This modification achieved a steady-state plasma concentration similar to that of nonsmokers receiving 150 mg/d, but did not reduce the probability of resistance to levels comparable with that of never smokers. These predictions were also mirrored when considering the expected number of resistant cells as a function of time in the case of preexisting resistance; smokers on 150 mg/d and 300 mg/d were predicted to have larger pools of resistant clones than nonsmokers on a 150 mg/d dose. Collectively, our modeling approach predicts that pharmacokinetic effects may play a crucial but previously unappreciated role in the dynamics of acquired resistance to erlotinib. In addition to smoking, a variety of reasons such as diet, lifestyle, other medications,²³ inherited differences, etc. could give rise to variability in pharmacokinetic rates. We envisage that personalized pharmacokinetic profiling of erlotinib metabolism could further help to minimize the chances of developing resistance in individual patients.

We also considered the effects of missed doses during the 150 mg/d standard schedule, given that if no preexisting resistance is present, missed doses significantly increase the probability of developing resistance even though the overall debulking of the tumor is not significantly affected. Taking make-up doses on subsequent days after missing doses does not significantly alter the probability of resistance, and therefore, patient compliance is an important factor in preventing resistance.

We also investigated the effects of treatment withdrawal and modifications after POD because of drug resistance on the standard 150 mg/d schedule. We considered the options of (1) drug withdrawal, (2) continuation on the 150 mg/d schedule, and (3) switch to 1600 mg/week plus 75 mg on days 2 to 7.³ We found that treatment withdrawal would result in the fastest rebound kinetics of the overall tumor population. In contrast, both continuation of standard therapy and switching to a high-dose pulsed with continuation schedule would impede the growth rate of the tumor population size.

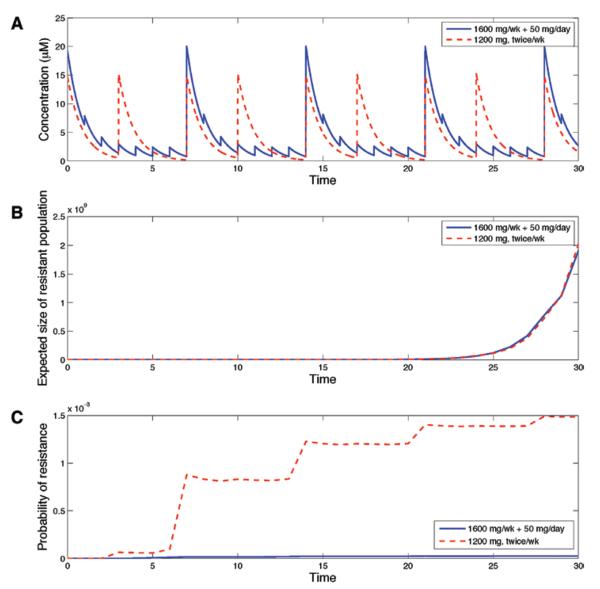
Finally, a phase I dose-escalation study demonstrated that for a twice-weekly treatment schedule, the dose-limiting toxicity was 1200 mg, whereas the maximum tolerated dose was 1000 mg.²⁴ To model the effect of the highest twice-weekly pulsed regimen, we performed comparisons of the schedule of 1600 mg/week plus 50 mg on days 2 to 7 with a 1200 mg twice-weekly schedule (doses on days 1 and 4). Figure 6A shows the corresponding drug concentration temporal profile for each of these schedules. Figure 6B displays the expected number of resistant cells in the scenario in which 100 out of 10⁶ cells are drug resistant at the start of therapy. These two schedules produced very similar outcomes. Figure 6C shows the probability of resistance as a function of time for the scenario in which initially all tumor cells are sensitive. We observed that the 1600 mg/week plus 50 mg/d schedule is superior to the 1200 mg twice-weekly schedule. Because the 1200 mg twice-weekly schedule has a significantly higher overall drug intake but does not produce a better outcome in either scenario, we conclude that the high-dose pulse of 1600 mg followed by low doses on subsequent days is a superior choice. Correspondingly, doses less than 1200 mg twice a week would be even less effective.

FIGURE 6.

A high-dose pulsed strategy with low-dose continuation is superior to 1200 mg twice a week. A, Drug concentration in plasma over time (in μ M) for a high-dose pulsed schedule of 1600 mg/week plus 50 mg on days 2 to 7. B, The expected size of the resistant clone as a function of time for the schedules shown in (A), assuming 100 preexisting resistant cells. C, Probability of resistance for each of these schedules assuming no preexisting resistant cells. For all panels, the mutation rate is μ =10⁻⁸ per cell division and the initial population size is M = 10⁶ cells with no preexisting resistance.

A limitation of our approach is the use of in vitro growth kinetics for the sensitive and resistant cell populations, because of the difficulty of obtaining similar measurements in vivo. We are therefore unable to make absolute quantitative predictions about realistic time scales for the emergence of resistance because growth kinetics in the in vitro setting occur on a time scale orders of magnitude more rapid than in in vivo settings. However, our approach allows a complete set of detailed measurements of in vitro cell populations for a wide panel of drug concentrations; this in turn enables the model to predict the resistance dynamics under a wide variety of treatment schedules. The relative benefits and comparisons among the various treatment schedules can then be assessed; these predictions are valid in the in vivo setting as long as the relative differences in growth rates are constant between in vivo and in vitro situations.

In summary, our study demonstrates the power of mathematical modeling in predicting improved treatment schedules with existing drugs. Such modeling may prove to be a useful tool for screening potential drug compounds and designing clinical trials. Of note, our data could help inform prospective clinical trials of erlotinib or other agents, but should not be used to make treatment decisions. An important aspect of such studies is the characterization of toxicity limits in human patients. If detailed toxicity constraints are known, then mathematical modeling can be used to exhaustively and rapidly search the space of tolerated schedules to optimize for biological endpoints such as the maximal delaying of POD, maximal tumor reduction, etc. Because toxicity constraints for each patient may be intrinsically tied to their pharmacokinetic processes, this further underscores the importance of incorporating pharmacokinetic modeling into evolutionary models of resistance. This approach could be applied to any cancer for which acquired resistance to targeted therapies exists, for example, imatinib, dasatinib, or nilotinib in BCR-ABL-driven CML, crizotinib in anaplastic lymphoma kinase fusion-driven NSCLC, and vemurafenib in mutant BRAF-driven melanoma. Incorporation of modeling in parallel with drug development could potentially lead to faster optimization of therapeutic outcomes.