State-of-the-Art Direct ¹³C and Indirect ¹H-[¹³C] NMR Spectroscopy In Vivo

Abstract

Carbon-13 NMR spectroscopy in combination with ¹³C-labeled substrate infusion is a powerful technique to measure a large number of metabolic fluxes non-invasively in vivo. It has been used to quantify glycogen synthesis rates, establish quantitative relationships between energy metabolism and neurotransmission and evaluate the importance of different substrates. All measurements can, in principle, be performed through direct ¹³C NMR detection or via indirect ¹H-[¹³C] NMR detection of the protons attached to ¹³C nuclei. The choice for detection scheme and pulse sequence depends on the magnetic field strength, whereas substrate selection depends on the metabolic pathways that are studied. ¹³C NMR spectroscopy remains a challenging technique that requires several non-standard hardware modifications, infusion of ¹³C-labeled substrates and sophisticated processing and metabolic modeling. Here the various aspects of direct ¹³C and indirect ¹H-[¹³C] NMR are reviewed with the aim of providing a practical guide.

INTRODUCTION

Knowledge about the relation between neuronal activity and cerebral energy metabolism is essential for the understanding of brain function. It is well known that under normal conditions the oxidation of glucose is the primary mechanism for cerebral energy production (1). Autoradiography (2, 3) and positron emission tomography (4, 5) (PET) have been used to assess regional glucose uptake in animal and human brain, respectively, by measuring the distribution of radioactivity following infusion of radioactive glucose analogues, 2-deoxy-D-glucose (DG) and 2-fluoro-2-deoxy-D-glucose (FDG). The information provided by glucose analogs is limited as they may not accurately reflect glucose metabolism and cannot provide flux information through metabolic pathways, like glycolysis. Furthermore, methods that utilize radioactively labeled glucose cannot distinguish the non-specific radioactivity of glucose and glucose metabolites. Nuclear magnetic resonance (NMR) spectroscopy overcomes these limitations by detecting specific chemical groups of metabolites through the chemical shift. Infusion of stabile ¹³C-labeled substrates, like [1-¹³C]-glucose, then allows detection of the appearance of ¹³C signal in all metabolites (of sufficient concentration) of glucose metabolism.

Previous in vivo ¹³C NMR spectroscopy in combination with intravenous [1-¹³C]-glucose infusion has shown abundant labeling of [4-¹³C]-glutamate and [4-¹³C]-glutamine, both in animal (6–10) and human (11–14) brain. These experiments, in combination with previous knowledge on compartmentalized glutamate metabolism (15, 16) allowed the development of quantitative, mathematical models of glucose metabolism. These studies have made important contributions to linking neuronal energy production to glutamatergic neurotransmission and establishing the importance of a glutamate–glutamine neurotransmitter cycle between neurons and astroglia.

In general the detection of ¹³C-label turnover involves a number of practical considerations and decisions that determine the exact information content and sensitivity of the experiment. These considerations include (1) the choice of ¹³C-labeled substrate, (2) the use of direct ¹³C-[¹H] or indirect ¹H-[¹³C] NMR detection and (3) the exact details of the metabolic model. The nomenclature for the various NMR methods is that the spins of the non-bracketed nucleus, e.g. ¹H, give rise to the observed NMR signal, whereas the spins of the bracketed nucleus, e.g. ¹³C in ¹H-[¹³C], require one or more RF pulses to successfully complete the NMR method. Examples include ¹H RF pulses used in concert with ¹³C RF pulses in ¹³C-[¹H] polarization transfer methods or ¹³C RF pulses during broadband decoupling in ¹H-[¹³C] methods. Additional considerations are the infusion protocol, RF power deposition, availability of a ¹³C channel and spectral fitting. This review will discuss the practical aspects of performing ¹³C NMR experiments in vivo. While the general nature of dynamic ¹³C NMR allows applications to a wide range of tissues, this review will focus on applications to study cerebral energy metabolism and neurotransmission.

METHODS

General system setup

In order to perform dynamic ¹³C NMR spectroscopy the MR system must be equipped with several non-standard features like (1) a ¹³C-[¹H] or ¹H-[¹³C] RF coil, (2) ¹H and ¹³C filters and (3) a console capable of handling two frequencies. While there are exceptions to the minimal requirements, as discussed in the section on alternative detection methods, these features are most commonly used for successful ¹³C NMR spectroscopy.

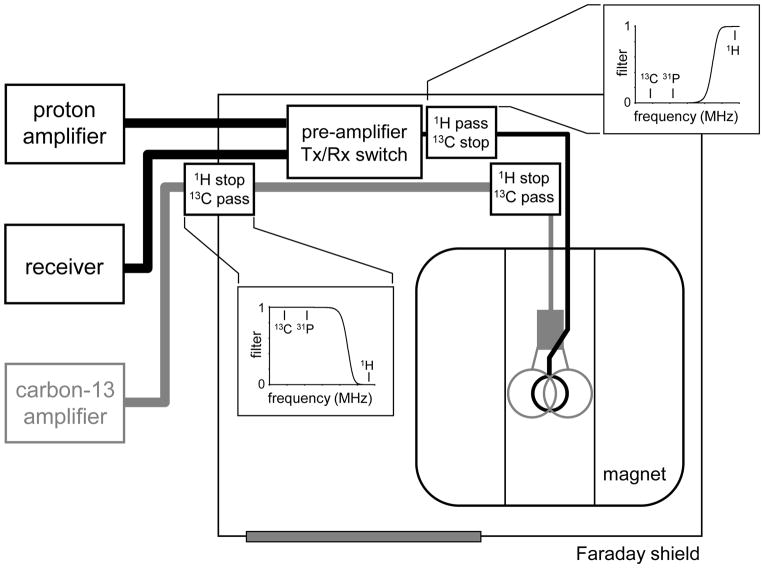
Perhaps the largest difference between conventional ¹H NMR spectroscopy and dynamic ¹³C NMR spectroscopy is the need for a RF coil that can simultaneously operate at both the ¹³C as well as the ¹H NMR frequency. For direct ¹³C-[¹H] NMR acquisitions, operation at the ¹H NMR frequency is necessary for coherence transfer, broadband decoupling, spatial localization, shimming and MR imaging. For indirect ¹H-[¹³C] NMR acquisitions, operation at the ¹³C NMR frequency is required for coherence transfer and broadband decoupling. Fig. 1 shows the most commonly used design for a ¹³C-[¹H] RF coil as originally described by Adriany and Gruetter (17). The ¹³C NMR coil is a simple, circular surface coil (14 and 80 mm diameter for rodent and human studies, respectively) that can be placed adjacent to the area of interest for optimal sensitivity. The ¹H NMR coil consists of two larger surface coils (21 and 130 mm diameter for rodent and human studies, respectively) placed at an approximate 90° angle relative to each other and driven in quadrature for optimal B₂ efficiency. The sensitive volume of the ¹H RF coil is always larger than that of the ¹³C RF coil, such that all spatial positions detected during a ¹³C-[¹H] NMR acquisition can be properly decoupled. For ¹H-[¹³C] NMR studies the two coils are simply reversed. The popularity of the design depicted in Fig. 1 can, besides the extended spatial coverage, also be explained by the reduced amount of coil interaction, high B₁ and B₂ efficiency and the absence of local hot spots in the B₂ field. See (17–19) for additional review and discussion of the RF coil setup.

Figure 1.

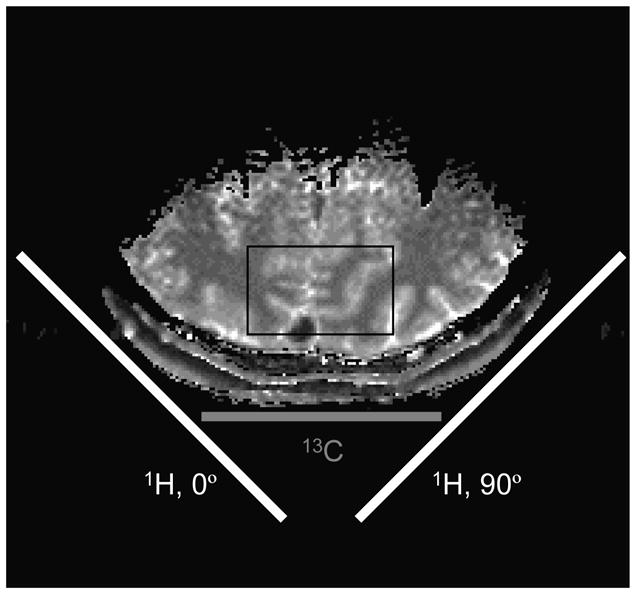
RF coil setup for direct ¹³C-[¹H] NMR on human brain. The ¹³C RF coil is a single loop surface coil. The two circular ¹H RF coils are positioned at a 90° angle and driven in quadrature for improved B2 efficiency. The indicated box is a typical volume size for direct ¹³C NMR detection.

Despite the reduced interaction of the two coils as a result of the geometric configuration, the interference between the two coils and the connected RF cables is typically strong enough to cause a significant increase in noise level when broadband decoupling is attempted. Even though the ¹H and ¹³C NMR frequencies are well separated, the decoupling channel can carry spurious signals at the observe frequency. As decoupling is always performed during signal acquisition, even small imperfections lead directly to a degradation of the observed signal.

For almost all heteronuclear experiments involving broadband decoupling it is therefore crucial to apply filters on the decoupling channel to filter out the frequencies that lead to noise in the observe channel. A typical setup for ¹H-[¹³C] NMR is shown in Fig. 2. At least one, but often two filters are required on the decoupling ¹³C channel to remove spurious signal at the ¹H frequency. Even though band-pass filters can be used, low-pass filters typically have a better performance in terms of reduced signal loss at the desired frequency. This so-called insertion loss is less than 0.5 dB for good filters. A good low-pass filter achieves at least 60 dB attenuation at the ¹H NMR frequency. While somewhat counter-intuitive, a high-pass filter on the observe channel prior to the pre-amplifier often greatly decreases the noise injection during ¹³C decoupling. This is likely due to non-linear elements in the pre-amplifier-T/R-switch that can multiply spurious signals at the ¹³C NMR frequency to the observed ¹H NMR frequency. For ¹³C-[¹H] NMR the filters should, of course, be reversed with high-pass filters on the decoupling ¹H channel and a low-pass filter on the ¹³C channel. While the exact filter combination and placement is often site-specific, the combination of filters should lead to negligible degradation of the signal-to-noise ratio during decoupling.

Figure 2.

Filter, amplifier and RF coil setup for indirect ¹H-[¹³C] NMR. A ¹H stop/¹³C pass filter is typically placed in the ¹³C transmit channel at the position of the filter plate (i.e. the Faraday shield). An identical filter is often placed closer to the RF coil for improved performance. For ¹H-[¹³C] NMR a ¹H pass/¹³C stop filter is typically required prior to the preamplifier to prevent ¹³C-to-¹H noise amplification. Exact filter placement is system-specific and must be determined empirically.

In addition to the location and the insertion loss, another important specification of RF filters is the limit on maximum peak and average power. For typical NMR sequences the filter must be able to handle both high peak power RF pulses (several kW for 1–5 ms) and high average power (several 100 W during 100–300 ms) during decoupling. As one of the most common problems with heteronuclear NMR is breakdown of RF filters under high power conditions, it is advised that high-quality RF filters capable of handling a sufficiently large RF power range are used.

Substrates

One of the most important considerations in dynamic heteronuclear in vivo NMR is the choice of substrate as this largely determines the information content that the experiment can provide. The exact ¹³C label position within the substrate is equally important.

Given that glucose is the primary substrate for cerebral energy metabolism under normal conditions, it is not surprising that glucose has been the most commonly used substrate in dynamic ¹³C NMR studies. However, in more recent years it is recognized that glucose does not provide information on all metabolic pathways in the brain. In addition, under a variety of conditions the brain also utilizes other substrates, such as β-hydroxybutyrate (BHB) and lactate.

[1-¹³C]-glucose and [1,6-¹³C2]-glucose

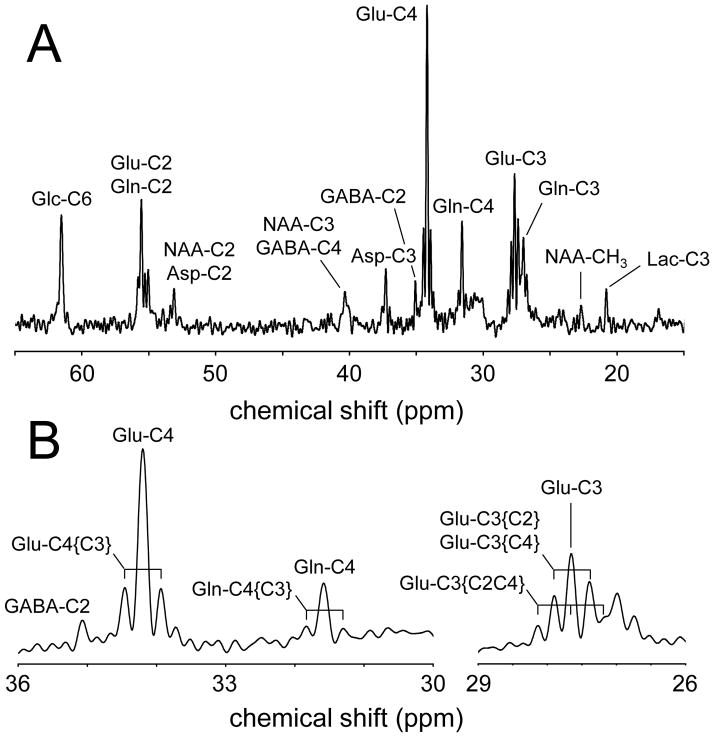
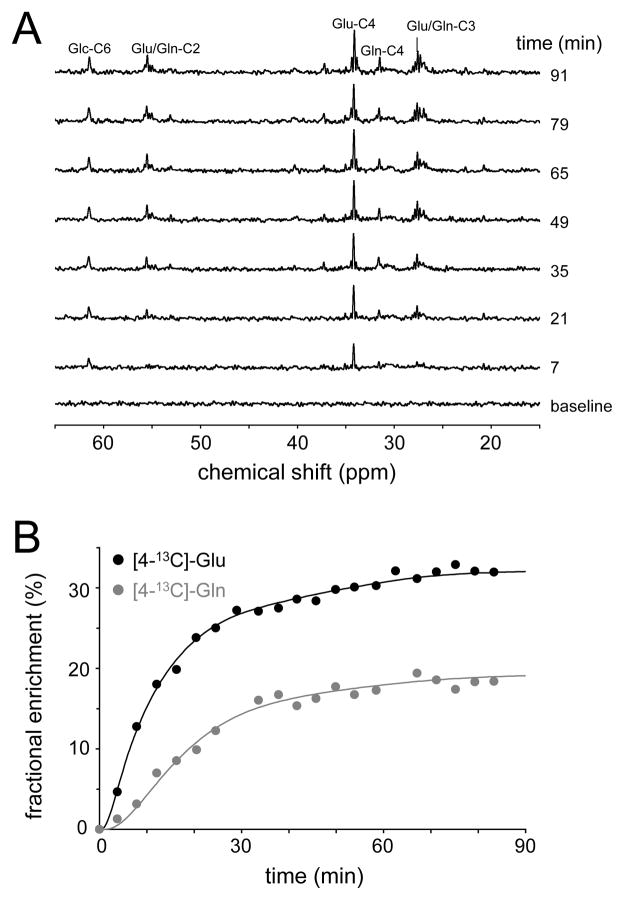
The majority of ¹³C NMR studies in vivo have used [1-¹³C]-glucose as the substrate. Besides the economic consideration that [1-¹³C]-glucose is the least expensive ¹³C-labeled form of glucose, the choice for [1-¹³C]-glucose is governed by the fact that the transfer of ¹³C label to [4-¹³C]-glutamate is indicative of the most active energy-producing metabolic pathways, namely glycolysis and the neuronal TCA cycle (see Fig. 3). While the labeling pattern of metabolites from [1,6-¹³C₂]-glucose is nearly identical to that from [1-¹³C]-glucose, the fractional enrichment of pyruvate and hence of all subsequent metabolic pools will be twice as high, leading to an improved detection sensitivity. [1,6-¹³C₂]-glucose is more expensive than [1-¹³C]-glucose, but this is only a minor consideration when considering the small amounts of material used to study cerebral metabolism in rat brain. For human experiments, [U-¹³C₆]-glucose is a less expensive alternative when performing ¹H-[¹³C]-NMR. For direct ¹³C NMR detection [U-¹³C₆]-glucose is not recommended as the NMR spectrum will be complicated by the multiple homonuclear ¹³C-¹³C scalar couplings, giving rise to isotopomer resonances. Label transfer from [1,6-¹³C₂]-glucose to [4-¹³C]-glutamate is detectable within minutes following the start of glucose infusion. Provided that the exchange between the mitochondrial 2-oxoglutarate and cytosolic glutamate pools is rapid, the label transfer is indicative of the TCA cycle rate. Note that through simultaneous quantification of [3-¹³C]-glutamate the TCA cycle rate can be determined even if the mitochondrial/cytosolic exchange rate is slow (13, 20). With a small time lag, label is subsequently transferred from [4-¹³C]-glutamate to [4-¹³C]-glutamine. Based on the location of specific enzymes as well as the size of the neuronal glutamate and astroglial glutamine pools, this has been interpreted as reflecting a glutamate–glutamine neurotransmitter cycle, and has subsequently been confirmed in many studies (6–10, 13, 14). Figure 4 shows a typical ¹³C NMR spectrum acquired from rat brain during the infusion of [1,6-¹³C₂]-glucose. Following 90 minutes of glucose infusion, a wide range of metabolites is labeled, including [n-¹³C]-glutamate and glutamine (n = 2, 3 or 4), [2-¹³C]-aspartate, [3-¹³C]-aspartate, [1,6-¹³C₂]-glucose and [n-¹³C]-GABA (n = 2, 3 or 4). Besides the singlet ¹³C NMR resonances, the NMR spectrum also contains several doublet and triplet resonances. These so-called isotopomer resonances are due to homonuclear ¹³C-¹³C scalar coupling in molecules where two ¹³C nuclei are immediately adjacent to each other, like in [3,4-¹³C₂]-glutamate. This situation occurs when [4-¹³C]-glutamate labeled in the first TCA cycle is labeled again at the C3 position in the second TCA cycle. The chance that this occurs increases with the duration of the infusion. The infusion for regular ¹³C turnover studies is between 90 and 150 minutes, leading to several isotopomers, in particular [2,3-¹³C₂], [3,4-¹³C₂] and [2,3,4-¹³C₃]-glutamate and glutamine (Fig. 4). However, for much longer infusion times, as required to detect ¹³C-glycogen turnover (21–23), the ¹³C NMR spectrum is dominated by isotopomer resonances (24). Analysis of the exact isotopomer patterns can provide complementary information that obtained from dynamic ¹³C turnover.

Figure 3.

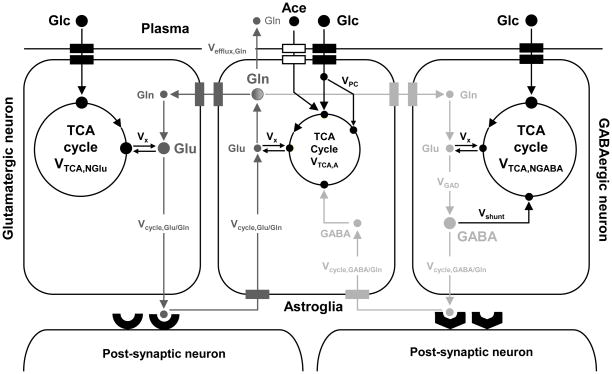
Four-compartment metabolic model compromising the blood, glutamatergic neurons, GABAergic neurons and astroglia. Glucose enters the brain with the aid of glucose transporter in the blood-brain barrier. In the glycolytic pathway, glucose is broken down into two pyruvate molecules which enter the tricarboxylic acid (TCA) cycle. Acetate only enters the astroglial compartment and enters the TCA cycle via acetyl-CoA. One of the TCA cycle intermediates, 2-oxoglutarate, is in rapid exchange with a large glutamate pool that can be observed with NMR. The TCA cycle flux can be obtained from the glutamate turnover and is denoted VTCA. Due to compartmental localization of specific enzymes, the fate of glutamate differs in each of the three cellular compartments. In glutamatergic neurons, glutamate acts as an excitatory neurotransmitter and is released into the synaptic cleft in response to an action potential. Following interaction with post-synaptic receptors, the glutamate is taken up by the astroglia and converted to glutamine. Glutamine is ultimately transported back to the glutamatergic neuron, where it is converted back to glutamate, thereby completing the so-called glutamate-glutamine neurotransmitter cycle. The flux through this cycle, Vcycle, Glu/Gln, can be obtained by following the glutamine turnover. In the GABAergic neuron, the glutamate is first converted to GABA which is the primary inhibitory neurotransmitter. Similar to the glutamatergic neuron, a GABA-glutamine neurotransmitter exists between GABAergic neurons and astroglia. A metabolic pathway specific to astroglia is the carboxylation of pyruvate catalyzed by the astroglia-specific enzyme pyruvate carboxylase. Note that the letter size roughly corresponds to the metabolic pool size of the corresponding metabolite (e.g. a large glutamine pool resides in astroglia). Metabolite abbreviations are given for: Ace, acetate; GABA, γ-aminobutyric acid; Glc, glucose; Gln, glutamine; Glu, glutamate

Figure 4.

(A) ¹H-decoupled, ¹³C NMR spectrum of rat brain in vivo obtained with polarization transfer between 120 and 150 min following the onset of intravenous infusion of [1,6-¹³C2]-glucose. Besides the singlet resonances, the ¹³C NMR spectrum is (B) characterized by doublet and triplet resonances arising from isotopomers. In particular glutamate and glutamine exhibit several isotopomers of which the C3-C4 combination is most abundant.

[2-¹³C]-glucose

In order to determine the rate of the glutamate–glutamine cycle from the glutamine synthesis rate, one must distinguish glutamine labeling via the glutamate–glutamine cycle from other metabolic pathways that may contribute to the flow through glutamine synthetase. The glutamate–glutamine cycle and anaplerosis are the only two pathways that provide carbon skeletons for glutamine synthesis. Glutamine efflux is the primary pathway of nitrogen removal from the brain. Since the glutamine concentration is constant, any loss of glutamine by efflux to the blood must be compensated by synthesis de novo of glutamine through anaplerosis. For synthesis of glutamine de novo by anaplerosis pyruvate derived from glucose is converted to oxaloacetate by carbon dioxide fixation (see Fig. 3), a reaction catalyzed by the astroglial enzyme pyruvate carboxylase. Through the action of the TCA cycle, oxaloacetate is converted to 2-oxoglutarate, which is converted to glutamate. Astroglial glutamate is then converted to glutamine by glutamine synthetase. A limitation of using [1-¹³C]-glucose as a labeled precursor to measure the glutamate–glutamine cycle flux is that ¹³C label entering glutamine by this pathway cannot be easily distinguished from ¹³C label that enters glutamine from the anaplerotic pathway or the astroglial TCA cycle. [1-¹³C]-glucose labels [4-¹³C]-glutamate through the action of pyruvate dehydrogenase and labels [2-¹³C]-glutamate through pyruvate carboxylase. However, the carbon label of [4-¹³C]-glutamate is quickly transferred to [2-¹³C]-glutamate in subsequent turns of the overwhelming neuronal TCA cycle, thereby obscuring [2-¹³C]-glutamate labeling by astroglial anaplerosis. Using [2-¹³C]-glucose as a label precursor offers a highly sensitive alternative to measuring the fluxes though anaplerosis and the astroglial TCA cycle. [2-¹³C]-glucose labels astroglial [3-¹³C]-glutamate/glutamine through pyruvate carboxylase and labels [5-¹³C]-glutamate/glutamine through the action of pyruvate dehydrogenase. However, the C5 position of the TCA cycle intermediates is ultimately lost as carbon dioxide in subsequent turns of the TCA cycle. Therefore, the accumulation of (astroglial) [3-¹³C]-glutamine is a direct indication of anaplerotic activity, without contamination by neuronal TCA cycle metabolism. Under most conditions the anaplerotic pathway constitutes only a small fraction of the TCA cycle flux.

[2-¹³C]-acetate

Since glucose is transported and metabolized in both neurons and astroglia and extensive mixing of the label occurs through the glutamate–glutamine cycle, the TCA cycle fluxes in the neuronal and astroglial compartments are convolved. The formation of [4-¹³C]-glutamate will be heavily weighted by the neuronal TCA cycle, making the glucose experiment relatively insensitive to the smaller astroglial TCA cycle flux. Neuronal and astroglial metabolism can be more directly distinguished by using acetate as a substrate. It has been shown that acetate is almost exclusively metabolized in astroglia due to a far greater transport capacity (25). Therefore, [2-¹³C]-acetate will be selectively transported into the astroglial compartment and converted to [2-¹³C]-acetylCoA, which labels the astroglial TCA cycle intermediates. Next, the small (0.5–1.0 mM) astroglial glutamate pool is labeled after which the ¹³C label arrives at the large glutamine pool. The large neuronal glutamate pool is subsequently labeled from astroglial [4-¹³C]-glutamine that is transported to the neuronal compartment as part of the glutamate–glutamine neurotransmitter cycle. [2-¹³C]-acetate experiments on human and animal brain have confirmed earlier observations made through the use of [1-¹³C]-glucose and have determined that the astroglial TCA cycle is only a small fraction of the neuronal TCA cycle.

Other substrates

In addition to glucose and acetate there have been a number of reports that have used alternative substrates, such as β-hydroxybutyrate and lactate. It is well-known that under conditions of prolonged fasting, strenuous exercise or ketogenic diets β-hydroxybutyrate can readily be utilized by the brain. Using [2,4-¹³C₂]-β-hydroxybutyrate, Pan et al (26) demonstrated significant ¹³C label accumulation in [4-¹³C]-glutamate and glutamine with a pattern closely resembling glucose metabolism. In addition to alternative substrates, it is sometimes also advantageous to use combinations of substrates. Using a co-infusion of [1,6-¹³C₂]-glucose and [1,2-¹³C₂]-acetate, Deelchand et al (27) were able to simultaneously measure neuronal and astroglial metabolism in rat brain through the specific ¹³C-¹³C isotopomer resonances.

Infusion protocol

While the description of the infusion protocol will be focused on rodent experiments, the setup is similar for human studies. Noticeable differences will be mentioned wherever applicable. Following the commonly employed preparations (general anesthesia and tracheotomy or intubation) two small lines are placed in the femoral artery and vein or tail vein for periodic sampling of arterial blood and intravenous infusion of substrates, respectively. In human studies, the two lines are typically placed in the antecubital vein of each arm, one of which is often wrapped in a warm water blanket to aid in blood drawing.

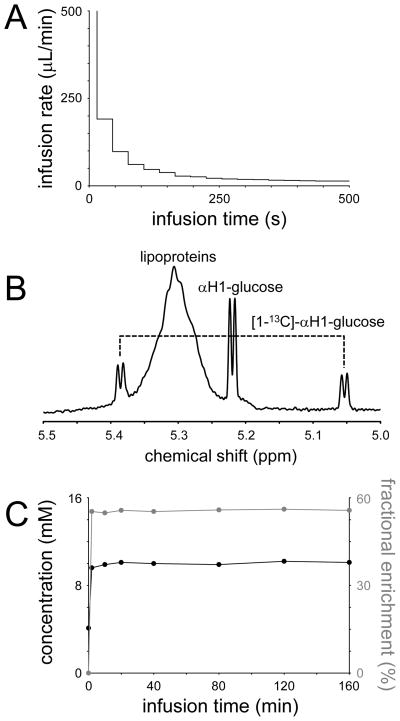
The infusion protocol is typically designed to quickly reach a high and stabile isotopic enrichment of the substrate. Fig. 5A shows a practical glucose infusion protocol for an adult rat that is designed to increase the intravenous glucose concentration from euglycemic levels (circa 4 mM following an overnight fast) to hyperglycemic levels (10 – 12 mM), while reaching a 50–70% fractional enrichment of the glucose within 1 minute. However, exact knowledge of the time course of substrate concentration and isotopic enrichment is critical for a quantitative evaluation of ¹³C labeling time courses. Without exact knowledge of the input function, the rate of ¹³C-label appearance in metabolites like glutamate and glutamine cannot be interpreted since the entry rate of labeled ¹³C substrate is a prerequisite in the metabolic modeling. The substrate concentration and isotopic enrichment time courses can be obtained through periodic sampling of arterial blood followed by quantitative analysis with a combination of methods, like glucosometer analysis, gas chromatography mass spectrometry (GC-MS) and high-resolution NMR spectroscopy. Fig. 5B shows a typical ¹H NMR spectrum from a rat blood plasma samples following 90 min of [1-¹³C]-glucose infusion. The lack of spectral overlap of the αH1-glucose resonance at 5.22 ppm readily allows the calculation of the ¹³C fractional enrichment as well as the absolute concentration. Fig. 5C shows a summary of typical blood glucose concentration and fractional enrichment time courses. It should be noted that in high-field ¹H-[¹³C] NMR studies (10) the αH1-glucose resonance can be detected directly in vivo, thus eliminating the need for blood plasma analysis.

Figure 5.

(A) Infusion protocol for intravenous administration of a 0.75 M glucose solution in order to raise the blood glucose level to circa 10 mM in an adult rat. (B) In vitro ¹H NMR spectrum of unfiltered blood plasma obtained 90 min after the onset of [1,6-¹³C2]-glucose infusion. The αH1-glucose resonance at 5.22 ppm is readily observable, together with the two satellites for [1-¹³C]-αH1-glucose. The ¹³C fractional enrichment for this sample was determined at 43%. (C) Measured blood glucose concentration (black line) and ¹³C fractional enrichment (gray line) in an adult rat (200 gram) during the infusion protocol shown in (A).

In response to the elevated glucose levels, endogenous insulin is secreted from the pancreas in order to stimulate glucose uptake in the liver. In order to suppress this effect and reduce the experimental costs of the expensive ¹³C-labeled glucose, the glucose infusion in human studies is frequently combined with an intravenous infusion of somatostatin, a hormone that inhibits insulin release. In order to maintain basal insulin levels, insulin can be co-infused. Experimental costs can be further reduced by switching to 50–70% ¹³C-enriched substrate once the initial substrate bolus has been given. Human ¹³C turnover studies can be greatly simplified by oral administration of the substrate (28). While this gives comparable metabolic rates as the studies using administration through intravenous infusion, the uncertainties on the metabolic rates are increased.

Direct ¹³C NMR methods

The next consideration for successful dynamic ¹³C NMR is the choice of a NMR pulse sequence, which is largely determined by whether the ¹³C NMR signals will be detected directly or indirectly through the attached protons. The choice is often determined by balancing the increased sensitivity of ¹H NMR detection against the increased spectral resolution of ¹³C NMR detection. Additional considerations are that ¹H NMR also allows the detection of protons attached to ¹²C (i.e. the total metabolic pools), whereas ¹³C NMR allows the detection of ¹³C-¹³C isotopomers.

Methods for the direct detection of ¹³C NMR signals generally fall into one of two categories, namely (1) polarization transfer (14, 29–33) or (2) direct excitation (22, 34–36), possibly in combination with nuclear Overhauser enhancement (37, 38). Polarization transfer methods are typically used to detect NMR signal from ¹³C nuclei that are directly attached to one or more protons, such as the C2, C3 and C4 positions in GABA, glutamate and glutamine. Direct excitation methods are typically chosen for glycogen or for ¹³C nuclei without directly attached protons, such as the C1 and C5 positions in GABA, glutamate and glutamine.

Direct ¹³C excitation

The main advantage of direct ¹³C excitation over polarization transfer is that signal acquisition starts immediately following excitation, thus allowing the detection of compounds with short T₂ relaxation times, like glycogen (21–23, 39). In addition, since polarization transfer requires an echo-time in the order of 1/J_CH, compounds with very small heteronuclear scalar couplings, like the C1 and C5 positions in GABA, glutamate and glutamine (²J_CH = 3.5 – 5.2 Hz), would require very long TE and, therefore, can realistically only be detected through direct excitation.

The main challenges of ¹³C NMR through direct excitation are limited sensitivity and spatial localization. The low gyromagnetic ratio of ¹³C NMR equates with a low NMR sensitivity. The primary method to enhance the ¹³C NMR sensitivity is, besides polarization transfer, through the use of the nuclear Overhauser enhancement. Irradiation of protons that have dipolar coupling with the ¹³C nuclei of interest will lead to a redistribution of the ¹³C spin populations and an enhancement of the ¹³C signal by a factor 1 + (γ_H/2γ_C) = 2.988. However, if dipolar relaxation only accounts for a fraction of all relaxation mechanism, the nucleur Overhauser enhancement is proportionally reduced. For in vivo applications, typically enhancements for ¹³C NMR are 1.3 – 2.9. The enhancement must be empirically determined and it should be considered whether the additional sensitivity sufficiently offsets the need for additional measurements.

Spatial localization for ¹³C NMR through direct excitation is a challenge because of the large chemical shift dispersion of ¹³C NMR and the absence of spin- and stimulated-echo-based localization methods. For example, when a frequency selective RF pulse with bandwidth BW and offset ν relative to glutamate-C4 at 34.2 ppm is executed during a magnetic field gradient of amplitude G, a slice of thickness (BW/G) at position (ν/G) is selected. However, for α-glucose-C1 at 92.7 ppm, the frequency offset at 7 Tesla is (92.7 − 34.2) ×75 = 4,388 Hz (= Δν) higher. For α-glucose-C1 the same slice selection thus results in a position offset (ν + Δν)/G, which means that the NMR signal from different resonances originates from different spatial positions. This so-called chemical shift displacement effect increases with field strength. It can only be minimized by using the highest possible gradient strength. In order to maintain the same slice thickness the highest possible RF bandwidth has to be used. Since, for a given pulse length, the RF amplitude scales with the RF bandwidth, a second limiting factor in minimizing the chemical shift displacement artifact, besides limitations in gradient strength, is often the available RF peak power.

Spatial localization for direct ¹³C NMR is often based on outer volume suppression (OVS), possibly extended by ISIS (image-selected in vivo spectroscopy) localization. The chemical shift displacement is minimized by using high bandwidth adiabatic RF pulses.

Polarization transfer

The main advantage of polarization transfer over direct excitation methods is the consistent signal-to-noise increase and ease of spatial localization. Direct ¹³C NMR in combination with nuclear Overhauser enhancement requires an empirical determination of the exact enhancement factor. However, the signal enhancement during polarization transfer only depends on the echo-time relative to the known and constant scalar coupling constant and can thus be quantitatively calculated.

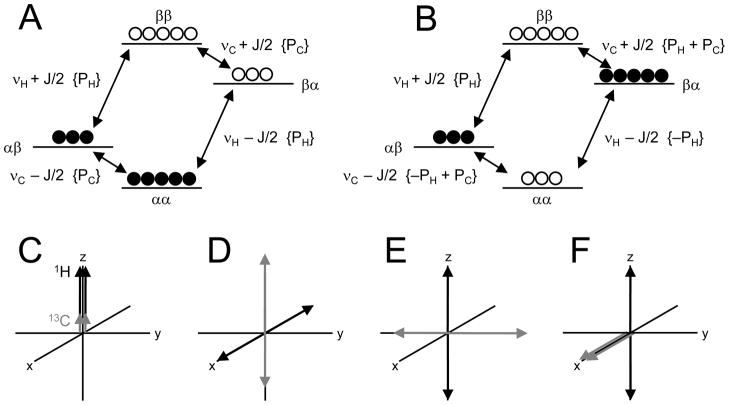
The polarization transfer experiment is readily described and understood with the product operator formalism (40). However, a thorough description of that formalism is outside the scope of this review. Fortunately, the product operator formalism for polarization transfer methods can be readily visualized through vector diagrams and considerations of relative spin populations. The principle of signal enhancement can be explained by considering the selective polarization inversion experiment (41) where a frequency-selective 180° spin inversion is applied to a single NMR transition (i.e. a single resonance line in a multiplet structure like a doublet). Consider a scalar-coupled heteronuclear two-spin system consisting of four energy levels and giving rising to two doublet signals (Fig. 6A). At Boltzmann equilibrium the spin populations of the levels are given by −0.5P_H − 0.5P_C for the highest energy level (level 1, ββ), −0.5P_H + 0.5P_C for level 2 (βα), 0.5P_H − 0.5P_C for level 3 (αβ) and 0.5P_H + 0.5P_C for the lowest energy level (level 4, αα), where P_H and P_C are the proton and carbon-13 spin populations. Two of the energy level differences give rise to proton resonances at frequencies ν_H ± ¹J_HC/2 with intensity P_H, whereas the other two energy level differences give rise to carbon-13 resonances at frequencies ν_C ± ¹J_HC/2 with intensity P_C. Selective inversion of the populations involved with one of the proton resonances, for example 2 – 4, will lead to a redistribution of the spin populations (Fig. 6B). While the frequencies of all transitions remain the same, the intensities of the carbon-13 transitions, which were not directly affected by the selective 180° inversion, are now −P_H + P_C and P_H + P_C, respectively. The changes in signal intensity are thus ±P_H/P_C which is proportional to ±γ_H/γ_C. In other words, selective inversion of a single ¹H transition leads to a circa four-fold enhancement of the carbon-13 resonances. Unfortunately, the selective polarization inversion experiment is not generally applicable to achieve uniform signal enhancement over a range of different metabolites. Polarization transfer achieves the same final situation, i.e. selective inversion of a single proton transition, without the use of selective RF pulses. Fig. 7 shows a practical INEPT-based polarization transfer sequences for in vivo NMR applications. Figs. 6C-F show the vector diagrams for the evolution of the proton and carbon-13 magnetization. Following excitation, the proton magnetization starts to evolve under the effects of frequency offsets and scalar couplings. Since the ¹H 180° pulse refocuses the effect of frequency offsets, i.e. magnetic field inhomogeneity and chemical shift evolution (Review 1, Comment 4), the magnetization is only affected by scalar coupling at the echo-time TE1. When TE1 = 1/(2¹J_CH) the proton magnetization has evolved into a state of anti-phase coherence in which protons bound to carbon-13 in the α-state have accumulated a 180° phase difference relative to protons bound to carbon-13 in the β-state (Fig. 6D). A second 90° pulse will bring the anti-phase coherence to the longitudinal axis where the same situation has been created as during the selective polarization inversion experiment, i.e. one of the ¹H NMR transitions has been selectively inverted (Fig. 6E). Therefore, at that point in time the ¹³C NMR signal is enhanced by a factor ±γ_H/γ_C, which can be revealed by a ¹³C excitation. Unfortunately, the carbon-13 magnetization appears in a state of anti-phase coherence. Application of broadband decoupling to this state will lead to a collapse of the doublet structure to a singlet of zero intensity. Applying another spin-echo delay TE2 = 1/(2¹J_CH) will evolve the anti-phase signal into an in-phase doublet (Fig. 6F), after which broadband decoupling can be applied for additional signal enhancement and spectral simplification. The sequence shown in Fig. 7 is referred to as ‘refocused INEPT’. For CH₂ and CH₃ resonances, the echo-time TE2 should be 1/(4¹J_CH) and ~1/(5¹J_CH), respectively, for optimal signal refocusing.

Figure 6.

(A) Energy level diagram and thermal equilibrium populations for a heteronuclear scalar-coupled two-spin-system. Closed and open circles represent a relative abundance and shortage of nuclear spins. The spin populations at thermal equilibrium correspond to +½PH + ½PC (αα), +½PH − ½PC (αβ), − ½PH + ½PC (βα) and − ½PH − ½PC (ββ). The difference between spin populations for a given transition determines the spectral intensity, indicated in parentheses. (B) Following an inversion of proton transition (αα ↔ βα), the intensities of the carbon-13 transition redistribute to {PH + PC} and {−PH + PC} thereby leading to an enhancement of ±γH/γC. Vector diagrams of the ¹H and ¹³C magnetizations at times (C) t = 0, before excitation, (D) t = TE1 = 1/(2¹JCH) before the second 90° pulse, (E) TE1 after the second 90° pulse and (F) t = TE1 + TE2 are shown. The situation in (F) is achieved after a two-step phase cycle of the second ¹H 90° pulse to remove the contribution of directly excited ¹³C magnetization.

Figure 7.

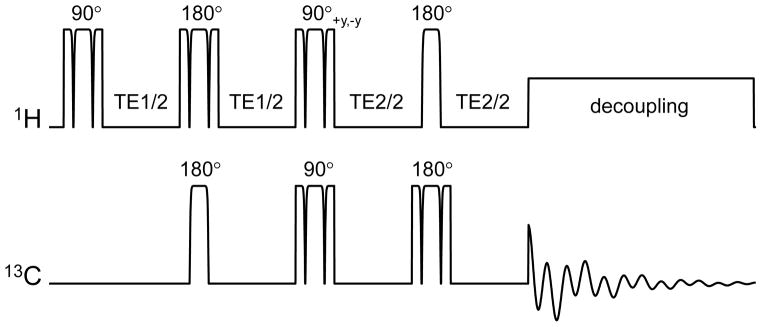
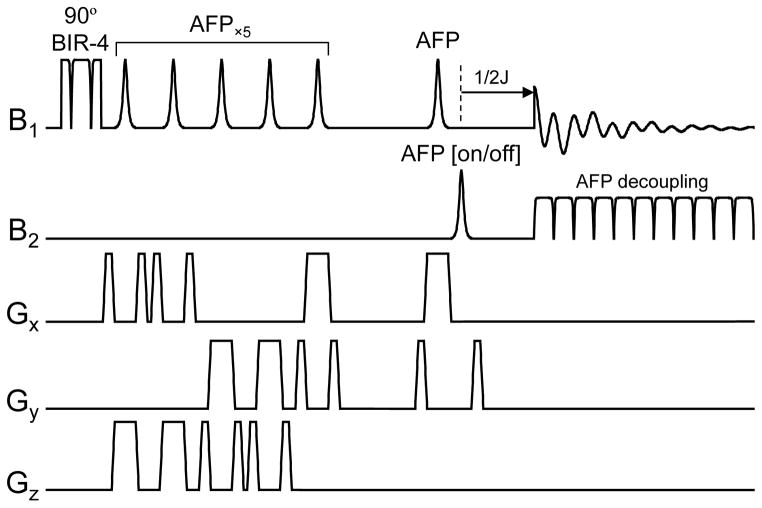
Polarization transfer sequence based on adiabatic AFP and BIR-4 pulses. The acquisition phase should be phase-cycled in concert with the second ¹H 90° pulse in order to retain the transferred polarization and cancel the direct ¹³C magnetization. All RF pulses are executed with BIR-4 waveforms, except for the first ¹³C and last ¹H RF pulses, which are executed as shorter AFP pulses, thereby reducing RF power deposition. WALTZ-16 is often used for broadband decoupling during acquisition.

Whereas the original polarization transfer methods were implemented with hard pulses, this would not be optimal for in vivo NMR applications. Almost all in vivo polarization transfer studies are performed with surface coils for maximum RF power efficiency and the highest receive sensitivity. However, the high RF inhomogeneity associated with surface coils leads to incorrect nutation angles and thus signal loss and artifacts. Executing the sequence with adiabatic RF pulses as shown in Fig. 7 will guarantee a constant nutation angle independent of the applied RF power, above a minimum required RF power level. An explanation of the exact choice for specific RF pulses is outside the scope of this review and interested readers are referred to the original literature (42–44) and reviews on adiabatic RF pulses (19, 45, 46). An additional consideration for in vivo ¹³C NMR spectroscopy is the need for spatial localization. In many cases the ISIS method is chosen in combination with outer volume suppression. Since the polarization transfer scheme begins on the ¹H channel, spatial localization can also be performed on the ¹H channel with a correspondingly smaller chemical shift artifact.

Indirect ¹H-[¹³C] NMR methods

Indirect ¹³C NMR refers to methods that detect protons that are directly attached to ¹³C nuclei. The main advantage of this approach is that the larger gyromagnetic ratio of protons leads to a significantly higher sensitivity. In addition, ¹H NMR detection allows the detection of both the total (¹²C + ¹³C) and the ¹³C fraction of a given metabolite, such that the direct calculation of in vivo ¹³C fractional enrichments is straightforward.

Indirect ¹H-[¹³C] NMR methods can be broadly divided into single-shot multiple-quantum-coherences-based methods (MQC) (47–50) and J-difference-based methods (10, 51–53). The MQC-based methods selectively detect the ¹H NMR signals attached to ¹³C nuclei by destroying (i.e. dephasing) all other ¹H NMR signals in a single scan. However, the removal of all other ¹H NMR signals prevents the calculation of ¹³C fractional enrichments and the monitoring of metabolites without ¹³C label incorporation. Because of these serious drawbacks only indirect ¹H-[¹³C]-NMR methods based on J-difference editing will be discussed further.

J-difference editing

The principle of J-difference editing is based on different reactions of a scalar-coupled spin-system to non-selective (¹H and ¹³C refocusing) and selective (only ¹H refocusing) spin-echo methods. Evolution due to scalar couplings will commence normally during a non-selective spin-echo sequence leading to an inversion of heteronuclear coupled spins relative to uncoupled spins when the echo-time TE equals 1/¹J_CH (= 7.1 ms for ¹J_CH = 140 Hz). A non-selective spin-echo typically has 180° RF pulses on both ¹H and ¹³C channels, such that all spins are equally affected. When the 180° RF pulse on the ¹³C channel is removed, the spin-echo becomes selective for ¹H. In this case evolution due to scalar coupling is completely refocused, such that heteronuclear coupled spins are in-phase with uncoupled spins. When the two experiments (non-selective and selective) are performed and stored separately, the difference can be calculated which will display all ¹H NMR resonances that are directly coupled to ¹³C nuclei. All ¹H NMR resonances not coupled to ¹³C nuclei are removed during the subtraction.

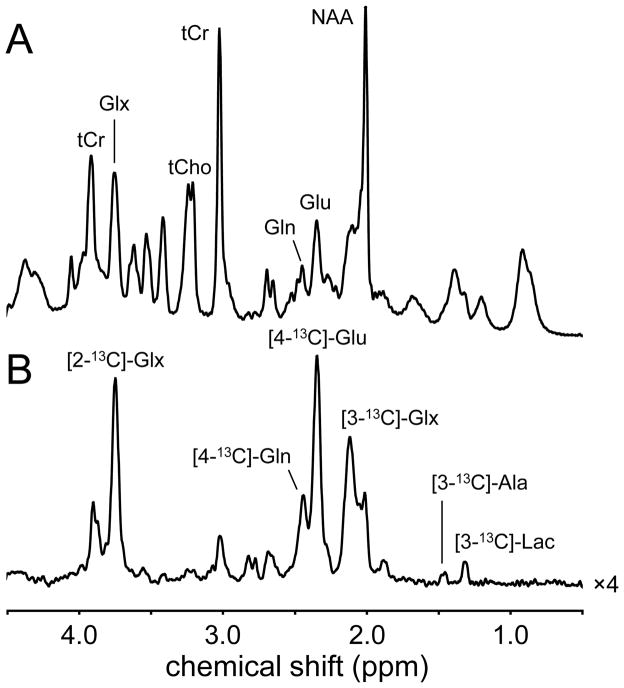
Indirect ¹H-[¹³C]-NMR detection via J-difference editing of course has to deal with all the common challenges of in vivo ¹H NMR such as spatial localization and water suppression. The NMR sequence shown in Fig. 8 is one of several possibilities to obtain high-quality ¹H-[¹³C] NMR spectra in vivo. The sequence is based on the LASER localization scheme (54, 55), extended with a ¹³C inversion pulse that is present during half of the scans when the sequence generates a non-selective spin-echo. Because the first five 180° pulses are selective for ¹H in all scans, all heteronuclear scalar coupling evolution is refocused. Therefore only the echo-time around the last 180° pulse is adjusted to TE = 1/¹J_CH ~7–8 ms. Fig. 9 shows an example of ¹H-[¹³C] NMR spectra of the rat brain following the infusion of [1,6-¹³C₂]-glucose. An additional feature of Fig. 8 is the presence of ¹³C RF pulses during ¹H acquisition to achieve broadband decoupling which will be discussed next.

Figure 8.

Proton-observed, carbon-edited J-difference sequence based on 3D LASER localization with adiabatic full passage (AFP) RF pulses. In order to attain the adiabatic nature of the method, an adiabatic broadband decoupling sequence is used during acquisition.

Figure 9.

(A) ¹H and (B) ¹H-[¹³C] NMR spectra acquired from rat brain at 9.4 T in the presence of adiabatic broadband decoupling. The spectra are acquired circa 90 min following the start of [1,6-¹³C2]-glucose infusion. Similar to the direct ¹³C NMR spectrum of Fig. 4, the [4-¹³C]-glutamate resonance is the most intense, reflecting the cerebral TCA cycle activity.

Broadband decoupling

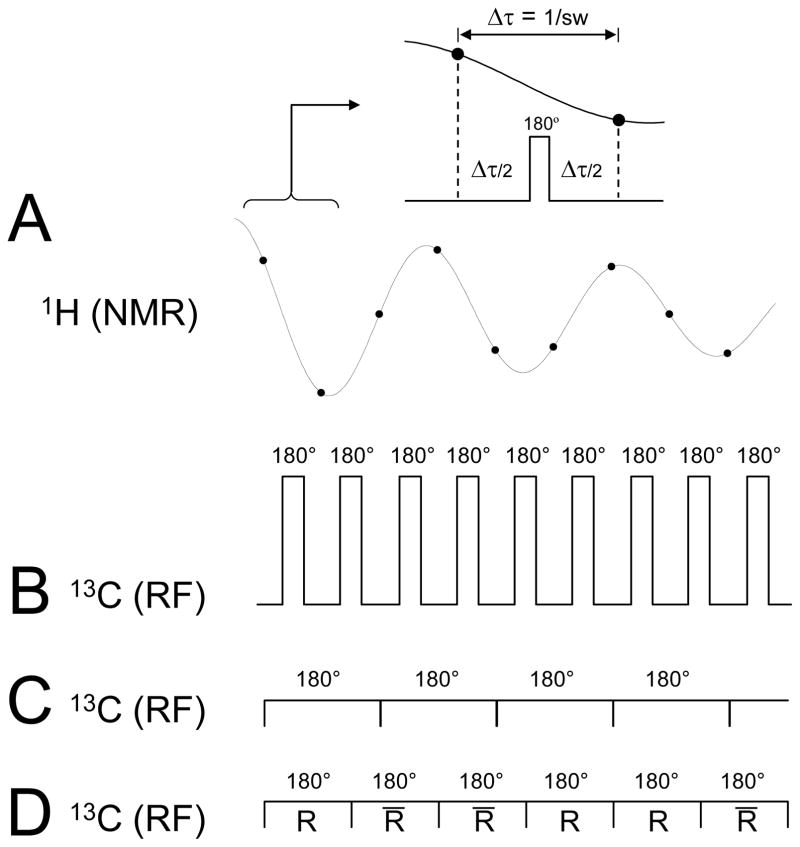
Decoupling aims at removing the splitting of resonances due to heteronuclear ¹H-¹³C scalar coupling in order to enhance the sensitivity and achieve spectral simplification. The principle behind decoupling is relatively simple and is based on the fact that a 180° RF pulse selective for one of the two spins, either ¹H or ¹³C, refocuses scalar coupling evolution over the time period symmetrical around the 180° pulse. This principle is similar to that used in J-difference editing. Therefore, when acquiring ¹H NMR signal the application of a short 180° pulse on the ¹³C channel in the middle of each dwell time would completely refocus heteronuclear scalar coupling at each acquisition point (Fig. 10A/B). Unfortunately, the large number of high-powered 180° pulses would lead to unacceptable sample heating and is never used in reality. The decoupling performance only slightly degrades when the 180° pulse spans a few dwell times. In the case that the delay between 180° pulses becomes zero, the decoupling method is referred to as continuous wave (CW) decoupling (Fig. 10C). Since the 180° pulses are stretched over a longer time with a proportional reduction in peak RF amplitude, CW decoupling is a feasible option for in vivo decoupling as far as RF power deposition and sample heating are concerned. However, the main drawback of CW decoupling is that a 180° rotation is only achieved very close to on-resonance. For selected applications, like ¹³C glycogen detection, this may be a viable option. However, for the far majority of in vivo applications, multiple metabolites across a range of chemical shifts require simultaneous decoupling. In these cases, on-resonance CW decoupling is inadequate and broadband decoupling methods must be employed.

Figure 10.

Principle of heteronuclear decoupling during ¹H-[¹³C]-NMR. (A) A continuous ¹H time domain signal is sampled at discrete points separated by the dwell-time Δ τ. (B) The application of short 180° pulses on the ¹³C channel in the middle of each dwell-time would lead to complete refocusing of heteronuclear scalar coupling evolution at each data acquisition point and to perfect decoupling. (C) RF power restrictions necessitate lengthening of the 180° ¹³C RF pulses over several dwell times, which would lead in the extreme case to continuous wave decoupling. (D) In order to improve the off-resonance performance, the regular 180° pulses are typically substituted with pulse combinations, composite or adiabatic RF pulses (denoted R, where the overbar represents a 180° phase inversion) and combined to form so-called decoupling super cycles.

Broadband decoupling methods make optimal use of the flexibility to stretch a 180° pulse beyond a single dwell-time by executing longer and more complicated RF pulses with inherent compensation towards imperfections (Fig. 10D). Traditionally the most popular decoupling sequences are MLEV-16 (56–58) and WALTZ-16 (59–61). The basic building block for MLEV and WALTZ decoupling are the composite pulses 90°(+x)180°(+y)90°(−x) and 90°(+x)180°(−x)270°(+x), respectively. Composite RF pulses are a collection of square RF pulses that achieve the same on-resonance rotation as a single square pulses but with compensation towards off-resonance effects and RF inhomogeneity. Fig. 11 shows the performance of square, MLEV and WALTZ RF pulses as a function of RF amplitude and frequency offset. Whereas the sensitivity of WALTZ towards RF inhomogeneity is identical to that of a square RF pulses, MLEV also has an increased insensitivity towards incorrect RF power settings (Fig. 11A). Even though MLEV and WALTZ RF pulses are significantly longer than a square pulse for the same on-resonance 180° rotation, they achieve a much wider inversion bandwidth (Fig. 11B). Since typical acquisition times are in the order of 100–300 ms, many composite RF pulses are required. The performance of these pulses is very poor when executed as a continuous train for the entire duration of the acquisition window. The poor performance can be traced back to the fact that the inversion frequency profile for individual composite RF pulses, while better than a square RF pulse, has significant imperfections (Fig. 11). These imperfections propagate through a decoupling pulse train, giving rise to large accumulative errors in the final frequency profile. Since minor imperfections are unavoidable, specific pulse phase schemes have been designed to minimize error propagation throughout decoupling sequences. These so-called decoupling sequences are essential to broadband decoupling. The specific 16-step decoupling super cycle that is used in combination with WALTZ composite RF pulses gives rise to the so-called WALTZ-16 decoupling scheme (59–61), demonstrating greatly enhanced performance over the frequency profile. Shorter, but less effective cycles are used in WALTZ-4 and WALTZ-8 decoupling.

Figure 11.

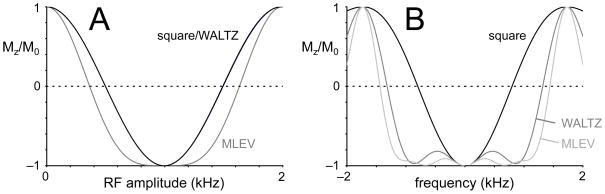
(A) RF amplitude and (B) frequency dependence of square, MLEV and WALTZ inversion pulses. The RF amplitude of square and WALTZ pulses are identical, whereas MLEV pulses have a decreased sensitivity towards the RF amplitude for inversions. The off-resonance performance of both MLEV and WALTZ pulses is significantly better than that of a square pulse.

Up to this point, the fact that decoupling pulses are allowed to run over several dwell-times has been ignored, given that the scalar coupling evolution is a relatively slow process compared to the data acquisition rate. However, restrictions on RF power deposition limit the available RF amplitude, typically leading to a lengthening of the RF pulse duration. For example, the RF amplitude for decoupling in the human brain at 4 T may be limited to 500 Hz, making an individual WALTZ element 3.0 ms in duration. During this relatively long pulse, the coherences will evolve under the effects of heteronuclear scalar coupling giving rise to small signal oscillations in the detected NMR signal, which in turn lead to so-called decoupling or cycling sidebands in the NMR spectrum (Fig. 12). The decoupling sidebands have two undesirable effects on the appearance of the NMR spectrum. Firstly, the multiple decoupling sidebands increase the effective noise level, leading to a reduced signal-to-noise ratio. Secondly, the intensity of the main resonance is redistributed across multiple smaller decoupling sidebands, leading to a reduction in the main decoupled signal. It is therefore desirable to minimize the decoupling sidebands and maximize the main decoupled resonance. Besides these two parameters, other often conflicting considerations include the minimum decoupling bandwidth, the allowable RF power deposition, the maximum available RF peak power and the sensitivity towards experimental imperfections like RF inhomogeneity. These parameters can be optimized and/or balanced with four basic variables, namely length, amplitude and shape of the decoupling pulse and the decoupling scheme. A rigorous comparison and evaluation of decoupling methods most commonly used for in vivo NMR has been given by de Graaf (62). Most noticeable, for RF amplitudes suitable for human applications at 4 Tesla (i.e. B_2max = 500 Hz), the classic MLEV-16 and WALTZ-16 provide the best performance with an effective decoupling bandwidth of circa 1.7B_2max for a 90% decoupling efficiency (i.e. the main decoupled resonance is at least 90% of a perfectly decoupled resonance). Furthermore, at higher RF amplitudes suitable for animal applications, many other decoupling methods involving adiabatic RF pulses become available (62).

Figure 12.

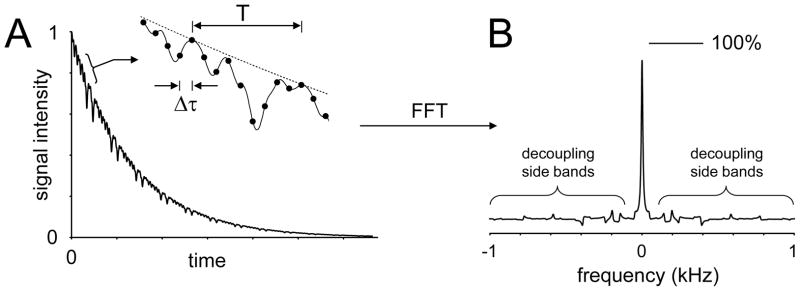
Time and frequency domain features of broadband decoupling. (A) In most realistic cases the length of the decoupling RF pulses span several dwell times Δ τ, such that the effects of heteronuclear scalar coupling evolution are not refocused until the end of the pulse. As a result part of the scalar coupling evolution is captured by the data acquisition points covering the length of the RF pulse. (B) These small modulations give rise to so-called decoupling or modulation side bands following Fourier transformation, potentially obscuring other, smaller resonances. The decoupling sidebands necessarily also lead to a reduction in the peak height of the main decoupled resonance (100% represents the maximum intensity in the case of perfect on-resonance CW decoupling).

Specific Absorption Rate (SAR)

Electrical fields associated with the RF probe during pulse transmission induce local currents in conductive media, such as human or animal tissues. In the presence of electrical resistance these circulating currents lead to power loss and subsequently to so-called ohmic or induction heating of the local tissue.

The amount of RF power deposition in tissues, expressed as the specific absorption rate (SAR), is limited by guidelines imposed by several government institutions, like the US Food and Drug Administration (FDA). Current guidelines state that the RF power deposition should not exceed 4 W/kg averaged over 15 min over the entire body which are relaxed to 12 W/kg averaged over 5 min for the extremities. For the head the guidelines are somewhat stricter with a maximum RF power deposition of 3 W/kg averaged over 10 min over the entire head and 8 W/kg in any gram of tissue averaged over 5 min. The average SAR is relatively easy to obtain by monitoring the total amplifier RF power output and determining the total tissue volume in which the RF power is deposited. RF power losses along the cables, filters and T/R switches do not reach the RF probe and should be subtracted from the total RF power seen by the RF probe. Furthermore, the coil is not 100% efficient in transferring the RF power to the subject. This efficiency can be measured by measuring the loaded and unloaded coil Q values (17). Other factors that affect the RF power delivery are power reflection and radiation losses. However, to attain the highest level of subject safety it is often best to be conservative and assume that all RF power from the amplifier, minus the losses over cables, filters and T/R switches, reaches the subject. The local SAR levels are much more difficult to obtain, since the electrical fields responsible for tissue heating cannot be readily measured in vivo. Especially the last criterion is most difficult to comply with due to local ‘hotspots’.

There are two kinds of electrical fields associated with an RF probe, namely a coil-specific, conservative field which arises from the charge distribution of the RF coil (i.e. the geometry of the RF probe) and sample-specific, non-conservative or induced fields which arise from the time-varying magnetic B₁ field within the sample. The conservative electrical field can and should be minimized through proper RF probe design (e.g. distributed capacitance). The inductive electrical E₁ field is closely associated with the magnetic B₁ field that is essential for NMR and can therefore not be eliminated. Whereas the exact distribution of the magnetic B₁ field can be readily mapped through MRI methods (19), the distribution of the electrical field depends on a number of parameters, like conductivity, and is not readily accessible in vivo. Furthermore, the relationship between B₁ and E₁ is complex at high magnetic fields which, together with the fact that the remaining conservative electrical E₁ field is typically unknown, leads to the experimental realization that electrical E₁ fields are not readily mapped in vivo. As a result, local SAR values must be obtained through finite difference time domain (FDTD) numerical methods for electromagnetism (63, 64).

Whereas the local temperature elevation is ultimately related to patient safety, guidelines have been established for SAR as non-invasive temperature mapping is for many techniques even more complicated. However, the chemical shift of the water resonance has a temperature sensitivity of −0.01 ppm/°C and has been used to perform non-invasive MRI-based temperature mapping of tissues in vivo (65).

Alternative detection methods

¹H NMR without ¹³C pulses or decoupling

Many clinical MR platforms are limited to a single proton channel and do not routinely provide access to a decoupling channel. However, this has not prevented some groups from performing ¹H-[¹³C] NMR spectroscopy without decoupling (66). In the absence of broadband decoupling, the ¹H NMR spectral signature of ¹³C-labeled compounds is different from that of the non-labeled compounds due to the heteronuclear scalar coupling. Therefore, during the infusion of ¹³C-labeled substrates, e.g. [1-¹³C]-glucose, the glutamate and glutamine metabolic pools are slowly replaced with ¹³C-labeled glutamate and glutamine. Through the use of advanced spectral fitting procedures, like LCModel, it is possible to separate the ¹³C labeled and unlabelled compounds based on their spectral pattern. The absence of broadband decoupling necessarily leads to a reduced sensitivity and increased spectral complexity, as all resonances are now split into doublets by the heteronuclear scalar coupling.

¹³C NMR without or with low-power ¹H decoupling

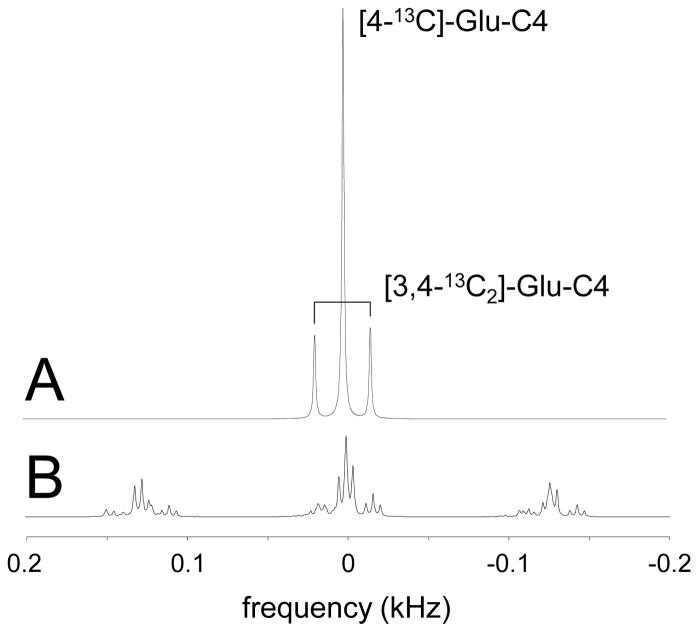
Recently several reports have appeared that performed ¹³C NMR without (67) or with low-power ¹H decoupling (35, 36). The absence of broadband decoupling in ¹³C NMR typically comes with a stronger penalty in spectral complexity and sensitivity than for ¹H NMR. This is because, whereas protons are always connected to a single ¹³C nucleus and thus forming a doublet signal, ¹³C nuclei are often connected to multiple protons. This leads to significantly more complicated spectral patterns (triplets, quartets, doublet of doublets) and a subsequent larger reduction in sensitivity. Fig. 13 shows an example of decoupled and non-decoupled ¹³C NMR spectra of [4-¹³C]-glutamate and [3,4-¹³C₂]-glutamate. It is apparent that the absence of decoupling leads to greater spectral complexity and reduced peak intensity (Fig. 13B). Nevertheless, with accurate knowledge of one, two and three-bond heteronuclear scalar couplings (19, 67) and least-squares-based spectral fitting it has been shown that ¹³C NMR in the absence of decoupling can be quantified, albeit with a reduced sensitivity (67).

Figure 13.

¹³C NMR spectra of [4-¹³C]-glutamate and [3,4-¹³C2]-glutamate in (A) the presence and (B) the absence of broadband decoupling. ¹H decoupling in (A) removed all splitting except the ¹³C-¹³C isotopomer splitting. In the absence of decoupling the ¹³C NMR spectrum becomes much more complicated with many low-intensity resonances, but can still be quantitatively described if all scalar coupling constants are known.

An alternative strategy that eliminates the spectral complexity obtained without decoupling while minimizing the RF power deposition from decoupling is to observe only ¹³C NMR signals from ¹³C nuclei without directly coupled protons, like [1-¹³C]- and [5-¹³C]-glutamate. As detailed earlier the RF power requirements of broadband decoupling are high because the 180° pulses must be short relatively to the heteronuclear scalar coupling evolution (~ 1/¹J_CH). Because ¹J_CH is very large for ¹³C nuclei with directly coupled protons (¹J_CH = 120 – 170 Hz), the 180° pulses must be in the order of 1 – 5 ms at a correspondingly high RF power. The heteronuclear scalar coupling between ¹³C nuclei and protons attached to the adjacent carbon nucleus is much smaller (²J_CH = 3 – 5 Hz), such that the pulse length conditions during decoupling can be greatly relaxed. In these cases low-power ‘noise’ decoupling has been used to remove the small long-range splitting and obtain high-quality ¹³C NMR spectra. Using [2-¹³C]-glucose as a substrate provides identical information on TCA cycle activity as the more conventional [1-¹³C]-glucose. The primary disadvantage of the outlined technique is that signal enhancement techniques, like polarization transfer, cannot be employed such that the overall sensitivity is lower than that achievable through polarization transfer methods.

Sensitivity and resolution

The choice for direct ¹³C-[¹H] or indirect ¹H-[¹³C] NMR is ultimately determined by a number of factors of which spectral sensitivity and resolution are often the most important. When factors arising from relaxation, nuclear Overhauser enhancement, and polarization transfer are ignored, ¹H NMR detection provides a 16 times (= (γ_H/γ_C)²) higher signal-to-noise ratio (SNR) than ¹³C NMR detection for equal number of spins (19). However, ¹³C NMR detection is often enhanced by polarization transfer which together with relaxation parameters reduces the SNR advantage of ¹H NMR detection to 3–4 fold. For more complicated spin systems, like CH₂ and CH₃ groups, the polarization transfer efficiency decreases whereas the ¹H NMR detection efficiency increases linearly. The sensitivity enhancement of ¹H over ¹³C NMR detection is thus dependent on many variables and may be difficult to determine exactly. However, it is safe to state that indirect ¹H-[¹³C] NMR detection provides several fold higher SNR. Of course, the accuracy of the detected metabolites is not only determined by the noise level, but also by the frequency separation of resonances. Since ¹H NMR has a spectral dispersion of less than 5 ppm, overlap of resonances is the rule, especially at lower magnetic fields. ¹³C NMR on the other hand has a spectral dispersion of >100 ppm, which gives adequate separation of resonances even at low magnetic fields. For dynamic ¹³C NMR studies a crucial factor for the decision may be the separation of [4-¹³C]-glutamate from [4-¹³C]-glutamine. The H4 resonances of glutamate and glutamine essentially overlap in ¹H NMR spectra at 4 T and lower making indirect ¹H-[¹³C] NMR less desirable. However, at 7 T and higher these resonances become resolved such that indirect detection may become preferable over direct ¹³C NMR detection.

Hyperpolarized ¹³C NMR

As mentioned in the previous section, the sensitivity of ¹³C NMR is ultimately limited by the low nuclear polarization obtained at thermal equilibrium. Whereas indirect ¹H-[¹³C] NMR can improve this several-fold, the thermal equilibrium nuclear polarization at currently available magnetic field strengths represents less than 0.01% of the potential, complete polarization. A number of methods have been proposed to enhance the nuclear polarization of spins to a significant fraction of unity. These methods, which are collectively referred to as hyperpolarization techniques, have recently begun to show potential for in vivo applications. The two techniques that show the greatest promise to study in vivo metabolism are para-hydrogen-induced polarization (68, 69) and dynamic nuclear polarization (70, 71). Since great detail about these methods can be found in many of the other articles in this special issue of NMR in Biomedicine, discussion of these methods is outside the scope of this review. However, it is informative to highlight some of the differences between the conventional and hyperpolarized ¹³C NMR methods.

As soon as the large ¹³C spin polarization is exposed to thermal equilibrium conditions the polarization will decay through T₁ relaxation. At the current state of compound and technique development the longest T₁ relaxation times are in the order of minutes. This means that a slow infusion protocol as depicted in Fig. 5A to build up a steady-state concentration of substrate in the blood is not feasible. Instead, all hyperpolarized compounds are currently administered as a high-concentration bolus. The substrate signal, of course, continues to decay as it travels through the vasculature and enters the various tissues. Similar to conventional ¹³C NMR the substrate is then converted to a range of products. In the case of [1-¹³C]-pyruvate typical products include [1-¹³C]-lactate and [1-¹³C]-alanine. At the current state of technique development products further downstream, e.g. glutamate, have not been detected, presumably because of signal loss due to T₁ decay. Studying cerebral metabolism through hyperpolarized ¹³C NMR has proved difficult, possibly due to the slow blood-to-brain transport across the blood-brain barrier.

Since protons directly attached to a carbon-13 nucleus typically reduce the ¹³C T₁ relaxation, the substrates studied to date, like [1-¹³C]-pyruvate, are hyperpolarized in the proton-free carbon position. This choice significantly simplifies NMR sequences as broadband decoupling is no longer required. Since the greatly increased sensitivity allows a much higher spatial resolution, signal localization is almost always performed in a spatially resolved manner, such as ¹³C MR spectroscopic imaging. However, since the hyperpolarized ¹³C NMR signal does not recover via T₁ relaxation following excitation, special care in sequence development much be taken to optimally utilize the available ¹³C polarization. Typical solutions involve using low-angle excitation pulses or single-shot localization methods like echo-planar imaging (EPI).

Hyperpolarized ¹³C NMR is only in its infancy when compared to conventional ¹³C NMR. It has already displayed excellent spatial resolution and spectral dynamics in a number of applications. And while the quantitative aspects of hyperpolarized ¹³C NMR, which will have to include T₁ relaxation, are currently unresolved, there is no doubt that it will provide unique new information about fast metabolic processes.

Metabolic modeling

Following the repeated acquisition of NMR spectra (averaged over 5–10 min) during the ¹³C-labeled substrate infusion one ends up with a series of spectra displaying the dynamic incorporation of ¹³C label in various products (Fig. 14A). In order to obtain absolute metabolic fluxes through the various pathways one has to quantify the NMR spectra in terms of total and ¹³C-labeled metabolite concentrations. This can be done with any of the publicly or commercially available spectral fitting software programs, such as jMRUI (72) and LCModel (73). The dynamical changes of ¹³C-labeled metabolite levels then form the input for metabolic modeling. Metabolic modeling refers to a set of procedures which express a collection of metabolic pathways as mathematical differential equations in order to obtain absolute fluxes through these pathways. Fig. 3 schematically shows the metabolic pathways involved in cerebral glucose metabolism and glutamatergic and GABAergic neurotransmitter cycling. The time dependence of each metabolic pool is given by a differential equation describing the flow in and out of that pool. For example, the time dependence of the neuronal glutamate [Glu_N] pool is given by

Figure 14.

(A) Time resolved ¹H-decoupled, ¹³C NMR spectra from rat brain in vivo following the intravenous infusion of [1,6-¹³C2]-glucose. Spectra are acquired with an adiabatic INEPT sequence (TR = 4000 ms, 200 uL) at 7.05 T. (B) Turnover curves of [4-¹³C]-glutamate and [4-¹³C]-glutamine. Dots represent measured fractional enrichments as obtained through spectral quantification of the data shown in (A), whereas the solid line represents the best mathematical fit to a three-compartment (blood, glutamatergic neurons and astroglia) metabolic model.

$$\frac{\text{d}[{\text{Glu}}_{\text{N}}]}{\text{dt}}={\text{V}}_{\text{cycle},\text{Glu}/\text{Gln}}+{\text{V}}_{\text{x}}-\left({\text{V}}_{\text{cycle},\text{Glu}/\text{Gln}}+{\text{V}}_{\text{x}}\right)=0$$ [1]

whereby the first two terms are metabolic flows into the glutamate pool from glutamine and 2-oxoglutarate, respectively. The last two terms represent the metabolic flows out of the glutamate pool. The differential equation [1] is equal to zero because the total neuronal glutamate pool does not change over time, i.e. the neuronal glutamate pool is at metabolic steady-state. Eq. [1] is a so-called mass-balance equation as it describes the flow of all mass (¹²C or ¹³C) to and from the neuronal glutamate pool. While Eq. [1] is trivial for the steady-state case, there are conditions where the metabolite levels are not constant over time. In those cases the mass-balance equations provide a quantitative description of the temporal dynamics of metabolite levels. For a complete description of the experiment, one also needs to track the flow of ¹³C isotope, which is done with isotope-balance equations. These equations are specific to the position of the carbon atom within a molecule, since different carbon positions will label at different rates depending on the substrate and metabolic pathways. The isotope-balance equation for the C4 position of neuronal glutamate [Glu_N4*] is given by

$$\frac{\text{d}[{\text{Glu}}_{\text{N}}4\ast ]}{\text{dt}}=\frac{[{\text{Gln}}_{\text{N}}4\ast ]}{[{\text{Gln}}_{\text{N}}]}{\text{V}}_{\text{cycle},\text{Glu}/\text{Gln}}+\frac{[2{\text{OG}}_{\text{N}}4\ast ]}{[2{\text{OG}}_{\text{N}}]}{\text{V}}_{\text{x}}-\frac{[{\text{Glu}}_{\text{N}}4\ast ]}{[{\text{Glu}}_{\text{N}}]}\left({\text{V}}_{\text{cycle},\text{Glu}/\text{Gln}}+{\text{V}}_{\text{x}}\right)$$ [2]

Mass and isotope balance equations similar to Eqs. [1]– [2] can be constructed for all metabolic pools, thereby making up the metabolic model. The model describing the metabolic pathways shown in Fig. 3 is referred to as a four compartment model, as it is composed of a blood compartment, and compartments for the glutamatergic neuron, GABAergic neuron and astroglia. Using the blood or brain glucose levels and fractional enrichments, the metabolic pool sizes and the measured fractional enrichment curves allow the calculation, through non-linear least-squares optimization, of a number of important fluxes like the neuronal and astroglial TCA cycles and the glutamate-glutamine and GABA-glutamine neurotransmitter cycles (Fig. 14B). For more details on cerebral metabolic models and turnover data analysis the reader is referred to the literature (9, 13, 74–76).

Abbreviations used

Ace

acetate

AFP

adiabatic full passage

BHB

β-hydroxybutyrate

BIR-4

B1 independent rotation using 4 segments

BW

bandwidth

CW

continuous wave

DG

2-deoxy-D-glucose

FDG

2-fluoro-2-deoxy-D-glucose

GABA

γ-aminobutyric acid

GC-MS

gas chromatography-mass spectrometry

Glc

glucose

Gln

glutamine

Glu

glutamate

INEPT

insensitive nuclei enhanced by polarization transfer

ISIS

image-selected in vivo spectroscopy

PET

positron emission tomography

LASER

localization by adiabatic spin-echo refocusing

MQC

multiple-quantum-coherences

OVS

outer volume suppression

SAR

specific absorption rate

SNR

signal-to-noise ratio

TCA

tricarboxylic acid

T/R

transmission/reception