Quantum-state transfer from an ion to a photon

Abstract

One model for quantum networks^1,2 is based on the probabilistic measurement of two photons, each entangled with a distant node, e.g., an atom or atomic ensemble^3–7. A second, deterministic model transfers information directly from an atom onto a cavity photon, which carries it to a second node⁸, as recently demonstrated with neutral atoms⁹. In both cases, the challenge is to transfer information efficiently while preserving coherence. Here, following the second scheme, we map the quantum state of an ion onto a photon within an optical cavity. Using an ion enables deterministic state initialization^10,11, while the cavity provides coherent coupling to a well-defined output mode^12–15. Although it is often assumed that a cavity-based quantum interface requires the strong-coupling regime, we show transfer fidelities of 92% in the presence of non-negligible decoherence and characterize the interplay between fidelity and efficiency. Our time-independent mapping process offers a promising route toward ion-based quantum networks.

Information transfer between distant quantum computers would enable distributed quantum information processing^16–18 and quantum communication^19,20. In the original proposal for quantum-state transfer⁸, a photonic qubit comprises the number states |0 and |1. Such a qubit was subsequently employed for the cavity-based mapping of a coherent state onto an atom²¹. However, due to losses in a realistic optical path, it is advantageous instead to encode the qubit within a degree of freedom of a single photon; we choose the polarization degree of freedom. The target process then maps an electronic superposition of atomic states |S and |S′ to the photon polarization states |H and |V ,

$$(\cos \alpha \mid S\rangle +e^{i\phi }\sin \alpha \mid S^{\prime }\rangle )\otimes \mid 0\rangle \to \mid D\rangle \otimes (\cos \alpha \mid H\rangle +e^{i\phi }\sin \alpha \mid V\rangle ),$$ (1)

preserving the superposition’s phase and amplitude, defined by φ and α; |D is a third atomic state. By coupling two initial atomic states to one final state, no information remains in the ion after the mapping.

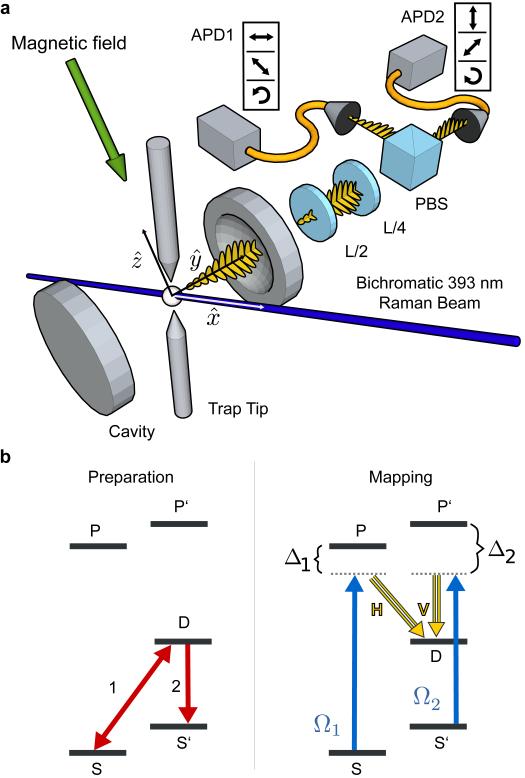
As an atomic qubit, we use two electronic states of a single ⁴⁰Ca⁺ ion in a linear Paul trap within an optical cavity²² (Fig. 1a). Any superposition state of the atomic qubit can be deterministically initialized via coherent laser manipulations^10,11, where this initialization is independent of the ion’s interaction with the cavity field. Following optical pumping to the Zeeman state |S ≡ |4²S_1/2, m_J = −1/2, the atomic qubit is encoded in the states |S and |S′ ≡ |4²S_1/2, m_J = +1/2 via two laser pulses on the quadrupole transition that couples the 4²S_1/2 and 3²D_5/2 manifolds (Fig. 1b). The length and phase of a first pulse on the |S ↔ |3²D_5/2, m_J = −1/2 transition set the amplitude and phase of the initial state. The state is subsequently transferred back to the S manifold via a π-pulse on the |3²D_5/2, m_J = −1/2 ↔ |S′ transition.

Figure 1. Experimental configuration and mapping sequence.

a, A ⁴⁰Ca⁺ ion is confined in a linear Paul trap (indicated schematically by two trap tips) and positioned at the antinode of an optical cavity. A bichromatic 393 nm field drives a pair of Raman transitions, generating a single cavity photon. The beam is linearly polarized in the $\widehat{z}$ direction and propagates along $\widehat{x}$. An external magnetic field is chosen parallel to $\widehat{z}$, orthogonal to the cavity axis $\widehat{y}$, in order to drive π transitions. The measurement basis of photons exiting the cavity is set by half- and quarter-waveplates (L/2, L/4). Photons are then separated by a polarizing beamsplitter (PBS) for detection on avalanche photodiodes (APD1, APD2). Tables indicate the polarization of photons at APD1 and APD2 corresponding to three measurement bases. b, Two laser pulses at 729 nm (1,2) prepare the ion in a superposition of levels S and S′. This superposition is subsequently mapped onto the vertical (V ) and horizontal (H) polarization of a cavity photon. The 393 nm laser and the cavity field couple S and S′ to the metastable D level. The bichromatic laser field is detuned from levels P and P′ by Δ₁ and Δ₂ (approximately 400 MHz) and has Rabi frequencies Ω₁ and Ω₂.

To implement the state-mapping process of Eq. 1, we drive two simultaneous Raman transitions in which both states |S and |S′ are coupled to the same final state |D via intermediate states |P ≡ |4²P_3/2, m_J = −1/2 and |P′ ≡ |4²P_3/2, m_J = +1/2 (Fig. 1b). One arm of both Raman transitions is driven by a laser, the second arm is mediated by the cavity field, and a single photon is generated in the process^12–15, where the single-photon nature of our system has been verified in Ref. ¹⁵. If the initial state was |S, this photon is in a vertically polarized state |V; if it was |S′, a horizontally polarized photon |H is generated.

We have recently generated ion–photon entanglement using a similar Raman process²³, which was robust to atomic decoherence. In contrast, here, the coherent transfer of the ion’s initial superposition state is sensitive to spontaneous decay. The crux of this mapping problem is to maintain amplitude and phase relationships during the transfer process in the presence of spontaneous decay, the dominant rate in the system. In this context, we explore both the efficiency and fidelity of the mapping process. The interplay between these quantities allows us to characterize the potential of our experimental apparatus for direct state transfer in a quantum network.

A magnetic field of 4.5 G lifts the degeneracy of electronic states |S and |S′, so that the two Raman transitions have different resonance frequencies, allowing them to be individually addressed. A phase-stable bichromatic driving field with detunings Δ₁ and Δ₂ from |P and |P′, respectively, is applied (Fig. 1b). If the difference frequency Δ₁–Δ₂ is equal to the energy splitting of the qubit states |S and |S′, both Raman transitions are driven resonantly.

The mapping process is characterized via process tomography, in which the bichromatic Raman transition is applied to four orthogonal initial states of the atom: |S, |S′, |S–S′ |S+iS′. For each input state, we measure the polarization state of the output photon via state tomography, using three orthogonal measurement settings²⁴ selected with two waveplates before a polarizing beamsplitter (Fig. 1a). Avalanche photodiodes detect photons at both beamsplitter output ports.

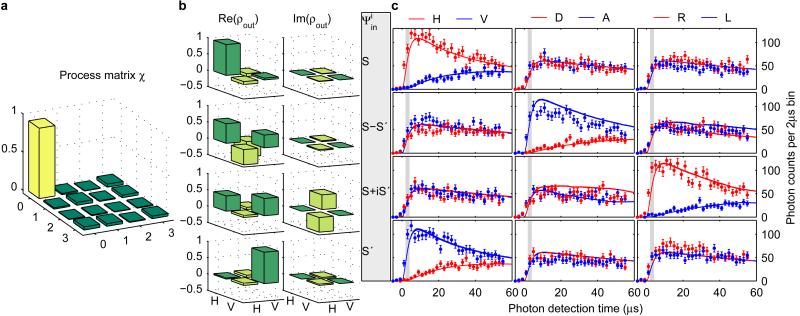
Process tomography extracts the process matrix χ, which parameterizes the map from an arbitrary input density matrix ρ_in to its corresponding output state ρ_out in the basis of the Pauli operators ${\sigma }_{0,1,2,3}\equiv \{1,{\sigma }_x,{\sigma }_y,{\sigma }_z\}:{\rho }_{\mathrm{out}}={\sum }_{i,j}{\chi }_{i,j}{\sigma }_i{\rho }_{\mathrm{in}}{\sigma }_j$. As the ideal mapping process preserves the qubit, the overlap χ_0,0 with the identity should be equal to one. We identify χ_0,0 as the process fidelity, which quantifies the success of the mapping. A maximum likelihood reconstruction²⁵ of χ is plotted in Fig. 2a for a 2 μs window of photons exiting the cavity. Here the matrix element χ_0,0 indicates a process fidelity of (92 ± 2)%, well above the classical threshold of 1/2. Other diagonal elements χ_1,1 = (3±1)% and χ_3,3 = (4±2)% reveal a minor depolarization of the quantum state.

Figure 2. Process and state fidelities of the ion–photon mapping.

a, Absolute values of the process matrix χ reconstructed from cavity photons detected between 2 μs and 4 μs after the bichromatic field is switched on at time = 0. b, Reconstructed density matrices of photons in the same time window for the four input states |S, |S–S′, |S+iS′, and |S′, shown in rows from top to bottom. c, Each state tomography corresponds to measurements in the three bases H/V, D/A, and R/L (columns). For each input state, the temporal shapes of single photons are plotted in red for polarizations H, D, R and in blue for polarizations V, A, L. Error bars represent one s.d. based on Poissonian statistics. In each row, in two of three columns, photons are equally distributed over both detectors, while in the third, photons are generated ideally with a single polarization. Master-equation simulations (red and blue lines) successfully reproduce the observed dynamics. The grey shaded area indicates the time window used for tomography.

For each of the four atomic input states, the reconstructed photonic output states ${\rho }_{\mathrm{out}}^i$ are shown in Fig. 2b, using the same photon collection window as in Fig. 2a. We now consider ${\rho }_{\mathrm{out}}^i$ as a function of detection time. In Fig. 2c, we plot the temporal shape of the emitted photon in each of three measurement bases, a total of 12 cases. For each input state, there exists one polarization measurement basis in which photons would ideally impinge on only one detector. If the ion is prepared in the state |S and measured in the H/V polarization basis, for example, the mapping scheme of Fig. 1b should only produce the photon state |V. However, a few microseconds after the Raman driving field is switched on, we see that the photon state |H appears and is generated with increasing probability over the next 55 μs. The mechanism here is off-resonant excitation of the 4²P_3/2 manifold and decay to the previously unpopulated state |S′, followed by a Raman transition generating the ‘wrong’ polarization. If the ion is prepared in |S′, the temporal photon shapes are inverted and symmetric, with the initial state |H followed by the gradual emergence of |V. We have confirmed this process through master-equation simulations of the ion–cavity system, also plotted in Fig. 2c. Scattering in the case of input states |S – S′ and |S + iS′ is described in the Methods.

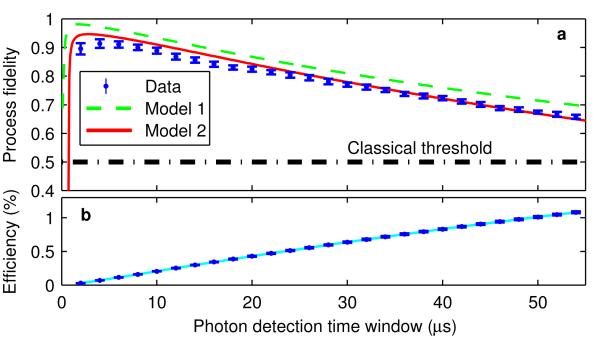
The accumulation of scattering events over time suggests that the best mapping fidelities can be achieved by taking into account only photons detected within a certain time window. Such a window is used for the preceding analysis of process and state fidelities. For each attempt to prepare and map the ion’s state, the probability to detect a photon within this window is 4 · 10⁻⁴, which we identify as the process efficiency. This efficiency can be increased at the expense of fidelity by considering a broader time window. Fig. 3 shows both the cumulative process fidelity and efficiency as a function of the photon-detection window. The cumulative process fidelity reaches a maximum between 2 μs and 4 μs after the bichromatic driving field is switched on, the time interval used to analyze the data of Fig. 2a and b. The fidelity then slowly decreases as a function of time due to the increased likelihood of off-resonant scattering.

Figure 3. Time dependence of process fidelity and efficiency.

a, Cumulative process fidelity and b, process efficiency are plotted as a function of the photon-detection time window, where error bars represent one s.d. (See Supplementary Information.) A green dashed line indicates the simulated process fidelity for the same parameters as in Fig. 2. To this model, we now add the effects of detector dark counts, imperfect state initialization, and magnetic-field fluctuations, quantified in independent measurements, with the result indicated by a red line. A fit to the process efficiency is used to weight the effect of dark counts. The second model agrees well with the data, while the first one represents achievable values for this ion–cavity system.

If all photons detected within 55 μs are taken into account, the process efficiency exceeds 1%, while the process fidelity of (66±1%) remains above the classical threshold of 1/2. This process efficiency includes losses in the cavity mirrors, output path, and detectors. The corresponding probability for state transfer within the cavity is 16%. Efficiencies of up to 55% could be reached by using a longer detection time window, where scattering to the 3²D_5/2 and 3²D_5/2 manifolds keeps this value below unity. In this case, however, the process fidelity approaches the classical threshold, limited by the finite strength of the ion–cavity coupling in comparison to spontaneous decay rates. The fidelity for the 2 μs detection window is primarily limited by detector dark counts at 5.6 Hz, imperfect state initialization with a fidelity of 99%, and magnetic-field fluctuations corresponding to an atomic coherence time of 110 μs. Simulations that include these three effects, plotted in Fig. 3, agree well with the data. A second simulation, also plotted, omits these effects in order to estimate the maximum fidelity possible, yielding a value of 98% for the 2 μs detection window.

The atomic superposition of |S and |S′ experiences a 12.6 MHz Larmor precession, which corresponds to a rotation of the states’ relative phase. One might expect that as a result, it would not be possible to bin data from photons generated from this superposition across a range of arrival times as described above. However, because the frequency difference Δ₁ – Δ₂ of the bichromatic Raman field matches the frequency difference between the two states, the Raman process generates a photon that preserves the initial states’ relative phase, independent of photon detection time. This transfer scheme thus offers advantages for any quantum system in which a magnetic field lifts the degeneracy of the states encoding a qubit. Such non-degeneracy is often required for controlled qubit rotations at a quantum node⁹.

Following the deterministic initialization of an atomic qubit within a cavity, we have shown the coherent mapping of its quantum state onto a single photon. The mapping scheme achieves a high process fidelity, and by accepting compromises in fidelity, we increase the efficiency of the process within the cavity up to 16%. To achieve both near-unit efficiency and high transfer fidelity simultaneously, stronger coupling between ion and cavity is necessary, accessible only with a different cavity geometry, i.e., a different apparatus. For experimentally feasible values of g = 2π × 5 MHz and κ = 2π × 0.1 MHz, simulations yield a photon-generation efficiency of 97% at a process fidelity of 87%. In our current intermediate-coupling regime, the fidelity could also be improved by encoding the stationary qubit across multiple ions²⁶. A direct application of this bichromatic mapping scheme is state transfer between two remote quantum nodes^8,9. Furthermore, via a modified bichromatic scheme, a single ion-cavity system can act as a deterministic source of photonic cluster states²⁷, an essential resource for measurement-based quantum computation²⁸.

Methods

Mean state fidelity

In addition to process fidelity, another metric for quantum processes is the mean state fidelity, which evaluates the state fidelities $\langle {\psi }_{\mathrm{in}}^i\mid {\rho }_{\mathrm{out}}^i\mid {\psi }_{\mathrm{in}}^i\rangle$ for a set of input states $\mid {\psi }_{\mathrm{in}}^i\rangle$, where ${\rho }_{\mathrm{out}}^i$ represent the corresponding photon output states. The mean state fidelity can also be directly extracted from the process fidelity for an ideal unitary process²⁹. For each of our four input states, the reconstructed density matrix of the output photon is shown in Fig. 2b. The corresponding state fidelities are (96±1)% for |S, (94±2)% for |S′, (97±2)% for |S – S′, and (95±2)% for |S + iS′, yielding a mean of (96±1)%. This agrees with the value of (95±1)% extracted from the process fidelity and exceeds the classical threshold²⁹ of 2/3.

Temporal evolution of the superposition states

In the second and third row of Fig. 2c, we plot the temporal pulse shape of the emitted photons for the superposition input states |S – S′ and |S + iS′. Here, the mapping generates a photon with antidiagonal polarization $A=(H-V)∕\sqrt{2}$ and right-circular polarization $R=(H+iV)∕\sqrt{2}$, respectively. Thus, photons impinge predominantly on one detector in the diagonal(D)/antidiagonal(A) and right(R)/left(L) bases, where $D=(H+V)∕\sqrt{2}$ and $L=(H-iV)∕\sqrt{2}$. Here, as for states |S and |S′, photons with the ‘wrong’ polarization are due to off-resonant scattering before the mapping occurs. In this case, scattering destroys the phase relationship between the S and S′ components. (Note that for eight of the cases in Fig. 2c, the measurement basis projects the photon polarization onto the two detection paths with equal probability.)

Process fidelity at short times

In Fig. 3, which shows the cumulative process fidelity as a function of time, the fidelity initially increases because at short times (< 100 ns), photons are produced primarily via the off-resonant rather than the resonant component of the Raman process and thus are not in the target polarization state. This coherent effect, which we have investigated through simulations, is quickly damped due to the low amplitude of off-resonant Raman transitions.