Haplotype assembly in polyploid genomes and identical by descent shared tracts

Abstract

Motivation: Genome-wide haplotype reconstruction from sequence data, or haplotype assembly, is at the center of major challenges in molecular biology and life sciences. For complex eukaryotic organisms like humans, the genome is vast and the population samples are growing so rapidly that algorithms processing high-throughput sequencing data must scale favorably in terms of both accuracy and computational efficiency. Furthermore, current models and methodologies for haplotype assembly (i) do not consider individuals sharing haplotypes jointly, which reduces the size and accuracy of assembled haplotypes, and (ii) are unable to model genomes having more than two sets of homologous chromosomes (polyploidy). Polyploid organisms are increasingly becoming the target of many research groups interested in the genomics of disease, phylogenetics, botany and evolution but there is an absence of theory and methods for polyploid haplotype reconstruction.

Results: In this work, we present a number of results, extensions and generalizations of compass graphs and our HapCompass framework. We prove the theoretical complexity of two haplotype assembly optimizations, thereby motivating the use of heuristics. Furthermore, we present graph theory–based algorithms for the problem of haplotype assembly using our previously developed HapCompass framework for (i) novel implementations of haplotype assembly optimizations (minimum error correction), (ii) assembly of a pair of individuals sharing a haplotype tract identical by descent and (iii) assembly of polyploid genomes. We evaluate our methods on 1000 Genomes Project, Pacific Biosciences and simulated sequence data.

Availability and Implementation: HapCompass is available for download at http://www.brown.edu/Research/Istrail_Lab/.

Contact: Sorin_Istrail@brown.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

The genome sequence of a human individual can be modeled as 23 pairs of sequences of four nucleotide bases, A, C, G and T, representing the 22 pairs of autosomes and the sex chromosomes. However, ∼99.5% of any two individuals’ genome sequences is shared within a population. The ∼0.5% of the nucleotide bases varying within a population range from single-nucleotide polymorphisms (SNPs) to more complex structural changes, for example, deletions or insertions of genomic material. A sequence of genomic variants, typically SNPs, with the non-varying DNA removed is referred to as a haplotype.

Standard genome sequencing workflows produce contiguous DNA segments of an unknown chromosomal origin. De novo assemblies for genomes with two sets of chromosomes (diploid) or more (polyploid) produce consensus sequences in which the relative haplotype phase between variants is undetermined. The set of sequencing reads can be mapped to the phase-ambiguous reference genome and the diploid chromosome origin can be determined but, without knowledge of the haplotype sequences, reads cannot be mapped to the particular haploid chromosome sequence. As a result, reference-based genome assembly algorithms also produce unphased assemblies. However, sequence reads are derived from a single haploid fragment and thus provide valuable phase information when they contain two or more variants. The haplotype assembly problem aims to compute the haplotype sequences for each chromosome given a set of aligned sequence reads to the genome and variant information. The haplotype phase of variants is inferred from assembling overlapping sequence reads [Browning and Browning (2011); Halldórsson et al. (2003); Schwartz (2010)].

The input to the haplotype assembly problem is a matrix M whose rows correspond to aligned read fragments and columns correspond to SNPs (Fig. 1). The quality of M’s construction depends on the parameters of the sequencing workflow and the accuracy of the read alignment algorithms. Misaligned read fragments can introduce erroneous base calls or sampling biases so the careful alignment of sequence reads is necessary for high-quality haplotype assemblies. Without read alignment or sequencing errors, the haplotype assembly problem can be solved in time linear in the size of M by partitioning the fragments in two sets whereby no fragments internal to a set share an SNP and differ in the allele called. To address erroneous base calls or misplaced alignments, three primary haplotype assembly optimizations have been developed: minimum error correction (MEC), minimum SNP removal (MSR) and minimum fragment removal (MFR). The goal is to convert M into a state such that the fragments (rows of M) can be distributed into two sets corresponding to the two haplotypes. All fragments in a set must agree on the allele at each SNP site and this is accomplished using the minimum number of SNP allele flips (0 to 1 or vice versa - MEC), SNP (columns of M) removals (MSR) or fragment (rows of M) removals (MFR).

Fig. 1.

Construction of the input to the haplotype assembly problem

Lancia et al. (2001) and Rizzi et al. (2002) provide a theoretical foundation for the MFR and MSR optimizations and describe the fundamental SNP and fragment conflict graph structures. The first widely available haplotype assembly software package was presented in Panconesi and Sozio (2004) in which the authors describe the Fast Hare algorithm, which optimizes the ‘Min Element Removal’ problem. Bansal et al. (2008) describe a Markov chain model with Metropolis updating rules to sample a set of likely haplotypes under the MEC optimization. In a follow-up, the authors present a much faster algorithm on a related graph model that relates maximum cuts to SNP allele flips (in the MEC model) [Bansal and Bafna (2008)]. Still other authors have suggested reductions to the well-known maximum satisfiability problem [He et al. (2010); Mousavi et al. (2011)] The Levy et al. (2007) algorithm is a well-known heuristic that was used to haplotype assemble the HuRef genome; it assigns fragments to haplotypes in a greedy fashion and iteratively refines the solution by comparing the set of fragments to the assembled haplotypes using majority rule phasings. In a recent survey, Geraci (2010) describes the Levy et al. (2007) algorithm as, arguably, the best performing algorithm tested.

The first extension of the haplotype assembly problem that addressed the simultaneous assembly of multiple diploid chromosomes was presented in Li et al. (2006); however, the benefits of multi-haplotype assembly are not clear for a set of unrelated individuals. Halldorsson et al. (2011) continued development of this theory by describing methods for assembling individuals who share a haplotype identical by descent (IBD) using relationships among the reads.

Aguiar and Istrail (2012) introduced a new graph data structure, algorithmic framework and the minimum weighted edge removal (MWER) optimization, which together have several advantages over existing methods. Recall that the rows of M correspond to sequence read fragments with the non-polymorphic bases removed such that only SNPs remain. The HapCompass model defined in Aguiar and Istrail (2012) is composed of the compass graph G_C core data structure, which summarizes the rows of M using edges weights and the MWER optimization that aims to remove a minimum weighted set of edges from G_C such that a unique phasing may be constructed. The algorithm operates on the spanning-tree cycle basis of G_C to iteratively remove errors that are manifested through a particular type of simple cycle [Deo et al. (1982); Mac Lane (1937)].

In this work, we prove a number of theoretical results for the previously described MWER optimization on compass graphs. The main result proves MWER is NP-hard and motivates the use of our heuristic algorithms. Further, we demonstrate how extensions to the generalized diploid HapCompass model can enable (i) usage of different optimizations, for example, MEC and MWER, to be used in the local optimization step, (ii) simultaneous assembly of two individuals sharing a haplotype tract IBD and (iii) haplotype assembly of a single polyploid organism. Finally, we evaluate our methods on 1000 Genomes Project, Pacific Biosciences and simulated data.

2 METHODS

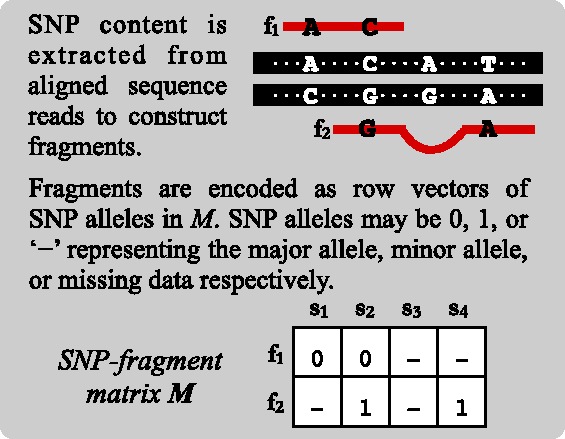
Let a fragment f be a sequence read with the non-polymorphic bases removed such that only SNPs remain. Fragments may be either a single contiguous region of DNA or contain any number of gaps between contiguous regions (for example, one gap between two contiguous regions in paired-end sequencing). Each SNP must be heterozygous and each row must cover at least two SNPs to be able to extract useful haplotype phase information from sequence reads. An SNP allele is encoded as 0 or 1 corresponding to the major or minor allele. The k^th base of the i^th fragment is referred to as . If f_i does not include the base k in the sequence read (within the gap of a paired-read, for instance), then 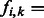‘–'. Let M be the 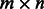SNP-fragment matrix with m rows corresponding to the m fragments and n columns corresponding to n SNPs. Two fragments f_i and f_j are in fragment conflict if

(1)

Informally, fragment conflict represents two fragments that include the same SNP but differ in the allele. The fragment conflict graph G_F has a vertex for each fragment in M and an edge between two fragments if they are in fragment conflict. M is feasible if a bipartition exists in G_F or, equivalently, the fragments of M can be partitioned in two sets such that no two fragments within each set are in fragment conflict.

2.1 The MWER optimization and HapCompass models

The HapCompass model defined in Aguiar and Istrail (2012) is composed of the compass graph G_C data structure and optimizations on the spanning-tree cycle basis of this graph. G_C is a graph with a vertex for each SNP and an edge between two SNPs if at least one read contains both SNPs (Fig. 2). The weight on the edge, defined by the function f_MWER, is the difference between the number of fragments that suggest a 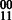phasing and the number of fragments that suggest .

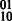Fig. 2.

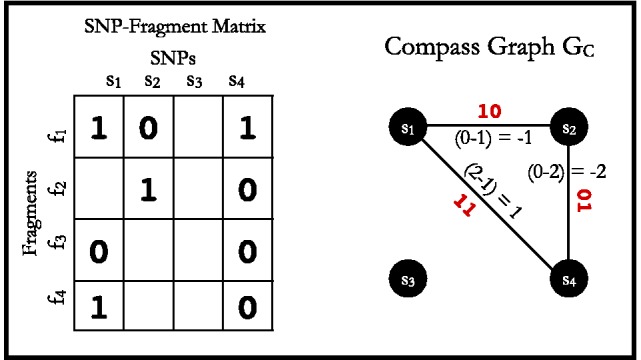
Construction of the compass graph from SNP-fragment matrix M. The SNP-fragment matrix M (left) contains four fragments and four SNPs. Each SNP’s pairwise phasing relationship defined by the fragments is represented on the edges of the compass graph (right). The majority rule phasing for one of the haplotypes is shown in red on the compass graph edges

A path in G_C corresponds to a phasing of the SNP vertices by concatenating the phasings on the edges. For example, the 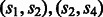path in Figure 2 corresponds to the concatenation of the 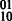phasing with the 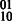phasing, yielding the 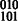phasing. A number of subtle combinatorial properties of the diploid read information define the contiguity of the assembly; in haplotype assembly of polyploid genomes where more than two haplotypes exist, these combinatorial properties will be made explicit and generalized as a basis for the development of polyploid haplotype assembly algorithms.

A spanning tree in G_C corresponds to a valid phasing of the SNPs of G_C. Simple cycles in G_C have the property of being non-conflicting, whereby every path in the cycle including the same set of vertices corresponds to the same phasing, or conflicting, whereby there is no unique phasing. Aguiar and Istrail (2012) show that a simple cycle is conflicting if and only if there is a 0-weight edge or an odd number of negative weight edges and non-conflicting otherwise. For the MWER optimization, the HapCompass algorithm constructs a spanning-tree cycle basis of G_C and removes edges of small weight (in absolute value) from conflicting cycles until G_C is void of conflicts.

The generalized HapCompass model described in this work supports multiple optimizations on compass graphs, joint haplotype assembly of individuals sharing a haplotype tract IBD and haplotype assembly of polyploid organisms. To support these algorithmic extensions, we examine key concepts of the HapCompass model and describe their generalizations.

The core of the HapCompass framework constructs the compass graph G_C, a spanning-tree cycle basis of G_C, and then corrects conflicting cycles. One such method for correcting conflicting cycles was presented in Aguiar and Istrail (2012) where edge weights are used to compute a set of edges whose removal would eliminate conflicting cycles (the MWER optimization). In principle, other methods may be used to remove edges, or entirely new optimizations may be employed, for example, MEC. Specifically, we implement an algorithm for the MEC optimization on compass graphs. However, before an implementation of an MEC algorithm on compass graphs can be realized, the HapCompass framework must be generalized to allow for corrections to fragments.

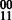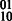Concept 1: edge weights. The HapCompass framework proposed in Aguiar and Istrail (2012) defines edge weights as the difference between the number of reads indicating the and phasings. The generalized model includes a vector for edge e, v_e, consisting of four integers corresponding to the four possible haplotypes between two SNPs: 00, 01, 10, 11. A function, f(e), maps the vector to a meaningful value interpreted by the HapCompass algorithm. 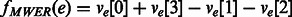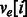For example, in the MWER HapCompass algorithm, where is the count of the phasings 00, 01, 10, 11 for 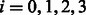, respectively.

2.2 An MEC HapCompass optimization

The MEC optimization on G_C aims to flip the minimum number of alleles such that all of the cycles are non-conflicting. The MEC algorithm proceeds by building a spanning tree cycle basis of the compass graph. The following steps are repeated until each edge is non-conflicting. (i) For each edge e in the set of conflicting cycles: let v₁ and v₂ be the two vertices adjacent to e. (ii) If 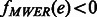, we check the fragments that include both v₁ and v₂, and temporarily flip the fragment alleles of v₁ (v₂ in following iteration) to indicate 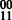phasings. The other alleles in the fragments cause edges adjacent to v₁ (v₂) to change weight as well. We record the number of conflicting cycles resolved and created by checking each cycle in the cycle basis including an edge that was modified by the flipping of a fragment allele. (iii) The case of 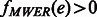is handled analogously with the exception of flipping the alleles to indicate 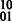phasings. (iv) Let the number of conflicting cycles resolved by processing e be 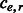and the number of conflicting cycles created be 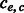. If 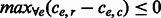, then there does not exist a favorable switching of fragment alleles and an edge is removed following the MWER algorithm. Otherwise, the fragment changes giving 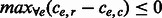are introduced in G_C. (v) When all cycles are non-conflicting, we output the phasing defined by any spanning tree.

The primary data structure change in G_C introduces a mapping of edges to fragments. The primary addition to the HapCompass framework is a definition of optimization function to remove conflicting cycles from G_C.

2.3 IBD tracts and haplotype assembly

Thus far, the HapCompass framework has only been defined for a single diploid individual. The generalization of haplotype assembly to multiple genomes must be selective for which individuals to assemble jointly. For example, if two individuals do not share a haplotype by descent, one individual’s set of reads does not provide any information for the other. However, when two individuals do share a haplotype by descent, the shared haplotype provides phasing information across homozygous sites as long as one individual remains heterozygous (Fig. 3). Regions of homozygosity in an individual, which would otherwise disconnect SNPs and partition haplotype solutions, can be phased together as long as the jointly assembled genotype has heterozygous SNPs within the interval.

Fig. 3.

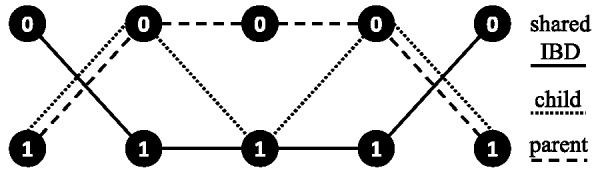
A graph of the haplotype transitions defined by the majority rule phasings of a compass graph. SNPs 1, 2, 3, 4 and 5 (left to right) are shown with both alleles (vertices), and edge transitions are encoded by a specific type of line depending on whether the haplotype is shared IBD or unique to the child or parent. The genotype of the parent and child are 22 222 and 22 122, respectively (where the two corresponds to the heterozygote and 0 and 1 correspond to homozygous for the major and minor alleles, respectively)

Concept 2: multiple genotypes. The problem of joint assembly of two individuals who share a haplotype IBD (hereafter referred to as a pair) is different from jointly assembling two individuals who do not share a haplotype. In the compass graph, two unrelated genotypes have the effect that both individuals can be heterozygous but have completely different phasings. However, if they share a haplotype, a transition from a doubly heterozygous SNP to another doubly heterozygous SNP forces exactly two phasings, namely 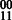or 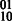(for example, SNP transitions (1,2) and (4,5) in Fig. 3). For the doubly heterozygous to singly heterozygous transitions, we may have exactly three of the four possible 2-SNP haplotypes. In Figure 3, the child’s genotype is 22 122 and to phase this block using the child’s data alone, we require a read to cover at least one of the first two SNPs and at least one of the last two SNPs, which may be impossible depending on the distance between the SNPs and sequence read insert length. However, if we assemble the parent with the child, we can use the shared haplotype to decode the parent’s phase across SNPs 2, 3 and 4 to be 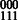. Because they share a haplotype, the 111 haplotype must be the shared haplotype and it can be inferred that the child’s phased haplotypes are .

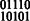Joint haplotype assembly in HapCompass is thus encoded as follows. Each edge now has two sets of vectors corresponding to the 2-SNP haplotype transitions of the parent and child. For a doubly heterozygote to doubly heterozygote transition, the weight function can be computed as before using the coverage from both individuals (because there are exactly two disjoint phasings). For a singly heterozygote to doubly heterozygote transition (or vice-versa), the weight function can solely use the heterozygous–heterozygous transmission data from a single individual.

2.4 Haplotype assembly of polyploid genomes

The research literature concerning polyploid haplotype assembly is essentially non-existent. The analysis of k-ploid genomes (k sets of chromosomes) has been hindered by the complexity of sequencing and assembling k chromosomes concurrently. With high-throughput sequencing technologies, genotype inference in polyploid organisms is manageable; sequence reads are mapped to a reference genome, and the relative quantities of alleles at an SNP can be inferred from sequence coverages. However, the basic assumption that there exists exactly two phasing between two SNPs no longer holds. We note that the polyploidy assembly problem is similar to a number of problems in other areas of haplotype reconstruction (when the number of haplotypes is known or unknown) such as modeling metagenomics (organism identification), HIV (viral quasispecies identification in the ‘metagenome’ of patients), cancer (tumor and plasma) and epigenetics (regulatory region methylation reconstruction similar to ‘probabilistic haplotype’ inference).

Concept 3: uniqueness and disjoint phasings. One difficulty of polyploid haplotype assembly emerges from the non-disjointness of phasing solutions between SNPs. With the assumption that SNPs are biallelic, at least one haplotype will be shared by two or more phasings between two SNPs. In the diploid case, a read suggesting the 00 phasing could be interpreted as evidence for 11 on the other haplotype (uniqueness of phasing) and also evidence contradicting the 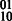phasing (disjointness of haplotypes in phasing solutions). In the tetraploid case, for example, if the genotype for each of 2 SNPs is 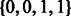then there exists three possible haplotype phasings: (00,00,11,11), (01,01,10,10), (00,01,10,11).

In general, the number of haplotype phasings on an edge is a function of the ploidy of the organism and the alleles at each SNP. As in the diploid case, each SNP must have at least one of each allele or else the SNP is homozygous and sequence observations of an allele do not provide any phasing information. As a result, every 2-SNP haplotype includes eithe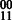r or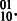

However, unlike in the diploid case, the extension from one edge in G_C to the next may not be deterministic. For example, in diploid assembly, if a reads suggest a 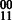phasing for SNPs 1 and 2, and a 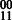phasing for SNPs 2 and 3, the extension would give us a phasing of 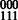. A conflicting cycle in G_C could then be generated if reads connecting SNPs 1 and 3 disagreed with this phasing. For the polyploid case, if the genotypes for each of SNP 1 and 2 are (0,0,1), then both the (00,00,11) phasing and (00,01,10) phasing are valid. Assume that we can compute the phasings between SNPs 1 and 2 and SNPs 2 and 3 to be (00,00,11); we can extend as we did in the diploid case to create the phasing (000,000,111). Then, if a read suggests a 01 phasing between SNPs 1 and 3, we again generate a conflicting cycle. However, if the SNPs were phased using (00,01,10) for SNPs 1,2 and 2,3, then either phasing (000,010,101) or (001,010,100) is possible. Both are completely valid phasings consistent with the genotype and read data but fragments connecting SNPs 1 and 3 may constrain the phasing solution to be unique.

Concept 4: polyploid edge decidability. The polyploid HapCompass model retains the axiom that each edge is decidable; that is, each edge has a unique and computable phasing as defined by the reads. The compass graph and spanning tree cycle basis is built from the input genotypes and reads as before. The distribution of haplotype configurations between two SNPs are defined by the genotypes, and a singular configuration is computed using the available read data. The first approach attempts to assign reads into haplotype bins that represent the haplotype distribution for a valid phasing between two SNPs. Given a 2-SNP genotype, a binning is an assignment of reads to haplotypes. For example, if two SNPs both had two 0 alleles and two 1 alleles, there would exist three haplotype phasings: (00,00,11,11), (01,10,11,00), (01,10,01,10), each with 4 bins. The phasing (00,00,11,11), for instance, would contain two 00 bins and two 11 bins.

Greedy binning algorithm. Input: a maximum distance d between any two bins, a set of haplotype phasings P and a set of reads R. Output: the haplotype phasing most supported by the reads.

1. For each haplotype phasing

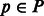
2. For each haplotype bin 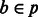, do steps (3–5).

3. Loop through steps (4–5) until all read fragments have been assigned.

4. Select a read 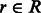such that the edit distance between r and an available haplotype bin 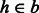is minimal.

5. Place r in the selected bin h and remove this read from the read set.

6. Report the haplotype phasing with the binning of minimum total edit distance as the optimal phasing.

We enforce that the difference of haplotypes in each bin must be at most d haplotypes to avoid always preferring diverse haplotype phasings [e.g. (10,10,01,01) versus (00,11,10,01)]. This condition defines which haplotype bin is available during each iteration.

Probabilistic binning algorithm. Alternatively, probabilities of each phasing given the set of reads can be computed and uncertainty can be accounted for when extending phase to adjacent edges. In particular, we wish to compute the likelihood of a phasing given the set of input sequence reads. Let p_i be the i^th phasing for two adjacent SNPs, P the set of all possible phasings for the two SNPs, r_j be the j^th read and s_e the probability of a sequencing error. Then, the likelihood of a particular phasing p_p is

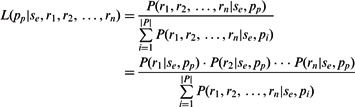which may be computed using the assumption that sequence reads are independent. The probability of a read r_i given sequencing error s_e and phasing p can be computed by marginalizing over all possible haplotypes h sampled for phasing p:

(2)

Thus, the edge is decisive for the haplotype phasing with the maximum likelihood for all reads that span the two SNPs. The original diploid scoring scheme can be recreated with a manipulation of the unnormalized phasing likelihoods: .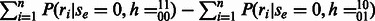

Concept 5: conflicting cycles and phase extensions. Both the greedy and probabilistic binning algorithms decide the haplotype phase of edges. In the diploid case, the extension of phasings from edges to paths was unambiguous because for each of the two phasings, exactly one haplotype begins with 0 (or 1) and exactly one haplotype ends with 0 (or 1). Therefore, the computation of phasings for paths and conflicting cycles was easily determined given the decided edges. In polyploid genomes, each SNP variant in G_C is still assumed to have only two possible alleles but each edge has three or more haplotypes. When extending phase from one edge to an adjacent edge, the haplotypes on different edges that share an allele can be used for extending phase. If this allele is present in k haplotypes, then there are 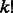possible extensions.

Phase extension algorithm. We introduce the chain graph G_h, which is defined on a path or cycle in G_C for a k-ploid genome. Let 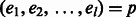denote a path of edges in G_C of length l. Each edge e_i is phased (by the greedy or probabilistic method) and each haplotype in the phasing introduces a vertex in G_h at level i. Thus, G_h contains k vertices for each 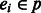and a total of 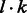vertices in total. Two haplotype vertices are connected by an edge if and only if they share an SNP position and allele. Because haplotypes at adjacent levels uniquely share an SNP position in G_h, edges only exist between adjacent levels and a path through the chain graph corresponds to a joining (or extension) of haplotypes. Therefore, there is always a valid phasing for a G_h defined on a path of G_C.

Cycles introduce complexity in G_h. G_h defined on a cycle retains the characteristics of the path chain graph, but also includes source and sink nodes: and , respectively. Let 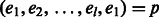denote any path of edges in G_C of length l with the addition of the 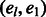edge. Source nodes are connected arbitrarily to haplotypes on level 1 but haplotypes on level l are only connected to sink nodes if the shared variant position agrees with the haplotype the source was connected to; for example, in Figure 5 Top, t2 is connected to both 00 haplotypes at level l because s2 is connected to a haplotype starting with 0. The sources and sinks represent the 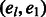edge and a path from s_i to t_i represents one valid haplotype. This intuition enables the formulation of the k vertex disjoint paths problem on chain graphs. If there exists k vertex disjoint, s_i to t_i paths for 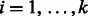, we have k valid phasings for the cycle; otherwise, the cycle is conflicting and there is no valid phasing.

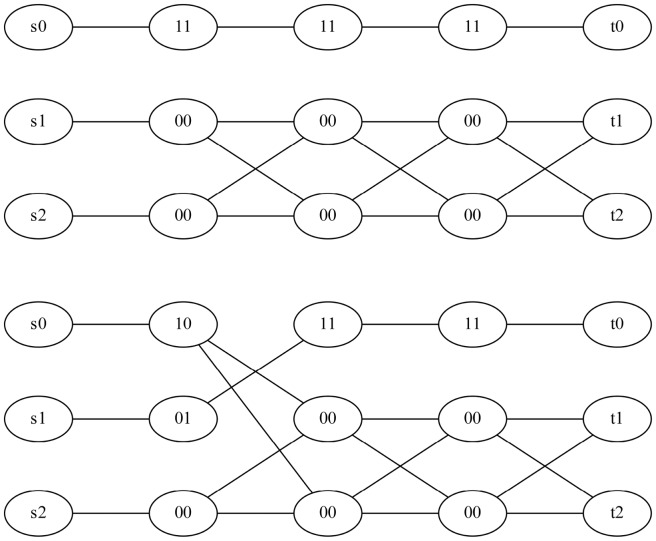
Fig. 5.

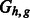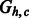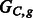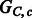The chain graphs (top) and (bottom) corresponding to and , respectively

To further build intuition, consider a conflicting cycle of G_C and G_h in the diploid case. A cycle was conflicting if the number of negative weighted edges in G_C was odd. Relating this to the chain graph G_h, an s_i node would be connected to a 0 (or 1) and each negative edge would flip the next bit. So, a conflicting cycle has an odd number of negative edges, which translates into an odd number of bit flips resulting in no s_i to t_i path for 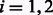. Figure 4 gives an example of non-conflicting and conflicting cycles in polyploid compass graphs and Figure 5 their chain graphs.

Fig. 4.

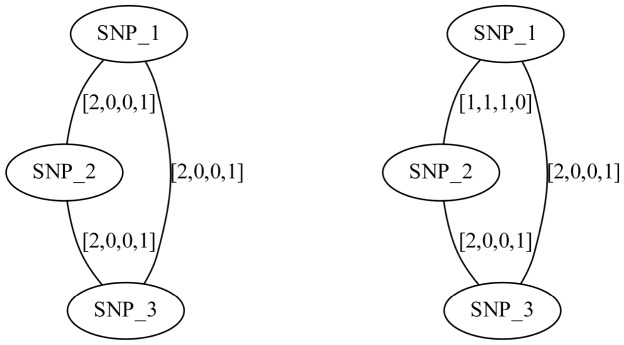
Compass graphs 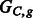, a non-conflicting polyploid cycle (left), and 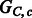, a conflicting polyploid cycle (right). The vector on the edge corresponds to the haplotype counts for an edge in the format [00,01,10,11]. In both compass graphs, the haplotypes are 000, 000 and 111, while the reads in 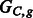are 000, 000 and 111, and the reads in 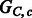are 00–, 01–, 10–, –00, –00, –11, 0–0, 0–0 and 1–1

G_h enables the (i) determination of conflicting cycles and (ii) computation of the phased haplotypes for a path or cycle using disjoint paths. The k-disjoint paths problem is a well-studied optimization in the field of discrete mathematics [Robertson and Seymour (1995)]. A polynomial-time solution is known to exist for the node disjoint paths problem when k is known as part of the input [Robertson and Seymour (1995); Kawarabayashi et al. (2012)], but these algorithms require manipulation of enormous constants rendering them difficult to implement in practical settings.

Fortunately, the structure of G_h enables a much more efficient solution to the problem. All paths from s_i to t_i can be computed by a modified depth first search algorithm. A depth first search is started from each source s_i and the path from source to the current node is stored. Each node contains a list of integers initially empty. When the algorithm either encounters the sink node t_i, or a node already labeled with i, all nodes on the current path have i added to their list. After each source–sink pair is processed, each node contains a label i if there is an s_i to t_i path that includes the node. The runtime of this algorithm is O(kve) where k is the ploidy, and v and e are the number of vertices and edges in G_h, respectively.

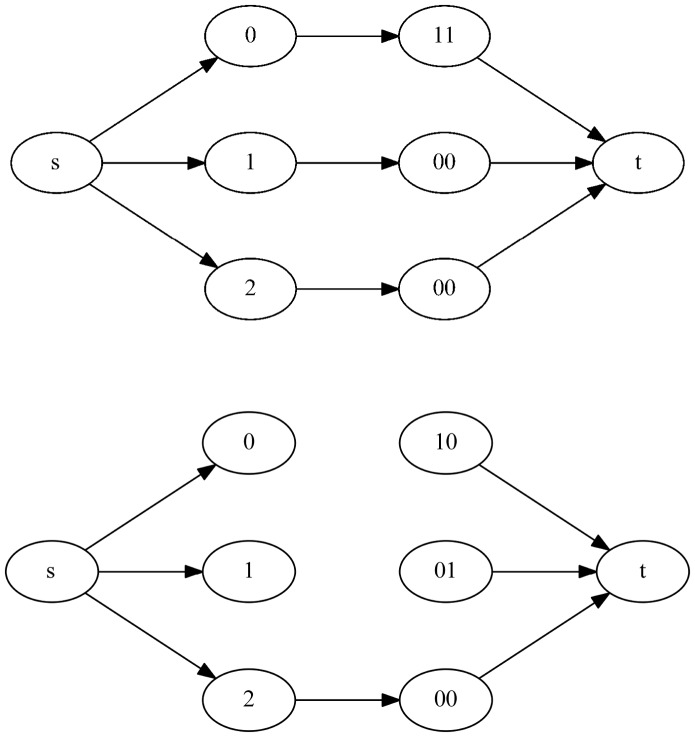
After all nodes are labeled, we iterate through each level of G_h and create an auxiliary flow graph 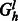where l is the level. 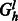defines a bipartite graph where one set of vertices corresponds to the source haplotype paths, which are connected to a set of vertices corresponding to the haplotypes of the phasing level l. A flow in 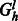of total value k where each edge has capacity 1 corresponds to a maximum matching and thus a valid assignment of haplotype paths to haplotypes of the phasing at level l. This flow can be found in time linear in the size of the edge set of 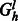. If every level of the chain graph has a valid bijection, then the cycle is non-conflicting and the path given by the matchings define a valid phasing. Figure 6 give an example of the auxiliary flow graphs for level 1 of the chain graphs defined in Figure 5.

Fig. 6.

The auxiliary flow graphs (top) 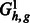and (bottom) 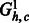. For a k-ploid organism (in this case k = 3), a flow of k with 1 capacity on each edge corresponds to a valid assignment of haplotype paths to haplotypes of the phasing a level 1

3 RESULTS

3.1 Theoretical

We first present results on the complexity of the MWER optimization, and related minimum weighted vertex (SNP) removal (MWVR) problems on the compass graph G_C. These results motivate the usage of our heuristics for the diploid and polyploid algorithms. Let 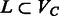be a subset of vertices in G_C, and let 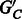be the resulting graph created from removing L from V_C. The MWVR optimization aims to compute an L such that the following conditions are satisfied:

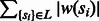1. is minimal where 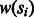is the weight of the i^th SNP (cost of removed vertices is minimal);

2. All edges in 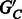are decisive (each edge has a majority rule phasing);

3. Choosing a phasing for each edge in 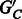by majority rule gives a unique phasing for .

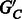We omit the straightforward proofs that the MWVR and MWER problems are in NP. It remains to be shown that known NP-hard problems can be reduced to MWVR and MWER.

We restate the conflict graph generality lemma from Lippert et al. (2002).

Lemma 1 —

Let be an arbitrary graph. Then there exists an SNP-fragment matrix M such that .

Proof —

Introduce a fragment f_i for each vertex . For every two adjacent vertices , introduce a new SNP column s_k in M where and .

Let M be the SNP-fragment matrix constructed from Lemma 1, G_F the corresponding fragment conflict graph of M and G_C the compass graph of M.

Lemma 2 —

Every simple cycle of odd length in G_F produces exactly one conflicting simple cycle in G_C.

For the proof of Lemma 2 please see Supplementary Appendix Proof of Lemma 2.

Lemma 3 —

Every conflicting simple cycle in G_C includes exactly one odd length simple cycle in G_F.

Proof —

We now interpret conflicting cycles in G_C as a set of vertices of G_C, which define a set of edges in G_F.

Because of the previous lemma, every conflicting cycle in G_C can be resolved by removing an edge of G_F, which corresponds to removing a vertex in G_C.

Corollary 1 —

There exists no conflicting cycles in G_C if and only if there are no cycles of odd length in G_F.

Lemma 4 —

Given an M produced from Lemma 1, the compass graph is the line graph of with weights of G_C as defined by the phasing relationships of the fragments of M.

Proof —

The SNPs (columns) of M contain exactly two alleles from two fragments that conflict. Therefore, in G_F, each SNP uniquely defines an edge, and in G_C, each SNP uniquely defines a vertex. All that remains is to show that every two adjacent edges in G_F produce an edge in G_C. Consider an SNP s whose conflicts involve fragments f_i and f_j. The edge defined by s in G_F is adjacent to edges defined by the other conflicts of f_i and f_j. The vertex s in G_C is defined exactly as the pairwise phasing relationships as defined by the SNP s and other SNP alleles in fragments f_i and f_j, which in turn define the adjacencies in G_F.

Because G_C is the line graph of G_F, if k simple cycles in G_C share an edge then k simple cycles in G_F share a vertex.

Theorem 1 —

MWVR is NP-hard.

Proof —

See the MWVR Proof section in Supplementary Appendix.

Theorem 2 —

MWER is NP-hard.

Proof —

The reduction is from the problem of removing the minimum number of edges of a graph to make it bipartite. Let G be an arbitrary graph and M the SNP-fragment matrix as defined in Lemma 1. We modify by adding two additional degree 2 vertices to each edge, effectively converting each edge to a length 3 path. Cycles of odd (even) length retain their odd (even) length, thus odd length cycles still create conflicting cycles in G_C. All vertices of degree k produce cliques of size k in G_C, which do not correspond to any cycles in . Therefore, we label all edges of clique vertices produced from a single vertex with weight . All paths of G_F will be encoded with two edges of G_C; both of which cannot be removed in an optimal solution to MWER. Given a solution to the MWER optimization, we can determine the minimum number of edges in G_F to make it bipartite.

3.2 Experimental

We evaluate the HapCompass MEC, HapCompass IBD and polyploid HapCompass algorithms using 1000 Genomes Project [The 1000 Genomes Project Consortium (2010)], Pacific Biosciences and simulated data.

Metrics. To evaluate the accuracy of our diploid haplotype assembly methods, we use the following measures, which capture different aspects of haplotype assembly quality. In Aguiar and Istrail (2012), we introduce the fragment mapping phase relationship (FMPR) distance, which counts the number of pairwise phase relationships (as defined by the input read fragments) that do not exist in the solution. The related boolean fragment mapping (BFM) distance counts the number of read fragments that do not map back to the solution. The third evaluation criteria we use is the MEC measure, which counts the number of allele flips in the fragments required to produce the phased haplotype assembly solution. In all previously described measures, lower values are desired. These metrics are similar to read mapping metrics in genome and transcriptome assembly, where good-quality assemblies will allow for many reads to map back to them.

3.3 Pacific biosciences data

Single molecule sequencing has great potential to become a preferred method for haplotype assembly, but current algorithmic techniques are untested on data with high error rates. We downloaded the chromosome 20 data from individuals HG00321, HG00577, HG01101, NA18861, NA19313, NA19740, NA20296 and NA20800 [PacBio Data (2013)]. Haplotype assembly solutions were produced by HapCompass, Levy et al. (2007) and HapCUT to obtain the results in Table 1 (run times can be found in the Pacific Biosciences run times section in Supplementary Appendix). HapCompass outperforms the competition in terms of MEC using both optimizations. Interestingly, the Levy et al. (2007) algorithm is the most accurate in terms of FMPR and BFM. This is likely due to the Levy et al. (2007) algorithm processing entire read fragments each iteration while HapCompass focuses on correcting multiple fragments at adjacent SNPs. Because the Pacific Biosciences read lengths are long (several kb), more emphasis is placed on matching reads with large overlaps on the same haplotype. This result further suggests that it is important to consider the input data and the desired results when preparing data for a haplotype assembly experiment.

Table 1.

The total FMPR, BFM and MEC scores aggregated across individuals HG00321, HG00577, HG01101, NA18861, NA19313, NA19740, NA20296 and NA20800 in the Pacific Biosciences data

	HapCompass MWER	HapCompass MEC	Levy	HapCUT
FMPR	163 799	169 385	153 433	169 890
BFM	39 827	40 470	38 318	41 006
MEC	48 631	49 591	66 299	50 164

3.4 1000 genomes project data

To further evaluate the HapCompass MEC implementation, we haplotype assembled the genome of 1000 Genomes Project NA12878 CEU child using our implementation of the Levy et al. (2007) method, HapCUT (v0.5) and the HapCompass MWER and MEC algorithms. Table 2 shows that the HapCompass MWER algorithm clearly performs best overall. The full table for all chromosomes is given in Supplementary Appendix (section 1000 Genomes Project Results). Surprisingly, even though the MWER algorithm does not directly optimize the MEC measure, it produces the best haplotypes in respect to this measure for all but two chromosomes.

Table 2.

Haplotype assembly results for the 454 data from 1000 Genomes Project NA12878 individual for chromosomes 1–22 and algorithms HapCompass MWER, HapCompass MEC, Levy et al. (2007) and HapCUT

HapCompass MWER			HapCompass MEC			Levy			HapCUT
FMPR	BFM	MEC	FMPR	BFM	MEC	FMPR	BFM	MEC	FMPR	BFM	MEC
64 128	36 578	37 597	68 623	39 221	40 269	64 789	39 832	40 946	65 724	37 606	38 372

Note: The full table is given in the section 1000 Genomes Project Results in Supplementary Appendix.

3.5 IBD haplotype assembly

Jointly assembling the haplotypes of related individuals has considerable benefits. The first benefit comes from the extra coverage on the shared haplotype, which helps with differentiating true phasings from sequencing errors. However, the most notable advantage is being able to extend phasing past homozygous blocks. We compared the size of the phased haplotype blocks when assembling chromosome 22 of the NA12878 child in the 1000 Genomes Project data alone versus jointly with the mother. Figure 7 compares the maximum achievable haplotype block sizes of any single individual haplotype assembly algorithm to IBD haplotype assembly; it demonstrates that larger haplotype blocks are achievable by assembling two individuals with a shared haplotype together rather than separately.

Fig. 7.

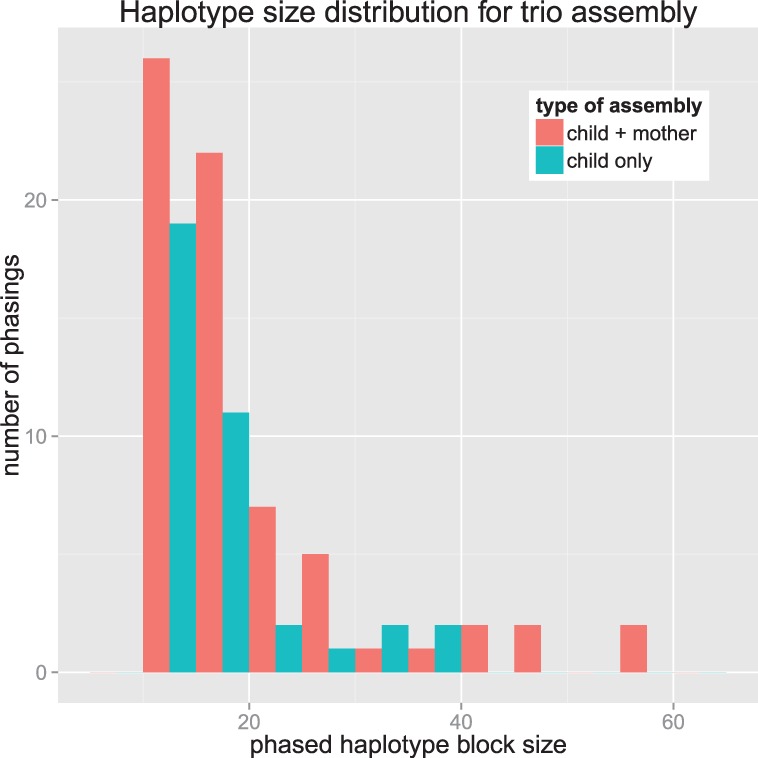
Comparison between haplotype assembling the child individually versus with a parent. The haplotype size is number of SNPs in the component of G_C, which represents the maximum number of SNPs that may be phased together

3.6 Polyploid algorithm

Finally, to evaluate the polyploid algorithm, we simulated three haplotypes at random and simulated reads from these haplotypes. The simulated reads were guaranteed to contain two SNPs (assuring they are useful for haplotype assembly) and given normally distributed insert sizes. The polyploid algorithm was run using both the greedy and probabilistic binning algorithms for deciding edge phasings. Figure 8 demonstrates two interesting results: (i) for a small number of reads, the quality of haplotype phasing is independent of the choice of binning method and (ii) that the probabilistic algorithm produces a more accurate phased solution than the greedy binning method for a large range of simulated read counts.

Fig. 8.

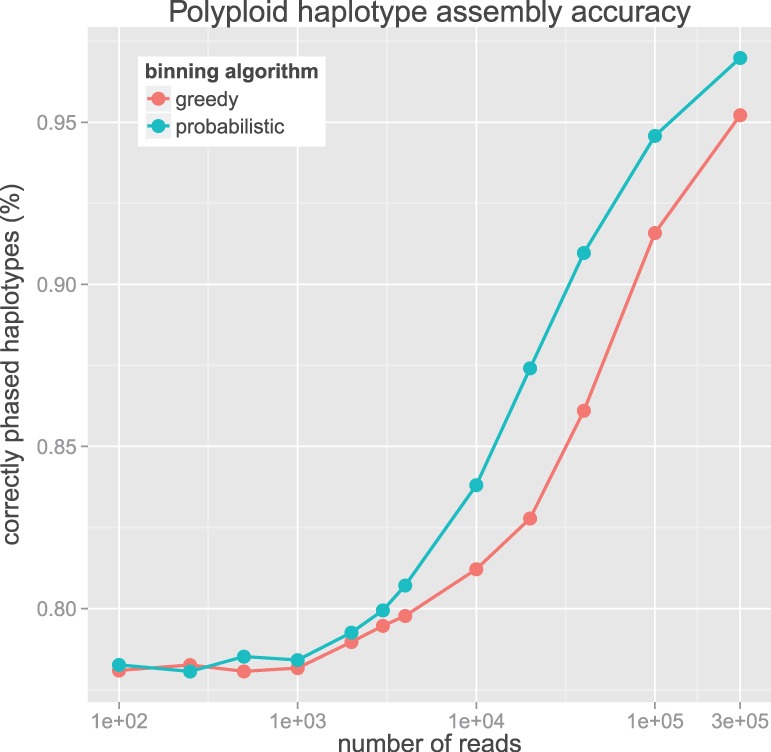
Comparison of the percentage of correctly phased polyploid SNP pairs for the greedy and probabilistic binning algorithms for varying number of input reads

4 DISCUSSION

Diploid haplotype inference is still a difficult task, in part due to the exponentially many solutions given the input genotype or sequence reads. HapCompass is a proven framework for haplotype assembly but there are a number of extensions that may improve results. For instance, we did not mention the usage of base call or read mapping quality scores in our computations. HapCompass can filter based on user-defined thresholds but a more elegant solution would be to convert the base call quality score for a particular allele call into a probability the base was called correctly. This probability can then define the contribution of weight to the edges of G_C rather than the current weight contribution of 1 for each SNP allele called. Also we demonstrated in the Pacific Biosciences experiments that the choice of assembly method should be informed by the sequencing technology and desired result. The Levy et al. (2007) method mapped more fragments error free than HapCompass but contained many more single base changes in fragments required to reproduce the inferred haplotypes. Considering the Pacific Biosciences data has high error rates and generating an error-free read is unlikely, a solution with the minimum number of corrected errors is likely preferred over a solution that successfully maps more fragments without errors.

The size of the haplotype blocks produced and, ultimately, the quality of the assembled haplotypes is a function of several factors. The primary difficulty for obtaining large haplotype blocks is the small nature and lack of diversity of insert lengths. We demonstrated a novel modeling and computational method that begins to address this difficulty by exploiting shared IBD haplotype structure. In general, assembling the haplotypes of related individuals has considerable benefits, which help overcome undesirable properties of the sequencing data. The first benefit comes from the extra coverage on the shared haplotype, which helps in differentiating actual phasings from sequencing errors. However, the most notable advantage is being able to include more SNPs into the haplotype assembly, which helps extend the assembly (past regions of low read coverage for example). But, the major advances in block sizes will likely be the result of novel experimental procedures and technologies; for instance, not only do the single molecule sequencers promise larger read lengths, they also enable the inclusion of multiple and large insert lengths.

Organisms having more than two sets of homologous chromosomes are becoming the target of many research groups interested in studying the genomics of disease, phylogenetics and evolution [Chen and Ni (2006); Leitch and Leitch (2008)]. Polyploidy occurs in human disease usually due to the duplication of a particular chromosome, for example, in Edwards, Patau and Down syndrome. While far fewer mammalian organisms are polyploid, specific mammalian cells may undergo polyploidization, for example, in human liver hepatocytes [Gentric et al. (2012)]. In addition, polyploid organisms are ubiquitous in the Plant and Fungi clades, present in crops that we ingest, convert into bioenergy and feed to livestock. Understanding the genomics of both the desirable—e.g. increased crop yield—and undesirable—e.g. susceptibility to disease—properties of plants may lead to critical advances in many research areas but requires untangling the polyploid genome and its variation. As more polyploid data becomes available, our approach may be used to infer haplotypes and begin to understand what effects haplotype variation may influence.

Funding: This work was supported by the National Science Foundation [1048831 to S.I.].

Conflict of Interest: none declared.