Supervised de novo reconstruction of metabolic pathways from metabolome-scale compound sets

Abstract

Motivation: The metabolic pathway is an important biochemical reaction network involving enzymatic reactions among chemical compounds. However, it is assumed that a large number of metabolic pathways remain unknown, and many reactions are still missing even in known pathways. Therefore, the most important challenge in metabolomics is the automated de novo reconstruction of metabolic pathways, which includes the elucidation of previously unknown reactions to bridge the metabolic gaps.

Results: In this article, we develop a novel method to reconstruct metabolic pathways from a large compound set in the reaction-filling framework. We define feature vectors representing the chemical transformation patterns of compound–compound pairs in enzymatic reactions using chemical fingerprints. We apply a sparsity-induced classifier to learn what we refer to as ‘enzymatic-reaction likeness’, i.e. whether compound pairs are possibly converted to each other by enzymatic reactions. The originality of our method lies in the search for potential reactions among many compounds at a time, in the extraction of reaction-related chemical transformation patterns and in the large-scale applicability owing to the computational efficiency. In the results, we demonstrate the usefulness of our proposed method on the de novo reconstruction of 134 metabolic pathways in Kyoto Encyclopedia of Genes and Genomes (KEGG). Our comprehensively predicted reaction networks of 15 698 compounds enable us to suggest many potential pathways and to increase research productivity in metabolomics.

Availability: Softwares are available on request. Supplementary material are available at http://web.kuicr.kyoto-u.ac.jp/supp/kot/ismb2013/.

Contact: goto@kuicr.kyoto-u.ac.jp

1 INTRODUCTION

The importance of metabolomics research is growing fast in recent years. Metabolomics can provide sensitive and thorough metabolic signatures as effective biomarkers for the diagnosis of diseases such as cancer. The knowledge about metabolism (e.g. reaction networks, fluxes, drug metabolism) has proven useful for performing rational drug design (Cascante et al., 2002; Hellerstein and Murphy, 2004). Some metabolites of plants and fungi have long been of vital use to drug leads in the pharmaceutical industry (Simmond and Grayer, 1999). In addition, systematic simulation studies on metabolic pathways rely on accurately predefined reaction network models. However, a large number of metabolic pathways remain unknown, and many reaction steps are still missing even in known pathways. For example, detailed analysis of human metabolome (Sreekumar et al., 2009) implies that even well-investigated species like human have many unknown metabolic pathways. As the experimental verification of reaction networks remains daunting, there is a strong need to develop in silico methods to infer unknown but possible metabolic pathways.

A variety of computational methods for reconstructing metabolic pathways have been developed thus far, which can be categorized into the three frameworks, as shown in Figure 1. The most traditional one is ‘reference-based framework’ (Fig. 1A). In this framework, many known pathways are collected from literatures to construct a combined pathway, named ‘reference pathway’, which only considers chemical transformations without distinguishing the difference of organisms (Fig. 1A, left). For an organism of interest, enzyme genes are assigned to appropriate positions in predefined reference pathways based on orthologous information (and some other evidences if available) about genes across different species (Bono et al., 1998; Dandekar et al., 1999; Forst and Schulten, 1999; Galperin and Koonin, 1999) (Fig. 1A, right). However, such reference pathway information is available only for a limited set of genes, enzymes and metabolites, and it is inherently incomplete owing to the lack of experimentally identified compounds and homology information. These missing reaction steps may cause misleading interpretations in practice. Therefore, the most important challenge in metabolomics research is de novo reconstruction of metabolic pathways, which includes the elucidation of previously unknown reactions to bridge the metabolic gaps (Darvas, 1988; Greene et al., 1999; Talafous et al., 1994).

Fig. 1.

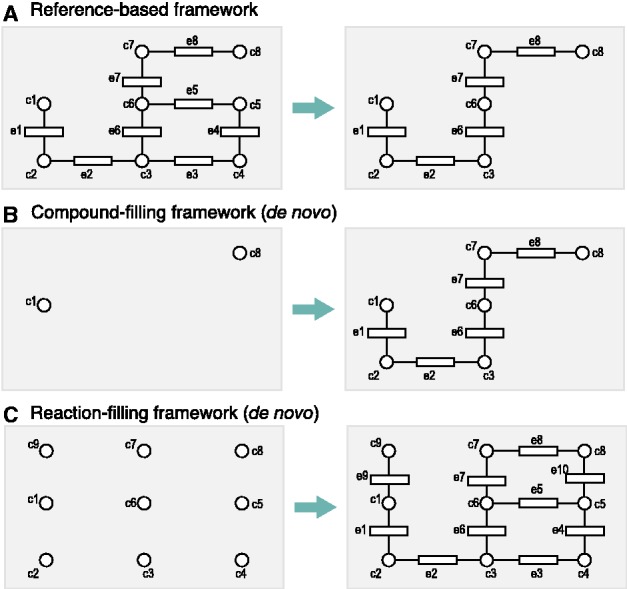
Metabolic pathway reconstruction frameworks. Circles c1–c9 and rectangles e1–e10 represents chemical compounds and enzyme proteins, respectively. Left and right panels represent inputs and outputs, respectively. The reference-based framework (A) extracts an organism-specific pathway from a pre-fixed pathway map with orthologous information about enzyme genes, whereas the compound-filling framework (B) and the reaction-filling framework (C) are the de novo methods to reconstruct a new pathway where reference information is not available

The previous studies on the de novo reconstruction can be classified based on different aspects, i.e. whether it automatically hypothesizes the compounds that are not identified yet, whether it relies on pre-defined chemical transformation patterns and whether the target (and/or source) compound(s) has/have to be specified, as shown in Table 1. One framework is ‘compound-filling framework’ (Fig. 1B), which predicts pathways by hypothesizing intermediate compounds necessary between the source and target compounds. Many of the prediction systems based on this framework are not freely available (Darvas, 1988; Greene et al., 1999; Talafous et al., 1994), but there are some free web servers such as PathPred (Moriya et al., 2010) and University of Minnesota Pathway Prediction System (UMPPS; Gao et al., 2011). A serious limitation of the compound-filling framework is that it is not suitable for predicting pathways for many compounds at a time owing to prohibitive computational cost.

Table 1.

Relationship between different studies on de novo metabolic pathway reconstruction

	Rule-based	Target/Source
Compound-filling framework
Darvas (1988)	Yes	Specified
Talafous et al. (1994)	Yes	Specified
Greene et al. (1999)	Yes	Specified
Moriya et al. (2010)	Yes	Specified
Gao et al. (2011)	Yes	Specified
Reaction-filling framework
Hatzimanikatis et al. (2005)	Yes	Unspecified
Kotera et al. (2008)	No	Unspecified
Tanaka et al. (2009)	No	Unspecified
Nakamura et al. (2012)	Yes	Specified
Kotera et al. (this study)	No	Unspecified

Note: ‘Yes’ and ‘No’ represent whether the studies are predefined rule-based, respectively. ‘Specified’ and ‘Unspecified’ represent whether target (or source) compounds needs to be specified, respectively. There are many previous studies in the reference-based framework, but they are not regarded as de novo metabolic pathway reconstruction.

Another framework for the de novo reconstruction is ‘reaction-filling framework’ (Fig. 1C), which predicts pathways by filling in reactions among many existing compounds at a time. Some of the previous methods depend on predefined chemical transformation patterns (Hatzimanikatis et al., 2005; Nakamura et al., 2012). The other previous methods reduce this dependency by comparing chemical graph structures of all compounds in databases and by determining possible chemical transformations (Kotera et al., 2008; Tanaka et al., 2009), but they suffer from huge computational costs. Thus, large-scale prediction is not computationally feasible (Kotera et al., 2008), or its applicability is limited only to ring-structured compounds (Tanaka et al., 2009).

In this article, we develop a novel method for a de novo reconstruction of metabolic pathways from a large compound set in the reaction-filling framework. We define feature vectors representing the chemical transformation patterns of compound–compound pairs in enzymatic reactions using chemical fingerprints. We apply a sparsity-induced classifier and support vector machine (SVM) to learn what we refer to as ‘enzymatic-reaction likeness’, i.e. whether a compound–compound pair is possibly converted to each other by enzymatic reactions. The originality of our method lies in the search for potential reactions among many compounds at a time, in the extraction of chemical transformation patterns and in the large-scale applicability owing to the computational efficiency. In the results, we demonstrate the usefulness of our proposed method on the de novo reconstruction of metabolic pathways in the Kyoto Encyclopedia of Genes and Genomes (KEGG) database (Kanehisa et al., 2012). Our comprehensively predicted reaction networks enable us to suggest many potential pathways and to increase research productivity in metabolomics.

2 MATERIALS AND METHODS

2.1 Enzymatic reactions and metabolic pathways

Enzymatic reactions and the associated chemical compounds were retrieved from the KEGG LIGAND database (Kanehisa et al., 2012). Chemical compounds in KEGG are given ID numbers consisting of a letter ‘C’ and five numerals, e.g. C00002 for ATP. The number of all chemical compounds with structure information in KEGG LIGAND is 15 698. Metabolic pathway information were retrieved from the KEGG PATHWAY database (Kanehisa et al., 2012), where pathways are divided into maps with ID numbers, such as Glycolysis and Gluconeogenesis (map00010), TCA Cycle (map00020) and Pentose Phosphate Pathway (map00030). We focus on 134 pathway maps involving at least 10 compounds in this study. These pathway maps are classified into 11 categories, such as carbohydrate metabolism and energy metabolism.

2.2 Compound fingerprints

Chemical structures of compounds were encoded by chemical fingerprints corresponding to chemical substructures and various physicochemical properties; therefore, each compound was represented by a high-dimensional binary vector. We used the Chemistry Development Kit (CDK) version 1.4.9 (Steinbeck et al., 2003) to calculate the following eight fingerprints; CDK fingerprint, CDK extended fingerprint, CDK graph-only fingerprint, CDK hybridization fingerprint, E-state fingerprint, Klekota-Roth fingerprint, MACCS fingerprint and PubChem fingerprint, and their dimensions are 1024, 1022, 1024, 1024, 71, 4860, 164 and 879, respectively, where the feature elements absent from the compound set are merged. Chemically identical compounds with the same structures (duplicates) were removed; therefore, structures of all compounds in the dataset were unique.

2.3 Reactant pairs

In addition to the conventional reaction equation format, KEGG stores ‘reactant pair’ format (Kotera et al., 2004) to describe enzymatic reactions. A reactant pair represents a pair of substrate and product with conserved chemical moiety in the reaction. For example, the reaction equation ‘glucose + ATP = glucose 6-phosphate + ADP’ consists of the following three reactant pairs: ‘glucose<=>glucose 6-phosphate’ (conserving a glucose moiety), ‘ATP<=>ADP’ (conserving an ADP moiety) and ‘ATP<=>glucose 6-phosphate’ (conserving a phosphate moiety). The compound pair ‘glucose<=>ADP’ cannot be defined as a reactant pair because these two compounds do not conserve any atoms in a reaction. As of November 2012, there were 13 564 reactant pairs stored in the KEGG RPAIR database, which was used as the gold standard dataset.

Reactant pairs are classified into five types, main, trans, cofac, leave and ligase, depending on the context in metabolic pathways, the topology of the reactant pair graph (the pattern of substrate-product relations in the reaction representing the flow of atoms) and the atomic element information. The main type is given manually for at least one of the pairs in the reactant pair graph, representing the main flow of atoms, which generally includes the flow in the pathway diagram and/or the flow of organic carbon atoms. We used the reactant pair that was given main types in this study.

2.4 Compound–compound pairs

A compound–compound pair has to be described in two distinct directions, i.e. forward and backward, to avoid to miss the similarity between a forward direction of a reaction and a backward of another reaction. Considering the distinction of forward and backward reactions, the number of all possible compound pairs is n(n−1) = 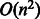, where n is the number of compounds. The computational cost of searching for similar compound–compound pairs would be 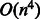. Among all possible compound–compound pairs, those involved in enzymatic reactions (reactant pairs) found in all enzymatic reactions in KEGG were 13 564 (as of November 2012). The number of compounds involved in these reactions was 6729; thus, the number of all the combination of compounds (compound–compound pairs) was 45 272 712. The number of all possible compound–compound pairs in KEGG LIGAND (involving 15 698 compounds) is 246 411 506.

3 METHODS

We formulate the de novo metabolic pathway reconstruction as a series of reaction predictions (estimation of the enzymatic-reaction likeness) of each pair of chemical compounds on a metabolic pathway, where the reaction prediction is solved as the following supervised classification problem. Given a collection of 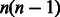compound–compound pairs 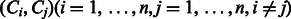, we estimate a function 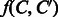that would predict whether a chemical compound C is converted to another compound 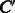in an enzymatic reaction. In addition, we aim to extract biochemical features contributing to the reaction prediction. In this section, we present a general approach to solve these problems in a unified framework. Our approach consists of three major components: (i) prediction model, (ii) vector representation of compound–compound pairs and (iii) binary classifier.

3.1 Prediction model

Linear models are a useful tool for classification and regression especially for high dimensional data. Basically, a linear model represents an object O by a feature vector 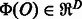, and then defines a linear function 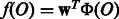, where 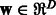is a weight vector. The weight vector is estimated such that it can correctly predict the class of objects. The object O is classified into positive or negative by thresholding the computed value of f(O). Linear models also have an interpretability of features. As each element of a feature vector 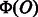corresponds to an element of the weight vector , we can extract effective features contributing to the prediction by sorting elements of 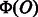according to the corresponding values of the weight vector .

The prediction of enzymatic-reaction likeness is not trivial because the object corresponds to a compound–compound pair in this study. Let C and 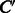be two chemical compounds. To apply the previous machine learning approach to this problem, we need to represent a compound–compound pair by a feature vector 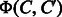and then estimate a linear function 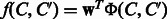. The weight vector is estimated such that it can correctly predict enzymatic-reaction likeness of compound–compound pairs. Finally, the reaction between C and 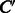is predicted by thresholding the value of .

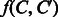3.2 Vector representation of compound–compound pairs

The design of feature vectors is crucial for the classification ability and interpretability of features in the linear model. We propose two kinds of feature vectors for each compound–compound pair based on the biochemical knowledge about enzymatic reactions.

Compounds C and 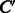are represented by D-dimensional fingerprints (binary vectors) as 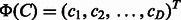and 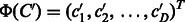, respectively, where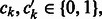 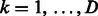. Let I(cond) be an indicator function, where 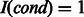if cond is true and otherwise 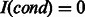. Here, we define two operations for the fingerprints as follows:

and

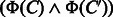represents the common features in 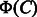and 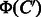, which is referred to as common feature vector. On the other hand, 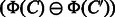represents the features present in 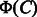and absent in 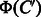, which is referred to as differential feature vector. Thus, the both feature vectors are expected to capture chemical transformation patterns between compounds C and 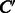. Using these feature vectors, we propose two kinds of feature vectors of any compound–compound pair as follows:

and

We shall refer to 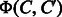and 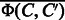as diff-common feature vector and diff-only feature vector, respectively. The diff-common and diff-only feature vectors are different in that the diff-common feature vector has common features in addition to differential features. The diff-only feature vector is expected to capture substructure changes around the reaction center in the conversion of a chemical compound to another compound. The diff-common feature vector is expected to additionally capture core substructures kept in the conversion of a chemical compound to another compound.

For example, if 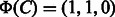and 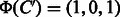are given, the corresponding feature vectors are computed as 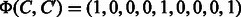and 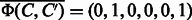. The both feature vectors are asymmetry, i.e. 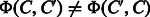and .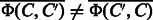

3.3 Binary classifier

We apply linear SVM as a binary classifier. Models are typically learned to minimize the objective function with a regularization for SVM. It is well-known that the use of regularization is necessary to achieve a model that generalizes well to unseen data, particularly if the dimension of features is high. One common regularization is L₂-regularization, which keeps most elements in the weight vector to be non-zeros; therefore, one can suffer from interpreting features from learned weights. Another possible regularization is L₁-regularization that makes most elements in the weight vector to be zeros; therefore, one can interpret a limited number of informative features. In this study, we introduce linear SVM with L₁-regularization for its high interpretability.

Given a collection of compound–compound pairs and their labels 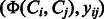where 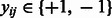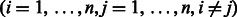, linear SVM is formulated by the following unconstrained optimization problem:

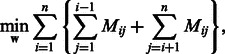where

To enhance the interpretability of linear models, the weight vector is optimized with L₁-regularization as follows:

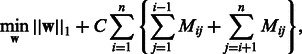where 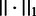is L₁ norm (the sum of absolute values in the vector) and C is a hyper-parameter. L₁-regularization has an effect of making the weights of uninformative features zeros without loss of classification accuracy. L₁-regularized linear SVM is referred to as L1SVM, whereas L₂-regularized SVM is referred to as L2SVM.

Learning weight vectors from compound–compound pairs is a difficult problem. As the number of compound–compound pairs is the product of all the compounds in a dataset, the problem becomes extremely large-scale. In fact, our dataset consists of 15 698 compounds; thus, there are 246 411 506 possible compound–compound pairs in total. The previous studies on classifying object pairs (e.g. compound–protein and protein–protein pairs) have used kernel SVM, where the input of the SVM classifier is the kernel similarity matrix (Ben-Hur and Noble, 2005; Faulon et al., 2008; Jacob and Vert, 2008). However, it is difficult to apply the kernel SVM to large-scale applications. This is because the time complexity of the quadratic programming problem for the kernel SVM is 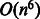, where n is the number of compounds, and the space complexity is 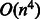, which is just for storing the kernel matrix. Moreover, the kernel SVM does not have an interpretability of features. Another crucial observation is that 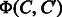and 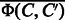are a sparse binary vector. For such sparse binary vectors, weight vectors can be learned via efficient optimization algorithms (Hsieh et al., 2008). In this study, we used an efficient algorithm named LIBLINEAR, which is available from http://www.csie.ntu.edu.tw/cjlin/liblinear/.

In practical applications, we regarded known reactant pairs as positive examples and the other compound–compound pairs as negative examples because it is impossible to obtain true negative data for enzyme reactions in reality. In the learning phase, we randomly selected negative examples for computational efficiency, where the ratio of negative examples against positive examples is set to five in this study.

3.4 Baseline method

The most straightforward method for the reconstruction is a similarity-based approach, assuming that reactive compound–compound pairs are likely to share high chemical structure similarity. Actually, a substrate compound and a product compound in an enzyme reaction tend to have a big core structure, and their different region tend to be small (Kotera et al., 2008). Tanimoto similarity (Jaccard similarity) between compound fingerprints can often be considered as a measure of chemical structure similarity between two compounds. A direct strategy is therefore to predict the enzyme-reaction likeness between two compounds whenever the Tanimoto similarity value between these compounds is above a threshold to be determined. We refer to this approach as BASELINE.

4 RESULTS AND DISCUSSION

4.1 Performance evaluation on enzymatic-reaction likeness

We tested L1SVM and L2SVM and BASELINE on their abilities to predict the enzymatic-reaction likeness of given compound–compound pairs from their chemical fingerprint data. We performed the following 5-fold cross-validation. (i) We randomly split compound–compound pairs in the gold standard data into five subsets of roughly equal sizes. We regarded known reactant pairs as positive examples and the other compound–compound pairs as negative examples. (ii) We took each subset as a test set and the remaining four subsets as a training set. (iii) We trained a predictive model based only on the training set. (iv) We computed the prediction scores for compound–compound pairs in the test set. (v) Finally, we evaluated the prediction accuracy over the five folds.

We evaluated the prediction performance by the receiver operating characteristic curve, which is a plot of true positives as a function of false positives based on various thresholds, where true positives are correctly predicted reactions and false positives are positively predicted pairs that are not present in the gold standard reactions. We summarized the performance by the area under the receiver operating characteristic curve (AUC) score, where 1 is for a perfect inference and 0.5 is for a random inference. We repeated the cross-validation experiment five times and computed the average of the AUC scores over the five cross-validation folds. The parameters involved in the methods were optimized with the AUC score as the objective function.

Table 2 shows the resulting AUC scores and their standard deviations. Among the eight fingerprints, the PubChem fingerprint achieved the highest AUC scores in some conditions. The AUC scores of the diff-common feature vector were slightly higher than those of the diff-only feature vector in both L1SVM and L2SVM. This result implies that it is important to take into account not only substructure transformation patterns but also common substructures in the reaction prediction. L1SVM and L2SVM outperformed BASELINE, which suggests that supervised learning with the proposed feature vectors is meaningful.

Table 2.

AUC scores on 5-fold cross validation experiments for enzymatic-reaction likeness on the whole gold standard data

	Diff-common feature vector		Diff-only feature vector
Fingerprint	L1SVM	L2SVM	L1SVM	L2SVM	BASELINE	RANDOM
CDK
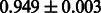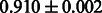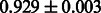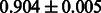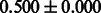CDK extended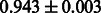
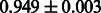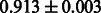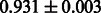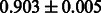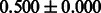CDK graph-only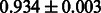
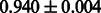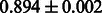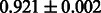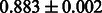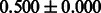CDK hybridization
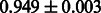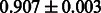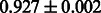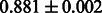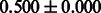E-state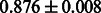
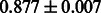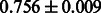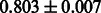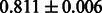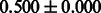KlekotaRoth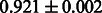
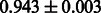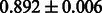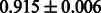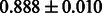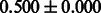MACCS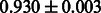
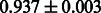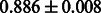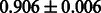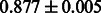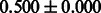PubChem

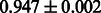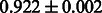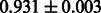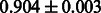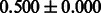L1SVM has a strong advantage over L2SVM in terms of high interpretability of features. Although the AUC scores of L1SVM are comparable or slightly worse than those of L2SVM, the number of features with non-zero weights in L1SVM is significantly smaller than that in L2SVM owing to sparsity constraints. Figure 2 shows a comparison of the number of extracted features between L1SVM and L2SVM in the case of using the PubChem fingerprint, where ALL means the number of all elements in the feature vectors. It was observed that L1SVM extracted a limited number of features, compared with L2SVM. This allows meaningful analysis of the extracted features for biological interpretation, which is shown in Section 4.4.

Fig. 2.

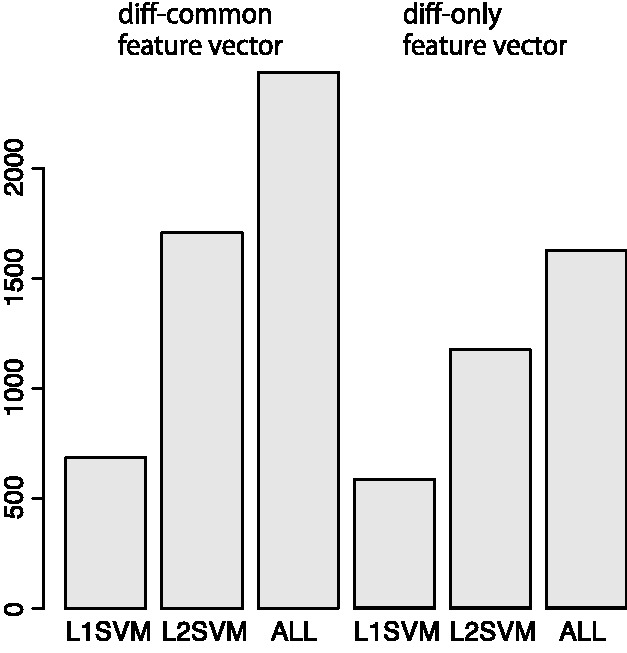
Comparison of the number of extracted features among different methods

The AUC scores of BASELINE were fairly high, regardless of fingerprints (except E-state fingerprint, probably owing to the small dimensions compared with other seven fingerprints), which validated the fact that a core substructure is shared between a substrate compound and a product compound in a reactant pair. Another explanation about the high AUC scores of BASELINE is that negative examples (all possible compound pairs except for reactant pairs in the gold standard data) include many structurally dissimilar compound pairs. As most of such compounds are unlikely to be converted to each other in a reaction, BASELINE (a standard similarity-based method) can easily classify them into negative class. To avoid such trivial predictions, we removed compound pairs whose Tanimoto coefficient (Jaccard coefficient) is less than 0.5 from the gold standard data and constructed a filtered dataset consisting of compound pairs whose structures are similar to some extent. Classification is more difficult for the filtered data. We performed the same cross-validation experiment on the filtered data, and the AUC scores are shown in Table 3. The result shows that the proposed method clearly outperforms the BASELINE method.

Table 3.

AUC scores on 5-fold cross validation experiments for enzymatic-reaction likeness on the filtered gold standard data

	Diff-common feature vector		Diff-only feature vector
Fingerprint	L1SVM	L2SVM	L1SVM	L2SVM	BASELINE	RANDOM
CDK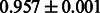
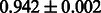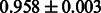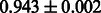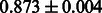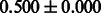CDK extended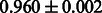
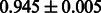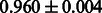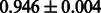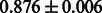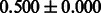CDK graph only
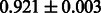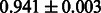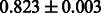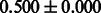CDK hybridization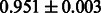
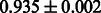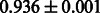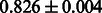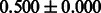E-state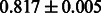
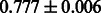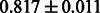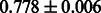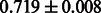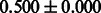KlekotaRoth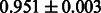
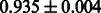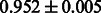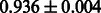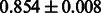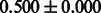MACCS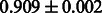
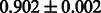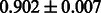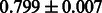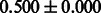PubChem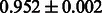

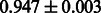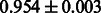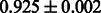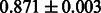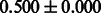4.2 Performance evaluation on pathway reconstruction

We tested the proposed L1SVM method with the PubChem fingerprint on its ability to reconstruct pathways from a given compound set, assuming the situation where we want to detect a series of reactant pairs comprising a metabolic pathway.

We performed the following pathway-based cross-validation. (i) We took known reactant pairs on the same pathway as a test set. We regarded the reactant pairs as positive examples and the other compound pairs as negative examples. (ii) We took the remaining sets of reactant pairs and compound pairs (which are absent from the pathway of the test set) as a training set. (iii) We trained a predictive model based only on the training set. (iv) We computed the prediction scores for all possible compound–compound pairs in the test set. (v) Finally, we evaluated the prediction accuracy over the known reactant pairs. We repeated the above steps on each of the 134 metabolic pathway maps in KEGG pathway.

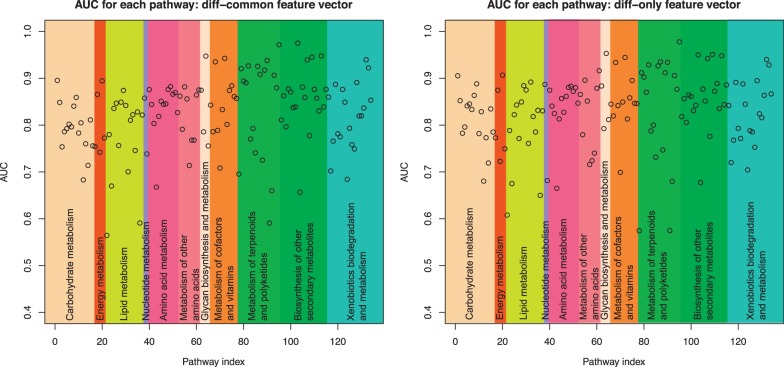
Figure 3 shows the resulting AUC scores by the pathway-based cross-validation, where the left panel is the result of using the diff-common feature vector and the right panel is the result of using the diff-only feature vector. Each point in the panels corresponds to the result of each pathway map, where each pathway map belongs to one of the 11 pathway categories. The AUC scores tend to be lower than those in the 5-fold cross-validation for all known reactant pairs (in Section 4.1), which implies that pathway reconstruction is a more difficult problem. For example, metabolism of terpenoids and polyketides involve pathways specific to a limited group of organisms. Removal of such pathways from the training set results in low predictive performance, indicating the difficulty to model exotic metabolism in newly found organisms. Additionally, although diff-only feature vector resulted in lower AUC scores than diff-common feature vector in the 5-fold cross-validation, diff-only feature vector performed slightly better than diff-common feature vector in some pathway maps including those in carbohydrate metabolism and lipid metabolism and so forth. One explanation is that, because compounds in the same pathway tends to be structurally similar to each other, removal of all compounds in the target pathway from the training set may sometimes lose the effectiveness of the common feature vector in the training set for the pathway-based cross-validation, and differential feature vector becomes relatively important. Nevertheless, it was shown that the proposed method worked well to some extent even when all reactions in a pathway map are not known. There was no significant difference between different pathway categories or between different feature vectors. These results suggest the usefulness of the proposed method not only for filling in the reaction gaps among existing pathways but also for de novo reconstruction of a series of reactions.

Fig. 3.

AUC scores for each pathway map with diff-common feature vectors (left panel) and diff-only feature vectors (right panel)

4.3 Interpretation of the chemical transformation patterns

In a reaction, some substructures are formed, whereas other substructures are eliminated. Here, we examined the importance of such chemical substructure transformations according to the weights learned by the L1SVM method. We focused on the substructure components in the PubChem fingerprint, removing the components that do not represent substructures (those in Hierarchic Element Counts and in Extended Smallest Set of Smallest Rings set).

Figure 4 is a network representation of such chemical substructure transformations with positive weights that contributed to estimate the enzyme-reaction likeness. In Figure 4, nodes represent the substructure components, the node size is proportional to the weight and edges represent the top 100 co-occurring (one formed and one eliminated) substructures. For example, the substructure with the highest contribution was labeled as ‘C(∼H)(∼O)(∼O)’, meaning a carbon atom attaching with a hydrogen atom and two oxygen atoms, which includes (hemi)acetal group, (hemi)ketal group, carboxyl group, O-formyl group and so forth. This substructure is connected with the substructures labeled as ‘C(∼C)(∼O)’, including hydroxy group, aldehyde group and so forth. The connection between these two includes frequently occurring transformations ‘aldehyde <=>hemiacetal’ and so forth. This substructure transformation network is useful when interpreting the frequently occurring chemical transformations. Nevertheless, many fingerprints including PubChem put some distinctive functional groups in the same fingerprint component (such as the one labeled as ‘C(∼H)(∼O)(∼O)’). This may lead to the flexibility of the prediction, but at the same time to the increase of false positives. Additionally, it is not possible to deal with the chemical transformations that cannot be described in the existing fingerprints. A more suitable fingerprint would be needed for improving the reliability of the de novo metabolic pathway reconstruction in the future work. A possible solution would be to include a number of different levels of substructure (or functional group) classification.

Fig. 4.

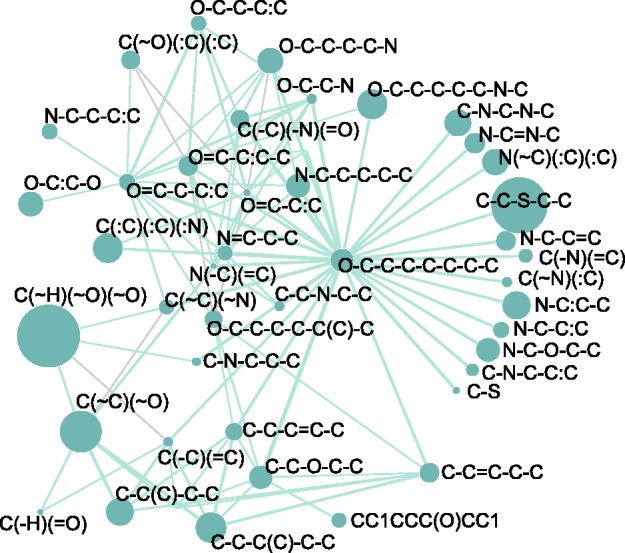
Substructure transformation network. Nodes represent the PubChem fingerprint components that contributed to the prediction with diff-only feature vectors, where the size of the nodes is proportional to the weights in L1SVM. Edges represent the top 100 frequently pairs of substructures, where the one is formed and the other is eliminated in a reaction

4.4 Newly predicted reactions and chemical transformations

Having confirmed the usefulness of our method, we conducted a comprehensive reaction prediction for all possible compound pairs. We trained a predictive model using all known reactant pairs in the gold standard data. We then predicted potential reactions for 246 397 942 compound–compound pairs involving 15 698 compounds in KEGG LIGAND (13 564 known reactant pairs are excluded). All the prediction results can be obtained from the supplemental materials from http://web.kuicr.kyoto-u.ac.jp/supp/kot/ismb2013/. The prediction times of L1SVM with the diff-common and the diff-only feature vectors were 1.4 and 1.1 h, respectively, for all possible compound pairs, which demonstrates the practical feasibility of our methods for large-scale compound data. We used one core of a Quad-Core AMD Opteron Processor (3.1 GHz) linux machine with 512 GB memory. The computational time of the proposed method was remarkably smaller than that of the rule-based method (Nakamura et al., 2012) that needed 0.03 s per pair (corresponding to ∼2000 h for all possible compound pairs). The same task is not feasible by other reaction-filling framework methods because of their methodological limitation (Kotera et al., 2008; Tanaka et al., 2009). The compound–filling framework methods (Gao et al., 2011; Moriya et al., 2010) needed tens of seconds per compound (corresponding to thousands of hours for all possible compound pairs).

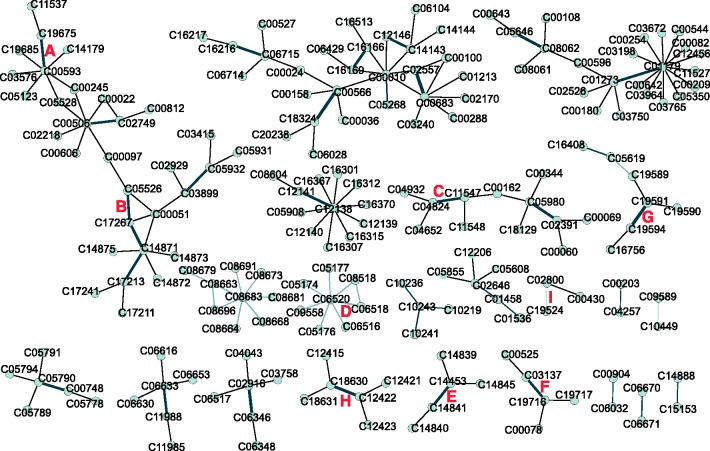
We examined the newly generated reaction network in detail (Figs 5 and 6). Among the predicted pairs connected with existing pathways, some pairs formed triangles with existing pathways (e.g. pair B in Fig. 5), meaning that some predicted pairs may represent two- or more-step reactions. With the closer look at the chemical structures (Fig. 6), it was also assumed that some pairs (D, E, G and H) would be possibly converted in more than one reaction steps. Some pairs were found to have the same chemical transformations as those in known reactions (e.g. pairs A, B and C), which looks reasonable to occurr. Among those without known chemical transformations (e.g. pairs D, E, F, G, H, I), it would be safe to say some pairs (e.g. pairs D, E and F) are false positives, and it would not be for other pairs (e.g. pairs G, H and I). It was found that using chemical fingerprints can easily produce chemically unrealistic false predictions, which can possibly be filtered out using graph isomorphism. The effective integration of the speed of the fingerprints and the accuracy of the graph isomorphism would be one of the important future developments.

Fig. 5.

Part of the generated de novo reactions combined with existing network, where nodes and edges represent compounds and reactions, respectively. Black thin lines represent the reactions existing in KEGG. Gray lines represent 50 new reactions with high scores predicted by diff-common and diff-only feature vectors. The width of the gray edges is proportional to the predictive score. Predicted reactions (A–I) are given detailed explanation in Figure 6

Fig. 6.

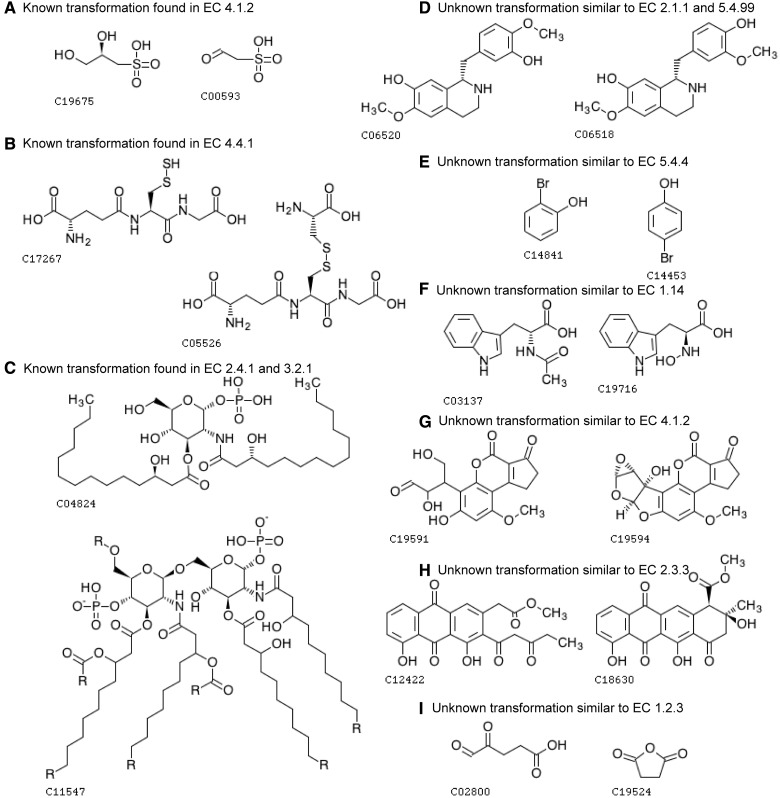
Examples of the predicted pairs taken from Figure 5. The chemical transformation patterns in pairs (A–C) are already known and described in KEGG reactant pairs (Note that these reactions are not known, but the transformation patterns are known), whereas pairs (D–I) have unknown patterns. (A) C-C bond accompanied with secondary alcohol group is degraded and forms an aldehyde group, which is a reaction typically found in EC sub-subclass 4.1.2 (aldehyde-lyases). (B) C-S bond in disulfide bond is degraded and forms an S-mercapto group, which is found in EC sub-subclass 4.4.1 (carbon-sulfur lyases). (C) This chemical transformation pattern is found in many reactions in EC 2.4.1 (glycosyltransferases) and EC 3.2.1 (glycosidases). (D) This pattern is not found in known reactions. At the first sight, this pair may look like two steps of methylation/demethylation (EC 2.1.1) or intramolecular transfer of a methyl group (part of EC 5.4). With closer investigations of Isoquinoline alkaloid biosynthesis pathway (map00950, which these compounds belong to), it looks more natural to occur the two steps of metylenedioxy ring formation/cleavage (EC 1.14.21 or 1.21.3) because some metylenedioxy ring formation reactions are known to take place in this pathway. However, in any case, methylation and metylenedioxy ring formation occurs in the context of biosynthesis, whereas demethylation and metylenedioxy ring cleavage occurs in the context of biodegradation. In that sense, this compound–compound pair may be an example of false positives when taking account of the reaction flow in the pathway level. (E) This compound–compound pair may look intramolecular transfer of a hydroxy group, which is typically found in EC 5.4.4 (hydroxymutases), but the transfer of hydroxy group from a position to another in an aromatic ring is not found in any known reactions stored in KEGG. This pair may be another example of false positives because the substitution of hydroxy group in aromatic ring is much harder to occur than the addition of hydroxy group. It is known that some anaerobic bacteria have 4-hydroxybenzoyl-CoA reductase (EC 1.3.7.9) that catalyzes the substitution of hydroxy group in aromatic ring. However, we assume it would be hard to catalyze intramolecular transfer of hydroxy group in substituted aromatic ring. (F) Although there are many varieties of hydroxylases (part of EC 1.14), there is no known pattern to produce hydroxyl amine from amide group. (G) For this reaction to occur, there need to be more than one reaction steps, and an important step would be similar to EC 4.1.2 (aldehyde-lyases). (H) There are similar EC 2.3.3 (acyl transferases) reactions in polyketide synthesis. (I) Some of EC 1.2.3 (oxidases) catalyze similar reactions

We further investigated the distribution of possible Enzyme Commission (EC) numbers for the predicted reactions, and it was clearly shown that the distribution of predicted reactions is different from that of known reactions, and diff-common and diff-only feature vectors favor different molecules or reactions (see Supplementary Material). For example, diff-common feature vector found compound–compound pairs that are possibly catalyzed by EC3, and diff-only feature vector found those by EC4. It is supposed that this bias is partly due to the given compound sets and partly due to the reaction types that the proposed method can deal with. We assume that the former is the main reason of the bias in the new prediction because the re-assignment experiments did not show significant difference from the original EC classifications compared with new predictions.

As described earlier in the text, our method based on supervised reaction-filling framework has the potential to suggest possible reactions among large number of known chemical compounds not only with known chemical transformation patterns but also with unknown transformation patterns. Reaction reversibility is not considered in this study. One reason is that only small numbers of enzymatic reactions are known irreversible in vitro, and the direction of the reactions in vivo may change according to the context in pathways and conditions. The other reason is, more importantly, the purpose of this study is generating the pathways that can be used as a template for modeling metabolic flux. Testing the generated pathways with metabolic flux analysis is an interesting and unavoidable future direction of this study.

5 CONCLUSION

We presented a novel de novo metabolic pathway reconstruction method in the reaction-filling framework. The proposed method does not require manually predefined rules, i.e. it automatically learns a statistical model to predict enzymatic reaction likeness for any compound pairs based on all possible existing knowledge. This method can deal with any compounds (even if they are not found in KEGG) as long as they are represented in chemical fingerprints.

An advantage of our method lies in finding potential reactions among many compounds at a time. The previous study (Kotera et al., 2008) used graph isomorphism, which contributed to the accuracy of the method but took much more calculation time. The current study used fingerprints (instead of graph isomorphism) to improve calculation time and deal with vast amount of compounds. For more accurate prediction, we are going to develop the two-step prediction, where fingerprints are applied to filter out vast amount of negative pairs in the first step, and graph isomorphism is applied to refine the predicted pairs in the second step.

In principle, our method (i.e. reaction-filling framework) is insufficient to correctly predict a multi-step pathway, which can be better dealt with the other framework (i.e. compound-filling framework). This does not imply which framework is superior; these two frameworks can complement each other for more successful de novo metabolic pathway reconstruction. We assume the proposed study is an important preliminary step toward the hybrid framework.

Further improvement of the de novo metabolic pathway reconstruction method would enable the on-demand integration of reaction network and gene (or protein) networks derived from metabolome and other omics, e.g. genome, transcriptome and proteome.