Simple topological properties predict functional misannotations in a metabolic network

Abstract

Motivation: Misannotation in sequence databases is an important obstacle for automated tools for gene function annotation, which rely extensively on comparison with sequences with known function. To improve current annotations and prevent future propagation of errors, sequence-independent tools are, therefore, needed to assist in the identification of misannotated gene products. In the case of enzymatic functions, each functional assignment implies the existence of a reaction within the organism’s metabolic network; a first approximation to a genome-scale metabolic model can be obtained directly from an automated genome annotation. Any obvious problems in the network, such as dead end or disconnected reactions, can, therefore, be strong indications of misannotation.

Results: We demonstrate that a machine-learning approach using only network topological features can successfully predict the validity of enzyme annotations. The predictions are tested at three different levels. A random forest using topological features of the metabolic network and trained on curated sets of correct and incorrect enzyme assignments was found to have an accuracy of up to 86% in 5-fold cross-validation experiments. Further cross-validation against unseen enzyme superfamilies indicates that this classifier can successfully extrapolate beyond the classes of enzyme present in the training data. The random forest model was applied to several automated genome annotations, achieving an accuracy of 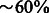in most cases when validated against recent genome-scale metabolic models. We also observe that when applied to draft metabolic networks for multiple species, a clear negative correlation is observed between predicted annotation quality and phylogenetic distance to the major model organism for biochemistry (Escherichia coli for prokaryotes and Homo sapiens for eukaryotes).

Contact: j.pinney@imperial.ac.uk

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Misannotation in sequence databases has been a recognized problem for more than a decade. Early studies reported the emergence of this issue (Brenner et al., 1999; Galperin et al., 1998) and estimated that up to 30% of proteins were misannotated in public databases (Devos and Valencia, 2001). More recent studies have confirmed that this problem is still a reality (Jones et al., 2007) and some even suggest that it has been getting worse over time (Schnoes et al., 2009), identifying overprediction and error propagation as the main sources of error. As experimental verification of gene function is expected to remain a highly time-consuming process, it is unlikely that it will be able to keep pace with the increasing amount of genome sequence data being deposited in public databases. More accurate computational methods for functional annotation and assessment of confidence in gene annotations are, therefore, increasingly necessary.

In the area of automated functional annotation, several approaches moving beyond basic sequence similarity are now available (Jones et al., 2007). Some recent annotation software will classify proteins based on locally conserved sequence patterns that are normally related with function (Forslund and Sonnhammer, 2008). Other approaches take into account the evolutionary relationships between proteins by integrating evidence across phylogenetic trees (Engelhardt et al., 2009) or use additional information, such as protein–protein interaction data (Ta and Holm, 2009) or genomic correlations (Hsiao et al., 2010).

However, functional annotation is still mainly based on sequence similarity. Given this fact, the accuracy of existing annotations has a crucial impact on that of future annotations (Jones et al., 2007). This dependency can lead to error propagation and a consequent increase in the number of annotation errors (Gilks et al., 2002). Moreover, as information on the origin of annotation is often scarce, this error propagation does not have an easy solution. The problem becomes even clearer when we note that the proportion of manually annotated proteins is <5% and continues to decrease (Frishman, 2007).

Any evidence that is independent of sequence may, therefore, be useful for discriminating between true and false functional annotations. The concept of gene function implies interaction with some part of the cell or the environment, and almost all functions of interest are the result of interactions among several components (Hartwell et al., 1999). Modelling these interactions by means of networks and studying their topological properties is, therefore, one way to understand the context of these molecular functions.

One easily accessible example of a well-defined molecular network derived from a set of gene annotations is a draft metabolic network, such as those available in the KEGG database (Kanehisa and Goto, 2000; Kanehisa et al., 2006, 2008). The topological properties of these networks have been studied previously in the contexts of network evolution (Wagner and Fell, 2001) and drug target discovery (Yeh et al., 2004). For example, the metabolic networks of parasitic species are known to be distinguishable from non-parasitic species on the basis of their topology (Borenstein and Feldman 2009; Nerima et al., 2010). Intuitively, any problems in such a network, for example, dead ends or disconnected components, could be an indication of misannotation (Poolman et al., 2006). However, each individual type of evidence can be relatively weak (e.g. dead ends may also be due to the uptake of nutrients from the environment) and difficult to discern by manual inspection.

In this work, we propose a supervised machine-learning methodology to assess the accuracy of assigned molecular functions, based on simple topological properties of an organism’s draft metabolic network. We show that our approach is able to separate correct annotations from incorrect ones with accuracy of up to 86%. Being entirely independent of sequence properties, it can be used to complement existing approaches and, hence, contribute to the detection and correction of errors in functional annotation.

2 METHODS

2.1 Metabolic networks

Bipartite (reaction and compound) graphs were used to represent metabolic networks, generated using the KEGG LIGAND database (Kanehisa et al., 2008). To reconstruct the metabolic network for each species, all gene functions annotated for that species were collected. The reactions mapped to each function were then retrieved. Finally, the compounds attached to each reaction were added to produce a bipartite metabolic network for each species. All reactions were considered as being reversible. Network topological properties were calculated using the NetworkX library in Python.

2.2 Training data

Schnoes et al. (2009) previously examined the annotation errors in four large public protein databases (KEGG, GenBank NR, UniprotKB/TrEMBL and UniProtKB/SwissProt). From their correct and incorrect annotation data, only the annotations with EC number were considered. In total, there were 834 correct and 477 incorrect annotations from six different superfamilies. For each annotation, the dataset presents the species, KEGG KO group, EC number and the part of the protocol that the annotation failed to pass. Each annotated function was mapped to a reaction according to KEGG. Where an EC function was mapped to more than one reaction, one of these was chosen at random. To evaluate the topological properties of each of the annotations, KEGG species networks were used.

2.3 Machine learning

The approach used to separate correct from incorrect annotations was the random forest. A random forest is an ensemble of decision trees. During the training process, to achieve a variety of different decision trees, a random subset of parameters is selected for each node. Afterwards, as in a standard decision tree, the parameter chosen at each node is the one that most increases the entropy. To predict the label of an entry, the entry is assessed by every tree of the ensemble. The distribution of label votes returned is the random forest prediction. In our case, the probability of an annotation being correct is taken as the proportion of trees that labelled it as correct.

The random forest used was the one implemented in the randomForest R package (Liaw and Wiener, 2002). The algorithm implemented is as described in Breiman (2001). The parameters used in both the randomForest and predict functions were the default ones. For building the receiver–operator characteristic (ROC) curves, the type = ‘prob’ option in the predict function was used.

2.3.1 The 5-fold cross-validation

The cross-validation process used was to start with the original data (D) and divide it in five equal sets. Each of the sets was used as an independent test set (D_test). The random forest algorithm considering all available features was applied to the remaining four sets (D_train). The random forest predictor built was then tested on D_test.

2.3.2 Inter-superfamily cross-validation

The training data were grouped by enzyme superfamily. Because of the paucity of data in most superfamilies, only the four most populated superfamilies were taken forwards to cross-validation. Each superfamily in turn was removed from the balanced dataset SF to form the test set SF_test. The random forest algorithm was applied to the remainder (SF_train). The model built was then tested on SF_test.

2.3.3 Final classifier

The random forest was trained on the whole of the original data using all the features. The importance function from the randomForest R package was used to assess each feature’s individual performance after training the model with the full training set.

2.4 Comparison against curated models

To further validate the classifier, it was applied to 24 KEGG metabolic networks, and the results were compared with curated genome-scale metabolic models for these species (Table 4). The species used were the set with whole-genome models listed in Feist et al. (2009) for which functions were labelled with EC numbers. For each KEGG model considered, each annotated function was mapped to a reaction according to KEGG. Where an EC function was mapped to more than one reaction, one of these was chosen at random. The classifier was applied to these KEGG data, and the results were compared with the curated models, verifying the presence or absence in the curated models of the functions assigned in the KEGG models.

Table 4.

Genome-scale model validation results

KEGG ID	Species name	AUC	Citation
ani	Aspergillus nidulans	0.56	David et al., 2008
ath	Arabidopsis thaliana	0.57	de Oliveira Dal’Molin et al., 2010
bsu	Bacillus subtilis	0.61	Oh et al., 2007
buc	Buchnera aphidicola	0.68	Thomas et al., 2009
det	Dehalococcoides ethenogenes	0.60	Islam et al., 2010
eco	E.coli K-12	0.55	Reed et al., 2003
hsl	Halobacterium salinarum	0.60	Gonzalez et al., 2008
lpl	Lactobacillus plantarum	0.64	Teusink et al., 2006
mge	M.genitalium	0.43	Suthers et al., 2009
nme	Neisseria meningitidis	0.58	Baart et al., 2007
nph	Natronomonas pharaonis	0.60	Gonzalez et al., 2010
pfa	P.falciparum	0.59	Plata et al., 2010
pgi	Porphyromonas gingivalis	0.60	Mazumdar et al., 2009
pic	Pichia stipitis	0.48	Caspeta et al., 2012
sau	Staphylococcus aureus	0.52	Lee et al., 2009
sce	S.cerevisiae	0.56	Herrgård et al., 2008
sce	S.cerevisiae	0.53	Förster et al., 2003
sco	Streptomyces coelicolor	0.64	Borodina et al., 2005
sco	S.coelicolor	0.63	Alam et al., 2010
son	Shewanella oneidensis	0.55	Pinchuk et al., 2010
syn	Synechocystis PCC6803	0.57	Nogales et al., 2012
vvu	Vibrio vulnificus	0.52	Kim et al., 2011
ypm	Yersinia pestis	0.55	Navid and Almaas, 2009
zmo	Zymomonas mobilis	0.61	Widiastuti et al., 2011

Note: The final classifier was applied to KEGG metabolic models, and the results were compared with curated genome-scale metabolic models for these species.

2.5 Tree of life analysis

Ciccarelli et al. (2006) have reconstructed a highly resolved tree of life. Their species tree is built from a concatenation of 31 unambiguous orthologues present in 191 species. This tree and the multiple alignments used to build it were downloaded from iTOL (Letunic and Bork, 2007, 2011). iTOL also provides other types of data related to these species, including genome sizes, domains per genome and publication dates. The multiple alignment was used to calculate the distances between the species using protdist from PHYLIP (Felsenstein, 1993), a package of programs for inferring phylogenies. The classifier was applied to the metabolic networks present in KEGG for each species included in the iTOL phylogeny.

3 RESULTS AND DISCUSSION

In this study, metabolic networks are represented by bipartite digraphs (with nodes for each reaction and compound). A network was built for each organism in the study, based on a template taken from the KEGG LIGAND database (Kanehisa et al., 2008).

As with any supervised machine-learning task, it is necessary to choose a machine-learning method and a set of features from which to learn. The random forest (Breiman, 2001) was found to be a suitable machine-learning approach for our aims. The advantages of using random forests in this work are their ability to process both numerical and categorical data and the interpretability of their output (a so-called ‘white box’ model). In contrast to other machine-learning methods, such as neural networks or support vector machines, random forests can provide insights into the signals that are useful for classification.

Training and testing data sets were taken from the work of Schnoes et al. (2009), which provide gold-standard sets of correct and incorrect EC number assignments within 331 species in KEGG, across six enzyme superfamilies. In addition to sequence similarity approaches at the superfamily and family levels, the authors used information on functionally important residues to infer misannotations, making this one of the most reliable data sources suitable for our purposes.

3.1 Features

In total, 22 different network topological features were considered in training the classifier. These features can be placed into three broad groups: local, semi-local and global features (Table 1).

Table 1.

Classification features

Group	Feature	Definition
1	m	Number of compounds connected to >2 reactions.
	u	Number of unpaired compounds.
	t	Reaction type: 1—unpaired compounds on both sides of the reaction, 2—unpaired compounds on only one side, 3—no unpaired compounds.
	h	Number of chokepoint compounds.
	c	Number of compounds.
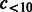		Number of compounds connected to >2 and <10 reactions.
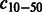		Number of compounds connected to 10–50 reactions
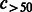		Number of compounds connected to >50 reactions.
	R	Number of other reactions sharing a compound with this reaction.
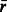		Mean number of other reactions connected to each compound.
	r1	Number of connections of the least connected compound.
	r2	Number of connections of the second least connected compound.
	r3	Number of connections of the third least connected compound.
	r4	Number of connections of the fourth least connected compound.
2	e	Eccentricity using unweighted edges,
		Normalized eccentricity using unweighted edges.
	ew	Eccentricity using weighted edges
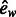		Normalized eccentricity using weighted edges
	b	Betweenness using unweighted edges
	bw	Betweenness using weighted edges
	N	Number of reactions in the connected component.
3		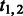Fraction of reactions of type 1 or 2 in the network.
4	G	Domain: 1—Bacteria, 2—Eukaryota, 3—Archaea.
	D	1—species is related to disease, 0—species is not related to disease.

Note: The features chosen were divided into four groups as shown: 1—local, 2—semi-local, 3—global and 4—non-topological.

Local topological features capture the properties of the immediate neighbourhood of each reaction. Several of these features are related to the compounds involved in the reaction, each of which can be classified according to its connectivity (degree) as an unpaired, chokepoint or ‘normal’ metabolite (Supplementary Fig. S1). Based on this classification, several integer attributes were defined for each reaction. We noticed that the connectivity of compounds involved in a reaction tends to vary depending on enzyme class; therefore, four additional features were defined to capture this variation. These features correspond to the ranked connectivities of the reaction’s four least-connected compounds.

The semi-local topological features describe the position of each reaction within the network. These features are based on the graph theoretical concepts of betweenness centrality and eccentricity. The betweenness of a node is the fraction of shortest paths (geodesics) between all pairs of nodes in the network that include that node, whereas the eccentricity of a node is the length of the longest geodesic between the node and all other nodes in the network. In both cases, these values were also calculated including weights on the edges of the networks. Weighted metabolic networks have previously proved useful in the automatic identification of biologically meaningful pathways within a metabolic network (Croes et al., 2006). This is a simple way to exclude spurious links via highly connected compounds, such as water or adenosine triphosphate. Here, we place a weight on each compound equal to its connectivity. To take variations in network size into account, we also considered a variant of eccentricity that is normalized by dividing by the diameter of the connected component to which the reaction belongs.

In addition to these reaction-based features, some global topological features of the network may be relevant, for example, if the amount of human curation varies between species. We use the proportion of reactions that have a dead-end compound on one or both sides as a proxy for the overall reliability of the network.

Two non-topological features were also considered: taxonomic domain (Archaea, Bacteria or Eukaryota) and whether the organism is implicated in a disease. The reason for including these two features was to allow for potential topological differences between different domains and between pathogens and non-pathogens. It has previously been shown that metabolic network topology can be affected by variations in the selection pressures experienced during evolution (Borenstein and Feldman, 2009; Kreimer et al., 2008; Parter et al., 2007).

To gain intuition of which features may have a bigger influence on the results, the performance of each individual feature was evaluated independently. Histograms of the correct and incorrect annotation data provide a visual summary (Fig. 1 and Supplementary Fig. S2). A quantitative evaluation of each feature’s performance was also obtained using the importance function from the randomForest package (Liaw and Wiener, 2002). This function evaluates the accuracy decrease and the entropy decrease when each feature is left out, with results shown in Supplementary Figure S3.

Fig. 1.

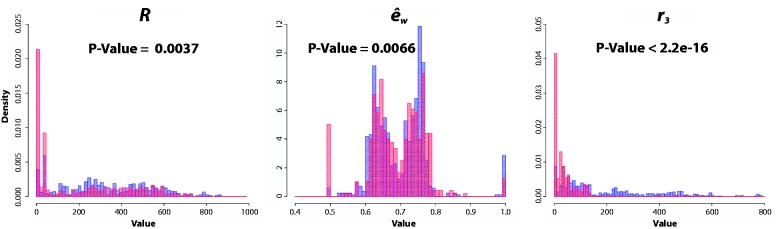
Feature histograms. Visualization of the potential value of each attribute in distinguishing the correct functional assignments from the incorrect ones (red—incorrect annotations; blue—correct annotations). The Kolmogorov–Smirnov test shows that each of these attributes has a significantly different distribution for the correct and incorrect annotations. The corresponding P-values are shown on each histogram. Similar histograms for the remaining features are shown in Supplementary Figure S2

All metrics show a similar ranking between the features, with those based on the concepts of betweenness and eccentricity seen to be the most highly predictive. It is possible that these semi-local features are able to capture relevant differences in relative network position (e.g. higher eccentricity indicates reactions that lie towards the periphery of the network). The weighted network factor seems to improve the performance of both eccentricity and betweenness features, although it is more clearly seen in the case of eccentricity.

The taxonomic domain is the least informative feature. This may imply that the features already considered, such as the connected component size, may already be capturing any differences between species from different domains. The same might be happening with the disease-related feature. For example, parasitic species may be expected to have a larger number of unpaired compounds and smaller connected components, making this feature less informative. However, both features still show some predictive power.

3.2 Cross-validation

The performance of the classifier on unseen data was assessed using two types of cross-validation. In 5-fold cross-validation experiments (Table 2), the model obtained has an accuracy of ∼86%. Supplementary Figure S4 shows the ROC curves obtained for each of the cross-validation folds. The mean area under the ROC curve (AUROC) was 0.92%. Another important aspect of performance is how well the predictor would be expected to perform on enzymes from unseen superfamilies. To this end, a second cross-validation was performed using the four most represented superfamilies present in the Schnoes et al. dataset: Enolase, Vicinal Oxygen Chelate, Haloacid Dehalogenase and Amidohydrolase. The cross-validation used the enzymes from three out of the four superfamilies as a training set and tested on the enzymes from the fourth (Table 3). In this experiment, with the exception of the Vicinal Oxygen Chelate superfamily, the accuracy of the predictor was consistently >60%. Supplementary Figure S5 shows the ROC curves for each superfamily. The area under the curve varied between 0.59 and 0.68. These results suggest that the functional classes covered in the training data do have an effect on the rules obtained. For example, enzyme classes may occupy topologically distinct positions in the network, and/or be subject to particular types of misannotation. However, these results indicate that the classifier trained on the entire available data set should still be informative when applied more generally.

Table 2.

The 5-fold cross-validation results

	Mean (SD)
Accuracy	0.86 (0.005)
Precision	0.91 (0.009)
Recall	0.88 (0.011)
AUC	0.92 (0.007)

Note: The predictive model performance was assessed by a 5-fold cross-validation. The table shows the accuracy, precision, recall and AUC of this analysis and their standard deviations.

Table 3.

Superfamily cross-validation results

Superfamily	Accuracy	Precision	Recall	AUC
Enolase	0.60	0.57	0.97	0.60
Vicinal oxygen chelate	0.52	0.86	0.51	0.59
Haloacid dehalogenase	0.60	0.77	0.46	0.67
Amidohydrolase	0.66	0.69	0.74	0.68

Note: To test performance on unseen enzyme classes, the classifier was assessed in a leave-one-out cross-validation at the superfamily level. The table shows the accuracy, precision, recall and the AUC of each analysis, where each superfamily in turn was used as the test dataset.

3.3 Comparison to a manually curated network

To assess the performance of the model, the classifier was applied to the 24 KEGG genome annotations. These results were compared with recent manually curated genome-scale metabolic models as gold standards (Table 4 and Supplementary Fig. S6). The species used were the whole-genome models listed in Feist et al. (2009) for which enzyme functions were labelled with EC numbers. The AUC results were consistently >0.5, showing a performance better than random. In fact, in almost half of the species tested, the classifier produced an AUC of ≥0.6. There were only two cases where AUC was found to be <0.5. The worst result was found with Mycoplasma genitalium, perhaps related to the fact that this is the smallest prokaryote genome sequenced.

3.4 Case study: an atypical orthologue

An interesting example of the successful identification of an unexpected enzyme function is given by Dittrich et al. (2008). This work was based on the idea that an evolving enzyme has more chance to acquire the function of structurally similar enzymes. A bioinformatic protocol was followed to draw up a shortlist of candidate functional analogues of a missing enzyme (dihydroneopterin aldolase, DHNA) in the Plasmodium falciparum folate biosynthesis pathway.

During the process, the authors found two candidates for filling the role of the missing enzyme. Both enzymes already had an assigned function in KEGG: PFF1360w is annotated as a putative 6-pyruvoyl tetrahydropterin synthase (PTPS) and PFL1155w as GTP cyclohydrolase I (GTPCH-I). Although PFF1360w was subsequently experimentally validated as performing the missing DHNA function, KEGG has not yet updated this annotation. This enables us to apply the classifier to the KEGG P.falciparum metabolic network to study this case.

Taking a closer look at the two annotated reactions in their network context (Supplementary Fig. S14), it can be seen that the PTPS reaction seems to be a dead end, indicating that this annotation is unlikely to be correct. In contrast, the GTPCH-I enzyme not only has its reactants produced and its products consumed, as seen in the figure, but is also assigned to four chokepoint reactions.

Applying our classifier to these two enzymatic functions, it returned a probability of 0.94 for the GTPCH-I reaction, indicating that this function seems to make biological sense within its network context. On the other hand, the PTPS reaction scores only a probability of 0.21 to be a correct annotation. This simple case study shows that the classifier has successfully captured the same network topological features that provided evidence for an incorrect annotation in the published manual analysis of this enzyme.

3.5 Comparison of predicted annotation quality across multiple species

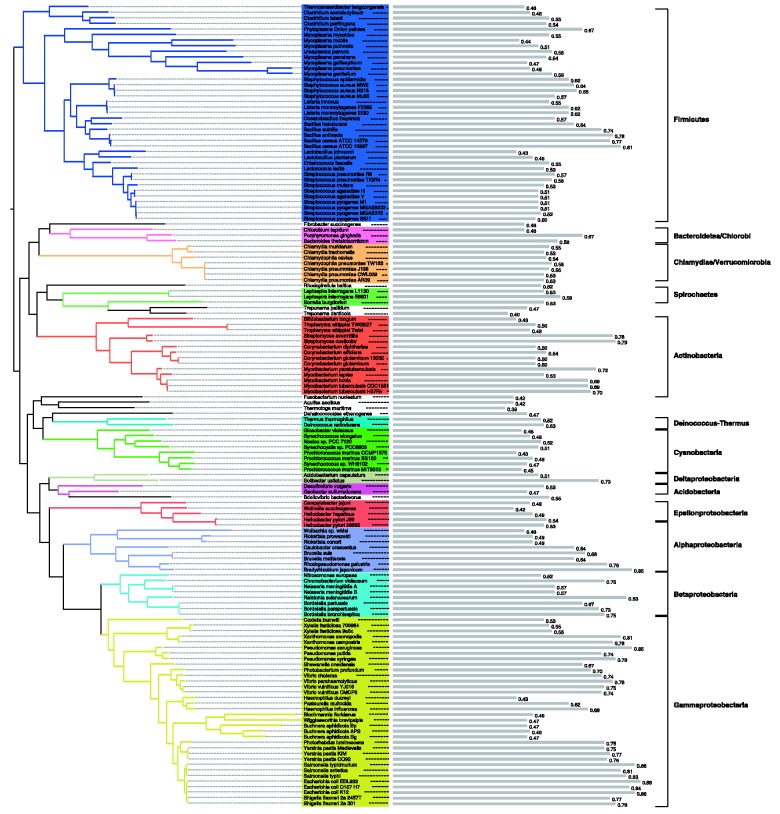
To investigate how annotation quality varies between species, the classifier was applied to the KEGG metabolic networks of the species present in the tree of life provided by iTOL (Letunic and Bork, 2007, 2011). The proportion of enzymatic functions predicted to be correctly annotated in the network of each species (i.e. the predicted precision of the set of enzymatic functions reported by KEGG for that organism) was taken as a measure of annotation quality. Figure 2 shows the prokaryote phylogenetic tree and quality scores for each of the species. The Escherichia coli strains and the most closely related species produce the highest scores, indicating their higher levels of curation. With the exception of Chlamydiae/Verrucomicrobia and the Cyanobacteria, all phyla show a wide variety of quality scores.

Fig. 2.

Predicted quality of draft metabolic networks across a prokaryote phylogeny. The classifier was applied to all prokaryote species present in the iTOL phylogeny (Letunic and Bork, 2007, 2011). Coloured clades represent the different phyla present (only phyla with more than one species were coloured). The names of the phyla are shown to the right. Predicted annotation quality values are represented by grey bars next to the species name

The number of eukaryotic species provided by iTOL is much smaller than the number of prokaryotes. Supplementary Figure S7 shows the eukaryote phylogenetic tree and the quality scores of the KEGG metabolic networks for each of the species. The vertebrates and plants produce higher scores than the other species. An unexpected result is the relatively low scores reported for Saccharomyces cerevisiae and Drosophila melanogaster (both 0.73), especially when compared with those achieved by the vertebrates. However, this most probably reflects the massive amount of study that human biochemistry has received relative to any other eukaryote, including these two important model organisms.

It is reasonable to expect that the quality of a draft metabolic network should be better for species that are closely related to organisms with well characterized biochemistry. Figure 3 shows that this is indeed the case: there is a clear negative correlation () between the predicted annotation quality in prokaryotes and the phylogenetic distance to E.coli and an even stronger negative correlation () between the predicted annotation quality in eukaryotes and the phylogenetic distance to Homo sapiens.

Fig. 3.

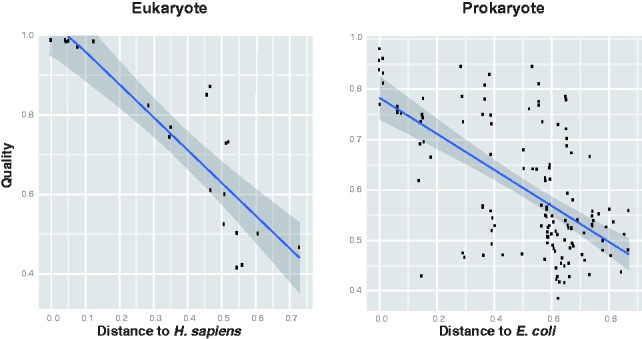
Variation of predicted annotation quality with phylogenetic distance to model organism. Left: Scatter-plot showing predicted annotation quality (precision of annotated reactions according to the classifier) for eukaryotes against phylogenetic distance to H.sapiens. Right: Scatter plot showing predicted annotation quality for prokaryotes against phylogenetic distance to E.coli (Ciccarelli et al., 2006). The shaded region shows the 95% confidence interval for the regression line

To check for any dependency between annotation quality and genome size, a similar scatter plot was drawn (Fig. 4). Although a positive correlation is present, this may be partially explained by other factors. In particular, the intracellular obligate species (highlighted in green in Fig. 4) and the well-curated species (highlighted in orange), constituted by the E.coli strains and closely related species (Salmonella and Yersinia), have distinctly low- and high-quality scores, respectively. As intracellular obligate species will tend to have lost many genes that are necessary for free-living organisms (Ochman and Moran, 2001), their genomes are smaller than average: intracellular obligates are almost exclusively at the bottom left of the plot. The low-quality scores for this group of species (Fig. 4) may indicate either an increased difficulty in reconstructing their metabolic networks by automatic methods or simply the known general topological differences between their metabolic networks and those of the other prokaryotes (Ochman and Moran, 2001). These two groups of species tend to enhance the correlation between predicted annotation quality and genome size. Without these species, the correlation becomes slightly weaker (changing from 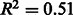to ).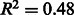

Fig. 4.

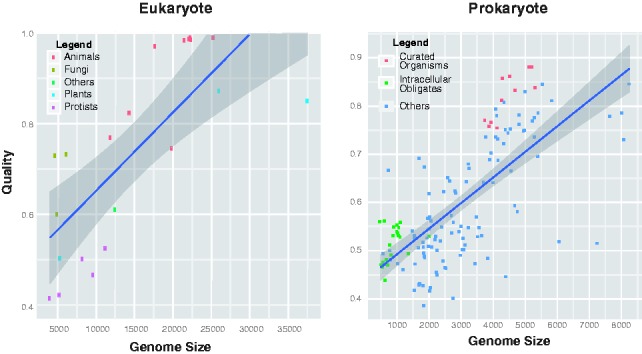
Variation of predicted annotation quality with genome size. Left: Scatter plot showing predicted annotation quality against genome size in eukaryotes: species are classified as animals, fungi, plants, protists and others. Right: Scatter plot showing predicted annotation quality against genome size in prokaryotes: orange—well-studied species (E.coli strains and the closely related species Salmonella and Yersinia); green—intracellular obligate species. The shaded region shows the 95% confidence interval for the regression line

In addition to the intracellular obligates and well-studied bacteria, the box plots in Figure 5 show the predicted annotation quality for two further sets of species: those with available manually curated genome-scale reconstructions (GENREs) (Price et al., 2004) and those that are facultatively intracellular. We can clearly see the low-quality scores in the obligate (although not the facultative) intracellular species (P = 1.16e-08) and the high accuracy scores in the well-studied species set (P = 3.06e-06). However, the extra curation possibly provided by the existence of a GENRE is not seen to be reflected in the semi-automated annotations within KEGG.

Fig. 5.

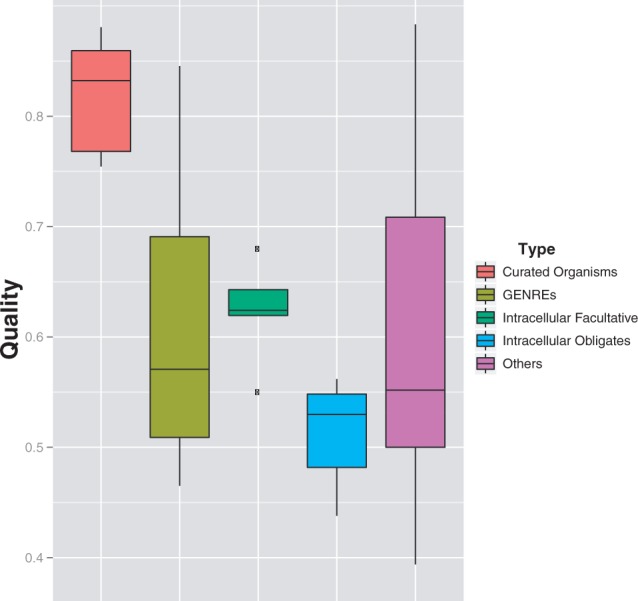
Variation of predicted annotation quality with organism type. Box plot of the distribution of quality scores in different sets of prokaryote species: orange—well-studied species (E.coli strains and the closely related species Salmonella and Yersinia); olive—species for which there is a GENRE (Price et al., 2004) available; green—facultative intracellular species; blue—intracellular obligate species; magenta—all other species

For prokaryotes, possible dependencies on other species attributes were also considered: motility, phylum, pathogenicity, oxygen requirement and habitat (Supplementary Figs S8–S12). The quality scores do not seem to depend on these attributes, with the exception of habitat: the species living in specialized habitats have lower accuracy scores compared with all other species (P = 4.33e-08). As stated earlier in the text, specialized environments may be responsible for differences in selective pressures that could result in detectable differences in metabolic network topologies.

The possible link between annotation quality and genome size was also checked in eukaryotes. As show in Figure 4, a positive correlation is present. However, closer inspection shows that there are two well-defined groups that contribute to this correlation. Towards the bottom left (small genomes, low-annotation quality) are the protists and the fungal species, and at the top right are a group of animals (mostly vertebrates) and plants. Taken together with the fact that the number of species present is small, there does not seem to be strong evidence for a direct link between genome size and annotation quality in eukaryotes.

For both eukaryotes and prokaryotes, other possible dependencies were studied, including the number of publications found in PubMed for each species and the year that the genomes considered were published. However, no significant correlations were found between the quality of the model and these factors (Supplementary Figs S15–S17).

4 CONCLUSION

Our results have demonstrated that simple topological features can be used to predict incorrect functional annotations within metabolic networks. The random forest classifier has not only achieved high overall cross-validation accuracy but has also been shown to be informative when applied to enzymes belonging to superfamilies that were not used in training. This approach is entirely independent of sequence properties; hence, it could be used to support automated metabolic reconstruction pipelines, as well as helping to identify incorrectly annotated enzymes within public databases. Subsequent improvements in the accuracy of the genome-scale metabolic models obtained will be of benefit in their downstream analysis, for example, using constraint-based methods, such as flux balance analysis (Oberhardt et al., 2009).

For both prokaryotes and eukaryotes, it seems that the quality of automated metabolic reconstruction decreases with phylogenetic distance to the major model organism for biochemistry, E.coli and human, respectively. However, differences in network topology between free-living organisms and obligate intracellular species may make the classifier less accurate when applied to the latter group of species. Given a larger amount of training data, it should be possible to produce separate classifiers for each of these two groups.

Funding: R.L. is funded by a studentship from the Fundação para a Ciência e a Tecnologia, Portugal. J.W.P. is funded by a University Research Fellowship from the Royal Society.

Conflict of Interest: none declared.