Automated Peak Detection and Matching Algorithm for Gas Chromatography–Differential Mobility Spectrometry

Abstract

A gas chromatography–differential mobility spectrometer (GC-DMS) involves a portable and selective mass analyzer that may be applied to chemical detection in the field. Existing approaches examine whole profiles and do not attempt to resolve peaks. A new approach for peak detection in the 2D GC-DMS chromatograms is reported. This method is demonstrated on three case studies: a simulated case study; a case study of headspace gas analysis of Mycobacterium tuberculosis (MTb) cultures consisting of three matching GC-DMS and GC-MS chromatograms; a case study consisting of 41 GC-DMS chromatograms of headspace gas analysis of MTb culture and media.

Today, modern analytical chemistry is dominated by the use of analytical instrumentation, e.g., coupled chromatography for data acquisition. This system is very powerful, producing multidimensional signals with rich sources of information.^1,2 In the era of rapid development of analytical instruments, gas chromatography– differential mobility spectrometry (GC-DMS) has marked another milestone for advancement in analytical methods. It is a relatively new technology where chemical substances are characterized based on differences between ion mobilities under high and low electric fields at ambient pressure.^3–6

GC-DMS has been employed in various applications such as arson investigation,⁷ environmental analysis,⁸ and disease diagnosis.^9–13 This hyphenated system produces data in the form of a matrix whose rows correspond to GC retention times, RT, and columns to DMS compensation field strength, Vc (V/cm). Usually, the GC-DMS data handling involves using a total chromatographic profile where the resultant signal cannot directly be interpreted in terms of specific chemical compounds. Recent publications also revealed another approach for analysis of GC-DMS chromatograms i.e., wavelet transforms.^14,15 Peak detection can be another alternative to the traditional approach, but it is laborious when a large volume of data is involved. In fact, peak detection procedures have received considerable attention in many other application areas such as GC-MS,¹⁶ GC-GC,¹⁷ LC-MS,¹⁸ etc. For GC-DMS, it remains unexplored and would certainly be useful for biomarker and pattern recognition study.

This paper reports an automated peak detection and matching algorithm for GC-DMS. The algorithm is demonstrated in three case studies: a simulated case study; a case study of headspace gas analysis of Mycobacterium tuberculosis (MTb) culture with three matching GC-DMS and GC-MS chromatograms; a case study of 41 GC-DMS chromatograms of headspace gas analysis of MTb culture and media.

CASE STUDIES

Case Study 1: Simulations

Case study 1 consists of 300 matrices, each representing a GC-DMS chromatogram, with dimensions 2000 (corresponding to elution times, represented by i) × 250 (corresponding to compensation field strength, represented by j) each in turn, consisting of between 10 and 40 simulated peaks (the numbers of peaks in each chromatogram being generated using a random uniform distribution).

The shape of each peak is modeled by a 2D Gaussian function

$$f({\phi }_i,{\phi }_j)=\vartheta \exp \left(-\frac{{({\phi }_i-{\phi }_{i\max })}^2}{2{\sigma }_i^2}-\frac{{({\phi }_j-{\phi }_{j\max })}^2}{2{\sigma }_j^2}\right)$$

where ν is the underlying intensity at the peak maximum; φ_imax, φ_jmax are the positions of the peak maxima in each dimension; and σ_i, σ_j relate to the width of each peak in each dimension.

The simulated data are created as follows:

1. The peak intensities, ν, are generated using a random normal distribution characterized by an underlying mean and standard deviation of 0.04 and 0.01. Because the mean is four times the standard deviation, no peaks of negative intensity are generated (in the contingency these would be replaced by 0).

2. The values of σ are obtained from an underlying random normal distribution with an underlying mean of 8 and standard deviation of 2 for RT dimension and mean of 12 and standard deviation of 3 in data points in the Vc dimension. These peaks are relatively narrow in the RT dimension compared to the Vc dimension.

3. The underlying peak maxima φ_imax and φ_jmax are obtained using a random uniform distribution between 100 to 1800 data points in the RT dimension and 80 to 200 data points in the Vc dimension.

4. Gaussian noise with a mean of 0 and a standard deviation of 0.002 in each 2D data matrix is added to each data point.

These simulated peaks were based on observed peak shapes in the experimentally obtained chromatograms.

Case Study 2: Matching GC-DMS and GC-MS

Case study 2 consists of three matching GC-DMS and GC-MS chromatograms of headspace gas analysis of Mycobacterium tuberculosis (MTb) cultures which are designated S1, S2, and S3. MTb cultures were prepared in SPME vials by inoculating BACTEC 12B media with MTb strain-2. The cultures were well-defined with a known concentration of 1 × 10⁸ bacilli/mL. The samples were incubated for 24 hours at 37 °C to allow volatiles to accumulate in the headspace of the vials. The extractions were performed for 30 min using a 50/30 μm divinylbenzene/Carboxen coating on a polydimethylsiloxane (PDMS/DVB/Carboxen) SPME fiber. The SPME fibers were purchased from Supelco Inc. (Bellefonte, PA) and the field portable SPME holder, TuffSyringe, from Field Forensics (St. Petersburg, FL). Prior to use, the fibers were conditioned as recommended by the manufacturer in the GC injector port at 250 °C for 1 h and reconditioned for 1 h in between each run to minimize carryover effects. Following extraction, all fibers were UV irradiated to prevent cross-contamination of MTb particles. During the entire process, blank fibers were exposed to the ambient atmosphere to check for extraneous volatile contamination. All fibers were reused following conditioning according to manufacturers’ instructions (1 h at 250 °C) with internal confirmation that we did not have carryover by running fibers immediately after conditioning. All fibers were used for a maximal amount of cycles according to the manufacturers’ instructions (up to 150 ×) unless they were deemed damaged by visual inspection.

In this case study, the DMS compensation field strength was scanned from −520 V/cm to +160 V/cm with an interval of 5.35 V/cm. The dimensions of GC-DMS chromatograms were 1044 (elution times) × 128 (compensation field strengths); note that we use compensation field strength^19–21 which is a common alternative to compensation voltage. The scan rate in the GC dimension was 1.297 s/scan over 22.5 min. Although both positive and negative ion spectra are available, there is limited information in the negative ion spectra, so we report only results on the positive ion chromatograms in this paper. For the matching GC-MS chromatograms, the dimensions were 7066 (elution times) × 262 (mass numbers) with a scan rate of 0.19 s/scan (0–22.5 min) over the mass range of 39 to 300.

Case Study 3: GC-DMS of MTb Cultures and Control

This case study consists of 41 GC-DMS chromatograms of which 18 were media (control) and 23 were MTb cultures. The MTb cultures were prepared using the media described of case study 2, and the media samples were control consisting of media alone. Both sets of samples were incubated for 24 hours at 37 °C to allow volatiles to accumulate in the headspace of the vials. The volatiles were extracted from the headspace of the vials by solid-phase microextraction, and further details are provided in the previous section. The aim of the MTB culture and media experiments is to be able to distinguish controls from inoculated cultures. Samples were analyzed within 5 days of extraction.

The DMS compensation voltages were scanned from −520 V/cm to +160 V/cm. The dimensions of GC-DMS chromatograms were 1044 (elution times) × 128 (compensation voltages) with a scan rate of 1.297 s/scan over 22.5 min over a compensation voltage range of −520 V/cm to +160 V/cm with an interval of 5.35 V/cm. As in case study 2, only the positive ion chromatograms are used.

The MTb and media samples were run in a randomized order. The instrumental drift and sample carryover was monitored by running a blank (22.5 min) followed by a VOC (volatile organic compound) standard (Supelco Inc., Bellefonte, PA; Supelco Inc., Bellefonte, PA) at the beginning and end of each day.

INSTRUMENTATION

All experiments were performed on a duel detector Cyro-GC system consisting of a Agilent 6890N (Agilent Technologies, Palo Alto, CA) gas chromatograph interfaced to a differential mobility spectrometer (Model SVAC-V, Sionex Corporation, Bedford, MA) and Agilent 5975 quadrupole mass spectrometer (Agilent Technologies, Palo Alto, CA). The Cryogenic Trap Enrichment System (CTE) was purchased from GERSTEL (Baltimore, MD).

GC was carried out on a Rtx-200MS (trifluoropropylmethyl polysiloxane) (Restek Corporation, Bellefonte, PA) wall-coated open tubular column (30 m × 0.32 mm i.d., 1 μm film thickness). The GC injector was operated at 250 °C. The samples were thermally desorbed in splitless mode for 2 min with a purge delay of 2 min. The front of the GC column was cooled cryogenically with liquid nitrogen to −125 °C for 2 min and ramped at 20 °C/s to 240 °C. The GC oven was programmed from 50 °C (2 min hold) increased to 170 °C (3 min hold) at 4 °C/min and then to 230 °C (3 min hold) at 20 °C/min. The GC carrier gas was helium at a flow rate of 2 mL/min. Data was acquired between 0 and 22.5 min. Data after 22.5 min was excluded because the compounds coming off at these higher temperatures were from column bleed.^22,23

A Y-connector (Restek Corporation, Bellefonte, PA) was used to split the column eluent to MS and DMS. The MS operated under vacuum pressure but the DMS operated at atmospheric pressures, so care was taken to ensure the analyte reach both detectors simultaneously by adjusting the length of the transfer lines from the Y-connector. To account for the differences in operating conditions, the total length of the transfer line from the Y-connector to the MS and DMS was 0.5 and 1 m, respectively. A differential mobility spectrometer with an electrode gap of 0.5 mm was used as the GC detector. The DMS was operated at a dispersion voltage of 22 kV/cm. The compensation voltage was scanned over a range of −520 to +160 V/cm with a step duration of 10 ms and a 2 ms step settle time. The scan duration was 1.297 s. The makeup drift gas for the DMS was nitrogen at a flow rate of 400 mL/min. The DMS sensor was operated at 85 °C. The part of the transfer gas line that was exposed to the atmosphere was heated to 180 °C to prevent sample condensation along the line. The mass spectrometer was equipped with an electron impact ionization source operated at 150 °C. The quadrupole was operated at 230 °C.

The GC-DMS data in Excel worksheets was converted to Matlab version 7.0 (The Mathworks, Inc., Natick, MA) into data matrices with rows correspond to GC retention times (RT) and columns to DMS compensation voltages (Vc). The matching GC-MS chromatograms in netcdf format were converted to Matlab version 7.0 (The Mathworks, Inc., Natick, MA) as matrices with dimensions 7066 × 262 with a scan range of m/z 39 to 300 and a scanning rate of 0.19 s/scan. The GC-MS chromatograms were subjected to the automated peak detection algorithm reported by Dixon et al.¹⁶

All software in this paper was developed in-house in Matlab.

DATA ANALYSIS

Peak Detection

A table of notation is presented in Table 1 listing the symbols and variables used in this paper. The schematic of the overall peak detection algorithm is illustrated in Figure 1.

Table 1.

Notation

variables/symbols	description
	Preprocessing
Vc	compensation field strength
RT	retention time
X (I×J)	matrix representation of a chromatogram
U (I×J)	matrix of baseline corrected and aligned data
D (I×(J–4))	matrix of Savitzky-Golay first derivative of U, horizontally
E ((I–4) J)	matrix of Savitzky-Golay first derivative of U, vertically
I	number of scans in a chromatogram
J	number of compensation field strength channels in a chromatogram
N	number of samples
C	number of variables in an unfolded data matrix
	Peak Detection
t i × a	threshold at RT i
a	peak noise factor
m	position of the peak start in Vc dimension
r	position of the peak maximum in Vc dimension
s	position of the peak end in Vc dimension
g	position of the peak start in RT dimension
h	position of the peak end in RT dimension
Y (P × Q)	peak detail table
P	number of peaks detected in the entire voltagram
Q	characteristics of peaks found (peak start, peak maximum and peak end from RT and Vc dimension)
	Peak Merging
ϕ	overlap ratio
p	overlap region (in data points)
q 1	length of the target peak
q 2	length of the candidate merging peak
K init	yij – ycj (where i = 2;c = 1 and j = 1)
W	matrix recording the one-dimensional features of a 2D peak
Z (R × S)	peak region table
β1, β2,.. ., β7	peak maximum of each voltagram for example in Figure S-3, Supporting Information
δ	mean difference of a 2D feature
ω	number of 1D peaks forming a 2D feature
	Peak Matching
L (T × G)	matrix containing peaks in dimensions detected in all samples
T	the number of unique peaks detected
G(G = 4)	characteristics of each peak (origin of peak (indicates by 1,.. ., n), RT, Vc, and peak area
H	peak table (rows corresponding to variables and columns to samples)
F	matrix recording the RT and Vc of each unique peaks
V 1	tolerance window of RT (data points)
V 2	tolerance window of Vc shift (data points)
	Simulations
ν	underlying intensity at the peak maximum
φimax,φjmax	positions of the peak maxima in each dimension
σi, σj	width of each peak in each dimension

Figure 1.

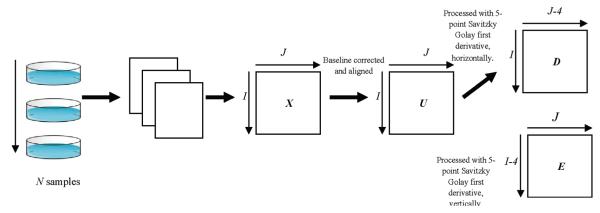
Peak detection overview.

Baseline Correction

The original matrix, X of dimensions I × J where I refers to retention time scans (RT dimension) and J to voltage scans (Vc dimension), is baseline corrected and aligned yielding a matrix U. For baseline correction, each column vector x_j is divided into windows of 100 points and 10% intensity quantile of each window is determined. These points are then modeled with Piecewise Cubic Hermite Interpolating Polynomial (PCHIP) function.²⁴ The baseline is then subtracted from the data.

Alignment

The peak alignment procedure is based on that described by Krebs et al.;²⁵ the details are not discussed for brevity. In summary, a reference chromatogram is chosen automatically using discrete coordinates simplex-like optimization routines;²⁶ the remaining chromatograms are aligned according to the reference. This procedure aligned data in two dimensions using a rigid shift in the Vc dimension, allowing a flexible shift in RT dimension. The data is shifted based on the maximum cross-correlation value for Vc dimension, and the RT dimension is aligned with respect to the reference by identifying the common landmarks (found in both sample and reference) and interpolating according to piecewise linear function. The resulting matrix, U, is subjected to further analysis.

Detecting Features in Each Voltagram

The key to feature detection is to find features at each voltagram obtained at each RT scanned. Matrix U is first processed with a quadratic Savitzky-Golay 5-point first derivative filter,^27,28 both horizontally and vertically, producing matrices D and E of dimensions (I × (J – 4)) and ((I – 4) × J), respectively. The next step involves computing a value, t, at each RT i by taking the average absolute change of derivative over the trace as follows.²⁹

$$t_i=\frac{\sum _{j=1}^{J-3}\mid d_{\mathit{ij}}-d_{i(j+1)}\mid }{J-4}$$

The first step of peak detection is to identify potential features in each voltagram at individual RT.

1. The peak detection algorithm examines each row, i, of matrix D in turn. For each vector, the algorithm proceeds iteratively one point at a time from j = 2,.. .,(J – 3). A feature start is identified when (d_ij > 0), (d_i(j+1) > d_ij), and (d_ij > t_i a): t_i is defined as above, and a is a user-defined peak noise factor. The threshold at RT i is t_i × a. The peak start is denoted by j = m. The variable a is a tunable noise level multiplier used to determine the potential signal threshold: in this paper, a is set at 5. Only peaks whose intensity are a-fold more than t_i are detected; some features in row vectors of matrix D might be rejected especially those at the edges of a two-dimensional peak.

2. Next, the algorithm searches for a maximum for each feature; the maximum satisfies both (d_ij < 0) and (d_i(j+1) < 0), defined by j = r. For a perfect peak shape, the center corresponds to the zero-crossing point in the derivative where the signal crosses the x-axis going from positive to negative (d_ij = 0).

3. The algorithm continues to detect the end of the feature which is found when (d_ij > 0) and (d_i(j+1) > 0). At the end of feature, j = s.

4. The maximum of the peak between the start and the end is determined; the number of data points the maximum is away from s is given by M (equivalent to the left half width of the peak).

   Each potential peak (or feature) detected in the voltagram is a candidate to be part of a true 2D peak which should consist of several features at successive RTs.

   In order to determine whether this feature is a component of a true peak or an artifact, there must be a corresponding feature in the chromatographic dimension at column variable j = r. The algorithm then searches for features in the chromatographic dimension using matrix E. The aim is to take each feature in row i corresponding to a single data point to see whether there is a corresponding feature in the second dimension. If so, this feature is potentially part of a 2D peak, whose start and end in the RT dimension can be defined.

5. The next stage of the algorithm is to locate the feature start and end in the RT dimension. The row variable i is denoted by u. The start is characterized by (e_ur > 0) and (e_(u–1)r < 0) where u = i – 1,i – 2,.. .2 and the end is the point where (e_ur < 0) and (e_(u–1)r > 0) where u = i + 1,i + 2,.. .I – 3. The positions of the start and end (RT dimensions) are denoted by g and h, respectively. If a feature is not found, the candidate peak is rejected.

6. If the candidate feature is accepted, the algorithm continues to search for another peak start in the voltagram at RT, i, from position j = s until j > (J – 3).

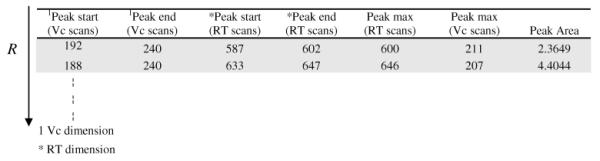
7. The positions of feature start, maximum, and end determined from both dimensions are presented in a ‘peak detail table’, Y = a matrix of dimensions (P × Q) where P is the number of features found over the entire voltagram and the columns (Q = 7) describe the characteristics of the features (Table 2). Note that at this stage all that has been done is to identify which features in each RT voltagram are part of potential peaks and to identify the start and end (in time) for each of these features.

Table 2.

Example of Feature Detail Table, Y: Two Peaks Are Illustrated (the values are data points in the Vc and RT dimensions)^a

row vector, i	peak start, mb	peak max, rb	peak end, sb	peak start, gc	peak end, hc	peak intensity
599	193	212	240	586	599	0.0465
600	192	211	238	587	600	0.0481
601	191	210	242	587	601	0.0481
602	191	210	242	587	602	0.0443
603	194	212	241	586	603	0.0395
604	191	211	234	587	604	0.0316
605	195	207	240	587	605	0.0183
644	187	207	241	633	644	0.0715
645	188	207	237	633	645	0.0793
646	188	207	240	633	646	0.0841
647	188	208	239	633	647	0.0796
648	191	210	238	633	648	0.0534
649	192	211	240	633	649	0.0216

^aThe peaks separated by a horizontal space indicate a peak in dimensions. The italic cells are selected and transferred onto peak region table, Z, indicating the border of a peak in dimensions.

^bVc dimension.

^cRT dimension.

The peak detection algorithm is illustrated in Supporting Information Figure S-1.

Peak Merging

The next step is to put together features at successive RTs to obtain a 2D peak characterized by a region in both dimensions. The peaks list in Y are one-dimensional peaks which do not yet represent peaks in two dimensions; a peak merging algorithm is used to cluster the peaks into respective regions.¹⁷ The peak merging algorithm produces a ‘peak region table’ (Table 3), Z (R × S) where R denotes the number of 2D peaks and S = 7.

Table 3.

An Example of Peak Region Table, Z

8. The peak merging algorithm compares the first feature (y_c where c = 1) with the next, the second lists in Y (y_i where i = 2).

9. The first feature is a ‘target’ suggesting a start of a peak in the RT dimension. A true peak consists of several features at successive RTs. The algorithm searches for features eluting at successive RTs after the target. If the difference between y_ij and y_cj (j = 1) is ≤ K_init (initially set to 2), this implies that the features are found at successive RTs and can be merged to form part of a 2D peak (in Table 2, for example, (y_ij – y_cj) = 600 – 599). The parameter for finding the neighboring features, K_init, begins from 2 (data points) as some features at the edge could be missed during peak detection when noisy chromatograms are involved.

10. Some features may be found at successive RTs; however, they do not represent the same 2D profile. For example, a target is found at row 100 (RT data point) eluting between columns 120 and 130 in the Vc dimension and a successive feature at row 101, between columns 200 and 210, although adjacent in rows are well apart in the Vc dimension suggesting they originate from two different peaks. For this reason, it is necessary to confirm whether features found at successive RTs are from the same two-dimensional profile using the overlap ratio, ϕ. The overlap ratio is calculated as p/[(q₁ + q₂)/2] where q₁ and q₂ are the length (in data points) of the target and the candidate merging peak while p is the overlapping region. The calculation is modified from that reported by Peters et al.¹⁷ (overlap ratio = p/q₁). The stability of the algorithm is believed to be improved with the modification. As an example, two peaks in the Vc direction eluting at different RTs are compared, the top (high RT) one between data points 1–10 and the bottom (low RT) between data points 6–11. According to Peters’s equation, the top-to-bottom configuration yields an overlap ratio of 5/10 but the bottom-to-top configuration is 5/6. The overlap ratios for both configurations are reasonably different. With the modified calculation, the overlap ratios from both directions are maintained at 5/8; in addition, the overlapping region is compared to an average peak rather than relying completely on the edge peak. In this paper if ϕ ≥ 0.7, the peaks are considered to originate from the same 2D peak and are merged.

11. The algorithm next constructs a matrix, W, to record the one-dimensional features that represent the same 2D profile, in this case, row vectors y_c and y_i are the input of W. Row vector y_i is then discarded from Y.

12. The comparison is performed with a new y_i where i = 2 and K_init = K_init + 1. For every successive RT, the data point that satisfies the neighboring and overlap criteria, y_i is added to matrix W and is subsequently discarded from Y; K_init is increased by 1 each time. If the neighboring criterion is not obeyed, the algorithm continues to search for peaks in Y that is characterized by a higher row, maintaining the value of K_init. If no further feature is found that can merge with a target, a 2D peak is considered fully described in both dimensions.

13. The algorithm then evaluates matrix W to determine the edges of the 2D peak. The limits of the peak are reported as the median of the one-dimensional features (starts and peak ends) forming the 2D peaks in both Vc and RT dimensions. The peak maximum is designated as the data point with the highest intensity within a peak region, and the peak area is reported as the sum of intensities for all data points within a peak region. An example is presented in Table 2 and Table 3 where two peaks are obtained from the peak detail table, Y, and the peak regions are recorded in the peak region table Z.

14. The target y_c is discarded from Y. A new y_c is used as a target and K_init is reset to 2.

15. Matrix Y is reduced until all peaks are assigned to their respective two-dimensional profiles.

The flow diagram of the peak merging algorithm is depicted in Supporting Information Figure S-2.

In order to protect against an atypical edge, each peak in the peak detail table, Y, is evaluated from both ends: top-to-bottom and bottom-to-top (in the RT dimension). For each configuration, the mean differences in Vc are calculated for all 2D peaks found. Supporting Information Figure S-3 illustrates a sample consisting of seven one-dimensional peaks where the peak maximum of each voltagram is denoted by β₁ to β₇. The peak merging algorithm finds two features when the peak detail table is examined from top-to-bottom; the reverse configuration (bottom-to-top) however identifies three features. The mean difference for each 2D feature (only those involving more than one one-dimensional peak), δ, is calculated as

$$\delta =\frac{\sum _{j=1}^{\omega -1}\mid {\beta }_j-{\beta }_{j+1}\mid }{\omega -1}$$

where ω is the number of one-dimensional features forming a 2D peak. The overall mean differences for both configurations are compared; the configuration that gives the lower overall mean difference is preferred.

Peak Matching

The third step is to determine which peaks in different DMS analyses originate from the same compound. This is done by seeing whether RTs and Vcs of successive peaks are within a given tolerance window, and if so, they are considered to have the same chemical origin.

For N samples, the algorithm above results in creation of N peak region tables, Z. To determine the number of unique peaks over all samples, a peak matching algorithm is applied.

16. Each peak in each sample is characterized by its RT and Vc in scan numbers.

17. Peaks found in all samples are extracted onto a matrix, L (T × 4 where T is the total peaks found over all N samples). The first column represents the origin of the peak according to sample 1,.. ., N, columns 2 and 3 detail the RT and Vc of the peak maxima, and the last column details the peak area.

18. Matrix L is sorted according to RT (column 2) in ascending order.

19. A sparse matrix, H with N columns is constructed and the tolerance window of the RT and Vc, V₁ and V₂, are determined.

20. The first peak in L is compared to the subsequent peaks found in different samples, i.e., the first peak in L is found in sample 1, the second and the third peaks are detected in samples 2 and 1, respectively. The algorithm compares the first peak with the second peak but comparison with the third is ignored.

21. Peaks differing within the allowable windows are considered originating from the same source and the peak area are placed in matrix H at columns corresponding to the sample number. The average characteristics RT and Vc are recorded in matrix F.

22. If more than one candidate matching peak from a sample is detected, the algorithm selects the one that has closer Vc and RT relationship to the target peak.

23. When relevant peaks are matched, the target peak and the matching peaks are removed from L. The algorithm repeats with a new target peak listed in L (i = 1) until all peaks are matched. Matrix H is transposed to give a peak table. This method finds matching peaks according to an ordered list of L.

The peak table H is of dimensions N × M where M is the number of detected peaks. All case studies are subjected to peak detection with the tunable parameters a = 5; K_init = 2 and ϕ = 0.7. For case study 3, the tolerance window of RT and Vc, V₁ and V₂, are 20 scans (25.94 s) and 7 scans (37.45 V/cm), respectively.

Unfolding

The unfolding method³⁰ is used to compare the 2D peak table obtained from the 41 = N samples of case study 3 with the raw GC-DMS chromatographic profiles. This method is conventionally used for analysis of GC-DMS chromatograms. In this study, each chromatogram is baseline corrected as discussed in Baseline Correction, and the negative values attributable to instrumental noise are replaced with 0s at the outset. Small misaligments by a few data points can have adverse consequences for pattern recognition, so it is usual to average the intensity over a small window of data points, called a bucket, to remove the influence of small RT shifts. The bucketed time window was varied between 5 and 30 scans, and the window that gives the best separation PCA scores plot was considered optimal and found to be 25 data points. The chromatograms are then bucketed in the RT direction at a window of 25 data points (32.43 s) and column-centered prior to formation of the 3D array (the 42nd bucket consisting of data points 1026 to 1044). After that, the three-dimensional array is unfolded into a 2D matrix, denoted B which is of dimensions N × C or 41 × 5376 where 5376 = 128 (Vc) × 42 (RT buckets) = C or the number of columns in the unfolded data matrix.

RESULTS AND DISCUSSION

Case Study 1

The algorithm was applied to 300 simulated data matrices. A graph of the number of peaks detected using the algorithm versus the underlying number of peaks in each simulation is presented in Figure 2a and has a correlation coefficient squared of 0.966. Figure 2b is of the estimated peak intensity versus the true peak intensity for all peaks that were correctly detected using the algorithm and the correlation coefficient squared obtained is 0.927. The maximum difference in number of peaks detected, $\mid (R-\widehat{R})\mid$, is 9 and the minimum difference is 0 peaks with the mean difference being 2.21 peaks. The mean of all true peak intensities is 0.0416, and the root mean square (RMS) error in the estimation of the intensity is 0.0045, corresponding to 10.82% of the overall mean.

Figure 2.

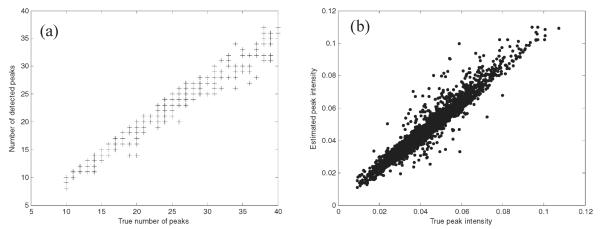
(a) Number of detected peaks versus the true number of peaks. (b) Estimated peak intensity versus the true peak intensity for simulations of case study 1.

A DMS analyzer often has a limited resolving power in comparison with MS; the peaks are generally broad and overlapped. Nevertheless, the performance of the peak detection algorithm is comparable to the algorithm reported by Dixon et al.¹⁶ for GC-MS where the correlation coefficient squared between the estimated numbers of peaks versus the true number of peaks reported is 0.9025.

Case Study 2

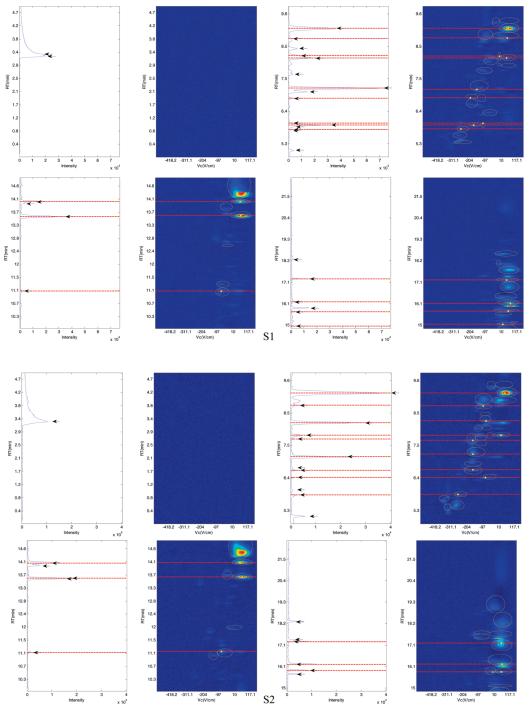
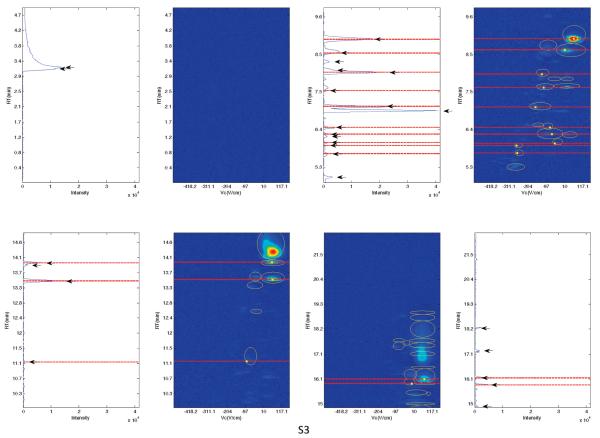
In this case study, we compare the peaks detected using GC-MS and GC-DMS. For GC-DMS, the identities of the compounds found at specific RT and Vc cannot be identified without the use of standards. It is anticipated that there will be peaks detected in common using both techniques,³¹ but due to the different detectors we do not expect to be able to detect all peaks by both methods. Peaks of GC-MS and GC-DMS with a RT difference of less than 10 s were matched for each individual sample. The topological plots of S1, S2, S3 and the total ion chromatograms (TIC) of GC-MS are shown in Figure 3 between 0 and 22.5 min with red dashed lines indicating the matching peaks using a 10 s RT shift criterion. For the GC-DMS chromatograms, the peaks identified with our algorithm are circled in yellow; the centers of the peaks matched with the MS analysis are in addition marked with filled yellow circles representing the positions of the peak maxima. For MS chromatograms, the peaks detected are indicated using black arrows.

Figure 3.

The topological plots of S1, S2, and S3 with the TIC of the matching GC-MS chromatograms where the dashed lines indicate the matching peaks using a 10 s tolerance.

Visual observation suggests that the algorithm described above can effectively identify peaks eluted in the GC-DMS chromatograms, with most of the peaks detected in GC-MS chromatograms also detected using GC-DMS. Nevertheless, there are some unmatched unique peaks using both DMS and MS detectors, suggesting differences in detection abilities between detectors. DMS offers resolution in the compensation voltage dimension so that compounds eluting at similar RTs with differing Vc can be distinguished; this is a consequence of formation of multiple ion peaks as a result of fragmentation of parent molecules or clustering of ionized species.⁹ However, it is observed that peaks detected using MS at earlier RTs (<5 min) are not found in the DMS chromatograms. Subsequent analysis of the MS data revealed that early eluting compounds are less susceptible to detection using DMS, as these compounds with low proton affinity could exhibit low spectral intensity.^8,32

Case Study 3

The peak detection algorithm can be tested on case study 3 by seeing whether the MTb culture samples can be distinguished from the media samples, using a peak table, and how this offers an advantage over the using of unfolded (raw) data.

Shuffling

The algorithm produces a peak table of dimensions 41 × 102 with the rows corresponding to samples and columns to variables. The repeatability of the peak table is assessed by shuffling the original order of the chromatograms and performing the peak matching on newly shuffled data. The shuffle test is used to see how close the peak table of the shuffled data correspond to that of the unshuffled data. In addition, it can be used to demonstrate that target peaks are extracted irrespective of the order of the list.¹⁶ In this study, the list of peaks is shuffled for 100 iterations and is subjected to independent peak matching. Using the original order of the GC-DMS chromatograms, 102 unique peaks are detected. When changing the order, the mean number of peaks detected is 100, suggesting that the order of the chromatograms is not significant. This is an important test of the robustness of the algorithm.

Principal Components Analysis

When using a peak table, H, the data is square rooted and the columns of the data matrix are standardized. Square rooting aims at reducing the influence of elements with high concentrations and to deal with the heterosedastic noise.^33–35 Standardization however ensures that each variable (representing a chromatographic peak) has a similar influence.³³ Standardization involves mean centering and diving by the population standard deviation.^33,36,37 The unfolded data matrix B is column centered but not standardized or square rooted. These choices are made by visual examination of the PC scores plot.

Principal component analysis (PCA) is performed using the NIPALS algorithm,^38,39 decomposing the data into scores T of dimensions N × A and loading matrices P of dimensions A × M or A × C (unfolded data matrix) and A is the number of PCs. For graphical visualization in 2D, we set A = 2.

The scores plot (Figure 4a) demonstrates that MTb and media samples can be distinguished using the peak table where four media samples are likely to be misclassified. The scores plot of the unfolded data matrix however indicates that MTb and media samples are less distinguishable because peaks of GC-DMS are often broad and overlapped (Figure 4b):⁴⁰ unfolding the entire chromatographic profile could result in mismatching RTs between chromatograms, as they are not stable, whereas peak picking takes this problem into account.

Figure 4.

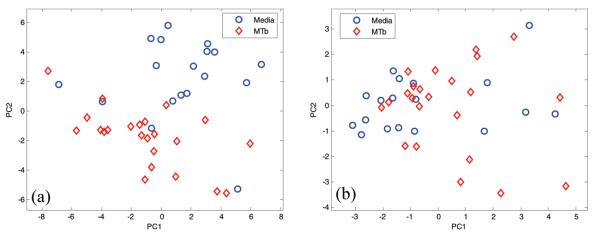
The scores plots of PC2 against PC1 for case study 3, with samples indicated according to groups (MTb cultures and media) for (a) peak table and (b) unfolded data matrix.

CONCLUSIONS

Peak detection (and integration) is one of the key steps in the analysis process especially in metabolomic studies.⁴¹ As illustrated in Figure 3, the algorithm is able to detect most of the characteristic peaks, but there are limitations dependent on the choice of tunable parameters as follows.

The number of detected peaks is dependent on correct choice of the detection threshold, t_i × a. If a is too low, there may be some false positives, whereas a high value can lead to false negatives. The peak detection method is based on the first derivative. Hence, problems may arise with closely eluting peaks, especially when there is only a shoulder between two coeluting peaks. In addition, the peaks are relatively narrow along the time axis. If a chromatographic peak is only represented by 3–5 data points in the RT dimension, it will not be recognized: this is because a peak identified in the Vc dimension is confirmed as a true peak only if a corresponding feature is found in the RT dimension.

Also, the one-dimensional peaks identified in both dimensions are merged to represent a two-dimensional feature based on the overlapping ratio, ϕ. A low value of this ratio may result in two overlapping peaks to be identified as a single 2D feature.

Third, there is a risk of mismatching if the tolerance shifts V₁ and V₂ are not chosen carefully, as these reflect the user’s estimate of how peak positions shift in the chromatogram.

As in almost all published approaches, the performance of the peak detection method is parameter dependent. The limitations of the two-step peak detection method (detecting peaks in a one-dimensional form and merging the peaks to represent a two-dimensional feature) are further described by Vivó-Truyols and Janssen.⁴² Although automated peak detection methods are rarely as effective as visual identification of peaks, the increase in the size of analytical data often makes manual investigation infeasible. When complex chromatograms are analyzed, the number of peaks can easily exceed thousands. If there are 100 peaks in 50 chromatograms, this would involve 5000 visual checks which at 5 min per check would take a total of 416 h, hence the need for automated methods.

Although there have been recent reports of using GC-DMS in the literature,^7–10,12 these primarily involve looking at whole profiles rather than individual peaks. In this paper, we have reported an automated peak detection and matching algorithm which we demonstrate on three case studies. The method demonstrates promising efficiency on the simulated case study. The parallel setup further allows verification of the algorithm; the results suggest that peaks can be effectively identified in the GC-DMS chromatograms and most of them are also detected using GC-MS despite some differences in detection abilities between detectors. The peak detection algorithm is automated, allowing pattern recognition study where necessary.

GC-DMS has a great potential to be used for disease diagnosis, offering a more cost-effective alternative to GC-MS. The availability of an automated approach for deconvoluting the GC-DMS chromatograms would allow automated interpretation of the data if the technique is used in routine field analysis.