Abstract
Many cellular stress-responsive signaling systems exhibit highly dynamic behavior with oscillatory features mediated by delayed negative feedback loops. What remains unclear is whether oscillatory behavior is the basis for a signaling code based on frequency modulation (FM) or whether the negative feedback control modules have evolved to fulfill other functional requirements. Here, we use experimentally calibrated computational models to interrogate the negative feedback loops that regulate the dynamic activity of the transcription factor NF- B. Linear stability analysis of the model shows that oscillatory frequency is a hard-wired feature of the primary negative feedback loop and not a function of the stimulus, thus arguing against an FM signaling code. Instead, our modeling studies suggest that the two feedback loops may be tuned to provide for rapid activation and inactivation capabilities for transient input signals of a wide range of durations; by minimizing late phase oscillations response durations may be fine-tuned in a graded rather than quantized manner. Further, in the presence of molecular noise the dual delayed negative feedback system minimizes stochastic excursions of the output to produce a robust NF-
B. Linear stability analysis of the model shows that oscillatory frequency is a hard-wired feature of the primary negative feedback loop and not a function of the stimulus, thus arguing against an FM signaling code. Instead, our modeling studies suggest that the two feedback loops may be tuned to provide for rapid activation and inactivation capabilities for transient input signals of a wide range of durations; by minimizing late phase oscillations response durations may be fine-tuned in a graded rather than quantized manner. Further, in the presence of molecular noise the dual delayed negative feedback system minimizes stochastic excursions of the output to produce a robust NF- B response.
B response.
Author Summary
Many signaling events are controlled by negative feedback circuits: as a result they are highly dynamic and in some cases show oscillations The presence of oscillations has led to the hypothesis that signaling pathways convey information about the stimulus via the frequency of oscillations and spikes of activity, analogous to frequency modulated (FM) radio signals. One such signaling protein is NF-kB which controls the inflammatory and immune response to cytokines and pathogens. We show here that the topology of the negative circuit does not allow for frequency modulation by the signaling input. Instead, we show that a second negative feedback circuit may be tuned to dampen the oscillations. In fact, the resulting dual negative feedback motif allows for better tracking of the duration of the incoming signal than the single negative feedback circuit, as well as better buffering of noise present in the incoming signal. Thus we propose that the negative feedback topology has evolved to provide complex dynamics of NF-kB in vertebrate animals and not for the purposes of oscillations.
Introduction
Many important signal transduction pathways contain a negative feedback motif consisting of an activator that activates its own repressor. Activated repression is capable of generating oscillatory behavior [1] and has been observed to do so in biological systems such as the Hes1 regulatory protein which controls neuronal differentiation [2], the p53-Mdm2 system that mediates the DNA damage response [3], and the NF- B (Q04207) signaling network that governs the immune response and inflammation [4], [5].
B (Q04207) signaling network that governs the immune response and inflammation [4], [5].
The role of activated repression is well understood in the context of transient signaling as functioning to limit the duration of the induced activity. Indeed, misregulation of the negative feedback mechanisms that control NF- B and p53 has been shown to generate prolonged inflammatory or genotoxic stress responses, respectively, that lead to cell death or chronic disease [6], [7]. Further, negative feedback can sensitize and speed-up responses to weak or transient input signals [8] when compared to constitutive attenuation mechanisms.
B and p53 has been shown to generate prolonged inflammatory or genotoxic stress responses, respectively, that lead to cell death or chronic disease [6], [7]. Further, negative feedback can sensitize and speed-up responses to weak or transient input signals [8] when compared to constitutive attenuation mechanisms.
In contrast, the physiological role of oscillatory signaling behavior remains poorly understood. Recent work has shown that, in the calcium stress pathway in yeast, the frequency of nuclear localization of a stress-response transcription factor can be modulated by the magnitude of the extracellular calcium concentration, and this frequency modulation results in a coordinated expression of target genes [9]. In the NF- B and p53 signaling systems, the function of oscillations is still unknown. Oscillations in p53 activity were proposed to represent a counting mechanism that quantizes the response, ensuring a robust but appropriate amount of activity for a specific degree of DNA damage [10]. An alternate view was proposed in which oscillations of the p53-controlling ATM kinase activity allow for periodic sampling of the damaged DNA to track its repair and, if necessary, drive further p53 signaling to sustain the repair programs [11]. Oscillations in NF-
B and p53 signaling systems, the function of oscillations is still unknown. Oscillations in p53 activity were proposed to represent a counting mechanism that quantizes the response, ensuring a robust but appropriate amount of activity for a specific degree of DNA damage [10]. An alternate view was proposed in which oscillations of the p53-controlling ATM kinase activity allow for periodic sampling of the damaged DNA to track its repair and, if necessary, drive further p53 signaling to sustain the repair programs [11]. Oscillations in NF- B activity were proposed to determine which genes would be transcriptionally induced, thereby representing a temporal code that conveys information about the stimulus to gene promoters [5]. However, it is not clear whether or not the frequency encodes information in this systems as no differences in NF-
B activity were proposed to determine which genes would be transcriptionally induced, thereby representing a temporal code that conveys information about the stimulus to gene promoters [5]. However, it is not clear whether or not the frequency encodes information in this systems as no differences in NF- B target gene expression were observed between oscillating and non-oscillating genetic variants [12].
B target gene expression were observed between oscillating and non-oscillating genetic variants [12].
Recent work has demonstrated that oscillations in NF- B activity can be generated by pulsatile stimulation with TNF
B activity can be generated by pulsatile stimulation with TNF (P06804) [13]. However, an analysis of the repeated activation of NF-
(P06804) [13]. However, an analysis of the repeated activation of NF- B that is driven by an oscillating signal provides little information about the role of oscillations that naturally arise with persistent stimulation. Thus, the role(s) of oscillations in NF-
B that is driven by an oscillating signal provides little information about the role of oscillations that naturally arise with persistent stimulation. Thus, the role(s) of oscillations in NF- B activity remains unclear and several questions are still unanswered: Do these oscillations convey information encoded in the frequency to downstream processes? Do they function to generate a periodically recurring phase of sensitivity to stimuli or regulatory crosstalk representing a potential “counting” mechanism? Do they “quantize” the output signal, thus specifying robust units of activity? Or, are the oscillations caused by persistent signaling simply a non-functional by-product of the requirement for the negative feedback architecture to enable sensitive, fast responses to transient stimuli?
B activity remains unclear and several questions are still unanswered: Do these oscillations convey information encoded in the frequency to downstream processes? Do they function to generate a periodically recurring phase of sensitivity to stimuli or regulatory crosstalk representing a potential “counting” mechanism? Do they “quantize” the output signal, thus specifying robust units of activity? Or, are the oscillations caused by persistent signaling simply a non-functional by-product of the requirement for the negative feedback architecture to enable sensitive, fast responses to transient stimuli?
Mathematical models comprised of a small number of equations have led to a greater understanding of biological processes in terms of molecular interactions, diffusion, dose responses, gradient sensing, the role stochasticity in gene expression and in fate decisions [14]–[17]. Although several models of networks with autoregulation have been developed [18]–[20], most of these networks do not incorporate delays. In signaling, however, such elegant models often do not faithfully reproduce the dynamic behavior of the signaling system because actual biological networks involve many molecular interactions that tend to slow overall signal processing. Larger models comprised of many molecular species and parameters have proven useful in exploring dynamic signaling behavior via computational simulations in conjunction with experimental studies, but they are analytically intractable and therefore do not provide the degree of conceptual insights that small models do.
Here we pursue an alternative approach to modeling NF- B signaling. We construct a new model that replaces cascading reactions with a single but delayed compound reaction that enables both recapitulation of experimentally observed dynamics and the use of powerful analytical tools. With these tools, we explore the physiological function of the dynamic behavior of NF-
B signaling. We construct a new model that replaces cascading reactions with a single but delayed compound reaction that enables both recapitulation of experimentally observed dynamics and the use of powerful analytical tools. With these tools, we explore the physiological function of the dynamic behavior of NF- B produced by the activated repression mechanism mediated by its inducible inhibitors, I
B produced by the activated repression mechanism mediated by its inducible inhibitors, I B
B (Q9Z1E3) and I
(Q9Z1E3) and I B
B (O54910). The mathematical analysis results in predictions that are addressed experimentally and thus lead to fundamental insights about the function and origins of this signaling system.
(O54910). The mathematical analysis results in predictions that are addressed experimentally and thus lead to fundamental insights about the function and origins of this signaling system.
Results
NF- B model formulation
B model formulation
The basic structure of the NF- B signaling module is shown in Figure 1 A
[4]. In resting cells, NF-
B signaling module is shown in Figure 1 A
[4]. In resting cells, NF- B is sequestered in the cytoplasm by I
B is sequestered in the cytoplasm by I B proteins. Cellular stimulation leads to activation of the I
B proteins. Cellular stimulation leads to activation of the I B kinase (IKK) which phosphorylates I
B kinase (IKK) which phosphorylates I B proteins thus targeting them for degradation. Upon degradation of I
B proteins thus targeting them for degradation. Upon degradation of I B proteins, NF-
B proteins, NF- B moves into the nucleus and activates hundreds of target genes including the predominant I
B moves into the nucleus and activates hundreds of target genes including the predominant I B isoform, I
B isoform, I B
B . Synthesized I
. Synthesized I B
B enters the nucleus, binds to NF-
enters the nucleus, binds to NF- B, and the I
B, and the I B
B -NF-
-NF- B complex is exported back to the cytoplasm. Thus, the core feature of the NF-
B complex is exported back to the cytoplasm. Thus, the core feature of the NF- B signaling module is a negative feedback loop mediated by I
B signaling module is a negative feedback loop mediated by I B
B . This can be abstracted to a simple motif in which
. This can be abstracted to a simple motif in which  (NF-
(NF- B) activates
B) activates 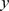 (I
(I B
B ),
),  represses
represses  , and repression of
, and repression of  by
by 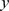 is relieved by
is relieved by  (active IKK) (Figure 1B
).
(active IKK) (Figure 1B
).
Figure 1. Oscillatory behavior from a system with a single negative feedback loop.
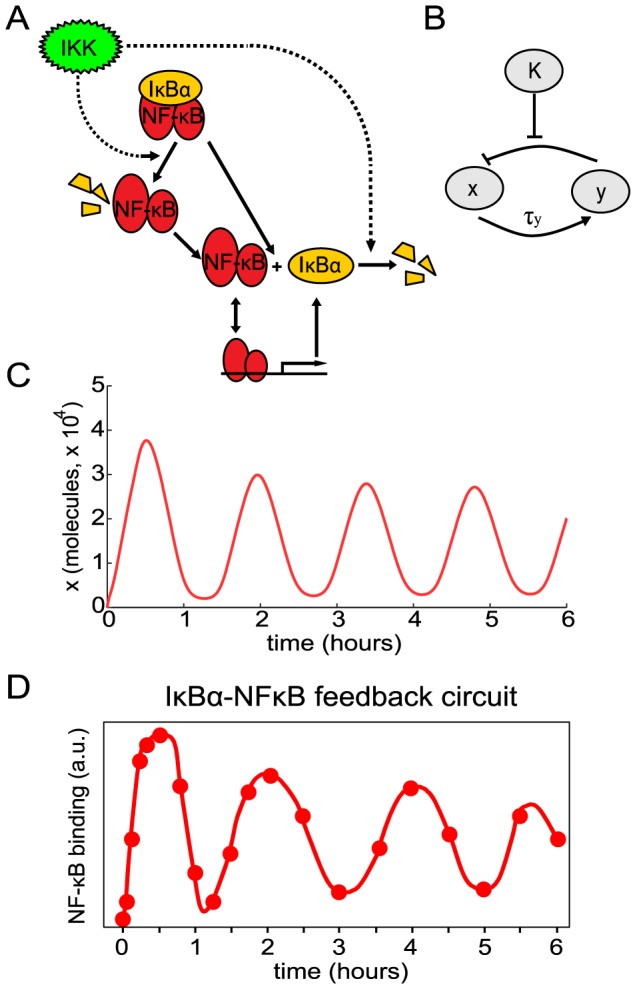
(A) Diagram of the I B
B - NF-
- NF- B signaling module. (B) Diagram of a system with a single delayed negative feedback loop. (C) Nuclear NF-
B signaling module. (B) Diagram of a system with a single delayed negative feedback loop. (C) Nuclear NF- B levels (
B levels ( ) in response to persistent stimulation as a function of time produced using our delayed feedback model. (D) Experimental levels of nuclear NF-
) in response to persistent stimulation as a function of time produced using our delayed feedback model. (D) Experimental levels of nuclear NF- B (determined by EMSAs) in cells with only the I
B (determined by EMSAs) in cells with only the I B
B -mediated negative feedback loop intact (data from [4]).
-mediated negative feedback loop intact (data from [4]).
Using this motif as a guide, we formulated our model of the I B
B -mediated NF-
-mediated NF- B response as a set of 9 reactions and 6 variables (Tables 1, 2). Specifically, the model assumes that the total number of the NF-
B response as a set of 9 reactions and 6 variables (Tables 1, 2). Specifically, the model assumes that the total number of the NF- B molecules (
B molecules (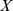 ) is conserved, however they can exist either in free/nuclear form (
) is conserved, however they can exist either in free/nuclear form ( ) or sequestered outside of nucleus within the I
) or sequestered outside of nucleus within the I B
B -NF-
-NF- B complex (
B complex (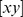 ). The model contains non-delayed reactions for the binding of free NF-
). The model contains non-delayed reactions for the binding of free NF- B to the unbound I
B to the unbound I B
B promoter (
promoter (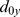 ) to form the bound I
) to form the bound I B
B promoter (
promoter (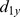 ), binding of I
), binding of I B
B protein (
protein (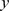 ) to free NF-
) to free NF- B to form the I
B to form the I B
B -NF-
-NF- B complex, constitutive degradation of I
B complex, constitutive degradation of I B
B , and induced degradation of free and bound I
, and induced degradation of free and bound I B
B proteins by the active I
proteins by the active I B kinase IKK (
B kinase IKK (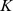 ) producing free NF-
) producing free NF- B. In contrast, a compound delayed reaction describes the synthesis of I
B. In contrast, a compound delayed reaction describes the synthesis of I B
B protein. This reaction involves a time delay
protein. This reaction involves a time delay 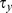 , which represents the time needed for transcription, translation, nuclear import and export, and protein-protein interactions.
, which represents the time needed for transcription, translation, nuclear import and export, and protein-protein interactions.
Table 1. Single feedback model variables.
| Variable | Description |

|
nuclear NF- B (nM) B (nM) |
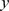
|
free I B B (nM) (nM) |
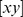
|
NF- B -bound I B -bound I B B (nM) (nM) |
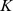
|
active I B kinase (IKK) B kinase (IKK) |
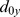
|
unbound I B B promoter* promoter*
|
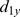
|
NF- B -bound I B -bound I B B promoter* promoter*
|
average numbers of corresponding promoters.
Table 2. Single feedback model reactions.
| Reaction | Rate | Description |
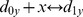
|
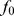 , , 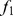
|
NF- B binds (and unbinds) I B binds (and unbinds) I B B promoter promoter |
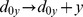
|
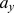
|
constitutive synthesis of I B B (delayed reaction) (delayed reaction) |
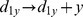
|
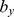
|
induced synthesis of I B B (delayed reaction) (delayed reaction) |
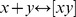
|
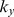 , , 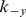
|
I B B association (and dissociation) with NF- association (and dissociation) with NF- B B |
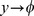
|
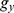
|
constitutive degradation of I B B
|
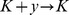
|
|
IKK-mediated degradation of I B B
|
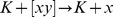
|
|
IKK-mediated degradation of NF- B-bound I B-bound I B B
|
Using experimentally validated assumptions, we reduced the set of mass-action kinetics equations for the 9 reactions to a single delay-differential equation:
| (1) |
where 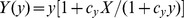 is the total I
is the total I B
B concentration (the sum of free I
concentration (the sum of free I B
B (
(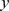 ) and I
) and I B
B bound to NF-
bound to NF- B),
B), 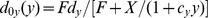 ,
,  , are the probabilities for the I
, are the probabilities for the I B
B promoter to be free or bound to NF-
promoter to be free or bound to NF- B, respectively,
B, respectively,  ,
, 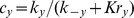 , and the subscript
, and the subscript  denotes the variable taken at time
denotes the variable taken at time 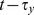 (see Methods for details of the derivation). The rates of individual reactions
(see Methods for details of the derivation). The rates of individual reactions 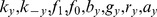 are defined in Table 2.
are defined in Table 2.
Mirroring the biological system, the non-dimensional time-dependent parameter 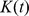 , which characterizes the active IKK concentration, is used as the proxy input signal. The first term in the r.h.s. of Eq. 1 represents constitutive synthesis from the unbound I
, which characterizes the active IKK concentration, is used as the proxy input signal. The first term in the r.h.s. of Eq. 1 represents constitutive synthesis from the unbound I B
B promoter, the second term represents induced synthesis from the NF-
promoter, the second term represents induced synthesis from the NF- B-bound I
B-bound I B
B promoter, the third term represents constitutive degradation of I
promoter, the third term represents constitutive degradation of I B
B protein, and the fourth term represents IKK-induced degradation of I
protein, and the fourth term represents IKK-induced degradation of I B
B . Values of
. Values of  correspond to the rate of IKK-induced degradation of NF-
correspond to the rate of IKK-induced degradation of NF- B-I
B-I B
B complex which is of the same magnitude as unbound I
complex which is of the same magnitude as unbound I B
B . Nuclear NF-
. Nuclear NF- B level
B level  at any time can be determined directly from I
at any time can be determined directly from I B
B levels via
levels via 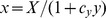 . The time delay
. The time delay 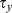 is incorporated in the synthesis terms: we assume that the rate of production of new proteins at time
is incorporated in the synthesis terms: we assume that the rate of production of new proteins at time  depends on the state of the system at time
depends on the state of the system at time 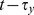 . Incorporating this time delay allows us to explore the behavior of the negative feedback loop without simulating the full set of reactions associated with it. We obtained values for the time delay and for the other model parameters by calibrating the behavior of the model with experimental results (Table S1). As a starting point, we used parameter values from biochemical measurements [21]. However, some modifications were necessary because these values represent the rates of single reaction steps and the model contains compound reactions.
. Incorporating this time delay allows us to explore the behavior of the negative feedback loop without simulating the full set of reactions associated with it. We obtained values for the time delay and for the other model parameters by calibrating the behavior of the model with experimental results (Table S1). As a starting point, we used parameter values from biochemical measurements [21]. However, some modifications were necessary because these values represent the rates of single reaction steps and the model contains compound reactions.
To validate the model, we compared it to experiments. In response to a persistent input signal (starting at time 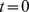 ), our simulations of the I
), our simulations of the I B
B -mediated negative feedback system show pronounced oscillations in nuclear NF-
-mediated negative feedback system show pronounced oscillations in nuclear NF- B levels with an oscillation period of about 90 minutes (Figure 1 C
). Oscillations with a similar period were observed experimentally when mutant cells containing only the I
B levels with an oscillation period of about 90 minutes (Figure 1 C
). Oscillations with a similar period were observed experimentally when mutant cells containing only the I B
B feedback loop were persistently stimulated with the inflammatory cytokine TNF (Figure 1D
).
feedback loop were persistently stimulated with the inflammatory cytokine TNF (Figure 1D
).
To address the dynamics of the wild-type NF- B system that feature both I
B system that feature both I B
B and I
and I B
B feedback loops, we expanded the model to include an additional 9 reactions and 4 variables involving I
feedback loops, we expanded the model to include an additional 9 reactions and 4 variables involving I B
B (Tables 3, 4). Following the same reduction procedure (see Methods for derivation), we derived a deterministic model consisting of two coupled delay-differential equations for the concentrations of the two I
(Tables 3, 4). Following the same reduction procedure (see Methods for derivation), we derived a deterministic model consisting of two coupled delay-differential equations for the concentrations of the two I B isoforms, I
B isoforms, I B
B (
(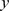 ) and I
) and I B
B (
( ),
),
| (2) |
| (3) |
where 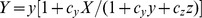 ,
, 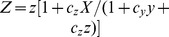 ,
, 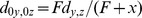 ,
, 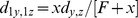 ,
, 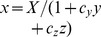 ,
, 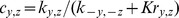 , and
, and 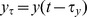 ,
, 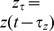 . Parameter
. Parameter 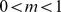 here is the scaling factor which characterizes the relative strength of the secondary feedback loop.
here is the scaling factor which characterizes the relative strength of the secondary feedback loop.
Table 3. I B
B feedback model variables.
feedback model variables.
average numbers of corresponding promoters.
Table 4. I B
B feedback model reactions.
feedback model reactions.
| Reaction | Rate | Description |
|
 , , 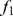
|
NF- B binds (and unbinds) I B binds (and unbinds) I B B promoter promoter |
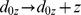
|
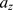
|
constitutive synthesis of I B B (delayed reaction) (delayed reaction) |
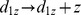
|
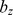
|
induced synthesis of I B B (delayed reaction) (delayed reaction) |

|
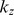 , , 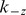
|
I B B association (and dissociation) with NF- association (and dissociation) with NF- B B |
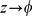
|
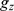
|
constitutive degradation of I B B
|
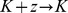
|
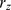
|
IKK-mediated degradation of I B B
|
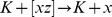
|
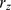
|
IKK-mediated degradation of NF- B-bound I B-bound I B B
|
In Eqs. 2 and 3, 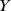 represents total I
represents total I B
B (the sum of free I
(the sum of free I B
B (
(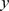 ) and I
) and I B
B bound to NF-
bound to NF- B (
B (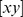 ), and
), and 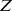 represents total I
represents total I B
B (the sum of free I
(the sum of free I B
B (
( ) and I
) and I B
B bound to NF-
bound to NF- B (
B (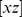 )). The terms in the r.h.s. of Eqs. 2 and 3 again represent constitutive synthesis from the identical unbound I
)). The terms in the r.h.s. of Eqs. 2 and 3 again represent constitutive synthesis from the identical unbound I B
B and I
and I B
B promoters, induced synthesis from the NF-
promoters, induced synthesis from the NF- B-bound promoters, constitutive degradation of I
B-bound promoters, constitutive degradation of I B
B and I
and I B
B proteins, and IKK-induced degradation of I
proteins, and IKK-induced degradation of I B
B and I
and I B
B . Nuclear NF-
. Nuclear NF- B levels are determined directly by I
B levels are determined directly by I B
B and I
and I B
B levels. Parameter values for the I
levels. Parameter values for the I B
B -mediated reactions were determined in the previous section. For the I
-mediated reactions were determined in the previous section. For the I B
B feedback reactions, we use the same parameter values except for the constitutive synthesis and the constitutive degradation rates, which were chosen based on experimental measurements [21] (Table S1).
feedback reactions, we use the same parameter values except for the constitutive synthesis and the constitutive degradation rates, which were chosen based on experimental measurements [21] (Table S1).
Is the oscillation period a function of the stimulus?
The advantage of our modeling approach is that it allows for analytical studies of the network dynamics. Here, we perform a linear stability analysis of the delay-differential equation (1) to identify the characteristic period and decay rate of NF- B oscillations produced when input signal is present (
B oscillations produced when input signal is present (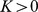 ). For sufficiently large
). For sufficiently large 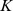 , induced synthesis and degradation are much stronger than basal ones, so the latter can be neglected (
, induced synthesis and degradation are much stronger than basal ones, so the latter can be neglected (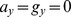 ).
).
Expressing 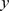 via
via  and substituting it into
and substituting it into 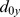 ,
, 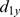 yields a closed equation for
yields a closed equation for 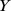 in the form
in the form
| (4) |
where 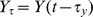 and the function
and the function 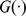 has the form
has the form
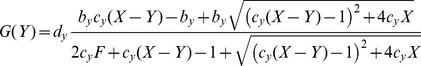 |
(5) |
The fixed point 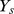 (stationary solution) of this equation is given by the algebraic equation
(stationary solution) of this equation is given by the algebraic equation
| (6) |
The stability of this solution is determined by the eigenvalue of the linearized equation (4) linearized near the fixed point 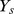 (see Methods for details). The corresponding eigenvalue can be found in terms of the Lambert function
(see Methods for details). The corresponding eigenvalue can be found in terms of the Lambert function 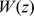 defined via
defined via 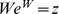 ,
,
| (7) |
The imaginary part of  gives the oscillation frequency
gives the oscillation frequency 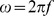 , and the (negative) real part of
, and the (negative) real part of 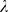 gives the decay rate
gives the decay rate  of oscillations. Plotting the period (
of oscillations. Plotting the period (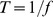 ) (Figure 2A
) and decay (
) (Figure 2A
) and decay ( ) (Figure 2B
) of the oscillations as a function of the delay reveals a strong dependence. In contrast, the signaling perturbation
) (Figure 2B
) of the oscillations as a function of the delay reveals a strong dependence. In contrast, the signaling perturbation 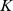 (the active IKK kinase) that acts as the input for the model determines the amplitude of the response but only negligibly affects the period or the oscillation decay (Figure 2B
). The mathematical reason for this asymmetry is that the imaginary part of the Lambert function
(the active IKK kinase) that acts as the input for the model determines the amplitude of the response but only negligibly affects the period or the oscillation decay (Figure 2B
). The mathematical reason for this asymmetry is that the imaginary part of the Lambert function 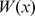 for negative values of its argument changes very weakly for arguments below
for negative values of its argument changes very weakly for arguments below 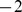 (
(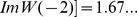 ,
, 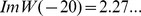 ) and asymptotically approaches
) and asymptotically approaches  for very large negative values of the argument. This is why the period of dampened oscillations (
for very large negative values of the argument. This is why the period of dampened oscillations (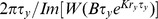 ) depends strongly on delay
) depends strongly on delay 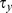 and only very weakly on
and only very weakly on 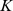 . Meanwhile, the real part of the eigenvalue
. Meanwhile, the real part of the eigenvalue  (the decay rate) is linearly proportional to
(the decay rate) is linearly proportional to 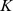 because of the second term in Eq.(7) and also strongly depends on
because of the second term in Eq.(7) and also strongly depends on 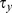 because of the first term. Thus, we find that the period is highly dependent on the delay but is rather insensitive to changes in the input level. This is confirmed by direct simulations of the full nonlinear equation (1), where time series of
because of the first term. Thus, we find that the period is highly dependent on the delay but is rather insensitive to changes in the input level. This is confirmed by direct simulations of the full nonlinear equation (1), where time series of  are plotted for several different values of
are plotted for several different values of 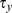 and
and 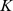 (Figure S1). Since variations of stimulus do not lead to significant frequency modulation of NF-
(Figure S1). Since variations of stimulus do not lead to significant frequency modulation of NF- B activity, oscillations of NF-
B activity, oscillations of NF- B are unlikely to encode information about the stimulus.
B are unlikely to encode information about the stimulus.
Figure 2. Period and decay rate of oscillations produced by the I B
B -mediated negative feedback system.
-mediated negative feedback system.
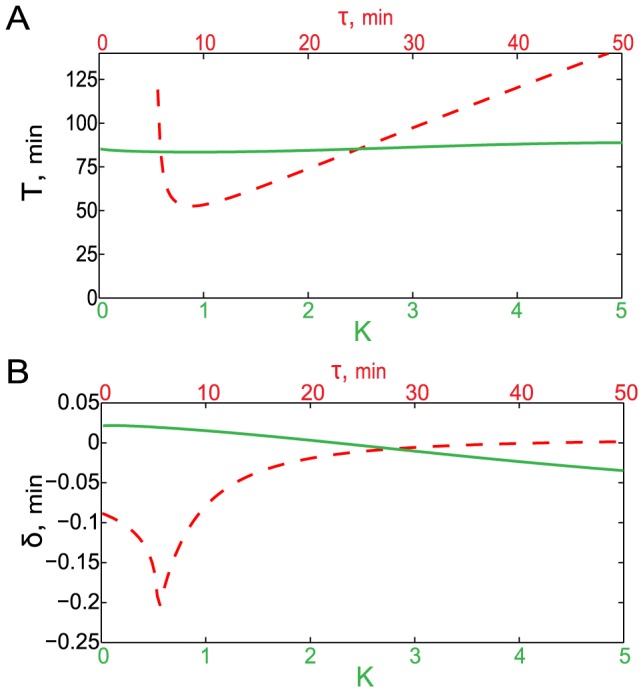
(A) The oscillation period  as a function of
as a function of  with
with  min (green line) and as a function of
min (green line) and as a function of  with
with 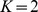 (red dashed line). (B) The oscillation decay rate
(red dashed line). (B) The oscillation decay rate  as a function of
as a function of 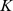 with
with 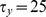 min (green line) and as a function of
min (green line) and as a function of 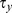 with
with 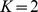 (red dashed line).
(red dashed line).
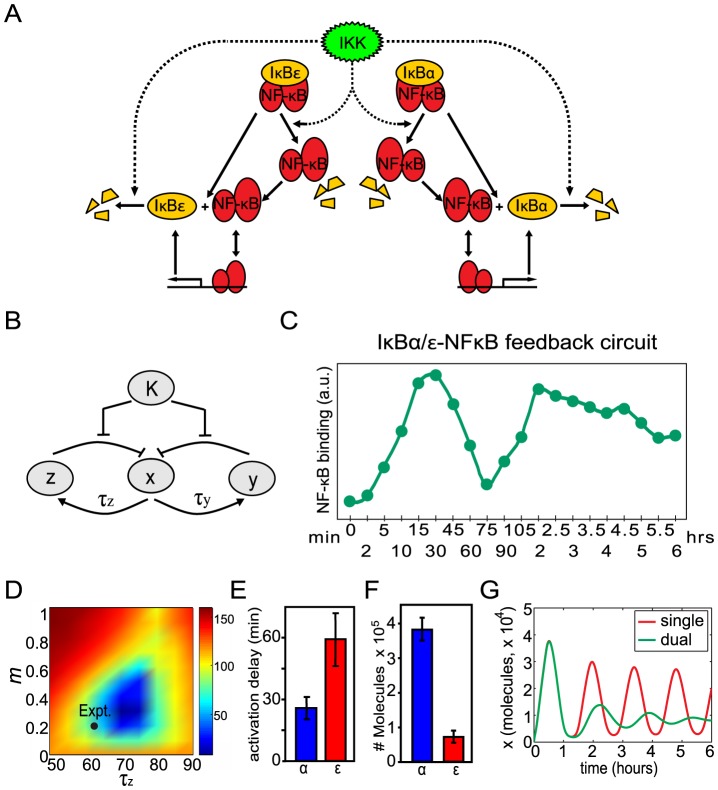
Damping of oscillations in a dual delayed feedback loop system
The main qualitative difference between the one-loop system considered in the previous section, and the wild-type NF- B module is the presence of another I
B module is the presence of another I B isoform, I
B isoform, I B
B , which also provides negative feedback regulation on NF-
, which also provides negative feedback regulation on NF- B activity (Figure 3A, B
), however with slower kinetics [21]. Experimental and computational work has shown that I
B activity (Figure 3A, B
), however with slower kinetics [21]. Experimental and computational work has shown that I B
B -mediated feedback can cause damping of I
-mediated feedback can cause damping of I B
B -mediated oscillations [21] and (Figure 3C
). More recent computational work has predicted that I
-mediated oscillations [21] and (Figure 3C
). More recent computational work has predicted that I B
B -mediated feedback desynchronizes oscillations but does not dampen oscillations in single cells [13]. Thus, the mechanism by which I
-mediated feedback desynchronizes oscillations but does not dampen oscillations in single cells [13]. Thus, the mechanism by which I B
B -mediated feedback produces damped oscillations at the population level is not well established. Furthermore, it is unknown whether the damping function of the I
-mediated feedback produces damped oscillations at the population level is not well established. Furthermore, it is unknown whether the damping function of the I B
B -mediated feedback loop has evolved to achieve a specific regulatory function or may simply be a secondary consequence of another function. We hypothesize that the primary role of the second feedback loop is to mitigate oscillatory behavior produced by the first feedback loop.
-mediated feedback loop has evolved to achieve a specific regulatory function or may simply be a secondary consequence of another function. We hypothesize that the primary role of the second feedback loop is to mitigate oscillatory behavior produced by the first feedback loop.
Figure 3. Damped oscillations with a dual negative feedback system.
(A) Diagram of the dual feedback system with both I B
B - and I
- and I B
B -mediated negative feedback loops. (B) Diagram of a system with dual delayed negative feedback loops. (C) Experimental levels of nuclear NF-
-mediated negative feedback loops. (B) Diagram of a system with dual delayed negative feedback loops. (C) Experimental levels of nuclear NF- B (determined by EMSAs) in wild-type cells containing both I
B (determined by EMSAs) in wild-type cells containing both I B
B -and I
-and I B
B -mediated negative feedback (data from [17]). (D) Optimization of the parameters of the second feedback loop
-mediated negative feedback (data from [17]). (D) Optimization of the parameters of the second feedback loop  and
and 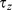 towards maximizing the oscillations damping. The optimization method minimizes peak-minus-trough differences six hours after the onset of stimulation, the global minimum occurs at
towards maximizing the oscillations damping. The optimization method minimizes peak-minus-trough differences six hours after the onset of stimulation, the global minimum occurs at 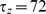 min,
min, 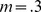 . The black dot indicates the experimentally measured parameter values (
. The black dot indicates the experimentally measured parameter values (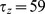 min,
min, 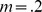 ). Note that
). Note that  was not measured directly. The value of
was not measured directly. The value of  corresponding to the experimentally measured value of
corresponding to the experimentally measured value of 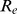 was determined with the model (Figure S3). (E) Experimental measurements of I
was determined with the model (Figure S3). (E) Experimental measurements of I B
B and I
and I B
B synthesis delays. (F) Experimental values for peak I
synthesis delays. (F) Experimental values for peak I B
B and I
and I B
B protein levels. (G) Simulated time course of nuclear NF-
protein levels. (G) Simulated time course of nuclear NF- B levels (
B levels ( ) for the single feedback system and for the optimized dual feedback system in response to persistent stimulation with
) for the single feedback system and for the optimized dual feedback system in response to persistent stimulation with 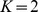 .
.
To address our hypothesis that I B
B -mediated feedback specifically evolved to dampen I
-mediated feedback specifically evolved to dampen I B
B -mediated oscillations, we performed a parameter optimization procedure on the wild-type model (Eqs. 2 and 3) to determine the I
-mediated oscillations, we performed a parameter optimization procedure on the wild-type model (Eqs. 2 and 3) to determine the I B
B synthesis parameters that result in maximum damping. To characterize the degree of damping, we chose the maximum peak-trough difference after 6 hrs as a metric for the persistence of oscillations. According to the definition of this performance metric, “optimal damping” occurs when this metric is minimized. In our optimization procedure, we varied two important parameters, the time delay of the second feedback loop
synthesis parameters that result in maximum damping. To characterize the degree of damping, we chose the maximum peak-trough difference after 6 hrs as a metric for the persistence of oscillations. According to the definition of this performance metric, “optimal damping” occurs when this metric is minimized. In our optimization procedure, we varied two important parameters, the time delay of the second feedback loop 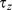 and the scaling factor
and the scaling factor  which simultaneously varies the rates of constitutive and induced synthesis of I
which simultaneously varies the rates of constitutive and induced synthesis of I B
B . Choosing
. Choosing  is equivalent to the complete removal of the I
is equivalent to the complete removal of the I B
B -mediated negative feedback loop while
-mediated negative feedback loop while 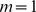 represents the case in which the inducible synthesis rates for I
represents the case in which the inducible synthesis rates for I B
B are the same as for I
are the same as for I B
B . The two-dimensional optimization search is shown in a color map (Figure 3D
) indicating that the performance metric is minimized at
. The two-dimensional optimization search is shown in a color map (Figure 3D
) indicating that the performance metric is minimized at 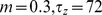 . Time course simulations with the optimized parameter set show a high degree of damping (Figure 3G
) similar to what is observed experimentally (Figure 3C
).
. Time course simulations with the optimized parameter set show a high degree of damping (Figure 3G
) similar to what is observed experimentally (Figure 3C
).
To determine whether these optimized parameter values correspond to observations, we measured relevant parameter values experimentally. The synthesis delays for I B
B and I
and I B
B were determined by measuring I
were determined by measuring I B
B and I
and I B
B mRNA levels in a time course of TNF-treated murine embryonic fibroblasts (MEFs) in multiple independent experiments (Figure 3E
, S2
A,B). The measured delay for I
mRNA levels in a time course of TNF-treated murine embryonic fibroblasts (MEFs) in multiple independent experiments (Figure 3E
, S2
A,B). The measured delay for I B
B was
was 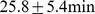 , and
, and 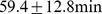 for I
for I B
B , which agrees well with the model prediction for optimal damping.
, which agrees well with the model prediction for optimal damping.
Since it is difficult to measure the promoter strength experimentally, we employed an implicit way of comparing experiment with the model. To relate the parameter value  to experimental measurements, we set
to experimental measurements, we set 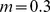 in the model and calculated the ratio of peak values for I
in the model and calculated the ratio of peak values for I B
B and I
and I B
B proteins
proteins 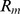 , which we found to be equal 3.9. Then we measured the ratios of basal (unstimulated) to peak protein levels for I
, which we found to be equal 3.9. Then we measured the ratios of basal (unstimulated) to peak protein levels for I B
B and I
and I B
B in experiment via quantitative Western blots of whole cell lysates generated during a TNF time course. These were compared to recombinant protein standards to derive absolute molecule number per cell. Peak I
in experiment via quantitative Western blots of whole cell lysates generated during a TNF time course. These were compared to recombinant protein standards to derive absolute molecule number per cell. Peak I B
B protein levels were measured to be 379,800 molecules per cell, and I
protein levels were measured to be 379,800 molecules per cell, and I B
B 71,300 molecules per cell, with both values being subject to an estimated 25% error (Figure 3F
, S2
C,D). These protein levels correspond to the experimental peak values ratio
71,300 molecules per cell, with both values being subject to an estimated 25% error (Figure 3F
, S2
C,D). These protein levels correspond to the experimental peak values ratio 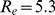 which is close to the model prediction
which is close to the model prediction 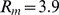 .
.
Duration encoding in a dual delayed negative feedback loop system
We next addressed why the NF- B signaling module may have evolved to produce oscillatory behavior if the oscillation frequency is not a function of the stimulus and does not constitute a signaling code. We first simulated persistent stimulation of a variant NF-
B signaling module may have evolved to produce oscillatory behavior if the oscillation frequency is not a function of the stimulus and does not constitute a signaling code. We first simulated persistent stimulation of a variant NF- B system without feedback (we assume that I
B system without feedback (we assume that I B
B is constitutively produced, so
is constitutively produced, so 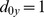 ,
, 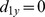 in Eq. 1) and found that this system produces long term, non-oscillatory NF-
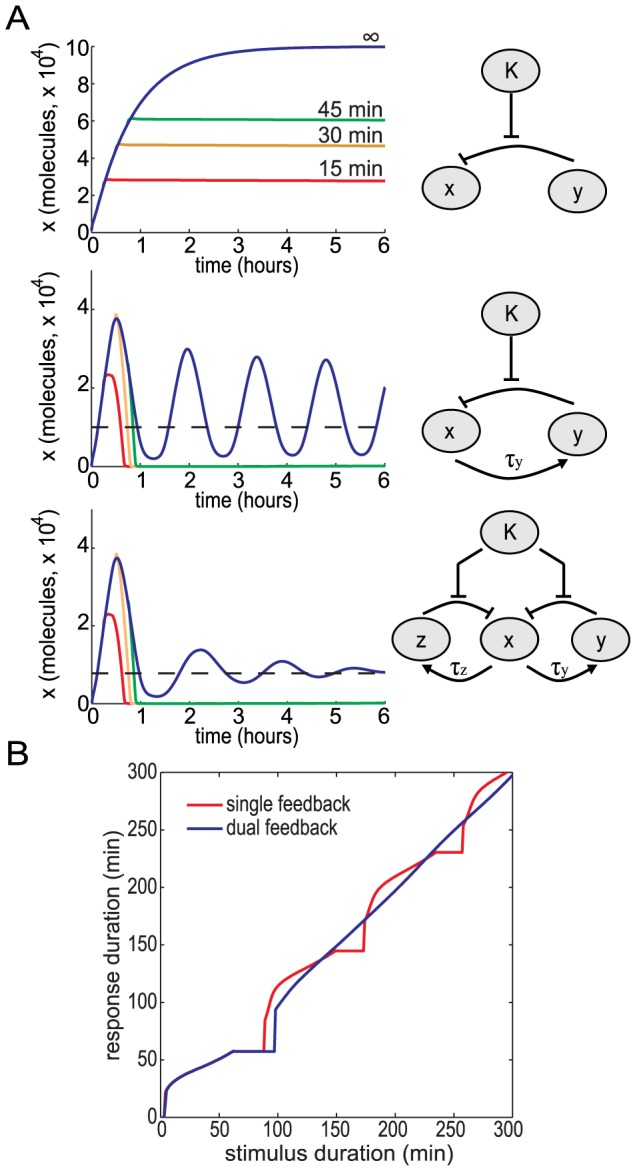
in Eq. 1) and found that this system produces long term, non-oscillatory NF- B activity (Figure 4A
Top, blue line). As TNF is secreted in bursts and therefore perceived by surrounding cells as transient or pulse stimulation, we then performed stimulations of pulses 15, 30, and 45 min in duration. In the negative feedback-deficient NF-
B activity (Figure 4A
Top, blue line). As TNF is secreted in bursts and therefore perceived by surrounding cells as transient or pulse stimulation, we then performed stimulations of pulses 15, 30, and 45 min in duration. In the negative feedback-deficient NF- B system, the pulses resulted in transient responses that were attenuated very slowly. Faster attenuation can be achieved by increasing the constitutive synthesis rate,
B system, the pulses resulted in transient responses that were attenuated very slowly. Faster attenuation can be achieved by increasing the constitutive synthesis rate, 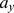 . Increasing
. Increasing 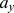 by two orders of magnitude results in pulse NF-
by two orders of magnitude results in pulse NF- B responses to transient stimuli, but the responsiveness (in amplitude) is much reduced (Figure S4).
B responses to transient stimuli, but the responsiveness (in amplitude) is much reduced (Figure S4).
Figure 4. Response of the NF- B signaling module to transient inputs with magnitude
B signaling module to transient inputs with magnitude  ,
,
(A) Time series of  for a system with all feedback removed (top), a system with I
for a system with all feedback removed (top), a system with I B
B -mediated negative feedback (middle), and a system with both I
-mediated negative feedback (middle), and a system with both I B
B - and I
- and I B
B -mediated negative feedback (bottom) in response to 15 min (red), 30 min (orange), 45 min (green), and persistent (blue) stimulation. (B) The response duration as a function of the stimulus duration for the single feedback and dual feedback systems. The response duration is the amount of time
-mediated negative feedback (bottom) in response to 15 min (red), 30 min (orange), 45 min (green), and persistent (blue) stimulation. (B) The response duration as a function of the stimulus duration for the single feedback and dual feedback systems. The response duration is the amount of time  exceeds a threshold level of 50 (as indicated by the dashed black lines in the graphs shown in (A).
exceeds a threshold level of 50 (as indicated by the dashed black lines in the graphs shown in (A).
We then performed similar simulations in a single negative feedback loop NF- B system and found that this network topology allows for a rapid shutdown of NF-
B system and found that this network topology allows for a rapid shutdown of NF- B activity for transient inputs (Figure 4A
Middle). This suggests that the NF-
B activity for transient inputs (Figure 4A
Middle). This suggests that the NF- B network may have evolved from a pathway without feedback to a pathway with a single negative feedback loop to allow for a more sensitive transient response. Although the negative feedback indeed allows for greater sensitivity, a secondary consequence is that pronounced oscillations arise when the input signal persists for a long time period (Figure 4A
Middle, blue line). The addition of a second negative feedback loop with a different time delay can help to dampen these oscillations, while preserving the responsiveness of the signaling module to transient stimuli (Figure 4A
Bottom).
B network may have evolved from a pathway without feedback to a pathway with a single negative feedback loop to allow for a more sensitive transient response. Although the negative feedback indeed allows for greater sensitivity, a secondary consequence is that pronounced oscillations arise when the input signal persists for a long time period (Figure 4A
Middle, blue line). The addition of a second negative feedback loop with a different time delay can help to dampen these oscillations, while preserving the responsiveness of the signaling module to transient stimuli (Figure 4A
Bottom).
By plotting the duration of the response (above a given threshold) we investigated what may be called “temporal dose response curves” of the single and dual feedback systems (Figure 4B
). The dual feedback system has a response duration close to 60 min for short pulses ( min), and a duration proportional to the input duration for longer pulses. The single feedback system has the same behavior as the dual feedback system for short inputs, but for longer inputs the single feedback system produces a quantized response with the same output duration for several different input durations. Our analysis indicates that a dual feedback system is able to produce temporally graded responses, whereas a single feedback system that oscillates does not. Given that the duration of the second phase of the NF-
min), and a duration proportional to the input duration for longer pulses. The single feedback system has the same behavior as the dual feedback system for short inputs, but for longer inputs the single feedback system produces a quantized response with the same output duration for several different input durations. Our analysis indicates that a dual feedback system is able to produce temporally graded responses, whereas a single feedback system that oscillates does not. Given that the duration of the second phase of the NF- B response to TNF is a critical determinant of gene expression programs [4], we suggest that the NF-
B response to TNF is a critical determinant of gene expression programs [4], we suggest that the NF- B system has evolved a dual feedback system that allows for NF-
B system has evolved a dual feedback system that allows for NF- B activity whose duration is more closely related to the duration of the cytokine stimulus.
B activity whose duration is more closely related to the duration of the cytokine stimulus.
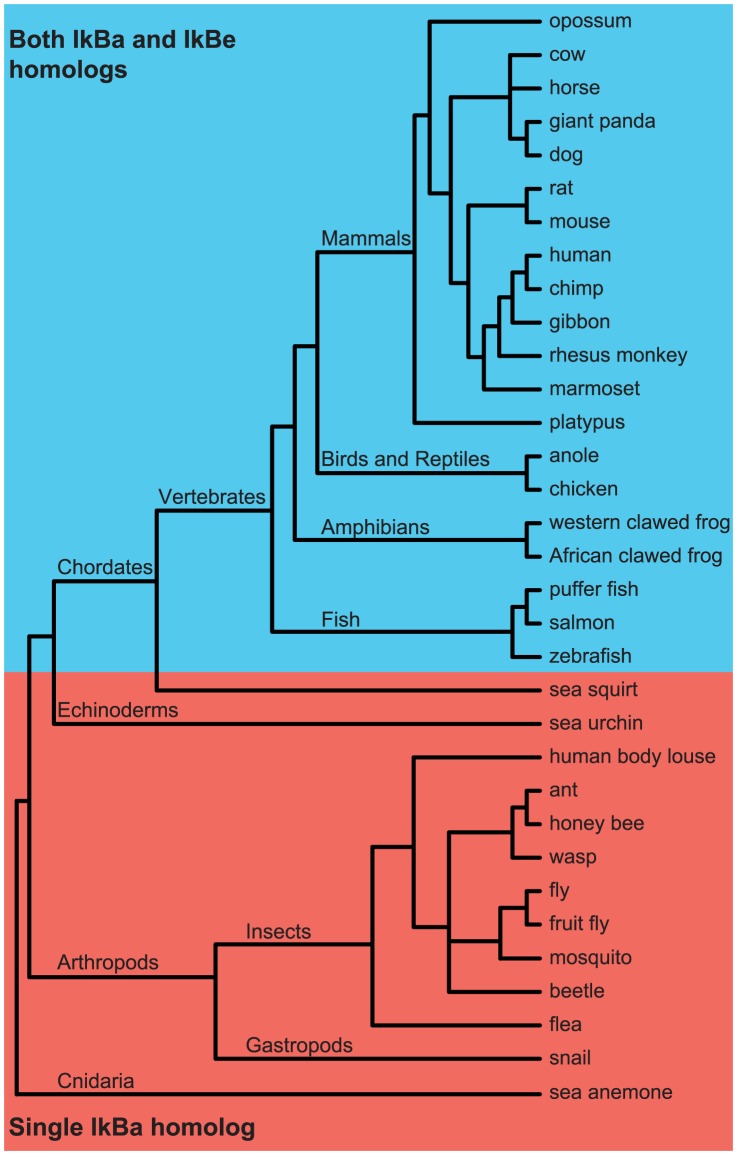
This fine temporal control, achieved via dual negative feedback, may be critical for complex cytokine-mediated cell-to-cell interactions involved in the adaptive immune response present in vertebrates, but may not be necessary for innate patogen-induced immune responses. We hypothesized that, on an evolutionary timescale, the appearance of dual negative feedback loops that regulate NF- B activity may coincide with the transition from an innate to an adaptive immune system. To address this hypothesis, we used BLASTP with an E-value cutoff of 1e-25 to search for homologs of the mouse I
B activity may coincide with the transition from an innate to an adaptive immune system. To address this hypothesis, we used BLASTP with an E-value cutoff of 1e-25 to search for homologs of the mouse I B
B and I
and I B
B protein sequences in other organisms (see Methods). We found homologs for both I
protein sequences in other organisms (see Methods). We found homologs for both I B
B and I
and I B
B , not only in other mammals (such as chimp, dog, platypus), but also in other vertebrate classes including fish, amphibians, and birds (Figure 5). Thus, dual negative feedback regulation of NF-
, not only in other mammals (such as chimp, dog, platypus), but also in other vertebrate classes including fish, amphibians, and birds (Figure 5). Thus, dual negative feedback regulation of NF- B activity appears to be present in all organisms with adaptive immunity. In contrast, we did not find any invertebrate organisms with homologs for both I
B activity appears to be present in all organisms with adaptive immunity. In contrast, we did not find any invertebrate organisms with homologs for both I B
B and I
and I B
B (Figure 5). Therefore, invertebrates, which lack adaptive immunity, also appear to lack the potential for dual negative feedback regulation of NF-
(Figure 5). Therefore, invertebrates, which lack adaptive immunity, also appear to lack the potential for dual negative feedback regulation of NF- B mediated by I
B mediated by I B
B and I
and I B
B suggesting that the temporal control achieved with this regulatory architecture is not necessary for innate immune responses.
suggesting that the temporal control achieved with this regulatory architecture is not necessary for innate immune responses.
Figure 5. Schematic of a phylogenetic tree showing organisms in which I B homologs were found using BLASTP.
B homologs were found using BLASTP.
Organisms with homologs for both I B
B and I
and I B
B are in blue shaded region and organisms with a single homolog are in red shaded region. The branches in the schematic phylogenetic tree are not drawn to scale. (For simplicity, not all organisms with single or dual homologs are shown here. A complete list is provided in Table S6).
are in blue shaded region and organisms with a single homolog are in red shaded region. The branches in the schematic phylogenetic tree are not drawn to scale. (For simplicity, not all organisms with single or dual homologs are shown here. A complete list is provided in Table S6).
Robustness to fluctuations in a dual delayed negative feedback loop system
Thus far, we have examined the response of the network to transient stimulation in the absence of fluctuations. However, it is well known that noise in gene expression can cause significant variability in cellular responses [18], [22]–[26]. Sometimes this variability can be beneficial [27], but in most cases, noise has a detrimental effect on the robustness of cellular functions. Mechanisms have presumably evolved to mitigate the unwanted effects of noise, especially in signaling pathways. In this section we examine the variability in the response of the NF- B module that arises due to intrinsic and extrinsic noise, and we demonstrate that the dual-feedback loop architecture allows for a more robust response than the single feedback loop system. Further, we investigate how the relative contribution of intrinsic and extrinsic fluctuations depends on the size of the system.
B module that arises due to intrinsic and extrinsic noise, and we demonstrate that the dual-feedback loop architecture allows for a more robust response than the single feedback loop system. Further, we investigate how the relative contribution of intrinsic and extrinsic fluctuations depends on the size of the system.
The concentration of signaling molecules such as NF- B can vary significantly between cells [28]. This variability in protein levels represents a source of extrinsic noise. We examined the variability in the response of the network to fluctuations in the total level of NF-
B can vary significantly between cells [28]. This variability in protein levels represents a source of extrinsic noise. We examined the variability in the response of the network to fluctuations in the total level of NF- B and fluctuations in the IKK input level by simulating the network behavior with total NF-
B and fluctuations in the IKK input level by simulating the network behavior with total NF- B levels and active IKK levels distributed within a certain rage around their nominal values. The coefficient of variation (CV) in peak nuclear NF-
B levels and active IKK levels distributed within a certain rage around their nominal values. The coefficient of variation (CV) in peak nuclear NF- B levels and the CV in late-phase nuclear NF-
B levels and the CV in late-phase nuclear NF- B levels is defined as
B levels is defined as 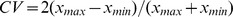 where
where 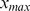 (
(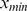 ) are the maximum (minimum) values of NF-
) are the maximum (minimum) values of NF- B at the peak or during the late phase. NF-
B at the peak or during the late phase. NF- B late-phase response is defined as the nuclear NF-
B late-phase response is defined as the nuclear NF- B level following the trough after the first peak response. In Text S1 we compare the extrinsic CV in the peak and the late phase for various values of IKK and NF-
B level following the trough after the first peak response. In Text S1 we compare the extrinsic CV in the peak and the late phase for various values of IKK and NF- B (see Figure S5).
B (see Figure S5).
Intrinsic noise arises from the stochastic nature of biochemical processes such as transcription and translation [24]. To examine the response of the NF- B signaling module in the presence of intrinsic genetic noise, we used the Gillespie algorithm [29] modified according to [30] to perform stochastic simulations of both regular and delayed biochemical reactions included in our delayed feedback model. These latter reactions are initiated at times dictated by their respective rates, but the numbers of molecules are only updated after the time delay since the reaction initiation.
B signaling module in the presence of intrinsic genetic noise, we used the Gillespie algorithm [29] modified according to [30] to perform stochastic simulations of both regular and delayed biochemical reactions included in our delayed feedback model. These latter reactions are initiated at times dictated by their respective rates, but the numbers of molecules are only updated after the time delay since the reaction initiation.
We ran stochastic simulations of both a single and dual feedback system and estimated the ensemble average 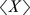 of the number of NF-
of the number of NF- B molecules
B molecules 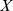 and the magnitude of fluctuations as characterized by the standard deviation
and the magnitude of fluctuations as characterized by the standard deviation 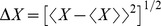 and the coefficient of variation
and the coefficient of variation 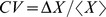 . To determine how the variability in the response varies with the magnitude of the input and the size of the system, we determined the CV in peak nuclear NF-
. To determine how the variability in the response varies with the magnitude of the input and the size of the system, we determined the CV in peak nuclear NF- B levels and the CV in late-phase nuclear NF-
B levels and the CV in late-phase nuclear NF- B levels for several values of IKK (Figure 6A,C
) and for systems with up to 100,000 NF-
B levels for several values of IKK (Figure 6A,C
) and for systems with up to 100,000 NF- B molecules (Figure 6B,D
). In Figure 6, we also plot CV values for extrinsic variations (
B molecules (Figure 6B,D
). In Figure 6, we also plot CV values for extrinsic variations (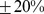 ) in total NF-
) in total NF- B at several values of IKK (Figure 6A,C
) and CV values for extrinsic variations in IKK (
B at several values of IKK (Figure 6A,C
) and CV values for extrinsic variations in IKK (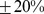 ) for several different system sizes (Figure 6B,D
). We find that, even with this relatively low level (
) for several different system sizes (Figure 6B,D
). We find that, even with this relatively low level ( ) of extrinsic variability in IKK and NF-
) of extrinsic variability in IKK and NF- B protein levels [28], variability in the response of the network is dominated by extrinsic noise for large systems (
B protein levels [28], variability in the response of the network is dominated by extrinsic noise for large systems (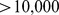 NF-
NF- B molecules).
B molecules).
Figure 6. The coefficient of variation (CV) in nuclear NF- B levels due to extrinsic and intrinsic fluctuations.
B levels due to extrinsic and intrinsic fluctuations.
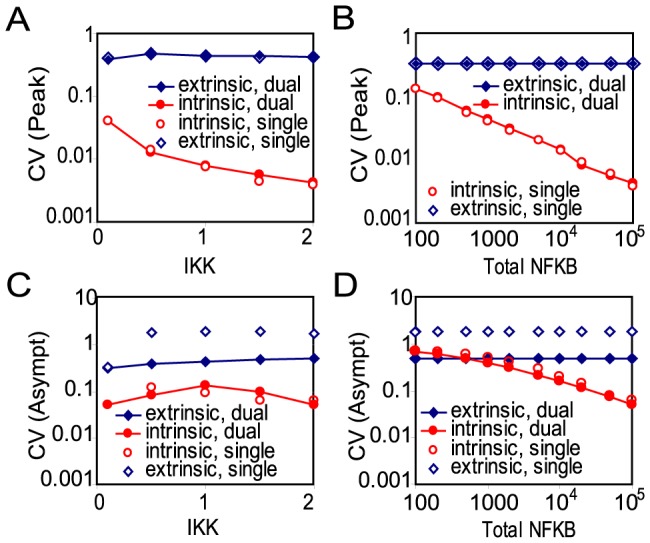
The CV was calculated for peak (A,B) and late-phase (C,D) nuclear NF- B levels for both single and dual feedback systems. The CV due to intrinsic fluctuations was determined from at least 50 runs of the stochastic simulations at each value of IKK (A,C) and total NF-
B levels for both single and dual feedback systems. The CV due to intrinsic fluctuations was determined from at least 50 runs of the stochastic simulations at each value of IKK (A,C) and total NF- B (B,D). The CV due to extrinsic fluctuations in total NF-
B (B,D). The CV due to extrinsic fluctuations in total NF- B and IKK levels was determined by varying the total NF-
B and IKK levels was determined by varying the total NF- B level by
B level by 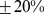 for each value of IKK (A,C) and by varying IKK by
for each value of IKK (A,C) and by varying IKK by 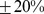 for value of total NF-
for value of total NF- B (B,D).
B (B,D).
The CV in late-phase nuclear NF- B levels is similar for extrinsic and intrinsic noise when the size of the system is reduced to 1000 NF-
B levels is similar for extrinsic and intrinsic noise when the size of the system is reduced to 1000 NF- B molecules. Next, we investigated the behavior of the NF-
B molecules. Next, we investigated the behavior of the NF- B signaling module in this regime where intrinsic noise levels become significant by analyzing stochastic simulations produced with a system with total NF-
B signaling module in this regime where intrinsic noise levels become significant by analyzing stochastic simulations produced with a system with total NF- B levels set to 1000 molecules. We ran stochastic simulations of all three systems studied deterministically above: no-feedback, single negative feedback, and dual negative feedback (Figure 7). Note that ensemble-averaged time series agree with the deterministic simulations very well (Figure S6). In the case of no feedback (Figure 7A
) there is a strong robust response to the incoming persistent signal as characterized by the low values of the coefficient of variation. However, as we have seen above in Figure 4A
, the major flaw of this system is its slow response to the pulse-like signals. Next, we simulated the 9 biochemical reactions included in the I
B levels set to 1000 molecules. We ran stochastic simulations of all three systems studied deterministically above: no-feedback, single negative feedback, and dual negative feedback (Figure 7). Note that ensemble-averaged time series agree with the deterministic simulations very well (Figure S6). In the case of no feedback (Figure 7A
) there is a strong robust response to the incoming persistent signal as characterized by the low values of the coefficient of variation. However, as we have seen above in Figure 4A
, the major flaw of this system is its slow response to the pulse-like signals. Next, we simulated the 9 biochemical reactions included in the I B
B -mediated single negative feedback loop (Figure 7B
). In single runs the first peak in nuclear NF-
-mediated single negative feedback loop (Figure 7B
). In single runs the first peak in nuclear NF- B levels appears to be very robust, as illustrated by Figure 7B
Top. The CV is lowest (
B levels appears to be very robust, as illustrated by Figure 7B
Top. The CV is lowest (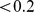 ) during the first peak in nuclear NF-
) during the first peak in nuclear NF- B indicating that this portion of the response is very robust. Subsequent peaks in this undamped system lead to higher CV (
B indicating that this portion of the response is very robust. Subsequent peaks in this undamped system lead to higher CV (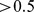 ) in the later portion of the response.
) in the later portion of the response.
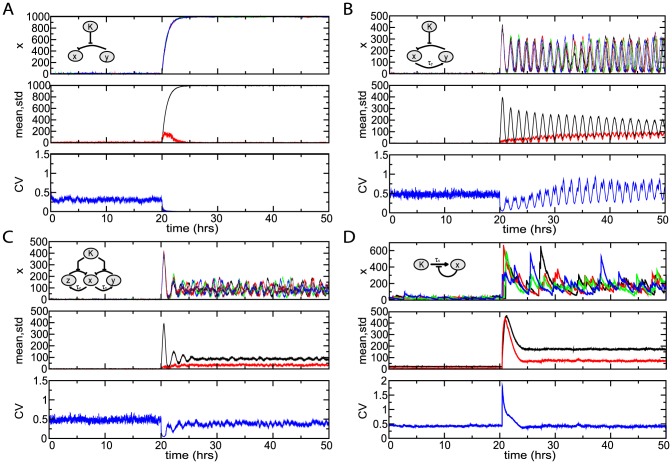
Figure 7. Stochastic model simulation results for various network architectures (with 1000 total NF- B molecules).
B molecules).
The architectures analyzed are the NF- B network with no feedback loops (A), only I
B network with no feedback loops (A), only I B
B -mediated negative feedback (B), the NF-
-mediated negative feedback (B), the NF- B network with both I
B network with both I B
B - and I
- and I B
B -mediated negative feedback (C), and an alternative auto-repressive network (D). The top panel in each group shows four typical runs of stochastic simulations for each network, the middle panel shows the mean and standard deviation for 200 runs of each network, and the bottom panel shows the corresponding coefficient of variation. The input signal, K(t), is switched from
-mediated negative feedback (C), and an alternative auto-repressive network (D). The top panel in each group shows four typical runs of stochastic simulations for each network, the middle panel shows the mean and standard deviation for 200 runs of each network, and the bottom panel shows the corresponding coefficient of variation. The input signal, K(t), is switched from 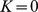 to
to 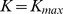 at
at 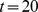 hrs. In A-C, the magnitude of external signal
hrs. In A-C, the magnitude of external signal 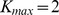 , in D,
, in D, 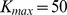 .
.
Next, we performed stochastic simulations of the 18 biochemical reactions included in the dual delayed feedback model (with both I B
B - and I
- and I B
B -mediated feedback) (Figure 7C
). In the dual feedback model, as in the single I
-mediated feedback) (Figure 7C
). In the dual feedback model, as in the single I B
B -mediated feedback model, there is a very robust first peak. However, unlike the single I
-mediated feedback model, there is a very robust first peak. However, unlike the single I B
B -mediated feedback model, in the dual feedback system the noise levels remain at a low level (
-mediated feedback model, in the dual feedback system the noise levels remain at a low level (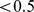 ) following the first peak in nuclear NF-
) following the first peak in nuclear NF- B (Figure 7C
Bottom). Thus, the dual feedback architecture allows for lower noise levels also in the later portion of the response.
B (Figure 7C
Bottom). Thus, the dual feedback architecture allows for lower noise levels also in the later portion of the response.
What is the underlying reason for the robustness of the initial response from this circuit? The main source of intrinsic noise lies in the transcription and translation of I B isoforms, since they are transcribed from single genes. In contrast, fluctuations in protein degradation and transport processes are relatively small, because the copy numbers of the corresponding molecules are large. In the NF-
B isoforms, since they are transcribed from single genes. In contrast, fluctuations in protein degradation and transport processes are relatively small, because the copy numbers of the corresponding molecules are large. In the NF- B network, the peak in nuclear NF-
B network, the peak in nuclear NF- B levels that occurs following stimulation is produced via the degradation of I
B levels that occurs following stimulation is produced via the degradation of I B proteins that bind and sequester NF-
B proteins that bind and sequester NF- B in the cytoplasm. Thus, we argue that robustness of the initial response of the NF-
B in the cytoplasm. Thus, we argue that robustness of the initial response of the NF- B circuit is explained by the fact that it uses the sequestering mechanism and does not rely on the protein production.
B circuit is explained by the fact that it uses the sequestering mechanism and does not rely on the protein production.
To test this hypothesis, we simulated the behavior of an alternative network that relies on transcription of auto-repressor, rather than the degradation of inhibitor proteins, for signaling (Figure 7D
). This system can be modeled with two variables:  , the number of repressor molecules, and
, the number of repressor molecules, and 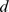 , the binary state of the promoter (
, the binary state of the promoter (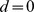 corresponds to the unbound promoter and
corresponds to the unbound promoter and 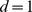 corresponds to bound promoter), and with four reactions (binding and unbinding of the repressor to the promoter, degradation of the repressor, and delayed synthesis of the repressor with rate
corresponds to bound promoter), and with four reactions (binding and unbinding of the repressor to the promoter, degradation of the repressor, and delayed synthesis of the repressor with rate 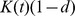 where
where 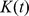 is the external signal (Tables S2, S3). The input signal activates the production of the auto-repressor which after a certain time delay binds to the promoter and terminates further synthesis. Deterministically, this circuit also provides a desired response to a persistent stimulation with a large well-defined first peak. However, stochastic simulations reveal significant differences in the noise performance of this design as compared with the NF-
is the external signal (Tables S2, S3). The input signal activates the production of the auto-repressor which after a certain time delay binds to the promoter and terminates further synthesis. Deterministically, this circuit also provides a desired response to a persistent stimulation with a large well-defined first peak. However, stochastic simulations reveal significant differences in the noise performance of this design as compared with the NF- B circuit (note that the agreement between deterministic and stochastic simulations is less accurate in this case because of the strong promoter fluctuations (Figure S6
D). Activation of the auto-repressor network is much less robust than the activation of the NF-
B circuit (note that the agreement between deterministic and stochastic simulations is less accurate in this case because of the strong promoter fluctuations (Figure S6
D). Activation of the auto-repressor network is much less robust than the activation of the NF- B network (cf. Figure 7D
and Figures 7B,C
). In fact, in the auto-repressor network, the coefficient of variation is highest (
B network (cf. Figure 7D
and Figures 7B,C
). In fact, in the auto-repressor network, the coefficient of variation is highest (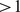 ) during the initial peak (Figure 7D
Bottom). These results confirm our conjecture that the sequestering mechanism incorporated in the design of the NF-
) during the initial peak (Figure 7D
Bottom). These results confirm our conjecture that the sequestering mechanism incorporated in the design of the NF- B network gives rise to a much more robust activation of NF-
B network gives rise to a much more robust activation of NF- B than alternative networks that rely on transcription for activation and signaling. This finding is in accord with recent work [31] where the sequestering of Cdc20 protein was also implicated in the noise resistance of the spindle assembly checkpoint.
B than alternative networks that rely on transcription for activation and signaling. This finding is in accord with recent work [31] where the sequestering of Cdc20 protein was also implicated in the noise resistance of the spindle assembly checkpoint.
As we mentioned previously, recent computational work has suggested that persistent oscillations are present in wild-type cells with both I B
B - and I
- and I B
B -mediated feedback but stochastic variability leads to desynchronization among individual cells and therefore produces damped oscillations at the population level [13], [32]. Our computational results demonstrate that, although stochastic oscillations are still present in individual cells with both I
-mediated feedback but stochastic variability leads to desynchronization among individual cells and therefore produces damped oscillations at the population level [13], [32]. Our computational results demonstrate that, although stochastic oscillations are still present in individual cells with both I B
B - and I
- and I B
B -mediated feedback (Figure 7C
), the oscillatory propensity can be greatly reduced by the second feedback loop in the wild-type NF-
-mediated feedback (Figure 7C
), the oscillatory propensity can be greatly reduced by the second feedback loop in the wild-type NF- B signaling module. Further, stochastic simulations of the dual-feedback network reveal highly synchronized damped oscillations (Figure S7
C) with cellular variations due to intrinsic noise becoming significant only when the system size is drastically reduced (Figure 7C
).
B signaling module. Further, stochastic simulations of the dual-feedback network reveal highly synchronized damped oscillations (Figure S7
C) with cellular variations due to intrinsic noise becoming significant only when the system size is drastically reduced (Figure 7C
).
To show that our results are not limited to the conceptual NF- B model introduced above, we simulated the more detailed stochastic NF-
B model introduced above, we simulated the more detailed stochastic NF- B model formulated in [32], which explicitly incorporates IKKK/IKK signaling cascade and NF-
B model formulated in [32], which explicitly incorporates IKKK/IKK signaling cascade and NF- B shuttling between the nucleus and the cytoplasm (see Methods and Figure S8
A). One of the key assumptions made in the model [32] is that the strong stochasticity of the NF-
B shuttling between the nucleus and the cytoplasm (see Methods and Figure S8
A). One of the key assumptions made in the model [32] is that the strong stochasticity of the NF- B response is caused by the slow and stochastic binding/dissociation of NF-
B response is caused by the slow and stochastic binding/dissociation of NF- B to the corresponding promoters of I
B to the corresponding promoters of I B
B , I
, I B
B , and A20 target genes. The slow rates chosen by the authors for these reactions lead to the high variability of oscillatory dynamics among cells (Figure S8
B). However, there is experimental evidence that the binding time of NF-
, and A20 target genes. The slow rates chosen by the authors for these reactions lead to the high variability of oscillatory dynamics among cells (Figure S8
B). However, there is experimental evidence that the binding time of NF- B may be significantly shorter, at least in certain types of cells. According to Fluorescence Recovery After Photobleaching (FRAP) measurements in HeLa cells [33], the typical time scale of NF-
B may be significantly shorter, at least in certain types of cells. According to Fluorescence Recovery After Photobleaching (FRAP) measurements in HeLa cells [33], the typical time scale of NF- B binding to the target promoters is on the order of a second rather than minutes, suggesting more rapid equilibration between the NF-
B binding to the target promoters is on the order of a second rather than minutes, suggesting more rapid equilibration between the NF- B-bound promoters and the pool of unbound nuclear NF-
B-bound promoters and the pool of unbound nuclear NF- B molecules. We found that increasing the binding and dissociation rates by
B molecules. We found that increasing the binding and dissociation rates by 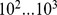 times profoundly changes the dynamics of the signaling system. NF-
times profoundly changes the dynamics of the signaling system. NF- B trajectories become more regular, suggesting that the behavior of individual cells translates more directly into the behavior of the population (Figure S8
C). After adjusting the binding/dissociation rates along with a few other parameters (Table S5), the updated model recapitulated the population response to chronic TNF
B trajectories become more regular, suggesting that the behavior of individual cells translates more directly into the behavior of the population (Figure S8
C). After adjusting the binding/dissociation rates along with a few other parameters (Table S5), the updated model recapitulated the population response to chronic TNF stimulation under various genetic conditions (WT,
stimulation under various genetic conditions (WT, 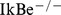 , and
, and 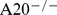 ) (Figure S9) in agreement with earlier experimental results [4], [21], [34].
) (Figure S9) in agreement with earlier experimental results [4], [21], [34].
To quantify the magnitude of the late oscillatory NF- B response to a chronic TNF
B response to a chronic TNF stimulation, we chose as a metric the average maximum peak-trough difference 5 hrs after initial stimulation. This quantity can be computed in two different ways. The mean single-cell variability can be characterized by the magnitude
stimulation, we chose as a metric the average maximum peak-trough difference 5 hrs after initial stimulation. This quantity can be computed in two different ways. The mean single-cell variability can be characterized by the magnitude 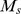 found by computing the maximum peak-trough differences for individual trajectories, and then averaging them over all trajectories:
found by computing the maximum peak-trough differences for individual trajectories, and then averaging them over all trajectories:
| (8) |
The population-level variability can be characterized by the magnitude 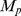 which is found by first computing an average trajectory and then computing its maximum peak-trough difference:
which is found by first computing an average trajectory and then computing its maximum peak-trough difference:
| (9) |
If the stochasticity is small, these two measures are similar, however for strong stochasticity they may differ significantly. Using these metrics, we first confirmed that for the parameter values adopted by [32], the model shows significant single-cell oscillations both in the 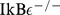 and in the WT, independently of the time delay in the I
and in the WT, independently of the time delay in the I B
B loop (
loop (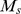 , Figure 8A
), but the population-averaged response shows significant oscillation dampening for the time delay around 45 min (
, Figure 8A
), but the population-averaged response shows significant oscillation dampening for the time delay around 45 min (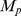 , Figure 8C
). However, for our re-parameterized model with fast binding/dissociation, the stochasticity of individual trajectories is small, and both metrics show similar trend: the amplitude of oscillations in the WT is strongly suppressed at the optimal time delay of 45 min both for the population average (Figure 8B
) and the individual cells (Figure 8D
), which falls within the margin of error of our experimental results (Figure 3D
).
, Figure 8C
). However, for our re-parameterized model with fast binding/dissociation, the stochasticity of individual trajectories is small, and both metrics show similar trend: the amplitude of oscillations in the WT is strongly suppressed at the optimal time delay of 45 min both for the population average (Figure 8B
) and the individual cells (Figure 8D
), which falls within the margin of error of our experimental results (Figure 3D
).
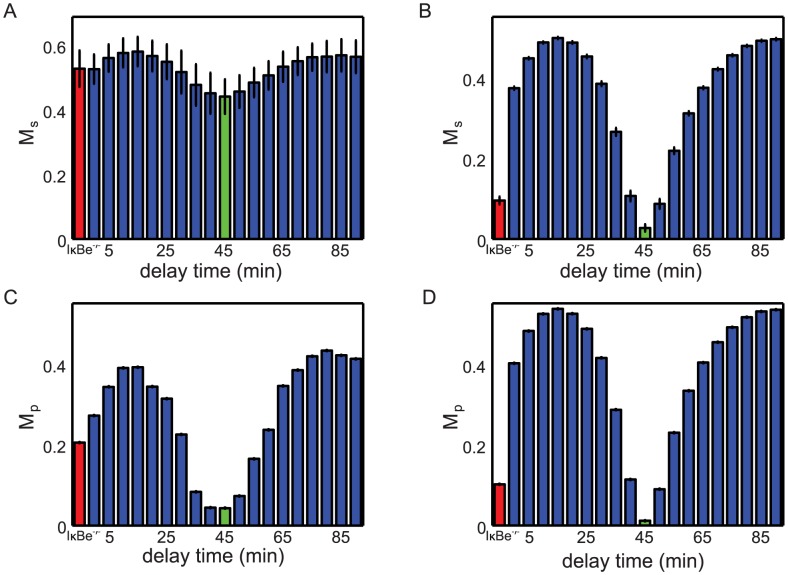
Figure 8. Effect of delay time on damped NF- B oscillations in the detailed NF-
B oscillations in the detailed NF- B model.
B model.
Magnitudes of single-cell oscillations 5 hours after stimulation (A,B) and of population averaged oscillations (C,D) are shown for the 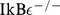 knockout (red bar) and in the WT for different time delays in the I
knockout (red bar) and in the WT for different time delays in the I B
B feedback loop (blue bars) with original (A,C) and adjusted (B,D) parameter values. The optimal time delay of 45 min is shown by the green bar. Each bar represents the average of nuclear NF-
feedback loop (blue bars) with original (A,C) and adjusted (B,D) parameter values. The optimal time delay of 45 min is shown by the green bar. Each bar represents the average of nuclear NF- B variation for 500 single cell trajectories. Error bars represent
B variation for 500 single cell trajectories. Error bars represent  one standard deviation.
one standard deviation.
Discussion
In this work we have developed a minimal model of the NF- B signaling pathway that uses a small number of reactions (some of them compound) thus making it amenable to mathematical analysis. Previously, another simplified model of NF-
B signaling pathway that uses a small number of reactions (some of them compound) thus making it amenable to mathematical analysis. Previously, another simplified model of NF- B signaling was developed in which a massive overshoot in I
B signaling was developed in which a massive overshoot in I B
B resulted in an effective slowing of signaling dynamics [35], and produced spiky oscillations that are not seen in physiological conditions. Our model, which utilizes an explicit time delay, recapitulates experimentally observed signaling behavior. It demonstrates that models with explicit time delays can be useful for investigating the mechanistic basis of the dynamic behavior of signaling pathways.
resulted in an effective slowing of signaling dynamics [35], and produced spiky oscillations that are not seen in physiological conditions. Our model, which utilizes an explicit time delay, recapitulates experimentally observed signaling behavior. It demonstrates that models with explicit time delays can be useful for investigating the mechanistic basis of the dynamic behavior of signaling pathways.
Using this model, we explored the potential role of NF- B oscillations which are observed in a variant of the NF-
B oscillations which are observed in a variant of the NF- B signaling module with the secondary negative feedback loop involving I
B signaling module with the secondary negative feedback loop involving I B
B , disabled. In particular, we addressed the question of whether the frequency of these oscillations contains information, as in neurons which sometimes encode information in the frequency of action potentials [36] and in the activation of the transcription factor NF-AT which is responsive to the number of
, disabled. In particular, we addressed the question of whether the frequency of these oscillations contains information, as in neurons which sometimes encode information in the frequency of action potentials [36] and in the activation of the transcription factor NF-AT which is responsive to the number of  pulses [37]. By analyzing the oscillatory response of a system regulated solely by the I
pulses [37]. By analyzing the oscillatory response of a system regulated solely by the I B
B -mediated negative feedback loop, we found that both the frequency and the decay rate of the oscillations produced by this system are highly dependent on the internal parameters of the circuit, but are not sensitive to changes in the input signal levels. This result suggests that the oscillatory frequency does not encode information about the stimulus. Hence, stimulus-specific gene expression is unlikely determined by stimulus-specific frequencies of NF-
-mediated negative feedback loop, we found that both the frequency and the decay rate of the oscillations produced by this system are highly dependent on the internal parameters of the circuit, but are not sensitive to changes in the input signal levels. This result suggests that the oscillatory frequency does not encode information about the stimulus. Hence, stimulus-specific gene expression is unlikely determined by stimulus-specific frequencies of NF- B oscillations. If there is a temporal code for stimulus-specific gene expression it is unlikely to involve frequency modulation, but may involve amplitude modulation over time.
B oscillations. If there is a temporal code for stimulus-specific gene expression it is unlikely to involve frequency modulation, but may involve amplitude modulation over time.
When a second feedback regulator, I B
B , is added to the model, the oscillations caused by a persistent stimulation are significantly dampened, in agreement with our earlier findings [21]. By performing an optimization procedure, we determined that the specific experimentally observed parameter values for the synthesis delay and peak protein abundance of both I
, is added to the model, the oscillations caused by a persistent stimulation are significantly dampened, in agreement with our earlier findings [21]. By performing an optimization procedure, we determined that the specific experimentally observed parameter values for the synthesis delay and peak protein abundance of both I B isoforms correspond to maximal efficiency of damping. These findings suggest that the second feedback (I
B isoforms correspond to maximal efficiency of damping. These findings suggest that the second feedback (I B
B ) has evolved to produce damping of the oscillatory behavior of the first feedback (I
) has evolved to produce damping of the oscillatory behavior of the first feedback (I B
B ). Furthermore, we demonstrated that this finding is not limited to our simple model, but can be expanded to more complex models. For example, in a recent model by [32] with fast binding/unbinding rates of NF-
). Furthermore, we demonstrated that this finding is not limited to our simple model, but can be expanded to more complex models. For example, in a recent model by [32] with fast binding/unbinding rates of NF- B the secondary I
B the secondary I B
B feedback leads to a reduction in NF-
feedback leads to a reduction in NF- B oscillations in individual cells. However, cell-cell variability and extrinsic noise can further reduce NF-
B oscillations in individual cells. However, cell-cell variability and extrinsic noise can further reduce NF- B oscillations on a population level.
B oscillations on a population level.
From the evolutionary perspective, we have a peculiar situation in which a signaling module apparently first developed a negative feedback loop that made it prone to oscillations, and then added a secondary loop which mitigated these oscillations. This brings the question, if oscillatory responses are not beneficial to the cell, why has the primary negative feedback appeared in the system in the first place? By comparing transient response of several variants of signaling modules (0-, 1- and 2-feedback loop designs) in the presence of stochastic fluctuations we showed that the primary negative feedback loop involving the release of sequestered NF- B proteins created a strong, rapid, and robust response to short pulses of active IKK signal. However, for longer signals a single-feedback-loop system exhibits a suboptimal “temporal dose response behavior” that leads to a quantized response to signals of different durations. In contrast, the dual feedback network generates response durations that are proportional to the stimulus input durations. Fine-tuning of the response duration may be reflective of a signaling code in which duration of NF-
B proteins created a strong, rapid, and robust response to short pulses of active IKK signal. However, for longer signals a single-feedback-loop system exhibits a suboptimal “temporal dose response behavior” that leads to a quantized response to signals of different durations. In contrast, the dual feedback network generates response durations that are proportional to the stimulus input durations. Fine-tuning of the response duration may be reflective of a signaling code in which duration of NF- B activity may be a key determinant of stimulus-specific gene expression program.
B activity may be a key determinant of stimulus-specific gene expression program.
Cytokines such as TNF facilitate adaptive responses at the effector stages [38]. The evolution of cytokines is associated with the evolution of an adaptive immune system to allow for coordination of various cell types [39]. Unlike pathogen exposure, cytokines are produced during varying amounts of time thereby generating time-varying signals. Our analysis showed that the dual negative feedback module is more capable at distinguishing differences in the duration of incoming signals. This function is important for the transduction of cytokine signals, but not pathogen signals. Our BLASTP analysis indeed demonstrates that the evolution of the dual negative feedback system may correlate with the evolution of adaptive immunity.
facilitate adaptive responses at the effector stages [38]. The evolution of cytokines is associated with the evolution of an adaptive immune system to allow for coordination of various cell types [39]. Unlike pathogen exposure, cytokines are produced during varying amounts of time thereby generating time-varying signals. Our analysis showed that the dual negative feedback module is more capable at distinguishing differences in the duration of incoming signals. This function is important for the transduction of cytokine signals, but not pathogen signals. Our BLASTP analysis indeed demonstrates that the evolution of the dual negative feedback system may correlate with the evolution of adaptive immunity.
Methods
Derivation of the deterministic model
Using mass action kinetics, the full set of reactions for the dual feedback loop NF- B system (Tables 2, 4) can be expressed by the following ODEs:
B system (Tables 2, 4) can be expressed by the following ODEs:
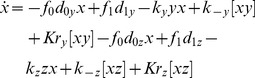 |
(10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
The total number of 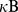 binding sites on each promoter is conserved:
binding sites on each promoter is conserved:
| (19) |
| (20) |
We assume that the total amount of NF- B in the cell
B in the cell 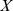 is conserved
is conserved
| (21) |
Since the number of binding sites available for NF- B protein is small, we can neglect the amount of NF-
B protein is small, we can neglect the amount of NF- B bound to the I
B bound to the I B
B and I
and I B
B promoters, so
promoters, so
| (22) |
Solving Eq. 22 for  yields:
yields:
| (23) |
DNA binding reactions are usually fast, so we can assume that they are at quasi-equilibrium at all times,
| (24) |
| (25) |
Using Eqs. 19 and 20, substituting into Eqs. 24 and 25, and solving for 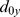 ,
, 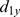 ,
, 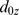 ,
, 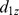 yields:
yields:
| (26) |
| (27) |
| (28) |
| (29) |
where 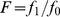 .
.
We also assume quasi-equilibrium for I B NF-
B NF- B binding reactions,
B binding reactions,
| (30) |
| (31) |
Substituting 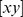 and
and 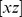 from Eqs. 30 and 31 into Eq. 23 yields:
from Eqs. 30 and 31 into Eq. 23 yields:
| (32) |
Now we can solve Eq. 32 for 
| (33) |
and substitute it in Eqs. 12 and 16. These equations contain both fast and slow terms. However, it is easy to see that rate equations for variables 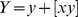 and
and 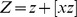 contain only slow terms:
contain only slow terms:
| (34) |
| (35) |
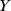 and
and 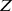 can in turn be expressed via
can in turn be expressed via 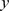 and
and  by:
by:
| (36) |
| (37) |
where 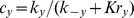 and
and 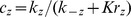 . Equations 34–35 combined with definitions Eqs. 26–29, 33, 36, and 37 represent a closed system of two delay-differential equations 2, 3 for the dual-feedback NF-
. Equations 34–35 combined with definitions Eqs. 26–29, 33, 36, and 37 represent a closed system of two delay-differential equations 2, 3 for the dual-feedback NF- B module. Setting
B module. Setting 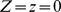 in these equations leaves us with a single delay-differential equation for the single feedback loop system Eq. 1.
in these equations leaves us with a single delay-differential equation for the single feedback loop system Eq. 1.
Details of the linear stability analysis
The fixed point  of Eq. (4) is given by the algebraic equation (6). Unfortunately, Eq. (6) does not permit finding
of Eq. (4) is given by the algebraic equation (6). Unfortunately, Eq. (6) does not permit finding  in explicit form. However, this calculation can be significantly simplified if the total number of NF-
in explicit form. However, this calculation can be significantly simplified if the total number of NF- B proteins is large, so
B proteins is large, so 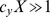 , then
, then  can be neglected as compared with total
can be neglected as compared with total  . Then
. Then 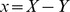 , and
, and 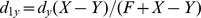 , and expression (5) for
, and expression (5) for  simplifies:
simplifies:
| (38) |
Now the stationary level of  can be obtained explicitly
can be obtained explicitly
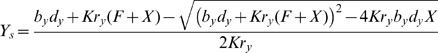 |
(39) |
The stability of this stationary solution is determined by the linearized equation (4) for a small perturbation  near
near 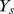 ,
,
| (40) |
where 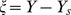 , subscript
, subscript  again indicates the delayed value of
again indicates the delayed value of  taken at time
taken at time  , and
, and  . Using formula (38) we obtain
. Using formula (38) we obtain
| (41) |
where 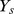 is given by Eq. (39). The eigenvalue
is given by Eq. (39). The eigenvalue 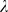 of the linearized equation (40) is found by substituting
of the linearized equation (40) is found by substituting 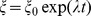 , yielding the transcendental equation
, yielding the transcendental equation
| (42) |
whose solution is given by Eq. (7).
Stochastic model formulation
For the analysis of a full NF- B system, we adopted the basic structure of the NF-
B system, we adopted the basic structure of the NF- B model formulated in [32] which in turn was based on the population-level model first proposed in [4]. The structure of the model is shown in Figure S8
A. In resting cells, NF-
B model formulated in [32] which in turn was based on the population-level model first proposed in [4]. The structure of the model is shown in Figure S8
A. In resting cells, NF- B is sequestered in the cytoplasm by I
B is sequestered in the cytoplasm by I B proteins. In response to TNF
B proteins. In response to TNF stimulation, IKKK protein becomes active, and activates IKK kinase. IKK phosphorylates I
stimulation, IKKK protein becomes active, and activates IKK kinase. IKK phosphorylates I B proteins targeting them for degradation. Upon degradation of I
B proteins targeting them for degradation. Upon degradation of I B proteins, NF-
B proteins, NF- B moves into the nucleus and activates hundreds of target genes. In the model, we focus on the dynamics of three genes associated with the negative feedback of the system. Following NF-
B moves into the nucleus and activates hundreds of target genes. In the model, we focus on the dynamics of three genes associated with the negative feedback of the system. Following NF- B activation, synthesized A20 proteins attenuate TNF
B activation, synthesized A20 proteins attenuate TNF signal by repressing IKKK and IKK transitions into their active states. NF-
signal by repressing IKKK and IKK transitions into their active states. NF- B also binds I
B also binds I B
B and I
and I B
B protein promoters, which following translation in the cytoplasm, translocate back into the nucleus and bind free NF-
protein promoters, which following translation in the cytoplasm, translocate back into the nucleus and bind free NF- B sequestering it out of the nucleus. In addition, I
B sequestering it out of the nucleus. In addition, I B proteins are directly responsible for NF-
B proteins are directly responsible for NF- B dissociation from the DNA.
B dissociation from the DNA.
The biological processes in the model were interpreted through stochastic and deterministic representations similar to [32]. Nuclear transport, complex formation, synthesis, transcription, and translation were described through a set of ordinary differential equations (Text S1). Regulation of gene activity through NF- B binding and dissociation from DNA was modeled using stochastic representation. The time-evolution of the system was accomplished through a hybrid simulation algorithm that uses Gillespie algorithm [29] to evaluate the state of stochastic processes and an ODE solver to compute the state of deterministic processes.
B binding and dissociation from DNA was modeled using stochastic representation. The time-evolution of the system was accomplished through a hybrid simulation algorithm that uses Gillespie algorithm [29] to evaluate the state of stochastic processes and an ODE solver to compute the state of deterministic processes.
Details of the BLASTP search for I B
B and I
and I B
B homologs
homologs
We performed two BLASTP searches (using default parameters) to search for I B
B and I
and I B
B homologs. The mouse I
homologs. The mouse I B
B protein sequence (gi28386026) was used as the query for the first search. The mouse I
protein sequence (gi28386026) was used as the query for the first search. The mouse I B
B protein sequence (gi2739158) was used as the query for the second search. We used an E-value of 1e-25 as a cutoff for both searches. Homologs for I
protein sequence (gi2739158) was used as the query for the second search. We used an E-value of 1e-25 as a cutoff for both searches. Homologs for I B
B were found in the organisms listed in Table S6, and homologs for I
were found in the organisms listed in Table S6, and homologs for I B
B were found in the organisms listed in Table S7.
were found in the organisms listed in Table S7.
Note that we selected only unique homologs for both I B
B and I
and I B
B in all vertebrates. We did not find unique I
in all vertebrates. We did not find unique I B
B homologue for several vertebrates. We expect that this is due to the fact that complete genomes are not currently available for these organisms. Table S8 lists the genome status (as of 6/1/11) of all organisms for which I
homologue for several vertebrates. We expect that this is due to the fact that complete genomes are not currently available for these organisms. Table S8 lists the genome status (as of 6/1/11) of all organisms for which I B
B or I
or I B
B homologs were found (http://www.ncbi.nlm.nih.gov/genomes/leuks.cgi).
homologs were found (http://www.ncbi.nlm.nih.gov/genomes/leuks.cgi).
Cell culture experiments
Immortalized murine embryonic fibroblasts [4] were chronically stimulated with 10 ng/mL TNF (Roche) and I B
B and I
and I B
B mRNA and protein levels were monitored by RNase Protection Assay (RPA) and Western Blot, respectively, as previously described [21]. RPA results for each time course were quantitated using ImageQuant software (GE Healthcare) and used to determine the time of half-maximal inducibility between basal and peak mRNA levels for I
mRNA and protein levels were monitored by RNase Protection Assay (RPA) and Western Blot, respectively, as previously described [21]. RPA results for each time course were quantitated using ImageQuant software (GE Healthcare) and used to determine the time of half-maximal inducibility between basal and peak mRNA levels for I B
B and I
and I B
B (Figure S2
A,B). Western Blot results were also quantitated with ImageQuant software and used to determine the time point of peak expression. The basal abundances of I
(Figure S2
A,B). Western Blot results were also quantitated with ImageQuant software and used to determine the time point of peak expression. The basal abundances of I B
B and I
and I B
B protein were determined via comparison to a standard curve of recombinant I
protein were determined via comparison to a standard curve of recombinant I B protein (R Tsu, JD Kearns, C Lynch, D Vu, K Ngo, S Basak, G Ghosh, A Hoffmann in preparation). The peak abundances of I
B protein (R Tsu, JD Kearns, C Lynch, D Vu, K Ngo, S Basak, G Ghosh, A Hoffmann in preparation). The peak abundances of I B
B and I
and I B
B were determined via multiplication of the basal value by the fold inducibility at the peak time point (Figure S2
C,D). Experimental levels of nuclear NF-
were determined via multiplication of the basal value by the fold inducibility at the peak time point (Figure S2
C,D). Experimental levels of nuclear NF- B in cells with only the I
B in cells with only the I B
B -mediated negative feedback loop intact and in wild-type cells containing both I
-mediated negative feedback loop intact and in wild-type cells containing both I B
B - and I
- and I B
B -mediated negative feedback were determined by EMSAs in [4].
-mediated negative feedback were determined by EMSAs in [4].
Supporting Information
Oscillations produced by the I
 B
B
 -mediated negative feedback system. (A)
-mediated negative feedback system. (A) 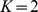 for
for 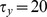 min,
min, 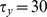 min, and
min, and 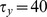 min and with (B)
min and with (B) 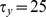 min for
min for 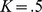 ,
, 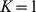 , and
, and 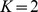 .
.
(EPS)
Representative experimental data for I
 B
B
 and I
and I
 B
B
 synthesis delays and feedback strengths. (A) mRNA synthesis for I
synthesis delays and feedback strengths. (A) mRNA synthesis for I B
B and I
and I B
B were measured by RNase Protection Assay in wild-type immortalized MEF cells in response to 10 ng/mL TNF chronic stimulation. (B) The RPA results were quantitated to determine the intensity of each band in the gel (ImageQuant, GE Healthcare). The highest intensity band in each set was set to 100% Activation and the other bands were normalized accordingly. The delay time to reach half maximal synthesis was calculated as the time at which the activation curve crossed the 50% level. A set of N = 10 replicate experiments were performed to calculate the global average. (C) The protein abundances for I
were measured by RNase Protection Assay in wild-type immortalized MEF cells in response to 10 ng/mL TNF chronic stimulation. (B) The RPA results were quantitated to determine the intensity of each band in the gel (ImageQuant, GE Healthcare). The highest intensity band in each set was set to 100% Activation and the other bands were normalized accordingly. The delay time to reach half maximal synthesis was calculated as the time at which the activation curve crossed the 50% level. A set of N = 10 replicate experiments were performed to calculate the global average. (C) The protein abundances for I B
B and I
and I B
B at their respective activation peaks in wild-type immortalized MEF cells chronically stimulated with 10 ng/mL TNF were measured by Western Blot analysis (I
at their respective activation peaks in wild-type immortalized MEF cells chronically stimulated with 10 ng/mL TNF were measured by Western Blot analysis (I B
B at 1 h and I
at 1 h and I B
B at 6 h) . Fold induction vs. basal state are shown below each gel and were calculated by quantitation of the band intensities and normalization to the 0 h band. (D) Bar plot of the average protein abundances from multiple Western Blot experiments for peak levels of I
at 6 h) . Fold induction vs. basal state are shown below each gel and were calculated by quantitation of the band intensities and normalization to the 0 h band. (D) Bar plot of the average protein abundances from multiple Western Blot experiments for peak levels of I B
B (N = 7) and I
(N = 7) and I B
B (N = 5). The basal state abundances were measured by comparison to a standard curve of recombinant I
(N = 5). The basal state abundances were measured by comparison to a standard curve of recombinant I B
B or I
or I B
B protein (JD Kearns, S Basak, C Lynch, A Hoffmann in preparation). Peak abundances were calculated by multiplying the quantitated fold induction (as in C) by the basal abundance. Error bars on the peak bars represent one standard deviation.
protein (JD Kearns, S Basak, C Lynch, A Hoffmann in preparation). Peak abundances were calculated by multiplying the quantitated fold induction (as in C) by the basal abundance. Error bars on the peak bars represent one standard deviation.
(EPS)
The ratio of peak I
 B
B
 protein levels to peak I
protein levels to peak I
 B
B
 protein levels (
protein levels (
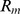 ) versus
) versus
 .
.
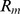 was determined for several values of
was determined for several values of  in the model simulations to determine the value of
in the model simulations to determine the value of  corresponding to
corresponding to 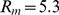 (The experimentally measured value for the ratio is
(The experimentally measured value for the ratio is 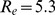 ). This value of
). This value of  (
(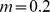 ) was used to plot the point in Figure 3D which indicates the experimental values of
) was used to plot the point in Figure 3D which indicates the experimental values of  and
and  .
.
(EPS)
Response of a no-feedback system with constitutive I
 B
B
 synthesis increased from
synthesis increased from
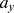 = 0.00185 nM/min to
= 0.00185 nM/min to
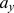 = 0.3 nM/min. The time series of
= 0.3 nM/min. The time series of  is shown for 15 min (red), 30 min (orange), 45 min (green), and persistent (blue) stimulation.
is shown for 15 min (red), 30 min (orange), 45 min (green), and persistent (blue) stimulation.
(EPS)
Coefficient of variation (CV) of nuclear NF-
 B levels. Comparison of the CV for peak and late-phase nuclear NF-
B levels. Comparison of the CV for peak and late-phase nuclear NF- B levels due to extrinsic variability in total NF-
B levels due to extrinsic variability in total NF- B (A,C) and IKK (B,D) for the single feedback and dual feedback network.
B (A,C) and IKK (B,D) for the single feedback and dual feedback network.
(EPS)
Comparison of ensemble-averaged runs of stochastic simulations with deterministic simulations for four different circuits. (A) no-feedback model, (B) single negative feedback model, (C) dual feedback system, (D) and auto-repressor system. Lines - deterministic simulations, symbols - stochastic simulations averaged over 200 runs.
(EPS)
Stochastic simulation results with 100,000 total NF-
 B molecules. Four NF-
B molecules. Four NF- B networks were considered: no feedback loops (A), only I
B networks were considered: no feedback loops (A), only I B
B -mediated negative feedback (B), the NF-
-mediated negative feedback (B), the NF- B network with both I
B network with both I B
B - and I
- and I B
B -mediated negative feedback (C), and an alternative auto-repressive network (D). The top panel in each group shows four typical runs of stochastic simulations for each network, the middle panel shows the mean and standard deviation for 200 runs of each network, and the bottom panel shows the corresponding coefficient of variation. The input signal, K(t), is switched from
-mediated negative feedback (C), and an alternative auto-repressive network (D). The top panel in each group shows four typical runs of stochastic simulations for each network, the middle panel shows the mean and standard deviation for 200 runs of each network, and the bottom panel shows the corresponding coefficient of variation. The input signal, K(t), is switched from 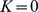 to
to 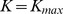 at
at 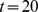 hrs. In A–C, the magnitude of external signal
hrs. In A–C, the magnitude of external signal 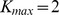 , in D,
, in D, 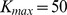 .
.
(EPS)
Oscillatory behavior from NF-
 B signaling system. (A) Diagram of the NF-
B signaling system. (A) Diagram of the NF- B signaling network model adopted from Paszek et. al (2010). In resting cells, NF-
B signaling network model adopted from Paszek et. al (2010). In resting cells, NF- B is sequestered in the cytoplasm by I
B is sequestered in the cytoplasm by I B proteins. In response to TNF
B proteins. In response to TNF stimulation, IKKK protein becomes active, activating IKK kinase. In turn, IKK phosphorilates I
stimulation, IKKK protein becomes active, activating IKK kinase. In turn, IKK phosphorilates I B proteins targeting them for degradation. Upon degradation of I
B proteins targeting them for degradation. Upon degradation of I B
B , NF-
, NF- B moves into the nucleus and activates hundreds of target genes. In the model, we describe the dynamics of three genes associated with the negative feedback of the system. Following NF-
B moves into the nucleus and activates hundreds of target genes. In the model, we describe the dynamics of three genes associated with the negative feedback of the system. Following NF- B activation, synthesized A20 proteins attenuate TNF
B activation, synthesized A20 proteins attenuate TNF signal by repressing IKKK and IKK transitions into their active states. NF-
signal by repressing IKKK and IKK transitions into their active states. NF- B also binds I
B also binds I B
B and I
and I B
B protein promoters, which following translation in the cytoplasm, translocate back into the nucleus and bind up free NF-
protein promoters, which following translation in the cytoplasm, translocate back into the nucleus and bind up free NF- B sequestering it out of the nucleus. In addition, I
B sequestering it out of the nucleus. In addition, I B proteins are directly responsible for NF-
B proteins are directly responsible for NF- B dissociation from the DNA. (B) Nuclear NF-
B dissociation from the DNA. (B) Nuclear NF- B levels in response to persistent stimulation as a function of time computed using Paszek et. al (2010) wildtype model. (C) Nuclear NF-
B levels in response to persistent stimulation as a function of time computed using Paszek et. al (2010) wildtype model. (C) Nuclear NF- B levels in response to persistent stimulation as a function of time computed using our re-parameterized model. Black curve represents an average of 500 cell trajectories.
B levels in response to persistent stimulation as a function of time computed using our re-parameterized model. Black curve represents an average of 500 cell trajectories.
(EPS)
Nuclear NF-
 B response in A20 and I
B response in A20 and I
 B
B
 knockout models to chronic TNF
knockout models to chronic TNF
 stimulation. The results for the updated model (C,D) shows close similarity, in NF-
stimulation. The results for the updated model (C,D) shows close similarity, in NF- B population dynamics, to the results obtained using Paszek et. al (2010) wildtype model (A,B) for both I
B population dynamics, to the results obtained using Paszek et. al (2010) wildtype model (A,B) for both I B
B knockout (A,C) and A20 knockout (B,D) models. Black trajectories represent the average of 500 cell trajectories.
knockout (A,C) and A20 knockout (B,D) models. Black trajectories represent the average of 500 cell trajectories.
(EPS)
Auto-repressor network reactions.
(PDF)
Auto-repressor network parameter values.
(PDF)
Organisms with homologs for I
 B
B
 . BLASTP analysis results.
. BLASTP analysis results.
(PDF)
Organisms with homologs for I
 B
B
 . BLASTP analysis results.
. BLASTP analysis results.
(PDF)
Additional model details. Extrinsic noise in dual negative feedback loop system and details of the full stochastic model.
(PDF)
Acknowledgments
We thank Matthew Bennett and William Mather for valuable discussions.
Funding Statement
This work was supported by the NIH, grants R01GM089976 and P50GM085764 (San Diego Center for Systems Biology). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Tyson JJ, Chen KC, Novak B (2003) Sniffers, buzzers, toggles and blinkers: dynamics of regulatory and signaling pathways in the cell. Current opinion in cell biology 15: 221–231. [DOI] [PubMed] [Google Scholar]
- 2. Shimojo H, Ohtsuka T, Kageyama R (2008) Oscillations in notch signaling regulate maintenance of neural progenitors. Neuron 58: 52–64. [DOI] [PubMed] [Google Scholar]
- 3. Lahav G, Rosenfeld N, Sigal A, Geva-Zatorsky N, Levine AJ, et al. (2004) Dynamics of the p53-mdm2 feedback loop in individual cells. Nature genetics 36: 147–150. [DOI] [PubMed] [Google Scholar]
- 4. Hoffmann A, Levchenko A, Scott ML, Baltimore D (2002) The IκB-NF-κB signaling module: Temporal control and selective gene activation. Science 298: 1241–1245. [DOI] [PubMed] [Google Scholar]
- 5. Nelson DE, Ihekwaba AEC, Elliott M, Johnson JR, Gibney CA, et al. (2004) Oscillations in NF-κB signaling control the dynamics of gene expression. Science 306: 704–708. [DOI] [PubMed] [Google Scholar]
- 6. Vogelstein B, Lane D, Levine AJ (2000) Surfing the p53 network. Nature 408: 307–310. [DOI] [PubMed] [Google Scholar]
- 7. Tergaonkar V (2006) NFκB pathway: A good signaling paradigm and therapeutic target. The International Journal of Biochemistry & Cell Biology 38: 1647–1653. [DOI] [PubMed] [Google Scholar]
- 8. Savageau MA (1974) Optimal design of feedback control by inhibition. Journal of Molecular Evolution 4: 139–156. [DOI] [PubMed] [Google Scholar]
- 9. Cai L, Dalal CK, Elowitz MB (2008) Frequency-modulated nuclear localization bursts coordinate gene regulation. Nature 455: 485–490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Ma L, Wagner J, Rice JJ, Hu W, Levine AJ, et al. (2005) A plausible model for the digital response of p53 to dna damage. Proceedings of the National Academy of Sciences of the United States of America 102: 14266–14271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Batchelor E, Mock C, Bhan I, Loewer A, Lahav G (2008) Recurrent initiation: a mechanism for triggering p53 pulses in response to dna damage. Molecular cell 30: 277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Barken D, Wang CJ, Kearns J, Cheong R, Hoffmann A, et al. (2005) Comment on “oscillations in NF-κB signaling control the dynamics of gene expression”. Science 308: 52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Ashall L, Horton CA, Nelson DE, Paszek P, Harper CV, et al. (2009) Pulsatile stimulation deter-mines timing and specificity of NF-κB-dependent transcription. Science 324: 242–246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Lander AD, Nie Q, Wan FY (2002) Do morphogen gradients arise by diffusion? Developmental Cell 2: 785–796. [DOI] [PubMed] [Google Scholar]
- 15. Kruse K, Pantazis P, Bollenbach T, Jlicher F, Gonzlez-Gaitn M (2004) Dpp gradient formation by dynamin-dependent endocytosis: receptor trafficking and the diffusion model. Development 131: 4843–4856. [DOI] [PubMed] [Google Scholar]
- 16. Arkin A, Ross J, McAdams HH (1998) Stochastic kinetic analysis of developmental pathway bi-furcation in phage λ-infected escherichia coli cells. Genetics 149: 1633–1648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Aurell E, Brown S, Johanson J, Sneppen K (2002) Stability puzzles in phage λ. Phys Rev E 65: 051914. [DOI] [PubMed] [Google Scholar]
- 18. Lipshtat A, Perets HB, Balaban NQ, Biham O (2005) Modeling of negative autoregulated genetic networks in single cells. Gene 347: 265–271. [DOI] [PubMed] [Google Scholar]
- 19. Ramsey SA, Smith JJ, Orrell D, Marelli M, Petersen TW, et al. (2006) Dual feedback loops in the gal regulon suppress cellular heterogeneity in yeast. Nature genetics 38: 1082–1087. [DOI] [PubMed] [Google Scholar]
- 20. Kim JR, Yoon Y, Cho KH (2008) Coupled feedback loops form dynamic motifs of cellular networks. Biophysical Journal 94: 359–365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Kearns JD, Basak S, Werner SL, Huang CS, Hoffmann A (2006) IκBε provides negative feedback to control NF-κB oscillations, signaling dynamics, and inflammatory gene expression. The Journal of Cell Biology 173: 659–664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Thattai M, Van Oudenaarden A (2001) Intrinsic noise in gene regulatory networks. Proceedings of the National Academy of Sciences 98: 8614–8619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Swain PS, Elowitz MB, Siggia ED (2002) Intrinsic and extrinsic contributions to stochasticity in gene expression. Proceedings of the National Academy of Sciences 99: 12795–12800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Elowitz MB, Levine AJ, Siggia ED, Swain PS (2002) Stochastic gene expression in a single cell. Science Signalling 297: 1183–1186. [DOI] [PubMed] [Google Scholar]
- 25. Rosenfeld N, Young JW, Alon U, Swain PS, Elowitz MB (2005) Gene regulation at the single-cell level. Science Signalling 307: 1962–1965. [DOI] [PubMed] [Google Scholar]
- 26. Volfson D, Marciniak J, Blake WJ, Ostroff N, Tsimring LS, et al. (2005) Origins of extrinsic variability in eukaryotic gene expression. Nature 439: 861–864. [DOI] [PubMed] [Google Scholar]
- 27. Hasty J, Pradines J, Dolnik M, Collins JJ (2000) Noise-based switches and amplifiers for gene expression. Proceedings of the National Academy of Sciences 97: 2075–2080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Dower S, Qwarnstrom E (2003) Signalling networks, inflammation and innate immunity. Biochemical Society Transactions 31: 1462–1471. [DOI] [PubMed] [Google Scholar]
- 29. Gillespie DT (1977) Exact stochastic simulation of coupled chemical reactions. Journal of Physical Chemistry 81: 2340–2361. [Google Scholar]
- 30. Bratsun D, Volfson D, Tsimring LS, Hasty J (2005) Delay-induced stochastic oscillations in gene regulation. Proc Natl Acad Sci U S A 102: 14593–14598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Doncic A, Ben-Jacob E, Barkai N (2006) Noise resistance in the spindle assembly checkpoint. Molecular systems biology 2: 2006.0027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Paszek P, Ryan S, Ashall L, Sillitoe K, Harper C, et al. (2010) Population robustness arising from cellular heterogeneity. Proc Natl Acad Sci U S A 107: 11644–11649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Bosisio D, Marazzi I, Agresti A, Shimizu N, Bianchi ME, et al. (2006) A hyper-dynamic equilibrium between promoter-bound and nucleoplasmic dimers controls nf-[kappa]b-dependent gene activity. EMBO J 25: 798–810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Werner SL, Kearns JD, Zadorozhnaya V, Lynch C, ODea E, et al. (2008) Encoding NF-κB temporal control in response to TNF: distinct roles for the negative regulators IκBα and a20. Genes & Development 22: 2093–2101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Krishna S, Jensen MH, Sneppen K (2006) Minimal model of spiky oscillations in nf-κb signaling. Proceedings of the National Academy of Sciences 103: 10840–10845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Bean BP (2007) The action potential in mammalian central neurons. Nature Reviews Neuroscience 8: 451–465. [DOI] [PubMed] [Google Scholar]
- 37. Dolmetsch RE, Xu K, Lewis RS, et al. (1998) Calcium oscillations increase the efficiency and specificity of gene expression. Nature 392: 933–935. [DOI] [PubMed] [Google Scholar]
- 38. Medzhitov R, Janeway CA Jr (1997) Innate immunity: impact on the adaptive immune response. Current opinion in immunology 9: 4–9. [DOI] [PubMed] [Google Scholar]
- 39.Murphy KM, Travers P, Walport M, et al.. (2012) Janeway's immunobiology, volume 7. New York, NY, USA : Garland Science.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Oscillations produced by the I
 B
B
 -mediated negative feedback system. (A)
-mediated negative feedback system. (A) 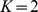 for
for 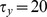 min,
min, 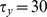 min, and
min, and 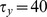 min and with (B)
min and with (B) 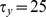 min for
min for 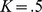 ,
, 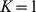 , and
, and 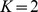 .
.
(EPS)
Representative experimental data for I
 B
B
 and I
and I
 B
B
 synthesis delays and feedback strengths. (A) mRNA synthesis for I
synthesis delays and feedback strengths. (A) mRNA synthesis for I B
B and I
and I B
B were measured by RNase Protection Assay in wild-type immortalized MEF cells in response to 10 ng/mL TNF chronic stimulation. (B) The RPA results were quantitated to determine the intensity of each band in the gel (ImageQuant, GE Healthcare). The highest intensity band in each set was set to 100% Activation and the other bands were normalized accordingly. The delay time to reach half maximal synthesis was calculated as the time at which the activation curve crossed the 50% level. A set of N = 10 replicate experiments were performed to calculate the global average. (C) The protein abundances for I
were measured by RNase Protection Assay in wild-type immortalized MEF cells in response to 10 ng/mL TNF chronic stimulation. (B) The RPA results were quantitated to determine the intensity of each band in the gel (ImageQuant, GE Healthcare). The highest intensity band in each set was set to 100% Activation and the other bands were normalized accordingly. The delay time to reach half maximal synthesis was calculated as the time at which the activation curve crossed the 50% level. A set of N = 10 replicate experiments were performed to calculate the global average. (C) The protein abundances for I B
B and I
and I B
B at their respective activation peaks in wild-type immortalized MEF cells chronically stimulated with 10 ng/mL TNF were measured by Western Blot analysis (I
at their respective activation peaks in wild-type immortalized MEF cells chronically stimulated with 10 ng/mL TNF were measured by Western Blot analysis (I B
B at 1 h and I
at 1 h and I B
B at 6 h) . Fold induction vs. basal state are shown below each gel and were calculated by quantitation of the band intensities and normalization to the 0 h band. (D) Bar plot of the average protein abundances from multiple Western Blot experiments for peak levels of I
at 6 h) . Fold induction vs. basal state are shown below each gel and were calculated by quantitation of the band intensities and normalization to the 0 h band. (D) Bar plot of the average protein abundances from multiple Western Blot experiments for peak levels of I B
B (N = 7) and I
(N = 7) and I B
B (N = 5). The basal state abundances were measured by comparison to a standard curve of recombinant I
(N = 5). The basal state abundances were measured by comparison to a standard curve of recombinant I B
B or I
or I B
B protein (JD Kearns, S Basak, C Lynch, A Hoffmann in preparation). Peak abundances were calculated by multiplying the quantitated fold induction (as in C) by the basal abundance. Error bars on the peak bars represent one standard deviation.
protein (JD Kearns, S Basak, C Lynch, A Hoffmann in preparation). Peak abundances were calculated by multiplying the quantitated fold induction (as in C) by the basal abundance. Error bars on the peak bars represent one standard deviation.
(EPS)
The ratio of peak I
 B
B
 protein levels to peak I
protein levels to peak I
 B
B
 protein levels (
protein levels (
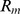 ) versus
) versus
 .
.
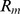 was determined for several values of
was determined for several values of  in the model simulations to determine the value of
in the model simulations to determine the value of  corresponding to
corresponding to 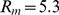 (The experimentally measured value for the ratio is
(The experimentally measured value for the ratio is 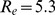 ). This value of
). This value of  (
(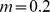 ) was used to plot the point in Figure 3D which indicates the experimental values of
) was used to plot the point in Figure 3D which indicates the experimental values of  and
and  .
.
(EPS)
Response of a no-feedback system with constitutive I
 B
B
 synthesis increased from
synthesis increased from
 = 0.00185 nM/min to
= 0.00185 nM/min to
 = 0.3 nM/min. The time series of
= 0.3 nM/min. The time series of  is shown for 15 min (red), 30 min (orange), 45 min (green), and persistent (blue) stimulation.
is shown for 15 min (red), 30 min (orange), 45 min (green), and persistent (blue) stimulation.
(EPS)
Coefficient of variation (CV) of nuclear NF-
 B levels. Comparison of the CV for peak and late-phase nuclear NF-
B levels. Comparison of the CV for peak and late-phase nuclear NF- B levels due to extrinsic variability in total NF-
B levels due to extrinsic variability in total NF- B (A,C) and IKK (B,D) for the single feedback and dual feedback network.
B (A,C) and IKK (B,D) for the single feedback and dual feedback network.
(EPS)
Comparison of ensemble-averaged runs of stochastic simulations with deterministic simulations for four different circuits. (A) no-feedback model, (B) single negative feedback model, (C) dual feedback system, (D) and auto-repressor system. Lines - deterministic simulations, symbols - stochastic simulations averaged over 200 runs.
(EPS)
Stochastic simulation results with 100,000 total NF-
 B molecules. Four NF-
B molecules. Four NF- B networks were considered: no feedback loops (A), only I
B networks were considered: no feedback loops (A), only I B
B -mediated negative feedback (B), the NF-
-mediated negative feedback (B), the NF- B network with both I
B network with both I B
B - and I
- and I B
B -mediated negative feedback (C), and an alternative auto-repressive network (D). The top panel in each group shows four typical runs of stochastic simulations for each network, the middle panel shows the mean and standard deviation for 200 runs of each network, and the bottom panel shows the corresponding coefficient of variation. The input signal, K(t), is switched from
-mediated negative feedback (C), and an alternative auto-repressive network (D). The top panel in each group shows four typical runs of stochastic simulations for each network, the middle panel shows the mean and standard deviation for 200 runs of each network, and the bottom panel shows the corresponding coefficient of variation. The input signal, K(t), is switched from 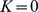 to
to 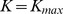 at
at 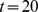 hrs. In A–C, the magnitude of external signal
hrs. In A–C, the magnitude of external signal 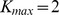 , in D,
, in D, 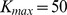 .
.
(EPS)
Oscillatory behavior from NF-
 B signaling system. (A) Diagram of the NF-
B signaling system. (A) Diagram of the NF- B signaling network model adopted from Paszek et. al (2010). In resting cells, NF-
B signaling network model adopted from Paszek et. al (2010). In resting cells, NF- B is sequestered in the cytoplasm by I
B is sequestered in the cytoplasm by I B proteins. In response to TNF
B proteins. In response to TNF stimulation, IKKK protein becomes active, activating IKK kinase. In turn, IKK phosphorilates I
stimulation, IKKK protein becomes active, activating IKK kinase. In turn, IKK phosphorilates I B proteins targeting them for degradation. Upon degradation of I
B proteins targeting them for degradation. Upon degradation of I B
B , NF-
, NF- B moves into the nucleus and activates hundreds of target genes. In the model, we describe the dynamics of three genes associated with the negative feedback of the system. Following NF-
B moves into the nucleus and activates hundreds of target genes. In the model, we describe the dynamics of three genes associated with the negative feedback of the system. Following NF- B activation, synthesized A20 proteins attenuate TNF
B activation, synthesized A20 proteins attenuate TNF signal by repressing IKKK and IKK transitions into their active states. NF-
signal by repressing IKKK and IKK transitions into their active states. NF- B also binds I
B also binds I B
B and I
and I B
B protein promoters, which following translation in the cytoplasm, translocate back into the nucleus and bind up free NF-
protein promoters, which following translation in the cytoplasm, translocate back into the nucleus and bind up free NF- B sequestering it out of the nucleus. In addition, I
B sequestering it out of the nucleus. In addition, I B proteins are directly responsible for NF-
B proteins are directly responsible for NF- B dissociation from the DNA. (B) Nuclear NF-
B dissociation from the DNA. (B) Nuclear NF- B levels in response to persistent stimulation as a function of time computed using Paszek et. al (2010) wildtype model. (C) Nuclear NF-
B levels in response to persistent stimulation as a function of time computed using Paszek et. al (2010) wildtype model. (C) Nuclear NF- B levels in response to persistent stimulation as a function of time computed using our re-parameterized model. Black curve represents an average of 500 cell trajectories.
B levels in response to persistent stimulation as a function of time computed using our re-parameterized model. Black curve represents an average of 500 cell trajectories.
(EPS)
Nuclear NF-
 B response in A20 and I
B response in A20 and I
 B
B
 knockout models to chronic TNF
knockout models to chronic TNF
 stimulation. The results for the updated model (C,D) shows close similarity, in NF-
stimulation. The results for the updated model (C,D) shows close similarity, in NF- B population dynamics, to the results obtained using Paszek et. al (2010) wildtype model (A,B) for both I
B population dynamics, to the results obtained using Paszek et. al (2010) wildtype model (A,B) for both I B
B knockout (A,C) and A20 knockout (B,D) models. Black trajectories represent the average of 500 cell trajectories.
knockout (A,C) and A20 knockout (B,D) models. Black trajectories represent the average of 500 cell trajectories.
(EPS)
Auto-repressor network reactions.
(PDF)
Auto-repressor network parameter values.
(PDF)
Organisms with homologs for I
 B
B
 . BLASTP analysis results.
. BLASTP analysis results.
(PDF)
Organisms with homologs for I
 B
B
 . BLASTP analysis results.
. BLASTP analysis results.
(PDF)
Additional model details. Extrinsic noise in dual negative feedback loop system and details of the full stochastic model.
(PDF)