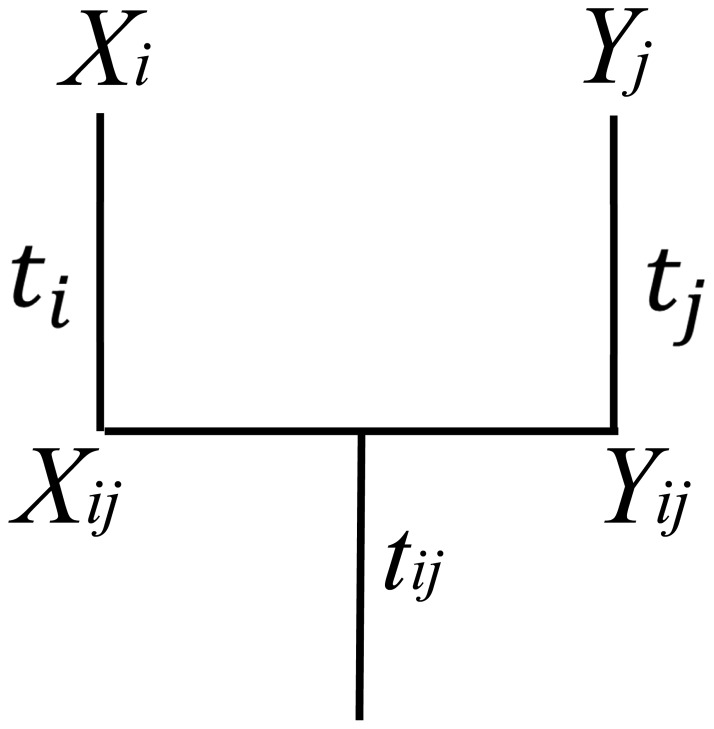Abstract
Background
Phylogenetic comparative methods (PCMs) have been applied widely in analyzing data from related species but their fit to data is rarely assessed.
Question
Can one determine whether any particular comparative method is typically more appropriate than others by examining comparative data sets?
Data
I conducted a meta-analysis of 122 phylogenetic data sets found by searching all papers in JEB, Blackwell Synergy and JSTOR published in 2002–2005 for the purpose of assessing the fit of PCMs. The number of species in these data sets ranged from 9 to 117.
Analysis Method
I used the Akaike information criterion to compare PCMs, and then fit PCMs to bivariate data sets through REML analysis. Correlation estimates between two traits and bootstrapped confidence intervals of correlations from each model were also compared.
Conclusions
For phylogenies of less than one hundred taxa, the Independent Contrast method and the independent, non-phylogenetic models provide the best fit.For bivariate analysis, correlations from different PCMs are qualitatively similar so that actual correlations from real data seem to be robust to the PCM chosen for the analysis. Therefore, researchers might apply the PCM they believe best describes the evolutionary mechanisms underlying their data.
Introduction
Over the past 20 years, many methods have been developed for incorporating phylogenies in comparative analysis. One of the most popular methods was proposed by Felsenstein and is known as the Felsenstein Independent Contrasts method (FIC), which assumes that trait values change according to the Brownian-motion process [1].
Cheverud et al. applied a general network autocorrelation model (PA) to phylogenetic comparative analysis, dividing the trait value (T) into an inherited phylogenetic value (P) and an independent specific value (S) [2] (see also [3]). Martins and Hansen proposed a phylogenetic generalized least square model (PGLS) assuming an Ornstein-Uhlenbeck (OU) process for the evolutionary change along the phylogeny. Such a model imagines that there is a rubber-band like process drawing extreme values back towards a common optimum mean value for the trait [4]. More recent work continues to develop this OU model [5], [6]. The phylogenetic mixed model (PMM) was first proposed by Lynch [7] and clarified by Housworth et al. for a single trait [8], and in the univariate case is identical to Pagel's lambda method [9]. The model allows for one component of the trait to follow a Brownian motion process along the phylogeny and a second component to be independent of the phylogeny. The model estimates how much of the trait is due to each component.
The purpose of this article is to compare the fit of these various methods for incorporating the phylogeny to comparative data found in the literature. Can one tell, by examining data typically collected for a comparative analysis, that one comparative method is decidedly more appropriate than another? Furthermore, comparative methods are most commonly used to examine two or more traits measured on the same set of species, but not all comparative methods have had their bivariate analogs delineated. I describe the appropriate bivariate variance-covariance structure for each model, some of which were previously unknown. I consider the use of PCMs in bivariate analyses where the parameter of interest is the correlation between two traits for a group of species, with the goal of determining the effect of model choice on the estimates of correlations. Are the correlation estimates qualitatively concordant (having the same sign) or do the methods give wildly different correlation estimates for given real data sets?
Modifications are required to three of these methods in order for the AIC comparisons to be valid [10]. I make a trivial modification to FIC to get maximum likelihood rather than restricted maximum likelihood estimates. I make a more substantial modification to the autocorrelation model by not normalizing the data in advance of determining its error structure. As the OU process should recover the Brownian motion process when the constraint parameter tends to zero, I make a modification to the PGLS as given in [4] so that this property is preserved. This same modification was used in [5].
Methods and Materials
Data Selection
I searched for published phylogenetic data sets in JEB, Blackwell Synergy and JSTOR using the keywords: ((Comparative methods OR Comparative analysis) AND independent contrasts) for 2002–2005. I included only articles that contained a phylogeny and the raw data for continuously distributed traits. All data sets contained averaged trait values; some also provided sample sizes and standard deviations or standard errors. These criteria yielded 43 articles, which were pruned further by eliminating studies where the species were from more than one order (so as to increase the chance that the species experienced a single model of evolution). Note that the choice of order as the cut-off is arbitrary; other authors have used other cutoffs such as families [11] and genera [5]. The final assemblage of data sets included 122 traits (some papers had multiple traits) and 47 phylogenetic trees. Data set size ranged from 9 to 117 species. The flow of information through the different phases of a systematic review is reported in Figure S1 in supporting information section. The references for the data sets are listed in Table [11]–[34].
Table 1. References for the meta analysis.
| References | Size | Species |
| [11] | 20 | Centrarchid fishes |
| [12] | 17 | Tropical Savannah bat |
| [13] | 19 | Tribe collinsieae |
| [14] | 37 | Tinamous |
| [15] | 24 | Lizards |
| [16] | 34 | Lizards |
| [17] | 11 | Macaranga ant-plants |
| [18] | 27 | Ungulates macropods |
| [19] | 10 | Drosophila |
| [20] | 29 | Pine |
| [21] | 40 | Parasitoid wasps |
| [22] | 14 | Notothenioid fishes |
| [23] | 12 | Gobies |
| [24] | 14 | Snow skinks |
| [25] | 17 | Anurans |
| [26] | 20 | Drosophila |
| [27] | 17 | Lizard |
| [28] | 22 | Neotropical marsupials |
| [29] | 117 | Diurnal raptors |
| [30] | 21 | Cnidaria |
| [31] | 18 | Ungulates |
| [32] | 37 | Woodcreepers |
| [33] | 9 | Lizards |
| [34] | 42 | Figs |
Phylogenies and comparative data are collected from the literature. The sample sizes (the number of the taxa) are shown is the second column.
The Phylogenetic Similarity Matrix G
PCM approaches typically require a phylogeny with branch lengths. To recover this, I used a ruler to measure the branch lengths. Some of the phylogenies were chronograms, where branch length is proportional to time, and others were cladograms; the former would be expected to have better branch lengths for PCM. I converted each phylogeny into a similarity matrix G. The diagonal elements of G,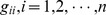 
, represent the correlation of a species with itself and so equal 1.0. The off-diagonal elements 
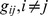, represent the relative evolutionary time shared by two species 
and 
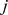so that 
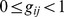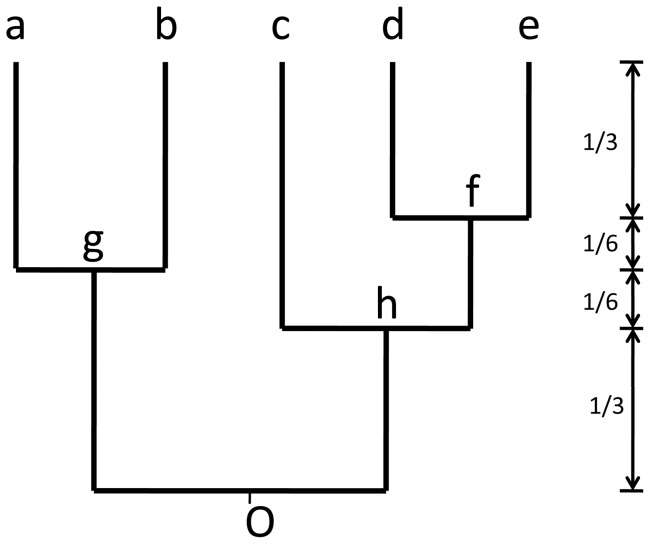
when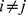 
. Figure shows a rooted phylogeny of 5 taxa with the assigned branch lengths.
Figure 1. A rooted phylogenetic tree of 5 taxa.
Tips a, b, c, d, e; interior nodes f, g, h and the root O.
The associated similarity matrix G is
 |
Statistical Model and Statistical Fit by MLE Estimation
Univariate Model
Given the assumption of a Markov process of trait evolution, trait values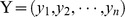 
are assumed to follow the multivariate normal distribution
 |
with the overall mean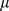 
and variance 
. 
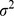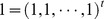is the vector of ones.
Each PCM results in a different variance-covariance structure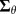 
, for the data:
ID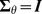 
, the identity matrix.
FIC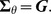 
PMM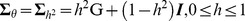 
.
PA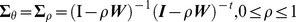
.
OU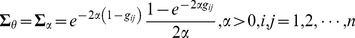 
.
Several of the PCMs have a free parameter (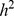
for PMM, 
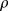for PA, 
for OU); for simplicity, I refer to this parameter as 
. Note that for FIC, I make a trivial modification to get maximum likelihood rather than restricted maximum likelihood estimates. For PA, W is the connectivity matrix [2]. For OU,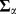 
is identical to the covariance structure in [5].
The negative log likelihood function is
 |
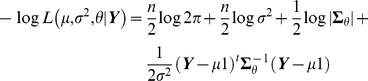where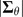 
is the determinant of 
.
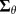The MLEs for the mean and variance are the function of 
where
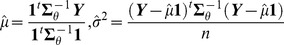, respectively.
The MLE estimator 
is obtained by optimizing the negative log likelihood function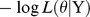 
on the domains: 
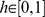for PMM, 
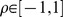for PA, and 
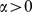for OU, respectively.
Bivariate Model
The bivariate model for traits X and Y measured at time t has a general form. Let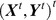 
follow a multivariate normal distribution with mean 
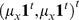and a 2n by 2n covariance matrix 
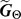where 
represents the model-specific parameters in the variance-covariance structure. The statistical model is
 |
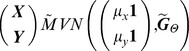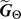for each model is
ID
 |
.
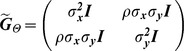FIC
 |
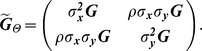PMM
 |
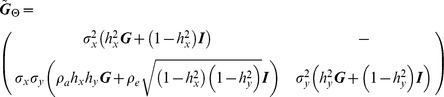where the correlation between traits X and Y is
 |
PA
 |
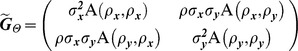where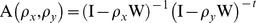 
.
OU
 |
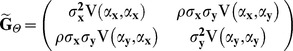where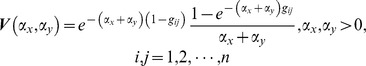 
.
The negative log likelihood function is
 |
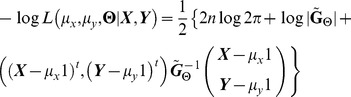where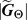 
is the determinant of 
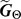. I use restricted maximum likelihood methods (REML) to estimate the correlation between two traits, as adjusted by the effect of the phylogeny. REML eliminates the need to estimate means and often produces less bias in the variances and correlation estimators. I used Powell's method to optimize the maximum likelihood estimators (after reducing the dimension of the search by solving for some parameters in terms of others; details available upon request). This method uses one-dimensional line searches in increasingly independent best directions, while periodically resetting the directions to be orthogonal. It is fast and efficient when the function is quadratic or close to quadratic, as likelihood functions often are close to their maximum [35]–[36]. There is no published maximum likelihood method for bivariate PA and OU. To create one, I propose the appropriate variance-covariance structure for these two methods:
PA:
The univariate phylogenetic autoregressive model proposed by Cheverud et al. [2] adapted the spatial autocorrelation model in [37]. The modified model I propose for univariate data analysis is
 |
where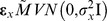 
and W is the phylogenetic connectivity matrix with zeros on the diagonal and rows that sum to one. The autocorrelation coefficient, 
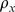, measures the impact of the phylogenetic effect on the traits. The residual 
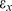is independent of 
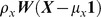and can be regarded as the value gained or loss due to non-phylogenetic component.
Transforming the equation, we have
 |
For bivariate analysis, let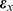 
and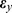 
be the residuals for the traits X and Y, respectively. As in the univariate case, the residuals 
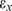and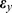 
are independent of the phylogenetic components 
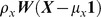and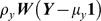 
. I now assume the correlation between the two residuals exists and let the correlation equal to
.
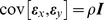Then, the covariance between the pair of traits is
 |
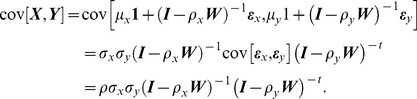The statistical model for the bivariate phylogenetic autoregressive model is therefore,
 |
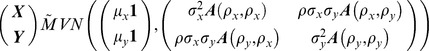where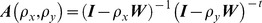 
.
OU:
Martins and Hansen considered species evolving under the OU process where a selection force pulls the trait back to an optimum. Thus, the OU process can be used to model stabilizing selection [4]. The univariate OU model assumes that the trait at time t,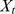 
, satisfies
 |
Where 
measures the magnitude selection force,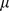 
is the optimum of the trait, and 
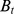is Brownian motion. The selection force acts strongly towards the optimum when the trait is far from the optimum and weakly if the trait is close to the optimum. For the bivariate analog, there are two constraining force parameters, 
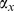for trait X and 
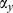for trait Y.
Assuming that the constraining force parameters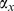 
and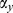 
are constants during the evolutionary process, I propose the bivariate statistical model
 |
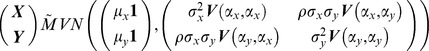where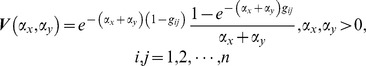 
.
The covariance structure is developed by the following mathematical property:
Theorem 1
Let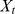 
and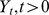 
be two OU process random variables. Given a rooted phylogeny for trait evolution, assuming that the constraining force parameters 
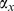and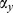 
are constants during the evolutionary process, the covariance between the trait 
of species i and the trait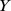 
of species j is
 |
where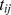 
measures the branch length from the root to the most common ancestor of species i and j; 
, 
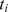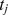are the branch lengths for species i and j since they diverged
(Figure 2). Proof of Theorem 1 is provided in appendix S1.
Figure 2. A two taxon phylogenetic tree of two species i and j with trait values.
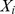and
. 
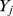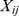and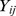 
are the trait values for the common ancestor of i and j. 
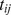measures the branch length from the root to the most common ancestor of species i and j. 
,
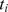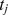are the branch length for species i and j since they diverged.
Model Selection for Univariate Data
For univariate data analysis, the fitted models were compared using the Akaike Information Criteria (AIC), in order to measure fit to data of a model [10].
 |
where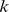 
is the number of parameters, 
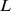is the likelihood function, and 
is the MLE estimator(s) in that model.
Hurvich and Tsai found AIC could over-fit models and be biased if there are too many parameters in comparison to the sample size. They proposed a modification of AIC when the ratio of sample size to the number of parameter does not exceed 40 (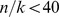
), AICc [38]:
 |
Since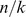 
in this study is always less than 40, I used AICc for model selection.
Another popular model selection method, Bayesian Information criterion (BIC) where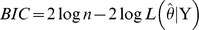 
, is based on an asymptotic result derived under the assumptions that the data distribution is in the exponential family [39]. BIC is not appropriate in model selection for biological phenotypic data sets because, when sample size is small, BIC tends to select unfitted models with large bias, which results in difficulty in inference [40].
Simulation
Do Some Models really fit better than others?
For a given dataset, one can get a ranked list of models, including the best model, by getting point estimates of AICc differences. However, it is also useful to get the confidence intervals for these differences. Thus, after determining which model fits a given data set best, I proceeded to test whether it fits significantly better than the other models by simulating the distribution of AICc differences, using a procedure suggested in [40]. Given a set of models indexed by 
, define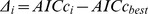 
where 
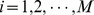is the model index and the term best is the index of the best model. In this study, 
represents ID, FIC, PMM, PA, or OU. I treated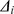 
as a random variable and suggested the following bootstrap technique for determining a confidence interval for 
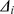. If FIC is the best model for the data Y, generate new bootstrap samples 
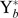from FIC using the MLE from the original data. For each sample, 
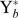, determine the AICc values for each model. Let 
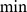be the index of the model with smallest AICc value for the bootstrapped data. Define the random variable 
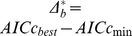. I then order the 
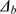in increasing order for the 
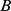bootstrapping samples. Re-using the index 
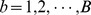but for the ordered values, the 
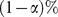confidence set for 
is CI = 
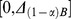. If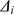 
(the original difference for model i versus the best model) falls outside this confidence interval, the null hypothesis that the two models fit the data equally well is rejected and I conclude that the best selected model under AICc is significantly better than model i. I set 
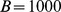to get a reliable result on the upper tail of 
.
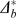Robustness
The comparative data sets usually consist of mean trait values derived from measuring a finite number of samples, which are subject to both measurement and sampling error. The phylogeny, even when given as a rooted molecular clock tree, also has uncertainty in branch lengths and topology because phylogenies are often obtained by a sample of DNA sequences from the species involved. Accordingly, I consider the robustness of my model selection results to perturbations of the trait values and the phylogeny. Both procedures are described below.
Perturbation of Comparative Data
Consider collecting m samples from a particular species yielding trait values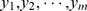 
. Let se be the standard error and let 
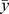be the sample mean. All of m, se, and 
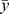are typically reported in the studies used in this analysis. I perturbed the species mean value by using the formula 
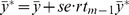where rt is a random sample from the t distribution with 
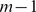degrees of freedom. This is a reasonable approach because the sample mean will be approximately t-distributed in most cases. However, biological data often follow a log normal distribution with a natural bound of zero and with no specific upper bound. On occasion, when the sample size is not large and the underlying data are log normal, using 
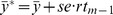to generate 
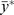can give impossible (negative) values with a substantial probability. Under such circumstances, I apply an alternative resampling technique aimed at reproducing the log normal data. Note that if 
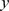is a log normal random variable, then 
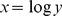is a normal random variable. The second order Taylor series approximation for the function 
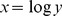at the point 
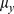is
 |
Given the sample mean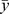 
and sample variance 
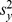for a log normal variable
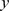, the distribution of the normal variable 
(with mean 
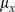and variance 
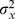) is approximately
 |
Using the linear part,
 |
the variance of 
can be approximated as
 |
I sampled from the normal distribution with appropriate mean and variance and exponentiated to get a sample from the log normal distribution. For a sample of size m, I simulate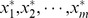 
from normal distribution with mean 
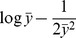and variance 
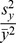. Then the perturbed data 
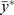can be obtained as
 |
Perturbation of Phylogeny
Stone considered the effect of local phylogenetic perturbations on the regression fit. He studied how tree misspecification could influence the phylogenetic regression given a Brownian motion model of evolution. He found that branch length misspecification can be easily explained in terms of the reweighting of contrast scores between subtrees [41]. I used a likelihood-based approach rather than regression to investigate how branch length misspecification could influence the model selection. To do this, I first perturbed the phylogenetic tree by randomly varying the branch lengths without changing the topology. Recall that the phylogenetic tree is scaled so that the length from the root to each tip is one. The unit length is decomposed into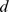 
segments with lengths 
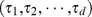by identifying each 
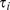as the time difference between two adjacent nodes in the phylogenetic tree. Thus, 
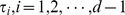are times between the 
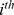and the 
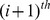speciation events and 
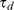is the time between the tip and the most recent node in the phylogenetic tree. In terms of the entries of the relationship matrix G, let 
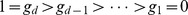be the ranking of the distinct entries in G, then we have 
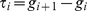. To perturb the branch lengths 
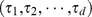but retain the topology of the original phylogeny, the procedure is described in the following. I first treated 
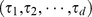as a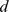 
-dimensional random variable from a Dirichlet distribution generated by drawing 
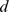independent random samples, 
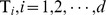, each from a Gamma distribution with rate parameter 
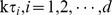where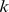 
is an arbitrary but positive constant. The desired 
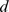- tuple sample 
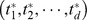from the Dirichlet distribution with parameter 
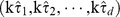is determined by
 |
Note that 
is an arbitrary scaling variable that always preserves the correct mean. That is,
 |
The Dirichlet distribution has a mode given by
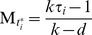, where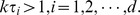 
The choice of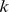 
is thus determined by 
.
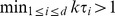I chose a positive integer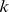
,
 |
where [a] returns the integer closest but less than a.
Because the mode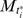 
of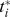 
is not equal to the expectation of 
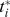, such choice of k does not guarantee that the distribution of 
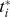is centered or symmetric around its mean 
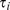. The mode converges to the expected mean when 
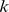approach to infinity (i.e. 
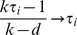as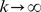 
). However, although choosing larger 
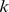helps to center the distribution around 
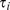, picking 
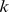too large will cause the samples 
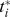to be tightly centered around the given estimate 
. My choice of 
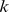is designed to be the minimal needed to prevent the phylogenetic tree from varying too wildly from the given one while still adequately testing robustness.
PCMs Comparison by Confidence Intervals for the Correlation
For bivariate data analysis, I generated the confidence interval by creating bivariate samples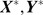 
using the MLE estimators of all the model parameters and re-estimating the correlation. I created 1000 pairs of samples 
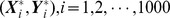and performed the REML analysis to obtain the MLEs
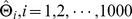. The 95 % confidence interval (CI) for the correlation under the hypothesis testing is constructed from the ordered MLEs for the correlation 
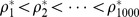with the cut off CI = 
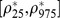. The correlation is significantly positive at the 5% level if 
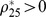, significantly negative at the 5% level if 
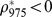and otherwise not significantly different from zero at the 5% level.
Results
Model Selection under AICc
I report the summary of the results from the simulation study in Table 2. By the first row of Table 2, most of the data sets are best described by either of the simplest models: the independent model (ID) or by Brownian motion (FIC). The entire table shows the performance of model-fitting of each model when competing with other models. If the best fit model is independent (no phylogenetic effect), then that model usually fits significantly better than other models. However, if the model that best fits the data is Brownian motion (FIC), then other models, except phylogenetic autocorrelation (PA), have a substantial probability of fitting the data as well. For other parameter-rich models, PMM and OU usually fit significantly better than other models; however, they do not fit statistically significant better than each other. PA fits significantly better than other models except for the independent (no phylogenetic model).
Table 2. Summary of the data sets that fit multiple models.
| IDb | FICb | PMMb | PAb | OUb | |
| (n = 36) | (n = 67) | (n = 4) | (n = 5) | (n = 10) | |
| ID | - | 0.48 | 1 | 0 | 0.8 |
| FIC | 0.86 | - | 0.75 | 0.8 | 0.7 |
| PMM | 0.94 | 0.06 | - | 0.8 | 0.4 |
| PA | 0.89 | 0.81 | 1 | - | 0.9 |
| OU | 0.86 | 0.12 | 0.5 | 0.8 | - |
In the first row of the table, n represents the number of data sets that best fit a particular model under AICc. In each column, the entries represent the ratio for which the best fit model fits significantly better than other models (see “Do some models really fit better than others?”). For instance, the second column shows that among 36 data sets that ID best fits the data, the ratio that ID fits significantly better than FIC, PMM, PA and OU are 0.86, 0.94, 0.89 and 0.86, respectively.
Robustness for Models under Perturbing Data and Phylogeny
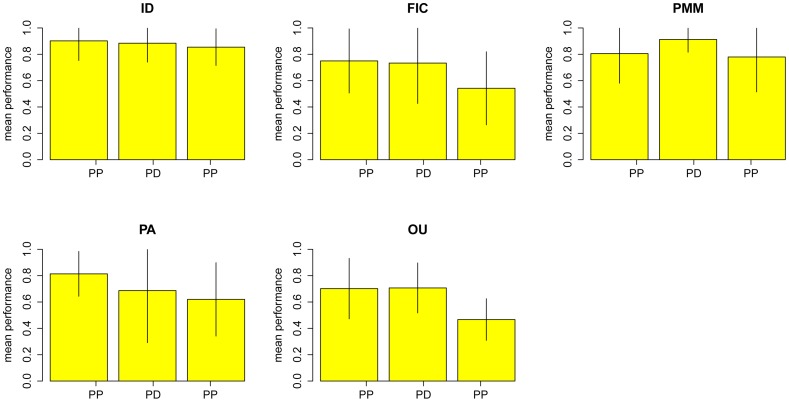
There were 64 traits for which standard error and sample size were reported. For each trait, I simulate one thousand perturbed data sets and phylogenies. The performance of the best model for a trait is evaluated by proportion of simulated data sets on which that model achieves the best fit. The mean performance is the average value of the performances across studies. The results of the perturbation analyses are shown in Figure 3. Data sets that best fit by the independent model are the most robust to perturbations while those whose best fit is a Brownian motion model (FIC) are less robust. Data sets that are best fit by the Brownian motion model (FIC), PMM, and OU seem to be more sensitive to perturbations in the phylogeny than to perturbations in the comparative data themselves.
Figure 3. Summary of the sensitivity analysis for perturbing comparative data and phylogeny.
The height for each bar graph represents the mean performance of the model where the vertical line on each bar graph represents the standard deviation of the performance. PP: Perturbing the phylogeny; PD: Perturbing the data only; PB: Perturbing both phylogeny and data.
Model Adequacy for PCMs
I also evaluated model adequacy for PCMs. The purpose is to investigate how well the model describes the underlying process that generated the trait data. Essentially, if a model simulates datasets that are indistinguishable from the observed datasets, the model adequately describes the data. I first simulated a thousand datasets by parametric bootstrapping using the MLE obtained from the empirical data under each model and then re-evaluated the likelihood from the simulated data for each model. The model is considered inadequate if the log likelihood for the empirical data falls out of the 95% confidence interval from the simulated data.
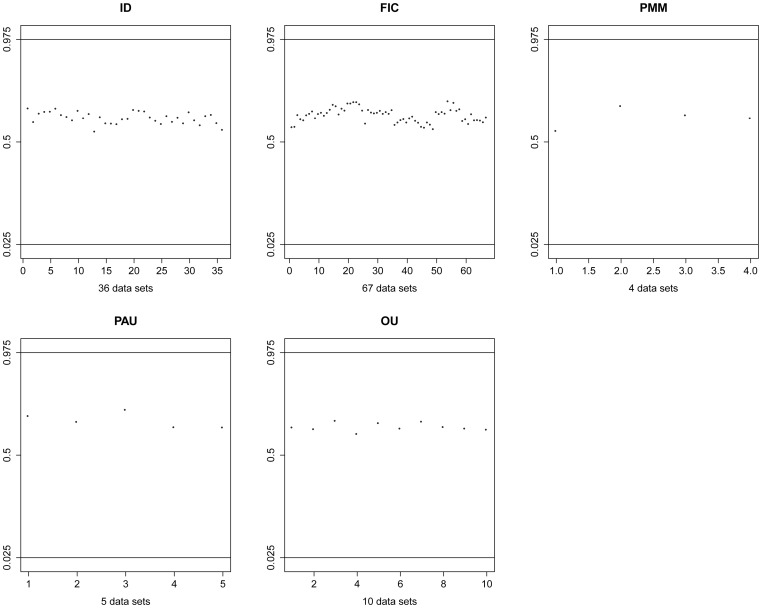
Figure 4 summarizes the result where scatter plots are shown to examine the adequacy of the AIC best model. The likelihood for the empirical datasets falls well within the 95% confidence interval for the simulated data from each model. Expressed as a percentile of the simulated scores, the empirical data averaged in the 61st percentile for ID, 62nd percentile for BM, 61st percentile for PMM, 66th percentile for PAU, and 63rd percentile for OU.
Figure 4. Summary of testing model adequacy.
In each plot the 95 % confidence interval is shown by two horizontal lines (0.025 and 0.975). Each point in the plot represents the rank in the 95 % confidence interval for the empirical data sets. In no cases are the empirical data sets outliers relative to the simulated datasets, suggesting model adequacy.
Assessing Goodness of Fit for PCMs
It might be the model for fitting data is over fitted. To investigate this, I simulate data using the true MLE under the best model. Then the fit of other models is then evaluated.
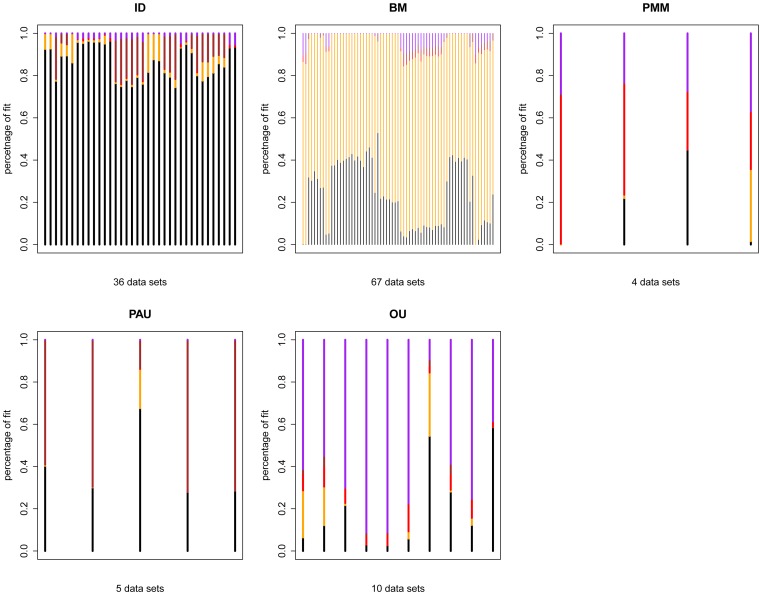
The result is shown in Table 3 and Figure 5. The diagonal entries in Table 3 show the average ratio of fit for the best model. Datasets simulated under ID have ID as the best fitting model 86% of the time, FIC has the best fit 72% of time. For more complicated models, datasets simulated under PMM have PMM as the best fitting model 45% of the time, PA has the best fit 57 % of time and OU has the best fit of 63 % of time which encounter over fitting issue. For PMM, as the combination model of ID and FIC, could be over fitted while the heritability parameter close to 0 or 1. In this case, ID and FIC would be the better fit. Similarly PA is an extended model for ID where the zero autocorrelation is detected.
Table 3. Average fit for model fitting.
| IDb | FICb | PMMb | PAb | OUb | |
| (n = 36) | (n = 67) | (n = 4) | (n = 5) | (n = 10) | |
| ID | 0.86 | 0.24 | 0.17 | 0.39 | 0.21 |
| FIC | 0.04 | 0.72 | 0.09 | 0.04 | 0.08 |
| PMM | 0.00 | 0.01 | 0.45 | 0.00 | 0.07 |
| PA | 0.08 | 0.01 | 0.57 | 0.57 | 0.02 |
| OU | 0.01 | 0.03 | 0.00 | 0.00 | 0.63 |
In the first row of the table, n represents the number of studies that best fit a particular model under AICc. In each column, the entries represent the average ratio for the best model across the studies.
Figure 5. Investigating over fitting issue for PCMs using the trait data from literature.
Each vertical line with different color in the plot represents the ratio of the fit: ID (black), BM (orange), PMM (red), PAU (brown), OU (purple).
Comparing Correlation Estimates from the PCMs
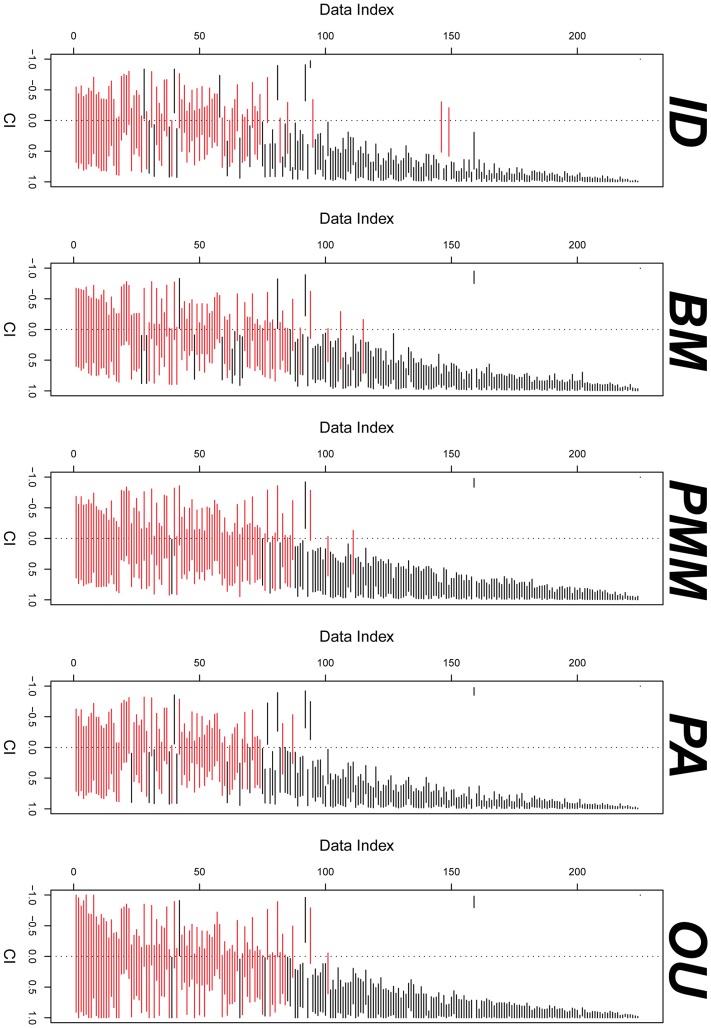
I analyzed 225 bivariate data sets with 23 phylogenies. Figure 6 gives the comparison of the confidence intervals for correlations. Correlations tend to be either positive or include zero in their confidence intervals.
Figure 6. The confidence intervals of correlation for PCMs.
Each line represents a confidence interval for a data set. Red lines include zero correlation in the confidence intervals.
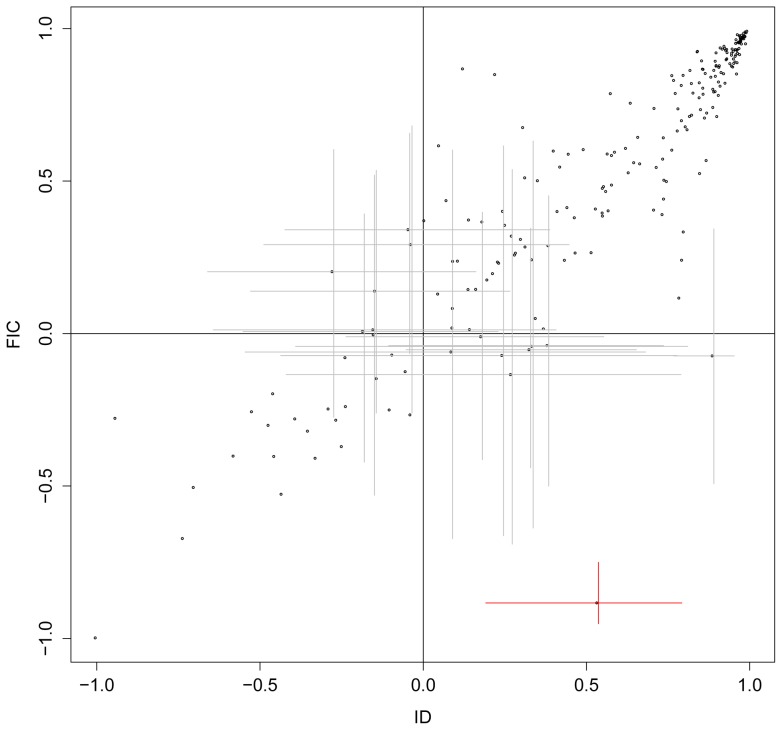
Figure 7 shows the comparison of correlation between ID and FIC. Most (93.4%) correlations have the same sign. There are only fourteen data sets for which there are estimated correlations of opposite signs that show the disagreement (the points in the second and the fourth quadrant) and for only one of these do the confidence intervals not include areas of agreement.
Figure 7. Comparison of correlation between ID and FIC.
On the plots, points in the second and the fourth quadrants are the correlations estimates estimated discordantly (different sign) by ID and FIC. Those points are then shown with the confidence interval. Only such one point, indicated in red, has confidence intervals for both correlations excluding zero, suggesting a difference in sign of the correlation that cannot be due just to uncertainty in the correlation estimates.
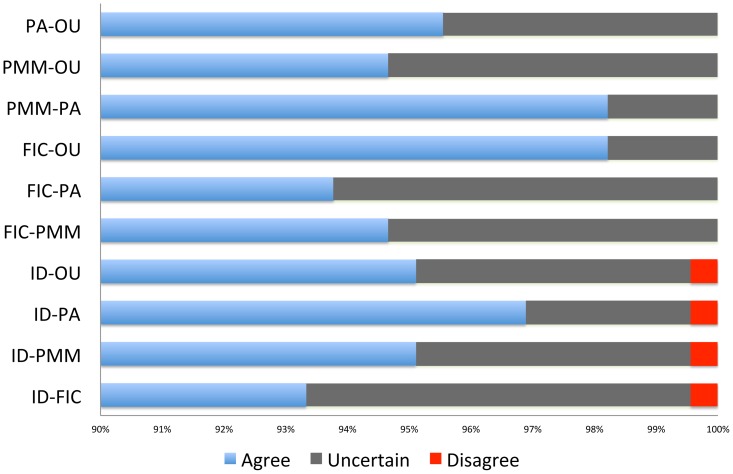
Figure 8 gives the summary of the concordance of the correlation estimates between PCMs by comparing the confidence intervals. Figure 6, Figure 7, and Figure 8 suggest that most estimated correlations are concordant. Thus, if there were a significant positive (or negative) correlation under one model, using a different model would also yield a significant positive (or negative) correlation. This is a very reassuring result for the use of PCMs. Similar results have been found, but for fewer models, by previous authors [42]–[43].
Figure 8. Concordance of the correlation estimates between PCMs.
Blue bars indicates agreement in sign in correlation. Dark grey bars indicate disagreement of sign for the point estimates of the correlation, but with agreement possible given the confidence intervals on the estimates. Red bars indicate conflict in sign that cannot be reconciled by accounting for uncertainty.
Discussion
Harmon et al. compared BM (Brownian motion), SSP (single stationary peak), and EB (early burst) models of morphological evolution and found little support for the EB model, whereas both other models, particularly that of SSP, were commonly supported [44]. In this work, I have looked at the most common bivariate models, but also created univariate versions of them to see how well they explain evolution of single traits: one expects that models that do not work well in the univariate case would also not perform well in the multivariate case, though this has not been formally shown.
I have shown that ID and FIC are most frequently chosen as the best model under the univariate analysis. This is in part due to the penalty AICc places on models with more parameters. If all else is equal (including the likelihood), then the AICc differences for a pair of models with one having one more parameter is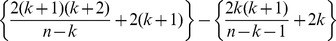 
. For two versus three parameters, the difference is 
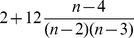where 
is the sample size. The number of species in the data sets under consideration in this study ranged from 9 to 117 and so this penalty ranged from 2.10 to 3.43. Some of these models are special cases of others. For instance, when the heritability parameter h in the PMM model converges to 0 or 1, PMM is identical to ID or FIC, and thus the likelihood for PMM and one of the extreme models would be identical in this case. However, AICc penalizes PMM for using an additional parameter. This also occurs for PA: when the autocorrelation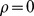 
, PA is identical to ID. Similarly OU is identical to FIC when 
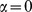. In these cases, simpler models (ID and FIC) provide a better fit for those data.
In the univariate case, it appears that when the best-fitting model is ID, other models will almost always fit more poorly. However, when the best model is slightly more complex, like FIC, it is usually hard to reject other models. This makes sense: FIC (based on likelihood rather than REML) is nested within other models with just one parameter, so it can be hard to distinguish them, especially in studies with moderate to small numbers of taxa. Researchers often just use a point estimate to determine the best model; however, I have shown there is often quite large uncertainty as to the best model. Modifying the phylogeny can result in dramatic shifts in the best model, but modifying the trait data had a much smaller effect. This suggests that when estimating the best model is important, a premium should be placed on estimating the phylogeny well. One caveat, though, is that the uncertainty added to the phylogenies was not based on empirical estimates. However, the magnitude used was fairly minimal (branch lengths differed from original branch lengths by 0.3 % on average with 3.2 % variation across different phylogenies) yet still had a major effect on model choice, suggesting that this may also be important in empirical analyses.
Despite the adequacy of models examined in this analysis, there are many ways in which the true evolutionary process may deviate from the models. For example, differing rates of evolution across taxa [45]; multiple optima [5]; or multiple optima, multiple rate and multiple attractors [6] may occur throughout a clade. Much work in this area uses parametric approaches, but non-parametric approaches may hold promise. Development of corresponding bivariate models may aid the exploration of correlation and appropriate alternative summaries of association in comparative analyses of multiple traits.
The results obtained here suggest caution when applying bivariate PCMs. In over half the cases, different PCMs give the same sign of correlation but in about a quarter of the cases, different methods resulted in correlations with different signs. Different methods gave non-overlapping confidence intervals for correlations in only a small proportion of cases. Price found that FIC and ID gave correlations with different signs in 14.7 % of cases [42], whereas I found this happened in 6.6 % of cases for those models. Such discrepancies occur with real data. For example, Fig. 3B and Fig. 3E in [46] showed an example in which leaf life span and leaf size in angiosperms and conifers had a negative correlation when using the ID and a positive relationship when using FIC; for most other traits, the sign of the correlation was the same regardless of model.
One surprising result is that all pairs of PCM agreed and disagreed by about the same amount, regardless of whether they were fairly similar models (FIC-PA) or very different (FIC-ID). Note that I have analyzed various univariate models in the same framework so as to allow model selection; this has yet to be done for the multivariate case. Revell has shown that one cannot just take univariate model selection results to infer the best multivariate model [47]. Thus, developing model selection approaches for the variety of available multivariate models remains important work for the future.
Supporting Information
Proof of Theorem 1.
(PDF)
Flow of information through the different phases of a systematic review.
(DOCX)
Checklist of items to include when reporting a systematic review or meta-analysis.
(DOCX)
Acknowledgments
I am grateful to Elizabeth Housworth and Brian O'Meara for helpful discussions. I also thank Steven Orzack and reviewers for their useful comments on this manuscript.
Funding Statement
This work was supported by the National Institute for Mathematical and Biological Synthesis, an Institute sponsored by the National Science Foundation, the U.S. Department of Homeland Security, and the U.S. Department of Agriculture through NSF (National Science Foundation) Award #EF-0832858, with additional support from The University of Tennessee, Knoxville, and the National Science Council grant #NSC-101-2118-M-035-001, Taiwan, ROC. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Felsenstein J (1985) Phylogenies and the comparative method. The American Naturalist 125: 1–15. [DOI] [PubMed] [Google Scholar]
- 2. Cheverud JM, Dow MM, Leutenegger W (1985) The quantitative assessment of phylogenetic constraints in comparative analyses: sexual dimorphism in body weight among primates. Evolution 39: 1335–1351. [DOI] [PubMed] [Google Scholar]
- 3. Gittleman JL, Kot M (1990) Statistics and a null model for estimating phylogenetic effects. Systematic Zoology 39: 227–241. [Google Scholar]
- 4. Martins EP, Hansen TF (1997) Phylogenies and the comparative method: a general approach to incorporating phylogenetic information into the analysis of interspecific data. The American Naturalist 149: 646–667. [Google Scholar]
- 5. Butler MA, King AA (2004) Phylogenetic comparative analysis: a modeling approach for adaptive evolution. American Naturalist 164: 683–695. [DOI] [PubMed] [Google Scholar]
- 6. Beaulieu JM, Jhwueng DC, Boettiger C, O'Meara BC (2012) Modeling stabilizing selection: expanding the Ornstein-Uhlenbeck model of adaptive evolution. Evolution 66: 2369–2383. [DOI] [PubMed] [Google Scholar]
- 7. Lynch M (1991) Methods for the analyses of comparative data in evolutionary biology. Evolution 45: 1065–1080. [DOI] [PubMed] [Google Scholar]
- 8. Housworth EA, Martins EP, Lynch M (2004) The phylogenetic mixed model. The American Naturalist 163: 84–96. [DOI] [PubMed] [Google Scholar]
- 9. Freckleton RP, Harvey PH, Pagel M (2002) Phylogenetic analysis and comparative data. The American Naturalist 160: 712–726. [DOI] [PubMed] [Google Scholar]
- 10. Akaike H (1974) A new look at the statistical identification model. IEEE Transactions on Automatic Control 19: 716–723. [Google Scholar]
- 11. Collar DC, Near TJ, Wainwright PC (2005) Comparative analysis of morphological diversity: does disparity accumulate at the same rate in two lineages of centrarchid fishes? Evolution 59: 1783–1794. [PubMed] [Google Scholar]
- 12. Aguirre L, Herrel A, Damme RV, Matthysen E (2002) Ecomorphological analysis of trophic niche partitioning in a tropical savannah bat community. Proceedings of the Royal Society B 269: 1271–1278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Armbruster WS, Mulder CPH, Baldwin BG, Kalisz S, Wessa B, et al. (2002) Comparative analysis of late floral development and mating-system evolution in tribe Collinsieae (Scrophulariaceae s.l.). American Journal of Botany 89: 37–49. [DOI] [PubMed] [Google Scholar]
- 14. Bertelli S, Tubaro PL (2002) Body mass and habitat correlates of song structure in a primitive group of birds. Biological Journal of the Linnean Society 77: 423–430. [Google Scholar]
- 15. Bonnie KE, Gleeson TT, Garland T Jr (2005) Muscle fiber-type variation in lizards (Squamata) and phylogenetic reconstruction of hypothesized ancestral states. The Journal of Experimental Biology 208: 4529–4547. [DOI] [PubMed] [Google Scholar]
- 16. Cruz FB, Fitzgrald LA, Esponoza RE, Schulte JA (2005) The importance of phylogenetic scale in tests of Bergmann's and Rapoport's rules: lessons from a clade of South American lizards. Journal of Evolutionary Biology 18: 1559–1574. [DOI] [PubMed] [Google Scholar]
- 17. Federle W, Rheindt FE (2005) Macaranga ant-plants hide food from intruders: correlation of food pre-sentation and presence of wax barriers analysed using phylogenetically independent contrasts. Biological Journal of the Linnean Society 84: 177–193. [Google Scholar]
- 18. Fisher DO, Blomberg SP, Owens IPF (2002) Convergent maternal care strategies in ungulates and macropods. Evolution 56: 167–176. [DOI] [PubMed] [Google Scholar]
- 19. Gibbs AG, Fukuzato F, Matzkin LM (2003) Evolution of water conservation mechanisms in Drosophila. The Journal of Experimental Biology 206: 1183–1192. [DOI] [PubMed] [Google Scholar]
- 20. Grotkopp E, Rejmánek M, Rost TL (2002) Toward a causal explanation of plant invasiveness: seedling growth and life-history strategies of 29 pine (Pinus) species. The American Naturalist 159: 396–419. [DOI] [PubMed] [Google Scholar]
- 21. Jervis MA, Ferns PN, Heimpel GE (2003) Body size and the timing of egg production in parasitoid wasps: a comparative analysis. Functional Ecology 17: 375–383. [Google Scholar]
- 22. Johnston IA, Fernadez DA, Calvo J, Vieira VLA, North AW, et al. (2003) Reduction in muscle fibre number during the adaptive radiation of notothenioid fishes: a phylogenetic perspective. The Journal of Experimental Biology 206: 2595–2609. [DOI] [PubMed] [Google Scholar]
- 23. Mazzoldi C, Petersen CW, Rasotto MB (2005) The influence of mating system on seminal vesicle variability among gobies (Teleostei, Gobiidae). Journal of Zoological Systematics and Evolutionary Research 43: 307–314. [Google Scholar]
- 24. Melville J, Swain R (2003) Evolutionary correlations between escape behaviour and performance ability in eight species of snow skinks (Niveoscincus: Lygosominae) from Tasmania. Journal of Zoology, London. 261: 79–89. [Google Scholar]
- 25. Monnet J M, Cherry MI (2002) Sexual size dimorphism in anurans. Proceedings of the Royal Society B 269: 2301–2307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Moreteau1 B, Gibert P, Pétavy G, Moreteau, GC, Huey RB, et al (2003) Morphometrical evolution in a Drosophila clade: the Drosophila obscura group. Journal of Zoological Systematics and Evolutionary Research 41: 64–71. [Google Scholar]
- 27. Niewiarowski PH, Angilletta MJ Jr, Leaché AD (2004) Phylogenetic comparative analysis of life-history variation among populations of the lizard Sceloporus undulates: an example and prognosis. Evolution 58: 619–633. [DOI] [PubMed] [Google Scholar]
- 28. Olifiers N, Vieira MV, Grelle CEV (2004) Geographic range and body size in neotropical marsupials. Global Ecology and Biogeography 13: 439–444. [Google Scholar]
- 29. Roulin A, Wink M (2004) Predator-prey relationships and the evolution of colour polymorphism: a comparative analysis in diurnal raptors. Biological Journal of the Linnean Society 81: 565–578. [Google Scholar]
- 30. Sánchez JA, Lasker HR (2003) Patterns of morphological integration in marine modular organisms: supra-module organization in branching octocoral colonies. Proceedings of the Royal Society B 270: 2039–2044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Toïgo C, Maillard JM (2003) Causes of sex-biased adult survival in ungulates: sexual size dimorphism, mating tactic or environment harshness? Oikos 101: 376–384. [Google Scholar]
- 32. Tubaro PL, Lijtmaer DA, Palacios MG, Kopuchian C (2002) Adaptive modification of tail structure in relation to body mass and buckling in woodcreepers. The Condor 104: 281–296. [Google Scholar]
- 33. Vanhooydonck B, Damme RV, Aert P (2002) Variation in speed, gait characteristics and microhabitat use in lacertid lizards. The Journal of Experimental Biology 205: 1037–1046. [DOI] [PubMed] [Google Scholar]
- 34. Weiblen GD (2004) Correlated evolution in fig pollination. Systematic Biology 53: 128–139. [DOI] [PubMed] [Google Scholar]
- 35. Powell MJD (1964) An efficient method for finding the minimum of a function of several variables without calculating derivatives, Computer Journal. 7: 155–162. [Google Scholar]
- 36.Press WH, Teukolsky SA, Vetterling WT, Flannery BP (2007) “Section 10.7. Direction Set (Powell's) Methods in Multidimensions”. Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8.
- 37. Ord JK (1975) Estimation Methods for Models of Spatial Interaction, Journal of the American Statistical Association. 70: 120–126. [Google Scholar]
- 38. Hurvich CM, Tsai C-L (1989) Regression and time series model selection in small samples. Biometrika 76: 297–307. [Google Scholar]
- 39. Schwarz G (1978) Estimating the dimension of a model. The Annals of Statistics 6: 461–464. [Google Scholar]
- 40.Burham KP, Anderson DR (2002) Model selection and multimodel inference. Springer-Verlag New York.
- 41. Stone EA (2011) Why the phylogenetic regression appears robust to tree misspecification Systematic Biology 2011. 60: 245–260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Price T (1997) Correlated evolution and independent contrasts. Philosophical Transactions of the Royal Society B: Biological Sciences. 352: 519–529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Martins EP, Hansen TF (1996) Phylogenies, spatial autoregression, and the comparative method: a computer simulation test. Evolution 50: 1750–1765. [DOI] [PubMed] [Google Scholar]
- 44. Harmon LJ, Losos JB, Davies TJ, Gillespie RG, Gittleman JL, et al. (2010) Early bursts of body size and shape evolution are rare in comparative data. Evolution 64: 2385–2396. [DOI] [PubMed] [Google Scholar]
- 45. O'Meara BC, Ane C, Sanderson MJ, Wainwright PC (2006) Testing for different rates of continuous trait evolution. Evolution 60: 922–933. [PubMed] [Google Scholar]
- 46. Ackerly DD, Reich P (1999) Convergence and correlations among leaf size and function in seed plants: a comparative test using independent contrasts. American Journal of Botany 86: 1272–1281. [PubMed] [Google Scholar]
- 47. Revell LJ (2010) Phylogenetic signal and linear regression on species data. Methods in Ecology and Evolution 1: 319–329. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Proof of Theorem 1.
(PDF)
Flow of information through the different phases of a systematic review.
(DOCX)
Checklist of items to include when reporting a systematic review or meta-analysis.
(DOCX)