Biomolecular Dynamics: Order-Disorder Transitions and Energy Landscapes

Abstract

While the energy landscape theory of protein folding is now a widely accepted view for understanding how relatively-weak molecular interactions lead to rapid and cooperative protein folding, such a framework must be extended to describe the large-scale functional motions observed in molecular machines. In this review, we discuss 1) the development of the energy landscape theory of biomolecular folding, 2) recent advances towards establishing a consistent understanding of folding and function, and 3) emerging themes in the functional motions of enzymes, biomolecular motors, and other biomolecular machines. Recent theoretical, computational, and experimental lines of investigation are providing a very dynamic picture of biomolecular motion. In contrast to earlier ideas, where molecular machines were thought to function similarly to macroscopic machines, with rigid components that move along a few degrees of freedom in a deterministic fashion, biomolecular complexes are only marginally stable. Since the stabilizing contribution of each atomic interaction is on the order of the thermal fluctuations in solution, the rigid body description of molecular function must be revisited. An emerging theme is that functional motions encompass order-disorder transitions and structural flexibility provide significant contributions to the free-energy. In this review, we describe the biological importance of order-disorder transitions and discuss the statistical-mechanical foundation of theoretical approaches that can characterize such transitions.

1. Introduction: The Biological Context for Physical Questions

The biomolecular origins of cellular dynamics occur over a wide range of length and time scales. Each biomolecule has specific functional properties that are governed by its energetics. Two well-studied classes of biomolecules (at the functional level) are proteins and nucleic acids. Both are linear polymer chains composed of specific sequences of monomers called “residues.” Proteins are composed of amino acid residues (Figure 1A), of which there are twenty naturally-occurring types. Ribonucleic acid (RNA, Figure 1B) chains and deoxyribonucleic acid chains (DNA) are composed of sugar-phosphate backbones and four types of nucleic acid side chains (A,U,C,G in RNA and A,T,C,G in DNA). While the primary role of DNA is to carry genetic information, RNA molecules can adopt well-ordered three-dimensional configurations, perform chemistry (1, 2) and function as molecular machines (3–5). In fact, in recent years it has been shown that the majority of the human genome is transcribed into RNA but not translated in protein, suggesting that functional noncoding RNAs may be equally important to cellular dynamics as proteins. Due to the functional importance of protein and RNA structural dynamics, this review will focus on their dynamics, though the concepts presented may be applicable to other biomolecular systems.

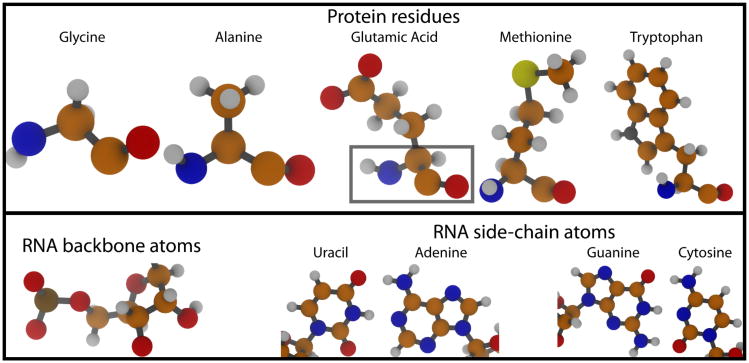
Figure 1. The diversity of protein and RNA residues (top).

Protein chains are composed of amino acid residues, which contain carbon (orange spheres), nitrogen (blue), oxygen (red), sulfur (yellow) and hydrogen (white) atoms. Each amino acid has a common set of C, N, O and H atoms (boxed). The range of chemical compositions of residues is depicted by the atomic structures of 5 of the 20 naturally-occurring) different amino acids. (bottom) RNA chains are composed of 4 type of nucleic acids. Each nucleic acid has a common set of backbone atoms (left). Canonical Watson-Crick base pairs are formed between A-U and C-G pairs (right). Structural figures were prepared with VMD (277).

Gene expression in the cell includes two fundamental steps: transcription and translation. Transcription is the process by which DNA is read and a complementary messenger RNA (mRNA) molecule is generated (Figure 2). In prokaryotes (single-celled organisms), mRNA is directly translated by ribosomes to produce proteins. In eukaryotes (multicellular organisms), precursor-mRNA (pre-mRNA) is produced during transcription. In eukaryotes, pre-mRNA is further modified by the cell (e.g. splicing (6)), which yields mature mRNA that is translated by ribosomes into protein sequences. In addition to this central dogma for the flow of genetic information, many feedback channels exist in the cell. For example, proteins and RNAs often regulate transcription and translation (7–13), as well as aid in heritable changes in gene expression by coordinating the structural reorganization of biomolecular assemblies (14, 15).

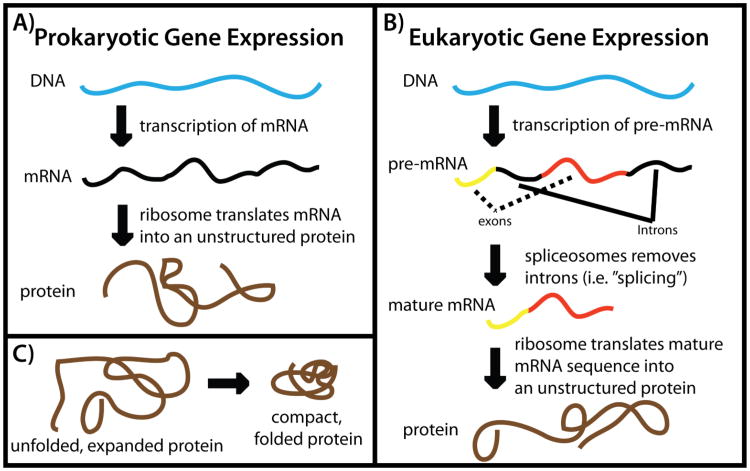
Figure 2. Gene expression in the cell.

The two fundamental steps of gene expression are transcription and translation. A) In prokaryotes, messenger RNA (mRNA) is transcribed and then read by ribosomes to produce proteins. B) In eukaryotes, precursor-mRNA is produced during transcription. Pre-mRNA is modified and transported in the cell and then mature mRNA is read by ribosomes. There are many types of post-transcriptional modifications that may be performed on pre-mRNA, though only splicing is depicted. During splicing, specific sequence of mRNA (introns) are removed from the pre-mRNA. C) Once a protein is synthesized by the ribosome, it folds to the lowest-energy “native” ensemble.

During transcription and translation the resulting linear polymers initially adopt unstructured (or partially-structured) ensembles of configurations. This is followed by a conformational search for the lowest-energy configuration. Since these polymers can have hundreds (even thousands) of residues (where each residue has several degrees of freedom) the accessible phase space of these molecules is large. The vastness of the available phase space led to the proposal of the so-called “Levinthal's Paradox.” (16) That is, if a polymer chain has N residues and each residue has M available conformations, the number of possible configurations of the polymer chain will be M^N. If each residue has only two possible conformations, then a 100 residue chain would have 2¹⁰⁰ ≈ 10³⁰ possible configurations. However, functional proteins and RNA molecules rapidly find a specific “native” three-dimensional structure (often on sub-second timescales). If the search process were completely random, and a configuration could be sampled every picosecond, then the average folding time would be $\frac{1}{2}{10}^{30}\times {10}^{-12}$ seconds ≈ 10¹⁸ seconds ≈ 10¹⁰ years. While considering the excluded volume of a biomolecule, or by assuming that proteins are initially collapsed (17), may reduce this counting problem, these arguments alone cannot account for the apparent eighteen orders of magnitude discrepancy in timescales. Accordingly, the search process must not be random. Identifying how proteins have evolved to fold to specific structures, with rapid rates, is often referred to as the “protein folding problem.” While the theoretical biological physics community has focused largely on protein folding, similar considerations apply for the folding of RNA (18).

To rationalize the kinetic disparities presented by Levinthal and biological timescales, the “funneled” energy landscape concept was introduced (19). Combined with The Principle of Minimal Frustration (20–22), this theoretical framework for the energy landscape of biomolecular dynamics has demonstrated that in order for proteins to be foldable, there must exist an ensemble of routes by which the molecule may reach the folded configuration. Folding then proceeds as a diffusive process over a relatively-smooth energy landscape (i.e. one that lacks large traps), and the ensemble of possible configurations continuously narrows as the native configuration is approached.

Since folding and functional dynamics occur on the same energy landscape, the principles developed to understand protein folding must extend to, and account for, biomolecular function. Many multi-domain proteins, such as Adenylate Kinase and kinesin, undergo conformational rearrangements during their function (23–27)). Accordingly, the energy landscapes of these molecules facilitate both, rapid folding and functional dynamics. Since the energy landscape (i.e. the Hamiltonian^‡) is determined by the chemical composition of the molecule, polymer sequences encode the energetics of the native configurations and large-scale functionally-relevant rearrangements, making it desirable to have a consistent theoretical framework for understanding both.

In this review, we provide a brief historical perspective (1970s-2000) on the development of the energy landscape theory of biomolecular motion, as developed in the context of glass-forming systems and protein folding. Next, we discuss recent work (2000-2010) to extend protein folding concepts and methods to describe functional dynamics of biomolecules. The focus of this discussion is on the use of theoretical models of energy landscapes that allow us to characterize the relationship between structure, folding and function. We will finish by discussing the role of order-disorder transitions in biomolecular functional dynamics.

2. Development of Energy Landscape Theory for Protein Folding

Grounded in statistical mechanics, the energy landscape theory of biomolecular dynamics (20–22, 28) has provided a general framework for understanding the folding and functional properties of biomolecules. For the Levinthal's Paradox to manifest, the energy landscape of a biomolecule must be relatively random. That is, if the landscape is “rough” ^§ (Figure 3), the Levinthal search problem could arise. When the stabilizing energy gap δE between the folded and unfolded ensembles is large, relative to the energetic roughness ΔE, the landscape can be described as an energetic “funnel.” (19) In a funneled energy landscape, configurations are locally connected (i.e. are kinetically accessible through simple moves) to states that are slightly more native and to those that are slightly less native. The degree of native content is also correlated with the stabilizing energy, resulting in a stabilizing energy gap that is much larger than the energetic barriers separating locally-connected states. In such a landscape, the diffusive walk is guided by the stabilizing energy and connectivity of states, and the Levinthal's paradox is averted.

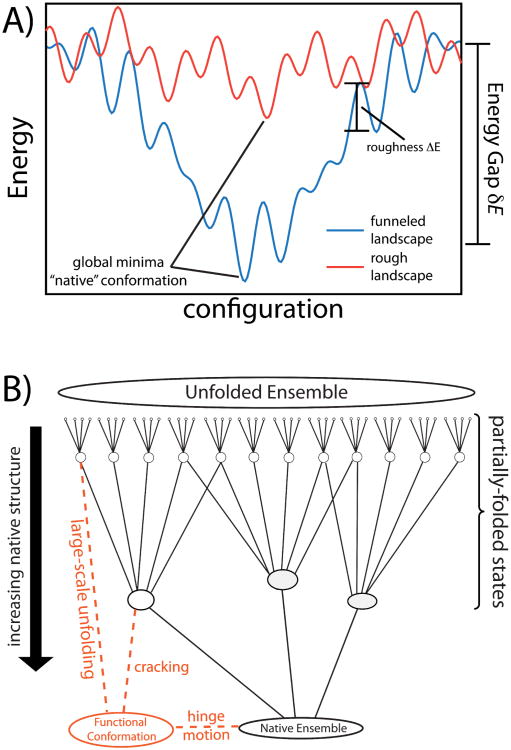
Figure 3. Energy landscapes of biomolecular folding.

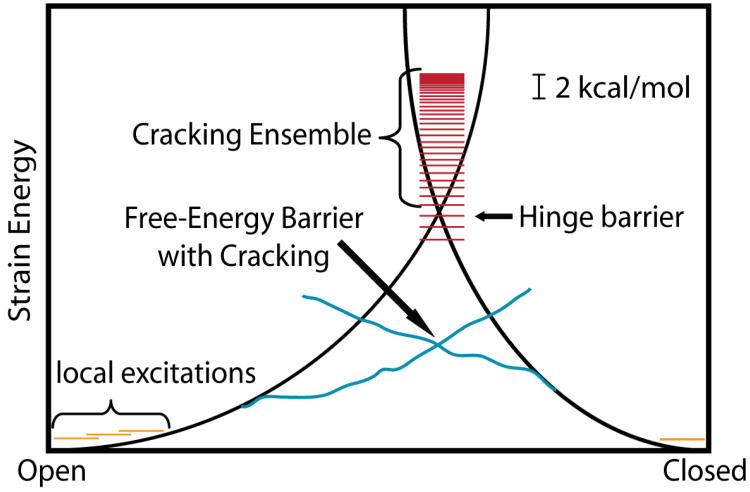
A) When the energy landscape of a system is rough red), the system must search randomly for the lowest-energy configuration and glass-like dynamics may arise. Biomolecules have evolved to have a large energy gap between the unfolded and folded ensembles δE, relative to the energetic roughness ΔE. “Funneled” energy landscapes (blue) enable rapid folding of biomolecules in vivo. B) An alternate representation of a funneled landscape that is extended to account for functional rearrangements. Functional biomolecules often possess multiple basins of attraction and there are many mechanisms by which functional transitions may occur. Cracking, hinge-motion and large-scale unfolding orange) encompass different degrees of molecular disorder and they result in differential forms of connectivity between the functional and native ensembles.

In many proteins, folding may be described as a pseudo-first order phase transition (22, 29) where the system goes from a disordered ensemble to an ordered ensemble by transitioning through partially-folded configurations that are not minima on the free-energy surface. The ensemble of configurations that separate the endpoints is known as the Transition State Ensemble (TSE). Phase transitions manifest throughout nature, suggesting that analogies between proteins and other physical system (such as spin glasses) may be identified. In spin systems, when the energetic roughness is small, the systems go through phase transitions to ordered states. Similar to glass-forming systems, when the energetic roughness in a protein is large (relative to the energy gap), the system is described as “frustrated” (22, 30–34). When there is a large degree of frustration, the fluctuations in energy that arise from non-zero temperatures are insufficient to escape from local minima and the timescales of the system's dynamics diverge.

2.1. Spin Glasses

To introduce the relationship between order-disorder transitions, glassy dynamics and energetic frustration, which are fundamental aspects of the energy landscape framework for biomolecular dynamics, we will discuss these properties in the context of spin glasses (35–37). This is not intended to be an exhaustive exploration of spin glasses and their dynamics. Rather, we will focus on features of order-disorder systems that will assist in our understanding of the energy landscapes of biomolecules.

The textbook example for discussing the statistical mechanics of phase transitions is the Ising model. (38) The Ising model represents a ferromagnetic material as being composed of a lattice of discrete sites (in any number of dimensions), where each site adopts a spin value of +1, or -1 (Figure 4). In its original formulation (39), each spin is coupled to the adjacent spins and the energy for an arbitrary-dimensional system is given by:

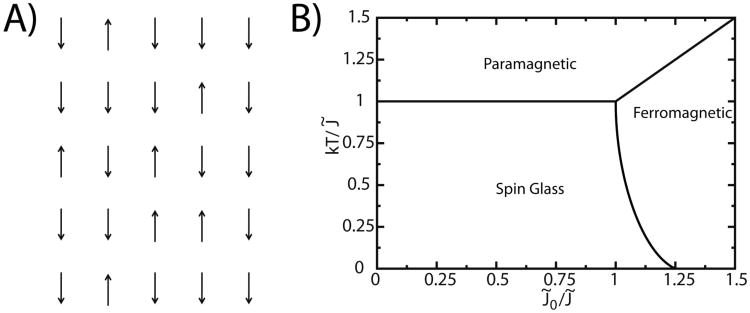
Figure 4. Spin systems and glass transitions.

A) A two-dimensional Ising spin model. B) Schematic of the phase diagram for the SK spin-glass model. In the SK spin-glass, three states can exist: paramagnetic, ferromagnetic, and glass. The balance of energetic roughness (J̃), ferromagnetic coupling (J̃₀) and temperature T determines which state the system adopts.

$$H=-\sum _{\left\{\mathit{\text{ij}}\right\}}{J}_{\mathit{\text{ij}}}{s}_i{s}_j,$$ (1)

where Σ_{ij} denotes the sum over all adjacent spins (s_i, s_j) and J_ij is the magnetic interaction energy of spins s_i and s_j. When J_ij > 0 (ferromagnetic interaction) for every pair, the lowest energy configuration of the system corresponds to all spins being aligned. If J_ij > 0, the system is described as “unfrustrated” since the interactions are consistent. That is, every microscopic interaction may be satisfied in the lowest energy configuration of the system and, at low temperatures, the magnitude of the average magnetization 〈m〉 approaches 1.

Ising systems of two or more dimensions (and J_ij > 0) undergo second-order phase transitions between disordered (〈m〉 = 0) and ordered states (|〈m〉| ≈ 1) (38) at the so-called critical temperature T_C. For T < T_C, the thermal fluctuations are sufficiently small that the stabilizing interactions are collectively satisfied and the majority of the spins align in a single direction. For T_C > T > 0 the system adopts a ferromagnetic state, though transient anti-ferromagnetic configurations are sampled. If J_ij is not constant for all pairs, then the probability of anti-ferromagnetic orientations are heterogeneously distributed across the system. Due to the Boltzmann weighting of configurations, this feature is obvious, though it is noted since biologically-relevant parallels will be drawn later.

In 1975, Sherrington and Kirkpatrick (SK) introduced an extended and exactly solvable Ising model that exhibits a glass phase (35). Rather than have J_ij ≠ 0 for only the adjacent pairs, the J_ij coupling constants are defined for all spin pairs (i.e. infinite-range interactions), and the probability distribution of the constants is given by:

$$p(J_{\mathit{\text{ij}}})={[{(2\pi )}^{1/2}J]}^{-1}\text{exp}[-{(J_{\mathit{\text{ij}}}-J_0)}^2/2J^2].$$ (2)

In the limit J → 0, the SK spin system reduces to the unfrustrated Ising model, and J_ij = J₀ for all pairs. As J → ∞ the interactions are completely random and the system does not exhibit long-range order (〈m〉 → 0). For large J (relative to J₀), the system is energetically frustrated, and not all interactions can be satisfied simultaneously.

There are several general features of the SK Ising model that are most relevant when describing the energy landscapes of biomolecules. Figure 4 shows the phase diagram for the SK model, in terms of the normalized quantities J̃₀ = NJ₀ and J̃ = N^1/2J, where N is the number of spins in the system. The axes correspond to ratios of competing energetic parameters: k_BT/J̃ and J̃₀/J̃. k_BT/J̃ is the ratio between thermally-accessible energetic fluctuations and the heterogeneity of the interaction weights. For large T, individual spins have sufficient thermal energy to take any value and the system enters a paramagnetic state (〈m〉 → 0). At low T, the system can enter a ferromagnetic state, or a spin-glass state. In the ferromagnetic state the individual spins are aligned (|〈m〉 → 1). In the spin-glass state, individual spins may align locally, but there is no long-range ordering. For low values of k_BT/J̃, J₀˜/J̃ determines whether the ferromagnetic or glass phase is adopted, where J̃₀ is the average coupling and J̃ is the dispersion of the coupling constants. When J̃₀/J̃ > 1, the system may adopt a ferromagnetic or paramagnetic state. If J̃₀ is large relative to J̃, then the majority of the system's interactions will be ferromagnetic, and every microscopic ferromagnetic interaction may be satisfied in a global ferromagnetic state. If the dispersion is large, relative to the average coupling (i.e. J̃₀/J̃ < 1), the system is composed of a mixture of ferromagnetic and anti-ferromagnetic interactions, and it is described as “energetically frustrated.” In frustrated systems, not all interactions can be satisfied simultaneously (i.e. where each microscopic interaction is a minimum). Accordingly, if J̃₀/J̃ and k_BT/J̃ are small, the system will enter a glassy state. Hallmark features of glassy systems are a lack of long-range ordering (〈m〉 → 0) and diverging relaxation times. Diverging relaxation times are due to interactions being satisfied locally, though the low-energy configurations are highly degenerate, which leads to competition of local structure formation. For a more detailed discussion on the thermodynamic properties of the SK model, we suggest the original manuscript (35).

Glass transitions are not isolated to Ising models. They are ubiquitous in nature and have been investigated computationally (40–42), theoretically (43–46) and experimentally (47–49) for a wide variety of systems. Here, we have limited the discussion to the general relationships between energetics, order-disorder transitions and glass dynamics, in order to guide our description of biomolecular dynamics.

2.2. Some Parallels Between Glasses and Protein Folding

While the energetics of biomolecules are not simply composed of spin-spin coupling interactions, analogous behaviors between biomolecular folding and glass transitions may be identified (49). Most proteins spontaneously fold under physiological conditions, and they do so in relatively short timescales (milliseconds). Similarly, in the Ising model, if the dispersion in the interactions is small, then a paramagnetic-to-ferromagnetic transition occurs without the formation of long-lived kinetic traps. In the SK spin model, when 1 < J̃₀/J̃ < 1.25, there are three accessible states. Consistent with this, in proteins, the adopted state is determined by the temperature-to-dispersion ratio k_BT/J̃. The paramagnetic:ferromagnetic:glass states thus correspond to unfolded:folded:misfolded ensembles. In polymers, glassy dynamics may emerge at low temperatures (50), where the glassy “state” is composed of many competing configurations and interconversion times between them is slow. Finally, for a given value of J̃₀/J̃ (between 1.0 and 1.25), these systems have well-defined order-disorder transition temperatures (paramagnetic-ferromagnetic transition, or folding-unfolding transition) and a glass transition temperatures (ferromagnetic-glass, or folded to glass/misfolded).

2.3. Energy Landscape Theory and The Principle of Minimal Frustration

The similarities between glass-forming systems and protein folding led to the proposal of The Principle of Minimal Frustration (19, 51, 52). That is, naturally occurring protein sequences are able to fold on short timescales, which indicates these sequences encode energetics for which the folding temperature T_f (i.e. the temperature at which the unfolded and folded ensembles are equally probable) is larger than the glass transition temperature T_g. Further, the principle states that nature has selected for protein sequences that maximize the ratio between T_f and T_g, which allows proteins to fold rapidly in vivo (i.e. T_g < T_cell < T_f). T_f/T_g in proteins parallels J̃₀/J̃ in the SK spin-glass model. J̃₀ is the average coupling strength of the spins, which is analogous to the average stabilizing energetic contribution of each native interaction in a protein. In the words of Gô (53), J̃₀ is similar to the degree of “consistency” between the native interactions in a protein. These consistent interactions lead to an energy gap δE between the disordered and ordered states (Figure 3). J̃ is the dispersion in the strength of the spin interactions and it is correlated with the degree of frustration in the system. In proteins, frustration manifests as stabilizing non-native interactions (34). According to these corresponding features of proteins and glasses, The Principle of Minimal Frustration states that by maximizing the ratio between the stabilizing energy gap δE and the energetic roughness ΔE (which determines the ratio T_f/T_g), nature has selected for protein sequences that are able to fold rapidly.

3. Modeling Approaches for Protein Folding

Over the last 20 years, many theoretical and computational studies have investigated the protein folding problem. Of particular relevance to this review are studies that have extended the energy landscape framework for biomolecular folding and function. We will focus on advances that have employed structure-based models (SBMs) (54–56), since these models are founded on The Principle of Minimal Frustration. A common theme throughout these investigations is that by accounting for simple geometrical considerations, such as excluded volume and chain connectivity, dynamic features of protein folding and function may be accurately described. That is, once a protein has evolved to have a dominant energetic basin (or several basins), the geometry of the protein is the primary determinant of the rate/mechanism.

Energy Landscape Theory provides a general physical framework for understanding the energetics of protein folding, which allows for many classes of theoretical models to be employed. Early work used lattice models of proteins, where each residue is described as a single bead that moves between lattice vertices. With such models, the interplay between global collapse, connectivity of states and energetics was elucidated. Subsequent work employed more easily transferable coarse-grained off-lattice models. Recently, we have developed models that combine all-atom resolution with the energy landscape framework. To clarify the utility of each approach, we will provide an overview of how each class of models has advanced our understanding of protein folding. By considering the advantages and limitations of each approach, future investigations may strategically utilize the models that are best suited for each question.

3.1. Lattice models of protein folding

Inspired by the glass-theoretical roots of The Principle of Minimal Frustration, early simulation models for protein folding also used lattice representations of polymer chains to explore the relationship between energetic frustration, kinetics and structural mechanisms (19, 57, 58). In these models, the polymer is treated as a connected chain, where each amino acid residue is a link that transits across a discrete set of lattice positions (Figure 5). The functional form of the Hamiltonian used in many studies is similar to an Ising spin model:

Figure 5. Lattice model for protein dynamics.

In lattice models of proteins, the residues (spheres) move between adjacent lattice positions. Similar to proteins in solution, backbone connectivity (grey) leads to sequential residues being adjacent in space. In this model, the degree of hydrophobicity is indicated by the sphere colors. The sequence shown is taken from Leopold et al., and it represents a maximally-compact configuration (19).

$$E=-\sum _{\left\{\mathit{\text{ij}}\right\}}∊(s_i,s_j)\Delta (i,j)+\sum _k\delta (|{\overrightarrow{r}}_k-{\overrightarrow{r}}_{k+1}|).$$ (3)

The chemical identity of the primary residue sequence S is defined as s₁,…, s_N, ∊(s_i, s_j) is the coupling constant between residue types, Δ(i, j) = 1 if the residues are on adjacent sites and Δ(i, j) = 0 otherwise. The summation over {ij} is the sum over all residue pairs (not a sum over all lattice sites). The second term sums over all residues that are adjacent in sequence, ensuring the connectivity of the backbone (grey lines in Figure 5) is maintained. δ = 0 if the residues are on adjacent sites and δ = ∞ if they are not. Changing notation reveals the similarities between this model and the Ising model:

$$E=-\sum _{\left\{\mathit{\text{ij}}\right\}}J(R(i),R(j))O_i{O}_j+\sum _{k=1}^{N-1}(|{\overrightarrow{r}}_k-{\overrightarrow{r}}_{k+1}|)$$ (4)

where {ij} is now defined for all adjacent lattice sites. O_i is the occupancy of each lattice site (1 if occupied and 0 if unoccupied), J(R(i), R(j)) defines the coupling between the types of residues in the sites, and R(i) is the type of residue at site i. R(i) carries the same type of information as s_i. However, R(i) is the type of residue at site i and s_i is the residue type in sequence position i. Accordingly, R(i) is not defined if site i is unoccupied, in which case O_i is also equal to zero. In this specific formulation, there are no long-range interactions, though alternate formulations have included a combination of long-range and short-range interactions (59, 60).

The only differences between the Ising spin Hamiltonian and protein lattice Hamiltonian are the connectivity restriction (δ function in Equations 3 and 4) and the intrinsic time dependence of the site-site coupling constants J(R(i), R(j)) ^‖. While these complications have impeded efforts to find an analytic solution for the model, the relatively small number of discrete configurations on the lattice allows all compact configurations to be explicitly enumerated for small system (i.e. a 27-mer) (29, 30, 61–63).

3.1.1. Utility of Lattice models

While lattice models employ a simplified representation of the atomic structure and energetics, they possess several features that allow for a general understanding of polymer folding to emerge. First, there is specificity in the sequence of the monomers. Not only do individual beads (residues) have unique energetic content, but adjacent residues (in sequence) are constrained to be on adjacent vertices (i.e. covalent geometry is maintained). Another physically valid constraint in the model is that monomers can not pass through one another. In an Ising system, it is possible for adjacent lattice sites to simultaneously exchange values (e.g. position i goes from spin -1 to +1 when position i +1 goes from +1 to −1). In lattice models of proteins (and in real proteins) the repulsive nature of atomic nuclei lead to an excluded volume that prevents this from occurring.

The low computational cost of Ising-like lattice models for protein folding has allowed for extensive exploration of the balance between energetic stability, entropic contributions and energetic frustration in protein folding (19, 64–68), and has elucidated new strategies for protein design (69). One of the most significant results stemming from lattice model studies was the folding funnel paradigm for biomolecular folding. This concept emerged from investigation into the energetic, thermodynamic and kinetic differences between “foldable” and “unfoldable” polypeptide sequences. To rationalize the apparent paradox implied by the arguments of Levinthal, Leopold et al. (19) used a lattice model to simulate folding for two protein sequences. While the beads were not assigned energetic values based on a particular polypeptide sequence, the energetic parameters were designed, such that one sequence was foldable. That is, the sequence was designed to meet the following criteria: 1) 20 unique bead “flavors” were used, which reflects the 20 naturally-occurring residue types in proteins, 2) the overall strength of each bead-bead interaction was on the scale of a few k_BT and 3) the potential energy had a dominant energetic basin. This small set of parametric requirements describe an “ideal” protein that has a unique native configuration. The non-foldable sequence was randomly assigned bead flavors, which represents a random heteropolymer that does not have a unique native configuration. While both sequences do have global energetic minima, it was shown that the folding time of the unfoldable sequence was far greater than in real proteins. This is consistent with the arguments of Levinthal, where the search for the native configuration on a rough energy surface is also random, and the likelihood of finding the native configuration becomes vanishingly small. In contrast, for the foldable sequence, folding could be described as a diffusive process over an initially broad ensemble of configurations (i.e. the unfolded ensemble), and the kinetically connected sub-ensembles decrease in size as the native basin is approached. Essentially, the energy landscape resembled a “funnel,” where the native ensemble resides at the bottom (Figure 3).

3.1.2. How to describe folding: Reaction coordinates

Prior to the advent of lattice models for protein folding, kinetic modeling of protein folding involved a traditional biochemical description, where the unfolded and folded basins are separated by a single transition state. Since the free-energy had not been evaluated or measured directly at that time, the landscape was considered in terms of a generalized, ideal reaction coordinate, where approximations are necessary to connect the folding rates and free-energy barriers. Since lattice models provide pseudo-atomic resolution of the folding dynamics, they necessitated rigorous methods for charactering the collective motion of biomolecular processes. That is, the energy landscape of a system is defined in terms of 3N degrees of freedom, where N is the number of atoms. In these landscapes, the free-energy barrier of folding is described by the transition state ensemble (TSE) that separates the unfolded and folded ensembles. One of the objectives of statistical mechanics is to describe the collective dynamics of complex system along a low number of reaction coordinates, or order parameters. In the case of protein folding, the first questions to address were: Are there simple structural reaction coordinates that can capture the essential properties of a folding process? And, what are the appropriate coordinates?

There are several requirements for an appropriate reaction coordinate. First, for a given system configuration, the coordinate must be uniquely defined. Second, each basin and TSE must have distinct values of the coordinate. Third, local moves in Cartesian space must map continuously onto the reaction coordinate. If this requirement is not satisfied, then this coordinate can not describe diffusive motion, since discontinuities will result in the projection of ballistic-like tunneling events in that coordinate space. For a given coordinate, the potential of mean force and diffusion coefficient must also be consistent with the kinetics of interconversion between the local basins (See Relationship between free-energy barriers and kinetics below). Finally, by definition, a configuration in the TSE must be equally likely to proceed to either of the adjacent free-energy minima, and the coordinate must be able to identify a TSE with this property. Since lattice models provided the first opportunity to use atomistic-based reaction coordinates, two intuitive reaction coordinates were introduced: the radius of gyration R_g and the fraction of native contacts Q. Following the initial studies that employed these coordinates, many subsequent studies have investigated the relationships between diffusion, barrier-heights and kinetics along them, in both lattice and off-lattice models (70–78). In the context of off-lattice models, it has been shown that Q can satisfy the above requirements when describing folding of two-state proteins (i.e. two basins separated by a single barrier) (79). In contrast, R_g is able to distinguish between the folded and unfolded configurations, but it is less able to distinguish between native and near-native configurations. However, by considering the folding as a function of both coordinates, folding may be well described as collapse (decrease in R_g) followed by reorganization (increase in Q) (19, 29, 57, 64, 65, 80–83).

3.2. Off-Lattice Models of Protein Folding

3.2.1. C_α models

While lattice models enabled a general characterization of heteropolymer collapse, real proteins do not reside on lattices. Rather, the coordinates of proteins take continuous values in three-dimensional space. To provide a continuous description of the phase space, simplified models that employ an off-lattice representation have been explored (31, 54, 84–92). Early off-lattice models employed a coarse-grained representation of the polymer, where each residue was represented as a single sphere (Figure 6C). With an off-lattice representation, it is possible to study specific proteins and not only model systems. That is, while it is possible to design lattice configurations that resemble the structures of specific proteins, the off-lattice description is transferable to any protein, which has enabled the exploration of the relationship between chain connectivity and excluded volume on the folding properties of many proteins.

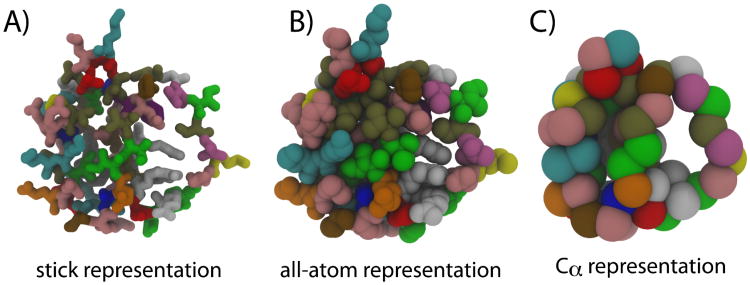
Figure 6. Multiple representations of proteins.

The protein Chymotrypsin Inhibitor 2 (CI2) pdb entry: 2ci2) shown in A) stick representation, B) all-atom representation excluding hydrogens) that depicts the excluded volume of the atoms, and C) C_α representation that is often used in molecule simulations. Each residue type is give a unique color, highlighting the heterogeneity of protein sequences.

The Principle of Minimal Frustration states that the energy gap between the unfolded ensemble and folded ensemble must be large, relative to the energetic roughness (i.e. frustration). Inspired by this, many off-lattice models employ forcefields that are completely specific to the native, folded configuration. These unfrustrated forcefields represent the limiting case of The Principle of Minimal Frustration. Similar to an ideal gas theory, these unfrustrated models represent a low-order approximation to a molecule's energetics, and thus provides a baseline framework upon which the role of energetic perturbations and roughness may be better understood (54, 81, 93–96). For example, this approach has been used to illuminate the effects of cellular crowding (97) and desolvation (81) on protein folding, folding under non-equilibrium conditions (87, 98–101), co-translational folding (102) and aggregation processes (103).

Clementi et al. introduced one of the most popular off-lattice models for protein folding, which is referred to as a Structure-Based Model (SBM), or a Go(x00302)-like model (54). In its initial formulation, the folded configuration is defined as the lowest-energy configuration. Each residue-residue interaction formed in the native configuration is assigned an attractive Lennard-Jones-like interaction, and the minimum energy corresponds to the residue-residue distances found in the native configuration. Adjacent residues are restrained by harmonic interactions, which account for the covalent backbone geometry of the system. The torsion angles formed by residues i, i + 1, i + 2, i + 3 are given cosine functions, each with a minimum corresponding to the native configuration. The functional form of this potential is:

$$V=\sum _i^{\mathit{\text{bonds}}}{∊}_r^i{(r^i-{\mathit{\text{r}}}_{\mathit{\text{o}}}^{\mathit{\text{i}}})}^2+\sum _i^{\mathit{\text{angles}}}{∊}_{\theta }^i{({\theta }^i-{\theta }_o^i)}^2+\sum _i^{\mathit{\text{dihedrals}}}{∊}_{\phi }^i\{[1-\mathit{\text{cos}}({\phi }^i-{\phi }_o^i)]+\frac{1}{2}[1-\mathit{\text{cos}}(3({\phi }^i-{\phi }_o^i))]\}+\sum _{\mathit{\text{ij}}}^{\mathit{\text{contacts}}}{∊}_C^{\mathit{\text{ij}}}[5{\left(\frac{{\sigma }^{\mathit{\text{ij}}}}{r}\right)}^{12}-6{\left(\frac{{\sigma }^{\mathit{\text{ij}}}}{r}\right)}^{10}]+\sum _{\mathit{\text{ij}}}^{\mathit{\text{non–contacts}}}{∊}_{\mathit{\text{NN}}}^{\mathit{\text{ij}}}{\left(\frac{{\sigma }_{\mathit{\text{NN}}}^{\mathit{\text{ij}}}}{r}\right)}^{12}$$ (5)

Where ${∊}_r^i=100,{∊}_{\theta }^i=20,{∊}_{\phi }^i=1,{∊}_C^{\mathit{\text{ij}}}=1,{∊}_{\mathit{\text{NN}}}^{\mathit{\text{ij}}}=1,$ and ${\sigma }_{\mathit{\text{NN}}}^{\mathit{\text{ij}}}=4.0\mathring{\text{A}}.{\mathit{\text{r}}}_{\mathit{\text{o}}}^{\mathit{\text{i}}},{\theta }_o^i,{\phi }_o^i$ and σ^ij are given the values found in the native structure. The bond and angle terms maintain the chain-like connectivity of the polymer. The 10-12 potential is used to model each native contact. While in this implementation the interactions are completely additive, other off-lattice models include non-additive (or, 3-body) interactions (104, 105), which is sometimes necessary to recover the proper degree of folding cooperatively.

In this model, since the solvent is not explicitly represented, the stabilizing 10-12 interactions are solvent-averaged effective interactions. That is, the native configuration has evolved to be the lowest free-energy configuration. Therefore, the native interactions are effectively stabilized, even though direct residue-residue interactions may be unfavorable. For example, it is possible for a native configuration to have two positively charged residues near each other, even though the direct interaction between like charges is repulsive. However, since these residues are in close proximity in the lowest free-energy configuration, the potential of mean force between them has a minimum at the native distance. According to this logic, the native interactions in these forcefields are “effective” interactions that are averaged over the contributions of water and non-native interactions.

Structure-based models have forcefully demonstrated that chain connectivity and excluded volume significantly restrict the possible folding routes of biopolymers. This restriction of phase space can lead to a feature known as “Topological Frustration” (31, 106–111). Topological frustration may be characterized as the requirement of particular subunits to fold first, regardless of the relative stabilities. That is, it is possible that formation of particular native interactions will impose strong structural constraints on the system, leaving insufficient space for the chain to reorganize and form additional native interactions. Topological frustration is not energetic in the classical sense, where attractive interactions lead to large escape barriers from non-native configurations. Rather, similar to how excluded volume may lead to caged dynamics, where large barriers are associated with reorganization in collapsed polymers (112), in a topologically-frustrated fold the early formation of specific interactions can introduce energetic barriers. If the “incorrect” contacts form prematurely, the excluded volume of each atom will lead to high-energy barriers that impede folding. Therefore, it would more likely that the protein will return to the unfolded ensemble than continue folding. Topologically frustrated proteins must search for the appropriate initial interactions that are able to facilitate additional native-structure formation.

To illustrate ways in which topological frustration can manifest, let us compare the folding mechanisms of two small proteins: Protein A and SH3 (Figure 7). Protein A is a three-helix bundle protein and SH3 is composed of several beta sheets. In the folding of protein A, the transition state ensemble has rather homogeneous structural content (113). This homogeneity of the transition state ensemble suggests that the order of structure formation not crucial. Protein A is composed of α-helices that are formed by many interactions between residues that are close in sequence. Each turn of the helix results in interactions between residue i and i+4. In addition to helical interactions, the interface between the helices introduces non-local interactions. By inspecting the native structure, one can easily envision how individual turns of the helix may be relatively disordered while some interface interactions are maintained. In contrast, SH3 has a very polarized transition state ensemble, where some regions are highly ordered and others are largely disordered.

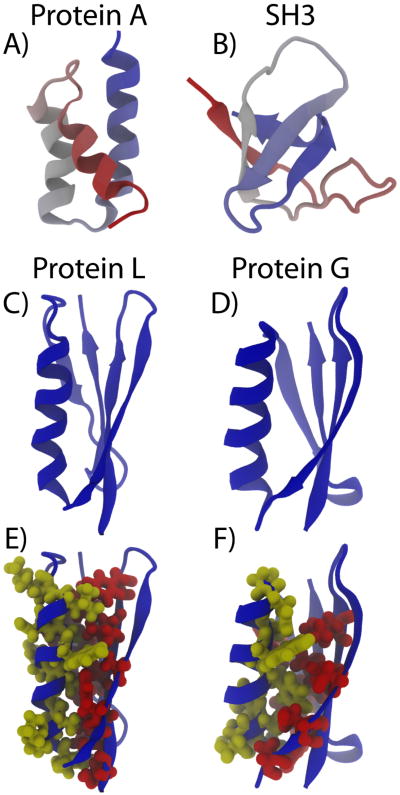
Figure 7. Protein structures vary in complexity.

A) Protein A pdb: 1BDD) is composed of three α-helices and is considered a simple fold. B) The SH3 domain of Src (pdb: 1FMK) is composed of two adjacent β-hairpins, which leads to more-complex folding dynamics. Protein L pdb: 2ptl) (panel C) and G (panel D) (pdb: 3gp1) share a common overall fold, but they exhibit different folding dynamics in solution. Inspection of the packing of residues in the core of the protein (E, F) shows that the fine details of these interactions are different. Side chains are shown explicitly for residues that are in contact between the helix and the sheet. These packing effects lead to unique folding dynamics of the proteins (122).

Two classes of proteins that are considered highly topologically frustrated are knotted proteins (114, 115) and the cytokine Interleukin family of proteins (108, 110, 116, 117) (Figure 8). A knotted structure may be defined by the following criteria: If the terminal ends of the chain are pulled in opposite directions, it will not reach a fully-extended structure. Rather, pulling results in a compact knot. Knots have been identified in a number of proteins and recent work has employed simplified models to characterize how complex native structures can be reached during folding (118, 119). Entropic considerations suggest that the most favorable way to fold would be to first form a loose loop and then thread the terminal end of the protein through the loop. Subsequent local rearrangements then lead to a completely folded configuration. If the loop were to close (i.e. fully form) early in the folding process, then there would be insufficient space for the threading process to occur, which highlights the topological difficulties associated with folding these proteins.

Figure 8. Topologically frustrated structures.

Two classes of proteins that are considered to be of “complex” folds are knotted proteins (top, stereo view. PDB: 2EFV) and the Interleukin family of proteins (bottom, stereo view. PDB: 6I1B). In the knotted protein, folding involves the formation of a loop and then threading of the terminal end through the loop. If the loop closes prematurely, then the threading process will be inhibited by excluded volume effects. In the Interleukin family, there is structural competition between regions during folding. If the C-terminal trefoil folds early, the protein “backtracks” and partially unfolds before full folding occurs.

The excluded volume of individual atoms can also lead to backtracking in proteins (91, 107, 120, 121), including knotted ones (118, 119). Backtracking is defined as a phenomenon where native structure forms, breaks and reforms during forward progress of the global folding process. In the case of IL-1β, when residues in the C-terminal trefoil region possess native structural content early, as folding continues to proceed, this region temporarily unfolds prior to it reaching a fully-folded configuration. As discussed above, one hallmark of topological frustration is that the protein returns to the unfolded ensemble if the “wrong” interactions form prematurely. In the case of IL-1β and backtracking, the unfolding is localized, where specific structural units reversibly unfold and refold as the forward global folding process takes place.

3.2.2. All-atom models

Following the progression from lattice to off-lattice C_α models, the next logical step was to extend biomolecular models to all-atom (AA) representations^¶. In all-atom structure-based models (56, 122–128), every heavy atom (and, in some cases, hydrogen atoms) is explicitly represented. Similar to its C_α counterpart, every interaction in the native configuration is stabilizing, which ensures the native structure is the lowest-energy configuration. Adopting this representation has two advantages that are immediately evident. First, by including all atoms, the excluded volume of the atomic structure is explicitly accounted for, which allows one to characterize the relationship between the details of atomic packing and the functional/folding properties. Through comparison with a C_α model, it was shown that side-chain packing can significantly influence the folding of some proteins. Specifically, proteins that have spatially-symmetric backbone configurations can have two or more apparently equivalent folding pathways, when described by a C_α models. A second motivation for using an AA model is that non-specific atomic interactions (i.e. interactions that are not formed in the native configuration) may be explicitly included, where the native-centric SBM would serve as a baseline model. That is, one may partition the effects of individual energetic contributions on the folding process (or other molecular processes) by comparing the dynamics in an unfrustrated model and a model where non-specific attractive interactions are included.

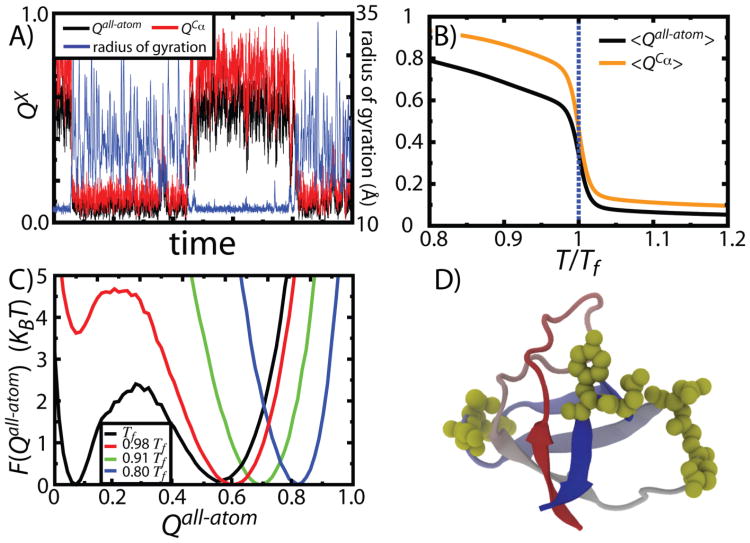
While the cooperative transition associated with protein folding encompasses a large change in configurational entropy of the backbone, the contribution of side chain entropy is less clear. We recently extended the C_α SBM to an all-atom representation and detected a partial separation between backbone ordering and side-chain ordering (56). These models yield a peak in the specific heat curve, indicative of a phase transition between the disordered (unfolded) and ordered (folded) ensembles, which is coincident with backbone ordering. However, this transition is accompanied by only partial ordering of the side chains. Figure 9 shows a typical trajectory for a single protein, described by the radius of gyration R_g (which measures chain collapse), the fraction of all-atom native contacts formed Q_AA (which characterizes side-chain packing) and the fraction of C_α – C_α contacts formed Q_Cα (which measures tertiary structure formation). Both 〈Q_AA〉 and 〈Q_Cα〉 undergo sharp transitions at T_f (Figure 9B), but 〈Q_Cα〉 is larger than 〈Q_AA〉. This separation of backbone and side-chain ordering has also been noted in recent explicit-solvent simulations (129), suggesting it is a robust feature of protein folding. Figure 9D shows which residues exhibit ordered backbones with disordered side chains in the folded ensemble (highlighted in blue). It is striking that disorder in the side chains is not homogeneous between all residues. Even though the residue-residue contacts indicate that the tertiary structure of the molecule is formed, specific regions have more highly-disordered side chains, which is similar to anisotropies in ferromagnetic-phase spin-glass systems. The disorder accessible in a folded protein raises the question: Since folding does not necessitate the ordering of all side chains, does side-chain mobility fulfill a functional purpose? Loop residues are often involved in protein recognition processes (130–132). The predicted flexibility of side-chain conformations in folded proteins is consistent with the notion that loop sequences may evolve in response to functional pressure that is independent of pressure to folding efficiently. Loop flexibility may also allow for conformational adaptability, which may enable proteins to participate in parallel signaling pathways. An alternative role of side-chain flexibility is that balancing order-disorder transitions in the side chains may be a way in which proteins modulate the free-energy barriers of interconversion between functional conformations (133–135).

Figure 9. Side-chain ordering and backbone collapse during protein folding.

A) A simulated folding trajectory of CI2, shown as a function of the radius of gyration R_g (blue), fraction of native all-atom contacts formed Q^all-atom (black) and fraction of native C_α contacts formed Q^Cα. R_g measures backbone collapse, which decreases when Q^all-atom and Q^Cα increase. Q^Cα reaches larger values than Q^all-atom indicating that the backbone is ordered, while the side chains are not in their native configurations. B) 〈Q^all-atom〉 and 〈Q^Cα〉 as function of T indicate that both coordinates capture the global folding transition. C) As temperature is reduced below T_f, there is continuous movement of the native basin to higher values of Q^all-atom. D) Residues in SH3 that have a larger fraction of C_α contacts formed than all-atom contacts are depicted by yellow spheres.

All-atom models have highlighted modes by which side-chain dynamics may guide the folding process. For example, the experimentally-characterized disparate folding properties of protein L and protein G (two proteins that share the same global fold. Figure 7) could be accounted for by subtle differences in packing interactions of the side chains (122). Since these β-sheet structures are symmetric at a coarse (i.e. residue) level, the details of the atomic packing (between the α helix and β-sheet) significantly influence the predicted folding rates and mechanisms. Recently, it was also shown how orientational information contained in side-chain packing reduces the prevalence of malformed knots in proteins (119). Specifically, at the residue level, the energetic penalty of “crossing” mistakes is small, which can lead to the native configuration becoming kinetically inaccessible.

Similar to studies with C_α models, using all-atom models, one may ask: What dynamic properties are robust, and which may be more easily manipulated in order to gain precise functional control? Using an all-atom structure-based model, we investigated the effects of energetic perturbations on the folding properties of several well-studied proteins: CI2, SH3 and Protein A (56). To no surprise, the thermodynamic quantities were sensitive to the energetic details. Consistent with the theoretical work of Portman and Wolynes (136), these models demonstrated how the balance between chain persistence length and non-local stabilizing interactions impacts the free-energy barriers of folding. That is, as the persistence length is increased, the free-energy barriers also increase. Consistent with the findings from C_α models (137, 138), the folding mechanisms were largely robust, though there was a small degree of variation. Protein A, which is considered a simple fold, was most sensitive to the distribution of energetics, while SH3 was most robust. This is consistent with the SH3 fold being topologically frustrated (106). In topologically frustrated folds, the phase space that the protein may sample en-route to the native configuration is reduced, relative to a simple fold. The fact that the SH3 folding mechanism was only marginally perturbed by changes in energetics is consistent with this highly restricted phase space.

4. Theoretical Approaches to Investigate Conformational Rearrangements

Recent work has expanded the energy landscape approach beyond folding, in order to describe large-scale conformational transitions associated with function. Oftentimes, biomolecules do not possess a single well-defined native configuration. Rather, there are competing basins of attraction and the balance between the conformations governs the biological functions of the molecule (139–141). Some enzymes undergo conformational rearrangements upon substrate binding (142, 143), taking the molecule from an enzymatically inert state to a conformation that is competent for chemistry. These rearrangements can even be rate limiting in the catalytic cycles of enzymes (144). In molecular machines, processive functions require conformational cycling through functional configurations, such as the “walking” of kinesin on microtubules (145) and the elongation cycle of the ribosome (146–148). Molecular machines that are not processive may also utilize large-scale rearrangements during function (e.g. the spliceosome (6)).

At first glance, it may be tempting to characterize functional rearrangements as rigid-body movements about well-defined “hinge” regions, since macroscopic machines function in this manner. While this approximation may be accurate in some cases (149), applying this framework to all biological systems can be misleading. In macroscopic machines, the rigid components are “infinitely” rigid (orders of magnitude stronger than the man-made hinges). The interactions that maintain macroscopic rigid bodies are extremely strong, relative to thermal energy, which allows macroscopic machines to maintain their structural integrity over a wide range of temperatures and conditions. Therefore, rigid macroscopic components undergo negligible changes in entropy during function. In contrast, biomolecules are only marginally stable, where a 10-20 % increase in temperature often results in high-entropy unfolding to occur. Further, in molecular machines, the weak interactions (i.e. on the scale of thermal fluctuations) that stabilize the folded configurations also govern the dynamics of functional motions. Since folding and function take place on a single energy landscape, we must expand our energy landscape approaches for folding to account for functional dynamics.

In this section, we will discuss current theoretical and computational approaches that are used to explore biomolecular functional energy landscapes. A challenge in these investigations is that in order for these molecules to interconvert between stable configurations, the native basin must not be uniquely defined. Since the folding and functional landscapes of a biomolecule are one and the same, the funneled energy landscape for folding (19) has to be extended to include competing basins. Similar to studies on protein folding, simple models allow for a low-order approximation to the energetics, which enables one to identify which features of the functional dynamics are most robust and which are most responsive to changes in energetics and cellular/experimental conditions. By partitioning the robust features, one may design new strategies to precisely target and regulate biomolecular dynamics.

4.1. Normal Mode Analysis

In normal mode analysis (NMA), the potential energy is expanded about a particular minimum to second order, and the local motions are described as a superposition of orthogonal oscillatory motions (150). In solution, biomolecules exhibit overdamped dynamics and their trajectories do not follow harmonic modes with precise frequencies. However, the energy local to the minimum may be expanded in terms of the modes:

$$E=\sum _n\frac{1}{2}{\omega }_n^2{q}_n^2,$$ (6)

where the normal coordinate of mode n, q_n, has a characteristic frequency ω_n. Each eigenvector of the Hessian matrix (i.e. the normal mode) corresponds to a single degree of freedom, and the equipartition theorem dictates that each mode has an average energy of 1/2k_BT. It then follows that $\langle q_n^2\rangle \propto {\omega }_n^{-1}$ , such that large-scale motions occur along the lowest-frequency modes. Interestingly, normal mode analysis of proteins has repeatedly demonstrated that low-frequency modes correspond to global deformations (151–153) that are in functionally-relevant directions (154).

A commonly-used potential energy function used for NMA of proteins is the Tirion potential (155). Similar to SBMs, the Tirion potential defines the native configurations as the lowest energy configuration and atoms that are near each other are assigned harmonic potentials, where the minima are assigned based on the initial configuration. Consistent with SBMs for folding, since the initial structure is typically a stable configuration, the Tirion potential provides a low-order approximation to the landscape about that minimum. Additionally, this simple approximation has been shown to accurately reproduce the local fluctuations about stable protein configurations (133, 143, 156–158).

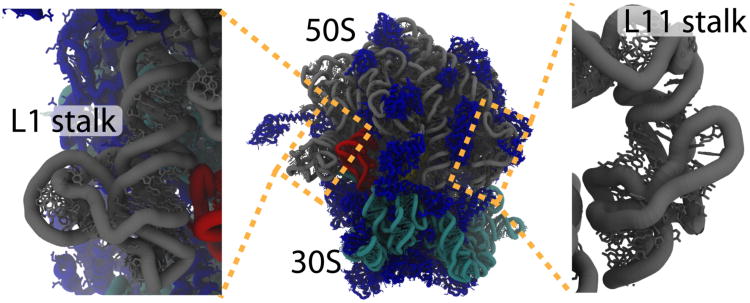
Low-frequency motions are largely determined by the global structure, and not specific energetic details (154). While individual interactions are important for the stability of the molecule, the connectivity of bonded and non-bonded interactions restricts the possible fluctuations, such that many Hamiltonians yield similar global motions about a chosen basin (159). These low-frequency motions in proteins and molecular complexes are also often correlated with functionally-relevant motions (160). In other words, the global structure determines the accessible local motions and these motions correlate with the large-scale changes required for function. Therefore, this provides a direct connection between molecular structure and function. The ribosome (Figure 10) is an excellent example that illustrates this relationship. Analysis of local-basin fluctuations have suggested that the movement of “stalk” regions is lower in energy than most other motions. While initial studies employed NMA with harmonic potentials (153, 153, 158, 161, 162), subsequent studies found similar results using all-atom structure-based simulations (163) and all-atom explicit-solvent simulations (164). These independent classes of theoretical models employ different assumptions and parameterizations. The fact that the fluctuations are so similar confirms that the dominant contributor to the local fluctuations is the overall structure of the molecular complex.

Figure 10. The Ribosome Center).

Atomic structure of an in-tact 70S ribosome (∼150,000 non-hydrogen atoms). Transfer (RNA tRNA, P-site tRNA shown in red) molecules read messenger RNA (mRNA) through interactions on the “small” (30S) subunit and add the incoming amino acid to the growing protein chain located in the “large” (50S) subunit. An additional tRNA i.e. the A-site tRNA) is buried deep inside of the ribosome. During protein synthesis, the 50S “stalks” assist movement of tRNA molecules. The L11 stalk (right) aids the entry of incoming tRNA molecules and the L1 stalk (left) facilitates the disassociation of tRNA molecules. NMA, simulations with SBMs and simulations with explicit solvent suggest that the stalks are very flexible (i.e. have low-energy displacements), relative to other components of the ribosome.

Since the local fluctuations described by NMA often correlate with functional motions, ongoing efforts are extending these methods to uncover the pathways between specified endpoints (133, 156, 165, 166). Miyashita et al. developed an iterative NMA approach to obtain a sequence of structures that represent a low-energy pathway between two functional configurations of the protein Adenylate Kinase (Figure 11). To do so, they first defined a Tirion potential for the initial configuration, calculated the normal modes and then displaced the structure along several low-frequency modes (where movement along each mode was proportional to the overlap with the displacements between endpoint configurations). After making a small displacement (such that the harmonic approximation was valid), the Tirion potential was re-defined for the new configuration, the modes were re-calculated and the system was displaced again. This process was repeated to generate a sequence of configurations along the modes that have the highest-overlap with the rearrangement. In this approach, only a few low-frequency modes were necessary to describe the majority of the global displacements. Following these initial studies, Adenylate Kinase has become the paradigm protein system for testing new concepts and methods in protein conformational transitions (133, 156, 165, 167–172). A common finding in these investigations is that the global motions are described well by low-frequency motions, though high-frequency motions are necessary to precisely organize catalytic sites.

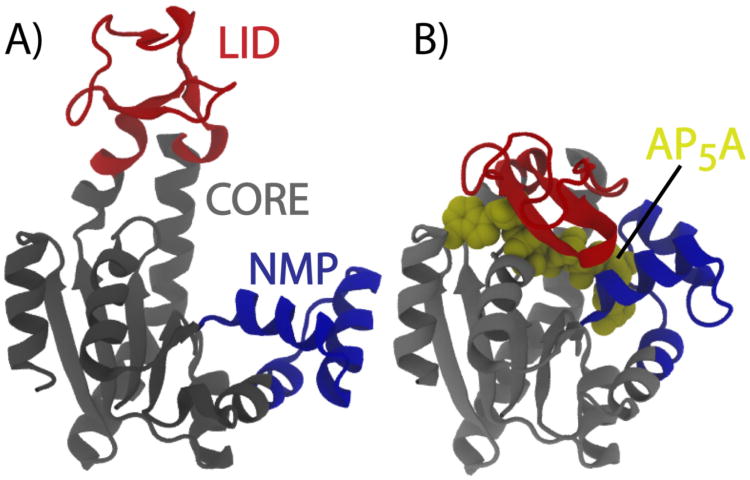
Figure 11. Functional configurations of Adenylate Kinase.

Adk is composed of three domains: LID (red), NMP (blue) and core (grey). A) When a ligand is not present, the dominant configuration has the domains arranged in a more extended fashion. B) Upon ligand binding, the molecule adopts a compact conformation, where the ligand is isolated and chemistry is permitted. AP₅A is a bi-substrate analogue that mimics the natural substrates of Adk: ATP and AMP.

4.2. Multi-basin Structure-based models

A physicist's approach to a new scientific question is to make the lowest-order approximation to the system's energetics, take that expansion to its limits of applicability and then expand to higher order. In this respect, the lowest-order approximation to a systems' dynamics is a static structure, which represents the average coordinates inside of a basin 〈r⃗ 〉. The first-order correction would be the isotropic dispersion in the coordinates $\langle \Delta {\overrightarrow{r}}_i^2\rangle$, which can be estimated from experimentally-accessible Debye-Waller factors (173). The dispersion may also be described in terms of anisotropic motions, where $\langle \Delta {\overrightarrow{x}}_i^2\rangle$, $\langle \Delta {\overrightarrow{y}}_i^2\rangle$ and $\langle \Delta {\overrightarrow{z}}_i^2\rangle$ are independent. The anisotropic dispersion characterizes the shape of the landscape about the average structure (173) and it can be obtained from normal mode analysis or from x-ray crystallographic refinement methods (174, 175). While the correlation between anisotropic motions and functional rearrangements has allowed NMA to identify low-energy paths between basins of attraction, when atomic displacements involve the breaking and formation of interactions, the harmonic approximation becomes increasingly inaccurate. To expand the description of the landscape to include large-scale conformational rearrangements, recently-developed modeling approaches represent the potential energy landscape as having a defined number of experimentally-identified basins of attraction (176–178). While there is a range of molecular modeling approaches available to study conformational rearrangements, we will focus our attention on investigations that use multiple structure-based potentials to define a single multi-basin potential. For those interested in alternative approaches, such as the use of semi-empirical forcefields (179, 180), there are many reviews available that may be of interest (181–184).

Multi-basin structure-based models allow one to explore the robustness of functional dynamics and develop energetic descriptions of the process that are quantitatively consistent with available experimental knowledge. In contrast to the application of SBMs to protein folding, where there is a single dominant basin (i.e. the native ensemble), these approaches extend the description of the landscape to include multiple basins of attraction. When there are multiple well-characterized conformations associated with a particular biomolecule, the model must possess a minimum for each conformation (Figure 12). The general strategy when building these models is to construct a structure-based forcefield for each configuration and then systematically merge the energetic terms into a single potential energy function.

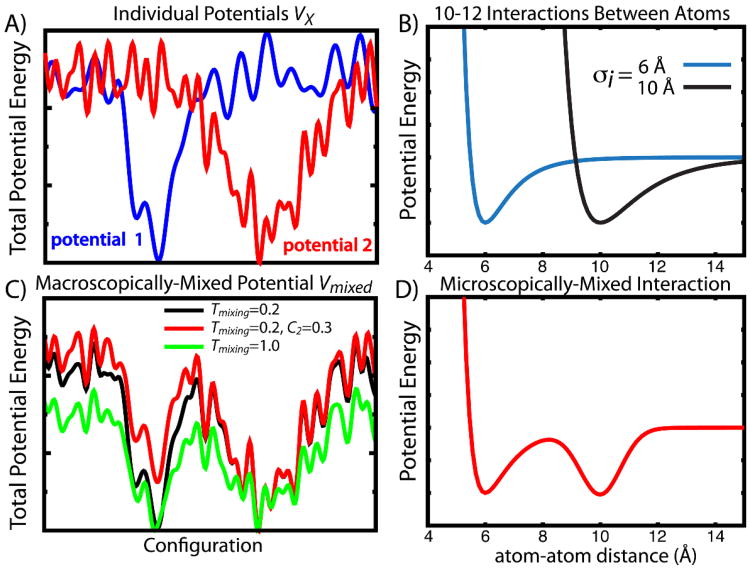
Figure 12. Macroscopic and Microscopic Mixing.

When combing two potential energy functions, one may combine them term-by-term, or in a global fashion. A) Two hypothetical potential energy surfaces, where each curve depicts the total energy in each potential, given in terms of an arbitrary coordinate. B) Two 10-12 interactions that are defined for the same atom-atom pair. This depiction represents a pair that is 6Å in one configuration and 10Å in the second. C) A macroscopically-mixed (Boltzmann) Hamiltonian, using the two potentials in (A) as input. Different values of the mixing temperature T_mixing and weighting factor C_i are shown. D) A microscopically-mixed atom-atom potential energy function that includes minima at both 6 and 10 Å. This representation uses a Gaussian function for the minimum at 10 Å.

Multi-basin approaches may be partitioned into two broad categories, which we will refer to as “microscopic” and “macroscopic” mixing. To illustrate the differences, we will first consider the functional form of a single-basin structure-based forcefield (Equation 5). Each experimental conformation can be used to uniquely define a structure-based energy function V_X. A multi-basin Hamiltonian is then obtained by combining the information stored in these forcefields. Since the bonded functions (r_o, θ_o, χ_o) are based on the covalent geometry of the molecules, and the chemical composition does not change during the processes described here, we will assume that the bonded functions are identical for all conformations. For ease of discussion, we will also neglect the changes in dihedral angles (φ_o), which reduces the relevant contribution to the non-local contact energies of potential X, $V_X^{\mathit{\text{contacts}}}.$

In a microscopic mixing model, the individual energetic terms are combined term-by-term, which allows the combined potential energy function to be decomposed in the following way:

$$V_{\mathit{\text{mixed}}}^{\mathit{\text{contacts}}}=\sum _i{f}_i(r_i),$$ (7)

where f_i(r_i) is a function that depends on a single degree of freedom (such as the distance between a specific atom-atom pair r_i). Let us consider an ideal protein that has two conformations and the only difference in these conformations is that atom pairs 1:20 and 30:60 (the numbers represent the sequence of the interacting atoms) are separated by different distances. In this example, the two degrees of freedom that determine the energetics of the system are the atom-atom distances r_1,20 and r_30,60. In a microscopic mixing model, the sum of the terms could be re-written as

$$V_{\mathit{\text{mixed}}}^{\mathit{\text{contacts}}}=f_{1,20}(r_{1,20})+f_{30,60}(r_{30,60})$$ (8)

In a macroscopically-mixed model, none of the energetic terms may be expressed as a function of a single degree of freedom. For our hypothetical system, the energy could only be expressed as

$$V_{\mathit{\text{mixed}}}^{\mathit{\text{contacts}}}=f(r_{1,20},r_{30,60}).$$ (9)

In the macroscopic-mixing case, the energetic contribution of each degree of freedom is explicitly coupled to the energetic contribution of every other degree of freedom.

The microscopic and macroscopic mixing models represent the limiting ways by which to combine energetics from two forcefields. In principle, there is a continuum of partially-microscopically mixed models, though they are not as commonly used as other methods of mixing and they will not be discussed further. For a given functional transition, one must consider the differences between the endpoint structures when determining whether a microscopic or macroscopic mixing model is most appropriate. While there are no established rules that dictate the use of each approach, we will outline some general considerations and implications for each.

4.2.1. Microscopic Mixing Models

In microscopic mixing models, the non-bonded energetics of the system may be expressed as a sum of functions that each depend on only one atom-atom distance (Equation 7). While microscopic mixing of multiple SBMs has been implemented in a variety of ways (138, 177, 185), we will describe two classes of models that will illustrate the strengths and limitations of each. For this discussion, we will focus on Adenylate Kinase (Adk), a three-domain protein that is known to populate at least two different configurations during function: the apo and ligand-bound forms (Figure 11).

The first microscopic mixing protocol uses “mutually exclusive” contact interactions (168, 177). In a mutually exclusive potential, the native atomic interactions for each conformation are combined, such that the total interaction between atoms i – j is identical to the potential in one of the single-basin potentials. The apo (ligand-free) and holo (ligand-associated) forms of Adk have 531 and 565 native contacts (177). For contacts that are common to both structures (i.e. same residue pairs at roughly the same distances), there is no need for mixing. For the unique contacts, one variant of a mutually-exclusively mixed forcefield would contain the union of the apo contacts Q_apo and the contacts unique to the holo form ${\mathit{\text{Q}}}_{\mathit{\text{holo}}}^{\mathit{\text{unique}}}$. One interpretation of this potential energy surface is that there is an energetic basin corresponding to the apo form, and “functional frustration” $\left({\mathit{\text{Q}}}_{\mathit{\text{holo}}}^{\mathit{\text{unique}}}\right)$ allows the holo form to be significantly populated. Since the protein has evolved to populate both of these conformations (i.e. these conformations are basins on the landscape), this describes the system as having competing internal interactions that favor either the apo, or ligand-bound, conformation. Another interpretation of this forcefield is that Adk has evolved the apo configuration to be the global basin and ligand binding introduces additional minima between holo atom pairs. From this perspective, there is energetic competition between ligand binding and the evolutionarily-selected energetic minimum of the isolated protein. Computational work that has employed non-structure-based forcefields (171, 186, 187), single-molecule experimental investigations (188) and x-ray crystallographic studies (189) have shown that in the absence of a ligand, Adk exhibits large-scale fluctuations that span all the way to closed configuration. These findings, in addition to the framework provided by the mixed-basin model, suggest that the apo basin is dominant and that residual stabilizing interactions of the holo atom pairs leads to partial sampling of the closed form.

In terms of the energy landscape of Adk, the above example suggests that minimally-frustrated proteins may contain residual frustration that contributes specifically to the functional dynamics. With advances in computing capabilities and algorithms (190–192), a question that should now be tractable is: Does the energetic roughness required for function influence folding mechanisms and rates, or are the folding properties robust? In other words, are function and folding governed by disparate features on the energy landscape? While we are unaware of a theoretical investigation that has explicitly probed this aspect of folding and function in Adk, ongoing work has aimed to identify regions of residual frustration, which may provide insights into the overlap of functional and folding energetics (34).

A second type of microscopic mixing has utility when contacts are formed in both conformations of the system, but the atom-atom distances of these pairs are significantly different (i.e. the differences can not be rationalized as local-basin fluctuations). For example, a contact between residue 10 and 35 may be formed in both conformations, but the atom pairs may be separated by 6 Å and 10 Å in the two conformations (Figure 12B). In these cases, it may be necessary to include a single potential energy function between the two atoms that has minima at both 6 and 10 Å (Figure 12D). This scenario is more frequently encountered in coarse-grained models (such as C_α models for proteins), where side-chain reorganization can lead to changes in the distance between C_α atoms of residues that are in contact. For example, it is possible for two Tryptophan residues (Figure 1) to be stacked, or be interacting in a extended orientation. At a coarse-grained level, the residues are considered “in-contact” in both conformations, though the distances between the C_α may change by ∼10Å. If both configurations are stable, the potential of mean force between the residues must have two minima and this type of multi-basin atom-atom interaction protocol would be appropriate.

When microscopically mixing N Hamiltonians (each with M_i minima), the total number of minima in the mixed potential is not necessarily equal to ${\sum }_i^N{M}_i$. Since the functional form of a microscopically-mixed potential energy function can be rewritten as a sum of functions, each of which only depends on a single degree of freedom r_i, minima on the energy surface must only satisfy:

$$\frac{\partial }{\partial x_k}{E}_{\mathit{\text{mixed}}}=\frac{\partial }{\partial x_k}\sum _{\mathit{\text{ij}}}{E}_{\mathit{\text{ij}}}^{\mathit{\text{contacts}}}(r_{\mathit{\text{ij}}})=\frac{\partial }{\partial x_k}\sum _i{E}_{\mathit{\text{ik}}}^{\mathit{\text{contacts}}}(r_{\mathit{\text{ik}}})=0$$ (10)

for all x_k, where $E_{\mathit{\text{ij}}}^{\mathit{\text{contacts}}}(r_{\mathit{\text{ij}}})$ is the function that describes the total interaction potential between atom-pair ij. While, in principle, this condition may only be satisfied in the endpoint configurations, that is not necessarily the case. For Adk, microscopic mixing models have suggested at least two additional minima (177) that are not captured by a macroscopic mixing scheme (169). That is, two domains of Adk (LID and NMP) are known to interconvert between open and closed configurations (193, 194). Microscopic-mixing models suggest that two possible intermediate basins may also exist, where one domain is closed in each basin. Similar configurations have been identified through x-ray crystallographic analysis (195) and theoretical analysis indicates these partially-closed configurations may increase the fidelity (156) and rate of catalysis (171).

4.2.2. Macroscopic Mixing Models

In macroscopic mixing models the minima are unambiguously defined a priori and all energetic contributions of each potential are coupled to one another. The simplest macroscopic mixing model would be defined by a simple “if”condition:

$$H_{\mathit{\text{mixed}}}^{\mathit{\text{macro}}}\left(\overrightarrow{x}\right)=\{\begin{array}{l}{H}_1\left(\overrightarrow{x}\right)\text{if}{H}_1\left(\overrightarrow{x}\right)<H_2\left(\overrightarrow{x}\right)\\ H_2\left(\overrightarrow{x}\right)\text{if}{H}_1\left(\overrightarrow{x}\right)>H_2\left(\overrightarrow{x}\right)\end{array}$$ (11)

where H₁(x⃗) and H₂(x⃗) are the potential energy functions being mixed and the coordinates of the system are given by x⃗. By definition, the combined potential energy function takes on the value of the lowest energy surface at each point in configuration space. This approach may be generalized to N potential energy functions as H(x⃗) = min(H₁(x⃗), …,H_N(x⃗)). Since the molecules are on a single potential energy surface H_X at each point, the set of minima on this combined landscape is simply the union of the minima in the individual H_i.⁺

There are several considerations when using a macroscopically-mixed Hamiltonian. First, when integrating the equations of motion, the first-derivative must be defined for all possible configurations, which necessitates methods that continuously transition between the potentials. Second, if one seeks to identify the robust features of functional dynamics, the versatility of macroscopic mixing models can be of utility. For example, by using macroscopically-mixed multi-basin models that are capable of explicit modulation of the barrier heights and the depths of each basin, one may determine the extent to which the observed structural mechanisms are determined by the precise distribution of stabilizing energetic interactions. To illustrate the utility of these approaches, we will describe two commonly-implemented macroscopic-mixing algorithms: the “Boltzmann Weighting” and “Superposition” approaches.

In the Boltzmann Weighting approach (176), the mixed Hamiltonian H_mixed (constructed from Hamiltonians H_i) is defined according the following relationship:

$$\mathit{\text{exp}}(-H_{\mathit{\text{mixed}}}{\beta }_{\mathit{\text{mixing}}})=\sum \mathit{\text{exp}}(-(H_i-C_i){\beta }_{\mathit{\text{mixing}}}).$$ (12)

β_mixing = 1/(k_BT_mixing) and C_i is an offset that increases/decreases the relative weight of H_i in the mixed-basin forcefield. Here, the barrier height and depth of each basin are governed by the parameters T_mixing and C_i. For a particular configuration, if (H₁ – C₁) – (H₂ – C₂) = 10k_BT_mixing, then H₂ would be weighted by a factor of e¹⁰ relative to H₁. For example, in Adk, a particular experimental measurement may suggest that the open conformation is more stable by several k_BT, a condition that may be imposed by adjusting the values of C_i(169). T_mixing is the “mixing temperature,” which is unrelated to the simulated temperature. T_mixing modulates the height of the barrier separating H₁ and H₂ by defining how sharp the transition is between potentials. For large values of T_mixing, the relative weight of each potential changes less with the difference between the potentials, and lower barriers are to be expected. Figure 12 shows an example of how two functions may be combined with the Boltzmann Weighting approach. For extensive discussion on specific applications of Boltzmann-weighted mixed potentials, we suggest additional reading (169, 176, 197).

In the Superposition approach (178, 196), a smooth potential, $H_{\mathit{\text{mixed}}}^S$ , is defined as the eigenvalue of the characteristic equation:

$$\left(\begin{array}{cc}{H}_1& \Delta \\ \Delta & H_2+C_2\end{array}\right)\left(\begin{array}{c}{c}_1\\ c_2\end{array}\right)=H_{\mathit{\text{mixed}}}^S\left(\begin{array}{c}{c}_1\\ c_2\end{array}\right)$$ (13)

where Δ is the coupling constant between H₁ and H₂, and (c1, c2) is the eigenvector. Δ governs the barrier height (similar to T_mixing in Boltzmann Mixing), and C₂ controls the relative weights of the input potentials. Solving for the secular equation yields the lowest-energy solution:

$$H_{\mathit{\text{mixed}}}^S=\frac{H_1+H_2+C_2}{2}-\sqrt{{\left(\frac{H_1-H_2-C_2}{2}\right)}^2+{\Delta }^2}$$ (14)

Similar to the Boltzmann Weighting approach, the Superposition approach ensures a smooth transition (i.e. defined first derivative) between potential energy surfaces and it allows the relative depths of each basin to be directly modulated.

4.2.3. Micro- vs. Macro-scopic mixing

Consideration must be given when deciding which mixing method best describes a particular transition. In the macroscopic mixing models, explicit declarations allow for straightforward calibration of some thermodynamic properties. Though, in these models, the “all-or-nothing” contribution of each potential is a restrictive constraint on the dynamics and may appear non-physical. In contrast, the flexibility of microscopic mixing approaches may necessitate a variety of qualitative decisions to be made, as well.

Each approach provides unique insights into the physics of the system. When we used a microscopic mixing model for Adenylate Kinase (177), we first asked whether or not a mixed set of contacts would provide sufficient information to encode the desired endpoints as energetic minima, while also exhibiting appropriate structural fluctuations about the endpoints. Since we were able to satisfy these conditions, the microscopic model provided an energetic framework to interpret the origins of Adk's functional transitions. However, with this approach, the free-energy barrier (potential of mean force as a function of inter-domain distance) was on the order of 1-2 k_BT, which may be a low estimate (described below). In contrast, in a macroscopically-mixed potential for Adk, it is possible to artificially increase the barrier height between the conformations. While the macroscopically-mixed potential has not yielded essential intermediate basins in earlier implementations (due to limitations on the available phase space in macroscopic mixing models), these approaches may be extended beyond the two-basin representation. Combing these approaches, one may use microscopic models to identify stable configurations that result from mixing and then use macroscopic models (with more than two minima) to tune the barrier heights further. Together, this layered approach may establish an overall picture of the energy landscape that is consistent with experimental knowledge that also provides an energetic/entropic characterization of the dynamics.

4.3. Relationship between free-energy barriers and kinetics

It is worth taking a moment to discuss the relationship between free-energy barriers and rates in biological molecules, since this is often where theoretical predictions and experimental kinetic measurements intersect. The barrier height of a conformational change may be related to the mean first passage time 〈τ〉 via the relationship (20, 198):

$$\langle \tau \rangle ={\int }_{Q_{\mathit{\text{initial}}}}^{Q_{\mathit{\text{final}}}}\mathit{\text{dQ}}{\int }_0^Q\mathit{\text{dQ}}\text{'}\frac{\text{exp}[\left(G\right(Q)-G(Q\text{'}\left)\right)/k_{B}T]}{D\left(Q\right)},$$ (15)

where G(Q) is the free-energy as a function of the reaction coordinate Q, D(Q) is the diffusion in Q-space, and Q_final and Q_initial are the values of the coordinate for the endpoint configurations. When the diffusion coefficient in Q-space is not available, and the free-energy profile is dominated by a single barrier of height ΔG, then it is useful to approximate this relationship as (199)

$$\langle \tau \rangle =\frac{1}{C}\text{exp}(\Delta G/k_{B}T).$$ (16)

C may be interpreted as the “attempt frequency” of barrier crossing. While we are not aware of an estimate of C for conformational transitions in Adk, estimates are available for protein folding (200, 201), RNA folding (18) and rearrangements in the ribosome (202). These independent theoretical, experimental, theoretical and computational studies suggest C is ∼ 1 – 10μs⁻¹ for many folding and functional transitions. Since conformational transitions in Adk occur on a smaller length-scale than tRNA rearrangements inside of the ribosome, it would be reasonable to expect C to be larger for Adk's transitions. The corresponding 〈τ〉 values would then represent an upper estimate (for a given ΔG). For example, free-energy barriers of 1-2 k_BT(177) and C = 1μs⁻¹ correspond to 〈τ〉 ∼ 10μs. Kinetic measurements indicate that these conformational transitions are rate limiting and that they occur on timescales of hundreds of microseconds (144), which is slightly slower than the rates predicted by the microscopic mixing model. However, an order of magnitude in timescale only corresponds to a 2.8 k_BT difference in barrier height and the observed deviation may be considered minor.

4.4. Computational considerations

Simulations allow one to enumerate the configuration space of a molecule, from which thermodynamic and kinetic properties may be calculated for a given model. With infinite computing time, one could exploit the ergodicity of these systems and simply wait for the full phase space to be sampled with a Boltzmann distribution. However, the energy landscapes of biomolecules are complex, and often possess many competing energetic basins. Therefore, when using conventional molecular dynamics (or, Monte Carlo) simulations, the majority of the calculation will be spent sampling the low-energy basins, and barrier-crossing events will be rare. Since the transition states between stable basins limit the overall functional dynamics, significant efforts have been dedicated to overcoming the sampling issues associated with high barriers. Some general strategies for characterizing transition states (or, transition state ensembles) are to enhance the overall sampling of the simulation (203–206), increase the sampling along particular coordinates (207), or to specifically search for the transition states (208–213).

In enhanced sampling approaches, system perturbations are introduced increase the sampling in particular regions of phase space and then statistical mechanical relationships are used to recover the physical quantities of the unperturbed system. For example, when using replica exchange methods, multiple copies of the system are simultaneously simulated, and each image is simulated with a unique Hamiltonian (H_i), or at a unique temperature (T_i). During the simulations, replicas are probabilistically interconverted (i.e. the copy at T_i goes to temperature T_i+1 and the replica at T_i+1 goes to T_i). The system at low temperature may then “jump” to the higher-energy configurations that are sampled at higher temperatures. Since these jumps are non-physical, the kinetics of the system are not directly observable. However, if the jumps between temperatures satisfy detailed balance, a canonical ensemble will be sampled. While this method has been very successful for biomolecular folding (214–220), where the relevant transition is temperature induced, there are limitations to its applicability. For example, when studying the interconversion between competing energetic basins, performing simulations at high temperature can lead to global unfolding of the system. More generally, temperature changes can be associated with phase transitions that are not relevant to the process of interest (e.g. global folding, or evaporation of explicit water). When applied to appropriate rearrangements, replica exchange methods can significantly increase the statistics of a given process.

An alternative to calculating the full range of possible configurations is to use path sampling approaches (208–213). Rather than allow the system to freely search all phase space, these algorithms search for the lowest-energy pathway that connects the predefined endpoints. To search for these low-energy paths, the system is described by a set of images, where adjacent images are coupled though energetic restraints, or constraints. As the calculation proceeds, the set of images evolves with time, such that the set of images converge onto the lowest energy (or, lowest free-energy) pathway. These methods are highly effective for describing transitions that possess a dominant low-energy pathway. When there are large changes in entropy as a function of the progress coordinate, then sampling the high-entropy regions has the potential to be computationally challenging. In nudged elastic band methods (210–213, 221), the replicas are coupled to one another, which restricts the relative mobility of adjacent images. If the given rearrangement has a high-entropy substate, then the harmonic coupling between images can limit the characterization of that space. To overcome this issue, these methods often use harmonic approximations to the local density of states, in order to estimate the local contribution to the entropy. For the reader interested in the detailed use of these approaches, we suggest additional reading (222). If there are multiple competing paths, then these estimations of entropy will not be accurate, since the harmonic approximation to the density of states is no longer valid. In string methods (209–212, 223), rather than couple each image to the others, the images are only required to be equispaced along a predefined set of reaction coordinates. As the calculation proceeds, the images are evolved until the lowest-energy path is found (in the defined coordinate space). Since each image is allowed to fluctuate in directions perpendicular to the reaction coordinates, the local phase space may be fully sampled. Thus, string methods can provide a more complete characterization of the minimum free-energy pathways than elastic band methods.

5. Roles of Order-Disorder Transitions in Biomolecular Functional Dynamics

Largely inspired by the seminal works of Haldane and Pauling (224, 225), a conventional view of biomolecular functional dynamics is that there are rigid regions of residues and rearrangements are facilitated by highly flexible “hinge” regions (27, 149, 165, 226, 227). This description is often enticing due to its similarities with macroscopic machines. Though, in contrast to macroscopic machines, where the rigidity of components spans orders of magnitude (i.e. hinges are often lubricated, leading to “flat” potential energy functions, and moving components are composed of solid-phase metals), the weak interactions that maintain biomolecular stability are the same interactions that facilitate functional dynamics. Since the non-bonded energetic interactions that maintain biomolecular structure are normally on the scale of a few k_BT, there is no reason to assume that a hinge/rod description will account for the full range of biomolecular functional dynamics.

Here, we discuss a variety of recent findings that expand our picture of biomolecular functional dynamics beyond the simple hinge/rod picture. Of particular interest is the biological relevance of order-disorder transitions. While energetic interactions are essential for dynamics, biomolecules may also exploit large changes in entropy through local, or global, folding/unfolding events. In doing so, biomolecules may tune their functional dynamics by evolving differential stabilities of particular subunits. To illustrate the biological role of heterogeneous biomolecular stability and flexibility, we will discuss several classes of order-disorder transitions that have been implicated in the functional dynamics of polypeptide and nucleic acid chains.

5.1. Conformational Rearrangements: Cracking

Early studies that employed iterative normal mode analysis to characterize the conformational transitions of Adenylate Kinase (133, 156, 165, 228) suggest that biomolecules may partially unfold and refold during conformational transitions. That is, it was predicted that internal “strain” energy accumulates during conformational rearrangements, and this strain is heterogeneously distributed across the protein. Not only was strain isolated to particular residues, but the level of strain energy would be sufficient to denature the protein (> 20 kCal/Mol). This high strain would also result in free-energy barriers would lead to biologically-irrelevant timescales (i.e. transitions would occur on hours, not milliseconds). To circumvent these high-strain states, it was proposed that these residues may “crack,” or locally unfold and refold during conformational transitions (133). By cracking, residues would release stabilizing interactions, enter a higher-entropy unfolded state and then refold in the alternate configuration. The increase in entropy would reduce the free-energy barrier of rearrangement, and would increase the kinetic rates (Figure 13) (134). At first glance, the cracking mechanism may appear too complex to increase the rates of interconversion. Though, as discussed above, the kinetic prefactor for protein folding is ∼ 1μs⁻¹. Since cracking is a smaller-scale process than folding of an entire protein, one should expect the timescale associated with the cracking transition to be less than 1 μs (assuming that interconversion between order-disorder does not introduce an additional significant free-energy barrier). The ability to transition between order and disorder on such timescales makes it clear that cracking should be a kinetically-accessible mechanism by which conformational rearrangements may occur.

Figure 13. Cracking during functional rearrangements.

Iterative normal mode analysis suggests large levels of strain energy accumulate (black) during conformational rearrangements. To relieve strain that is localized to specific residues, biomolecules may crack, or partially unfold and refold. By unfolding, a large number of unfolded configurations are accessible (red), which increases the entropy of the transition state ensemble and reduces the free-energy barrier associated with the transition (blue). X-ray crystallographic data and NMR measurements (27) probe the fluctuations local to a particular energetic basin (yellow lines), and the local excitations can have dynamics that are correlated with large-scale rearrangements (134).

When the cracking mechanism is employed, the balance between order and disorder for individual residues will determine the functional dynamics. Therefore, protein functional dynamics may be tuned by selecting for amino-acid sequences that have appropriate local stabilities. Analogous to the SK Ising model, each residue is uniquely coupled to the rest of the protein, which allows residues to have differential propensities to spontaneously unfold, even under native conditions (229, 230).

Following the original prediction of cracking, many studies have aimed to use more complex modeling approaches to characterize the location and scale of cracking in Adk. With a microscopically-mixed multi-basin Hamiltonian, we found that the degree of cracking in Adk is largest in the highest-strain regions that were predicted by Miyashita et al. (177). In contrast, simulations of Adk that employed macroscopic mixing models have suggested a lower-degree of cracking (169). As discussed above, this attenuated level of cracking may have been the result of the stringent restrictions imposed by macroscopic mixing models (See Macroscopic Mixing Models). These studies have employed coarse-grained models that represent each residue as a single bead, located at the position of the C_α atom. Therefore, in these studies, cracking was measured in terms of large-scale changes in backbone dynamics. Models that explicitly include all-atoms have demonstrated that protein folding transition may be described as a superposition of partially-separable transitions: backbone collapse and side-chain rearrangements (56, 129, 231). This separation of backbone and side-chain ordering suggests that the details of cracking may be more subtle than originally envisioned. Specifically, cracking may also involve the local disordering of side chains, with a more minor contribution from backbone cracking (186). Together, these studies suggest that multi-basin models that employ atomic resolution will reveal a broad range of cracking events that span from individual residue side chains, to regions of consecutive residues.

Cracking has also been identified in the motor protein kinesin. Kinesin molecules are able to “walk” on microtubules, which enables transport within the cell (26). During each “step,” kinesin binds ATP, undergoes relative displacement of ≈ 80 Å of the domains (145), hydrolyzes ATP and releases ADP. Simulation studies that employed time-dependent Hamiltonians showed that the power stroke in the kinesin head domain may be facilitated by cracking (232, 233). Hyeon et al. showed that a simple model for substrate directed walking is that ATP binding shifts the effective potential energy surface of the leading domain, such that it prefers to place the trailing domain “in front.” This leads to an internal conflict of domain energetics, which leads to partial disordering of the linker region that connects them. If flexibility of the linker were too high, then strain could not be transferred between the domains. Conversely, if the linker were rigid, it would not be capable of undergoing the conformational rearrangements associated with walking.

The potential importance of cracking has motivated the investigation of its role in other proteins' conformational dynamics, as well. Itoh and Sasai developed a dual-basin statistical mechanical model and found evidence of cracking in the C-terminal tail of Calmodulin (135). Similarly, Tripathi and Portman developed a variational model to describe conformational rearrangements in the N-terminal domain of Calmodulin and found that specific regions undergo significant changes in flexibility during rearrangements (234), which is consistent with the cracking paradigm. Using a coarse-grained model, Hyeon et al. also provided evidence of cracking during functional rearrangements in Protein Kinase A (235). Experimentally, biophysical measurements have implicated cracking during the functional dynamics of Adenylate Kinase (229, 236). Peng et al. used instantaneous normal mode (INM) calculations to guide conformational rearrangements in a simulation of Adk (237) and found that immediately preceding domain rearrangements, the INMs were dissimilar to those found in either of the end-state ensembles. This suggests that simple low-energy, rigid-body rearrangements are insufficient to account for Adk's functional dynamics and that cracking may occur. Finally, Okazaki et al. surveyed multiple proteins and showed that cracking appears to be a common feature in multiple protein rearrangements (196).

5.2. Biomolecular Association: Fly-Casting

The balance of many, often competing, kinetic processes is required for proper functional dynamics of the cell (238, 239). The highly non-equilibrium nature of cellular dynamics requires that signaling interactions be kinetically accessible and regulated. If bimolecular association events are simply 3-dimensional random walks, the only way to modulate the kinetics of association would be to evolve proteins of different shapes and sizes, thereby changing their diffusion coefficients. However, evolutionary pressure has led to nearly every aspect of the cell being tunable, including association kinetics.

To address the apparently limited tunability of bimolecular association, Shoemaker et al. proposed the “fly-casting” mechanism (240), where proteins partially unfold when isolated and the full structure forms upon substrate binding. Using a free-energy functional approach, they demonstrated that if part of the protein can unfold, and the unfolded form of the protein has a marginal affinity for the substrate, the exponential increase in phase space available for substrate capture can lead to increased rates of association. It was later demonstrated through molecular simulations (241, 242) that these changes in flexibility can impact the rates of bimolecular association events. Bioinformatic analysis of protein-RNA interactions have also suggested that the electrostatic composition of biomolecules have evolved to guide disordered regions during fly-casting events (243).

In addition to using fly-casting dynamics for bimolecular association, recent work has elaborated on the role of intrinsically-disordered regions during DNA “searching.” That is, the molecular flexibility that enables fly-casting may also facilitate “sliding” motions (95), where the protein “scans” the DNA when looking for the lowest-energy binding site (244). During these searches, proteins may utilize a combination of sliding and “hopping” between sites. During hopping, the protein dissociates from the DNA and reattaches itself via the fly-casting mechanism. The balance between flexibility, disorder and atomic energetics determines the extent to which each mechanism is utilized, which ultimately determines if the genetic messages may be expressed at the appropriate time.

Similar to cracking, the fly-casting mechanism provides a means by which a balance of local stabilities dictates the functional dynamics of a protein. However, in contrast to cracking, where the endpoints are stable configurations, in fly casting the folded configuration only needs to be stable upon substrate binding.

5.3. Protein Recognition: Global Unfolding and Refolding

While fly-casting and cracking involve partial unfolding of substructures (Figure 3B), in some cases, global order-disorder transitions may be linked to functional dynamics. The Repressor of Primer (Rop) dimer^* is formed by association of two alpha-helical protein chains that bind to “kissing” RNA hairpins and stabilize their interactions. Based on experimental kinetic data (245), it had been suggested that Rop and its mutants can adopt two symmetrically-related competing conformations during function (246). To study the dynamics of this process, a multi-basin potential energy function was employed to simulate the transitions between these competing configurations (247). Since a microscopically-mixed Hamiltonian was employed, it would have been possible for the protein to undergo this rearrangement through a sequence of local displacements, while the monomers remain in association with each other. Despite the energetic flexibility afforded by the microscopic model, these simulations indicate that the Rop dimer globally unfolds and then refolds during its conformational rearrangements. These predictions from simulations were later verified in single-molecule experiments (248). Consistent with cracking and fly-casting dynamics, this global denaturation is afforded by the marginal stability of proteins under physiological conditions. Global, or local increases in stability could make unfolding kinetically unfavorable, and functional regulation in Rop would then not be possible.

5.4. Riboswitch Signaling: Substrate-Assisted Ordering

Riboswitch aptamer domains are untranslated regions of mRNA that, in response to ligand binding, adopt well-defined three-dimensional configurations, whereas alternate ensembles of configurations are accessed in the absence of ligand. These conformational changes can even include large-scale unfolding and refolding of secondary structure, similar to the operation of the Rop dimer. The balance between these ligand-bound and ligand-free ensembles directly regulates transcription and translation (249, 250) (Figure 14A). Since the identification of riboswitches in bacteria (251), there has been vigorous investigation into the relationship between ligand binding, structure formation and gene expression. A frequently adopted framework for interpreting experimental data is that all secondary structure (i.e. helices), and some tertiary structure, is formed prior to substrate binding. For systems where this assumption holds, the role of ligand binding is relegated to facilitating minor rearrangements. That form of operating is reminiscent of allosteric protein function, where tertiary structure is usually fully formed and conformational transitions associated with ligand binding are limited to the repositioning of domains. However, bacterial riboswitches fold with the ligand in solution, suggesting that ligand binding may alter the dynamics of the global reorganization/folding processes, in addition to coordinating final atomic repositioning.

Figure 14. Riboswitch folding and ligand recognition.

A) Secondary structure of the SAM-1 riboswitch. The P1 helix is formed by the terminal residues, making it a non-local helix (125). B) Average fraction of native P1 contacts formed (〈Q_P1〉) as a function of the fraction of all native contacts being formed (Q_total) is shown in blue. Potential of mean force shown in green. The largest barrier in the pmf corresponds to folding of the P1 helix. C) Same as (B), but in the presence of the SAM ligand. The average fraction of ligand interactions 〈Q_ligand〉 is shown in magenta. Ligand binding induces earlier folding of P1 and it reduces the associated barrier. D) Structural representation of the final step of folding, when the SAM ligandis present. All secondary structure, along with some tertiary structure is formed, and the ligand binds prior to P1 structure formation.

Simulations with unfrustrated models have shown that entropic bottlenecks during folding can be directly perturbed by ligand association. In the case of the SAM-1 riboswitch, entropic contributions disfavor the formation of the P1 helix (Figure 14B), which is the step associated with the largest free-energy barrier during folding (125). This large difference in configurational entropy can be attributed to the connectivity of the helices. The strands composing P2, P3 and P4 helices are each connected by a few-residue “turn,” and the P1 helix is formed by the terminal residues in the domain (Figure 14A). While the P2/3/4 turns are composed of 4 residues, the P1 strands are connected by a linker of ∼80 residues, hence the designation of “non-local helix.” Thus, the configurational entropy of the unfolded P1 helix is much larger than the other helices. By simulating the process in the presence of the ligand, it was shown that this rate-limiting step is accelerated by ligand binding, suggesting that ligand binding can have a thermodynamic and kinetic influence on aptamer formation. Consistent with this prediction, recent chemical probing data has shown that in the absence of ligand, the P1 helix exhibits high mobility, and this mobility is attenuated by substrate binding (252).^# Single-molecule experiments indicate that ligand binding most strongly affects the dynamics of the P1 helix (253), which highlights the potential of SAM to direct P1 folding.

Coarse-grained simulations of a purine riboswitch also found that the non-local helix is least stable and its formation is rate limiting (254). Similarly, simulations of the preQ₁ riboswitch showed that the folding mechanisms can be redirected by substrate binding (255). Single-molecule experiments have also revealed that ligand binding has a focused effect on the non-local helix in a purine riboswitch (256). Each of these studies demonstrate the role that ligand binding has on folding, suggesting that substrate recognition and folding are concomitant.

Similar to protein recognition, substrate-assisted folding in RNA may encompass fly-casting-like dynamics. As discussed above, the principal effect of the fly-casting mechanism is to accelerate substrate binding rates by increasing the capture radius for the substrate. Riboswitch studies suggest that there may be a symbiotic relationship between folding and ligand association: fly-casting increases association rates and ligand association increases the biomolecular folding rates. Similar to fly-casting proteins, if aptamer domain formation is too fast, or stable, then there would be a separation of timescales between ligand binding and riboswitch folding. In that scenario, ligand binding may increase the folding rate slightly, but the presence/absence of ligand would only represent a minor perturbation. Together, these studies corroborate a general theme in molecular biophysics: biomolecular complexes have evolved to be marginally stable, allowing them to access higher-entropy states and increase the available phase space for regulation.

5.5. Molecular Machines: Entropically-Guided Rearrangements

The final example of the role of entropy in biomolecular functional dynamics that we will discuss is found in the elongation cycle of the ribosome. During translation, mRNA is read by the ribosome through the use of transfer RNA (tRNA) molecules, which produces proteins with specific amino acid sequences. The decoding process involves individual aminoacyl-tRNA (aa-tRNA) molecules that form 3-base-pair interactions (i.e. codon-anticodon interactions) with the mRNA, where each base pair is composed of two (Adenine-Uracil) or three (Guanine-Cytosine) hydrogen bonds. When accounting for competition with water, the hydrogen bonds of base pairs provide ∼ 1 – 2k_BT of stabilizing energy, each. Since four types of nucleic acids compose these base-pair interactions, there are 4³ = 64 unique messages that may be encoded by a single mRNA codon. With only 64 possible ways to encode 20 different naturally-occurring amino acids, where all possible base-pair interactions are on comparable energetic scales, thermodynamic differences between cognate (correct tRNA-mRNA pairs) and nearcognate (1 base-pair mismatch, such as a U on the tRNA and a G on the mRNA) can only account for an error rate of about 1 in 100. Since the error rate of the ribosome is approximately 1 in 10³ − 10⁴, additional proofreading mechanisms must be employed (257).

To explain the fidelity of ribosome dynamics, Hopfield proposed the “kinetic proofreading” mechanism (258). In this mechanism, by loading a marginally-stable intermediate via a driven process (such as GTP hydrolysis), the differences in kinetic accessibility of the initial and final configurations may be greater than the corresponding differences in thermodynamic stability. Kinetic proofreading was proposed as a general strategy by which molecular processes may increase the fidelity of a particular substrate selection step, though here we will only discuss it in context of ribosome fidelity (259). In the ribosome, elongation factor-Tu (EF-Tu) uses the energy stored in GTP to load the ribosome with aa-tRNA molecules (260–262) in an energetically-stained A/T configuration (163, 263). Upon EF-Tu release, cognate (i.e. correct) aa-tRNAs enter the ribosome (≈ 90 Å displacement) and adopt the “A/A” configuration, while noncognate aa-tRNAs are rejected. In the kinetic proofreading framework, the A/T configuration is loaded by EF-Tu, but both the A/A and dissociated configurations are more stable. The A/T-to-A/A transition (called “accommodation”) can then serve as the proofreading step in translation. Consistent with the kinetic proofreading mechanism, theoretical considerations have demonstrated that kinetics and fidelity impose competing limitations on ribosome dynamics (264). If the accommodation step were too fast (averaged over all tRNA species), large energetic factors would be necessary to remove the tRNA from the ribosome. However, no such factors are required for rejection. In contrast, if accommodation were too slow, then the dissociation of tRNA from the ribosome would be overly likely, even for cognate tRNAs.

Investigations into the balance of kinetics, energetics and fidelity of accommodation (265) have revealed atomic details of the endpoints (146, 261, 266), the transition state ensembles (260, 267, 268) and rates (265) of accommodation. These studies have provided many insights into the details of accommodation, including the role of disorder in the incoming aa-tRNA molecule. Using a modified SBM, we showed that the flexibility of the single-stranded 3′-CCA end (Figure 15) may lead to large changes in the configurational entropy during accommodation (Figure 15), which also facilitates a multi-step accommodation process (268). Upon dissociation of EF-Tu, the 3′-CCA end can adopt a disperse set of configurations within the A/T ensemble, which leads to an increase in configurational entropy. As the aa-tRNA enters the ribosome, the initial accommodation sub-step is aa-tRNA elbow movement towards an A/A-like configuration. This is followed by aa-tRNA arm movement and finally 3′-CCA end movement into the catalytic center of the ribosome (the peptidyltransferase center, PTC). During the elbow-association step, the accessible configurations of the 3′-CCA end appear to be constant, which indicates a negligible change in configurational entropy of the 3′-CCA end during this transition. As the tRNA arm moves into the A site, movement of the 3′-CCA end is partially restricted (Figure 15), suggesting that a decrease in configurational entropy resists such motions. Finally, as the 3′-CCA end enters the PTC, it becomes highly ordered, as required for the chemical step (peptide bond formation) to occur (3). This further decrease in configurational entropy represents an additional entropic penalty during accommodation.

Figure 15. Entropy changes in the 3′-CCA end of aa-tRNA during accommodation.

Atomic models of tRNA (A-site tRNA in yellow, P-site tRNA in red) and mRNA (green) at different points during accommodation. Amino acids attached to the ends of tRNA are shown in blue. A) Atomic model of the A/A configuration of tRNA, based on cryo-EM densities. Three reaction coordinates for describing accommodation (R_Elbow, R_Arm, R_3′) are indicated. B/C) Intermediate populations predicted from simulations (268) suggest that transient interactions are formed with the A loop (pink) and H89 (gray) of the large subunit. D) Endpoint of accommodation, as determined from x-ray crystallography. E) Pseudo-dihedral angle Φ₂ describes the configuration of the 3′-CCA end as it enters the center of the ribosome. F) During accommodation, the range of accessible configurations of the 3′-CCA end decreases, indicative of an entropic penalty for accommodation.

This order-disorder-order transition in the 3′-CCA end of the aa-tRNA can have profound biological implications. Specifically, changes in configurational entropy of the universally conserved (across all tRNA species) 3′-CCA end may provide an entropic counterweight that ensures 3′-CCA entry into the PTC is the last step during accommodation. Since the incoming amino acid is attached to the 3′-CCA end, once it accommodates the amino acid may be added to the growing peptide chain. By favoring the late entry of the 3′-CCA end, this entropic contribution can facilitate the use of additionally proofreading “machinery” prior to incorporating a potential mistake.

While previous simulations showed that flexibility in the 3′-CCA end is necessary for it to enter the PTC (267), this was the first time that configurational entropy of the 3′-CCA end was explicitly identified as contributing to the global tRNA dynamics. There are many signatures of a dynamic 3′-CCA end in tRNA may be found in the literature. For example, the 3′-CCA end of tRNA molecules are often not resolved in crystallographic structures (269), or the dispersion in their coordinates is large (as measured by the Debye-Waller factors) (270). In cryogenic electron microscopy studies there is often a low density obtained for the 3′-CCA end (271), indicating that the 3′-CCA end structure is composed of a diverse set of configurations, relative to other molecular components. The 3′-CCA end also interacts with many distinct binding partners (272), including synthetases (273), EF-Tu (274) and the ribosome (275), which necessitates that its conformation be easily adaptable.

These studies highlight the balance between stabilizing energetic interactions (that favor accommodation) and destabilizing entropic contributions (that resist the process). If flexibility of the 3′-CCA end were increased, it would be possible for accommodation to become too slow, and correct tRNA molecules would be rejected. Though, if 3′-CCA flexibility were decreased, it may not be possible for the tRNA molecules to navigate through the narrow corridor of the ribosome (267, 276).

6. Closing Remarks

Grounded in statistical mechanics, the energy landscape framework has enabled the quantitative characterization of biomolecular dynamics at the atomic level. Here, we have described the historical context surrounding the development of this framework, which originated in protein folding. Since then, it has been repeatedly extended to address biomolecular functional dynamics of increasing complexity. An exciting consequence of the energy landscape description is that there is an interplay between order-disorder transitions and the functional dynamics of biomolecules. From a wide range of studies, there are many examples demonstrating how the marginal stability of biomolecules allows them to adjust their unfolding properties as a mode for tuning the functional dynamics. Accordingly, these deceptively-complex molecular assemblies possess an extremely large range of phase space available for functional dynamics. In the future, we anticipate that this theme will be echoed in assembly/disassembly processes, transient formation of excited states, and large-scale collective motions in the cell. Eventually, the molecular description will reach scales that overlap with systemslevel biology, which will represent one of the next major challenges for the biological physics community.