Transient RNA structure features are evolutionarily conserved and can be computationally predicted

Abstract

Functional RNA structures tend to be conserved during evolution. This finding is, for example, exploited by comparative methods for RNA secondary structure prediction that currently provide the state-of-art in terms of prediction accuracy. We here provide strong evidence that homologous RNA genes not only fold into similar final RNA structures, but that their folding pathways also share common transient structural features that have been evolutionarily conserved. For this, we compile and investigate a non-redundant data set of 32 sequences with known transient and final RNA secondary structures and devise a dedicated computational analysis pipeline.

INTRODUCTION

The primary products of all DNA genomes are RNA transcripts. We know by now that almost all of the human genome is transcribed, yet only 2% of the genome is translated (1). The expression of protein-coding and non-coding genes can be regulated through RNA structural features that can influence key processes such as transcription, splicing, RNA editing, localization, degradation, translation initiation and translation efficiency (2). Many viral genomes depend on RNA structure for a wide variety of functions during their replication cycle (3). A functional RNA structure need not necessarily involve the entire transcript (global RNA structure, e.g. ribosomal RNA (4), transfer RNA (5)), but may be restricted to only part of it (local RNA structure, e.g. riboswitches in untranslated regions) (6)). RNAs can play catalytic roles (7,8). And a given transcript can have more than a single functional RNA structure, e.g. riboswitches that change between two distinct structural configurations on binding a metabolite or ligand (9,10,6).

Unlike for protein structures where we typically need to know their three-dimensional configuration, the potential functional roles of a given RNA can already be studied by only knowing its RNA secondary structure, i.e. the pairs of nucleotide positions involved in making base-pairs. These consensus base-pairs (G-C, A-U and G-U) can be viewed as the fundamental structural building blocks of RNA secondary structure.

As soon as an RNA transcript is synthesized from a DNA template, it starts to form RNA structural features co-transcriptionally (7,11,12). There is by now significant experimental evidence that the co-transcriptional folding process determines the formation of the functional RNA structure in vivo.

The speed of transcription is one factor that can influence structure formation. Depending on the underlying polymerase, the speed of transcription differs significantly: 200 nucleotides per second (nt/s) in phages, 20–80 nt/s in bacteria and 10–20 nt/s for human polymerase II (13). RNA folding can occur well within the time scale of transcription (14) (but kinetically trapped RNAs can persist for minutes or hours (14–16)). Altering the natural speed of transcription, e.g. by using a non-host polymerase, can yield different folding pathways and final structures and result in inactive transcripts (17–21). The speed of transcription need not be constant, but can be modulated, e.g. owing to transcriptional pausing at specific sites, which may be required for the efficient structure formation (22–24).

Any RNA transcript can influence its own co-transcriptional folding by engaging in cis interactions with itself through RNA structural features. Owing to the directional nature of transcription, base-pairs near the 5′ end of the transcript can form early on, whereas long-range base-pairs or those involving the 3′ end of the molecule can only form later in the transcription process (25,26). Structure elements that appear temporarily during the folding process (i.e. transient features) can guide the folding pathway (12,27,28), and modifying the flanking sequences of a transcript can significantly alter the folding pathway (29). In addition to experimental evidence, there is also statistical evidence that structured RNA genes not only encode information on their final functional RNA structure, but also on transient structural features of their co-transcriptional folding pathways (30).

In addition to these cis interactions, the co-transcriptional folding pathway can also be significantly influenced by trans interactions between the nascent transcript and various interaction partners. These can involve small metabolites whose binding can induce structural changes that influence transcription or translation (31–33), RNA-binding proteins that bind the transcript in a sequence- and/or structure-specific way (34,35) or other RNAs whose sequence- and/or structure-specific binding can influence diverse processes such as transcription, splicing, translation, degradation and RNA editing (36–38).

Experimental methods for RNA structure determination such as X-ray crystallography and nuclear magnetic resonance are time-consuming and comparatively expensive. Computational methods for RNA secondary structure prediction thus play a powerful role in assigning potential functional roles to large sets of transcripts and in helping to design more targeted follow-up experiments. These computational methods typically operate on the level of secondary structure rather than tertiary structure (i.e. three-dimensional configuration of all atoms in the transcript), as this level of detail is computationally easier to study in predictive models and usually provides enough insight into the potential functional role of the molecule.

Methods for RNA secondary structure prediction can be roughly categorized into comparative methods (e.g. Pfold (39), RNA-Decoder (40), RNAalifold (41), CARNAC (42,43), ILM (44) and SimulFold (45)) or non-comparative methods (e.g. RNAfold (46,47), Mfold (48), Sfold (49–51) and Contrafold (52)). Comparative methods take as input a set of homologous transcripts from evolutionarily related organisms (usually in the form of a multiple-sequence alignment (MSA)) and aim to detect the consensus RNA secondary structure that has been conserved during evolution. Non-comparative methods take a single RNA as input and, typically, predict the RNA secondary structure that minimizes the overall free energy (MFE methods), i.e. the thermodynamically most stable configuration. Comparative methods tend to outperform non-comparative methods in terms of prediction accuracy, but require a carefully selected set of input sequences to start with (53). Almost all of the currently existing methods for RNA secondary structure prediction, whether comparative or not, do not explicitly consider the effects of co-transcriptional RNA structure formation when generating predictions (54).

In addition to the aforementioned methods for RNA secondary structure prediction, a number of methods have been developed to explicitly predict the co-transcriptional RNA folding pathway (RNA folding pathway prediction methods). These methods typically model some aspects of folding kinetics over a simulated period, and consider only a single sequence as input, i.e. they are non-comparative. As output, they return a detailed list of structural configurations constituting a predicted folding pathway.

Most folding simulation methods use stochastic simulation (e.g. RNAKinetics (55–57), Kinfold (58) and Kinéfold (59–62)). These methods extend the RNA sequence at regular intervals and incorporate randomized structural changes (e.g. helix formation and disruption). Typically, the probability of each randomized change is related to the theoretical rate of that process. Although the overall design of these methods is similar, they differ in the details of their respective algorithm. In addition to these stochastic methods, Kinwalker (63) uses a deterministic algorithm that combines free energy minimization with a heuristic, which disallows transitions deemed kinetically infeasible. It successively extends the sequence from the 5′ end and combines structures predicted by free energy minimization for which the theoretical formation time is fast. Kinwalker returns all the structural configurations encountered during this process.

All of these methods have length limitations, as the errors are multiplicative: approximately 200 nt for the stochastic simulation methods, and 1000 nt for Kinwalker. Furthermore, they make a number of simplifying assumptions about the complex cellular environment. They assume transcription rate to be constant, which we know is not necessarily the case in vivo (22–24), and they do not model the various trans interaction partners (e.g. proteins, RNA or small molecules). In this work, we focus on Kinéfold, Kinwalker and RNAKinetics, as they represent the diversity of existing folding pathway prediction methods and are freely available.

In this work, we explore the hypothesis that conserved RNA structures from homologous non-coding RNA genes not only fold into similar functional structures, but that their co-transcriptional folding pathways also share common transient structural features. More specifically, we (i) provide evidence that transient features are conserved in related sequences, (ii) investigate if known final and transient structural features can be detected using a comparative analysis of folding pathway prediction methods and (iii) assess the ability of these methods to predict new conserved transient features.

For this, we investigate a comprehensive data set of 32 non-redundant sequences deriving from the following six functional RNA families for which we assembled the data and compiled a comprehensive and accurate RNA secondary structure annotation mostly ourselves.

Bacterial ribonuclease P Type A

Ribonuclease (RNAse) P is a ubiquitous ribonucleoprotein endowed with the ability to catalyze the cleavage of phosphodiester bonds in non-terminal positions of the RNA chain (64). Wong et al. (24) identified a transient structure in RNase P that forms upstream of a transcriptional pausing site, sequestering the 5′ nucleotides of six long-range helices until their downstream pairing partners are transcribed.

Bacterial signal recognition particle 4.5 S RNA

The bacterial signal recognition particle (SRP) functions as a molecular adapter for protein targeting (65). In the same study cited previously, Wong et al. (24) identified a transient structure upstream of a transcriptional pausing site in the SRP RNA’s folding pathway that may sequester the upstream portion of the molecule’s long-range helices.

Tryptophan operon leader

The tryptophan (trp) operon contains genes that function in the biosynthesis of the amino acid trp (66). Yanofsky (66) identified two alternative structures that form in the operon leader co-transcriptionally. When trp is plentiful, the leader forms a ‘terminator’ helix that terminates transcription of the operon; when trp is in short supply, the formation of the ‘anti-terminator’ helix permits transcription and translation of the downstream genes (66).

Hepatitis delta virus ribozyme

The last of the Rfam-derived alignments is that of the hepatitis delta virus (HDV), which possesses an RNA genome that encodes a self-cleaving ribozyme (67). Chadalavada et al. (67) identified a transient helix in the genomic RNA that forms co-transcriptionally and suppresses ribozyme self-cleavage, while a second alternative structure sequesters the upstream portion of the transient helix and permits ribozyme self-cleavage.

Levivirus maturation gene

Levivirus is a genus of single-stranded RNA bacteriophages whose maturation gene is generally un-translatable owing to a structure in the 5′ untranslated region that sequesters its Shine–Dalgarno sequence (68). Van Meerten et al. (68) demonstrated that the formation of the inhibitory structure of the Levivirus maturation gene is briefly postponed by the formation of a small transient helix, during which time translation may occur. As the Rfam database does not contain an alignment for the Levivirus maturation gene, we assembled it manually from scratch, see Supplementary Information for more information (80,81).

S-adenosylmethionine riboswitch

The SAM riboswitch undergoes structural reorganization on binding to the metabolite S-adenosylmethionine (SAM) (69). Its two alternative conformations regulate the expression of 26 genes in Bacillus subtlis and related species (69). The Rfam alignment for the SAM riboswitch (RF00162) features only one of the two alternative structures, and does not extend downstream to the region in which the second alternative structure is found (70). We therefore compiled a high-quality data set based on an alignment presented by Winkler et al. (69).

Our evaluation of folding pathway prediction methods on known transient and final RNA structure features constitutes the first comprehensive performance evaluation of these methods.

In the following sections, we describe the compilation of our data sets, the computational analysis pipeline for evaluating the RNA folding pathway prediction methods and the results generated by this approach.

MATERIALS AND METHODS

Compilation of the data sets

Few transient and alternative structures have been experimentally validated, and available MSAs for these structures typically lack multiple structural annotations. A comprehensive previous analysis suggests that the comparative helix prediction program Transat performs best in terms of prediction accuracy for input alignments with a corresponding total tree length of ideally more than 1 and sequences with an average pairwise percent-identity in the range of 70–80% (71). Based on these criteria, we compiled high-quality alignments for six non-coding families of RNAs, and mapped all known structures to these alignments. These constitute our six data sets from which we derive a non-redundant data set of 32 sequences that constitute the input to our analysis pipeline. In all cases, the selection criteria were imposed to optimize the alignment for the prediction of the known functional structure (or one of two alternative structures, if both are functional). Known transient and alternative structures were then mapped onto the resulting sequence alignment so as not to bias Transat for the prediction of known transient/alternative features. A detailed description of the alignment compilation process can be found in the Supplementary Information.

Alignments

Four of the six alignments were constructed based on seed or full alignments from the Rfam database (70): the bacterial RNase P type A RNA (RF00010), the bacterial SRP 4.5 S RNA (RF00169), the trp operon leader (RF00513) and the HDV ribozyme (RF00094). Two additional alignments were manually compiled using the Infernal software (72) and MUSCLE (79): the Levivirus maturation gene, which is not part of Rfam, and the SAM riboswitch, whose Rfam alignment is truncated upstream of the region with the alternative structure. All alignments were hand-curated in the end using 4SALE (82) to correct any obvious aligning error.

Reference sequences and structures

The reference sequence for the RNase P alignment was derived form Escherichia coli (accession number CP001509.3; start and end coordinates 3136788-3136410). The functional structure of RNase P has been solved by X-ray crystallography (73). Wong et al. (24) identified a transient structure in RNase P that forms upstream of a transcriptional pausing site, sequestering the 5′ nucleotides of six long-range helices until their downstream pairing partners are transcribed. The reference sequence for the SRP 4.5 S RNA was also derived from E. coli (accession number X01074.1; start and end coordinates 138-275) (24,78). The final structure of this RNA was determined by chemical probing (74) and X-ray crystallography (75). In the same study cited previously, Wong et al. (24) identified a transient structure upstream of a transcriptional pausing site in the SRP RNA’s folding pathway. Once again, this structure may function to sequester the upstream portion of the molecule’s long-range helices (24). An E. coli reference sequence was extracted for the trp operon leader alignment (accession number AE005174.2; start and end coordinates 2263095-2263188). The trp operon contains genes that function in the biosynthesis of the amino acid trp (66). Yanofsky (66) identified two alternative structures that form in the operon leader co-transcriptionally. Pausing of the polymerase provides time for the ribosome complex to initiate translation of the leader region (66). When the amino acid trp is in short supply, the ribosome stalls in the upstream portion of the operon leader, providing time for an RNA helix known as the ‘anti-terminator’ to form (66). This structure permits the RNA polymerase to complete transcription of the operon (66). Alternatively, when trp is plentiful, the ribosome continues translation past the first pausing site. An alternative RNA helix forms and signals the polymerase to terminate transcription (66). Finally, an HDV reference sequence was extracted for the HDV ribozyme alignment (accession number M28267.1; start and end coordinates 635-775). HDV possesses an RNA genome that encodes a self-cleaving ribozyme (67). Both the genomic HDV RNA and the anti-genomic transcript derived from this RNA encode a ribozyme, and the location of the two ribozymes is largely overlapping (67). Chadalavada et al. (67) identified a transient helix in the genomic RNA that forms co-transcriptionally and suppresses ribozyme self-cleavage. A second alternative structure sequesters the upstream portion of the transient helix and permits ribozyme self-cleavage (67). The functional structure of the ribozyme was also derived from Chadalavada et al. (67). The seed and full Rfam alignments featured both genomic and anti-genomic sequences (70). Genomic sequences were extracted from the Rfam full alignment because the seed alignment lacked sufficient diversity for our purposes once the anti-genomic sequences were removed.

Alignment statistics

Summary statistics for all six alignments can be found in Supplementary Table S1 and S2. Supplementary Tables S3–S8 specify the 32 sequences we select from the six alignments. The average number of sequences per alignment is 12, and the average number of characters in the alignments is 194. Our alignments have an average co-variation of 0.260 and a conservation value of 0.686 (76,77).

Kinetic folding approach

In this work, we investigate transient structural features by comparing the predictions of existing non-comparative RNA folding pathway prediction methods. For this, we have devised an analysis pipeline that performs folding simulations on several homologous sequences that derive from the same data set. We have chosen three simulation methods: Kinéfold (59–61), Kinwalker (63) and RNAKinetics (55–57). These represent the diversity of existing folding simulation methods, differ significantly in their simulation algorithms and are freely available.

Kinéfold and RNAKinetics both use stochastic simulation. They model transcription by extending the RNA sequence at regular intervals over a simulated time scale. Both methods capture the kinetics of RNA folding by allowing randomized events of helix formation and disruption, where the probability of each randomized change is related to the rate of that chemical process. Therefore, these methods explicitly mimic the co-transcriptional RNA folding process in vivo. Both Kinéfold and RNAKinetics operate on the level of entire helices, i.e. contiguous stretches of base-pairs without bulges and internal loops. Kinéfold allows pseudo-knotted structural configurations using a complex energy model, whereas RNAKinetics allows only pseudo-knot-free structures. Because a single simulation returns only a single randomized trajectory, it is necessary to consider many trials to determine the statistical significance of the result. We approximate the number of required trials for both RNAKinetics and Kinéfold as a quadratic function of the sequence length, as recommended by the creators of these programs. The methods can handle sequences up to roughly 200 nt in length. For both methods, we specify the total simulation time t as twice the transcription time to provide time for the methods to converge, where L denotes the sequence length in nucleotides, and r is the transcription rate in nt/s: .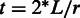

The raw output of the two programs differs significantly. Kinéfold returns a detailed list of structural configurations over simulated time for a single simulation. Conversely, RNAKinetics returns aggregated simulation data: for each helix encountered, it provides a series of probability values over simulated time points. This is generated by averaging data across all trials. The raw output from these two programs therefore has to be handled differently.

Kinwalker is a deterministic prediction method that is conceptually based on free energy minimization for RNA secondary structure prediction. It first predicts the minimum free energy structure for all subsequences, and successively merges these substructures starting from the 5′ end with one stipulation: the theoretical rate of each merger must be feasible to occur between transcription events according to a heuristic. That is, the change must be expected to complete within this period. Kinwalker thus incorporates kinetic aspects of RNA structure formation to predict the folding pathway of the input sequence in a deterministic manner. The raw output of Kinwalker is a list of structural configurations over the simulated time scale. The program can handle sequence of up to 1000 nt in length.

All three methods require a constant transcription rate parameter to be specified by the user. We use different values depending on the evolutionary domain of the sequence (13). We choose a transcription speed of 22.5 nt/s for RNase P Type A, the SRP 4.5 S RNA and the trp operon; 20 nt/s for the HDV ribozyme; 30 nt/s for the Levivirus, which is the replication speed of the positive RNA, and 75 nt/s for the SAM riboswitch. To interpret the different types of raw output that these three programs generate, we define simple metrics to aggregate simulations across related sequences and across multiple trials (described in the Analysis pipeline section).

Comparative approach

Transat is a comparative program designed to detect evolutionarily conserved helices, including final, transient and mutually exclusive structural features as well as pseudo-knots (71). The program takes as input an MSA and a phylogenetic tree, which quantifies the evolutionary distance between species represented in the alignment. Transat assigns a log-likelihood value to all predicted helices using the Felsenstein algorithm and probabilistic models of evolution that quantify how base-paired and unpaired nucleotides evolve over time. In addition, it also estimates a P-value for every predicted helix, which corresponds to the probability of seeing a random helix with the same log-likelihood value by chance.

Because Transat detects RNA structure features that have been evolutionarily conserved, it does not make complex assumptions about the cellular environment and RNA folding chemistry or folding dynamics. We use Transat to detect conserved, and potentially transient, structural features of the co-transcriptional folding pathway. For each of the six alignments, we extract the six helices predicted by Transat with the lowest P-values that have less than 50% overlap to the known structural features. These helices are thus not contained within the known final and transient structural structure features, but are supported by significant evolutionary evidence, as all have P-values of at most 0.03. We consider these putative new transient helices that constitute candidate helices for experimental confirmation.

Analysis pipeline

To detect evolutionarily conserved transient helices, we use the following analysis pipeline, see Figure 1. We use the three folding pathway prediction methods introduced previously to assign a score to each predicted structural feature. This score captures the outcome of folding pathway simulations for multiple non-redundant representative sequences derived from each alignment and thus comprises comparative information.

Figure 1.

The analysis pipeline. Solid black arrows represent the core analysis involving kinetic folding programs. For each non-coding RNA molecule examined, a reference sequence and known structural features were used to construct a multiple-sequence alignment (MSA). Non-redundant sequences were extracted from the MSA, and provided as input to three kinetic folding programs: Kinwalker, Kinéfold and RNAKinetics. The raw output, consisting of simulated folding pathways, was analyzed, and high-scoring helices were extracted. These predicted helices were mapped back onto the MSA. A comparison across programs then yielded helices with high scores from multiple programs. The dotted arrows represent an optional analysis involving the comparative helix prediction program Transat. A phylogenetic tree is required as input along with an MSA. FastTree2 is employed in our pipeline to estimate the phylogenetic tree based on the concatenated unpaired regions (83). The program detects and scores conserved helices, and outputs a ranked list of conserved helices with P-values. These are mapped onto the alignment along with the output of the three kinetic folding programs.

We use the following procedure to extract representative sequences from each input alignment. Each representative sequence is subsequently used as input to each of the three folding pathway prediction methods. We first order the sequences in each alignment by overall fit to the known reference structure, e.g. having few invalid base-pairs. We begin by extracting the best fitting sequence, and successively extract more sequences such that no pair of extracted sequences share a pairwise sequence identity greater than an alignment-specific threshold. Each set of representative sequences is thus not redundant, see the Supplementary Information for more information.

Each run of each program generates a list of base-pairs. Base-pairs predicted for each representative sequence are mapped back onto the corresponding sequence alignment to identify corresponding base-pairs that derive from different sequences, but from the same pair of alignment columns.

Kinéfold returns the detailed folding trajectory for each simulation, including the secondary structure configuration of the simulated RNA molecule over time. For each representative sequence in the alignment, we perform several simulations (with the number of simulations scaling approximately quadratically with the sequence length). Any base-pair that occurs during at least one simulation is assigned a score equal to the fraction of trials in which that base-pair was observed. This value aggregates across all alignment sequences.

RNAKinetics returns as raw output data that are already aggregated across several simulations. For each representative sequence, we first compile a list of helices, each with a series of probability values over time. For each of such helix, we identify the maximum probability from the corresponding profile of probability values over time. The maximum probability is subsequently assigned to each constituent base-pair of this helix, which we map to the corresponding alignment. The final score assigned to each base-pair along the alignment is then the average probability of the corresponding base-pairs from all representative sequences.

Kinwalker is a deterministic method that does not use randomization. For any given input sequence, it generates exactly one folding trajectory. We therefore simply generate the Kinwalker prediction by simulating one run for each representative sequence. Kinwalker’s output comprises a sequence of structural configurations over simulated time. The score assigned to any predicted base-pair is set to the fraction of representative sequences for which the base-pair occurs at any point in the simulation.

We thus define a metric for each kinetic folding method that aggregates predictions across many sequences within the alignment, and across many simulated trials (where applicable). The Kinéfold and Kinwalker scores are conceptually similar, as both indicate the fraction of predictions in which the base-pair occurs. RNAKinetics, however, is limited by the granularity of the output, and is incapable of generating an exactly equivalent score. Its score indicates the average peak probability across all sequences, and is therefore on a different scale than the others.

For evaluation of this approach, we compare the prediction metrics against several benchmarks. Each alignment in our data set is annotated with known final features and known transient features (in the case of alternative structures, we classify all of their base-pairs as transient). We use Transat (described previously) to identify potential novel conserved helices. In addition, we investigate the ability of RNA folding pathway prediction methods to predict these classes of structural features.

RESULTS

Known transient features of folding pathways are evolutionarily conserved

Functionally important RNA structures tend to be evolutionarily conserved in homologous sequences from related species. The conservation of base-pairing potential through compensatory mutations (i.e. covariation) is one indicator of the functional importance of a structure. The structure quality measures of the six alignments are shown in Table 1 for the known final and known transient structural features. Any base-pair that is shared by both a known transient structure and a known final structure is classified as belonging only to the final structure. For each structural category, we calculated the percentage of canonical base-pairs (i.e. G-C, A-U and G-U), covariation, primary sequence conservation and fraction of characters that are gaps.

Table 1.

Quality measures for known transient and known final structural features for all six data sets

Alignment	Known transient				Known final
	Can. bp	Covar.	Cons.	Gap.	Can. bp	Covar.	Cons.	Gap.
Levivirus	0.88	0.01	0.64	0.01	0.95	0.34	0.69	0.02
RNase P Type A	0.94	0.13	0.81	0	0.97	0.48	0.69	0.02
HDV ribozyme	0.88	−0.13	0.88	0.03	1.00	0.15	0.93	0
SRP 4.5 S RNA	0.88	0.11	0.79	0.01	0.99	0.39	0.79	0
Trp operon	0.97	0.20	0.84	0.01	0.97	0.20	0.84	0.01
SAM riboswitch	0.90	0.28	0.65	0.07	0.90	0.28	0.65	0.07
Average	0.91	0.10	0.77	0.02	0.96	0.31	0.76	0.02

Percent canonical base-pair (can. bp) indicates the proportion of base-pairs across all alignments that contain one of the three canonical pairs (A-U, G-U or G-C). Covariation (covar.) measures the relative frequency of compensatory mutations that retain the base-pairing potential, and indicates base-pairs that are functionally important. Covariation ranges from −2 to +2, and it is 0 when the paired columns have no variation, negative when they contain many invalid pairs and positive when they contain compensatory mutations. Conservation (cons.) indicates the mean pairwise percent identity between homologous sequence positions at paired columns. Percent gaps (gap.) indicates the proportion of paired sequence positions that contain gaps.

As shown in the average row of Table 1, both known transient and final structures maintain the canonical base-pairing potential well (with the pairing potential of known final structure only slightly higher by 5%). Known transient structures have a high canonical base-pair percentage of 0.91 and a positive covariation of 0.10. The covariation level of known transient structures is much lower than that of known final structures. While transient structures show a reduced covariation relative to final structures, they feature a higher fraction of conserved base-pairs.

To summarize, Table 1 indicates that the transient features are evolutionarily conserved on approximately the same level as final features based on the base-pairing potential.

Known transient features can be predicted computationally using folding pathway prediction programs

To assess the ability of folding pathway prediction programs to predict known transient features in a comparative manner, we define a value (described in Materials and Methods) for each program that is assigned to each predicted base-pair by combining the predictions for several representative homologous sequences. The known transient and final structures are merged into a non-redundant set, against which the predictions from each kinetic folding program are evaluated on base-pair level by imposing cutoffs between 0 and 1. The curves in Figure 2 show the variance of values of the Matthews’ correlation coefficient (MCC) for different cutoffs for the three kinetic folding programs (see the caption of Figure 2 for MCC definition).

Figure 2.

Matthews’ correlation coefficient (MCC) for known transient and final structural features as function of the cutoff value. A bold line is shown for Kinéfold (blue), RNAKinetics (green) and Kinwalker (red). For each program, we also show two additional lines in light blue (Kinéfold), light green (RNAKinetics) and orange (Kinwalker), which show the minimum and maximum MCC-values derived from six-fold cross-evaluation. The horizontal axis indicates the cutoff value for the kinetic folding programs, and its scale is shown at the bottom for Kinéfold and Kinwalker and at the top for RNAKinetics. MCC is a measure of both sensitivity and specificity and is defined as 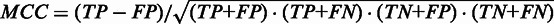. The optimal MCC values can be found at cutoff values 0.755 (Kinéfold, MCC = 0.656), 0.43 (Kinwalker, MCC = 0.676) and 0.0082 (RNAKinetics, MCC = 0.263). As the minimum and maximum lines show, the precise choice of these cutoff values does not have a large impact on the resulting performance. Our cutoff values should thus be viewed as robust general recommendation.

Kinwalker and Kinéfold have roughly the same optimal MCC, whereas RNAKinetics has the lowest one, see Figure 2. An analysis of the corresponding receiver-operating characteristic curves in Figure 3 confirms that Kinwalker and Kinéfold perform similarly. Overall, RNAKinetics accumulates more false-positives at low cutoff values, resulting in low specificity even with stringent cutoffs. These characteristics of RNAKinetics contribute to this program’s generally lower MCC values in Figure 2.

Figure 3.

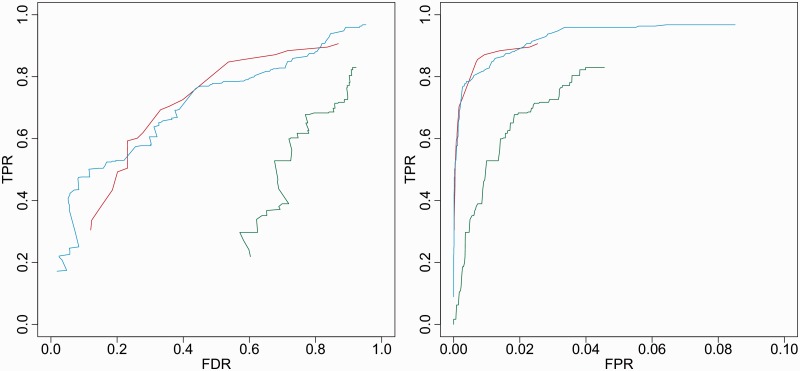
Receiver-operating characteristic curves indicating the performance for known transient and final structural features using folding pathway prediction methods for a broad range of cutoff values. In both plots, the vertical axis indicates the true-positive rate (. In the left plot, the horizontal axis indicates the false discovery rate, i.e. the proportion of predictions that are incorrect (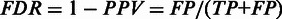). Kinwalker and Kinéfold reach a similarly high TPR at 0.907 and 0.968, which exceeds the maximum TPR of 0.830 achieved by RNAKinetics. In the right plot, the horizontal axis indicates the false-positive rate, i.e. the proportion of all potential negatives that are predicted (. Kinéfold is shown in blue, RNAKinetics in green and Kinwalker in red.

We use the program-specific cutoffs derived from Figure 2 to filter out lower-quality predictions. As the resulting performance is robust with respect to the precise choice of these cutoff values, see Figure 2, our cutoff values should be viewed as robust, general recommendation if no other specific training set of known structural features is available.

Using these cutoff values, a significant fraction of the known transient base-pairs can be detected by the three kinetic folding programs, although the three programs differ significantly in their ability to detect known transient and known final structures, see Table 2. Table 6 contains more detailed performance measures for each data set using the three folding pathway prediction programs at program-specific MCC-derived cutoff values.

Table 2.

TPR for known final and known transient structural features as predicted by Kinwalker, Kinéfold and RNAKinetics using the respective MCC-derived cutoff

Program	TPR
	Known transient	Known final
Kinwalker	0.428	0.762
Kinéfold	0.183	0.586
RNAKinetics	0.722	0.652

TPR is a measurement of sensitivity on base-pair level, and is defined as 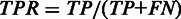. The program-specific MCC-derived cutoffs are applied to filter the predictions (see Figure 2 for details).

Table 6.

Detailed performance measures for each data set using the three folding pathway prediction programs at MCC-derived cutoff values

Program	Alignment	Known transient			Known final		All known			New transient
		Cutoff	TPR	PPV	TPR	PPV	TPR	PPV	MCC	TPR	PPV
Kinwalker	Levivirus	0.430	0	0	0.875	0.792	0.778	0.792	0.78	0	0
	RNase P Type A	0.430	0.538	0.167	0.679	0.679	0.664	0.698	0.68	0.160	0.114
	HDV ribozyme	0.430	0.258	0.267	0.633	0.463	0.443	0.551	0.49	0.172	0.227
	SRP 4.5 S RNA	0.430	0.286	0.083	0.903	0.560	0.789	0.577	0.67	0	0
	Trp operon	0.430	0.621	0.474	0.621	0.474	0.621	0.474	0.54	0.160	0.200
	SAM riboswitch	0.430	0.864	0.919	0.864	0.919	0.864	0.919	0.89	0	0
Kinéfold	Levivirus	0.755	0	NaN	0.396	1	0.352	1	0.59	0	NaN
	RNase P Type A	0.755	0	0	0.615	0.838	0.549	0.838	0.68	0	0
	HDV ribozyme	0.755	0.258	0.444	0.700	0.677	0.475	0.744	0.59	0	0
	SRP 4.5 S RNA	0.755	0	0	0.968	0.909	0.789	0.909	0.85	0	0
	Trp operon	0.755	0.310	0.900	0.310	0.900	0.310	0.900	0.53	0	0
	SAM riboswitch	0.755	0.530	0.921	0.530	0.921	0.530	0.921	0.70	0	0
RNAKinetics	Levivirus	0.0082	0.667	0.018	0.354	0.072	0.389	0.088	0.18	0.154	0.018
	RNase P Type A	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
	HDV ribozyme	0.0082	0.839	0.088	0.567	0.059	0.705	0.137	0.30	0.379	0.040
	SRP 4.5 S RNA	0.0082	0.571	0.014	0.806	0.084	0.763	0.096	0.26	0.360	0.032
	Trp operon	0.0082	0.759	0.154	0.759	0.154	0.759	0.154	0.34	0.680	0.140
	SAM riboswitch	0.0082	0.773	0.520	0.773	0.520	0.773	0.520	0.63	0.440	0.234

The table includes the cutoff value, true-positive rate (TPR), positive predictive value (PPV) and the Matthews’ correlation coefficient (MCC), see the captions of Figures 2 and 3 for their definitions. PPV is a measurement of specificity and is defined as PPV = TP/(TP + FP). NaN (not a number) is produced when the denominator in the ratio is 0. Data are not shown for RNase P Type A using RNAKinetics because the program did not complete due to the length limitation of the program, which is denoted as missing value (NA).

In a later section, see Table 3, we show how the complementarity of the three programs can be used to increase the overall performance accuracy.

Table 3.

Average TPR and PPV for all categories of structures using the three folding pathway prediction programs at MCC-derived cutoff values

Programs	Known transient		Known final		All known		New transient
	TPR	PPV	TPR	PPV	TPR	PPV	TPR	PPV
Kinwalker	0.428	0.318	0.762	0.648	0.693	0.667	0.0871	0.090
Kinéfold	0.183	0.378	0.586	0.874	0.501	0.885	0	NA
RNAKinetics	0.722	0.191	0.652	0.210	0.678	0.231	0.322	0.077
Kinwalker and Kinéfold	0.202	0.513	0.53	0.924	0.453	0.934	0	0
Kinéfold and RNAKinetics	0.138	0.511	0.39	0.932	0.334	0.945	0	0
Kinwalker and RNAKinetics	0.284	0.432	0.483	0.714	0.438	0.736	0.032	0.133
Any two programs	0.347	0.455	0.648	0.760	0.577	0.777	0.032	0.114

Performance measures are shown for Kinwalker, Kinéfold and RNAKinetics alone, in addition to the intersection of all pairs of programs. For this, we consider the set of predicted base-pairs as the intersection of the base-pairs predicted by each program at its optimal cutoff. See the caption of Figure 3 for the definitions of TPR and PPV.

Combining programs improves the prediction accuracy for known transient and final structural features

To further investigate the performance of the three folding pathway prediction programs, Table 3 summarizes the true-positive rate (TPR) and positive predictive value (PPV) for the four structural categories using different combinations of programs. The predictions by the three programs are first filtered using the cutoff values derived from the optimal MCC.

Additionally, we explore the performance using the intersection of predictions generated by two programs, resulting in more strict filtering. For this, a base-pair is considered a positive when predicted by both programs at the respective MCC-derived cutoffs. Table 3 shows performance for all possible intersections. Similarly, in the row of ‘any two programs’, a true positive (TP) refers to a base-pair that is predicted by at least two programs. As one alignment exceeds the length limits of RNAKinetics, only the remaining five alignments serve as input for this combinative analysis.

However, the PPV is greatly improved in all four structural categories, especially in known transient and final structures. For instance, RNAKinetics suffers from low PPV, while performing well in terms of TPR, see Table 3. When RNAKinetics is coupled with Kinwalker or Kinéfold,the PPV increases from 0.191 to 0.511 or 0.432, respectively, for known transient structures. Moreover, the PPV significantly increases from 0.210 to 0.932 and 0.714, respectively, for known final structures. The choice of any pair of programs tends to maximize the TPR, while sacrificing a certain amount of PPV. This choice generates a TPR comparable with that of the individual program and is higher than any of the pair-program combinations. In addition, the PPV is higher than using any individual program.

Overall, the numbers in Table 3 show the benefits of combining prediction programs in enhancing the PPV, while only slightly lowering the TPR.

There is evolutionary evidence for new transient helices

In addition to exploring known transient and final features, we used Transat to identify potential new transient helices that have been conserved during evolution. Transat output includes a list of conserved helices, each with a P-value that corresponds to the probability of seeing a random helix with the same log-likelihood value by chance. Helices with 50% or greater overlap with the known final and transient structural features are removed, and six helices with the most significant P-values are extracted from the resulting list to produce the set of candidate novel transient helices.

Table 4 shows different quality measures for these potential new transient helices. They contain few invalid base-pairs (95.4% canonical base-pairs versus 90.9% for known transient), and are highly conserved (91.5% percent identity versus 76.7% for known transient). However, they show less variation, indicated by a higher sequence conservation and a significantly lower covariation measure (0.036 versus 0.0987 for known transient). Covariation indicates the relative frequency of compensatory mutations that retain base-pairing potential, and is an indicator for conserved functional structures. Additionally, the new transient features contain fewer gaps (0.9%) compared with the known transient (2.31%).

Table 4.

Quality measures of potential new transient structural features for all alignments

Alignment	Can. bp	Covar.	Cons.	Gap.
Levivirus	0.907	−0.031	0.823	0.022
RNase P Type A	0.992	0.033	0.968	0
HDV ribozyme	0.993	0.056	0.960	0
SRP 4.5 S RNA	0.996	0.062	0.961	0
Trp operon	0.964	0.141	0.870	0
SAM riboswitch	0.872	−0.046	0.905	0.029
Average	0.954	0.036	0.915	0.009
Av. (known transient)	0.909	0.100	0.767	0.023
Av. (known final)	0.963	0.305	0.758	0.021

Percent canonical base-pair (can. bp) indicates the proportion of base-pairs across all alignments that contain one of the three canonical pairs (A-U, G-U or G-C). Covariation (covar.) measures the relative frequency of compensatory mutations that retain the base-pairing potential, and indicates base-pairs that are functionally important. Covariation ranges from −2 to +2, and it is 0 when the paired columns have no variation, negative when they contain many invalid pairs and positive when they contain many compensatory mutations. Conservation (cons.) indicates the mean pairwise percent identity between homologous sequence positions at paired columns. Percent gaps (gap.) indicates the proportion of paired sequence positions that contain gaps. New transient features comprise six helices predicted by Transat that have less than 50% overlap with the known structure and the most significant P-values.

Overall, we find that the potential transient helices predicted by Transat show strong evolutionary conservation in terms of primary sequence and base-pairing ability compared with known transient helices. Whether or not these putative transient helices play a functional role as transient helices in the living organisms requires experimental verification.

These potential new conserved transient helices can also be predicted computationally using methods for folding pathway prediction

Using the same MCC-derived cutoffs established for the known transient and final features, we evaluate the ability of the folding pathway prediction methods to identify the new transient features predicted by Transat. Table 5 shows the TPR for the three folding programs for the new transient features. RNAKinetics performs best, as it is able to identify 32.2% of the base-pairs. Kinwalker predicts 8.7% of the features, whereas Kinéfold predicts none of them.

Table 5.

TPR for new transient structural features for three different folding pathway prediction methods using the MCC-derived cutoff optimized over known features

Program	New transient
	TPR
Kinwalker	0.0871
Kinéfold	0
RNAKinetics	0.322

The TPR is evaluated on base-pair level, see the caption of Figure 3 for the definition. New transient features comprise six helices predicted by Transat that have less than 50% overlap with the known structure and the most significant P-values.

Figure 4 shows the performance for new transient helices for a broader range of cutoff values, as the MCC-derived cutoffs discussed previously are stringent. Kinéfold (blue) and RNAKinetics (green) performance is comparable, where RNAKinetics detects 76.5% of new transient features with a 7% false-positive rate (FPR), and Kinéfold detects 67.0% of the features with a 7% FPR. Overall, RNAKinetics achieves a higher TPR with fewer false-positives. Kinwalker (red) is unable to detect a large percentage of the new transient features at any cutoff value. It finds 28.1% of known features with a 4.0% FPR. Although the cutoffs derived from known features generate a small number of high-confidence predictions (Table 5), the folding pathway prediction programs are able to detect a significant proportion of these features when relaxing the cutoffs and accepting a higher FPR.

Figure 4.

Receiver-operating characteristic curve illustrating the predictive performance for potential new transient features using the three folding pathway prediction programs at a broad range of cutoff values. The vertical axis indicates the TPR and the horizontal axis indicates the FPR, see the caption of Figure 3 for the definitions. Note that the axes are plotted on different scales. Each line indicates the performance of one program for different cutoff values (Kinéfold in blue, RNAKinetics in green and Kinwalker in red). New transient features comprise the six top-scoring helices predicted by Transat that have less than 50% overlap with the known structure and the most significant P-values.

One interesting example is shown for the trp operon in Supplementary Figure S20. Transat predicts four novel transient helices also predicted by RNAKinetics (arcs with dotted lines below the horizontal lines representing the alignment, where the arc-plots are made using R-chie (84)), which are all incompatible with alternative structure 2. The Transat helix with the lowest P-value (purple) is also predicted by RNAKinetics with the highest averaged probability, which suggests that the evolutionarily conserved helix is also kinetically feasible during transcription. This helix could be a putative alternative structure in addition to the known alternative structure 1.

CONCLUSION AND DISCUSSION

We have shown that homologous RNA sequences not only fold into similar functional RNA structures, but that their co-transcriptional folding pathways also share common transient structural features that have been evolutionarily conserved. Our conclusions are based on a non-redundant data set of 32 sequences that derive from six RNA families with known final and transient RNA structural features, which constitutes the most comprehensive data set of this kind today. The transient structural features are conserved on approximately the same level as structural features of the final functional RNA structure. The lower covariation compared with that of known final structural features may be due to three different reasons. First, a significant portion of transient base-pairs comprise nucleotides that are also base-paired in the final RNA structure, and the dual evolutionary constraint on these nucleotides results in a higher primary sequence conservation and reduced covariation. Second, the alignments were optimized with respect to the known final structure only. The alignment in the regions outside this structure may thus have been more guided by primary sequence conservation than conservation of base-pairing potential. Third, the lower covariation could also be potentially explained by overlapping protein binding sites when these proteins bind the transient structures in a sequence-specific way. This hypothesis, however, would need to be tested in dedicated experiments and on a case-by-case basis.

We show that known transient features can be predicted in a comparative way by using existing methods for folding pathway prediction. These computational methods use diverse prediction algorithms and all work in a purely non-comparative way by analyzing one individual RNA input sequence at a time. It is therefore remarkable that combining the folding pathway predictions for individual homologous sequences allows us to computationally identify conserved transient features. Using this strategy, known transient features can be predicted with approximately the same prediction accuracy as features of the known final RNA structure. The specificity of this approach can be further increased by combining the predictions of two or more folding pathway prediction programs, which keeps the sensitivity almost unchanged.

We also propose a computational strategy for identifying potential new transient structural features and find significant evolutionary and computational evidence for a range of new transient helices that have not yet been experimentally confirmed. These features exhibit, on average, a higher primary sequence conservation and base-pair conservation than known transient features and a lower, yet positive, covariation.

Overall, we provide ample evidence that evolutionarily related transcripts not only fold into the same functional RNA structure, but that they also co-transcriptionally fold in a similar way in their in vivo environment. More specifically, co-transcriptional folding pathways of homologous transcripts share distinct transient structural features that have been evolutionarily conserved. These transient structural features probably constitute guiding lampposts that the co-transcriptionally folding transcript needs to reach to correctly and efficiently fold into the final functional RNA structure. These lampposts may, overall, provide enough guidance and robustness for the formation of the functional RNA structure. Overall, we thus do not expect closely related RNA transcripts to share identical folding pathways.

Co-transcriptional folding pathways have already been the subject of many dedicated experiments. Their results show the diversity of tricks that the cell uses to fold functional RNA structures robustly and efficiently. Even though computational methods for folding pathway prediction currently need to make a range of simplifying assumptions about the complex in vivo environment, we here show that we can identify conserved transient features by analyzing folding pathway predictions in a comparative way. The predicted features can hopefully help to perform more targeted experiments, e.g. to identify interaction partners that the computational folding pathway prediction methods currently cannot capture. For the future, we hope that adopting a comparative approach to the analysis of folding pathways may prove as successful as it is for RNA secondary structure prediction and that this will further our understanding of RNA structure formation in vivo.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online: Supplementary Tables 1–8 and Supplementary Figures 1–23.

FUNDING

Natural Sciences and Engineering Research Council (NSERC) of Canada and from the Canada Foundation for Innovation (CFI) (to I.M.M.); A.S. holds an Alexander Graham Bell Canada Graduate Scholarship (CGS) from NSERC, with additional funding from NSERC-CREATE through the Graduate Program in Genome Science and Technology (GSAT) at the University of British Columbia (UBC); J.R.P. holds a CGS from NSERC, with additional funding from the CIHR/MSFHR Bioinformatics Training Program at UBC; CIHR are the Canadian Institutes of Health Research and MSFHR is the Michael Smith Foundation for Health Research in Canada. Funding for the open access charge: NSERC of Canada.

Conflict of interest statement. None declared.