Influenza Transmission in Households During the 1918 Pandemic

Abstract

Analysis of historical data has strongly shaped our understanding of the epidemiology of pandemic influenza and informs analysis of current and future epidemics. Here, the authors analyzed previously unpublished documents from a large household survey of the “Spanish” H1N1 influenza pandemic, conducted in 1918, for the first time quantifying influenza transmissibility at the person-to-person level during that most lethal of pandemics. The authors estimated a low probability of person-to-person transmission relative to comparable estimates from seasonal influenza and other directly transmitted infections but similar to recent estimates from the 2009 H1N1 pandemic. The authors estimated a very low probability of asymptomatic infection, a previously unknown parameter for this pandemic, consistent with an unusually virulent virus. The authors estimated a high frequency of prior immunity that they attributed to a largely unreported influenza epidemic in the spring of 1918 (or perhaps to cross-reactive immunity). Extrapolating from this finding, the authors hypothesize that prior immunity partially protected some populations from the worst of the fall pandemic and helps explain differences in attack rates between populations. Together, these analyses demonstrate that the 1918 influenza virus, though highly virulent, was only moderately transmissible and thus in a modern context would be considered controllable.

The devastating impact of the 1918 “Spanish” influenza pandemic on global mortality and morbidity has been well documented (1). Analyses of historical data from that and later pandemics have strongly shaped our understanding of influenza epidemiology (2–12). Such analyses have been used for calibrating efforts to prepare for future influenza pandemics (4, 13–15) and provided prior information that informed the response to the 2009 pandemic (16).

In the current study, we gained new insight into the transmission of pandemic influenza from previously unpublished data from a survey of 7,287 Maryland households conducted in the fall of 1918. The survey was led by Wade Hampton Frost, a pioneer of both field and theoretical epidemiology (17, 18), who led the US Public Health Service’s investigation into the 1918 pandemic (17, 19) and developed one of the first mathematical models of infectious disease transmission (18). We extended Frost’s posthumously published mathematical model of disease transmission in households (18) and fitted a wide range of model variants to the data from 1918. This analysis yielded new insights into the epidemiology of the 1918 pandemic: We found that the epidemic was characterized by low rates of transmission within households (susceptible-infectious transmission probability (SITP) < 20%), that there was considerable interperson variability in infectiousness, and that up to 22% of the population of Baltimore may have been immune before the fall wave of influenza. In addition, we inferred that there appeared to have been very few (<6%) asymptomatic infections. Here we place our results into context by comparing them with seasonal influenza (20, 21) and a recent study of the 2009 pandemic (22). Our results demonstrate that influenza is consistently only moderately transmissible and thus potentially controllable. They also demonstrate the value of simple large-scale household surveys, such as Frost and Sydenstricker’s 1918 study (19), for disaggregating different clinically and epidemiologically relevant components of influenza transmission during the first months of a pandemic.

The most important parameter in epidemic control is transmissibility, which is often (but, as we will see, not always) measured using the basic reproduction number R₀, the number of secondary cases that 1 typical patient infects in an entirely susceptible population. Estimates of R₀ for pandemic influenza range from 1.5 to 2.5, indicating that 33%–60% of transmission (based on the conventional formula, (R₀ − 1)/R₀) would need to be blocked to control a pandemic completely, and also that lesser interventions would have a substantive mitigating impact (2, 4–6, 10, 11, 13–16).

While published estimates of R₀ have mostly been consistent, they share frailties. Time series of deaths (or, in some cases, morbidity reports) are analyzed to determine the rate of spread of the virus in the population. The first frailty is that estimates of R₀ are highly dependent on the generation time distribution (23), the distribution of times between subsequent infection events. There are no good estimates for the generation time of influenza in 1918, and there are only limited data for interpandemic influenza (23) and the 2009 H1N1 pandemic (22, 24). Second, methods for estimating R₀ have mostly been applied to highly aggregated data from large populations. Where outbreaks in small, isolated communities (e.g., military camps or ships) have been analyzed, estimates of R₀ have been more variable and typically higher (5, 6, 24, 25). Third, estimates of R₀ for the 1918 pandemic have been reported from places where nonpharmaceutical interventions were applied with some effect (7–9). Finally, prior immunity should be accounted for. The fall epidemic of 1918 was preceded in some locations by earlier waves of transmission that may have generated immunity (3, 11, 12, 26, 27). Similarly, prior immunity played an important role in mitigating the 2009 H1N1 pandemic (28). These frailties imply that the real transmissibility of pandemic influenza viruses could be higher than expected from published estimates of R₀, and thus there is a need to obtain more robust estimates.

MATERIALS AND METHODS

Additional details on our methods, data, sensitivity analyses, and time-series analysis are given in the Web Appendix, which is posted on the Journal’s Web site (http://aje.oxfordjournals.org/); here we report enough information to ensure reproducibility.

The study

In 1919, Frost and Sydenstricker (19) published results from a house-to-house canvass carried out in Baltimore, Maryland, between November 20, 1918, and December 15, 1918, immediately after the first peak of the lethal fall wave of the pandemic. We analyzed previously unpublished documents held by the Chesney Medical Archives of Johns Hopkins University (reproduced in the Web Appendix). Part of the data are summarized in Figure 1 and consist of contingency tables of final outcomes—that is, of the 7,140 households surveyed in Baltimore, the number k_(m,n) of households of size n reporting m cases.

Figure 1.

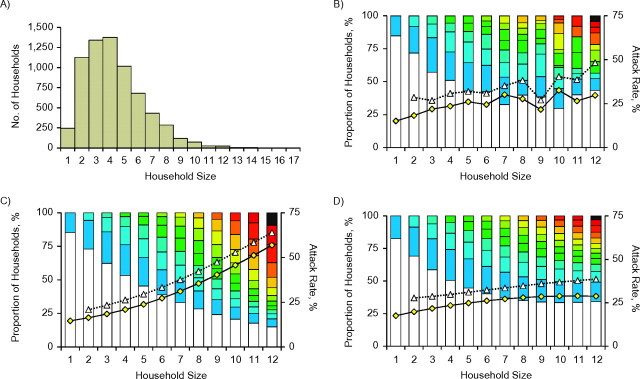
A) Sizes of the households included in a canvass of influenza cases in Baltimore, Maryland, 1918. We analyzed data from 6,753 households with a mean of 4.26 inhabitants per household. B) Distribution of the 7,140 recorded influenza cases within these households. For each household size, the bars show the proportion of households recording 0, 1, 2, or more cases, highlighted in colors ranging from cold (white/blue) to warm (red/black). The yellow diamonds show the attack rate for each household size (the overall attack rate was 24.7%), while the open triangles show the secondary attack rate (i.e., the attack rate for remaining persons after the introduction of 1 infected case); the overall mean was 32.5%. Data from households containing more than 12 people were sparse and are not shown. C) Graph equivalent to that in part B, showing the best-fitting basic Reed-Frost model. D) Predictions of the best-fitting extended model (which included the effects of prior immunity, variable infectiousness, and transmission rates scaling with household size).

Nonmathematical description of methods

For the sake of clarity, we briefly describe our methods in nonmathematical form. To model transmission in households, we used (and extended) a formalism developed by Wade Hampton Frost and Lowell Read, which predicts the progression of an epidemic in discrete generations of infection, with random infection events specified by predetermined probabilities (18). Once infected, individuals are considered infectious for 1 time step (the generation) and then recover to full immunity. Closed mathematical forms can be derived for the final size distribution of small epidemics (29, 30). The model has been shown, for this task of predicting epidemic sizes, to be equivalent to much more realistic models formulated in continuous time (31). It is thus ideally suited for analyzing household outbreak data.

The basic variant of the model has 2 parameters: the escape probability (Q), the probability that an individual is not “exposed” to infection outside the household, estimated cumulatively over the whole course of the epidemic; and the SITP. “Exposure” refers to events that result in infection if and only if the individual is susceptible at that point in time. The SITP quantifies infectiousness within the household, and it is defined for each infectious person in relation to each other susceptible individual in the household. The SITP is the probability of transmission occurring between each susceptible-infectious pair of individuals, measured over the whole period of infectiousness of the infectious individual and in the case when the susceptible individual is not infected by a third party during that period.

The basic model is extended to include various other effects, including variable infectiousness (including dependence on household size), asymptomatic infection (in both infectious and uninfectious states), systematic misreporting, prior immunity, and inclusion of classes of persons with higher infectiousness (e.g., children). By varying assumptions from this list, many different models are obtained. Each model’s ability to explain the data is assessed by maximizing the likelihood, defined as the probability that the model could have generated the data. The different models are compared with each other using an information theoretical method, in which (roughly speaking) the likelihood of the model is discounted by the number of parameters in the model, thus achieving the best-fitting, most parsimonious model.

To complement this analysis of household data, a time-series analysis is performed on the time series of incident disease cases reported by Frost and Sydenstricker (19), with the aim of estimating individual and household reproduction numbers over time. These reproduction numbers are defined as the numbers of individuals and households infected by each infectious individual and household, respectively. The method is based on estimating, on each day, the total number of infectious persons and the total number of newly infected persons and defining the reproduction number as the ratio of these 2 quantities (32). Finally, using simulations that integrate all of the estimates from the household and time-series analyses, we estimated the effect of nonpharmaceutical interventions and prior immunity in reducing the final attack rate in the city.

Mathematical models

We initially model these data with a generalized susceptible-infected-removed (SIR) epidemic model (29) that predicts the proportion 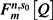of households of size n with s₀ initial susceptible individuals and reporting m cases, found by solving the system of equations

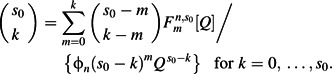(1)

Q is the probability of each individual’s not being infected from outside the household (a.k.a. the escape probability). ϕ_n(x) is the generating function for the distribution of infection rates within a household of size n. In the basic Reed-Frost model, this distribution is concentrated at a fixed infectiousness, β, while in our extended model it is a gamma distribution with mean β/n^α and shape k. Our extended model also allows for prior epidemic(s) generating cross-protective immunity with total escape probability Q_prior and similar in-house transmission parameters. Infection can be asymptomatic and infectious with probability p_asx, asymptomatic and uninfectious with probability p_pr, or symptomatic. Allowing for these additional effects, the distribution of final outcomes, denoted T_(m,n) and to be compared with the data k_(m,n), is given by

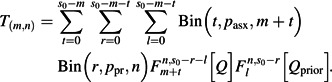(2)

Bin( ) is the standard binomial distribution. The basic model has 2 parameters (β and Q), while the extended model has 7 (β, Q, α, k, Q_prior, p_asx, and p_pr).

Statistical analysis

The models are fitted by finding the parameter values that maximize the likelihood, or alternatively minimize the deviance

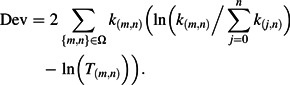(3)

Ω is the set of all values of m and n such that k_(m,n) > 0.

Models of intermediate complexity are obtained by considering all combinations of parameter limits which partially reduce the extended model to the simple one, that is, k → + ∞, α = 0, Q_prior = 1, p_pr = 0, and p_asx = 0. Altogether, the 32 resulting models are compared using the modified Akaike’s Information Criterion (AIC):

(4)

More model variants, as well as details of how the method was adapted to different data sets where it is known that there was exactly 1 infection external to the household, are described in the Web Appendix.

Time-series analysis

To complement our analysis of transmission within households, a time-series analysis was used to estimate time-varying reproduction numbers from the incidence of disease reported in the Frost and Sydenstricker study (19). The reproduction number is defined as the number of individuals (or households) infected, on average, by each infected individual (or household) over his or her (its) entire infectious period. It is determined from the time series of incident cases and the generation time distribution (the distribution of times between the infection of an index case and the times of infection of secondary cases). The method was adapted from Fraser (32). A likelihood was constructed by assuming that incidence was generated by a stochastic epidemic renewal process,

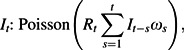(5)

where I_t is the incidence time series, R_t is the reproduction number, and ω_s is the (discrete) generation time distribution. The likelihood is then given by

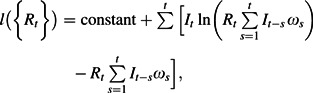(6)

which is maximized with respect to the reproduction numbers R_t. For the estimates used in the main text, R_t was considered piecewise constant over 10-day intervals, while for the estimates presented in Table 1, R_t was assumed to be constant before and after October 10. Different standard choices for the generation time distribution were used (as described in the Web Appendix). The household reproduction number, the number of households infected by each household, was estimated by substituting the simulated household generation time distribution into equation 6, following the scheme defined by Fraser (32).

Table 1.

Estimates of Key Quantities Describing Influenza Transmission in Baltimore, Maryland, During the 1918 Pandemic, as Inferred From the Best-Fitting Model

Quantity	Value or Estimate
	No.	95% CI	%	95% CI
No. of households sampled	6,753
No. of people included in sample	28,977
No. of people reported as cases	7,140
Overall attack rate for the fall wave			24.6
Proportion of households reporting at least 1 case			47.4
Secondary attack rate within affected households			32.5
Proportion of cases which are asymptomatic and uninfectious			0	0, 6
Proportion of cases which are asymptomatic and infectious			0	0, 3
Dispersion parameter for individual variability in infectiousness (k; lower values correspond to more variability)	0.94	0.59, 1.72
Scaling parameter for infectiousness as a function of household size (α, where in-house infectiousness decreases as 1/nα)	0.35	0.22, 0.49
Effective reproduction no. (September 1–October 10), R	1.38	1.33, 1.42
Basic reproduction no., R0	1.77	1.61, 1.95
Basic household reproduction no., R0*	2.47	2.25, 2.73
Proportion of the population immune prior to September 1			22.2	17.1, 27.0
Reduction in reproduction no. on October 10			42.1	38.2, 45.7
Attack rate for a hypothetical scenario in which:
There was no prior immunity			35.8
There was no reduction in R on October 10			44.9
There was neither immunity nor reduction in R			74.2

Abbreviation: CI, confidence interval.

RESULTS

The Frost and Sydenstricker study

Household studies of influenza are ideally suited for deriving disaggregated estimates of transmissibility which complement population-based estimates of R₀ (21, 29, 30). A key measure of transmissibility in households is the SITP, the probability that each infectious individual will infect each susceptible individual in a household during his or her infectious period. We begin by focusing on previously unpublished documents from the Wade Hampton Frost collection of the Chesney Medical Archives at Johns Hopkins University, which report the final outbreak size for households surveyed in a canvass conducted by Frost and Sydenstricker’s team (19) from November 20, 1918, to December 15, 1918. While the time series of cases has been analyzed (5, 10), detailed records collected during this study have not been previously published. The newly rediscovered data from Baltimore are summarized in Figure 1, parts A and B. More detail, as well as data from the smaller nearby city of Frederick, is provided in the Web Appendix.

Basic Reed-Frost model

To analyze these data, we started with the basic Reed-Frost model (18) of transmission in households (29, 30). This model assumes that an epidemic progresses through discrete generations of infection, in which each susceptible individual has a probability of being infected by each infectious individual in the household (the SITP (33)). After each generation, all currently infectious persons progress to immunity, and all newly infected persons progress to infectiousness. The ordering of events and the temporal variation in individual infectiousness are irrelevant for predicting the final number of persons infected (31). For the Baltimore data, the maximum likelihood estimate for the SITP was 14% (95% confidence interval (CI): 13, 15).

An extended model

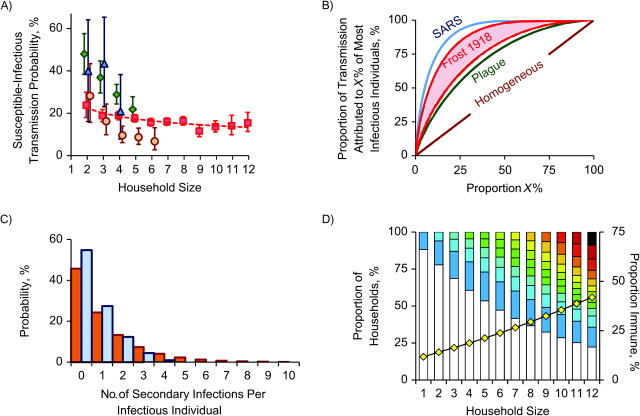
The basic Reed-Frost model is a poor fit to these data (Figure 1C and Web Appendix). We therefore extended the basic model to include other known or assumed features of influenza transmission, such as infectiousness that varies between individuals (34), contact rates that vary as a function of household size (4, 21), and asymptomatic infection (as either an infectious state or a noninfectious state) (35). We also allowed for prior immunity, which could be generated by the spring 1918 “herald” waves of infection (3, 11) or by cross-immunity arising from other sources (27). We used an information theoretical framework to select the best-fitting model variant; the fit for that model is shown in Figure 1D. All methods are described in the Web Appendix. The mean SITP was estimated to be 18% (95% CI: 15, 20) (Figure 2A; see Web Appendix for details of how this was computed from model parameters). Though it is difficult to compare different studies because of different case definitions (clinical vs. serologic), the estimated transmission probability is lower than similar estimates for seasonal influenza (Figure 2A), thus demonstrating that the influenza virus of 1918 was characterized by low person-to-person infectiousness within affected households. Conversely, transmission probabilities were generally higher in 1918 than for the 2009 H1N1 pandemic.

Figure 2.

A) Susceptible-infectious transmission probability for the 1918 influenza pandemic, by household size. In addition to results from the Baltimore, Maryland, study, which are shown in red (squares, nonparametric; line, parametric), results are also shown for a study of 2009 H1N1 pandemic influenza (22) (orange circles) and 2 further studies of seasonal influenza transmission (green diamonds, Epigrippe Study (21); blue triangles, Tecumseh Study (20)). The studies used different methods, so estimates are not exactly comparable; the comparison with the Tecumseh Study (20) may be the most valid, since we analyzed serologically confirmed infections in initially seronegative households. The 2 other studies were also comparable, since they were based on follow-up of symptomatic cases after an index case (21, 22). All of the studies show evidence of declining susceptible-infectious transmission probability in larger households, but this is less pronounced for the 1918 Frost and Sydenstricker study (19) than for the others, perhaps because of secular changes in the nature of the household (see Web Appendix). Bars, 95% confidence interval. B) Characterization of a measure of interperson variability in infectiousness by means of a plot of the proportion of transmission attributable to the X% most infectious individuals. The brown line corresponds to homogeneity (when all infected persons have identical infectiousness); the lower red line shows the best-fitting model. The upper red line corresponds to the estimate from a different but plausible model with misreporting (see Web Appendix), and thus the red shaded area corresponds to estimates with model uncertainty. The curves were compared with a previous analysis of several infectious diseases (34): The blue line shows the most variable of the infectious diseases studied (severe acute respiratory syndrome (SARS)) and the green line the least (pneumonic plague). C) Predicted number of secondary cases attributable to within-household transmission (blue bars) and between-household transmission (orange bars) for an index case living in a household of size 5, in the absence of prior immunity or public health interventions. An index case infects an average of 0.69 persons in his or her household and 1.22 persons outside of it. The distributions are highly overdispersed. D) Distribution of immune individuals within households of different sizes predicted by the best-fitting model, using the same color scheme as in Figure 1. The yellow diamonds show the average proportion of immune individuals.

Variable infectivity

We detected interperson variability in infectiousness. The parameter k in our model (see Web Appendix) is directly equivalent to the dispersion parameter introduced in an earlier study of variability in infectiousness for multiple diseases (34). To date, published microsimulations of pandemic influenza have used various assumptions regarding interperson variability in biologic infectiousness, without much empirical support (4, 13–15). The main effects of biologic heterogeneity in infectiousness operate in the early establishment phase of an epidemic (34) and in changing the predicted impact of contact tracing (36). If the source of biologic heterogeneity could be identified, so that more infectious individuals could be preferentially targeted for isolation and quarantine, then gains in epidemic mitigation might be substantial (34). Our estimate of k = 0.94 (Table 1) would imply that the most infectious 20% of the population would be responsible for 50% of infections in a homogenously mixing population (Figure 2B) and somewhat less when household structure is accounted for; this is an intermediate level of heterogeneity (Figure 2C). We were unable to determine whether age was an important source of this heterogeneity (see Web Appendix).

Preexisting immunity

Our analysis suggested a large role for preexisting immunity (Figure 2D), with 22.2% of the population estimated to have been immune prior to the lethal fall wave (Table 1). This is consistent with earlier studies of the 1918 pandemic in Scandinavia, which described high morbidity but a low mortality epidemic wave occurring during the spring or summer of 1918 (3, 11) and gave direct evidence of cross-protection (12). However, unlike the situation in Scandinavia (11), there is little direct evidence of a substantial spring wave of influenza in the United States outside of Army camps (12), though a minor mortality peak was observed in New York (3). If our estimates of the degree of prior immunity are accurate, then it had a major impact. We estimate that the 1918 fall wave had an attack rate of 22%, but in the absence of prior immunity, we predict that this might have risen to approximately 36% (Table 1). Interestingly, we were able to test these predictions using documents from the study of Frederick, Maryland, where we inferred very low levels of prior immunity and the observed attack rate was indeed substantially higher than in Baltimore, at 32.1% (see Web Appendix). This suggests that levels of prior immunity generated by earlier infections could have been very variable in different communities, and that this could partly explain variable attack rates in different localities (and very high attack rates experienced in some remote communities) (7, 8).

Asymptomatic infections

Our analysis of multiple model variants consistently indicated a very low proportion of asymptomatic infection, whether infectious or not (see Table 1 and Web Table 3 in the Web Appendix), with the best-fit value being 0%. Our estimate of a lack of asymptomatic infection can be imputed directly from the data with a much simpler analysis, since a fair proportion of even large households report all members experiencing symptomatic influenza (Figure 1). A simple binomial calculation shows that this outcome would be very unlikely with any appreciable frequency of asymptomatic infection. Of course, models could be devised to reconcile asymptomatic infections with this pattern (such as dose-dependent amplification in heavily affected households or shared genetic susceptibility), but they would be far less parsimonious than the models used here.

Potential misreporting

The results presented above assume full reporting of cases in the survey. To test the importance of this, we considered the impact of possible systematic misreporting. We assumed, plausibly, that a fraction of households falsely reported zero cases, perhaps to evade further questioning. This model could also be used to describe a situation wherein a proportion of households successfully isolated themselves entirely during the epidemic. This model also fitted the data well (indeed, slightly better than the model with prior immunity (see Web Table 3)). The best-fit parameters for this model are listed in Web Table 7 and are compared with the main model; the estimated secondary attack rate was very similar, but the interperson variability in infectiousness was larger (Figure 2B). The model did not include prior immunity; it proved impossible to independently estimate both prior immunity and misreporting, indicating that these phenomena have a similar impact on the predicted distribution of cases in households. Thus, the estimate of the degree of prior immunity presented above could be considered an upper bound if a significant fraction of households falsely reported no cases. Underreporting of infected individuals within households is equivalent (in the model) to asymptomatic infectious cases. Our analysis suggested a very low rate for such underreporting.

Comparison with seasonal influenza and the 2009 H1N1 influenza pandemic

We also fitted our model to published data on seasonal influenza and on the recent H1N1 pandemic (Figure 2A). For the pandemic studies, the overall SITP was estimated at 17.6% (95% CI: 15.2, 20.1) for the 1918 pandemic and 11.9% (95% CI: 7.1, 18.2) for the 2009 pandemic (22). In comparison, for the studies of seasonal influenza, it was 32.0% (95% CI: 15.2, 56.0) (Tecumseh Study (20)) and 34.0% (95% CI: 26.7, 39.4) (Epigrippe Study (21)). While some caution is needed in drawing strong conclusions because of differences in the study populations (the seasonal studies focused on households with children), duration of follow-up, and what was being measured (the Tecumseh Study investigators recorded seroconversion), this comparison suggests lower person-to-person transmission in both pandemics than in seasonal influenza and confirms the early finding that 2009 H1N1 influenza was particularly modestly transmissible (16). In addition, only Frost and Sydenstricker’s 1918 study had a sufficiently large sample size to permit estimation of anything beyond the most basic transmission parameters. Our analysis of the 2009 data could not identify parameters relating to asymptomatic infection or prior immunity, both likely to be important factors; a sensitivity analysis of these parameters is presented in the Web Appendix.

Population dynamic analysis

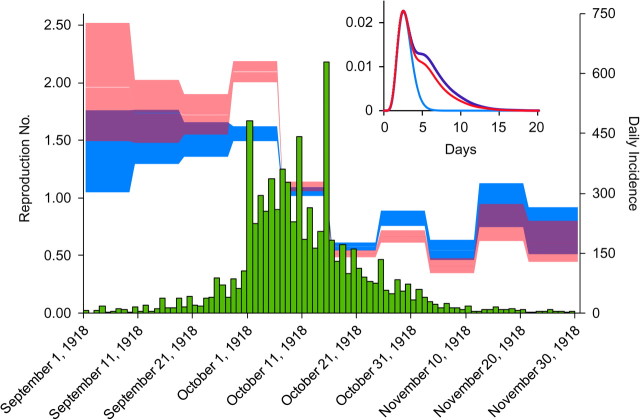
To complement our analysis of household transmissibility, we also estimated the effective reproduction number over different periods of the epidemic in Baltimore (Figure 3). The reproduction number estimated over the first period of epidemic growth in the fall of 1918 in Baltimore was 1.38 (Table 1); extrapolating this to a population without immunity gives an estimate of R₀ = 1.77. To account for the impact of household structure, we also calculated the basic household reproduction number R₀^*, the number of households infected by each household in the absence of immunity (32), estimated to be 2.47. The dependence of these estimates on the generation time distribution is explored in the Web Appendix.

Figure 3.

Time series of incident symptomatic influenza cases in a 1918 Baltimore, Maryland, canvass (19) (green bar chart). Estimates of the effective reproduction number R (how many people each infected person infects; the blue shaded area is the 95% confidence interval) and of the effective household reproduction number R^* (how many households each infected household infects; the pink shaded area is the 95% confidence interval) are shown. Inset: estimates of the generation time distribution for individuals (blue line; gamma distribution with mean 2.85 days (standard deviation (SD), 0.93)) and for households with no prior immunity (purple line; mean = 5.01 days (SD, 2.83)) or households with prior immunity (red line; mean = 4.68 days (SD, 2.69)). For clarity, the household generation time distribution is not normalized in the plot.

The final attack rate for the fall wave (24.6%) was lower than would be predicted for the effective R of 1.38 (which, even allowing for the effect of prior immunity, is 38.3% (95% CI: 33.1, 43.8)), suggesting that most of the reduction in transmission that occurred around October 10 (Figure 3) was due to the effect of nonpharmaceutical interventions rather than depletion of the pool of susceptible contacts, which is consistent with earlier analyses (7–9) but subject to the caveat that assortative mixing by age group can also skew the relation between R₀ and final attack rates. We can thus estimate the reduction in transmission that must have arisen around October 10 (Table 1). The precision with which we can estimate the date of reduction in transmission is limited by our method (in which the reproduction number is estimated over 10-day time periods (Figure 3)). However, and validating the approach taken here, this date is consistent with contemporary news reports citing a ramp-up in social distancing measures, starting on October 7 with school closures, followed by daily updated closures of meeting spaces, and culminating on October 11 with the closure of churches (7–9). We estimate that these measures reduced transmission by 42% and reduced the attack rate from 45% to 25% (Table 1); more timely and sustained responses would have had a greater effect in mitigating the epidemic (7–9).

DISCUSSION

The size of Frost and Sydenstricker’s study (19) allowed us to discriminate between hypotheses regarding influenza transmission in 1918, highlighting the power of a simple but effective study design augmented by modern statistical methods for gaining insight into the epidemiology of an infectious disease. Of the 4 household studies analyzed here, only Frost and Sydenstricker’s was large enough to estimate multiple parameters reliably. A particular strength of our study was that we fitted many different models to the data and used likelihood-based information theoretical methods to choose the most appropriate of the models we proposed; this can only be done reliably with large data sets. Of course, one cannot rule out the possibility of having missed even better models, and indeed some models we developed in a second iteration of analysis described the data better than the first set of models (without changing our main conclusions; see Web Appendix). Such is the process of iterative model development.

While features such as asymptomatic infection and prior immunity can now be assessed more reliably with serologic surveys, recent experience with the 2009 H1N1 pandemic shows that while serologic surveys are invaluable, they can also be slow and difficult to perform in the early stages of a pandemic (28). We suggest that rapidly performed large-scale household studies could generate many insights even during the first few months of a newly emergent epidemic.

At best, inference from 1918 will only ever be as reliable as the data themselves, which were collected over 90 years ago in the absence of any diagnostic test (or even correct knowledge of the etiologic agent). Nonetheless, the scale of the epidemic and the reported exceptional care taken by the chief investigators (17) give us some confidence in the data. The lack of asymptomatic infections and the low and consistent estimates of the SITP and of R₀, even when adjusting for the effect of prior immunity, all suggest that current plans for pandemic preparedness (4, 13–15) might overestimate the difficulty with which a highly pathogenic pandemic virus could be controlled. Particularly compelling in the light of these findings is the case for household-based isolation, quarantine, reactive household-wide prophylaxis (13, 37, 38), and perhaps even contact tracing. The recent H1N1 pandemic presented a particular challenge for control because of very low virulence (39), which made case-finding and diagnosis difficult and meant that disruptive nonpharmaceutical interventions would have been more costly than the epidemic they would have aimed to mitigate. Our findings of low transmissibility for 1918 pandemic influenza suggest that a severe pandemic caused by a novel virulent influenza virus could be comparatively easy to mitigate or even control in a modern setting if population compliance were high. Findings of higher transmissibility for seasonal influenza than for pandemics shed some light on the slow tempo and magnitude of the evolution of transmissibility that may take place in the years following a pandemic.

Glossary

Abbreviations

CI

confidence interval

SITP

susceptible-infectious transmission probability