Designed azurins show lower reorganization free energies for intraprotein electron transfer

Abstract

Low reorganization free energies are necessary for fast electron transfer (ET) reactions. Hence, rational design of redox proteins with lower reorganization free energies has been a long-standing challenge, promising to yield a deeper understanding of the underlying principles of ET reactivity and to enable potential applications in different energy conversion systems. Herein we report studies of the intramolecular ET from pulse radiolytically produced disulfide radicals to Cu(II) in rationally designed azurin mutants. In these mutants, the copper coordination sphere has been fine-tuned to span a wide range of reduction potentials while leaving the metal binding site effectively undisrupted. We find that the reorganization free energies of ET within the mutants are indeed lower than that of WT azurin, increasing the intramolecular ET rate constants almost 10-fold: changes that are correlated with increased flexibility of their copper sites. Moreover, the lower reorganization free energy results in the ET rate constants reaching a maximum value at higher driving forces, as predicted by the Marcus theory.

Electron transfer (ET) through proteins is central to biological energy conversion processes, from photosynthesis to respiration (1). ET rates between redox centers are tightly controlled and tuned in biological systems for efficiency and to avoid formation of deleterious products (2–5). An important parameter determining the ET rate is the reorganization free energy of the redox sites (6–8), which for biochemical ET reactions has evolved to low values, usually providing high rate constants. Despite many years of work, few efforts have succeeded in designing protein ET sites having reorganization free energies lower than those observed for the native ones. For example, numerous mutations proximal to the type 1 (T1) blue copper site have been introduced into azurin (Az) (9–19), a bacterial electron-mediating protein, but those that have lowered this barrier have not been reported yet.

Prominent among the theories developed to rationalize the control of ET reaction rates (20–22) is that of R. A. Marcus (23). A particularly intriguing element of this theory predicts that the ET rate reaches its maximum when the driving force of the reaction equals the reorganization free energy, after which an even higher driving force decreases ET rate, reaching the “Marcus inverted region.” It has been proposed that the dramatic difference in rates between some of the forward and backward ET reactions in the photosynthetic reaction center is a result of the latter being in the inverted region, which is reached because of exceptionally low reorganization free energies of the relevant ET sites (24).

In the present study, we aim at examining how the major changes in modifying the redox potential of the type 1 copper site in Az achieved by Marshall et al. (25) affect its ET reactivity. A major obstacle in rationally fine-tuning the properties of the metal ion coordination site is the difficulty in modifying only a single parameter controlling the ET reactivity of a redox site, e.g., its reduction potential, without significantly altering other properties (26). The copper site in Az contains three strong ligands—His46, Cys112, and His117—that form a trigonal planar geometry around the metal center (Fig. 1B). Recently, Az mutants were produced that left all three of these ligands intact yet replaced the weak axial ligand Met121 by a Gln or an Leu to tune the hydrophobicity around the copper. In addition, Asn47 was changed to Ser and Phe114 to Asn or Pro to modify the hydrogen bonding networks near Gly45, Cys112, and His117, which interact with the copper. The mutations tuned the reduction potential of the Cu center over a wide range (>500 mV) without significantly disrupting the copper binding site (25), providing a promising system for a quantitative examination of the relationship between ET driving force and rate constant. Here we report the results of studying intramolecular ET from a disulfide radical anion, produced by pulse radiolysis, to the Cu(II) center in several of these Az mutants. The results presented here suggest that the reactions proceed with a lower reorganization free energy compared with wild-type Az and other mutants studied so far (18). Furthermore, the ET rates in these mutants fit the curve predicted by the Marcus theory, and at the highest driving force of >1.0 eV, a decline in rate suggests entry into the Marcus inverted region.

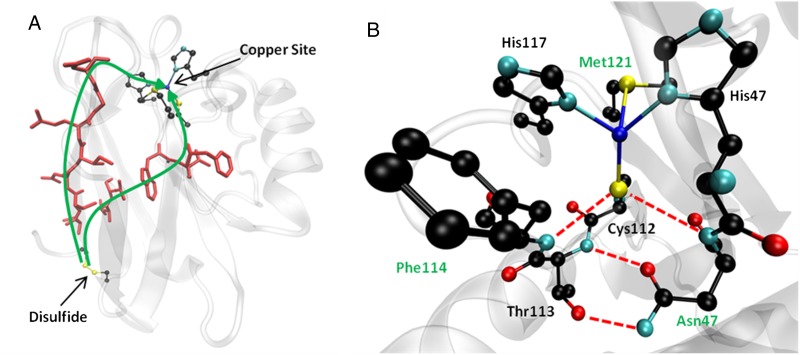
Fig. 1.

(A) Calculated ET pathways from the disulfide to the copper site. Residues involved in the ET pathway are shown in red. For reference, the disulfide bond and the copper site are shown in ball-and-stick representation. (B) The copper binding site of Az and surrounding secondary coordination sphere. Hydrogen bonding interactions relevant to this study are shown as red dashed lines. Residues that were mutated are denoted with green labels. The copper is shown as a dark blue sphere.

Results

Six mutants of Az previously shown to have a wide range of reduction potentials [0.11–0.64 V vs. the normal hydrogen electrode (NHE); Table 1] were constructed, expressed, and purified as described previously (25). Exposure of anaerobic Az solutions (75–200 μM, 100 mM sodium formate, 10 mM phosphate buffer, pH 7.0) to pulse radiolytically produced CO₂⁻ radical anions (18) caused reduction of either the single disulfide bridge (Cys3 and Cys26) to the disulfide radical anion (RSS*R^·−) (E⁰ = –0.41 V) (27), or the Cu(II) ion with essentially diffusion-controlled rate constants (k₁ ∼10⁹ M⁻¹⋅s⁻¹), as monitored by absorption changes at both 410 nm (RSS*R⁻ band, ε₄₁₀ = 10,000 M⁻¹⋅cm⁻¹) (27) and 625 nm [Cu(II) band, ε₆₂₅ ∼5,000 M⁻¹⋅cm⁻¹). After the initial reduction phases, a slower and concentration-independent intramolecular RSS*R^·− to Cu(II) ET takes place (18) (see Figs. S1 and S2):

The observed rate constants, k_ET (at 25 °C), and standard reduction potentials are presented in Table 1. The temperature dependences of the rate constants were measured in the range of 4–45 °C, and the activation parameters were derived (SI Text and Table S1). The activation parameters show similar values with small activation enthalpies and negative activation entropies common for long distance ET reactions and indicative of a shared mechanism.

Table 1.

Rate constants and reduction potentials

Mutant	kET, s−1 at 298 K	Reduction potential, mV
Phe114Pro/Met121Gln	81 ± 11	114 ± 49
Phe114Pro	191 ± 26	219 ± 8
Asn47Ser/Phe114Asn	387 ± 59	490 ± 12
Asn47Ser/Met121Leu	355 ± 51	509 ± 3
Phe114Asn/Met121Leu	287 ± 34	535 ± 11
Asn47Ser/Phe114Asn/Met121Leu	78 ± 12	641 ± 9
WT P. aeruginosa	44 ± 7	286 ± 8

In the nonadiabatic regime, the semiclassical ET theory for reactions between spatially fixed and oriented donors and acceptors provides a framework for analysis of rate constants (23):

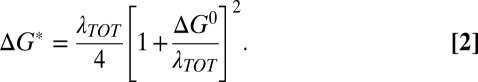In Eq. 1, κ(r) is the transmission coefficient at a fixed separation distance, r, and ν is a frequency. In the nonadiabatic limit, κ(r)ν is independent of the frequency of nuclear movements. ΔG* and ΔG⁰ are the activation free energy and standard free energy of reaction, respectively; λ_TOT is the reorganization free energy; and T is the temperature (in kelvins). When the driving force of the reaction equals the total reorganization energy, the rate constant reaches its maximum value, k_MAX. κ(r)ν decays exponentially with the separation distance (23); as such, we can estimate k_MAX by

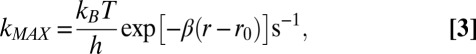where r is the donor-acceptor distance and r₀ is the value of r for a donor and an acceptor in direct (van der Waals) contact; the generally accepted value for r₀ is 0.3 nm (6, 28). A timetable for activationless electron tunneling in β-sheet proteins establishes a decay constant of β = 10 nm⁻¹ (28). For particular donors and acceptors, λ can be calculated by the Marcus cross-relation (23):

where λ_TOT, λ_D, and λ_A are reorganization energies of the whole system, ET donor, and ET acceptor, respectively. Eq. 3 thus provides the maximal value of the rate constant, k_MAX, for the given distance when the activation free energy is zero. Applying Eq. 3 and inserting the direct distance separating the electron donor and acceptor, r − r₀ = 2.38 nm, as well as the exponential decay constant, β = 10.0 ± 0.2 nm⁻¹ (see Discussion), a k_MAX = 290 s⁻¹ is calculated. This means that as long as this separation distance and β do not change (see Discussion), the rate constant of the intramolecular ET should not exceed this value of k_MAX. The separation distance has been derived from the 3D structures (see Fig. 1) of five of the seven variants shown in Table 1 and Fig. 2.

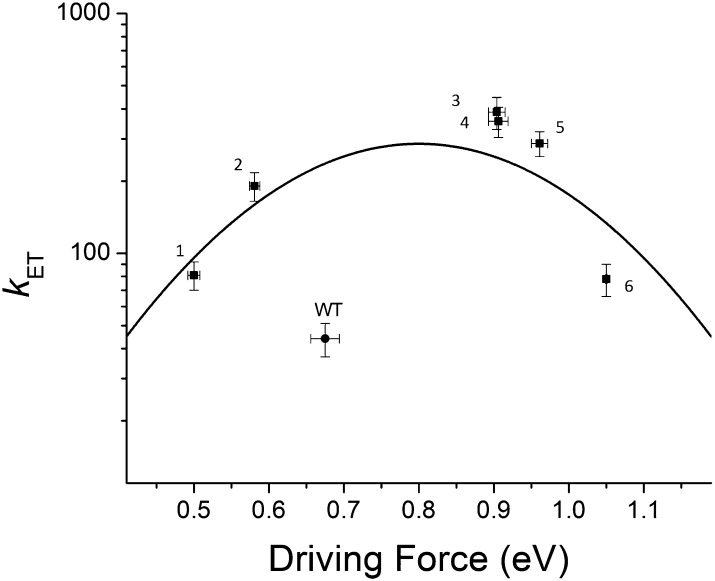
Fig. 2.

Logarithm of the ET rate constants as a function of the reactions’ driving force and the theoretically calculated, bell-shaped curve fit to the data with the parameters k_MAX = 290 (+90/−70) s⁻¹ and λ_TOT = 0.81 (+0.07/−0.05) eV. The mutants are indicated by ■ and, from left to right, are identified with those in Table 1, from top to bottom: 1, Phe114Pro/Met121Gln; 2, Phe114Pro; 3, Asn47Ser/Phe114Asn; 4, Asn47Ser/Met121Leu; 5, Phe114Asn/Met121Leu; and 6, Asn47Ser/Phe114Asn/Met121Leu. The ● represents WT Az.

A main element in the ET pathway to Cu(II) is the bond between the Cu(II) and the thiolate ligand. Changes in the extent of covalency of the Cu²⁺−S(Cys) bond in the mutants studied here could alter the coupling parameter. To examine our assumption that the electronic coupling between the donor and acceptor has not changed substantially, we analyzed electron paramagnetic resonance spectra of each of the mutants (Fig. S3) and the extended X-ray absorption fine structure (EXAFS; Fig S4) of the triple mutant (SI Text and Tables S2 and S3). The results of this analysis correlate well with the values collected via EXAFS spectroscopy for several variants containing the same mutations and support the above notion that the electronic coupling between electron donor and acceptor does not change significantly as a result of the mutations.

The experimental values of k_ET obtained for the Az mutants fit well to the theoretical curve calculated using the Marcus theory in the plot of the ET rate vs. the driving force shown in Fig. 2. The fit of the data to Eqs. 1 and 2 (Fig. 2), using nonlinear least squares analysis and the method of support planes (29), yields a value of k_MAX = 290 (+90/−70) s⁻¹ and a reorganization free energy of λ_TOT = 0.81 (+0.07/−0.05) eV. In this analysis, k_MAX is the preexponential term in Eq. 1, treated as a constant, and is consistent with the value calculated from Eq. 3. The reorganization free energies of the individual mutants also were calculated independently using the experimental activation parameters, ΔH^‡ and ΔS^‡ [the latter corrected for the entropic contribution from β(r − r₀)] (see SI Text and Tables S1 and S4). Using the values of the activation free energies ΔG*, the reorganization free energies λ_TOT for the individual variants then could be calculated applying Eq. 2. As seen in Table S4, the resultant values fit very well with the above-determined λ_TOT. For the five mutants with the lowest driving force (see Fig. 2 and Table S4), an average λ_TOT = 0.89 (+0.05/−0.07) eV was observed. For the last (triple) mutant, we calculate a reorganization free energy of 0.71 eV, which is considerably smaller than the driving force of 1.05 eV. The reorganization free energy includes contributions from both the T1 Cu site and the disulfide-radical ion. For the latter, we previously determined a λ_SS = 1.2 eV (30), which, from Eq. 4, leads to an average λ_Cu = 0.4 eV for the variants studied here, a significantly lower value than that previously determined for WT Pseudomonas aeruginosa Az (0.82 eV) (31). The difference in reorganization free energy between the Az mutants calculated here and that of WT Az (18) is illustrated in Fig. 2, in which the point for WT Az clearly falls below the bell-shaped curve.

Discussion

The bell-shaped curve in Fig. 2 illustrates that within reasonable accuracy, the reorganization free energy can be fitted to a single value for all the studied mutants, which is manifested as a lower activation barrier for the ET. This assumption is supported further by the similar λ_TOT values obtained when calculated for each individual mutant. The key feature shared by all these azurins is the mutations in the copper ion’s outer coordination sphere, affecting primarily the hydrogen-bonding network around Cys112, as described above. We attempted to identify structural features that may be responsible for the low ET activation barrier by analyzing additional properties of these proteins, including 3D structures, along with resonance Raman and X-ray absorption spectroscopic measurements of related mutants (see SI Text). A correlation between the lower reorganization energies and the flexibility of the ligand loops was observed when we examined the B factors of the ligand containing loops (B_loop) connecting Asn42 to Asn47 and Phe110 to Lys122. These two loops contain all the interactions of the primary coordination sphere with the copper ion (SI Text and Table S5). When these B values were normalized relative to the total average B factor for the protein (B_TOT), to account for any variations that affect the entire protein, such as temperature or crystal-packing variations, we observed a higher B_loop/B_TOT ratio of 0.9 for all the mutants, whereas the ratio remained at ∼0.6 for both loops in WT Az (Fig. S5). The analysis indicates that the relative conformational freedom has increased, or the rigidity has decreased, particularly around the copper binding site (SI Text and Table S5) (25).

A detailed theoretical analysis of the effect of structural flexibility (or stiffness) demonstrates that the reorganization free energy will increase with decreasing flexibility of the protein (32, 33). The reorganization free energy is proportional to the sum of terms in the form of k·(Δd)², where k is the force constant and Δd is the change in the associated bond length upon reduction (24). However, these two parameters are not independent of each other because, following the formalism of Marcus, enhanced flexibility is associated with a decrease in the force constant k. However, increased flexibility also may result in a higher Δd, so the final value for reorganization energy is a question of what the flexibility does to the composite expression k·(Δd)². An extreme example in which Δd was altered in Az was demonstrated previously in studies of intramolecular ET from the disulfide radical-ion to Cu(II) in a type 2Cu Az mutant, Cys112Asp. Here the copper site undergoes ligand loss and an ∼0.2-Å expansion in its inner coordination sphere upon reduction from Cu(II) to Cu(I) (34). From analysis of the ET kinetics, a reorganization energy of 2.1–2.3 eV was calculated. This relatively high λ is consistent with values for Cu(II)/(I) reorganization energies in unconstrained complexes; for example, λ for the Cu(II)/(I) (1,10-phenanthroline)₂ complex is 2.4 eV (35), and λ for unfolded WT Az is approximately the same (36). In contrast, intramolecular ET in the type 0 Cu Az mutant, Cys112Asp/Met121Leu, with a structurally more constrained copper site, is characterized by a much smaller reorganization energy (0.9–1.1 eV). A lower λ for Cys112Asp/Met121Leu is accompanied by a smaller ΔH^‡ (34). One possible explanation of the different ET rates is structural perturbation of the Cu–ligand interactions and thus in ET pathways of the different Az mutants. The observed 3D structures (25) and EXAFS data (SI Text) show minimal perturbation of the Cu–ligand distances or angles in the mutants compared with WT Az, which rule out this possibility as the main contributing factor in the variants studied here.

Another important parameter determining ET rates is the exponential decay constant, β (see Eq. 2), which also is included in the expression for the activation entropy, ΔS^‡ (23). Thus, the rate constant of intramolecular ET in Cys112Asp Az is twice that of the type 0 Cu Az mutant despite the higher reorganization free energy. A larger β for Cys112Asp/Met121Leu ET also is consistent with the highly unfavorable activation entropy relative to that for Cys112Asp (SI Text, Table S1, and ref. 34). Differences in β and thus ET rates and activation entropies in Az might occur even when a common pathway operates because of subtle differences in electronic coupling between the copper and the ligands, particularly if slight differences in the covalency of the Cu²⁺−S(Cys) bond exist. As shown in Table S2 and associated analyses in SI Text, the electronic coupling between electron donor and acceptor does not change significantly as a result of the mutations and therefore are unlikely to cause the observed decrease in rate constants at the highest driving force as illustrated in Fig. 2. However, small changes in the electronic coupling might be responsible for the scatter of the data in Fig. 2 (in addition to experimental errors). If the deviation between the experimental rate constants and the theoretical curve is entirely attributed to variation in β, then an average value = 10.0 ± 0.2 nm⁻¹ is calculated.

It is interesting that all the reactions studied here exhibit rather small activation free energies (ΔG* ∼0–0.04 eV; see Table S4). Furthermore, the three mutants with the highest rate constants (Asn47Ser/Phe114Asn, Asn47Ser/Met121Leu, and Phe114Asn/Met121Leu) have ΔG* ∼0 eV, as expected from Eq. 1. Table S4 shows the reorganization free energies calculated from the individual activation parameters of the mutants using Eq. 2. The average value is λ_calc = 0.86 ± 0.09 eV, in agreement with the value derived from the fitting to the parabola in Fig. 2. Furthermore, previous investigations of WT Az indicated that distinct temperature-dependent changes in the macromolecule, such as thermal expansion, play a role in activation entropy differences (37).

As stated above, if increased flexibility within a protein corresponds to a smaller force constant k, the reorganization energy would decrease (32). Our experimental results demonstrate that the total reorganization free energy is clearly lower in the present mutants compared with the WT. Although the B factors of the mutants (SI Text and Table S5) also indicate that decreased stiffness is correlated with the lower reorganization free energy, further studies are required to identify the origin of the latter finding.

It also is noteworthy that the mutant Az with the highest driving force (Asn47Ser/Phe114Asn/Met121Leu, 1.05 eV) and the one with the lowest driving force (Phe114Pro/Met121Gln, 0.52 eV) both exhibit the lowest ET rate measured, within experimental error. The other Az mutants, with intermediate driving forces, all exhibit significantly faster rates. The plot of the ET rate vs. the driving force for these mutants fits the curve predicted by Eqs. 1 and 2 (Fig. 2). The results lead to the suggestion that the ET rates in the latter mutants, including Phe114Asn/Met121Leu and Asn47Ser/Phe114Asn/Met121Leu, may lie in the inverted region. However, more mutants with ET driving force above 1 eV are required before such a conclusion can be reached. These observations are of particular significance in view of the fact that they were obtained for ET proceeding within a polypeptide matrix with no additional, external, or internal reaction partners involved, having relatively limited and well-defined structural changes made in these proteins.

Evolution clearly has used many ways of lowering the reorganization energy in biological metal sites. Earlier we showed that insertion of the mixed valence [Cu(1.5)–Cu(1.5)] Cu_A electron uptake site of cytochrome c oxidase into Az lowers λ to 0.4 eV (30), i.e., to a value similar to that observed for the T1 Cu in the present study. Given the structural similarity between this Cu_A Az model and the mutants examined in this study, it is tempting to postulate that the latter mutations might be introduced into the Cu_A Az scaffold to lower the ET reorganization energy further. In fact, a recent publication showed that such mutations have been introduced in Cu_A Az, and a similar but less dramatic impact on the redox potential was seen (38). Nevertheless, it is unclear whether these mutations also would lower the reorganization energy of the Cu_A site because of the distinct characteristics of the binuclear site.

The results presented here demonstrate that the reorganization free energies of intramolecular ET within the mutated azurins are indeed lower than that of WT Az, causing an increase in rate constants by almost one order of magnitude. The changes in the reorganization energies are correlated with the increased flexibility of the copper sites, suggesting a general strategy for producing mutants with lower reorganization energies than native proteins, yielding proteins that need not be derivatized for ET studies.

Methods

Protein Construction; Electrochemistry.

Protein mutants were constructed, expressed, and purified and their redox potentials were measured as previously reported (25). Briefly, mutations in the Az gene in the periplasmic expression vector pET-9a were generated via QuikChange PCR (Stratagene) and verified by sequencing the DNA at the Core DNA sequencing facility (Urbana, IL). Variants were expressed at 37 °C in liquid culture with an isopropyl β-D-1-thiogalactopyranoside (IPTG) promoter and extracted from the periplasmic space by a previously reported osmotic shock procedure. Crude protein-containing solutions were purified by chromatography on SP Sepharose resin (GE Healthcare), and the identity of the protein again was verified by electrospray ionization mass spectrometry (ESI-MS). Cu(II) then was added to the apoprotein by slowly adding aqueous CuSO₄ and monitoring the increase of the visible absorbance (600–635 nm) until there was no further increase upon Cu(II) addition. Holoprotein was separated from apoprotein and other contaminants by passing the reconstituted sample over Q Sepharose resin. Redox potentials then were determined by cyclic voltammetry with protein film voltammetry on an edge graphite electrode along with a platinum auxiliary electrode and an Ag/AgCl reference electrode. Data were collected in sodium phosphate buffer (pH 7.0) to resemble the conditions used in pulse radiolysis experiments and were found to agree with those published earlier within the experimental error (25).

Crystallography.

The crystal structures from which B factors were determined were reported previously (25, 39). We have made considerable efforts to obtain 3D structures of Asn47Ser/Phe114Asn/Met121Leu and Phe114Asn/Met121Leu Az and so far have not been successful in obtaining diffraction-quality crystals.

Kinetic Measurements.

Pulse radiolysis experiments were carried out using the Varian V-7715 linear accelerator at the Hebrew University of Jerusalem. Five megaelectronvolts accelerated electrons at pulse lengths in the range of 0.4–1.0 μs. All optical measurements were carried out anaerobically under purified N₂O using three light passes, resulting in an overall optical path length of 3 cm. A 150-W xenon lamp produced the analyzing light beam, and to avoid photochemistry and light scattering, an optical filter with a cutoff at 385 nm was used. The data acquisition system consisted of a Tektronix 390 analog-to-digital converter connected to a personal computer. The temperature range used in the kinetic studies, 4–45 °C, was controlled by a thermostat and continuously monitored by a thermocouple attached to the cuvette. The protein concentration was varied between 75 and 200 μM. All reactions were performed under pseudo–first-order conditions, typically with a 10-fold excess of oxidized protein over reductant. The concentration of Cu(II) was monitored at 600–635 nm (ε₆₂₅ ∼5,000 M⁻¹⋅cm⁻¹), whereas formation and decay of the RSS*R⁻ radical were followed at 410 nm (ε₄₁₀ = 10,000 M⁻¹⋅cm⁻¹). Aqueous solutions, 0.1 M in sodium formate, 10 mM phosphate, were deaerated and saturated with N₂O by bubbling directly in the cuvette. The pH was kept constant at 7.0. Afterward, the concentrated protein stock solution was added, and N₂O bubbling was continued for another 5 min before pulsing the protein solution. Each individual kinetic measurement was repeated at least three times at each temperature. The process is biphasic: the first step is reduction by the CO₂⁻ radicals in bimolecular processes [either disulfide reduction (410 nm) or Cu(II) reduction (∼600 nm)] followed by intramolecular ET, which is the process of interest (compare reaction scheme with Figs. S1 and S2). Therefore, all the results were analyzed by fitting to a sum of exponentials using a nonlinear least squares program written in MATLAB (MathWorks).