Solid surface tension measured by a liquid drop under a solid film

Abstract

We show that a drop of liquid a few hundred microns in diameter placed under a solid, elastic, thin film (∼10 μm thick) causes it to bulge by tens of microns. The deformed shape is governed by equilibrium of tensions exerted by the various interfaces and the solid film, a form of Neumann’s triangle. Unlike Young’s equation, which specifies the contact angles at the junction of two fluids and a (rigid) solid, and is fundamentally underdetermined, both tensions in the solid film can be determined here if the liquid–vapor surface tension is known independently. Tensions in the solid film have a contribution from elastic stretch and a constant residual component. The residual component, extracted by extrapolation to films of vanishing thickness and supported by analysis of the elastic deformation, is interpreted as the solid–fluid surface tension, demonstrating that compliant thin-film structures can be used to measure solid surface tensions.

When two immiscible liquids are brought into contact in air, at the point where the liquid–liquid and two liquid–vapor interfaces meet, the angles between these interfaces are governed by equilibrium of the three surface tensions. The geometric construction representing equilibrium of three surface tensions is known as Neumann’s triangle (1). If one of the surface tensions is measured independently, Neumann’s triangle can be used to obtain the other two. By contrast, for a liquid droplet resting on a rigid solid substrate, there is typically only one condition that relates two surface energies and the liquid–vapor surface tension, the well-known Young’s equation (1–3). For most solids, the component of the liquid surface tension normal to the surface causes negligible deformation and is ignored. Although the liquid–vapor surface tension is straightforward to measure separately, it still leaves Young’s equation as a single relationship with two unknown quantities.

That liquid surface tension can cause significant deformation in a compliant elastic solid has been known for some time (1, 4–6 and reviewed in ref. 7). Lester (8) and Rusanov (9) first solved the problem for deformation due to the normal component of the surface tension. Recently, Style et al. (10) showed that within a region governed by the elastocapillary length, γ/E, where E is Young’s modulus and γ is surface tension, a ridge forms with a local shape governed by Neumann’s triangle for the two fluids and solid, allowing determination of the solid–fluid surface tensions. The height of the ridge is approximately the elastocapillary length (11); for an elastomeric material with a modulus of a few kilopascals, this is a few microns. Therefore, depending on the measurement resolution, deformation due to the normal component of surface tension can be easily measured only for sufficiently compliant materials, with a modulus in the tens of kilopascals or lower, using optical measurement techniques.

However, the characteristic length scale for the deformation of a solid due to surface tension, γ/E, can be amplified dramatically by proper choice of geometry (5, 12), for example, by using cantilevers (13) or films (12). In this work, we show that liquid drops placed under a compliant film with a modulus of several megapascals induce deflections of the solid film in the tens of microns, which is observable by the naked eye. The combination of the liquid, solid film, and ambient air form a Neumann’s triangle, with the film playing the role of an interface between the fluids. [An early experiment involving liquid drops on a compliant graphite sheet was performed by Metois (14).] This allows direct determination of the tensions, which can be decomposed further into contributions from stretch and surface tension.

Although surface stress in stiff solids has long been a subject of theoretical and experimental investigation (13, 15–17), it has always been difficult to measure (1, 18), primarily because γ/E is typically a very small quantity. For compliant materials, this elastocapillary length can be many microns; thus, its effects are more significant and easily measured. Examples include the foregoing one on contact line deformation (6, 10, 19), mechanical instabilities in a gel (20), adhesion instabilities (21, 22), limitation on shape replication by compliant materials (23), flattening of a surface due to surface tension (12), effect on surface creasing (24), influence on cavitation rheology (25), and deformation of a compliant cylinder immersed in a liquid (26). By using a thin-film geometry, we circumvent the existing limitations in surface tension measurements and present a method for measuring the surface tension in relatively stiff solids.

Results and Discussion

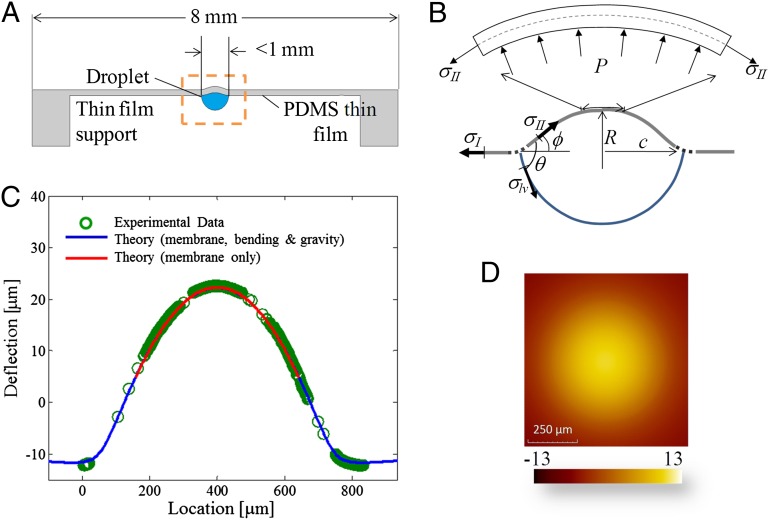
To study quantitatively the liquid surface tension-induced deformation on a thin solid film, we used simple geometry consisting of polydimethylsiloxane (PDMS) thin films ranging from 9 to 40 μm in thickness (t) suspended on PDMS substrates with holes typically 8 mm in diameter (Fig. 1A). We placed a droplet on the underside of the thin film and measured the surface profile of the top surface of the film via optical profilometry. The forces on the thin film are the droplet’s surface tension and Laplace pressure, as depicted in Fig. 1A, as well as gravity. We find that these forces cause significant film deformation (Fig. 1 C and D). In all previous studies of deformation due to a liquid drop (7), the deformation is cusp-like in the direction of the droplet’s line surface tension force. However, for our suspended thin-film geometry, deformation is mainly in the opposite direction, that is, in the direction of the Laplace pressure P (Fig. 1B). (The action of gravity causes overall deflection opposite to the Laplace pressure; however, our drops are sufficiently small that this deflection only shifts the datum for deflection, but not the shape of the deformed film, as shown below.)

Fig. 1.

Extraction of tension by measurement of deformation due to a drop placed under a solid film. (A) Schematic of experimental setup for surface tension experiments. The droplet is placed on the underside of a circular thin film that is 8 mm in diameter, with thickness in the range of 9–40 μm. (B) Schematic drawing shows the balance of forces near the axis of symmetry and at the triple line. Laplace pressure is denoted by P. Note that deformation is mainly in the direction of P, whereas all previous measurements of deformation due to a drop show the formation of a cusp in the direction of surface tension, opposed to P. θ is the internal angle between the film surface and the liquid drop, and ϕ is the angle of the deflected shape. (C) Comparison of measured and theoretical surface profiles. There is virtually no difference in the calculated shape of the deformed membrane near the axis of symmetry with or without bending and gravity, consistent with the assumption that the membrane essentially supports only in-plane tension. (D) Profile of the top surface of an 11.0-μm thick membrane with a drop on the underside showing a bulge of tens of microns.

Fig. 1C shows the surface profile for a drop of deionized water (DI) under an 11.0-μm thick PDMS film. Observe that the film bulges to a height of about 30 μm for an ∼350-μm radius drop. Although the PDMS used in this work is three orders of magnitude stiffer than the silicone gel used by Style et al. (10), the flexibility of the film results in deformation one order of magnitude greater than they reported. Fig. 1A shows schematically the nature of the deformed shape, along with the liquid drop; this is reminiscent of Neumann’s construction (Fig. 1B) but with a solid elastic film playing the role of two of the interfaces. Assuming that the solid elastic film supports tensions 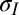just outside the droplet and 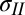inside it, equilibrium of tensions (in newtons per meter) in the radial and axial directions at the contact line requires

where θ is the internal angle between the solid film and the droplet surface at the contact line (it is also is the wetting angle that the liquid makes on a flat PDMS substrate) and 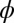is the angle of thin-film deflection at the contact line (Fig. 1B). Here, 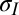and 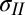are the total tensions in the film just outside and inside the contact line (in newtons per meter). As argued later, the value of tension has contributions due to stretch of the film and the sum of the solid surface tensions at the two film surfaces. In the limit of vanishing film thickness, the values of tensions approach the sum of the surface tensions of the two film surfaces. If the liquid–vapor surface tension 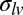is measured independently, Eqs. 1 and 2 can be used to obtain tensions 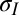and .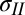

Eqs. 1 and 2 are based on the assumption that the film behaves like a membrane, supporting mainly in-plane tension. Because the elastic film has finite thickness and the drop has finite weight, a natural question arises about the influence of bending and gravity. To investigate this, we have analyzed the case where bending, in-plane tension, and gravity are all present [details are provided in SI Text, and previous related analyses are provided by Fortes (27) and Kern and Müller (28)]. The blue line in Fig. 1C shows excellent agreement between the theoretical prediction and experimental measurement of deformed shape for a film of thickness 11 μm. The tension, 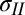, was estimated independently as described below. Other parameters were measured or are known independently. The red line, overlaid on the same plot, is the theoretical prediction (within a vertical offset) for the case where bending and gravity are neglected. Note that the shape of the membrane near its axis of symmetry is captured very well by either theoretical model (i.e., we may conclude that the membrane does mainly support tension and that its radius of curvature at the axis of symmetry is insensitive to bending and gravity).

More quantitatively, we have established theoretically (SI Text) that agreement between prediction based on membrane theory and measured shape is expected, except in a small boundary layer near r = c, the position of the contact line, if the parameter 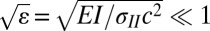, where E is the Young’s modulus, I is the area moment of inertia, and c is the radius of the contact line. We retained data only for cases where, a posteriori, 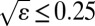. For example, the tensions were lowest in value when we conducted experiments with Dimethyl Sulfoxide (DMSO). In this case, for film thicknesses of 9, 25, and 40 μm, 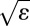takes the values 0.07, 0.25, and 0.42, respectively, for a drop with a radius of 0.5 mm. For this reason, we discarded all the data for 40-μm thick films.

Thus, we can neglect the influence of bending and gravity on the film shape near the axis of symmetry, where the film supports mainly biaxial tension. (We also independently confirmed, by direct computation based on measured deflection, that shear forces in the film are small compared with measured tension; SI Text). Let R be the radius of curvature at the axis of symmetry. Using the geometric relation 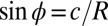, Eq. 2 is rewritten as

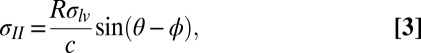in terms of measurable parameters. We obtain R by fitting a sphere to a small region near the center of deformation for various values of c (SI Text). The angle θ is measured independently via contact angle experiments on a flat PDMS slab, whereas the angle ϕ is measured by averaging angles from line scans of the vertical deflection at the contact line. Based on known values of the liquid surface tension of the liquids used in this work (29), Eq. 3 provides the tension in the region where the solid film is in contact with the liquid drop, 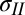. The radial equilibrium (Eq. 1) then gives us the tension in the film just outside the contact line, .

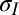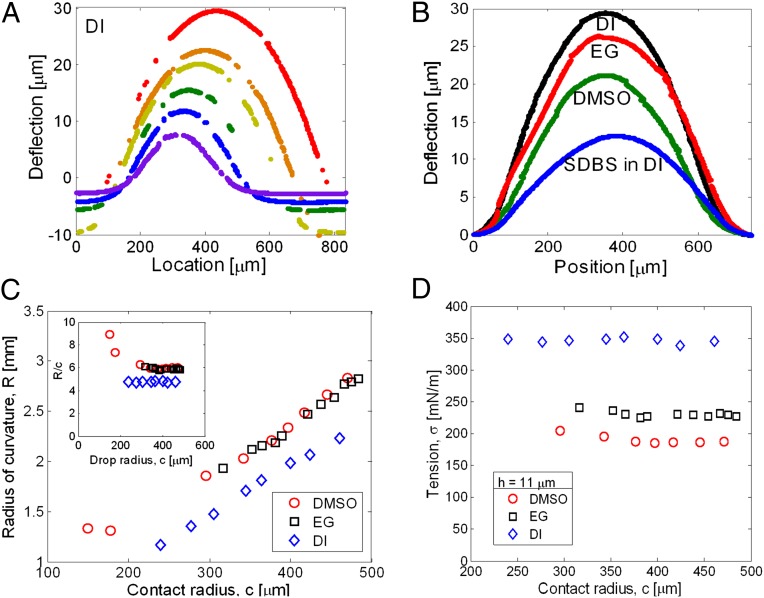
Fig. 2A shows the time evolution during evaporation of the deformed shape of the bulge for DI on an 11-μm thin film. The effects of gravity and bending result in vertical offsets that affect neither the measurement of the radius of curvature nor the angles used to calculate tension by Eq. 3 (SI Text). Fig. 2B shows, for a given drop size, that the deformed shape depends strongly on the type of liquid (in this case, the vertical offsets were removed to provide a common baseline for comparison). In our experiments, we use DI, ethylene glycol (EG), and Dimethyl Sufoxide (DMSO). These liquids were chosen because they are the least capable of absorbing into PDMS, essentially eliminating deformations due to swelling of the elastomer (30). In addition, we performed experiments with drying drops of these liquids on a flat PDMS slab and observed no measurable deformation in regions previously exposed to the liquid (at a resolution of ∼2 nm), supporting the conclusion that swelling was negligible.

Fig. 2.

Extraction of tension in the film from its measured deformation. (A) Time evolution during drying of the deformed shape of the bulge for DI. The deflection data have an arbitrary vertical offset that does not affect the measurement of the radius of curvature or the angles. (B) Bulge shape for different liquids on the same PDMS film and approximately the same drop radius (the deflection data have been shifted to a common datum of zero). SDBS, Sodium Dodecylbenzenesulfonate. (C) As the drop dries, its radius, c, reduces; the radius of curvature of the bulged film reduces in proportion. (Inset) Consistent with Eq. 3, the ratio R/c remains constant until the edge of the drop starts to pin. (D) Estimated value of tension in the solid film, 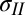, remains approximately constant as the drop dries, consistent with Eqs. 1–3.

Fig. 2C shows the radius of curvature, R, as a function of the position of the contact line, c, for the three liquids on an 11-μm thick film. Fig. 2C (Inset) shows the ratio of R/c as a function of c. We observe that the radius of curvature decreases linearly as a function of droplet contact radius and that the ratio is approximately a constant. Indeed, Eq. 3 implies that R/c is a material constant as long as 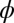is determined by Eq. 2, which assumes that the film outside the contact zone is flat. This would not be the case if bending were significant, and it further supports the assumption that the membrane supports mainly in-plane tension. In our experiments, we find that R/c is no longer constant either when the film is so thick that bending matters (SI Text) or when the contact line pins permanently and the contact angle decreases as the liquid evaporates away completely. Data in either case are discarded. Fig. 2D shows the measured tension 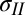as a function of contact radius for a film 11-μm thick during the phase when the contact line retracts freely. The finding that measured tension is approximately independent of the contact radius again supports the assumption that the film deforms as a membrane (i.e., it mainly supports only tension). (For a sufficiently thick film, where bending is expected to be important, Fig. S4 shows that the extracted tension is no longer independent of drop radius.) For a given film thickness and liquid, we performed three droplet experiments on three separate samples. The reported tension value is the average of the tension over three-drop radii from the three experiments. The tension in the solid film depends distinctly on the fluid used and is ranked according to the liquid–vapor surface tensions (78.3, 46.5, and 43.2 mN/m for DI, EG, and DMSO, respectively; ref. 29).

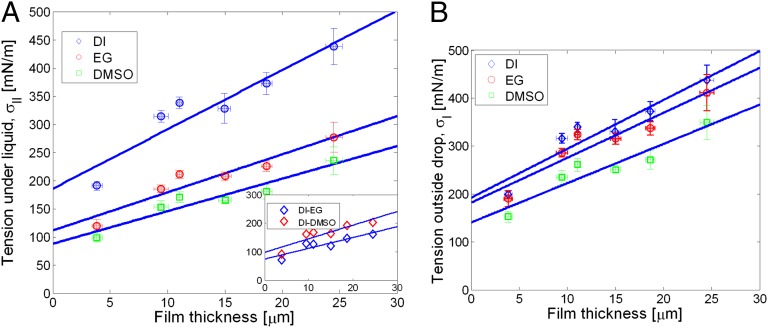
The experiments and their analysis discussed so far allow us to compute the tensions in the parts of the film inside and outside the liquid droplet. These tensions can arise due to the surface tension of the fluid–solid interfaces, stretching of the elastic film, and, potentially, bulk residual stresses. To separate out the contribution of tension due to stretching, we measured tension (newtons per meter) as a function of film thickness for three different liquids: DI, EG, and DMSO. Fig. 3A plots tension in the region of the film exposed to the liquid, and Fig. 3B plots tension in the region immediately outside the drop. We find that the measured tensions increase significantly with film thickness, presumably due to increasing contributions from film stretching. Extrapolation by straight-line fits to zero thickness yields values that we interpret as the surface tension. The values we obtain are shown in Tables 1–3. (In SI Text, we outline a model confirming that, in the limit of small film thickness, the contribution to tension due to stretch vanishes, supporting the interpretation of the intercept as the surface tension.)

Fig. 3.

Extrapolation of film tension to zero thickness yields surface tension. (A) Film tension in the region in contact with liquid as a function of film thickness. We find that all three cases exhibit a nonzero intercept, which we interpret as the surface tension. (Inset) There is a systematic difference on the same sample depending on the type of liquid in contact with the film. The data plotted here therefore represent the difference in film tension simply due to a change of the liquid in contact with the solid. (B) Film tension in the region immediately outside the contact line as a function of film thickness.

Table 1.

Tension in the film in the limit of zero thickness, interpreted as surface tension

Liquid	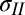, mN/m [tension inside the drop (intercept + 90% confidence interval)]
DI	185.3 (124.0, 246.6)
DMSO	87.3 (57.2, 118.2)
PEG	111.3 (76.4, 146.3)

Table 3.

Tension in the film just outside the drop extrapolated to zero thickness, interpreted as surface tension

Liquid	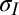, mN/m [tension outside the drop (intercept + 90% confidence interval)]
DI	192.1 (133.7, 250.5)
DMSO	140.3 (92.5, 188.1)
PEG	181.6 (127.0, 236.2)

Table 2.

Difference in tension in the film inside the drop extrapolated to zero thickness, interpreted as the difference in surface tension

Liquid	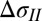, mN/m (intercept + 90% confidence interval)
DI-PEG	74.0 (43.1, 104.9)
DI-DMSO	97.6 (59.2, 135.9)

Intercept values for absolute tension and for the difference in tension between DI and EG or DMSO both show a significant dependence of tension inside the contact on the liquid used. These two observations support the notion that intercepts can be interpreted as surface tensions (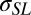 for the solid/liquid interface and 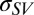for the solid/vapor interface, respectively). Fig. 3A (Inset) shows the difference in tension values inside the contact radius between experiments performed with DI and those performed with EG and DMSO. That there is a systematic difference in the intercept tension for the same sample (PDMS film), depending on the liquid, rules out the possibility of bulk residual stress playing an important role and further supports the assertion that we are measuring surface tension.

The intercept values should be compared with approximately the sum of the surface energy of the PDMS surfaces on two sides of the film. This sum should equal about 80–100 mJ/m² for the case where one side of the membrane is exposed to DI and the other to air. Of course, there is no necessity for surface tension and energy to hold the same value, but one might expect their magnitude to be similar. With significant confidence, we can accept the hypothesis that intercept values represent nonzero solid–fluid surface tensions. With similar confidence, we can conclude that replacing DI by EG or DMSO causes a significant change in surface tension. We note that unlike previous experiments with drops on thin films (31) that showed hoop buckling, we observe no such phenomenon. We ascribe this difference to the strong influence of the surface tension and the geometry of our setup, which keeps hoop stresses tensile.

The argument and method presented so far represent a direct, model-independent measurement of tension that relies only on force balance. Once it has been established that thickness is sufficiently thin, one ought to be able to dispense with the need for measuring films of different thickness. However, if one wishes to improve on the accuracy of the method, it may be possible to estimate the contribution to film tension due to film stretching in terms of measured parameters. As outlined in SI Text, this contribution is on the order of .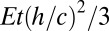

Conclusion

We studied liquid surface tension-induced deformation of films with a thickness of several micrometers spanning relatively large cylindrical holes. The interplay of liquid–vapor surface tension and tensions in the solid film results in a bulged membrane. Its equilibrium shape can be analyzed by force balance, a version of Neumann’s triangle, providing a method for estimating the film tension by measurement of bulge deformation. In the limit of vanishing membrane thickness, film tension may be interpreted as solid–fluid surface tension. The use of a compliant geometry provides several advantages. Because deflections are quite significant, it permits the use of PDMS, which is a relatively stiff material in this area of research but one that provides many conveniences. The geometry is straightforward to fabricate, and the experiment is easy to implement. By using this technique, one can measure the surface tension of thin films in contact with both liquid and air. Furthermore, this simple technique can potentially be used for measurements on a greater variety of materials by using an elastomeric thin film as a support substrate for stiffer and thinner (e.g., a few nanometers thick) materials.

Methods

Suspended Circular Thin Film.

A Plexiglas mold was used to create polydimethylsiloxane (PDMS) substrates a few millimeters thick with holes that were 8 mm in diameter. A PDMS (Sylgard 184) liquid thin film was spun onto a polystyrene-coated silicon wafer. The substrate was placed onto the thin film, and, together, they were cured at 80 °C for 2 h. To obtain various film thicknesses, we spin-coated the thin film at speeds in the range 2,000 to 500 rpm to obtain thicknesses in the range of 9–40 μm.

Displacement Measurements and Analyses.

Drops were placed below the film. Deformation was monitored from above using a white-light interferometer (Zegage; Zygo Corporation) with a resolution of about 2 nm. Data were extracted and analyzed using codes written in MATLAB (MathWorks).

Contact Angle Measurement.

Receding contact angles were measured on flat PDMS substrates by dispensing and withdrawing liquid using a syringe while monitoring the drop profile through a video camera. Images were subsequently analyzed to measure contact angle.