Global probabilistic annotation of metabolic networks enables enzyme discovery

Abstract

Annotation of organism-specific metabolic networks is one of the main challenges of systems biology. Importantly, due to inherent uncertainty of computational annotations, predictions of biochemical function need to be treated probabilistically. We present a global probabilistic approach to annotate genome-scale metabolic networks that integrates sequence homology and context-based correlations under a single principled framework. The developed method for Global Biochemical reconstruction Using Sampling (GLOBUS) not only provides annotation probabilities for each functional assignment, but also suggests likely alternative functions. GLOBUS is based on statistical Gibbs sampling of probable metabolic annotations and is able to make accurate functional assignments even in cases of remote sequence identity to known enzymes. We apply GLOBUS to genomes of Bacillus subtilis and Staphylococcus aureus, and validate the method predictions by experimentally demonstrating the 6-phosphogluconolactonase activity of ykgB and the role of the sps pathway for rhamnose biosynthesis in B. subtilis.

Introduction

Advances in DNA sequencing technologies and high-throughput experiments provide a unique opportunity to study cellular function at the systems level. The systems biology perspective seeks to understand how the interaction between multiple genomic components determines cellular physiology. Genome-scale metabolic networks serve as an important platform for such systems analyses and have been very successful in predicting various emergent properties of biological systems. They also have great potential for guiding metabolic engineering¹ and aiding drug target discovery². Unfortunately, accurate manual annotations of organism-specific metabolic networks are laborious and can take up to a year for a typical microbial genome. Efforts have been made to automate the reconstruction process, particularly the initial steps of genome annotation and network assembly^3-5.

The annotation process usually relies on sequence homology methods, in which the function of a metabolic gene is assigned based on sequence similarity to known enzymes⁶. Although homology methods have been successful overall, annotations established based solely on weak sequence identity are often unreliable due to frequent functional divergence between distant homologues. It was demonstrated that a sequence identity above 60% is usually required to accurately transfer a precise enzyme function, i.e. all four digits of an Enzyme Commission (EC) number⁷. Consequently, homology-based methods fail to assign functions to a substantial fraction of genes in completely sequenced genomes and have been known to produce multiple imprecise or incorrect annotations^8,9.

The metabolic network reconstruction for a given genome is usually performed based on a functional annotation of all metabolic genes. Functional databases such as BRENDA¹⁰, GeneCards¹¹, KEGG³, MetaCyc¹² or Swiss-Prot¹³ are useful resources for establishing initial associations between metabolic genes and corresponding biochemical reactions. Draft metabolic models are typically reconstructed by assembling annotated biochemical reactions into a network. One disadvantage of this two-step approach is that genes are annotated individually rather than being considered together in a proper network context. Therefore, some successful computational approaches utilize pre-defined or manually curated metabolic pathways⁵ and subsystems¹⁴ to annotate network reactions. Naturally, the accuracy of such methods depends both on the quality of the initial annotation and the evolutionary conservation of reference pathways.

Context based methods such as phylogenetic profiles¹⁵, protein fusions¹⁶, gene co-expression¹⁷, and chromosomal gene neighborhood¹⁸ capture conserved functional relationships and often provide information complementary to sequence homology¹⁹. The effectiveness of these methods has been shown by determining members of protein complexes, functional modules, and molecular pathways^20,21. Multiple studies have also demonstrated that context associations combined with local network structure can be used to identify genes responsible for orphan metabolic activities and to improve existing annotations of metabolic genes^22,23. Therefore, it is natural to combine sequence homology and context functional descriptors using a unified probabilistic framework.

Although powerful probabilistic approaches, such as Bayesian and Boolean networks, have been applied to reconstruction of regulatory and signaling networks based on high-throughput data²⁴, global probabilistic methods to annotate metabolic networks have not been developed. Here, we present such a global probabilistic approach that integrates sequence homology and context associations to annotate genome-scale metabolic networks. The method for Global Biochemical reconstruction Using Sampling (GLOBUS) not only provides annotation probabilities for each gene and each metabolic activity, but also suggests possible alternative functions. We applied GLOBUS to the genomes of Bacillus subtilis and Staphylococcus aureus, evaluated the accuracy of the reconstructed networks, and experimentally validated three B. subtilis predictions that have important functional consequences.

Results

Strategy of a global probabilistic reconstruction

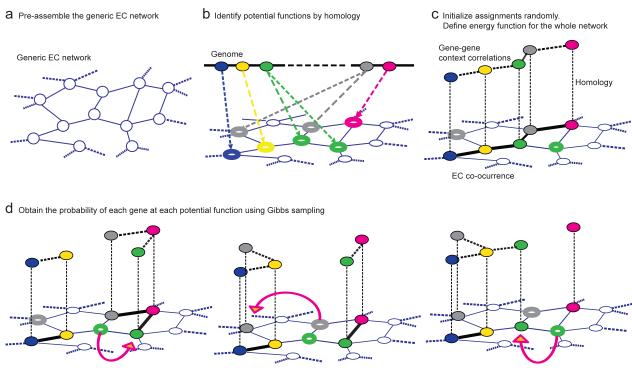
The conceptual outline of GLOBUS is shown in Figure 1. First, we built a generic metabolic network containing all possible metabolic activities characterized in the Enzyme Commission (EC) system (http://www.chem.qmul.ac.uk/iubmb/enzyme/). Nodes of this EC network represent known enzymatic activities (Fig. 1a), and network edges are established by metabolites shared between the activities either as substrates or products²⁵. The usage of the global EC network allowed us to consider gene function in a proper network context without predefining metabolic pathways. With the EC network as a scaffold, the global metabolic reconstruction for a given organism is equivalent to assigning metabolic genes to their correct network locations (Fig. 1b). In this way, organism-specific networks will occupy a subset of all possible locations (activities) in the global EC network.

Figure 1. Overview of the GLOBUS method.

(a) A generic Enzyme Commission (EC) network, where nodes represent all known biochemical activities and edges indicate metabolites shared between activities. (b) For a genome of interest, the potential network locations of each gene are assigned based on sequence homology to known enzymes. (c) Each gene is initially assigned randomly to one of its possible locations. A fitness function is defined such that assignments to locations with high sequence identity and good context correlations with neighboring genes correspond to higher values of the fitness function (higher probability). (d) Gibbs sampling is used to sample all possible assignments of genes to their candidate network locations. At each step of a Gibbs chain a random gene is selected and re-assigned to one of its possible locations (arrows). The marginal probabilities for assigning every gene to each candidate network location are derived from converged Gibbs chains.

A gene assigned to its correct network location usually has at least remote sequence identity to enzymes known to catalyze the corresponding activity. In addition, a correctly assigned gene often has good context correlations with its network neighbors. As we demonstrated previously, the genes with high mutual context correlations tend to be located closer in metabolic networks²². For example, we show that the higher a context correlation between a pair of S. cerevisiae genes, the more likely that the genes are direct network neighbors (Supplementary Results, Supplementary Figure 1).

In GLOBUS we used sequence homology and context correlations to evaluate a given global assignment of multiple metabolic genes into a set of network locations using a Markov-like fitness function. The contribution of each gene to the fitness function depends on the sequence identity to the assigned location and the context correlations with the genes assigned to neighboring network positions. The overall GLOBUS fitness function E(g₁, g₂, …., g_n) (see Methods), which is calculated based on a given assignment of metabolic genes (g₁, g₂, …., g_n), consists of the following terms:

$$E(g_1,g_2,\dots ,g_n)=-b_{\text{homology}}{f}_{\text{homology}}-b_{\text{orthology}}{f}_{\text{orthology}}-b_{\text{context}}{f}_{\text{context}}-b_{\text{ECco}-\text{occurrence s}}{f}_{\text{ECco}-\text{occurrence s}}$$ (1)

where f_s are various homology-based and context-based functional descriptors, and b_s are corresponding positive coefficients representing weights of each descriptor in the fitness function. For homology descriptors we used two separate terms: 1.) the highest sequence identity to a Swiss-Prot¹³ protein annotated to catalyze the corresponding activity in other species (annotations marked as based exclusively on computational methods were excluded), and 2.) a binary (0 or 1) descriptor indicating if a protein ortholog in another species is annotated to catalyze the activity. For context-based descriptors we used three types of gene-gene correlations: phylogenetic profiles (which quantify the co-occurrence of gene orthologs across species, see Methods), chromosomal gene clustering across sequenced genomes, and mRNA co-expression. For each context descriptor, we considered the maximum correlation Z-score (see Methods) between the gene under consideration and genes assigned to neighboring network locations. In addition, we also considered a context term describing the co-occurrence across sequenced genomes of various metabolic activities according to annotations available in the KEGG database.

Using the described fitness function, the global probability for a particular assignment of multiple genes into their network locations is given by P(g₁, g₂, …., g_n) based on the relationship used in statistical physics and Markov Random Fields (MRF)²⁶

$$P(g_1,g_2,\dots ,g_n)=\frac{1}{Z}\times e^{-E(g_1,g_2,\dots ,g_n)}$$ (2)

, where E(g₁, g₂, …., g_n) is the aforementioned fitness function, and Z is a normalizing partition function, which is necessary to insure that probabilities of all possible metabolic assignments sum to one. Using the defined probabilities we sampled from all possible assignments proportionally to their likelihood using Gibbs sampling²⁷. Gibbs sampling is a version of Markov Chain Monte Carlo (MCMC)²⁸ and has been successfully used in many computational biology applications, such as finding transcription factor binding sites in a set of DNA sequences²⁹. The efficiency of the Gibbs sampling in GLOBUS is due to the fact that although there is a combinatorially large number of possible metabolic assignments, the vast majority of them have very low probabilities. The Gibbs sampling allows to efficiently sample the most relevant global assignments according to their probabilities.

A step in a Gibbs chain was simulated by: 1.) selecting a random gene assigned to a particular network location, 2.) determining the probabilities for all possible locations of the selected gene, including the present location, and 3.) re-assigning the gene to a location according to the calculated probabilities (Fig. 1c,d). In the sampling we only considered the locations with at least remote sequence identity to the corresponding gene. In addition to possible locations in the network, a special out-of-the-network node was created, and in all Gibbs steps the move to the out-of-the-network node was also considered. The energy contribution to the fitness function for all genes located in the out-of-the-network node was the same. The energy in the out-of-the-network node is a parameter of the simulation (see below), it ensures that genes with little sequence identity or context correlation to any network location have a low probability of being assigned to an EC number. Importantly, we empirically established the absence of ergodicity problems in Gibbs sampling of microbial genomes. In other words, the annotation probabilities converged to essentially the same values for chains started from different random assignments; after about 20000 iterations the maximum probability difference across all genes was < 1%. Based on the convergent Gibbs chains we obtained the marginal probabilities for each metabolic assignment, consistent with the global fitness function.

Optimization of the fitness function parameters

The GLOBUS fitness function contains several important adjustable parameters b_s, that represent relative weights of several sequence and context correlations. The values of these parameters directly affect the sampling and the resulting gene annotation probabilities. To learn the parameters we applied a maximal likelihood approach using a well-annotated metabolic model of S. cerevisiae (iLL672³⁰). Specifically, following the approach commonly used in MRF²⁶, we optimized the fitness function parameters to maximally increase the product of the probabilities for correct gene assignments in the yeast network. Multiple simulated annealing³¹ runs were used to the search the parameter space for maximal likelihood values. Importantly, in searching for the parameters over-fitting was not an issue as many hundreds of known metabolic annotations (485 yeast genes with EC numbers in the iLL672 model) dominate the number of optimized parameters (7 parameters in total). As a result of the maximum likelihood optimization, the yeast genes in their correct network locations had a geometric mean probability of 0.617, and an overall prediction accuracy of 80.5%, i.e. the overlap with the iLL672 model when genes were assigned to their most probable locations. Using more recent metabolic models of S. cerevisiae (iMM904³²) or B. subtilis (iBsu1103³³) for optimization resulted in similar parameter values and similar GLOBUS probabilities (Supplementary Fig. 2). Thus, we used the parameters optimized with the iLL672 model for GLOBUS metabolic annotations in other species.

GLOBUS precision-recall performance

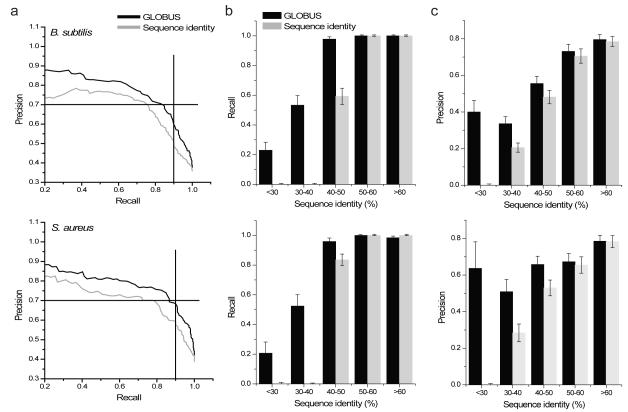
To understand the utility of GLOBUS for metabolic network annotations we applied it to the genomes of a gram-positive model bacterium, B. subtilis, and a medically important bacterium, S. aureus. The genomes of these bacteria contain 1244 (B. subtilis) and 854 (S. aureus) genes with at least remote sequence identity to known enzymes in other species. Several curated metabolic models are also available for these species: iYO844³⁴ and iBsu1103³³ for B. subtilis and iSB619³⁵ for S. aureus. The parameters optimized using the yeast model (see above) were used in Gibbs sampling of all possible metabolic assignments in the two bacteria. The GLOBUS annotation probabilities were generated and precision-recall curves calculated (Fig. 2a) based on comparison with the corresponding curated models. For comparison we also show in the figure the precision-recall curves calculated based only on sequence identity to enzymes in other species; similar results were obtained using either BLAST or PSI-BLAST³⁶ (Supplementary Fig. 3). The precision-recall calculations demonstrate that GLOBUS substantially outperforms homology in the areas of high recall and high precision.

Figure 2. GLOBUS precision-recall performance.

Using available metabolic models (iBsu1103³³ for B. subtilis and iSB619³⁵ for S. aureus) we compared predictions by GLOBUS to predictions made using sequence homology; predictions for B. subtilis are on the top, and predictions for S. aureus are on the bottom. (a) Precision–recall curves for GLOBUS (black lines) were calculated by ranking genes using assignment probabilities. Precision-recall curves for homology (red lines) were calculated by ranking genes using sequence identity. (b) Recall of known metabolic genes (at 70% precision) as a function of sequence identity to the closest enzymes from other species with the annotated functions. (c) Prediction precision (at 90% recall) for known metabolic genes as a function of sequence identity to the closest enzymes from other species with the annotated functions. In the figure error bars represent the S.E.M,

Further analysis (Fig. 2b,c) demonstrates that the main source of the superior GLOBUS performance lies in more accurate annotations of genes with low sequence identity to known enzymes. In Figure 2b we show the recall (at 70% precision) for gene annotations in B. subtilis and S. aureus as a function of sequence identity to known enzymes. GLOBUS recovers significantly more correct assignments compared to homology (10%, P < 4 × 10⁻⁴ for B. subtlis, and 14%, P < 5 × 10⁻⁵ for S. aureus, χ² test), especially for cases with less than 40% sequence identity. In Figure 2c we show that at the same level of recall (90%) GLOBUS achieves significantly higher precision (9% and 11% more, P < 8 × 10⁻⁵ and P < 5 × 10⁻³). The difference in precision is again highest for genes with low sequence identity to known enzymes, which constitutes a substantial fraction of all potential metabolic genes (Supplementary Fig. 4).

To investigate the contribution of individual context correlations to the GLOBUS performance, we optimized the coefficients of the fitness function without each context descriptor. We then compared the precision and recall values for predictions using all context correlations and predictions obtained without individual correlations (see Supplementary Fig. 5). This analysis showed that all correlations contribute to the method’s accuracy and that – similar to the complete fitness function - the effects of the individual context correlations are most apparent for cases with lower sequence identity.

We investigated the potential utility of GLOBUS for refining existing metabolic models by comparing two curated models of B. subtilis^33,34 (older iYO844, newer iBsu1103) and two models of S. cerevisiae^30,32 (older iLL672, newer iMM904). Specifically, we considered all annotations with non-zero GLOBUS probabilities that were not included in the older metabolic models. We then subdivided these non-zero GLOBUS annotations into those that were included in the newer models and those that were not included in the newer models for each species. This analysis showed (see Supplementary Fig. 6) that for both species, and across different sequence identity bins, higher GLOBUS probabilities corresponded to higher likelihoods of being included in the newer metabolic models.

Specific metabolic predictions and biochemical validation

GLOBUS results indicate that in many cases context correlations provide crucial functional evidence determining correct annotations, especially when sequence identity is small. One example is the B. subtilis gene hemD, known to be responsible for the uroporphyrinogen-III synthase activity³⁷ (EC 4.2.1.75). The sequence identity of hemD to the closest Swiss-Prot sequence performing its correct function is only ~24%; however, GLOBUS assigned a high probability (P=0.86) to the correct EC number because of the excellent context associations with its neighboring enzymes at this location: the gene clustering Z-score (defined as the number of standard deviations from the mean based on all gene-gene context scores, see Methods) is 21.2, the co-expression Z-score is 5.64. Context correlations are also helpful in selecting between potential functions with comparable sequence identity. For instance, the B. subtilis 8-amino-7-oxononanoate synthase bioF³⁸ has ~39% sequence identity to both its correct function (EC 2.3.1.47) and to glycine C-acetyltransferase (EC 2.3.1.29). GLOBUS selected the correct assignment (P=0.64 vs. 0.02) despite the equivalent sequence identity due to high clustering and co-expression Z-scores (16.6 and 4.3, respectively) in the correct location compared to the alternative location (1.1 and 2.4).

In Table 1 (B. subtilis) and Supplementary Table 1 (S. aureus) we list GLOBUS predictions without experimental validation that have high annotation probabilities despite low sequence identity to enzymes responsible for corresponding functions in other species. The annotations in the tables are ordered by averaging the prediction ranks sorted by decreasing annotation probability and the prediction ranks sorted by decreasing sequence identity distance to known enzymes. For each prediction in the table we also show the average Z-score for the three context correlations in the corresponding network location.

Table 1. Prediction of gene function in B. subtilis.

In the table we show predictions without experimental validation that have GLOBUS-assigned probabilities above 0.5 and protein sequence identity to known enzymes below 50%. The first three activities in the table were experimentally validated in this study. The remaining annotations in the table are ordered by averaging the prediction ranks sorted by decreasing annotation probability and the prediction ranks sorted by decreasing sequence identity distance to known enzymes. The last column shows the average Z-score of phylogenetic correlations, gene clustering and gene co-expression when all sequences are assigned to their most probable locations. The Z-score for each type of data was calculated using the maximum context correlation between a gene and its immediate network neighbors (see Methods).

Gene	EC number	Enzyme name	Probability	Identity (%)	Average Context Z-score
spsI	2.7.7.24	glucose-1-phosphate thymidylyltransferase	0.93	44.4	11.6
spsJ	4.2.1.46	dTDP-glucose-4,6-dehydratase	0.97	48	12.0
ykgB	3.1.1.31	6-phosphogluconolactonase	0.51	30.4	2.6
murF	6.3.2.10	UDP-N-acetylmuramoyl-tripeptide-D-alanyl-D-alanine ligase	0.98	32.8	9.0
spsL	5.1.3.13	dTDP-4-dehydrorhamnose-3,5-epimerase	0.95	33.1	8.4
ycgM	1.5.99.8	proline dehydrogenase	0.76	25.6	3.6
yfnG	4.2.1.45	CDP-glucose-4,6-dehydratase	0.76	27.5	11.0
birA	6.3.4.15	biotin-[acetyl-CoA-carboxylase] ligase	0.77	31.7	2.3
gcvPB	1.4.4.2	glycine dehydrogenase (decarboxylating)	0.97	41.5	12.3
yloI	4.1.1.36	phosphopantothenoylcysteine decarboxylase	0.99	44.5	2.6
fruK	2.7.1.56	1-phosphofructokinase	0.88	40.4	10.9
spsK	1.1.1.133	dTDP-4-dehydrorhamnose reductase	0.87	39.6	8.4
murB	1.1.1.158	UDP-N-acetylmuramate dehydrogenase	0.97	43	5.2
folK	2.7.6.3	2-amino-4-hydroxy-6-hydroxymethyldihydropteridine diphosphokinase	0.99	45.3	8.0
sul	2.5.1.15	dihydropteroate synthase	0.99	47	8.2
yitJ	2.1.1.13	methionine synthase	0.54	30.6	2.1
ybbF	2.7.1.69	protein-Npi-phosphohistidine-sugar phosphotransferase	0.85	40.5	11.3
yloI	6.3.2.5	phosphopantothenate-cysteine ligase	0.97	44.5	2.9
pheA	4.2.1.51	prephenate dehydratase	0.69	36.1	6.7
purK	4.1.1.21	phosphoribosylaminoimidazole carboxylase	0.89	43.5	13.3
ysnA	3.6.1.15	nucleoside-triphosphatase	0.56	33.3	7.7
ywbC	4.4.1.5	lactoylglutathione lyase	0.6	35.2	3.6
pucE	1.2.3.14	abscisic-aldehyde oxidase	0.62	35.8	1.0
ydhR	2.7.1.4	fructokinase	0.77	41.5	5.3
yfnH	2.7.7.33	glucose-1-phosphate cytidylyltransferase	0.88	43.2	11.0
ybbD	3.2.1.52	beta-N-acetylhexosaminidase	0.52	33.1	3.1
yngE	6.4.1.4	methylcrotonoyl-CoA carboxylase	0.64	36.2	8.6
kbl	2.3.1.29	glycine C-acetyltransferase	0.97	49	9.4
tenI	2.5.1.3	thiamine-phosphate diphosphorylase	0.7	40.6	6.6
pabB	4.1.3.27	anthranilate synthase	0.74	42.8	8.6

From the predictions listed in Table 1 we selected the genes spsI, spsJ, and ykgB for experimental validation. The first two genes were selected because they were predicted to catalyze the first two steps in a rhamnose biosynthesis pathway (Supplementary Fig. 7); the other two genes from the pathway (spsK and spsL, in Table 1) were also predicted by GLOBUS. Rhamnose is a main sugar component of the B. subtilis exosporium³⁹. The sps genes are transcribed from a σ^K-controlled promoter at late stages of B. subtilis sporulation when the outer components of the spore coat are being assembled⁴⁰. The gene ykgB was selected because GLOBUS predicted (with probability P=0.51) that this gene catalyzes the long elusive 6-phosphogluconolactonase activity of the B. subtilis pentose phosphate (PP) pathway. Despite a central role of PP pathway in the B. subtilis metabolism, this enzymatic activity remains without experimental validation in this important model organism.

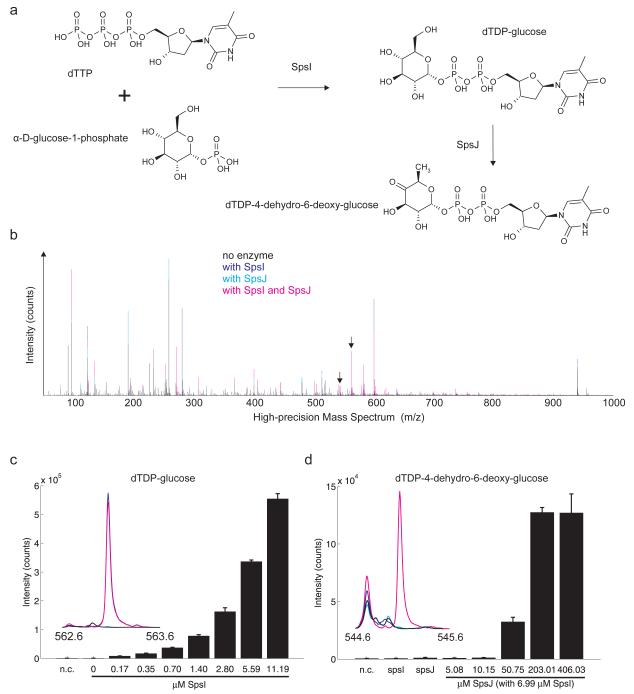
The three proteins selected for experimental validation were over-expressed in E. coli and purified by His-Tag affinity and anion exchange chromatography. The correct identity of the purified proteins was confirmed by in-gel tryptic digestion and subsequent peptide analysis using mass spectrometry (Supplementary Dataset 1). In vitro enzymatic assays for SpsI and SpsJ were performed using a published method⁴¹. Predicted SpsI substrates (dTTP and α-D-glucose-1-phosphate, Fig. 3a) were observed in negative ionization mode high-precision mass-spectra profiles at 259.022 m/z and 480.981 m/z (M-H⁺) respectively. Intensities of both dTTP and α-D-glucose-1-phosphate decreased only when SpsI was present in the assays, indicating that the enzyme uses these compounds as substrates (Supplementary Fig. 8). In addition, the predicted reaction product (dTDP-glucose) accumulated at 563.068 m/z (M-H⁺) only in the presence of SpsI (Fig. 3b,c). The product of SpsJ (dTDP-4-dehydro-6-deoxy-glucose) was observed at 545.058 m/z (M-H⁺) only in the presence of both SpsI and SpsJ (Fig. 3b,d), suggesting that SpsJ indeed converts dTDP-glucose into dTDP-4-dehydro-6-deoxy-glucose (Fig. 3a). Product accumulation, as well as substrate consumption, exhibited a clear dependence on the protein concentrations within a wide range around the estimated in vivo concentration of glucose-1-phosphate thymidylyltransferase (~1 μM for RfbA in Escherichia coli⁴²).

Figure 3. In vitro biochemical assays used to characterize activities of SpsI and SpsJ using high-precision mass spectrometry.

(a) Reaction diagram. (b) Mass spectrum plot showing intensities for masses corresponding to the products dTDP-glucose and dTDP-4-dehydro-6-deoxy-glucose of the reactions catalyzed by SpsI and SpsJ (black arrows, detailed in panel c). Observed masses deviated by less than 0.001 atomic mass units (amu) from the corresponding reference masses. Spectra were recorded from two independent assays. (c, d) Bar plots show dependency of dTDP-glucose and dTDP-4-dehydro-6-deoxy-glucose accumulation on protein concentration of SpsI and SpsJ, respectively. As negative control (n.c.), the protein free filtrate of 6.99 μM spsI or 203.01 μM SpsJ solution was used. Error bars represent standard deviations calculated using two independent assays.

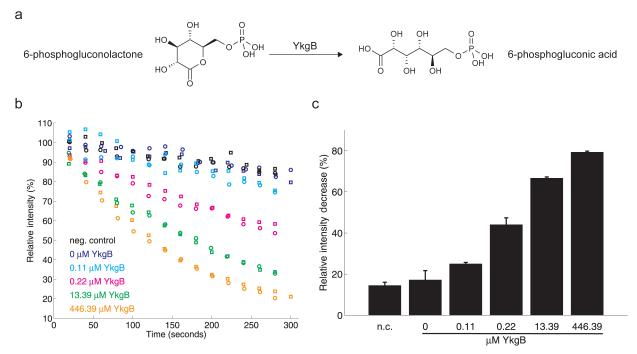
Similarly to SpsI/SpsJ, the YkgB activity (Fig. 4a) was followed by observing the 6-phospho-gluconolactone degradation with online flow injection into a high-precision mass-spectrometer operating in the negative ionization mode. The intensity at the mass of 257.007 m/z (M-H⁺), corresponding to 6-phospho-gluconolactone, decreased with rates faster than the rate of spontaneous background hydrolysis only when YkgB was present in the assays (Fig. 4b). The 6-phospho-gluconolactone degradation rate also exhibited a clear dependence on the protein concentration (Fig. 4c) within a wide range around the estimated in vivo 6-phosphogluconolactonase concentration (~1.5 μM for YbhE in Escherichia coli⁴²). Similarly, the production rate of 6-phosphogluconic acid was consistently higher than the background when YkgB was present in the assays (Supplementary Fig. 9). Interestingly, available expression and proteomic data show that the ykgB gene is transcribed during several environmental conditions^43,44, such as heat and phenol stress. This suggests that YkgB - similar to lactonases in other species⁴⁵ - is likely to play a role in removing toxic byproducts of the PP pathway.

Figure 4. In vitro biochemical assays used to characterize the 6-phospho-gluconolactonase activity of YkgB.

(a) Reaction diagram for 6-phospho-gluconolactonase. (b) Time courses of lactone degradation at different YkgB concentrations were recorded by direct flow injection analysis. Different symbols represent replicate assays. (c) Relative intensity increase from initial to final lactone intensities as a function of YkgB concentration. As negative control (n.c.), the protein-free filtrate of 223.2 μM YkgB solution was used. Error bars represent standard deviations calculated using two independent assays.

Discussion

Due to inherent uncertainty of computational annotations, predictions of biochemical function need to be treated probabilistically. Currently, most publicly available biochemical databases do not provide quantitative probabilities or confidence measures for existing annotations. This makes it hard for the users of these valuable resources to distinguish between confident assignments and mere guesses. As the application and impact of genome-scale metabolic networks rapidly expands¹, a probabilistic treatment of annotations is essential. The GLOBUS approach, which is based on statistical sampling of possible biochemical assignments, provides a principled framework for such global probabilistic annotations. The method assigns annotation probabilities to each gene, as well as suggests likely alternative functions.

We demonstrate that context correlations can significantly improve the accuracy of biochemical predictions, especially when annotations are based on distant sequence identity. Over half of potential metabolic genes, even in such well-studied model organisms as S. cerevisiae and B. subtilis, have remote sequence identity (<40%) to known enzymes (Supplementary Fig. 4). Application of GLOBUS to less-studied organisms should be straightforward, as context-based correlations, excluding gene co-expression, are calculated directly from genome sequences; the reduction in the overall accuracy due to the co-expression term is relatively small (<1%). The precision of other context correlations should only improve with the rapid growth of fully sequenced genomes.

Probabilistic predictions generated by GLOBUS can be directly used to annotate sequences and genomes. GLOBUS annotations can be also used by various gap identification and gap filling approaches^22,23,46,47 to produce simulation-ready flux balanced networks. In addition, recent advances in metabolomics, proteomics, and fluxomics offer complementary opportunities to expand and refine biochemical annotations and network reconstructions ⁴⁸. The flexibility of the GLOBUS framework makes it easy to integrate metabolomics and proteomics data. For example, as genes are moved through the network to sample possible assignments, available data for corresponding proteins and metabolites can be included in the global fitness function. Additional functional descriptors, for example based on protein structure and information about protein localization, can be also considered in the framework. Such probabilistic integration of diverse biochemical data will be crucial for exploiting the ongoing avalanche of genomic sequencing.

Methods

Construction of the generic EC network

In the construction of the EC (Enzyme Commission) network we considered 3284 EC numbers (http://www.chem.qmul.ac.uk/iubmb/enzyme/) responsible for biochemical activities involving small compounds as substrates and products; activities such as “RNA polymerase” or “protein kinase” were excluded. In the global EC network, nodes represent EC numbers connected by edges representing metabolites shared between reactions. Following a common procedure ²⁵, linkages through the top 40 most highly connected metabolites and cofactors were not considered (Supplementary Table 2).

Identification of potential metabolic genes and their functions

The program BLAST³⁶ (with E-value cutoff of 5*10⁻²) was used for homology searches against enzymes in Swiss-Prot¹³, excluding sequences that were: 1) from genomes of closely related species (species in the same taxonomic genus) or 2) likely annotated based exclusively on computational methods, i.e., annotations containing words probable, by similarity, hypothetical, like, or putative. Although many remaining annotations in Swiss-Prot are also derived using computational methods, they are usually curated, ensuring that the misannotation rate in this database is relatively low ^8,9.

To account for multi-functional enzymes, when non-overlapping regions of a query gene could be mapped to different enzymatic functions - indicating domains responsible for distinct metabolic activities - the mapped regions of the query gene were allowed to be assigned independently to different network locations.

The functional descriptors in the GLOBUS fitness function

Detailed description of the energy function and related calculations are given in Supplementary Methods. Denoting by n the total number of considered metabolic genes, the components of the fitness function used in GLOBUS are as follows:

Sequence homology. f_homology

As the sequence identity descriptor we used the logarithm of the conditional probability that the gene performs the assigned metabolic function, given the highest sequence identity to a Swiss-Prot ¹³ protein annotated to catalyze the corresponding activity:

$$f_{\text{homology}}=\sum _{i=1}^n\log P(\text{gene performs target function}\mid \text{highest sequence identity to annotated Swiss}-\text{Prot protein})$$ (3)

Orthology. f _orthology

An additional binary descriptor related to sequence homology was the likely gene orthology to a gene from another species annotated with the target activity. For each gene, the orthology term was either 1, if at least one possible ortholog was annotated in Swiss-Prot to perform the target activity, or 0, if no orthologs with the target activity could be identified.

Gene-gene context correlations. f _context

In GLOBUS we used the context correlations (phylogenetic profiles, chromosomal clustering, mRNA co-expression) by: 1.) transforming them into Z-scores⁴⁹ (number of standard deviations from the mean) using the distribution of correlations for all pairs of metabolic genes, and 2.) estimating the conditional probability that two genes are direct network neighbors, given their context association Z-score. The corresponding conditional probabilities were derived using the iLL672 yeast metabolic model (Supplementary Fig. 1a-c). In the GLOBUS fitness function, for each assigned gene we considered the maximum log probability among all network neighbors of the gene:

$$f_{\text{context}}=\sum _{i=1}^n\mathit{max}\left(\log P\right(\text{two genes are network neighbors}\mid \text{context correlation}\mathrm{Z}-\text{score between the genes}\left)\right)$$

EC co-occurrences. f_{ECco-ocurrence}

This descriptor measures the correlation between the occurrences of different metabolic activities (EC numbers) across sequenced species without considering specific genes assigned to the activities. In the GLOBUS fitness function for each assigned gene we considered the EC co-occurrence descriptor equal to the average correlation between the EC activity of the assigned gene and the EC activities for all its network neighbors. The EC co-occurrence term provides information additional to that available from direct sequence homology. The most relevant information about homology usually comes from annotated enzymes with the highest sequence identity to a protein under consideration. On the other hand, the EC co-occurrence reflects common presence and absence of metabolic activities across multiple KEGG genomes. Thus, this term quantifies tendencies of closely related activities to be filled together.

Experimental validation of biochemical predictions

Different amounts of purified SpsI or SpsJ were incubated at 37 °C in 1 mL of 10 mM potassium phosphate buffer pH 7.4, 2.5 mM MgCl₂, 1 mM glucose-1-phosphate (Sigma-Aldrich, >= 97% purity), 1 mM dTTP (Sigma-Aldrich, >= 96% purity) and 1 U pyrophosphatase⁴¹. The enzyme reaction samples were assayed after 4 hours by flow-injection into a time of flight mass spectrometer (6520 Series QTOF, Agilent Technologies) operated in the negative ionization mode. High-precision mass spectra were recorded from 50-1000 m/z and analyzed as described previously⁵⁰. Acquired masses were deviating less than 0.001 atomic mass units (amu) from the reference masses 259.022, 480.982, 545.058, and 563.068 for α-D-glucose-1-phosphate, dTTP, dTDP-glucose, and dTDP-4-dehydro-6-deoxy-glucose, respectively.

Purified YkgB was assayed in 1 mL 5 mM potassium phosphate buffer pH 7, 2.5 mM MgCl₂, and freshly prepared 6-phospho-gluconolactone. The lactone was prepared freshly from 6-phospho-gluconic acid (Sigma-Aldrich, >= 90% purity) by lyophilization, and its degradation due to the YkgB activity was followed by direct online flow-injection into a time of flight mass spectrometer as described above. Acquired masses were deviating less than 0.001 atomic mass units (amu) from the reference masses 257.007 and 275.017 for 6-phospho-gluconolactone and 6-phosphogluconic acid, respectively.

A detailed description of the cloning, purification and protein identification procedure is given in the Supplementary Methods.

Computational requirements and statistical analysis

The calculations were performed using the 3GHz Intel Xeon quad core processor with 256MB of RAM memory. GLOBUS run times depend both on the number of iterations and the number of genes considered for a given species. For the S. cerevisiae, S. aureus, and B. subtilis genomes, 10,000 iterations over all genes took about 10 minutes. The run time increased linearly with the number of iterations and number of genes. 20,000-50,000 iterations (20-50 minutes) were required to achieve 1% convergence of annotation probabilities, i.e. so that there were no gene assignments different in their annotation probabilities by more than 1% between different runs. Pre-computed GLOBUS predictions for 10 bacterial species of medical interest can be found at: http://vitkuplab.c2b2.columbia.edu/globus/index.html

P-values used to compare the precision-recall performances for GLOBUS and sequence identity were calculated using the one-tailed χ² test, N = 332 to 717 annotations.