A Semiparametric Approach to Dimension Reduction

Abstract

We provide a novel and completely different approach to dimension-reduction problems from the existing literature. We cast the dimension-reduction problem in a semiparametric estimation framework and derive estimating equations. Viewing this problem from the new angle allows us to derive a rich class of estimators, and obtain the classical dimension reduction techniques as special cases in this class. The semiparametric approach also reveals that in the inverse regression context while keeping the estimation structure intact, the common assumption of linearity and/or constant variance on the covariates can be removed at the cost of performing additional nonparametric regression. The semiparametric estimators without these common assumptions are illustrated through simulation studies and a real data example. This article has online supplementary material.

1. INTRODUCTION

Dimension reduction has been an active field of statistical research for the last 20 years and continues to be important due to the increasingly large amount of available covariates in various scientific areas. The goal of dimension reduction is to identify one or multiple directions represented by a matrix β, so that the response Y relates to the covariate vector x only through a few linear combinations x^Tβ. When the conditional distribution depends on x^Tβ, it is a problem of estimating the central space (Cook 1998); when the conditional mean E(Y | x) depends on x^Tβ, it is a problem of estimating the central mean space (Cook and Li 2002).

Started with the ingenious idea of sliced inverse regression (SIR) in the seminal article by Li (1991), many highly effective methods in the area of dimension reduction have been developed. For identifying the central space, see, for example, sliced average variance estimation (SAVE) (Cook and Weisberg 1991) and directional regression (DR) (Li and Wang 2007) and their variations such as kernel inverse regression (Zhu and Fang 1996), CANCOR analysis (Fung et al. 2002), and so on. These methods extend the inverse regression idea and are promising in recovering the central space. However, they all rely on certain conditions. These conditions mainly include the linearity condition, where E(x | x^Tβ) is assumed to be a linear function of x, and the constant variance condition, where cov(x | x^Tβ) is assumed to be a constant matrix. These conditions are not always satisfied, and sometimes could imply stringent assumptions on the joint distribution of x. To be precise, SIR requires the linearity condition; SAVE and DR require both the linearity condition and the constant variance condition. If the covariates do not satisfy these two conditions, current practice often relies on transformation (Box and Cox 1964) or reweighting (Cook and Nachtsheim 1994), which can restore these conditions sometimes. Li and Dong (2009) and Dong and Li (2010) successfully remove the linearity condition from the dimension-reduction problems while their estimators remain to be the inverse regression type. This is no doubt a great advancement. The residual issue is that they assumed E(x | x^Tβ) to be a polynomial function of x^Tβ and they still required the constant variance condition. These remaining requirements can still be stringent and difficult to check in practice. Zhu and Zeng (2006) introduced a dimension-reduction method to identify the central subspace through using Fourier transformations. Their method, however, requires one to estimate the joint probability density function (pdf) of x, which is typically infeasible in a high-dimensional environment. To circumvent this difficulty, they assumed x to be multivariate normal in implementations. Adapting the idea of minimum average variance estimation (MAVE) (Xia et al. 2002), Xia (2007) proposed a similar procedure (dMAVE) to recover the central space, and Wang and Xia (2008) proposed sliced regression (SR) for dimension reduction. However, their methods estimate the distribution function nonparametrically and heavily rely on the implicit assumption that all the covariates are continuous. Because all the existing dimension-reduction methods impose either the above two conditional moment conditions or distributional assumptions on the covariate vector in one form or another, new dimension-reduction methods which are free of any of these assumptions are highly in demand, particularly when some covariates are discrete or categorical.

Similarly, a large amount of literature exists for identifying the central mean space. For example, when the central mean space is one dimensional, Li and Duan (1989) suggested using the ordinary least squares (OLS), assuming x to satisfy the linearity condition. Härdle and Stoker (1989) and Power, Stock, and Stoker (1989) proposed the average derivative estimation, which requires x to be continuous. Horowitz and Härdle (1996) proposed a method that allows some covariates to be discrete; however, the number of levels in discrete variables cannot be large. Ichimura (1993) and Härdle, Hall, and Ichimura (1993) suggested using nonlinear least squares, which are essentially special cases of our proposal which will be described in the following. When the central mean space is possibly two or more dimensional, Xia et al. (2002) proposed the minimum average variance estimation method, which, similar to the constructive approach in Xia (2007) and the sliced regression in Wang and Xia (2008), requires x to be continuous. Li (1992) and Cook and Li (2002) proposed the method of principal Hessian directions which requires x to satisfy both the linearity condition and the constant variance condition, which are not always satisfied in practice. Assuming conditional normality of x on Y, Cook and Forzani (2009) proposed a likelihood-based method, and in the context of classification, Hernández and Velilla (2005) estimated the dimension reduction space via minimizing a criterion function which involves kernel density estimation. Yin and Cook (2005); Yin, Li, and Cook (2008); and Park, Sriram, and Yin (2010) proposed a method to recover the dimension-reduction space via minimizing a Kullback–Leibler distance.

In this article, we provide a completely different viewpoint for looking at the dimension-reduction problems. Our approach is through semiparametrics, which has not been considered in the literature. By casting the dimensional-reduction problem in the semiparametric framework, the dimension-reduction problems become semiparametric estimation problems. Therefore, powerful semiparametric estimation and inference tools become applicable. We use the geometric approach in Bickel et al. (1993) and Tsiatis (2006) to analyze these problems and derive the space of the influence functions. This enables us to construct a rich class of estimators. Many of the existing dimension-reduction methods turn out to be special cases in this class. In fact, the complete class of influence functions provide all the possible consistent estimators.

A direct consequence of the semiparametric analysis is the relaxation of the linearity condition and the constant variance condition. Using the semiparametric construction, we reveal that these conditions are not structurally necessary. Consequently, in all these existing dimension-reduction procedures, we can remove these two conditions, and instead replace the assumed quantity with nonparametric estimation of the corresponding conditional expectations. Thus, the semiparametric derivation allows us to obtain the dimension reduction spaces without any distributional assumption on the covariate vector. Another advantage of the semiparametric analysis is that we do not require all the covariates to be continuous.

In summary, the contributions of this article are:

1. We introduce a novel and drastically different approach to the dimension-reduction field. We anticipate to stimulate deeper and richer literature in this direction.

2. We derive the complete class of influence functions, which guarantees to yield all possible root-n consistent estimators for the column space of β. We demonstrate how to obtain several most popular dimension-reduction methods from this class. This further reveals the underlying connection between these different methods and provides a different and natural motivation for their construction.

3. We completely eliminate the linearity condition, the constant variance condition, the condition on the quadratic form of the covariates, or, in fact, any moment conditions on the covariates at all.

4. We eliminate the redundant continuity conditions on the covariates. The new approach can be readily used even when some covariates are categorical or discrete.

The outline of this article is the following. In Section 2, we describe the semiparametric approach to the central space estimation and derive a rich class of estimators. We establish their link and generalization to several existing dimension-reduction methods in Section 3. The analysis for central mean space estimation is given in Section 4. We explain the implementation details on estimation and on selecting the dimension of the central space/central mean space in Section 5. Extensive simulation studies are conducted in Section 6 to demonstrate the practical performance and the method is implemented in a real data example in Section 7. We finish the article with a brief discussion in Section 8. Technical derivations are collected in an appendix and the online supplementary document.

2. ESTIMATING THE CENTRAL SUBSPACE VIA SEMIPARAMETRICS

Let x be a p × 1 covariate vector and Y a univariate response variable. The goal of sufficient dimension reduction (Cook 1998) is to seek a matrix β such that

$$F(y|\text{x})=F(y|{\text{x}}^{\text{T}}\beta ),\text{for }y\in ℝ,$$ (1)

where $F(y|\text{x})\stackrel{\text{def}}{=}\text{Pr}(Y\le y|\text{x})$ denotes the conditional distribution function of Y given x. (1) implies that the response variable Y relates to x only through linear combinations x^Tβ. The column space of β satisfying (1) is called a dimension-reduction subspace. Because the dimension-reduction subspace is not unique, our primary interest is the central subspace, which is defined as the intersection of all dimension-reduction subspaces, provided that the intersection itself is a dimension-reduction subspace (Cook 1998).

Following the convention in the area of dimension reduction, we denote by S_Y|x the central subspace and assume β to satisfy β^Tcov(x)β = I_d. Note that β is more restrictive than before, however to avoid introducing a new notation, we keep the same notation. We also assume S_Y|x exists and is unique. Here, the number of columns in β, denoted by d, is the dimension of S_Y|x and is often referred to as the structural dimension. Our goal is to find S_Y|x through finding β ∈ ℝ^{p × d} which satisfies (1). To focus on the main issues of the dimension-reduction problems, we assume throughout our article that the covariate vector x satisfies E(x) = 0 and cov(x) = I_p. This assumption causes no loss of generality, thanks to an invariance property of the central subspace (Cook 1998, p. 106).

In model (1), the likelihood of one random observation (x, Y) is

$${\eta }_1(\text{x}){\eta }_2(Y,{\text{x}}^{\text{T}}\beta ),$$

where η₁ is a probability mass function (pmf) of x or a pdf of x, or a mixture, depending on whether x contains discrete variables, and η₂ is the conditional pmf/pdf of Y on x. Treating η₁, η₂ as infinite-dimensional nuisance parameters while β as the parameter of interest, this can be viewed as a semiparametric estimation problem. The essential idea in semiparametrics is to construct estimators through deriving influence functions. Influence functions can be viewed as normalized elements in a so called nuisance tangent space orthogonal complement Λ^⊥. Thus, if one can successfully derive Λ^⊥, one at least has the hope of characterizing the influence functions and constructing estimators. Because semiparametrics is not a familiar tool in the dimension-reduction community, we give a general and more precise explanation in Appendix 0. It is not a simple and straightforward tool to grasp and to master, and interested readers are encouraged to refer to Bickel et al. (1993) and Tsiatis (2006) for in-depth understanding. In model (1), using the semiparametric analysis, we characterize the space of the span of all possible score functions, had η₁, η₂ been replaced by all possible parametric submodels, to find the nuisance tangent space. We then derive its orthogonal complement to obtain

$$\begin{array}{c}{\Lambda }^{\perp }=\{\text{f}(Y,\text{x})-E\{\text{f}(Y,\text{x})|{\text{x}}^{\text{T}}\beta ,Y\}:E\{\text{f}(Y,\text{x})|\text{x}\}\\ =E\{\text{f}(Y,\text{x})|{\text{x}}^{\text{T}}\beta \},\forall \text{f}(Y,\text{x})\}\end{array}$$

See the detailed derivation in Appendix 1. The form of Λ^⊥ permits many possibilities for constructing consistent estimating equations. For example, for any functions g(Y, x^Tβ) and α(x), we can choose f(Y, x) to be

$$[\text{g}(Y,{\text{x}}^{\text{T}}\beta )-E\{\text{g}(Y,{\text{x}}^{\text{T}}\beta )|{\text{x}}^{\text{T}}\beta \}][\alpha (\text{x})-E\{\alpha (\text{x})|{\text{x}}^{\text{T}}\beta \}].$$

Here, f(Y, x) satisfies E{f(Y, x) | x^Tβ, Y} = 0 and is thus a valid element in Λ^⊥. Therefore, a general class of estimating equations can be obtained using the sample version of

$$E([\text{g}(Y,{\text{x}}^{\text{T}}\beta )-E\{\text{g}(Y,{\text{x}}^{\text{T}}\beta )|{\text{x}}^{\text{T}}\beta \}]\times [\alpha (\text{x})-E\{\alpha (\text{x})|{\text{x}}^{\text{T}}\beta \}])=0.$$ (2)

The resulting estimate is obviously $\sqrt{n}$-consistent (Newey 1990).

Remark 1. Equation (2) is only one convenient way to construct elements in Λ^⊥. Other constructions are also possible. For example, an arbitrary linear combination

$${\displaystyle \sum _{i=1}^k[{\text{g}}_i(Y,{\text{x}}^{\text{T}}\beta )-E\{{\text{g}}_i(Y,{\text{x}}^{\text{T}}\beta )|{\text{x}}^{\text{T}}\beta \}]\times [{\alpha }_i(\text{x})-E\{{\alpha }_i(\text{x})|{\text{x}}^{\text{T}}\beta \}]}$$

also provides a $\sqrt{n}$-consistent estimator because it is a valid element in Λ^⊥.

Remark 2. It is easy to see that solving (2) does not necessarily yield a unique solution. Theoretically, as long as we choose g and α so that the matrix A in Theorem 1 has rank p(p − d) and B is bounded, solving (2) can yield a basis of S_Y|x, although the basis may not be unique; and as long as the dimension-reduction problem is identifiable, such g and α always exist. Regarding the issue of multiple solutions in practice, there are two aspects to it. First, in a typical estimating equation approach, multiple roots issue presents a challenge. This problem almost always exists in a finite sample, even under the condition that at the population level a unique solution exists. There is no established method to handle it as far as we know. Almost in all the situations, empirical methods are used to select the most sensible root among several roots. Second, uniquely in the context of dimension reduction, even if the targeted central space S_Y|x is unique, its basis—which is what we solve for—is not. Fortunately, this level of multiple roots issue is not a concern. As any particular choice of the basis will yield the same space, and the space is what we really aim for.

In Appendix 2, we show that (2) has a double robustness property, in that the consistency is doubly assured by the term g − E(g | x^Tβ) and the term α − E(α | x^Tβ). We can misspecify either E{g(Y, x^Tβ) | x^Tβ} or E{α(x) | x^Tβ}, the estimator obtained from (2) will still be consistent. Specifically, if we replace E{α(x) | x^Tβ} with an arbitrary function h(x^Tβ), then (2) becomes

$$E([\text{g}(Y,{\text{x}}^{\text{T}}\beta )-E\{\text{g}(Y,{\text{x}}^{\text{T}}\beta )|{\text{x}}^{\text{T}}\beta \}]\{\alpha (\text{x})-\text{h}({\text{x}}^{\text{T}}\beta )\})=0,$$

which still yields a consistent estimator. Similarly, if we replace E{g(Y, x^Tβ) | x^Tβ} with an arbitrary function h(x^Tβ), then (2) becomes

$$E(\{\text{g}(Y,{\text{x}}^{\text{T}}\beta )-\text{h}({\text{x}}^{\text{T}}\beta )\}[\alpha (\text{x})-E\{\alpha (\text{x})|{\text{x}}^{\text{T}}\beta \}])=0,$$ (3)

which also yields a consistent estimator.

Remark 3. To ensure the consistency of the estimation of β, only one of the two expectations E{g(Y, x^Tβ) | x^Tβ} and E{α(x) | x^Tβ} can be misspecified. The other expectation needs to be calculated consistently, this typically requires specifying a correct parametric model or performing nonparametric regression.

Remark 4. In contrast to the existing literature on sufficient dimension reduction (Cook 1998), when using (2) or its misspecified versions to identify S_Y|x, no additional assumptions are made on the covariate vector. This means that (i) we do not need to assume a specific joint distribution for x; (ii) we do not need to assume the linearity condition or the constant variance condition; and (iii) we do not need to assume x to be continuously distributed. Although Cook and Li (2005) also considered noncontinuous covariates, they had to assume a parametric model for the distribution of the covariate vector x conditional on the response Y.

Remark 5. If we are willing to make additional parametric assumptions on E{α(x) | x^Tβ} in (3), for example, E{α(x) | x^Tβ} = Cx or E{α(x) | x^Tβ} = C for a quantity C that may or may not depend on β, then we will no longer need to perform a nonparametric estimation of E{α(x) | x^Tβ} when using (3). Such assumptions greatly simplify the computation. We suspect this is the implicit motivation behind the linearity condition and the constant variance condition, which are widely used in the sufficient dimension reduction literature. We will explore this issue in detail in the next two sections.

The double robustness property further allows us to obtain a $\sqrt{n}$-consistent estimator without any undersmoothing requirement even when d ≥ 3 through nonparametrically estimating both E{g(Y, x^Tβ) | x^Tβ} and E{α(x) | x^Tβ}. We state this result in Theorem 1 and provide the proof in the online supplementary document.

Theorem 1. Under conditions (C1)–(C4) given in Appendix 4, the estimator $\widehat{\beta }$ obtained from the estimating equation

$${\displaystyle \sum _{i=1}^n[\text{g}(Y_i,{\text{x}}_i^{\text{T}}\widehat{\beta })-\widehat{E}\{\text{g}(Y_i,{\text{x}}_i^{\text{T}}\widehat{\beta })|{\text{x}}_i^{\text{T}}\widehat{\beta }\}]\times [\alpha ({\text{x}}_i)-\widehat{E}\{\alpha ({\text{x}}_i)|{\text{x}}_i^{\text{T}}\widehat{\beta }\}]=0}$$

satisfies

$$\sqrt{n}\text{A}\text{vec}(\widehat{\beta }-\beta )\to {\rm N}(0,B)$$

in distribution, where

$$\begin{array}{l}\text{A}=E[\partial \text{vec}([\text{g}(Y,{\text{x}}^{\text{T}}\beta )-E\{\text{g}(Y,{\text{x}}^{\text{T}}\beta )|{\text{x}}^{\text{T}}\beta \}]\times [\alpha (\text{x})-E\{\alpha (\text{x})|{\text{x}}^{\text{T}}\beta \}])|\partial {\{\text{vec}(\beta )\}}^{\text{T}}],\hfill \\ \text{B}=\text{cov}\{\text{vec}([\text{g}(Y,{\text{x}}^{\text{T}}\beta )-E\{\text{g}(Y,{\text{x}}^{\text{T}}\beta )|{\text{x}}^{\text{T}}\beta \}]\times [\alpha (\text{x})-E\{\alpha (\text{x})|{\text{x}}^{\text{T}}\beta \}])\}.\hfill \end{array}$$

Here vec(M) denotes the vector formed by concatenating the columns of M.

3. CONNECTION WITH EXISTING METHODS

In this section, we will examine several popular existing sufficient dimension-reduction methods, and illustrate why they are special cases of the semiparametric estimation family. We will show that all these methods take advantage of the double robustness property. In addition, we will point out that the linearity condition and/or the constant variance condition are used in these methods to simplify the computation. To be specific, the linearity condition characterizes the mean of x conditional on x^Tβ by assuming

$$E(\text{x}|{\text{x}}^{\text{T}}\beta )=\text{Px},$$ (4)

and the constant variance condition characterizes the variance-covariance matrix of x conditional on (x^Tβ) by assuming

$$\text{cov}(\text{x}|{\text{x}}^{\text{T}}\beta )=\text{Q},$$ (5)

where P = β(β^Tβ)⁻¹β^T = ββ^T, Q = I_p − P. Note that here the two conditions are given in the context where E(x) = 0 and cov(x) = I_p. Here, both P and Q are symmetric matrices.

Before presenting the specific analysis on these methods, We first highlight two simple linear algebra results that will be used frequently in the remaining context. These are simple linear algebra results; hence, we only sketch the proofs in the online supplementary document.

Lemma 1. Assume Λ is a p × p symmetric matrix of rank d. If and only if β satisfies

$$\Lambda -\text{P}\Lambda \text{P}=0,$$

then the span of the columns in β is the eigenspace of Λ corresponding to the d nonzero eigenvalues.

Lemma 2. Assume Λ is a p × p symmetric nonnegative definite matrix of rank d. If and only if β satisfies

$$\text{Q}\Lambda \text{Q}=0,$$

then the span of the columns in β is the eigenspace of Λ corresponding to the d nonzero eigenvalues.

3.1 Sliced Inverse Regression

The classic SIR (Li 1991) requires x to satisfy the linearity condition (4). It uses the eigenvectors associated with the d nonzero eigenvalues of the matrix ${\Lambda }_{\text{SIR}}\stackrel{\text{def}}{=}\text{cov}\{E(\text{x}|Y)\}$ to span S_Y|x. For ease of illustration, we assume that Λ_SIR has rank d hence excluding some degenerated cases.

To obtain SIR as a semiparametric estimator, we set g(Y, x^Tβ) = E(x | Y) and α(x) = x^T in (2). The linearity condition promises a parametric form E{α(x) | x^Tβ} = x^TP, hence we can use the misspecified version (3) while selecting h(x^Tβ) = 0. This choice of g, α, and h in (3) yields E{E(x | Y)x^T}(I_p − P) = 0, or equivalently, Λ_SIRQ = 0. Because Λ_SIR is nonnegative definite and has rank d, hence Λ_SIRQ = 0 is equivalent to QΛ_SIRQ = 0. Lemma 2 indicates that this is equivalent to obtaining the eigenspace of Λ_SIR to span S_Y|x.

The above semiparametric derivation of SIR indicates clearly that the linearity condition is not structurally necessary for constructing SIR. When the linearity condition (4) does not hold, we simply lose the convenience of replacing E{α(x) | x^Tβ} by x^TP, everything else remains unchanged. Specifically, in this case, SIR becomes

$$\begin{array}{l}\text{SIR}:\hfill \\ E[\{E(\text{x}|Y)-E\{E(\text{x}|Y)|{\text{x}}^{\text{T}}\beta \text{}}\}{\{\text{x}-E(\text{x}|{\text{x}}^{\text{T}}\beta )\}}^{\text{T}}]=0,\hfill \end{array}$$

where E(· | x^Tβ) and E(· | Y) need to be estimated nonparametrically. This is what we propose as the semiparametric generalization of SIR in the absence of the linearity condition.

3.2 Sliced Average Variance Estimation

The SAVE (Cook and Weisberg 1991) assumes both the linearity condition (4) and the constant variance condition (5). Similar to SIR, SAVE uses the eigenvectors associated with the d nonzero eigenvalues of a matrix Λ_SAVE to span S_Y|x, where ${\Lambda }_{\text{SIR}}\stackrel{\text{def}}{=}E[{\{{\text{I}}_p-\text{cov}(\text{x}|Y)\}}^2]$.

To obtain SAVE from the semiparametric approach, we define g₁(Y, x^Tβ) = I_p − cov(x | Y), g₂(Y, x^Tβ) = g₁(Y, x^Tβ)E(x | Y) and α₁(x) = −x{x − E(x | x^Tβ)}^T, α₂(x) = x^T. As we have pointed out in Remark 1, ${\displaystyle {\sum }_{i=1}^2\{{\text{g}}_i(Y,{\text{x}}^{\text{T}}\beta )-E({\text{g}}_i|{\text{x}}^{\text{T}}\beta )\}\{{\alpha }_i(\text{x})-E({\alpha }_i|{\text{x}}^{\text{T}}\beta )\}}$ is an element in Λ^⊥, hence it yields a valid semiparametric estimating equation. In this construction, taking advantage of the double robustness, we are allowed to misspecify E(g₁ | x^Tβ) = 0 and E(g₂ | x^Tβ) = 0. Some algebra then yields

$$\text{SAVE}:E(\{{\text{I}}_p-\text{cov}(\text{x}|Y)\}[\{\text{x}-E(\text{x}|Y)\}{\{\text{x}-E(\text{x}|{\text{x}}^{\text{T}}\beta )\}}^{\text{T}}-\text{cov}(\text{x}|{\text{x}}^{\text{T}}\beta )])=0.$$ (6)

The linearity condition (4) and the constant variance condition (5) further allow us to replace E(x | x^Tβ) and cov(x | x^Tβ) with Px and Q, which directly simplifies (6) to

$${\Lambda }_{\text{SAVE}}\text{Q}=0.$$

Because Λ_SAVE is nonnegative definite, solving Λ_SAVEQ = 0 is equivalent to solving QΛ_SAVEQ = 0, which is equivalent to SAVE because of Lemma 2.

Relaxing the linearity condition and the constant variance condition is now obvious. Because (6) is obtained without using these two conditions, we can simply use (6) as the condition-free semiparametric generalization of SAVE, while in implementation, we need to estimate E(x | x^Tβ) and cov(x | x^Tβ) nonparametrically.

3.3 Directional Regression

Like SAVE, the DR (Li and Wang 2007) also assumes both the linearity condition (4) and the constant variance condition (5). It uses the eigenvectors associated with the d nonzero eigenvalues of the matrix Λ_DR to span S_Y|x. Here, ${\Lambda }_{\text{DR}}\stackrel{\text{def}}{=}E[{\{2{\text{I}}_p-\text{A}(Y,\stackrel{\sim }{Y})\}}^2],\text{A}(Y,\stackrel{\sim }{Y})=E\{(\text{x}-\stackrel{\sim }{\text{x}}){(\text{x}-\stackrel{\sim }{\text{x}})}^{\text{T}}|Y,\stackrel{\sim }{Y}\}$, and $(\stackrel{\sim }{\text{x}},\stackrel{\sim }{Y})$ is an independent copy of (x, Y).

To obtain DR from the semiparametric approach, we choose g₁(Y, x^Tβ) = I_p − E(xx^T | Y), g₂(Y, x^Tβ) = E{E(x | Y)E(x^T | Y)}E(x | Y), g₃(Y, x^Tβ) = E{E(x^T | Y)E(x | Y)}E(x | Y), α₁(x) = −x{x − E(x | x^Tβ)}^T and α₂(x) = α₃(x) = x^T. Remark 1 indicates that ${\displaystyle {\sum }_{j=1}^3\{{\text{g}}_j(Y,{\text{x}}^{\text{T}}\beta )-E({\text{g}}_j|{\text{x}}^{\text{T}}\beta )\}\{{\alpha }_j(\text{x})-E({\alpha }_j|{\text{x}}^{\text{T}}\beta )\}}$ is an element in Λ^⊥. Taking advantage of the double robustness property, we misspecify E(g_j | x^Tβ) = 0, for j = 1, 2, 3. The subsequent estimating equation is therefore the sample version of

$$\begin{array}{l}\text{DR}:\hfill \\ E[\{{\text{I}}_p-E(\text{x}{\text{x}}^{\text{T}}|Y)\}\{-\text{x}{\text{x}}^{\text{T}}+\text{x}E({\text{x}}^{\text{T}}|{\text{x}}^{\text{T}}\beta )+\text{cov}(\text{x}|{\text{x}}^{\text{T}}\beta )\}]+E[E\{E(\text{x}|Y)E({\text{x}}^{\text{T}}|Y)\}E(\text{x}|Y)\{{\text{x}}^{\text{T}}-E({\text{x}}^{\text{T}}|{\text{x}}^{\text{T}}\beta )\}]+E[E\{E({\text{x}}^{\text{T}}|Y)E(\text{x}|Y)\}E(\text{x}|Y)\{{\text{x}}^{\text{T}}-E({\text{x}}^{\text{T}}|{\text{x}}^{\text{T}}\beta )\}]=0.\hfill \end{array}$$ (7)

When both the linearity condition (4) and the constant variance condition (5) hold, we can insert E(x | x^Tβ) = Px and cov(x | x^Tβ) = Q in (7). Some algebra then leads to the equivalence between (7) and

$$\begin{array}{c}0=E[{\{{\text{I}}_p-E(\text{x}{\text{x}}^{\text{T}}|Y)\}}^2]\text{Q}+{[E\{E(\text{x}|Y)E({\text{x}}^{\text{T}}|Y)\}]}^2\text{Q}+E\{E({\text{x}}^{\text{T}}|Y)E(\text{x}|Y)\}E\{E(\text{x}|Y)E({\text{x}}^{\text{T}}|Y)\}\text{Q}\\ =2^{-1}{\Lambda }_{\text{DR}}\text{Q},\end{array}$$

where the last equality is due to Li and Wang (2007). Because Λ_DR is nonnegative definite, solving Λ_DRQ = 0 is equivalent to solving QΛ_DRQ = 0, which is equivalent to DR because of Lemma 2.

Similar to SAVE, as (7) is obtained without any of the linearity or constant variance condition, it can thus be used as a semiparametric generalization of DR.

Li and Dong (2009) and Dong and Li (2010) extended SIR, SAVE, and DR to the case when the linearity condition (4) is violated while the constant variance condition (5) is true. Similar analysis shows that these are also special cases of the semiparametric approach. These results are available in the supplementary document.

4. SEMIPARAMETRIC ESTIMATION OF THE CENTRAL MEAN SUBSPACE

In situations when one only concerns about the conditional mean of the response given the predictors, Cook and Li (2002) introduced the notion of the central mean subspace. They defined the column space of β as a mean dimension-reduction subspace if β satisfies

$$E(Y|\text{x})=E(Y|{\text{x}}^{\text{T}}\beta ).$$

The intersection of all mean dimension-reduction subspaces is defined as the central mean subspace, denoted by S_E(Y|x), if the intersection itself is also a mean dimension-reduction subspace. The conditional mean model assumes the mean of Y conditional on x relies on x^Tβ only. In other words, x contributes to the conditional mean of Y only through x^Tβ. Our main interest is to estimate S_E(Y|x), or equivalently, a basis matrix β which spans S_E(Y|x).

To facilitate the semiparametric analysis, we write the conditional mean model as

$$Y=\ell ({\text{x}}^{\text{T}}\beta )+\epsilon ,$$ (8)

where $\ell ({\text{x}}^{\text{T}}\beta )\stackrel{\text{def}}{=}E(Y|{\text{x}}^{\text{T}}\beta )$ is an unspecified smooth function and E(ε | x) = 0. We emphasize that because we make no assumptions on ε other than conditional mean zero, (8) is equivalent to the central mean subspace model. For the conditional mean model (8), the likelihood of one random observation (x, Y) is

$${\eta }_1(\text{x}){\eta }_2\{Y-\ell ({\text{x}}^{\text{T}}\beta ),\text{x}\},$$

where η₁ has the same meaning as in Section 2, ℓ(x^Tβ) is the mean function of Y conditional on x (or equivalently, on x^Tβ), and η₂ is the conditional pmf/pdf of the residual ε = Y − E(Y | x^Tβ) on x. Here, η₂ satisfies E(ε | x) = 0, and is otherwise unconstrained. Similarly, treating η₁, η₂, and ℓ as nuisance parameters while β as the parameter of interest, following the semiparametric analysis in Appendix 3, we obtain the nuisance tangent space orthogonal complement to be the class of the form

$${\Lambda }^{\perp }=\{\{Y-E(Y|{\text{x}}^{\text{T}}\beta )\}\{\alpha (\text{x})-E(\alpha |{\text{x}}^{\text{T}}\beta )\}:\forall \alpha \}.$$

Similar to (1), the form of Λ^⊥ allows us to take any α(x) to obtain

$$\{Y-E(Y|{\text{x}}^{\text{T}}\beta )\}\{\alpha (\text{x})-E(\alpha (\text{x})|{\text{x}}^{\text{T}}\beta )\}$$

as a valid element in Λ^⊥. Hence, a general class of estimating equations can be obtained using the sample version of

$$E(\{Y-E(Y|{\text{x}}^{\text{T}}\beta )\}[\alpha (\text{x})-E\{\alpha (\text{x})|{\text{x}}^{\text{T}}\beta \}])=0.$$ (9)

Similar to Appendix 2, we can easily show that (9) has a double robustness property, in that we can misspecify either E(Y | x^Tβ) or E{α(x) | x^Tβ}, the resulting estimator from (9) will still yield a consistent estimating equation.

4.1 Ordinary Least Squares

We first inspect the OLS (Li and Duan 1989) method, where the linearity condition (4) is assumed to hold. The OLS method uses cov(x, Y) to infer a subspace of the column space of β in (8).

From the semiparametric approach, we let α(x) = x in (9). Taking advantage of the double robustness, we misspecify E(Y | x^Tβ) = 0. Then (9) reduces to

$$0=E(\text{x}Y)-\text{P}E(\text{x}Y)=E(\text{x}Y)-\beta {({\beta }^{\text{T}}\beta )}^{-1}{\beta }^{\text{T}}E(\text{x}Y).$$

Note that (β^Tβ)⁻¹β^TE(xY) is a d × 1 vector. This directly yields cov(x, Y) as a one-dimensional subspace of S_E(Y|x), which is exactly the OLS estimation.

When the linearity condition (4) does not hold, (9) has the form

$$E[\{Y-E(Y|{\text{x}}^{\text{T}}\beta )\}\{\text{x}-E(\text{x}|{\text{x}}^{\text{T}}\beta )\}])=0$$

and can still be used to estimate β. A simple treatment is to set E(x | x^Tβ) = 0 and solve the sample version of the above display to obtain β.

4.2 Principal Hessian Directions

The principal Hessian directions (PHD) method (Li 1992) assumes both the linearity condition (4) and the constant variance condition (5). It uses the eigenvectors associated with d nonzero eigenvalues of Λ_PHD to form a basis of S_E(Y|x). Here, ${\Lambda }_{\text{PHD}}\stackrel{\text{def}}{=}E[\{Y-E(Y)\}\text{x}{\text{x}}^{\text{T}}]$. To obtain PHD from the semiparametric approach, we let α(x) = xx^T in (9). Taking advantage of the double robustness, we misspecify E(Y | x^Tβ) = E(Y). The linearity condition (4) and the constant variance condition (5) yield a simplification α(x) − E{α(x) | x^Tβ} = xx^T − Q − Pxx^TP, hence (9) reduces to

$$E[\{Y-E(Y)\}(\text{x}{\text{x}}^{\text{T}}-{\text{Pxx}}^{\text{T}}\text{P})]={\Lambda }_{\text{PHD}}-\text{P}{\Lambda }_{\text{PHD}}\text{P}=0.$$

Lemma 1 indicates that this is equivalent to the PHD method. When either (4) or (5) is not true, we can use

$$E[\{Y-E(Y|{\text{x}}^{\text{T}}\beta )\}\{\text{x}{\text{x}}^{\text{T}}-E(\text{x}{\text{x}}^{\text{T}}|{\text{x}}^{\text{T}}\beta )\}]=0$$

to estimate β, where we calculate E(Y | x^Tβ) and E(xx^T | x^Tβ) nonparametrically. We can opt to misspecify E(Y | x^Tβ) = 0 or preferably E(xx^T | x^Tβ) = 0 to simplify the computation. The second simplification

$$\text{PHD}:E[\{Y-E(Y|{\text{x}}^{\text{T}}\beta )\}\text{x}{\text{x}}^{\text{T}}]=0$$

will be considered as the semiparametric generalization of the PHD method without extra conditions.

5. IMPLEMENTATION

To focus on delivering the main message, we have avoided detailing the implementation details in practice, which we explain now.

The proposed semiparametric counterparts of SIR, SAVE, DR, PHD, and so on, which were respectively denoted by semi-SIR, semi-SAVE, semi-DR, and semi-PHD for ease of subsequent illustration, all have the similar components of estimating conditional expectation and solving estimating equations. Because the number of the estimating equations sometimes is larger than the number of parameters, the implementation is through minimizing their Frobenius norm. We use the familiar Newton-Raphson procedure to numerically obtain the minimizer. This essentially means that at the jth iteration β^(j), we perform nonparametric conditional estimation using, say, a kernel regression method to evaluate an estimating equation at β^(j), and use numerical difference to obtain the derivative of the estimating equation with respect to β evaluated at β^(j). We then update β^(j). This process iterates until the difference between two consecutive candidates are sufficiently small.

Because semi-DR has the most complicated form, we now outline an algorithm for semi-DR as a concrete illustration. We use β^(j) to denote the value of $\widehat{\beta }$ at the jth iteration, and use K(·) to denote a kernel function. Let K_h(·) = K(·/h)/h for any bandwidth h. We use the Epanechnikov kernel function in the implementation. Assume the observations are (x_i, Y_i) for i = 1, …, n.

1. Nonparametrically estimate E(xx^T | Y) and E(x | Y) using

   $$\begin{array}{c}\widehat{E}(\text{x}{\text{x}}^{\text{T}}|Y)=\frac{{\displaystyle {\sum }_{i=1}^n{\text{x}}_i{\text{x}}_i^{\text{T}}{K}_h(Y-Y_i)}}{{\displaystyle {\sum }_{i=1}^n{K}_h(Y-Y_i)}}\text{ and}\\ \widehat{E}(\text{x}|Y)=\frac{{\displaystyle {\sum }_{i=1}^n{\text{x}}_i{K}_h(Y-Y_i)}}{{\displaystyle {\sum }_{i=1}^n{K}_h(Y-Y_i)}}.\end{array}$$

   The bandwidth can be selected using the classic cross-validation procedure. We evaluate the above estimations at Y_i, for i = 1, …, n.

2. Form ${\text{A}}_i={\text{I}}_p-\widehat{E}(\text{x}{\text{x}}^{\text{T}}|Y_i)$, ${\text{b}}_i=n^{-1}{\displaystyle {\sum }_{j=1}^n\{\widehat{E}(\text{x}|Y_j)\widehat{E}({\text{x}}^{\text{T}}|Y_j)\}\widehat{E}(\text{x}|Y_i)}$ and ${\text{c}}_i=n^{-1}{\displaystyle {\sum }_{j=1}^n\{\widehat{E}({\text{x}}^{\text{T}}|Y_j)\widehat{E}(\text{x}|Y_j)\}\widehat{E}(\text{x}|Y_i)}$.

3. Pick an arbitrary starting value β⁽¹⁾, for example, the classical DR estimate.

4. At the jth iteration, form ${\text{t}}_i={\text{x}}_i^{\text{T}}{\beta }^{(j)}$ for i = 1, …, n.

5. Nonparametrically estimate E(x | x^Tβ^(j)) and cov(x | x^Tβ^(j)) using

   $$\widehat{E}(\text{x}|{\text{x}}^{\text{T}}{\beta }^{(j)})=\frac{{\displaystyle {\sum }_{i=1}^n{\text{x}}_i{K}_h({\text{x}}^{\text{T}}{\beta }^{(j)}-{\text{t}}_i)}}{{\displaystyle {\sum }_{i=1}^n{K}_h({\text{x}}^{\text{T}}{\beta }^{(j)}-{\text{t}}_i)}}$$

   and

   $$\widehat{\text{cov}}(\text{x}|{\text{x}}^{\text{T}}{\beta }^{(j)})=\frac{{\displaystyle {\sum }_{i=1}^n{\text{x}}_i{\text{x}}_i^{\text{T}}{K}_h({\text{x}}^{\text{T}}{\beta }^{(j)}-{\text{t}}_i)}}{{\displaystyle {\sum }_{i=1}^n{K}_h({\text{x}}^{\text{T}}{\beta }^{(j)}-{\text{t}}_i)-\widehat{E}(\text{x}|{\text{x}}^{\text{T}}{\beta }^{(j)})\widehat{E}({\text{x}}^{\text{T}}|{\text{x}}^{\text{T}}{\beta }^{(j)})}}.$$

   We use a same bandwidth to estimate the above two quantities to ensure that $\widehat{\text{cov}}(\text{x}|{\text{x}}^{\text{T}}{\beta }^{(j)})$ is positive definite. The bandwidth can be selected using the cross-validation procedure. Evaluate the above estimations at x^Tβ^(j) = t₁, …, t_n.

6. Form the sample version of the left-hand side of (7):

   $$r({\beta }^{(j)})=\frac{1}{n}{\displaystyle \sum _{i=1}^n[{\text{A}}_i\{-{\text{x}}_i{\text{x}}_i^{\text{T}}+{\text{x}}_i\widehat{E}({\text{x}}^{\text{T}}|{\text{t}}_i)+\widehat{\text{cov}}(\text{x}|{\text{t}}_i)\}+({\text{b}}_i+{\text{c}}_i){\{{\text{x}}_i-\widehat{E}({\text{x}}_i|{\text{t}}_i)\}}^{\text{T}}]}.$$

   Update β^(j) using the following Newton-Raphson steps.

7. Form the derivative of ∂{∥r(β)∥²}/∂{vec(β)} evaluated at β^(j) through numerical difference. Specifically, let δ be a small number and decide an order for the elements in β^(j). Let ${\beta }_{k+}^{(j)}={\beta }^{(j)}+\delta {\text{e}}_k$ and ${\beta }_{k-}^{(j)}={\beta }^{(j)}-\delta {\text{e}}_k$. Here e_k has the same size as β but has 1 in the kth entry and zero elsewhere. Repeat the procedure in Step 5 to obtain $r({\beta }_{k+}^{(j)})$ and $r({\beta }_{k-}^{(j)})$. Set the kth row of ∂{∥r(β)∥²}/∂{vec(β)} to be $\{\parallel r({\beta }_{k+}^{(j)}){\parallel }^2-\parallel r({\beta }_{k-}^{(j)}){\parallel }^2\}/(2\delta )$. Repeat this for all the entries in β^(j) For simplicity, we denote the resulting first derivative ∂{∥r(β^(j))∥²}/∂{vec(β)}. Following similar procedures, we obtain the second derivative ∂²{∥r(β)∥²}/∂{vec(β)}∂{vec(β)}^T.

   Practically, δ = 0.001 is sufficiently small to obtain a close approximation of the derivatives. If more precision is desired, one can simply opt for smaller δ.

8. Update to obtain

   $$\text{vec}({\beta }^{(j+1)})=\text{vec}({\beta }^{(j)})-{\left[\frac{{\partial }^2\{\parallel r{\beta }^{(j)}{\parallel }^2\}}{\partial \{\text{vec}({\beta }^{(j)})\}\partial {\{\text{vec}({\beta }^{(j)})\}}^{\text{T}}}\right]}^{-1}\times \frac{\partial \{\parallel r{\beta }^{(j)}{\parallel }^2\}}{\partial \{\text{vec}({\beta }^{(j)})\}}.$$

9. Repeat Steps 4 to 8 until convergence.

For identification, x must contain at least one continuous variable (Ichimura 1993; Horowitz and Hardle 1996). The above algorithm is applicable if the support of x^Tβ is connected. When the support consists of several disjoint regions, we need to carry out the kernel estimation in Step 5 in each region.

Another important component in dimension reduction is to decide the dimension d of S_Y|x or S_E(Y|x). To this end, the bootstrap procedure described by Dong and Li (2010) adapts the idea of Ye and Weiss (2003) by taking into account the variation of the covariates, and is very flexible. This is what we recommend for use in our context. Specifically, we can decide d through the following procedure. Let λ₁, …, λ_k be the nonzero eigenvalues of

$${\{\text{var}(\text{u})\}}^{-1/2}\text{cov}(\text{u},{\text{v}}^{\text{T}}){\{\text{var}(\text{v})\}}^{-1}\text{cov}(\text{u},{\text{v}}^{\text{T}}){\{\text{var}(\text{u})\}}^{-1/2},$$

where u and v are two generic random vectors. In addition, we let

$$r^2(\text{u},\text{v})=k^{-1}{\displaystyle \sum _{i=1}^k{\lambda }_i.}$$

For any working dimension k = 1, …, p − 1, we let ${\widehat{\beta }}_k$ be the estimate based on the original sample, and ${\widehat{\beta }}_{k,b}$ be the estimate based on the bth bootstrap sample, for b = 1, …, B. We then estimate the structural dimension d by maximizing over k = 1, …, p − 1

$${\overline{r}}_k^2=\frac{1}{B}{\displaystyle \sum _{b=1}^B{r}^2}\left({\widehat{\beta }}_k^{\text{T}}\text{x},{\widehat{\beta }}_{k,b}^{\text{T}}\text{x}\right).$$ (10)

Interested readers are referred to Dong and Li (2010) for more details.

6. SIMULATION STUDY

In this section, we conduct simulation studies to evaluate the performance of different estimation procedures. Unless otherwise stated, we repeat the experiments 500 times each with sample size n = 200 and reduced space dimension d = 2. Throughout the simulations, we used the Epanechnikov kernel and fixed $\widehat{\sigma }{(3n/4)}^{-1/(d+4)}$ as bandwidth, where $\widehat{\sigma }$ is the robust estimation of the standard deviation of x^Tβ, which is the default bandwidth selector implemented in Matlab routine ksdensity. We choose the predictor dimension p to be 6 and 12, and consider the following two cases for the covariate vector x = (X₁, …, X_p)^T.

Case 1: We generate (X₁, X₂)^T (corresponding to the case p = 6) and X₁, X₂, X₇, …, X_p)^T (corresponding to the case p = 12) from normal population with mean zero and variance-covariance matrix (σ_ij)_{(p − 4) × (p − 4)} where σ_ij = 0.5^{|i − j|}. We generate X₃ and X₄ from nonlinear models: X₃ = |X₁ + X₂| + |X₁| ε₁, and X₄ = |X₁ + X₂|² + |X₂| ε₂, where ε_i’s are independently generated from the standard normal population, X₅ from a Bernoulli distribution with success probability exp (X₂)/{1 + exp (X₂)}, and X₆ from another Bernoulli distribution with success probability Φ (X₂), where Φ(·) denotes the cumulative distribution function of standard normal population. Note that in this case, both the linearity condition (4) and the constant variance condition (5) are violated.

Case 2: We generate x from normal population with mean zero and variance-covariance matrix (σ_ij)_{p × p} where σ_ij = 0.5^{|i − j|}. Note that in this case, the covariates satisfy both the linearity condition (4) and the constant variance condition (5).

Let β be a basis matrix of S_Y|x and $\widehat{\beta }$ be its estimate. To assess the estimation accuracy of $\widehat{\beta }$, we use the Euclidean distance between $\widehat{\beta }$ and β, defined as the Frobenius norm of the matrix $\widehat{\beta }{({\widehat{\beta }}^{\text{T}}\widehat{\beta })}^{-1}{\widehat{\beta }}^{\text{T}}-\beta {({\beta }^{\text{T}}\beta )}^{-1}{\beta }^{\text{T}}$. In both cases, the distance ranges from zero to two, and a smaller distance indicates a better estimate.

6.1 Example 1

We generate the response variable using the following four different models:

$$\begin{array}{c}\text{model (I)}:Y=({\text{x}}^{\text{T}}{\beta }_1)/\{0.5+{({\text{x}}^{\text{T}}{\beta }_2+1.5)}^2\}+0.5\epsilon ;\\ \text{model (II)}:Y={({\text{x}}^{\text{T}}{\beta }_1)}^2+2|{\text{x}}^{\text{T}}{\beta }_2|+0.1|{\text{x}}^{\text{T}}{\beta }_2|\epsilon ;\\ \text{model (III)}:Y=\exp ({\text{x}}^{\text{T}}{\beta }_1)+2{({\text{x}}^{\text{T}}{\beta }_2+1)}^2+|{\text{x}}^{\text{T}}{\beta }_1|\epsilon ;\\ \text{model (IV)}:Y={({\text{x}}^{\text{T}}{\beta }_1)}^2+{({\text{x}}^{\text{T}}{\beta }_2)}^2+0.5\epsilon ,\end{array}$$

where β₁ and β₂ are p × 1 vectors with their first six components being ${(1,1,1,1,1,1)}^{\text{T}}/\sqrt{6}$ and ${(1,-1,1,-1,1,-1)}^{\text{T}}/\sqrt{6}$, respectively. When p = 12, the rest components of β₁ and β₂ are identically zero. The error term ε has a standard normal distribution. Models (I)–(IV) are chosen to compare, respectively, SIR, SAVE, DR, and PHD with their semiparametric counterparts. We also include dMAVE (Xia 2007) and MAVE (Xia et al. 2002) into our comparison as they are often used as a benchmark. To make a fair comparison on the core methodologies of these proposals, we estimate the kernel matrices of the classical SIR, SAVE, DR by using kernel smoothing rather than the usual slicing estimation. This allows us to avoid selecting the number of slices which usually adversely affects the performance. Thus, SIR, SAVE, and DR are implemented in their improved form.

The boxplots of the Euclidean distances are reported in Figure 1. The results under Case 1 are presented in panels (A) and (C), where we show the boxplots of Euclidean distances for different estimation procedures when both the linearity condition (4) and the constant variance condition (5) are violated. In this case, we can see that the semiparametric estimates are substantially more accurate than their classical dimension-reduction counterparts across all four models, indicating the significant improvement when the violation of these conditions is taken into account. Note that dMAVE has very large variability in these settings and sometimes even perform worse than the classical dimension-reduction methods. This is because some covariates are discrete which violates the continuity requirement of dMAVE. Because the semiparametric estimation procedures do not require continuous covariates, and they do not rely on any conditional moment or distributional assumptions, their performance dominates the competitors in all scenarios. The results for Case 2 are in panels (B) and (D), which contain the boxplots of Euclidean distances when both the linearity condition (4) and the constant variance condition (5) are satisfied. We can see that, surprisingly, our semiparametric proposals are still superior to their classical counterparts in these particular examples. This reminds us of a quite interesting phenomenon where sometimes, estimating a quantity even if it is known brings gain (Henmi and Eguchi 2004). However, whether this gain is real, in general, or just in these specific examples deserves further theoretical investigation. On the other hand, our estimators seem to perform comparably with dMAVE, which usually produces very accurate estimates when all the covariates are continuous, such as the case here. Following the request of a referee, we also experimented the simulations with p = 50, which corresponds to 96 free parameters with the sample size n = 200. Unfortunately, none of the methods examined above can provide any reasonable results in this case. We believe that to handle p very large in comparison with n, additional assumptions such as sparsity is needed. The sparsity assumption assumes many rows of β are zeros, hence the corresponding variables in x simply have no effect on the response variable Y. Many existing methods are available to take advantage of the sparsity assumption (see, e.g., Li 2007; Wang and Wang 2010). Combining the sparsity techniques and the dimension reduction methods are promising future work.

Figure 1.

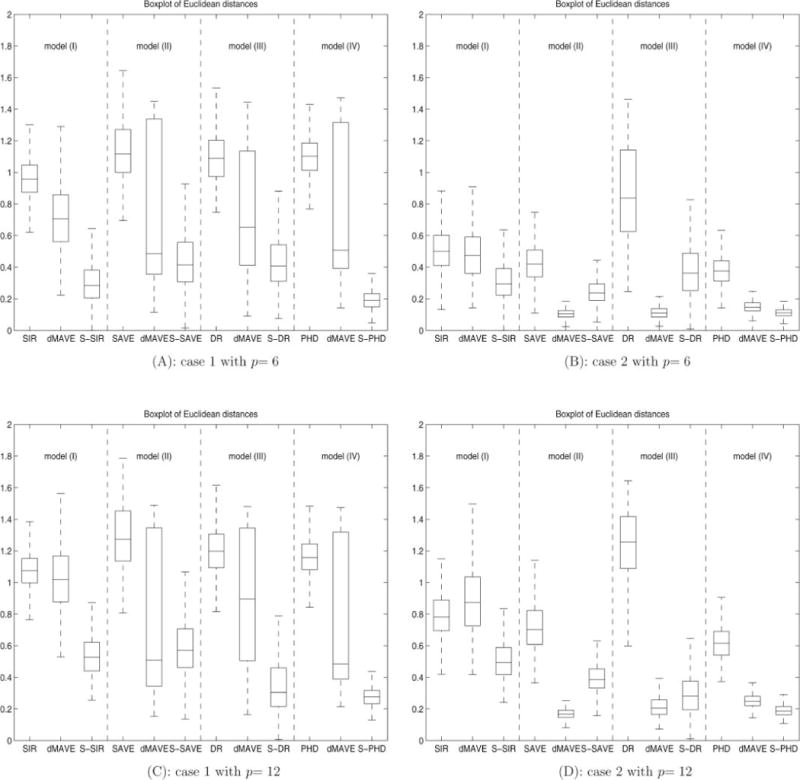
Boxplots of Euclidean distances for models (I)–(IV) with p = 6 and p = 12 in Example 1. Semi-SIR, Semi-SAVE, Semi-DR, and Semi-PHD are shorten to S-SIR, S-SAVE, S-DR, and S-PHD, respectively, in the labels.

6.2 Example 2

Next, we perform simulations to demonstrate the performance of the bootstrap procedure conjuncted with the semiparametric methods in estimating the structural dimension d. We continue to use models (I)–(IV) in Example 1, and generate the predictors x from case 1 when p = 6. We generated 100 datasets of sample size n = 200, with bootstrap size B = 100.

We report the relative frequency of the bootstrap selected dimensions for models (I)–(IV) in Table 1. It can be easily seen that with at least 95% accuracy the bootstrap method correctly chose the dimension, which we consider quite satisfactory.

Table 1.

Relative frequency of the estimated dimension $\widehat{d}$

Model	Method	$$\widehat{d}=1$$	$$\widehat{d}=2$$	$$\widehat{d}=3$$	$$\widehat{d}\ge 4$$
(I)	Semi-SIR	1%	99%	0%	0%
(II)	Semi-SAVE	1%	97%	0%	2%
(III)	Semi-DR	3%	97%	0%	0%
(IV)	Semi-PHD	5%	95%	0%	0%

7. REAL DATA APPLICATION

We illustrate further our semiparametric proposals through a dataset concerning the employees’ salary in the Fifth National Bank of Springfield (Albright, Winston, and Zappe 1999). The aim of this study is to understand how an employee’s salary associates with his/her personal characteristics. To this end, an employee’s annual salary is the response variable Y, and six covariates are possibly associated with the salary: the employee’s current job level, where a larger number indicates a higher rank (X₁); the employee’s working experience at current bank, which is measured by the number of years of the employment (X₂); the employee’s age (X₃); the experience of an employee at another bank prior to working at the Fifth National, which is measured by the number of years at other banks (X₄); the employee’s gender (X₅); and a binary variable indicating whether the employee’s job is computer related (X₆). We removed an obvious outlier in this dataset, leaving 207 observations in the subsequent analysis.

Under various working dimensions k = 1, …, 5, we implement the proposed semi-DR method given in (7) in association with the bootstrap method described in Section 5, with bootstrap size B = 1000. The results are presented as boxplots in Figure 2. It is clear that bootstrap method favors d = 1, which indicates that the six covariates affect the salary through one single linear combination direction. We present the estimation of this direction in Table 2. For comparison, we also implement the dMAVE and the classical DR with kernel smoothing. We emphasize here that dMAVE requires the covariates to be continuous, which is not the case for gender (X₅), and DR requires linearity condition and constant variance condition, which are not satisfied in this example (see Figure 3). Hence, both results should not be fully trusted.

Figure 2.

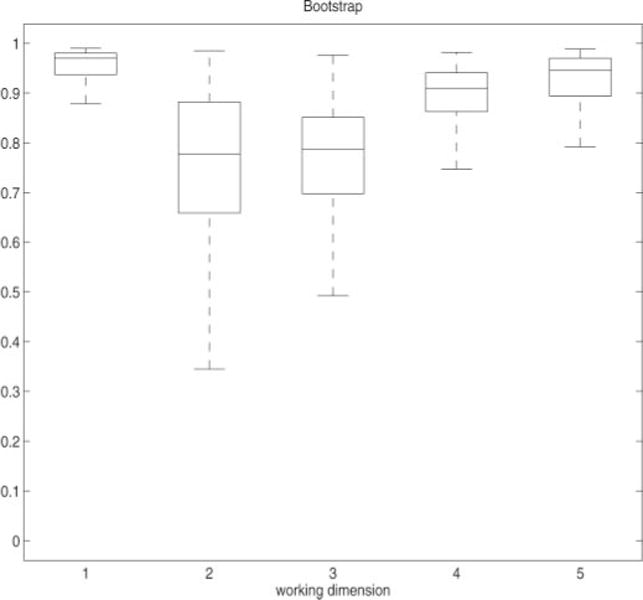
Boxplot of the ${\overline{r}}_k^2$ values defined in (10) from 1000 bootstrapped Semi-DR.

Table 2.

Estimated coefficients of x

Method	X1	X2	X3	X4	X5	X6
Semi-DR	0.7330	0.5794	0.2523	0.0147	0.1830	0.1723
dMAVE	0.8388	0.4404	0.2295	0.0417	0.1373	0.1711
DR	0.2673	0.8596	0.2829	−0.1023	0.3050	0.0782

Figure 3.

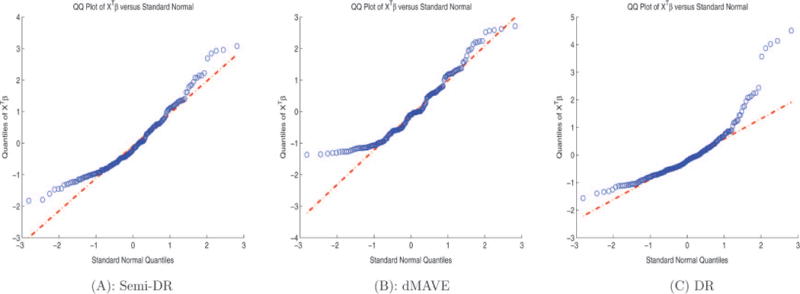
The Q–Q plot of ${\text{x}}^{\text{T}}{\widehat{\beta }}_1$, with ${\widehat{\beta }}_1$ estimated from Semi-DR, dMAVE, and DR. (The online version of this figure is in color.)

To see the dimension-reduction effect from a different perspective, in Figure 4, we present the scatterplots of Y versus ${\text{x}}^{\text{T}}\widehat{\beta }$, where $\widehat{\beta }$ denotes the estimate obtained from Semi-DR, dMAVE, and DR. We can see that the estimates obtained from Semi-DR and dMAVE exhibit a more obvious pattern than DR in that the data cloud appears more compact. We also include in Figure 4 three curves (the dashed lines) fitted from a quadratic function on $({\text{x}}_i^{\text{T}}\widehat{\beta },Y_i),i=1,\dots ,n.$. These fit the data cloud rather well and illustrate a homoscedastic error pattern. Thus, we further used the fitted curves to perform a cross-validation procedure to calculate the prediction error. The resulting prediction errors from Semi-DR, dMAVE and DR are, respectively, 21.3191, 23.4481, and 47.0288, which further illustrate the advantage of the Semi-DR method. All these evidences support the conclusion that Semi-DR has successfully reduced the dimension from p = 6 to d = 1 and has found the right linear combination of the covariates in terms of establishing the association between salary and an employee’s characteristic.

Figure 4.

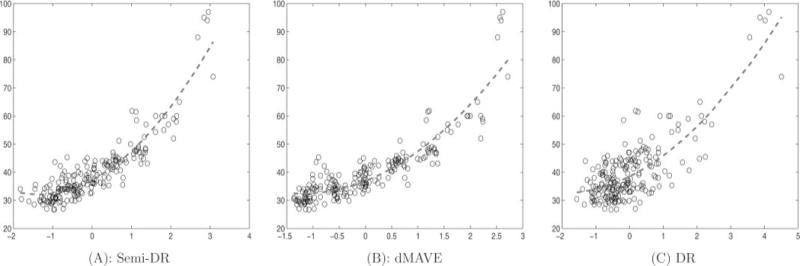
Scatterplot of Y versus ${\text{x}}^{\text{T}}{\widehat{\beta }}_1$, with ${\widehat{\beta }}_1$ estimated from Semi-DR, dMAVE, and DR. The dash lines are fitted curves based on quadratic regression modeling.

8. DISCUSSION

It is worth mentioning that (2) and (9) only differ in the first component. For (2), this component can be constructed from any function of Y and x^Tβ, namely, any g(Y, x^Tβ), while for (9), the only valid choice is g(Y, x^Tβ) = Y. Thus, the family of estimators provided by (2) is much richer than the one provided by (9). In fact, it includes the family of (9) as a subfamily of estimators. This is easy to understand intuitively as model (1) assumes more structures than model (8), consequently one can have more ways to construct estimators for (1) and, therefore, model (1) has a larger subspace Λ^⊥. Because of this relation, any estimator for model (8) is necessarily also an estimator for (1). This also agrees with the dimension-reduction result that the conditional mean subspace S_E(Y|x) is a subspace of the conditional subspace S_Y|x, because if (1) holds for β, then (8) also holds for β or a submatrix of β.

For illustration, we have chosen to derive SIR, SAVE, and DR as examples for the central subspace problem and OLS and PHD as examples for the central mean subspace from the semiparametric approach, mainly due to their popularity in the dimension-reduction literature. Because Λ^⊥ contains all the influence functions, hence every root-n consistent method must correspond to a special choice of the functions in Λ^⊥. In this sense, the families given in Sections 2 and 4 are complete.

Finally, we acknowledge here that the linearity condition and the constant variance condition, when assumed to hold only at the true value of β, can be mild and often hold approximately, especially when p is large (Hall and Li 1993). However, our simulations in Case 1 have shown that this approximation may not be sufficient to justify making and using these assumptions. In other words, if we assume the linearity condition and/or constant variance condition to hold exactly at the true β while, in fact, they are only approximately true, the subsequent estimation of the central subspace or central mean subspace can be quite different. In addition, even if the linearity and constant variance conditions do hold exactly, our limited numerical results seem to indicate that it might be still beneficial not to use them if one is concerned more about the estimation quality than the computational cost. Investigation on whether this is indeed a general phenomenon or some special isolated instances is a worthy endeavor.

APPENDIX: SOME TECHNICAL DERIVATIONS

A.1. General Introduction to Semiparametrics

Consider the Hilbert space H consisting of all the mean zero, finite variances, length m vector functions of x, Y, where the inner product between two functions h, g is defined as E(h^Tg). Here and in the following definitions, all the expectations are calculated under the true distribution. The nuisance tangent space Λ is a subspace of H defined as the mean squared closure of all the elements of the form B S, where S is an arbitrary nuisance score vector function, and B is any conformable matrix with m rows. Here the nuisance score vector functions are calculated conventionally in every possible valid parameterization of the infinite-dimensional nuisance parameter, where a “valid parameterization” means that there exists one parameter value which yields the truth. Furthermore, Λ^⊥ is defined to be the orthogonal complement of Λ in H.

Semiparametric theory ensures that every regular, asymptotic linear, root n consistent (RAL) estimator corresponds to an influence function, and every influence function is a normalized element in Λ^⊥, where the normalization is to ensure $E(\varphi S_{\beta }^{\text{T}})={\text{I}}_m$. Here, S_β is the usual score vector with respect to the parameter of interest β, and we use ϕ to denote an influence function and I_m to denote the size m identity matrix. This link between the complete family of RAL estimators and the space Λ^⊥ allows one to derive estimators through characterizing Λ^⊥ and identifying members in Λ^⊥. Every explicit identification of one function in Λ^⊥ ensures the discovery of one estimator. This is the semiparametric approach that drives all our derivations.

A.2. The Derivation of Λ^⊥ in Model (1)

Denote the nuisance tangent space corresponding to η₁ and η₂, respectively, Λ₁ and Λ₂. We have

$$\begin{array}{c}{\Lambda }_1=\{\text{f}(\text{x}):\forall \text{f}\text{such that}E(\text{f})=0\},\\ {\Lambda }_2=\{\text{f}(Y,{\beta }^{\text{T}}\text{x}):\forall \text{f}\text{such that}E(\text{f}|\text{x})=E(\text{f}|{\beta }^{\text{T}}\text{x})=0\}.\end{array}$$

Obviously, Λ₁ ⊥ Λ₂, hence Λ = Λ1 ⊕ Λ2. It is easy to see that ${\Lambda }_1^{\perp }=\{\text{f}(Y,\text{x}):E(\text{f}|\text{x})=0\}\supseteq {\Lambda }_2$. We now show that ${\Lambda }_2^{\perp }=\{\text{f}(Y,\text{x}):E(\text{f}|{\beta }^{\text{T}}\text{x},Y)\text{is a function of}{\beta }^{\text{T}}\text{x}\text{only}.\}$. Obviously, functions having the required conditional expectation property are certainly elements in ${\Lambda }_2^{\perp }$. To show that elements in ${\Lambda }_2^{\perp }$ have to satisfy the conditional expectation requirement, consider any $\text{f}(Y,\text{x})\in {\Lambda }_2^{\perp }$. We let g = E(f | β^Tx, Y) − E(f | β^Tx). Obviously, g ∈ Λ₂ hence E(g^Tf) = 0. On the other hand,

$$\begin{array}{c}0=E({\text{g}}^{\text{T}}\text{f})=E\{{\text{g}}^{\text{T}}E(\text{f}|{\beta }^{\text{T}}\text{x},Y)\}\\ =E({\text{g}}^{\text{T}}\text{g})+E\{{\text{g}}^{\text{T}}E(\text{f}|{\beta }^{\text{T}}\text{x})\}\\ =E({\text{g}}^{\text{T}}\text{g})+E\{E{(\text{g}|{\beta }^{\text{T}}\text{x})}^{\text{T}}E(\text{f}|{\beta }^{\text{T}}\text{x})\}\\ =E({\text{g}}^{\text{T}}\text{g})+0.\end{array}$$

Hence g itself should be zero. This means f indeed satisfies the conditional expectation requirement.

We now show that

$$\begin{array}{c}{\Lambda }^{\perp }={\Lambda }_1^{\perp }\cap {\Lambda }_2^{\perp }=\{\text{f}(Y,\text{x})-E(\text{f}|{\beta }^{\text{T}}\text{x},Y):E(\text{f}|\text{x})\\ =E(\text{f}|{\beta }^{\text{T}}\text{x})\forall \text{f}\}.\end{array}$$

To see this, note that its form simply says for any element in Λ^⊥, it should satisfy the condition E(g | β^Tx, Y) = 0. Let us denote the set A = {f(Y, x) − E(f | β^Tx, Y) : E(f | x) = E(f | β^Tx) ∀ f}. Obviously, $A\subset {\Lambda }_2^{\perp }$. Because

$$\begin{array}{c}E\{\text{f}(Y,\text{x})-E(\text{f}|{\beta }^{\text{T}}\text{x},Y)|\text{x}\}\\ =E\{\text{f}(Y,\text{x})|\text{x}\}-E(\text{f}|{\beta }^{\text{T}}\text{x},Y)|\text{x}\}\\ =E(\text{f}|\text{x})-E\{E(\text{f}|{\beta }^{\text{T}}\text{x},Y)|{\beta }^{\text{T}}\text{x}\}\\ =E(\text{f}|\text{x})-E(\text{f}|{\beta }^{\text{T}}\text{x})=0,\end{array}$$

hence $A\subset {\Lambda }_1^{\perp }$ as well. Hence, A ⊂ Λ^⊥. On the other hand, for any f ∈ Λ^⊥, because $\text{f}\in {\Lambda }_2^{\perp }$, we have E(f | β^Tx, Y) = a(β^Tx) for some a. Writing this out, we obtain

$$\begin{array}{c}\text{a}({\beta }^{\text{T}}x)=\frac{{\displaystyle {\int }_{{\beta }^{\text{T}}\text{x}={\beta }^{\text{T}}x}\text{f}(Y,\text{x}){\eta }_1(\text{x}){\eta }_2(Y|{\beta }^{\text{T}}\text{x})d\mu (\text{x})}}{{\displaystyle {\int }_{{\beta }^{\text{T}}\text{x}={\beta }^{\text{T}}x}{\eta }_1(\text{x}){\eta }_2(Y|{\beta }^{\text{T}}\text{x})d\mu (\text{x})}}\\ =\frac{{\displaystyle {\int }_{{\beta }^{\text{T}}\text{x}={\beta }^{\text{T}}x}\text{f}(Y,\text{x}){\eta }_1(\text{x})d\mu (\text{x})}}{{\displaystyle {\int }_{{\beta }^{\text{T}}\text{x}={\beta }^{\text{T}}x}{\eta }_1(\text{x})d\mu (\text{x})}}.\end{array}$$

Now, we have

$$\begin{array}{c}\text{a}({\beta }^{\text{T}}\text{x})={\displaystyle \int \text{a}({\beta }^{\text{T}}x){\eta }_2(Y|{\beta }^{\text{T}}x)d\mu (Y)}\\ ={\displaystyle \int \frac{{\displaystyle {\int }_{{\beta }^{\text{T}}\text{x}={\beta }^{\text{T}}x}\text{f}(Y,\text{x}){\eta }_1(\text{x})d\mu (\text{x})}}{{\displaystyle {\int }_{{\beta }^{\text{T}}\text{x}={\beta }^{\text{T}}x}{\eta }_1(\text{x})d\mu (\text{x})}}{\eta }_2(Y|{\beta }^{\text{T}}x)d\mu (Y)}\\ =\frac{{\displaystyle {\int \int }_{{\beta }^{\text{T}}\text{x}={\beta }^{\text{T}}x}\text{f}(Y,\text{x}){\eta }_1(\text{x}){\eta }_2(Y|{\beta }^{\text{T}}x)d\mu (\text{x})d\mu (Y)}}{{\displaystyle {\int }_{{\beta }^{\text{T}}\text{x}={\beta }^{\text{T}}x}{\eta }_1(\text{x})d\mu (\text{x})}}\\ =\frac{{\displaystyle {\int }_{{\beta }^{\text{T}}\text{x}={\beta }^{\text{T}}x}{\displaystyle \int \text{f}(Y,\text{x}){\eta }_2(Y|{\beta }^{\text{T}}\text{x})d\mu (Y){\eta }_1(\text{x})d\mu (\text{x})}}}{{\displaystyle {\int }_{{\beta }^{\text{T}}\text{x}={\beta }^{\text{T}}x}{\eta }_1(\text{x})d\mu (\text{x})}}=0\end{array}$$

because E(f | x) = 0 due to $\text{f}\in {\Lambda }_1^{\perp }$. Thus, elements in Λ^⊥ indeed have the form f(Y, x) − E(f | Y, β^Tx). The requirement of these elements belonging to ${\Lambda }_1^{\perp }$ generates the second requirement of A, and we obtain Λ^⊥ ⊂ A. This completes the derivation of Λ^⊥.

A.3. The Double Robustness of (2)

Denote E*(g | x^Tβ) the misspecified function of E(g | x^Tβ). We have

$$\begin{array}{c}E[\{\text{g}(Y,{\text{x}}^{\text{T}}\beta )-E\ast (\text{g}|{\text{x}}^{\text{T}}\beta )\}\{\alpha (\text{x})-E(\alpha |{\text{x}}^{\text{T}}\beta )\}]\\ =E([E\{\text{g}(Y,{\text{x}}^{\text{T}}\beta )|\text{x}\}-E\ast (\text{g}|{\text{x}}^{\text{T}}\beta )]\{\alpha (\text{x})-E(\alpha |{\text{x}}^{\text{T}}\beta )\})\\ =E[\{E(\text{g}|{\text{x}}^{\text{T}}\beta )-E\ast (\text{g}|{\text{x}}^{\text{T}}\beta )\}\{\alpha (\text{x})-E(\alpha |{\text{x}}^{\text{T}}\beta )\}]\\ =E[\{E(\text{g}|{\text{x}}^{\text{T}}\beta )-E\ast (\text{g}|{\text{x}}^{\text{T}}\beta )\}E\{E(\alpha |{\text{x}}^{\text{T}}\beta )-E(\alpha |{\text{x}}^{\text{T}}\beta )\}]\\ =0.\end{array}$$

Denote E*(a | x^Tβ) the misspecified function of E(a | x^Tβ). We have

$$\begin{array}{c}E[\{\text{g}(Y,{\text{x}}^{\text{T}}\beta )-E(\text{g}|{\text{x}}^{\text{T}}\beta )\}\{\alpha (\text{x})-E\ast (\alpha |{\text{x}}^{\text{T}}\beta )\}]\\ =E([E\{\text{g}(Y,{\text{x}}^{\text{T}}\beta )|\text{x}\}-E(\text{g}|{\text{x}}^{\text{T}}\beta )]\{\alpha (\text{x})-E\ast (\alpha |{\text{x}}^{\text{T}}\beta )\})\\ =E[\{E(\text{g}|{\text{x}}^{\text{T}}\beta )-E(\text{g}|{\text{x}}^{\text{T}}\beta )\}\{\alpha (\text{x})-E\ast (\alpha |{\text{x}}^{\text{T}}\beta )\}]=0.\end{array}$$

A.4. The Derivation Λ^⊥ in Model (8)

Denote the nuisance tangent space corresponding to η₁, η₂, and m, respectively, Λ₁, Λ₂, and Λ_m. Straightforward derivation yields

$$\begin{array}{c}{\Lambda }_1=\{\text{f}(\text{x}):\forall \text{f}\text{such that}F(\text{f})=0\},\\ {\Lambda }_2=\{\text{f}(\epsilon ,\text{x}):\forall \text{f}\text{such that}E(\text{f}|\text{x})=0,E(\epsilon \text{f}|\text{x})=0\},\\ {\Lambda }_m=\left\{\frac{{{\eta }^{\prime }}_{20,\epsilon }(\epsilon ,\text{x})}{{\eta }_{20}(\epsilon ,\text{x})}\text{h}({\text{x}}^{\text{T}}\beta ):\forall \text{h}\right\}.\end{array}$$

Consequently, we have

$$\begin{array}{c}{\Lambda }_1^{\perp }=\{\alpha (\epsilon ,\text{x}):\forall \alpha \text{such that}E(\alpha |\text{x})=0\},\\ {({\Lambda }_1+{\Lambda }_2)}^{\perp }=\{\alpha (\text{x})\epsilon :\forall \alpha \}.\end{array}$$

To further derive Λ^⊥ ⊂ (Λ₁ + Λ₂)^⊥, we first inspect an α(x)ε ∈ Λ^⊥. For any h(x^Tβ), α(x) satisfies

$$\begin{array}{c}0={\displaystyle \int \alpha (\text{x})\epsilon \frac{{{\eta }^{\prime }}_{20,\epsilon }(\epsilon ,\text{x})}{{\eta }_{20}(\epsilon ,\text{x})}\text{h}({\text{x}}^{\text{T}}\beta ){\eta }_{10}(\text{x}){\eta }_{20}(\epsilon ,\text{x})d\mu (\epsilon )d\mu (\text{x})}\\ ={\displaystyle \int \alpha (\text{x})\text{h}({\text{x}}^{\text{T}}\beta ){\eta }_{10}(\text{x})\left\{{\displaystyle \int \epsilon {{\eta }^{\prime }}_{20\epsilon }(\epsilon ,\text{x})d\mu (\epsilon )}\right\}d\mu (\text{x})}\\ =-{\displaystyle \int \alpha (\text{x})\text{h}({\text{x}}^{\text{T}}\beta ){\eta }_{10}(\text{x})\left\{{\displaystyle \int {\eta }_{20}(\epsilon ,\text{x})d\mu (\epsilon )}\right\}d\mu (\text{x})}\\ =-E\{\alpha (\text{x})\text{h}({\text{x}}^{\text{T}}\beta )\}.\end{array}$$

This implies E{α(x) | x^Tβ} = 0. Therefore,

$$\begin{array}{c}{\Lambda }^{\perp }=[\{\alpha (\text{x})-E(\alpha |{\text{x}}^{\text{T}}\beta )\}\epsilon :\forall \alpha ]\\ =[\{Y-E(Y|{\text{x}}^{\text{T}}\beta )\}\{\alpha (\text{x})-E(\alpha |{\text{x}}^{\text{T}}\beta )\}:\forall \alpha ].\end{array}$$

A.5. Regularity Conditions for Theorem 1

(C1) The univariate kernel function K(·) is Lipschitz, has compact support. It satisfies

$$\begin{array}{c}{\displaystyle \int K(u)\mathrm{du}=1,{\displaystyle \int u^{i}K(u)\mathrm{du}=0,1\le i\le m-1,}}\\ 0\ne {\displaystyle \int u^{m}K(u)\mathrm{du}<\infty .}\end{array}$$

The d-dimensional kernel function is a product of d univariate kernel functions, that is, $K_h(\text{u})=K(\text{u}/h)/h^d={\Pi }_{j=1}^d{K}_h(u_j)={\Pi }_{j=1}^{d}K(u_j/h)/h^d$ for u = (u₁, …, u_d)^T. Here, we abuse the notation and use the same K regardless of the dimension of its argument.

(C2) Let r₁(x^Tβ) = E{α(x) | x^Tβ}f(x^Tβ) and r₂(x^Tβ) = E{g(Y, x^Tβ) | x^Tβ}f(x^Tβ). The mth derivatives of r₁(x^Tβ), r₂(x^Tβ) and f(x^Tβ) are locally Lipschitz-continuous.

(C3) The density functions of x and x^Tβ, denoted, respectively, by f_x(x) and f(x^Tβ), are bounded from below and above. Each entry in the matrices E{α(x)α^T(x) | x^Tβ} and E{g(Y, x^Tβ)g^T(Y, x^Tβ) | x^Tβ} is locally Lipschitz-continuous and bounded from above as a function of x^Tβ.

(C4) The bandwidth h = O(n^−κ) for 1/(4m) < κ < 1/(2d).