Automated Maximum Likelihood Separation of Signal from Baseline in Noisy Quantal Data

Abstract

Data recordings often include high-frequency noise and baseline fluctuations that are not generated by the system under investigation, which need to be removed before analyzing the signal for the system’s behavior. In the absence of an automated method, experimentalists fall back on manual procedures for removing these fluctuations, which can be laborious and prone to subjective bias. We introduce a maximum likelihood formalism for separating signal from a drifting baseline plus noise, when the signal takes on integer multiples of some value, as in ion channel patch-clamp current traces. Parameters such as the quantal step size (e.g., current passing through a single channel), noise amplitude, and baseline drift rate can all be optimized automatically using the expectation-maximization algorithm, taking the number of open channels (or molecules in the on-state) at each time point as a hidden variable. Our goal here is to reconstruct the signal, not model the (possibly highly complex) underlying system dynamics. Thus, our likelihood function is independent of those dynamics. This may be thought of as restricting to the simplest possible hidden Markov model for the underlying channel current, in which successive measurements of the state of the channel(s) are independent. The resulting method is comparable to an experienced human in terms of results, but much faster. FORTRAN 90, C, R, and JAVA codes that implement the algorithm are available for download from our website.

Introduction

During analysis of experimental data, it is often necessary to first remove from data records any baseline fluctuations (1–6) that are not generated by the phenomenon under study. If nothing is known about the signal beyond its power spectrum, then the best solution is a Wiener filter. But when the idealized signal takes on only certain values, such as in patch-clamp recordings of ion channels, maximum likelihood can be used to estimate the state of the channel(s) given some model for the noise. Experienced experimentalists are able to follow the quantal jumps by eye and subtract the drifting baseline by manually tracing out the baseline before processing by other automated methods.

In the studies of the gating behaviors of single protein ion channels using the powerful patch-clamp technique (7), instabilities in the gigaohm seals formed between isolated biological membrane patches and patch-clamp microelectrodes often result in substantial fluctuations in the magnitude of the observed current. Such baseline fluctuations are usually significantly slower than the abrupt changes in current magnitude caused by opening and closing of the protein channel, and have to be removed before the current traces can be analyzed by standardized algorithms such as QUB (8) and HJCFit (9) that model the channel gating characteristics based on idealized data. Existing baseline subtraction algorithms can require substantial time and/or user interaction as the program requires the user to laboriously check each individual fit by eye and/or to input nodes by hand. When this happens, the front-end to sophisticated time-series analysis algorithms (e.g., Milescu et al. (8), Qin et al. (9), and Colquhoun (10)) devolves to eyeballing and mouse clicking to indicate the baseline trajectory, which is susceptible to subjective bias. Here we develop a minimally parameterized maximum likelihood (11) approach for separating a quantal signal from a noisy and varying baseline, which gives results that largely agree with the mouse-based method and is much faster.

QUB has a set of techniques for baseline removal: linear interpolation between a set of user-defined nodes, and a combined Markov-Kalman process where QUB models the baseline as a continuous process with Markov channels superimposed. The Kalman filter tracks the baseline and the Markov idealization algorithm filters the channel kinetics from the baseline data. Qin et al. (9) use time-course fitting in which the response of the recording system to a step change in input is measured. The step response curve can then be used to estimate the response to arbitrary patterns of channel transitions. Time-course fitting requires checking the baseline before and after each opening, which is time-consuming. Burzomato et al. (12) report having obtained rate constants of ∼130,000/s, faster than the 30-kHz sampling rate (and 3 kHz filter frequency), with time-course fitting. The ability of time-course fitting to fit such fast rates was tested by repeated fits of simulated data (12,13).

Colquhoun notes:

“The most obvious danger of time-course fitting is that of over-ambitiousness. The risk of false events arising from an attempt to fit events that are too short is just the same as described above for the threshold crossing method, but the temptation to fit them may be greater. Not only genuine channel transitions, but any disturbance (artifactual or random noise), if sufficiently brief, will produce a signal that can plausibly be fitted by the time-course method” (1).

In time-course fitting, false events that arise from over-ambitiousness are subsequently removed upon imposing a maximum time resolution.

In addition, the time-course fitting approach requires an estimate of the impulse response function (the IRF or Green's function) of the recording apparatus. Whereas for patch-clamp recordings an estimate of the IRF is readily available, for other single molecule signals it might not be. An increasing variety of fluorescence techniques are being used to provide information on single or few molecule kinetics (14–22). It is not clear that IRF estimates can be obtained in all cases. Although patch-clamp recordings use a well-characterized filter, other single molecule systems may involve filtering intrinsic to the experimental methods used. In most single-molecule studies, the molecules of interest are immersed in a solution containing fluorescent indicators. Such signals involve various chemical reactions, which can themselves be considered as not particularly well-characterized filters.

Our method and the QUB Markov-Kalman method both yield a ranking: the likelihood. When these methods are run repeatedly with different initializations, one need only compare the likelihood scores to ascertain which output is best. There is virtually no subjectivity involved in this scenario. Moreover, maximum likelihood is asymptotically efficient. In the contemporary state of the art of patch-clamp data analysis, the use and application of these methods is not standardized. The method proposed here and some of the QUB methods are objective in the sense that they return a model-based maximum likelihood estimate for the data (by “model” we mean a decomposition of the data into baseline, signal, and noise), but as Box wrote: “all models are wrong” (23).

How does the innate incorrectness of the models weigh against the dangers involved in time-course fitting? We do not address the comparison of various methods in this article. Given the variety of single molecule signals researchers are obtaining, we believe that there is merit in new methods for solving this old problem, particularly ones as conceptually simple and fast as the method we put forth here.

Our technique treats the observed data as comprising three components:

• 1.A quantal current passing through ion channels;
• 2.A slowly varying baseline current that we model as a random walk; and
• 3.A white noise that represents noise within the patch-clamp amplifier and measurement apparatus.

We show in Results that the method can work equally well when the background signal is contaminated by nonwhite noise. The QUB Markov-Kalman method requires the user to provide estimates for baseline and channel properties and generates a Markov model for the channel gating kinetics. Our method does not generate a Markov model. In the case of a single channel, our method returns a conditional posterior probability that the channel is open at each time point. Thus, if the channel P_O (equilibrium open probability) changes abruptly for whatever reason, it does not pose difficulties for our method. Our method requires an initial guess for the baseline, which can be quite crude, plus an initial guess for each of three parameters corresponding to the three components of our model (as explained in Methods). These parameter initializations are automatically improved as the method runs.

The current passing through channels is given by the product of the single channel current and the number of open channels at each time point. We use the estimation/maximization (also known as the expectation maximization (EM) algorithm) to estimate the number of open channels, which is treated as missing data. The EM algorithm (24–27) was originally developed by Baum and Petrie (24) in the 1960s and formalized by Dempster et al. (27). We integrate out the baseline, which is equivalent to replacing it with a maximum likelihood estimate. In Methods, we lay out the basic theory for such a system, which yields a likelihood function for the baseline and the data that is similar to the path integral representation of the harmonic oscillator (28,29) or a Gaussian process (30). The Results section is broken down into two subsections corresponding to weak and strong filtering. We present applications of the technique to both synthetic (numerically generated) data and to ion-channel data obtained with the Axon Axopatch 200B patch-clamp amplifier (Molecular Devices, Sunnyvale, CA). We find that the algorithm works well on both weakly and strongly filtered data. The algorithm has a higher probability of error and can fail to converge on strongly filtered data.

Methods

We will describe the basic idea using the language for ion channels that are either open or closed, but the method can be used for any signal that can be reasonably approximated as consisting of some number of equally spaced steps. Both QUB and time-course fitting have methods for traces for which the channel has multiple step sizes. We have not yet developed code for unequal step sizes, but the generalization is straightforward. In this article we treat equal step sizes only. We first sketch the general theory, then signal/noise issues. This section closes with a brief explanation of the experiments that were undertaken to provide the data that the method was tested on. We remark here that one need not understand the mathematics of the general theory that underlies the technique to be able to apply the method or to use the code. For those who are interested more in using the technique than in the mathematics, we recommend reading the opening paragraph of Theory and then skipping to Signal/Noise.

Theory

We imagine an experiment producing a continuous time signal that we sample discretely at sampling frequency ν. The discrete sampling yields a data record d = (d₁,d₂,…d_T). We shall denote a generic time point in the record by d_t, where t ∈ (1,2,…,T). We assume that an open channel passes a current $\mathcal{I}$ and that a closed channel passes no current. In our model, if n_t channels are open at time t, the observed signal (the data: d_t) is given by d_t = b_t + $\mathcal{I}$n_t + σ_ξξ_t, where d_t is the baseline current flowing through the circuit although not necessarily through the ion channel, and ξ_t is discrete-time Gaussian white noise that has moments 〈ξ_t〉 = 0, 〈ξ_tξ_t′〉 = δ_tt′. Here δ_tt′ is the Kronecker delta and σ_ξ is the noise strength. We further assume that the baseline is undergoing a discrete time random walk, $b_t=b_{t-1}+{\sigma }_b{\tilde{\xi }}_t$, where ${\tilde{\xi }}_t$ is discrete-time white noise like ξ_t. Under these assumptions, it follows immediately that d_t − b_t − $\mathcal{I}$n_t and b_t+1 − b_t are zero mean Gaussian distributed random variables with variances ${\sigma }_{\xi }^2$ and ${\sigma }_b^2$, respectively. We remark that if the continuous time baseline is undergoing a continuous random walk, as modeled by a Wiener process (31), that the baseline variance should scale inversely with sampling frequency, ${\sigma }_b^2$ ∝ 1/ν. Analogous to the definition of d, we also define b and n: b = (b₁,b₂,…,b_T), n = (n₁,n₂,…n_T). Our primary goal is to obtain estimates of the n_t, but in doing so we will also obtain estimates of b, ${\sigma }_{\xi }^2$, σ²_b, and $\mathcal{I}$ as well. It turns out that it is simpler to parameterize the system in terms of ${\sigma }_{\xi }^2$ and R², where

$$R^2\equiv \frac{{\sigma }_b^2}{{\sigma }_{\xi }^2}$$ (1)

is the ratio of the baseline walk variance to the white-noise variance. We treat both n and b as missing data, although b is integrated out directly without the need of EM.

Our model implies that the joint distribution function for d, b, and n is given by

$$p\left(d,b,n;\theta \right)=\tilde{\mathcal{N}}{e}^{-\mathcal{H}\left(d,b,n;\theta \right)},$$ (2)

where $\mathcal{H}$ is an energy functional given by

$$\mathcal{H}\left(d,b,n,\theta \right)=\frac{1}{2{\sigma }_b^2}\sum _{t=1}^{T-1}{\left(b_{t+1}-b_t\right)}^2+\frac{1}{2{\sigma }_{\xi }^2}\sum _{t=1}^T{\left(d_t-b_t-\mathcal{I}{n}_t\right)}^2,$$ (3)

and where θ represents the parameters ${\sigma }_{\xi }^2$, ${\sigma }_b^2$, and $\mathcal{I}$. The value $\tilde{\mathcal{N}}$ is the normalization factor

$$\tilde{\mathcal{N}}=\frac{1}{\sum _n\int e^{-\mathcal{H}\left(d,b,n,\theta \right)}dddb},$$ (4)

where

$$\sum _n\equiv \sum _{n_1=0}^{N_{ch}}\sum _{n_2=0}^{N_{ch}}\cdots \sum _{n_T=0}^{N_{ch}}$$

and N_ch is an upper bound on the number of channels contained in the patch. The values dd and db represent the differentials of all the variables being integrated over, e.g.,

$$db=\prod _t^{T}d{b}_t.$$

In principle, we would like to maximize the likelihood of the data given the model, L(d;θ),

$$L\left(d;\theta \right)\equiv \sum _n\underset{b}{\int }p\left(d,b,n;\theta \right)db,$$ (5)

but this is unwieldy. Although the integral over T dimensions can be dealt with, the sum is over at least 2^T values and cannot be maximized in one step. Thus we employ the iterative estimation/maximization (EM) procedure. We made use of Fraser’s accessible discussion of the algorithm (32). The EM algorithm attempts to find the maximum likelihood estimate of L by first making an initial guess for $\theta =\tilde{\theta }$, and then iterating the steps

$$\begin{array}{c}Q\left({\theta }^{\prime },\tilde{\theta }\right)={\langle \log p\left(d,b,n;{\theta }^{\prime }\right)\rangle }_{p\left(b,n|d;\tilde{\theta }\right)},\\ \theta =\underset{{\theta }^{\prime }}{\arg \max }Q\left({\theta }^{\prime },\tilde{\theta }\right),\\ \tilde{\theta }=\theta .\end{array}$$ (6)

In the above, ${\langle \text{log}p\left(d,b,n;{\theta }^{\prime }\right)\rangle }_{p\left(b,n|d;\tilde{\theta }\right)}$ denotes the expectation of $\text{log}p\left(d,b,n;{\theta }^{\prime }\right)$ with respect to the distribution $p\left(b,n|d;\tilde{\theta }\right)$. The EM iteration is known to converge to, at worst, a local maximum likelihood estimate for L(d|θ).

Because of the simple dependence that the likelihood function has on b, we can integrate b out and then employ a slightly modified version of the EM algorithm to solve the remaining maximum likelihood problem,

$$p\left(d,n;\theta ,b^{\ast }\right)\equiv \int p\left(d,b,n;\theta \right)\prod _{i=1}^{T}d{b}_i=\tilde{\mathcal{N}}\int e^{-\mathcal{H}\left(d,b,n;\theta \right)}\prod _{i=1}^{T}d{b}_i=\mathcal{N}{e}^{-\mathcal{H}\left(d,b^{\ast },n;\theta \right)},$$ (7)

where b^∗ is the maximum likelihood estimate of b (or equivalently, the saddle-point) found by minimizing the energy $\mathcal{H}$,

$$-{\frac{\partial \mathcal{H}}{\partial b}|}_{b=b^{\ast }}=\frac{1}{{\sigma }_b^2}\Delta b^{\ast }+\frac{1}{{\sigma }_{\xi }^2}\left(d-b^{\ast }-\mathcal{I}n\right)=0,$$

and Δ is the finite difference Laplacian,

$$\text{Δ}{b}_i\equiv b_{i+1}+b_{i-1}-2b_i.$$

Thus

$$b^{\ast }\left(d,n,\theta \right)={\left(-\Delta +R^2\right)}^{-1}\left(d-\mathcal{I}n\right).$$ (8)

The Laplacian and associated boundary conditions are discussed in the Appendix. The normalization constant $\mathcal{N}$ is given by

$$\mathcal{N}\approx \frac{1}{{\left(1+N_{ch}\right)}^T}{\left(\frac{1}{2\pi }\right)}^{T/2-1/2}{\left(\frac{1}{{\sigma }_{\xi }^2}\right)}^{T/2-1/2}\frac{2^{T/2}R}{{\left(2+R^2+\sqrt{R^4+4R^2}\right)}^{T/2}}.$$ (9)

The steps leading from Eq. 7 to Eq. 9 are discussed in the Appendix. As written, the b^∗ in the argument of p(d,n;θ,b^∗) in Eq. 7 is redundant because b^∗ is a known function of d, n, and θ. The reason we have employed this seemingly redundant notation is just to make clear in the algorithm which value of b^∗ (old or updated) we used to compute the expected values of n.

We discuss the precise form that our implementation of the EM algorithm takes in the Appendix. The distribution $p\left(b,n|d;\tilde{\theta }\right)$, needed for Q in Eq. 6, becomes $p\left(n|d,\tilde{\theta },{\tilde{b}}^{\ast }\right)$ after integrating out b. To find $p\left(n|d,\tilde{\theta },{\tilde{b}}^{\ast }\right)$, we note that, in general, p(x|y) = p(x,y)/p(y). Thus,

$$p\left(n|d,\tilde{\theta },{\tilde{b}}^{\ast }\right)=\frac{p\left(d,n;\tilde{\theta },{\tilde{b}}^{\ast }\right)}{\sum _{n}p\left(d,n;\tilde{\theta },{\tilde{b}}^{\ast }\right)}=\frac{e^{-\mathcal{H}\left(d,{\tilde{b}}^{\ast },n;\tilde{\theta }\right)}}{\sum _n{e}^{-\mathcal{H}\left(d,{\tilde{b}}^{\ast },n;\tilde{\theta }\right)}}=\prod _{t=1}^{T}p\left(n_t|d_t,\tilde{\theta },t\right).$$ (10)

The quantity $p\left(n_t|d_t,\tilde{\theta },t\right)$ is the conditional probability that there are n_t channels open at the single time point t. To simplify the notation, we write $p\left(j|d_t,\tilde{\theta },t\right)$ to indicate the conditional probability that there are j channels open at time t,

$$p\left(j|d_t,\tilde{\theta },t\right)=\frac{\exp \left(-\frac{{\left(d_t-{\tilde{b}}_t^{\ast }-\tilde{\mathcal{I}}j\right)}^2}{{\tilde{\sigma }}_{\xi }^2}\right)}{\sum _{k=0}^{N_{ch}}\exp \left(-\frac{{\left(d_t-{\tilde{b}}_t^{\ast }-\tilde{\mathcal{I}}k\right)}^2}{{\tilde{\sigma }}_{\xi }^2}\right)}=\frac{1}{\sum _{k=0}^{N_{ch}}{e}^{{\eta }_{jt}-{\eta }_{kt}}},$$ (11)

where

$${\eta }_{mt}\equiv \frac{{\left(d_t-{\tilde{b}}_t^{\ast }-m\tilde{\mathcal{I}}\right)}^2}{2{\tilde{\sigma }}_{\xi }^2},m=0,1,2,3,\dots N_{ch}.$$

We will use angle brackets without subscripts to denote expectations with respect to $p\left(j|d_t,\tilde{\theta },t\right)$ so that

$$\langle n_t^s\rangle \equiv \sum _{j=0}^{N_{ch}}{j}^{s}p\left(j|d_t,\tilde{\theta },t\right).$$

For a single channel or single molecule recording, N_ch = 1 and Eq. 11 results in

$$\langle n_t\rangle =\frac{1}{e^{{\eta }_{1t}-{\eta }_{0t}}+1}.$$

For a single ion channel (or molecule) with multiple equally spaced conductance states, N_ch + 1 represents the total number of conducting states that the system can take.

At this point, we can write Q explicitly as

$$Q\left(\theta ,\tilde{\theta }\right)=\log \mathcal{N}-\frac{1}{2{\sigma }_b^2}\sum _{t=1}^{T-1}{\left(b_{t+1}^{\ast }-b_t^{\ast }\right)}^2-\frac{1}{2{\sigma }_{\xi }^2}\sum _{t=1}^T\langle {\left(d_t-b_t^{\ast }-\mathcal{I}{n}_t\right)}^2\rangle .$$ (12)

The dependence on $\tilde{\theta }$ is only through b^∗ and the angle brackets. The end result of this calculation is that we replace the dependence in $\mathcal{H}$ on powers of n_t with the expected value of those powers: n_t → 〈n_t〉 and n²_t → 〈n²_t〉. We maximize $Q\left(\theta ,\tilde{\theta }\right)$ by updating θ iteratively in the following steps:

Step 0 (Initialization)

Make initial guess for ${\tilde{b}}_t^{\ast },{\sigma }_{\xi }^2,\mathcal{I}$, and $R^2$: $\tilde{\theta }=\left({\sigma }_{\xi }^2,\mathcal{I},R^2\right)$.

Step I (Estimate or expectation)

Update the expected values of n_t and n_t² with respect to p(j|d_t,θ,t), which we will denote 〈n_t〉 and 〈n_t²〉,

$$\langle n_t^s\rangle =\sum _{j=0}^{N_{ch}}{j}^{s}p\left(j|d_t,\theta ,t\right).$$ (13)

At the end of this step, n_t and n_t² in $\mathcal{H}$ will be replaced by 〈n_t〉 and 〈n_t²〉, respectively.

Step II (Maximize)

A. Update baseline signal:

$$b^{\ast }={\left(-\Delta +{\tilde{R}}^2\right)}^{-1}\left(d-\tilde{\mathcal{I}}\langle n\rangle \right).$$

We obtain b^∗ with a standard tridiagonal matrix solver, which is very fast. Note the dependence in b^∗ is on $\tilde{\theta }$ rather than on θ. In substeps B, C, and D we update the parameters $\mathcal{I}$, σ²_ξ, and R² while keeping b^∗ fixed.

B. Update $\mathcal{I}$:

The derivative of Q with respect to $\mathcal{I}$ is

$$\frac{\partial Q}{\partial \mathcal{I}}=\frac{1}{{\sigma }_{\xi }^2}\sum _{t=1}^T\left(\langle n_t\rangle \left(d_t-b_t^{\ast }\right)-\mathcal{I}\langle n_t^2\rangle \right)\text{.}$$

To maximize Q with respect to $\mathcal{I}$, we set the above equation to zero, which yields

$$\mathcal{I}=\frac{{\sum }_{i=1}^T\left(d_t-b_t^{\ast }\right)\langle n_t\rangle }{{\sum }_{t=1}^T\langle n_t^2\rangle }\text{.}$$

C. Update ${\sigma }_{\xi }^2$.:

The derivative of Q with respect to 1/${\sigma }_{\xi }^2$ is

$$\frac{\partial Q}{\partial \frac{1}{{\sigma }_{\xi }^2}}=\frac{T{\sigma }_{\xi }^2}{2}-\frac{1}{2R^2}\sum _{t=1}^T{\left(b_t^{\ast }-b_{t-1}^{\ast }\right)}^2-\frac{1}{2}\sum _{t=1}^T\left({\left(d_t-b_t^{\ast }\right)}^2-2\left(d_t-b_t^{\ast }\right)\mathcal{I}\langle n_t\rangle +{\mathcal{I}}^2\langle n_t^2\rangle \right).$$

To maximize Q with respect to ${\sigma }_{\xi }^2$, we set the above equation to zero, which yields

$${\sigma }_{\xi }^2=\frac{1}{T}(\frac{1}{R^2}\sum _{t=1}^T{\left(b_t^{\ast }-b_{t-1}^{\ast }\right)}^2+\sum _{t=1}^T\left({\left(d_t-b_t^{\ast }\right)}^2-2\left(d_t-b_t^{\ast }\right)\mathcal{I}\langle n_t\rangle +{\mathcal{I}}^2\langle n_t^2\rangle \right).$$ (14)

D. Update R²:

The derivative of Q with respect to R² is

$$\frac{\partial Q}{\partial R^2}=\frac{\mathcal{B}}{2{\sigma }_{\xi }^2{R}^4}-T\frac{1+\frac{2+R^2}{\sqrt{4R^2+R^4}}}{2+R^2+\sqrt{4R^2+R^4}},$$

where $\mathcal{B}\equiv {\sum }_{t=1}^{T-1}{\left(b_{t+1}^{\ast }-b_t^{\ast }\right)}^2$. The updated R² is the single real positive root of ∂Q/∂R² = 0. At this point, $\tilde{\theta }=\left({\sigma }_{\xi }^2,\mathcal{I},R^2\right)$.

E. Return to Step I:

To summarize, we iterate the steps described above in the order Step 0 $\to$ Step I $\to$ Step II $\to$ Step I. So, in the E step, we compute the N_ch expectation values of n_t for each t and in the M step, we update the parameters based on maximizing Q in Eq. 27. FORTRAN 90, C, R, and JAVA programs that perform these calculations are available at our website.

Signal/noise

There are two noise sources in our model ξ_t and ${\tilde{\xi }}_t$, where ξ_t is the noise in the data (d_t = b_t + $\mathcal{I}$n_t + σ_ξξ_t) and ${\tilde{\xi }}_t$ is the noise in the baseline $\left(b_t=b_{t-1}+{\sigma }_b{\tilde{\xi }}_t\right)$,

$${\text{SNR}}_{\xi }\equiv \frac{\mathcal{I}}{{\sigma }_{\xi }},$$ (15)

$${\text{SNR}}_{\text{b}}\equiv \frac{\mathcal{I}}{{\sigma }_b\sqrt{\text{max}\left(N_O,N_C\right)}},$$ (16)

$$SNR=\frac{\mathcal{I}}{{\sigma }_{\xi }}\sqrt{\frac{1}{1+R^2\text{max}\left(N_O,N_C\right)}},$$ (17)

where N_O and N_C are the mean number of sampling intervals for open and closed events, respectively. SNR_ξ is a standard signal/noise ratio. SNR_b indicates how much the baseline drifts relative to the current during the average open or closed event. SNR is the combined signal/noise ratio:

$$SNR=\sqrt{SN{R}_{\xi }^2+SN{R}_b^2}.$$

SNR must be several times larger than unity for the reconstruction to be reliable.

Idealization

Technically the algorithm presented thus far does not yield an idealized record. In the case N_ch = 1, the output is simply the posterior probability that the channel is open at each time point. Thus to obtain the most probable record we need only take the value of j for which $p\left(j|d_t,\tilde{\theta },t\right)$ is maximal, so that we have

$$n_t=\underset{j}{\text{argmax}}p\left(j|d_t,\tilde{\theta },t\right),$$ (18)

which requires only the N_ch function evaluations at each time point.

Experiment

Experimental records of current passing through single inositol 1,4,5-trisphosphate (IP₃) receptor (IP₃R) channels, which are ubiquitous intracellular Ca²⁺-release protein channels localized mainly to the endoplasmic reticulum and outer nuclear membranes (33), were acquired by nuclear patch-clamp electrophysiology as described in Mak et al. (34,35). Currents passing through outer nuclear membrane patches isolated at the tips of micropipettes were amplified using an Axopatch 200B patch-clamp amplifier (Molecular Devices); filtered either at 1 kHz using a tunable low-pass four-pole Bessel filter (Frequency Devices, Ottawa, IL) or at 5 or 10 KHz using the internal tunable low-pass four-pole Bessel filter of the Axopatch amplifier (Molecular Devices). The current signals were digitized at 5 kHz using an ITC16 interface (HEKA Instruments, Bellmore, NY) and recorded directly onto a data acquisition computer using the Pulse + PulseFit software (HEKA Instruments).

Results

To illustrate the use of the technique we apply it to both simulated and experimental patch-clamp data. We found that the algorithm works best on data that is unfiltered/lightly filtered but that it works with a slight modification on heavily filtered data. The difficulty with heavily filtered data is that the filtering generates correlations in the noise ξ, which becomes harder to distinguish from a random walk. Larger R² values can give higher likelihoods but worse reconstructions on heavily filtered data because the model assumes no filtering. We found that for the heavily filtered data the algorithm performed better if we held R² fixed. Choosing a good value of R² takes some experience or repeated comparisons of the output (n) to the input data.

Synthetic data

To generate the synthetic data we need to simulate both signal and noise. The signal is simulated by first choosing the desired number of open/closed pairs and then choosing a desired equilibrium open probability (P_O) and mean open time with the open time specified in units of the sampling interval, N_O. Then the length of each open event is chosen randomly to give the selected mean. Closed event lengths with a mean closed interval N_C are determined in the same way. In the simulation presented here, we added two twists to make the simulated data more challenging by having it violate the model in a few plausible ways:

First, we chose the P_O for the first-half of the record to be 0.1 and to be 0.2 for the second-half of the record. This was done to simulate nonstationarity of the channel behavior.

Second, in addition to the noise ξ, we also treated $\mathcal{I}$ as a random variable with a well defined mean, $\langle \mathcal{I}\rangle$, and variance σ²_ξ. This was done because ion channel signals are usually noisier when the channel is open than when it is closed. Thus the effective σ_ξ, σ_ξeff, is ${\sigma }_{\xi \text{eff}}=\sqrt{2}{\sigma }_{\xi }$ because of the extra noise when the channel is open. (The variance doubles so the standard deviation goes up by $\sqrt{2}$.)

We then chose to use a total of 10,000 open/closed pairs. For the simulation discussed here, this gave us n_t for ∼T = 151,000 time points. Next we construct a random walk for the baseline according to $b_t=b_{t-1}+{\sigma }_b{\tilde{\xi }}_t$, where ${\tilde{\xi }}_t$ is a unit norm, zero mean normal deviate. We construct simulated data according to

$$d_t=b_t+{\mathcal{I}}_t{n}_t+{\sigma }_{\xi }{\xi }_t,$$

where ξ_t is a unit norm, zero mean normal deviate. We chose $\langle \mathcal{I}\rangle$ = 40, σ_ξ = 5, and σ_b = 2. We used N_O = 2 for the entire record, and the mean closed interval, N_C, switched from 18 to 8 half-way through the simulation (so that the P_O switched from 0.1 to 0.2 half-way through the record). In this case, R² = ${\sigma }_{\xi }^2$/σ²_eff ≈ 0.08 and $\mathcal{I}$/σ_ξeff = 7.07 so that

$$SNR=\frac{40/{\sigma }_{\xi eff}}{\sqrt{1+R^2\text{max}\left(N_O,N_C\right)}}\approx 3.6.$$

This was meant to be challenging for the algorithm. For most runs we were able to find an estimate of n that was accurate to >$1\text{\%}$. In Fig. 1, a and b, the thin lines show a snippet of the time series we generate by this process. The thick line in Fig. 1 a is the algorithm’s estimate of 〈n_t〉. The thick line in Fig. 1 b is the algorithm’s estimate of b. With these challenging parameters we occasionally have to play with the starting guesses for the parameters, particularly the initial single channel current, $\mathcal{I}$, before the algorithm returns a reasonably accurate estimate of n. Whether an estimate of n is reasonably accurate or not is determined by visual comparison between the estimated n and the raw data.

Figure 1.

Simulated data. (a) (Thin line) Simulated signal d. (Dashed line) Algorithm’s estimate of b_t + $\mathcal{I}$〈n_t〉. (Dotted line) Estimated baseline, b_t. (b) (Thin line) Simulated signal d. (Thick line) Estimate for b that the algorithm found.

Unfiltered synthetic data

For this case we took the data as described above and applied our algorithm to it. We found that we sometimes need to alter the initial guess for the baseline to reach a better solution. For the results presented here we chose b_t = 0.95 d_t for the initial guess for the baseline. There is nothing fundamental about the choice of initial baseline. It is probably wise to try several different guesses, particularly if one is having difficulty generating a visually satisfactory estimate of n. The initial guesses for the other parameters were R² = 0.1, ${\sigma }_{\xi }^2$ = 20, $\mathcal{I}$ = 505, and N_ch = 1. With these guesses the algorithm converged in 38 iterations (which took a few seconds) and gave estimates for the current of $\mathcal{I}$^est = 39.9558, P_O^est = 0.131128, σ^est2_ξ = 28.1459, and R² = 0.141. The true $P_O^{\text{true}}=0.1316$. We found the total error

$$\sum _t\left|n_t-n_t^{\text{est}}\right|$$

was ∼100, which means >$99.9\text{\%}$ correct despite the SNR of 3.6. Snippets of the data are shown in Fig. 1. The upper graph shows 500 time points. The thin line is the raw synthetic data. The dashed line is the reconstruction b_t^est + $\mathcal{I}$^estn_t^est. The dotted line is b_t^est. As general rule we recommend comparing d_t, b^est, and b_t^est + $\mathcal{I}$^estn_t^est. The lower graph is a larger sample of the data. The thin line is the raw data and the thick one is the estimate of the baseline that the algorithm returned.

Filtered synthetic data

We generated filtered data, $\tilde{d}$, beginning with unfiltered data, (d), from the previous subsection. We filtered diffusively through

$${\tilde{d}}_t^{\left(n+1\right)}={\tilde{d}}_t^{\left(n\right)}+D\left({\tilde{d}}_{t+1}^{\left(n\right)}+{\tilde{d}}_{t-1}^{\left(n\right)}-2{\tilde{d}}_t^{\left(n\right)}\right),$$

with $D=0.15$ for six steps where ${\tilde{d}}^{\left(0\right)}=d$. This produced the time series shown as the dark line in Fig. 2. The thin line in that figure is the unfiltered data (d) for the same snippet shown in the top panel of Fig. 1. In this case we made initial guesses of R² = 1, ${\sigma }_{\xi }^2$ = 20, $\mathcal{I}$ = 65.6, and b_t = 0.95 d_t. We held R² fixed because updating R² on this data results in an R² that appears to increase without bound. This appears to be an essential aspect of filtering that, in our view, is a significant corruption of the data. Filtering generates unwanted correlations in the noise. Consequently the algorithm has trouble distinguishing between the drifting baseline and the white noise. It tends to conclude that all the noise is baseline, thus R² → ∞ if we update R². Fig. 3 shows the best reconstruction we were able to produce in a few minutes of playing around with various initial parameters. The heavily filtered data used in Fig. 3 came from the same time series as the lightly filtered data used in Fig. 1. Fig. 1 a and Fig. 3 can be directly compared. The algorithm converged in 86 iterations (which took a few seconds) and generated the following estimates of $\mathcal{I}$^est,filtered = 12, P_O^est,filtered = 0.171, and (σ_ξ^est,filtered) = 5. The true P_O^true = 0.1316. The total error was ∼8800, which represents a fractional error of 8800/151,000 = 0.05. Note though that whereas the P_O is off by 0.04, the fractional error in P_O is ∼25%. Clearly we cannot compare the output likelihood scores for different R² values when using the algorithm with fixed R² on heavily filtered data. If the likelihood score cannot be trusted for filtered data then the only way to compare different candidate solutions is by visually comparing them to the input data and ranking them. This is arduous and time-consuming. Ultimately we recommend that the data not be filtered except for frequencies above the sampling rate.

Figure 2.

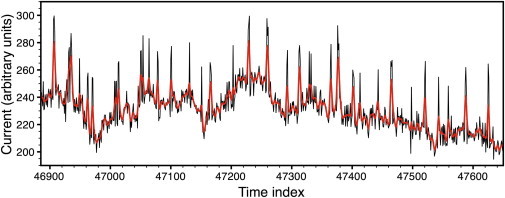
Simulated data. (Thin line) The same unfiltered synthetic data shown in Fig. 1a. (Thick line) Diffusively filtered data.

Figure 3.

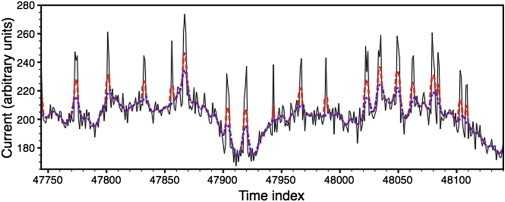
Synthetic filtered data. (Thin line) Unfiltered synthetic data. (Dashed line) Algorithm’s estimate of b_t + $\mathcal{I}$〈n_t〉. (Dotted line) Estimated baseline, b_t. This is the same segment as shown in Figs. 1 and 2. The algorithm had a fairly low error rate on this segment. The total summed error for the filtered data is 8801.

Synthetic data with nonwhite noise

Our method worked equally well on data contaminated by nonwhite noise. We filtered the white noise so that its power spectrum increases with frequency similar to the observed noise (Fig. 4) (see Fig. 1B of Shapovalov and Lester (36) for comparison) and contaminated the background signal with the resulting nonwhite noise. The unfiltered time-trace was generated as described above. We processed 1000 such time-series traces, each having more than 100,000 points and 10,000 events. The mean error was computed by averaging the total error for each run

$$\left(\sum _t\left|n_t-n_t^{\text{est}}\right|\right)$$

over the 1000 runs. The total error averaged over the 1000 runs with white and nonwhite noise was 65.235 and 65.127, respectively, meaning that only 65 time points out of 100,000 were classified incorrectly in either case.

Figure 4.

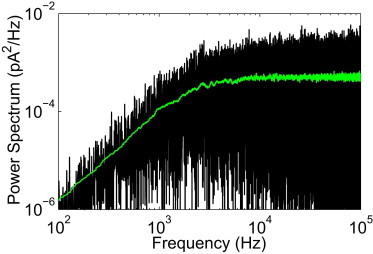
Power spectrum of unfiltered synthetic data with non-white noise. (Shaded line; green online) Averaged power spectrum using a moving box average with a window of 200 points.

Real data

The records shown in Figs. 5 and 6 are two segments from one of the nuclear patch-clamp experiments that studied homotetrameric recombinant rat type 3 IP₃R channels expressed in mutant chicken B cells deficient in the expression of all three of the endogenous IP₃R isoforms (37). Solution on the cytoplasmic side of the channel contained saturating [IP₃] (10 μM), optimal free [Ca²⁺] (2 μM), with physiological [K⁺] (140 mM) and free [ATP⁴⁻] (0.5 mM). Applied voltage used was 30 mV. The experiment was performed at room temperature. Two records of the same current trace but filtered with different corner frequencies of 1 and 5 kHz were acquired simultaneously. For this data we used an initial baseline guess b[j] = 18, which was an eyeball estimate of the baseline toward the end of the data. For the strongly filtered data (1 kHz corner frequency) we kept R² fixed at R² = 0.01. The other parameters were initialized to ${\sigma }_{\xi }^2$ = 0.1 and $\mathcal{I}$ = 15. This took ∼5 min of playing around with different initial parameters before a visually reasonable solution was found. The algorithm stopped after 137 iterations and returned values for the current of 13.37 pA and ${\sigma }_{\xi }^2$ of 3.13, and P_O of 0.856.

Figure 5.

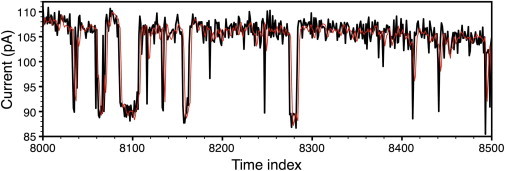
Experimental data. Sampling frequency: 5 kHz. (Thick line) Filter frequency 5 kHz. (Thin line) Filter frequency = 1 kHz.

Figure 6.

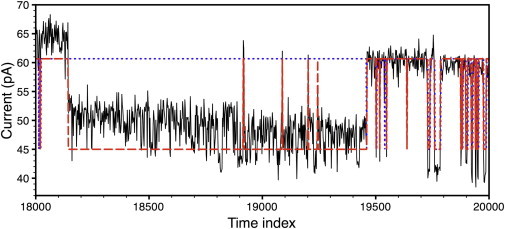
(Thin line) Raw data sampled at 5 kHz with a 5 kHz filter frequency. (Thick dashed line) The algorithm’s estimate of $\mathcal{I}$〈n_t〉 using the lightly filtered data as input. (Thick dotted line) The algorithm’s estimate of $\mathcal{I}$〈n_t〉 using the data filtered with the 1 kHz filter as input. This snippet was found by plotting running averages of the two estimates and looking for the regions where there were large differences.

The algorithm was then applied to the less filtered version of the same current trace with initial parameters R² = 0.000001, ${\sigma }_{\xi }^2$ = 0.1, and $\mathcal{I}$ = 15. In this case, we could update R². The algorithm converged in 105 iterations, which took a few seconds on the 88,000 time points. The final value for R² was 0.02 and ${\sigma }_{\xi }^2$ was 3.3. The current that was returned was 15.68 pA and P_O = 0.813. After idealization we found a mean open time of 25.4 sampling intervals. Thus the algorithm gives an estimate of the signal/noise ratios, SNR_ξ = $\mathcal{I}$/σ_ξ ≈ 8.6 and SNR ≈ 7. The fact that we obtained different values for P_O on the filtered and unfiltered data raises the question: which P_O value was more accurate?

One cannot directly compare the output for the two files because the input files are slightly shifted from each other because of the difference in filtering. Simply differencing the two data sets generates a large number of differences. Thus we computed 500-point running averages for the two output files and compared those. The running averages were largely indistinguishable, except for brief windows that stood out. In Fig. 6, we plot the raw data (thin line) with 5-kHz filtering overlain with the algorithms output for n for the 1-kHz filter frequency (thick dotted line) and the 5-kHz filter frequency (thick dashed line). In this region the channel was in a rare extended closed period. The output from the heavily filtered data missed it and estimated that the channel was open during this time, which accounts for the fact that the more heavily filtered data yielded a slightly higher P_O. Visual comparison between the output and the input is the only standard that we have for gauging the validity of a reconstruction. Thus we concluded that the signal obtained from the less filtered data is more accurate.

We also applied the method outlined to IP₃R Ca²⁺ channels from insect Sf9 cells observed in [IP₃] = 300 nM and free [Ca²⁺] = 70 μM (34,35). The top panel of Fig. 7 (black) shows 1 s of raw data (5000 sampling intervals) filtered at 5 kHz. (The raw data is available on our website in file N1_it.txt.) The middle panel of Fig. 7 (green) shows the same data after the baseline was removed by hand using spline fits. We did the spline fits for only half the file. This process took about two days for Mak, who considered this a particularly challenging data set. The bottom panel of Fig. 7 (red) shows 〈n_t〉 for the same data. This takes seconds for the algorithm to process with a few additional minutes required to find good initial guesses for the parameters and baseline.

Figure 7.

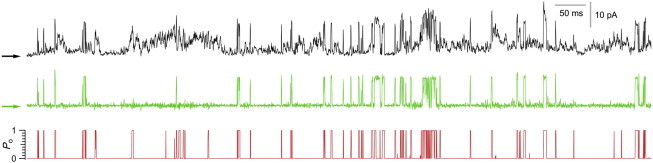
Comparison. (Top panel) Raw data. (Middle panel) Data with baseline subtracted by hand. (Bottom panel) Output of our EM algorithm.

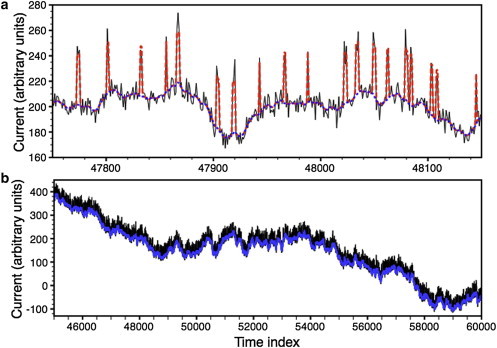
The method works equally well on patch-clamp data from multiple ion channels. Raw data (sampled at 5 kHz and filtered at 1 kHz) from a patch-clamp experiment on IP₃R from Sf9 cells ([IP₃] = 10 μM, free [Ca²⁺] = 70 μM) is shown by the thin line in Fig. 8 a, where up to three channels open simultaneously. The baseline extracted by the method is shown by the thick line in Fig. 8 a, whereas the idealized signal generated is shown in Fig. 8 b. An expanded view of a 1000 time-point segment of the raw and idealized time series from Fig. 8, a and b, is shown in Fig. 8, c and d, respectively. N_t = 0, 1, 2, and 3 in Fig. 8, b and d, represent zero, one, two, and three channels open simultaneously.

Figure 8.

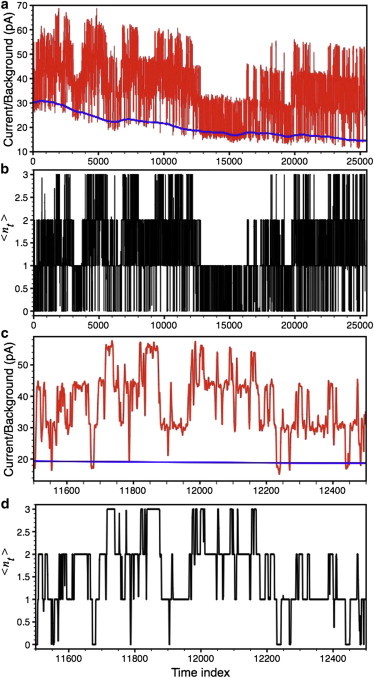
Patch-clamp data from multiple channel. (a) Raw time-series data from three simultaneously patch-clamped IP₃Rs in Sf9 cells (thin line) and the baseline extracted from the noisy data (thick line). (b) Processed signal generated by the method. (c and d) Expanded views of the traces in panels a and b, respectively.

Obtaining the codes and data

All files used in the creation of this article are available at ftp://ftp-t10.lanl.gov/pub/pearson/baseline.tar.gz. This archive includes working C and FORTRAN implementations of the baseline subtraction algorithm described in this article. It also includes R and JAVA versions that are currently under development. All other code and data used in generating this article is contained in this archive as well.

Conclusions

Baseline removal and idealization algorithms have been employed for decades(8,10). Despite that fact, many experimentalists still resort to performing this arduous task by hand. The discovery of green fluorescent protein (38) and its subsequent development by Shimomura et al. (38) has enabled experimentalists to obtain signals from a rapidly growing number of single molecules. Single molecule data is necessarily noisy. Algorithms are needed to extract signal out of the noise.

For lack of a simple automated method, experimentalists resort to the eye and mouse-based approach for processing noisy quantized signals such as the patch-clamp data representing the current through an ion channel in various conducting states. This laborious manual procedure sometimes costs experimentalists more time for processing the data than the actual experiment. Here we have developed a minimally parameterized likelihood method to process the noisy quantal data with a varying and drifting baseline. The underlying model we use assumes the data is the sum of three components: the current passing through open channels, a slowly varying baseline that we model as a random walk, and white noise.

We demonstrate the accuracy of our method by applying it to both real and synthetic time-series data. On unfiltered synthetic data we demonstrated that we could accurately reconstruct the underlying signal for a signal/noise ratio of SNR_ξ = 3.6 and SNR_ξ = 7. On heavily filtered synthetic data we were forced to hold R² fixed and the method overestimated the P_O.

When applied to experimental patch-clamp data we found SNR_ξ ≈ 8.6 and SNR_ξ ≈ 7. We had previously estimated that SNR_ξ in our patch-clamp system was between 10 and 20. We also applied the algorithm to a current trace that was recorded with two different filter frequencies. Based on visual comparison between the input data and the output data we found that the lightly filtered data yielded a more accurate solution. As expected, based on our simulations, we were forced to hold R² fixed on the more heavily filtered data but not on the lightly filtered data.

On another data set of heavily filtered experimental data, our method proved comparable to a mouse-based method in accuracy, but much faster. The method can easily be adopted for noisy quantized signals from other systems. For unfiltered/lightly filtered data, we found that we did not need to make visual comparisons between different candidate solutions. The one with the best likelihood score was always the one that gave the best visual comparison to the input data. Thus one can explore how different initial parameter values affect the outcome without needing to visually compare the different solutions. There is, however, one caveat to the likelihood score. The algorithm would occasionally return estimates of the single channel current, $\mathcal{I}$, that were near zero (femtoamps and smaller). For a single channel these solutions would always give P_O = 0.5 and they would tend to have the best likelihood scores for the data set. Ruling these bad solutions out did not require any effort because one needed only to read off the output current to know that the solution was bad. In a subsequent article, we will show that our approach can also be used on optical data.

Appendix

Normalization

Note that the energy functional has the same form as that for a driven discrete time-harmonic oscillator. Thus integrals over b are essentially path integrals for the harmonic oscillator process. Normalization requires that

$$\sum _n\int p\left(d,b,n\right)dddb=1,$$ (19)

thus

$$\tilde{\mathcal{N}}=\frac{1}{\sum _n}\frac{1}{\int e^{-\mathcal{H}\left(d,b,n,\theta \right)}dbdd},$$

where db = db₁db₂…db_T. The d differentials, dd, are defined similarly save for a minor technical point that we must discuss first.

It will prove convenient to rewrite the energy using Dirac’s notation as

$$\begin{array}{c}\mathcal{H}=\frac{1}{2{\sigma }_b^2}\langle b{\mathcal{D}}^{†}|\mathcal{D}b\rangle +\frac{1}{2{\sigma }_{\xi }^2}\langle d-b-\mathcal{I}n|d-b-\mathcal{I}n\rangle \\ =\frac{1}{2{\sigma }_b^2}\langle b|-\Delta |b\rangle +\frac{1}{2{\sigma }_{\xi }^2}\langle d-b-\mathcal{I}n|d-b-\mathcal{I}n\rangle ,\end{array}$$ (20)

where $\mathcal{D}$ is the differencing operator (with transpose $\mathcal{D}$^†),

$${\mathcal{D}}_{ij}=-{\delta }_{ij}+{\delta }_{ij+1}\text{for}i=1,2,\dots T-1,$$

$${\mathcal{D}}_{Tj}=0\text{for}j=1,2,\dots T,$$

and Δ is the discrete Laplacian, ${\text{Δ}}_{ij}=-2{\delta }_{ij}+{\delta }_{ij+1}+{\delta }_{i+1j}$ for i and j ≠ 1 or T and ${\text{Δ}}_{1j}=-{\delta }_{1j}+{\delta }_{2j}$ and ${\text{Δ}}_{Tj}=-{\delta }_{Tj}+{\delta }_{Tj+1}$.

If we could do all of the d integrals right now, we would then need to evaluate

$$\text{Int}\equiv \int \text{exp}\left(-\frac{1}{2{\sigma }_b^2}\langle b\left|-\text{Δ}\right|b\rangle \right)db.$$

A general result for Gaussian integrals of the above form is

$$\text{Int}\propto \frac{1}{\sqrt{\text{Det}\left(\text{Δ}\right)}},$$

but Δ is a singular operator; we cannot blithely do the d integrals. This is the technical difficulty that we alluded to above. We avoid this difficulty by choosing not to integrate over d₁, which is equivalent to choosing a reference current by which all others are measured.

We can rearrange the energy to single out the terms involving d₁ so that

$$\mathcal{H}=\frac{1}{2{\sigma }_b^2}\langle b|-\tilde{\Delta }|b\rangle +\frac{1}{2{\sigma }_{\xi }^2}\langle \tilde{d}-\tilde{b}-\mathcal{I}\tilde{n}|\tilde{d}-\tilde{b}-\mathcal{I}\tilde{n}\rangle +\frac{1}{2{\sigma }_{\xi }^2}\left({\left(d_1-\mathcal{I}{n}_1\right)}^2-2b_1\left(d_1-\mathcal{I}{n}_1\right)\right),$$ (21)

where $|\tilde{d}-\tilde{b}-\mathcal{I}\tilde{n}\rangle =|d_2-b_2-\mathcal{I}{n}_2,d_3-b_3-\mathcal{I}{n}_3\dots d_T-b_T-\mathcal{I}{n}_T\rangle$. The operator $-\tilde{\Delta }$ is identical to −Δ except $-{\tilde{\Delta }}_{11}=1+R^2$. Now the Gaussian integrals can be done by inspection. (First, do the d integrals over (d₂,d₃,…d_T), then all of b integrals.) This yields

$$\int e^{-\mathcal{H}}\prod _{i=1}^{T}d{b}_i\prod _{i=2}^{T}d{d}_i={\left(2\pi \right)}^{T-1/2}{\left({\sigma }_{\xi }^2\right)}^{T/2-1}{\left({\sigma }_b^2\right)}^{T/2}\frac{1}{\sqrt{\text{Det}\left(-\tilde{\Delta }\right)}},$$ (22)

where $\text{Det}\left(-\tilde{\Delta }\right)$ is the determinant of $-\tilde{\Delta }$. It is straightforward to show by induction that $\text{Det}\left(-\tilde{\Delta }\right)=R^2$. We have nearly determined $\tilde{\mathcal{N}}$ in Eq. 4:

$$\begin{array}{c}\tilde{\mathcal{N}}=\frac{1}{{\sum }_n}\frac{1}{\int e^{-\mathcal{H}}\prod _{i=1}^{T}d{b}_i\prod _{i=2}^{T}d{d}_i}\\ =\frac{1}{{\left(1+N_{ch}\right)}^T}{\left(\frac{1}{2\pi }\right)}^{T-1/2}{\left(\frac{1}{{\sigma }_{\xi }^2}\right)}^{T/2-1/2}{\left(\frac{1}{{\sigma }_b^2}\right)}^{T/2}R.\end{array}$$

The summation over n gave the factor of (1 + N_ch)^T. At this point we have managed to find the normalization factor for the full distribution function but we plan to integrate out b.

We need the marginal distribution p(d,n;θ), so we still have some work to do. Note that the energy functional has the same form as that for a discrete-time driven harmonic oscillator. Thus integrals over b are essentially path integrals for the harmonic oscillator process.

In what follows, we integrate out the b_t so that we can use maximum likelihood to find the other parameters. For the marginal likelihood we have

$$L\left(d,n;\theta \right)=\int e^{-\mathcal{H}\left(d,b,n,\theta \right)}\prod _{i=1}^{T}d{b}_i=\tilde{\mathcal{N}}\frac{{\left(2\pi {\sigma }_b^2\right)}^{T/2}}{\sqrt{\text{Det}\left(-\Delta +I{R}^2\right)}}{e}^{-\mathcal{H}\left(b^{\ast },d\right)}=\mathcal{N}{e}^{-\mathcal{H}\left(d,b^{\ast },n,\theta \right)},$$ (23)

where b^∗ is the maximum likelihood estimate of b, I is the T × T identity matrix, and

$$\mathcal{N}=\tilde{\mathcal{N}}\frac{{\left(2\pi {\sigma }_b^2\right)}^{T/2}}{\sqrt{\text{Det}\left(-\text{Δ}+I{R}^2\right)}}.$$

To calculate the determinant of −Δ + IR² we take advantage of the relationship to the path integral for the harmonic oscillator and find (29) that in the large T limit

$$\text{Det}\left(-\text{Δ}+I{R}^2\right)\approx {\left(\frac{1}{2}\left(2+R^2+\sqrt{R^4+4R^2}\right)\right)}^T,$$

so that

$$\mathcal{N}\approx \frac{1}{{\left(1+N_{ch}\right)}^T}{\left(\frac{1}{2\pi }\right)}^{T/2-1/2}{\left(\frac{1}{{\sigma }_{\xi }^2}\right)}^{T/2-1/2}\frac{2^{T/2}R}{{\left(2+R^2+\sqrt{R^4+4R^2}\right)}^{T/2}},$$ (24)

and then

$$\text{Log}\left(\mathcal{N}\right)=K+\frac{T-1}{2}Log\left(\frac{1}{{\sigma }_{\xi }^2}\right)+\text{Log}\left(R\right)-\frac{T}{2}\text{Log}\left(2+R^2+\sqrt{R^4+4R^2}\right),$$ (25)

where K is constant with respect to σ_ξ, R², and $\mathcal{I}$.

Our Implementation of the EM algorithm

Thus the form the EM algorithm takes for our model is to initialize $\theta =\tilde{\theta }$ and ${\tilde{b}}^{\ast }$, which is the starting guess for the baseline. Then we iterate the following steps:

$$b^{\ast }=\underset{b}{\text{argmin}}{\langle \mathcal{H}\left(d,b,n;\tilde{\theta }\right)\rangle }_{p\left(n|d,\tilde{\theta },{\tilde{b}}^{\ast }\right)},$$ (26)

$$Q\left({\mathcal{I}}^{\prime },{\sigma }_{\xi }^{\prime 2},R^{\prime 2},\tilde{\theta }\right)={\langle \log p\left(d,n;{\mathcal{I}}^{\prime },{\sigma }_{\xi }^{\prime 2},R^{\prime 2},b^{\ast }\right)\rangle }_{p\left(n|d,\tilde{\theta },{\tilde{b}}^{\ast }\right)},$$ (27)

$$\mathcal{I}=\underset{{\mathcal{I}}^{\prime }}{\text{argmax}}Q\left(\mathcal{I},{\sigma }_{\xi }^{\prime 2},R^{\prime 2},\tilde{\theta }\right),$$ (28)

$${\sigma }_{\xi }^2=\underset{{\sigma }_{\xi }^{\prime 2}}{\text{argmax}}Q\left(\mathcal{I},{\sigma }_{\xi }^{\prime 2},R^{\prime 2},\tilde{\theta }\right),$$ (29)

$$R^2=\underset{R^{\prime 2}}{\text{argmax}}Q\left(\mathcal{I},{\sigma }_{\xi }^2,R^{\prime 2},\tilde{\theta }\right),$$ (30)

$$\tilde{\theta }=\left(\mathcal{I},{\sigma }_{\xi }^2,R^2\right),$$

$${\tilde{b}}^{\ast }=b^{\ast }\text{.}$$

Note that b^∗ is fully specified by Eq. 8 because n is summed over in the expectation and d is given. Thus, in Eq. 27, b^∗ is simply a vector of constants, so that $Q\left(\theta ,\tilde{\theta }\right)$ is simply a function of σ²_ξ, R², and $\mathcal{I}$.