Accurate high-throughput structure mapping and prediction with transition metal ion FRET

Abstract

Mapping the landscape of a protein’s conformational space is essential to understanding its functions and regulation. The limitations of many structural methods have made this process challenging for most proteins. Here, we report that transition metal ion FRET (tmFRET) can be used in a rapid, highly parallel screen, to determine distances from multiple locations within a protein at extremely low concentrations. The distances generated through this screen for the protein Maltose Binding Protein (MBP) match distances from the crystal structure to within a few angstroms. Furthermore, energy transfer accurately detects structural changes during ligand binding. Finally, fluorescence-derived distances can be used to guide molecular simulations to find low energy states. Our results open the door to rapid, accurate mapping and prediction of protein structures at low concentrations, in large complex systems, and in living cells.

INTRODUCTION

To understand how a protein works, its underlying atomic structure and structural movements must be discovered. High-resolution X-ray and electron crystallography, along with nuclear magnetic resonance (NMR) spectroscopy, have provided unparalleled and systemic views of protein structures and dynamics. The structures of many proteins and protein families, however, have remained difficult to solve with these methods. Furthermore, even if crystallography provides detailed information regarding one state of a protein, alternate states can be difficult to solve. NMR has the advantage of providing dynamic information from a single sample and can thus provide access to multiple states, but residue assignments can be difficult, particularly for large proteins and protein complexes. For these and other reasons, alternate and complementary methods are needed to fully map the structures and structural transitions of proteins. This is particularly pertinent to the structure of proteins in complex chemical environments such as the membrane, large protein assemblies, or in living cells.

Förster resonance energy transfer (FRET) is a process where excitation energy is transferred by dipole-dipole resonance coupling from a donor fluorophore to an acceptor (Forster, 1949). The efficiency of energy transfer is equal to R₀⁶/(R₀⁶+ R⁶), where R is the distance between the donor and the acceptor, and R₀ is the distance at which the transfer efficiency is 50% for the two probes (Selvin, 1995b). This relationship makes FRET extremely sensitive to distance when the probes are spaced at distances near R₀. While FRET holds great promise as a tool for mapping molecular structures, it has been challenging to use classical FRET to map protein structures at the atomic scale for several reasons (Hillisch et al., 2001; Murchie et al., 1989; Stryer and Haugland, 1967). First, commonly used fluorescent dyes and fluorescent protein pairs have R₀values near 50 Å, and are thus most sensitive when the probes are spaced at distances between 30–70 Å. These distances are larger than many proteins. Second, standard fluorophores are large (15–30 Å), comparable to the size of many proteins or protein domains. Third, dyes are generally attached to proteins by long flexible linkers (10–15 Å). These linkers position the dipole of the dye far from the backbone of the protein. Long and flexible linkers also introduce considerable conformational uncertainty to the probes (Taraska et al., 2009a). Thus, probes can sample a large space surrounding their attachment sites, which makes the exact position of the fluorophore’s dipole relative to the protein backbone difficult to estimate, and the interpretation of FRET values problematic. Therefore, while the photo-physics of FRET makes it an attractive tool for structural biology; these and other issues with classical FRET have limited its use in structural biology.

Recently, we developed a method called transition metal ion FRET (tmFRET) that mitigates many problems associated with classical FRET (Richmond et al., 2000; Sandtner et al., 2007; Taraska et al., 2009a; Taraska et al., 2009b). In tmFRET, a colored transition metal ion (Ni²⁺or Cu²⁺) acts as an energy acceptor for small organic fluorophores such as bimane and tryptophan (Glaaser et al., 2012; Taraska et al., 2009a; Taraska et al., 2009b). Because metals have extremely low extinction coefficients, they have very short R₀ values and thus act as energy acceptors only over very short distances (Taraska et al., 2009a; Taraska et al., 2009b). This makes metal ions ideal probes for mapping short range and small-scale (5–20 Å) changes in distance within a protein. Additionally, the small donors used in tmFRET, and the ionic metal acceptors, are held close to the protein backbone, allowing them to better represent the underlying structure of the protein (Taraska et al., 2009a). Furthermore, sites used to coordinate the metal can bind Ni²⁺or Cu²⁺, and thus two different acceptors can be used to probe the same donor position. This feature helps optimize tmFRET measurements and cross-check distances. Also, the multipartite labeling scheme of tmFRET (dye linked to cysteine → metal bound to di-histidine) allows the donor and acceptor to be introduced into the protein at specific locations with flexibility and certainty. Finally, the acceptor ligand is non-covalently bound to the protein, and can thus be removed by chelators. Together, these features allow tmFRET to globally map large portions of the conformational space of a protein or protein complex.

Here, we developed a high-throughput tmFRET assay to rapidly screen multiple positions in parallel to systematically map a protein’s entire three dimensional structure and conformational changes. First, with distances generated through this screen, we determined the underlying accuracy and precision of tmFRET measurements in the protein Maltose Binding Protein (MBP) (Sharff et al., 1992). TmFRET-derived alpha carbon backbone distances were within a 1.4 Å to 3.6 Å root-mean-square deviation (RMSD) of the alpha carbon distances determined from the x-ray crystal structures of MBP. Thus, our results provide a comprehensive comparison between tmFRET measurements and high-resolution x-ray structural data. Second, we show that, along with structural mapping, tmFRET reports accurate open-to-closed distance changes in MBP in response to ligand binding. Finally, we use distances obtained from tmFRET to generate a model for the conformational transition in MBP using two different computational methods (Bermejo et al., 2009; Wu and Brooks, 2011b). Specifically, using tmFRET-based distances as constraints, we directed molecular simulations to efficiently generate the APO state configuration of MBP starting from the HOLO state with an accuracy of less than 2 Å. Combined, these methods provide the means for fast comprehensive high-resolution structure mapping with fluorescence.

RESULTS

Here, we systematically measure the structure and conformational movements of the model protein (MBP) with transition metal ion FRET (tmFRET). The availability of high-resolution structural data, along with the stability of MBP, its lack of endogenous cysteines, and its well-defined conformational transition in response to its ligand maltose, makes MBP an ideal system to test and calibrate tmFRET in proteins. Figure 1A shows the crystal structures of MBP in the open (APO, grey) and closed (HOLO, green) state (Quiocho et al., 1997; Sharff et al., 1992). MBP has two rigid domains joined by a hinge (Fig. 1A). When maltose binds between the two rigid domains, MBP closes through a hinge-bending motion, locking the maltose between the two fixed lobes of the protein (Fig. 1A).

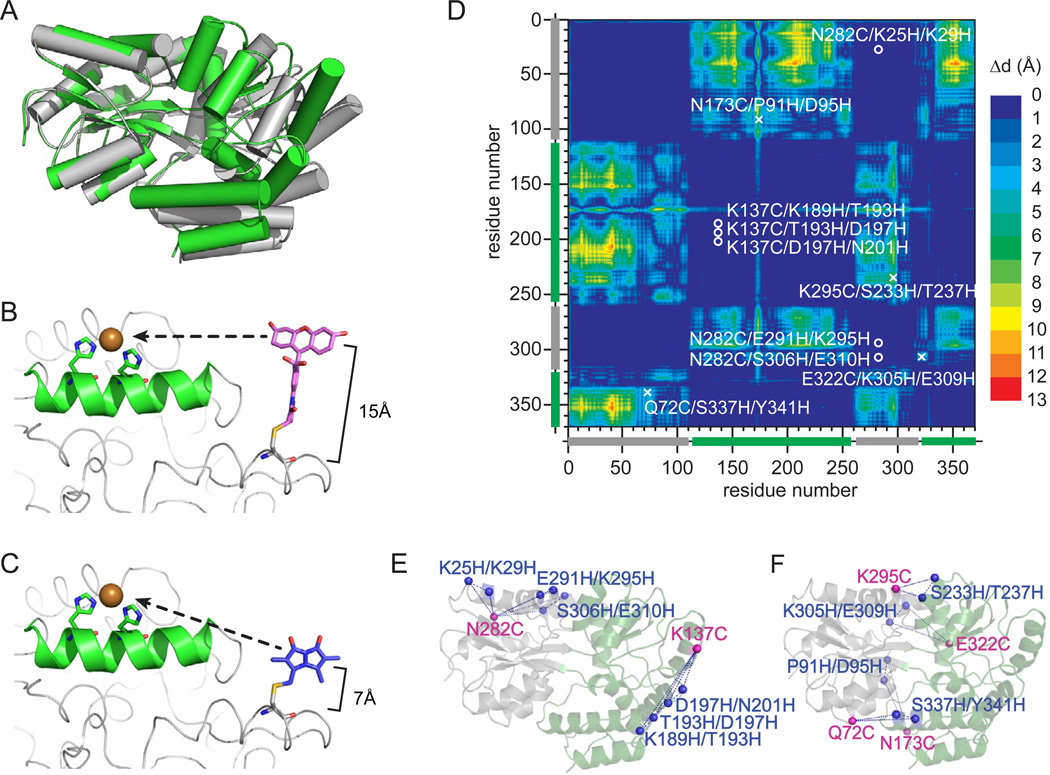
Figure 1.

Mapping the structure of MBP with tmFRET. a) The x-ray crystal structures of MBP in the APO (grey, protein data bank:1OMP) and HOLO (green, protein data bank:3MBP) states. b) Model of bi-functional labeleing of a single protein with a cysteine-linked dye fluoresceine-5-maleimide and a di-histidine coordinated metal ion or (c) cysteine-linked mono-bromobimane and a di-histidine coordinated metal ion. d) Dynamic distance map comparing the HOLO and APO state crystal structure of MBP. The colormap shows the amino acid to amino acid difference in distance between each state of the protein. The location of the chosen label sites are indicated as a circle (fixed pair) or an x (dynamic pair). d) Cartoon of the label sites in MBP. The pairs that map fixed disances are shown on the left and pairs that map dynamic distances are shown on the right.

With tmFRET, distances are measured between donor fluorophores and acceptor transition metal ions. Donor dyes are conjugated to proteins through cysteine chemistry and acceptor metals are bound to the protein by pairs of engineered histidines introduced at the i and i+4 positions on an alpha helix (Fig. 1B–C) (Taraska et al., 2009a). Here, we tested the ability of two cysteine-reactive dyes (fluorescein-5-maleimide, F5M and monobromobimane, mBBr) and two ionic metal acceptors (Cu²⁺ and Ni²⁺) to accurately map the structure and conformational movements of the protein MBP. Both F5M and mBBr have significant spectral overlap with colored transition metal ions, resulting in R₀ values of 12 Å (F5M → Ni²⁺), 16 Å (F5M → Cu²⁺), 10Å (mBBr → Ni²⁺), and 12Å (mBBr→ Cu²⁺) respectively (Taraska et al., 2009a; Taraska et al., 2009b). The molecular size, however, of these donors are different. F5M is larger than mBBr (Fig. 1B–C). Thus, the dipole of F5M in comparison to mBBr is positioned farther from the protein backbone (Taraska et al., 2009b).

To select sites in MBP to measure distances, we used three criteria. 1) The pair is within the effective tmFRET range of 5–20 Å; 2) both the cysteine and di-histidine mutation sites are solvent accessible; and 3) the di-histidine metal binding site is located on an alpha helix. As a second component in this work, we tested if tmFRET could reveal changes in structure. To identify pairs of residues that underwent a conformational change during ligand binding, we generated a dynamic distance map of the protein (Fig. 1D). This map visualizes a pair-wise comparison of alpha carbon to alpha carbon distances between the APO and HOLO crystal structures of MBP. The color index represents the size of the conformational change between each pair in the crystal structures (Fig. 1D). In this map, blue colors are pairs with little movement during the conformational transition (fixed pairs) and red color regions are pairs with large movements (dynamic pairs). Based on our above criteria, and this dynamic distance map, we selected 6 fixed pairs (Fig. 1E) and 4 dynamic pairs (Fig. 1F). Because we could use each pair with 4 dye/metal combinations in both the HOLO and APO state of MBP, this set of mutants could generate a total of 80 independent tmFRET measurements. Furthermore, because these pairs were scattered over the exposed surface of the protein, they constituted a network of sites which could be used to map the structure of the protein.

Sixteen mutant proteins were expressed and purified by amylose column chromatography. All these mutants bound to the column and were eluted with maltose, indicating that the engineered proteins retained their ability to bind maltose. The proteins were then unfolded in guanidine hydrochloride to remove the bound maltose, isolated, and then refolded. These purified and ligand-free proteins were then reacted with the cysteine-reactive dyes F5M or mBBr. The labeling efficiencies of these mutants were greater than 90%, and there was no background labeling for the wild-type cysteine-free MBP. The fluorescence anisotropy values for these mutants were measured to be between 0.05–0.20 (Supplementary Fig. 1). These low anisotropy values indicated that the dyes rotated freely around their cysteine attachment sites (Clegg, 1992; Klose et al., 2012). The addition of a saturating concentration of maltose did not substantially change the anisotropy values, demonstrating that ligand binding did not change the mobility of the probes, and affect FRET measurements by substantially changing the orientation of the dyes (Supplementary Fig. 1) (Clegg, 1992; Klose et al., 2012).

To determine distances between each pair of sites, we performed tmFRET measurements on the above dye-labeled proteins. The quantity of FRET was determined by measuring the quenching of the protein-attached fluorophores in a 96-well fiber-based micro-plate reader attached to a fluorometer (Fig. 2A). In the wells of the plate, we added increasing concentrations of metal (0 6 to 10 mM) to a constant concentration of the donor-labeled protein. For individual wells, emission spectra were collected (Fig. 2B). Thus, in one plate, 8 metal quenching curves were generated. In general, 4 rows in the same plate contained the same protein-metal pair, which provided quadruplicate measurements of each dose-response curve. This high-speed parallel fluorescence detection method vastly improved the rate and reproducibility of data acquisition compared to past FRET-based quenching methods (Klose et al., 2012; Majumdar et al., 2005; Taraska, 2012; Taraska and Zagotta, 2010).

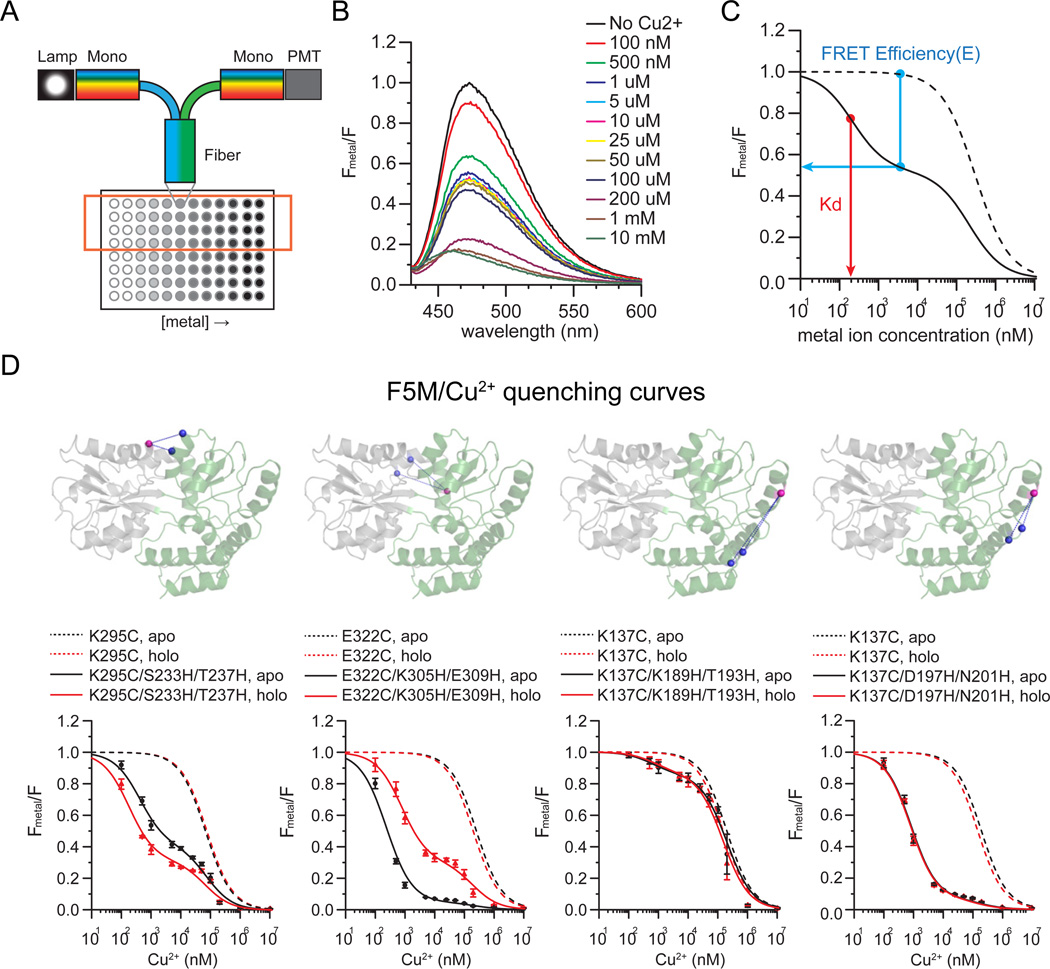
Figure 2.

tmFRET measurements of MBP. a) Cartoon of the experimental system. Fluorescence was measured in a 96 well plate through a fiber-optic launched fluorometer. Increasing concentrations of metal were added to a constant concentration of protein. b) Spectra were collected from each well and the quantity of quenching was measured. c) For analysis, spectra were normalized to the initial value at zero metal and the relative fluorescence from a di-histidine containing mutant (solid trace) was plotted as a function of metal concentration. All constructs were compared to cysteine-only controls (dotted lines). From these traces, FRET efficiencies and Kd could be determined. d) Representative quenching curves for di-histidine-containing MBP mutants (4 out of 10 are shown) compared to cysteine only controls. Spectra were collected for MBP in the absence (APO, black line) and presence (HOLO, red line) of maltose.

For analysis, fluorescence from proteins in the presence of metals (F_metal) were measured and normalized to the initial value without metals (F) (Fig. 2B). The amount of quenching at the peak (520 nm) of the spectrum (F_metal /F) was then plotted as a function of metal concentration (Fig. 2C). For each construct, fluorescence from the non-metal binding cysteine-only controls and the di-histidine-containing metal-binding mutants (Fig. 2D) were plotted. Figure 2D shows a set of tmFRET quenching experiments for MBP labeled with F5M and quenched with copper. The quenching effect observed at high metal concentration present in the controls (Fig. 2D, dotted lines) was likely due to collisional quenching between fluorophores and metal ions in solution, and could be fit with a single-site binding model (K_d1: F5M/Ni²⁺: 40.52 ± 13.61 mM, F5M/Cu²⁺: 0.14 ± 0.07 mM, mBBr/Ni²⁺: 52.63 ± 26.25 mM, mBBr/Cu²⁺: 0.39 ± 0.17 mM) (Taraska et al., 2009a). MBP mutants, however, containing di-histidine sites showed an additional higher-affinity quenching component (Fig. 2D, solid lines). This component is specific for the engineered histidines and is the result of FRET between fluorophores and bound metals (Taraska et al., 2009a; Taraska et al., 2009b). We fit the curve from di-histidine-containing mutants with a two-site binding model that accounted for both solution quenching and FRET-based quenching (Taraska et al., 2009a; Taraska et al., 2009b). Based on these fits, the FRET efficiency (E) and metal binding affinity (K_d) of the proteins could be measured. Measurements were taken for each of the 16 mutants labeled with the four sets of donor/acceptor combinations (F5M → Ni²⁺, F5M → Cu²⁺, mBBr → Ni²⁺, mBBr→ Cu²⁺) in both the APO and HOLO states (Supplementary Fig. 2, Supplementary Fig. 3, Supplementary Fig. 4, Supplementary Fig. 5). Clearly, the addition of the engineered histidines added a higher-affinity metal-dependent quenching component that was unique for each mutant. Furthermore, in some cases the amount of quenching was dependent of the presence of maltose, indicating that tmFRET was sensitive to conformational changes in MBP.

To compare distances derived from tmFRET to previous structural data we plotted all the tmFRET efficiencies taken from the 4 donor/acceptor combinations against distances from the crystal structures (Fig. 3A–D). For these comparisons, we plotted tmFRET data from the maltose-free and maltose-bound samples together. This resulted in 20 independent distance measurements for each dye-metal combination. When tmFRET efficiencies were plotted against the expected alpha-carbon distances from the crystal structures we observe a strong 1/R⁶ distance-dependence between the experimental tmFRET measurements and distances derived from the crystal structures for all dye metal combinations (Fig. 3A–D). Thus, our data followed the theoretical FRET behavior for both F5M (Fig. 3A–B) and mBBr (Fig. 3C–D). To further demonstrate that our data could be explained by a FRET mechanism, and not another type of quenching mechanism, we measured the fluorescence lifetime of a set of labeled constructs. Unlike static quenching, FRET shortens the fluorescence lifetime of a donor fluorophore in the presence of an acceptor (Lakowicz, 2006; Selvin, 1995a). For constructs within the tmFRET range, we observed a shortening of the fluorescence lifetime in the presence of metals that was dependent on the distance between the probe pairs (Supplementary Fig. 6). These data indicate that transition metal ions provide an alternate decay pathway for the excited state energy of the donor. Similar results has been observed for distance-dependent metal-dependent quenching of luminescent lanthanide ions (Sandtner et al., 2007). All these results are consistent with a FRET-based distance-dependent quenching mechanism of donor fluorophores by transition metal ions (Sandtner et al., 2007; Sutter et al., 2008; Taraska et al., 2009a; Taraska et al., 2009b). While other processes might occur at distances less than five angstroms, the data empirically fit a FRET-based model.

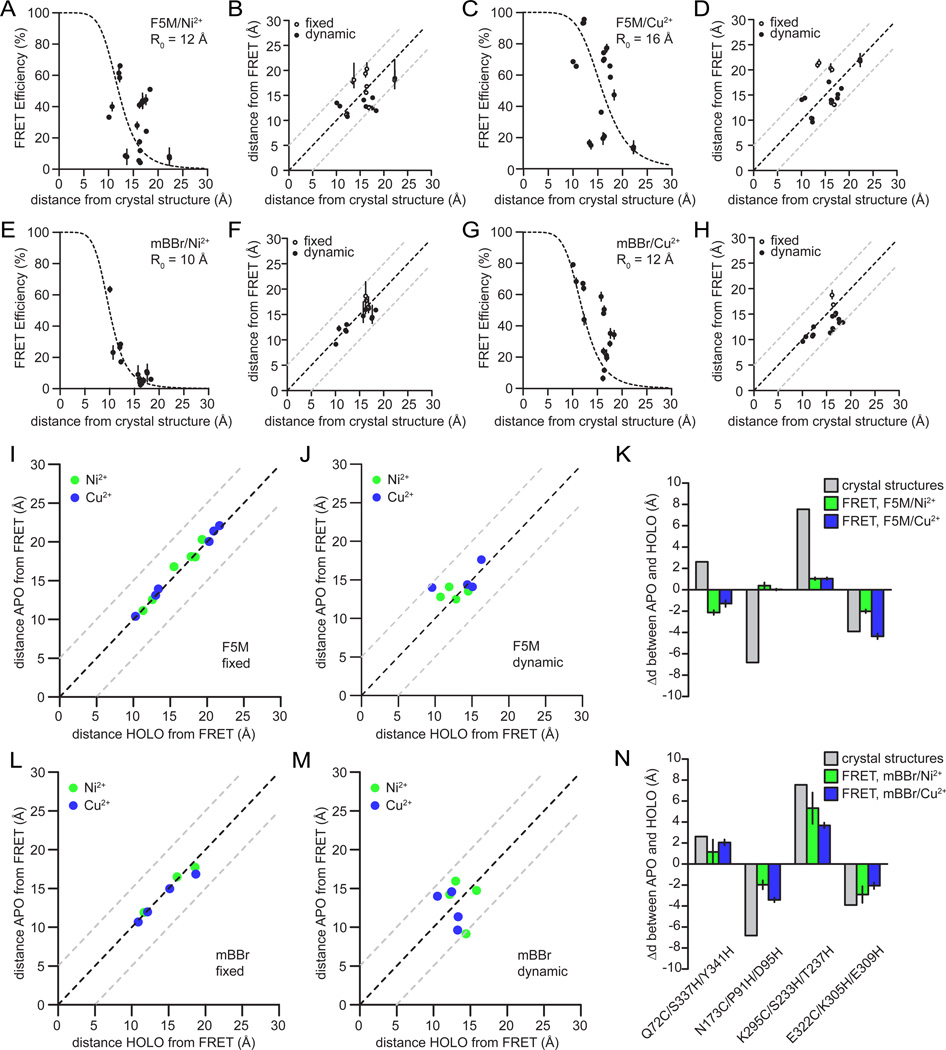
Figure 3.

Direct comparison between tmFRET distances and the x-ray crystal structure distances. a) Plot of FRET efficiences compaired to the calculated Cα-Cα distances in the crystal structure between F5M-labeled MBP mutants and nickel. The same measurements between F5M and copper (b), mBBr and nickel (c), and mBBr and copper (d). Plot of distances calculatd from FRET comapired to disntanes calulcated from the x-ray crystal structure for between F5M and nickel (e), F5M and copper (f), mBBr and nickel (g), and mBBr and copper (h). For comparisons, the probe pairs defined as fixed are shown as open circles and the dynamic pairs are shown as solid circles. i) Comparison between the APO state distances and the HOLO state distances for fixed pairs in F5M-labeled MBP donors with nickel (green) or copper (blue) acceptors. j) The same comparison for fixed pairs in mBBr-labeled MBP. k) comparison between the APO state distances and the HOLO state distances for dynamic pairs in F5M-labeled MBP donors with nickel (green) or copper (blue) acceptors. l) The same comparison for dynamic pairs in mBBr-labeled MBP. m) Measured distance changes for dynamic pairs labeled with F5M compaired to distance chages measured from the crystal structures. n) Calculated distance changes for dynamic pairs labeled with mBBr compaired to changes from the crystal structures.

Figure 3 shows the measured distances for each of the 10 constructs measured with both F5M and mBBr. These distances were strikingly similar to the distances measured from the crystal structures. The RMSD values between the tmFRET data and the crystal structures for F5M/Ni²⁺, F4M/Cu²⁺, mBBr/Ni²⁺ and mBBr/Cu²⁺ were 3.5 Å, 3.6 Å, 1.7 Å and 2.9 Å, respectively (Fig. 3E–H). These data demonstrate the accuracy and reproducibility of transition metal ion FRET compared to past FRET-based methods (Majumdar et al., 2005; Muschielok et al., 2008; Taraska, 2012; Taraska and Zagotta, 2007). Among all four dye/metal combinations, mBBr/Ni²⁺ showed the closest match to the crystal structure with an average RMS difference of 1.7 Å for APO (1OMP) and 1.8 Å for the HOLO (3MBP) structures (Fig. 3G). mBBr shows a better match to the backbone position of the crystal structure likely because of the dyes smaller size (Taraska, 2012; Taraska et al., 2009b). The measured distances, however, for both fluorophores correlated well with the alpha carbon-alpha carbon distances from the crystal structures. These data demonstrated that transition metal ion FRET can be used to determine distances between two backbone positions in a protein without the need to model the location of the dye’s dipole in space relative to the backbone.

As discussed above, we designed two classes of donor-acceptor sites for this study – fixed and dynamic. The distances between fixed pairs are not expected to change during the ligand-induced conformational change of MBP, while distances between dynamic pairs are expected to change. Figure 3i–n shows that transition metal ion FRET is able to report changes in distance between conformational states of MBP. Figures 3I & J show that the fixed pairs measured with both F5M and mBBr did not change when ligand was added to MBP. In contrast, the dynamic pairs showed substantial changes in FRET (Fig. 3K & L). While all the dynamic pairs measured with mBBr showed changes in distance, F5M did not show noticeable distance changes in two of the dynamic pairs (N173C/P91H/D95H and K295C/S233H/T237H) (Fig. 3M). Furthermore, one of the dynamic pairs for F5M showed the opposite direction of movement predicted from the crystal structure. We attribute these results to the larger size and longer linker of F5M compared to mBBr (Taraska et al., 2009b). The distance changes measured from mBBR, while slightly smaller than expected, closely match the distances and directions of changes predicted from the crystal structures to within a few angstroms (Fig. 3N). In conclusion, mBBr, likely due to its smaller size and shorter linkers, robustly and accurately detects the size and direction of protein backbone conformational changes (Taraska et al., 2009b).

To further demonstrate that tmFRET detects conformational changes, we measured changes in tmFRET as a function of the concentration of maltose. The binding constant of maltose to MBP has been reported to be 8.7 × 10⁵ M⁻¹, at 25 °C (Thomson et al., 1998). Here, we added increasing amounts of maltose to the N173C/P91H/D95H construct at a constant concentration of copper (10 µM) (Supplementary Fig. 7). Data were fit to a one-step reaction based on the receptor-ligand binding model (Brelidze et al., 2009; Cukkemane et al., 2007). The dissociation constant was calculated to be 15.8 × 10⁵ M⁻¹, which is close to the previous ITC data (Thomson et al., 1998). This shows that the amount of quenching measured in tmFRET is sensitive to the amount of protein in different conformational states, suggesting that tmFRET could be used to detect minor populations of conformations. Furthermore, tmFRET can be used to measure substrate binding affinities.

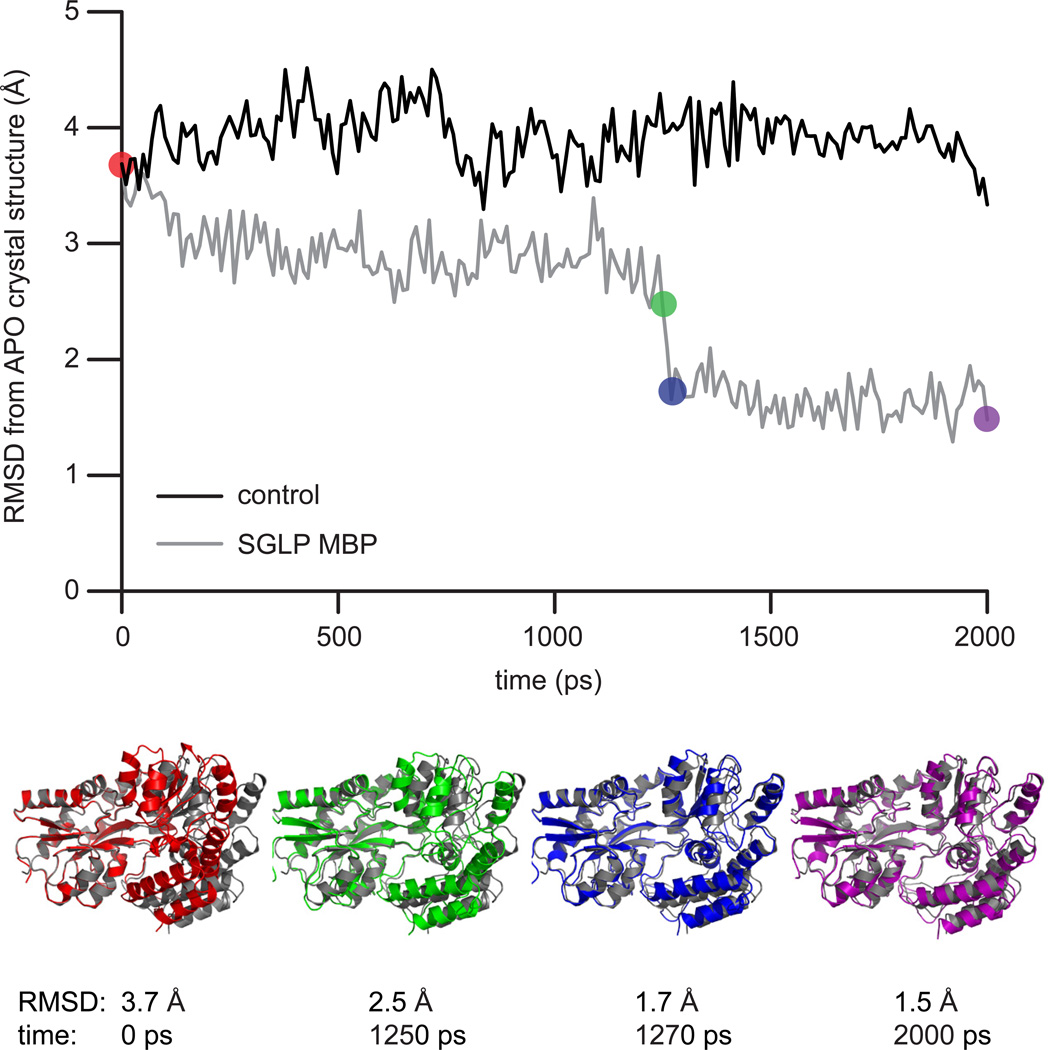
We next asked if tmFRET distances could be used to help generate the structure of an entire protein. With MBP as a model system, we used the molecular simulation method known as self-guided Langevin dynamics (SGLD) to simulate the transition of MBP from the HOLO to the APO state (Wu and Brooks, 2011b). Without any tmFRET-derived constraints, in a 2 ns simulation, MBP did not overcome the energy barrier separating the HOLO from the APO state (Fig. 4). When we, however, included six tmFRET-derived distance constraints to direct the simulation, MBP rapidly entered into the APO state (Fig. 4, Supplementary Video 1 & 2). The final simulated MBP structure matched the APO-state crystal structure with an RMSD of 1.5 Å for all backbone atoms. To confirm that our added tmFRET-derived values were influencing the simulation, we performed simulations with increasing guiding factors. These factors are the additional guiding forces added in self-guided Langevin dynamics, in comparison to Langevin dynamics, that increase the low frequency motion of the system and accelerate the conformational search. When the simulation included tmFRET constraints but no guiding force, the system did not adopt the APO conformation (Supplementary Fig. 8). With, however, increasing guiding factors, MBP rapidly entered into the APO state (Supplementary Fig. 8). The final structures for all simulations that contained the FRET constraints were closely matched, indicating that the simulation found one solution for the APO state structure (Supplementary Fig. 8). From these results, we conclude that high-throughput tmFRET measurements can help guide a molecular dynamics simulation to find the structure of an entire protein. This simulation method opens the door to determining unknown or rare states of proteins with distances generated from tmFRET.

Figure 4.

Using tmFRET distances to guide molecular simulations. a) Self-guided Langevin dynamics simulations of MBP starting in the HOLO state (PDB: 3MBP). Plot compares the RMSD during the simulation between the simulation conformation and the APO state crystal structure of MBP (PDB: 1OMP). After 2 ns of simulation, MBP does not find the APO state (black trace). With tmFRET-derived distance constraints added to the simulation, the simulation adopts the APO state within 2 ns (grey trace). Representative structures from the tmFRET-constrained simulation are shown below. The color of the simulated strucures match time-points on the graph. As a comparision, the grey structure is the APO state crystal structure.

Finally, as a comparison to the above simulation methods, we used an alternate method to model the structure of the APO state of MBP using tmFRET-based distance constraints and the HOLO state crystal structure as an initial model. This method, called rigid body/torsion angle simulated annealing, treats the two independent domains of MBP as rigid bodies and conformational motions are restricted to the torsion angles of the linkers connecting the two domains (Bermejo et al., 2012; Clore and Kuszewski, 2002; Nilges et al., 1988). This method has been used extensively for NMR structure calculations of multi-domain proteins, including the periplasmic binding protein family which MBP is a member (Madl et al., 2011; Tam and Saier, 1993) ENREF 29. When one hundred structures were generated with the addition of the four inter-domain tmFRET-derived constraints, the average RMSD between the computed structures and the APO state crystal structure was 1.48 +/− 0.13 Å (Supplementary Fig. 9). Because the two domains are treated as rigid bodies in these calculations, the intra-domain distances were not used. Without tmFRET constraints, the computed structures were within a RMSD of 3.30 +/− 0.24 Å of the APO state crystal structure (Supplementary Fig. 9). Thus, in protein systems where the conformational motion can be described as the movement of rigid bodies connected by a linker, the addition of several inter-domain tmFRET-derived constraints resulted in a two-fold improvement in structural folding.

DISCUSSION

Here we show that tmFRET is capable of measuring molecular distance and distance changes with precision and accuracy. Previous studies have shown that classical FRET measurements that use large fluorophores can mask small conformational changes and diverge from the expected structure (Majumdar et al., 2005; Taraska, 2012; Taraska et al., 2009b; Taraska and Zagotta, 2010). Transition metal ion FRET, however, tracks both fixed structures and conformational changes to within a few angstroms of those predicted from the backbone positions of crystal structures. Furthermore, these distances can be measured rapidly, in parallel, without the need to model the position of the donor or the acceptor. We show that a sparse matrix of distances generated from high-throughput tmFRET measurements can be used to model the global conformational motions of MBP with a computationally intensive self-guided Langevin dynamics simulation, and a simpler and faster rigid-body simulated annealing calculation. The final simulated structure matched the crystal structures of the APO state of MBP to within a few angstroms. Thus, tmFRET opens the door to mapping structures using nanomolar concentrations of protein, in complex systems such as the membrane, and in large macromolecular complexes. Combined with molecular simulations, fluorescence-based experimental data could help generate all-atom predictions of the complete conformational space sampled by a protein or protein complex. Similar methods have been used with EPR and NMR data (Alexander et al., 2008a; Bermejo et al., 2009; Hirst et al., 2011; Klose et al., 2012). TmFRET, however, works at protein concentrations 1000 fold less than NMR and x-ray crystallography, and 100 fold less than EPR.

The differences between tmFRET measurements and the X-ray crystal structure were between 1.7 Å and 3.6 Å RMSD ENREF 2. Here, we simplified the experimental system by considering only the Cα-Cα distances of the protein in the reference crystal structures. The dipoles of the probes, however, reside several angstroms from their Cα attachment sites. Furthermore, the rotation of the donors around their linkers creates a population of distances under which energy transfer can occur during the excited state lifetime (Lakowicz, 2006). FRET occurs more efficiently at shorter distances, biasing the measured (bulk) FRET to shorter distances. Taken together, these effects lead to a slight underestimation of the distances between attachment sites. Indeed, most bimane measurements fall below the diagonal in figure 3, highlighting this effect. While we did not model the position of the dipole in this work, modeling the conformational area occupied by the fluorophore could further reduce the differences between our tmFRET measurements and the crystal structure (Alexander et al., 2008b). However, even without extensive and complex modeling, tmFRET results in measurements that match the backbone positions with a difference less than 5 angstroms.

Here we show that fluorescein is less accurate than bimane as a donor probe for mapping distances with tmFRET. Very large common organic fluorophores on long linkers such as Alexa dyes or cyanine dyes would likely increase this error (Majumdar et al., 2005; Taraska et al., 2009b). Past work has attempted to solve this problem for large dyes by using Bayesian predictions to model a statistical cloud of possible fluorophore positions or molecular dynamics simulations (Margittai et al., 2003; Muschielok et al., 2008). From our data, we conclude that using smaller dyes such as bimane results in more accurate measurements of backbone distances in proteins without the need for complex modeling of fluorophore positions. Similar results should be obtained from native small fluorophores such as tryptophans (Glaaser et al., 2012). Both bimane and tryptophan, however, are fairly dim fluorophores. Thus, some compromise between size and brightness might need to be reached to detect extremely small amounts of protein. This would be important for tmFRET measurements in cells or in single molecule experiments.

It has been challenging to study minor conformational states of proteins. NMR has been one technique where minor sub-populations can be detected (Tang et al., 2007). Paramagnetic NMR has been used to show that a small population (5%) of MBP can exist in the closed state without ligand (Tang et al., 2007). These measurements indicated that MBP could sample the HOLO state without ligand. This, however, might not be a general rule for all periplasmic binding proteins (Bermejo et al., 2010). Like NMR, the steep distance-dependence of FRET should allow for the identification of minor populations of proteins. We, however, were unable to detect this small population of MBP in our tmFRET measurements. This could be due to the rarity of this state, the time scale under which these transitions occur, or the sensitivity of our assay for detecting very rare structural states. To experimentally observe minor populations, other measurement methods including lifetime measurements might be needed. Alternatively, single molecule measurements could be used to monitor stochastic changes in fluorescence from individual proteins.

Transition metal ion FRET measures molecular distances between 5 and 20 Å and is a powerful technique for protein structure mapping. The simple labeling scheme, combined with the easy high-throughput data acquisition and analysis, provides a robust yet sensitive method for measuring Å-scale molecular distances and conformational motions in proteins. These measurements have the potential to be done in complex biological systems, including membranes, large protein complexes, and cells. Combined with other structural methods including X-ray crystallography, small angle X-ray scattering, NMR, electron microscopy, and computational modeling, the full range of a protein’s conformational space should be revealed (Taraska, 2012; Taraska and Zagotta, 2010).

METHODS

Plasmids

Maltose Binding Protein (MBP) was subcloned from the pMAL-c5x vector (New England Biolabs). Minigenes with cysteine and di-histidine mutations were synthesized (Biobasic Inc.) and introduced into the wtMBP plasmid. A total of 16 MBP mutants (6 single-cysteine controls and 10 di-histidine mutants) were generated. All vectors were sequence confirmed.

Protein expression and purification

MBP control and mutant plasmids were transformed into BL21(DE3) competent cells (Stratagene). A single colony was suspended in 40 mL LB with ampicillin and incubated overnight at 37 °C with shaking at 250 rpm. 8 liters of bacteria were grown at 37 °C for 3.5 hours and induced with 1 mM IPTG at OD₆₀₀ of 0.4 – 0.8. Cultures were grown overnight at 18 °C and collected by centrifugation. Cell pellets were re-suspended and lysed with one c0mplete tablet (Roche) and 1 mM PMSF protease inhibitor. The supernatant was cleared by ultracentrifugation at 40,000 rpm and proteins were purified on an amylose column (New England Biolabs). The purity of the samples was confirmed by SDS-PAGE.

Fluorophore labeling

5 µL of 100 mM fluorescein-5-maleimide or monobromobimane (Invitrogen) stock solution was added to 1 mL aliquots of protein (50 µM) and incubated in the dark for 4 hours at room temperature or overnight at 4 °C. To remove maltose and unlabeled fluorophore, the protein samples were denatured and purified over a size-exclusion column in 2 M guanidine hydrochloride (Invitrogen) buffer. Buffers were then exchanged on a PD-10 column (GE Healthcare) using 6 mM HEPES (Sigma-Aldrich) and 260 mM NaCl pH 7.2 buffer (2× fluorescence buffer). The purified samples were further purified over a second size-exclusion column in fluorescence buffer to remove residual dye and denaturant. The unfolding and refolding of MBP was confirmed by circular dichroism (CD) spectra (data not shown). The amount of protein-attached fluorophore was calculated using the extinction coefficient of each dye (ε₄₉₅ = 68,000 M⁻¹ cm⁻¹ for F5M and ε₃₈₀ = 5,000 M⁻¹ cm⁻¹ for mBBr). After subtracting the contribution from the dye at 280 nm, the concentrations of MBP were calculated by measuring absorbance at 280 nm and using 64,720 M⁻¹ cm⁻¹ as its extinction coefficient. By this method, the samples had a labeling efficiency of more than 90%.

Anisotropy

Fluorescence spectra were measured on a Fluorolog fluorometer (Horiba Jobin Yvon). The labeled protein samples were diluted to a final concentration of 15 nM with and without 14 µM of maltose in fluorescence buffer. Excitation/emission values were taken at 485/519 nm for F5M-labeled samples and 390/477 nm for mBBr-labeled samples. Slits were set at 12 and 6 nm for excitation and emission, respectively. All measurements were done in triplicate, with the anisotropy module of FluorEssence.

Steady-state fluorescence

Fluorescence measurements were performed in a 96-well high-throughput plate reader attached to a fluorometer. For metal binding curves, 100 µL of MBP solution (600 nM in 2× fluorescent buffer) was mixed with an equal amount of metal solution in water. 12 wells of the 96-well plate contained metal solutions ranging from a final metal concentration of 0 to 10 mM. For measurements of the HOLO state, a 200-fold molar excess (60 µM) of maltose was added to each well. A narrowed emission window was used to speed up data-acquisition. These values were determined from the complete emission spectra measured in cuvettes. The windows were: F5M-labeled MBP, 485 nm excitation, 12 nm excitation silt, 500–525 nm emission, 6 nm emission slit; for mBBr-labeled MBP, 390 nm excitation, 12 nm excitation slit, 460–500 nm emission, 6 nm emission slit.

Data analysis

A window of 5 and 10 nm around the emission peak of F5M and mBBr were used to calculate intensity. All measurements were blank corrected and repeated at least four times. For every fluorophore/metal pair, values from 12 metal concentrations were used to fit the corresponding curve. For single-cysteine controls, the following single-site binding curve was used to account for nonspecific solution quenching of the fluorophore (Taraska et al., 2009a; Taraska et al., 2009b):

$$\frac{F_{\mathit{\text{metal}}}}{F}=\frac{1}{1+\frac{[\mathit{\text{metal}}]}{{\mathit{\text{Kd}}}_1}}$$

where F_metal and F are the fluorescence of the fluorophore with and without metal, respectively. K_d1 is the dissociation constant for solution quenching caused by free metal ions. For di-histidine mutants, a two-site binding curve fitting equation was used:

$$\frac{F_{\mathit{\text{metal}}}}{F}=(1-\frac{E}{1+\frac{{\mathit{\text{Kd}}}_2}{[\mathit{\text{metal}}]}})\left(\frac{1}{1+\frac{[\mathit{\text{metal}}]}{{\mathit{\text{Kd}}}_1}}\right)$$

where the first term on the right represents the FRET effect. E is the FRET efficiency and K_d2 is the dissociation constant for the engineered di-histidine metal binding site. The second term on the right is the same as in the single-site binding model, representing solution quenching. K_d1 was fixed at the same value as calculated from solution quenching of the control sample with the same cysteine mutation. The distance between the fluorophore and the metal binding site (R) was calculated by using the Förster equation:

$$R=R_0{(\frac{1}{E}-1)}^{\frac{1}{6}}$$

where R₀ is the Förster distance for a particular donor/acceptor pair(Selvin, 1995a; Taraska and Zagotta, 2007) ENREF 24. Values of 16 Å for F5M/Cu²⁺, 12 Å for F5M/Ni²⁺, 12 Å for mBBr/Cu²⁺ and 10 Å for mBBr/Ni²⁺ were used (Taraska et al., 2009a; Taraska et al., 2009b).

Lifetime measurements

PTI EasyLife LS fluorometer with an LED excitation source was used for lifetime measurements. The 445 nm and 340 nm LED sources were used for exciting F5M and mBBr-labeled samples, respectively. Appropriate filter sets were used to minimize the excitation light at the peak emission wavelength. For each test construct, the lifetimes in the presence of four Cu²⁺ concentrations (0, 10, 50, and 100 µM) were measured.

Maltose binding assay

The maltose binding assay was done with the high-throughput fluorometer. A 300 nM solution of the N173C/P91H/D95H construct with 10 µM Cu²⁺ were titrated with increasing concentrations of maltose (0.1 nM to 15 µM in 10 steps). All the values were normalized to the control well which contained protein and metal but no maltose. The data analysis and fitting were done in Origin (OriginLab).

SGLD Simulations

We used the CHARMM package (Brooks et al., 2009; Brooks et al., 1983) to build the simulation of maltose binding protein (MBP) from PDB structure: 3MBP (MBP HOLO state) (Quiocho et al., 1997). The PDB structure 1OMP (MBP APO state) (Sharff et al., 1992) was used as a reference to calculate RMSD values. In these simulations, the ligand was not included. The CHARMM all-atom force field (MacKerell et al., 1998) was used to describe their energy surfaces. The solvation effect was calculated with the FACT solvation model (Haberthur and Caflisch, 2008). Force-momentum based self-guiding Langevin dynamics (SGLDfp) method (Wu and Brooks, 2011a; Wu et al., 2012) was used for conformational search. This method was selected because it allows the facile crossing of barriers in the 10 Kcal/mol range while preserving the canonical ensemble. A friction constant of 1/ps was used to thermostat the systems. We used a local averaging time of 0.5 ps to focus the conformational search on domain motion. The guiding factor was set to 1 unless otherwise noted. 2 ns simulations were performed starting from the closed state and conformations were saved every 10 ps.

The FRET distance information was embedded into SGLDfp simulations similar to Nuclear Overhauser effect constraints from NMR data:

$$E_{\mathit{\text{FRET}}}=\{\begin{array}{cc}\hfill 0.5K_{\text{min}}{(r_{\mathit{\text{avg}}}-r_{\text{min}})}^2\hfill & \hfill r_{\mathit{\text{avg}}}<r_{\text{min}}\hfill \\ \hfill 0\hfill & \hfill r_{\text{min}}<r_{\mathit{\text{avg}}}<r_{\text{max}}\hfill \\ \hfill 0.5K_{\text{max}}{(r_{\mathit{\text{avg}}}-r_{\text{max}})}^2\hfill & \hfill r_{\text{max}}<r_{\mathit{\text{avg}}}<r_{\text{lim}}\hfill \\ \hfill F_{\text{max}}(r_{\mathit{\text{avg}}}-0.5(r_{\text{max}}+r_{\text{lim}}))\hfill & \hfill r_{\mathit{\text{avg}}}>r_{\text{lim}}\hfill \end{array}$$

$$r_{\text{min}}=r_{\mathit{\text{FRET}}}-2\AA$$

$$r_{\text{max}}=r_{\mathit{\text{FRET}}}+2\AA$$

The limit values, r_lim = 999Å, and F_max = 999kcal mol⁻¹ Å⁻¹, had no effect on the simulation. The constraining constant K_min and K_max were set to 1 kcal mol⁻¹ Å⁻².

Rigid Body Motion Simulations

Starting from the X-ray crystal of HOLO state MBP (PDB ID: 3MBP), the FRET-based structure of APO MBP in solution was calculated by a molecular dynamics/simulated annealing protocol that treated the backbone conformation of each domain as a rigid body, and gave the remainder of the molecule full torsion angle degrees of freedom. Calculations were performed with Xplor-NIH software (Schwieters et al., 2006; Schwieters et al., 2003), incorporating the experimentally determined FRET distances as restraints in the form of flat-bottom potentials:

$$E_{\mathit{\text{FRET}}}=\{\begin{array}{cc}{K}_{\mathit{\text{dist}}}{(L-r)}^2\hfill & \text{if }r<L\hfill \\ 0\hfill & \text{if }L<r<U\hfill \\ K_{\mathit{\text{dist}}}{(r-U)}^2\hfill & \text{if }r>U\hfill \end{array}$$

E_FRET is the potential energy associated with a FRET restraint, r is the distance between the alpha carbon of FRET donor cysteine and the mid position between the alpha carbons of FRET acceptor di-histidine during the course of a structure calculation, and L and U are the lower and upper restraint bounds, respectively. For each FRET-based target distance, d_FRET, L = d_FRET − error and U = d_FRET + error, where error is the experimental error (standard deviation) measured from the tmFRET experiments. The total energy term associated with all N FRET target distances is ${\displaystyle {\sum }_{i=1}^N}{\mathrm{E}}_{\text{FRET},i}$. Similarly, two hydrogen-bond distance restraints were applied to the beta-sheet portion of MBP’s linker region in order to preserve its integrity.

The structure computation protocol comprised the following stages: (i) high-temperature (3,500 K) torsion angle dynamics, the smallest of 15 ps or 15,000 timesteps in length, subject to the distance restraints (K_dist = 2 kcal mol⁻¹ Å⁻²), a statistical potential to bias torsion angles towards highly populated regions observed in databases of crystal structures (Bermejo et al., 2012) (K_db = 0.002 kcal mol⁻¹ rad⁻²), and van der Waals-like repulsions (Nilges et al., 1988) (K_vdw = 0.004 kcal mol⁻¹ Å⁻⁴; only Cα-Cα interactions active, with a van der Waals radius scale factor s_vdw = 1.2), where K_η represents the force constant of energy term η; (ii) torsion angle dynamics with simulated annealing, where the temperature is reduced from 3,500 to 25 K in steps of 12.5 K (the smallest of 0.2 ps/step or 200 timesteps/step), and K_dist, K_db, K_vdw, and s_vdw, are geometrically increased from 2 to 500 kcal mol⁻¹ Å⁻², 0.002 to 1 kcal mol⁻¹ rad⁻², 0.004 to 4 kcal mol⁻¹ Å⁻⁴, and 0.9 to 0.8, respectively (all van der Waals interactions active, a feature maintained in the subsequent stage, as well as the final values of force constants and s_vdw); (iii) 500 steps of Powell torsion angle minimization. 100 structures were computed with the above-described protocol and used for statistical analysis. Additionally, 100 control structures were generated with the same protocol except for the exclusion of the FRET distance constraints.

Supplementary Material

02

Supplementary Video 1. Front view of the tmFRET guided SGLD simulation of the conformational transition of MBP from the HOLO to the APO state. The simulation is colored red, the HOLO state crystal structure (PDB: 3MP) is colored grey, and the APO state crystal structure (PDB:1OMB) is colored blue.

03

Supplementary Video 2. Side view of the tmFRET guided SGLD simulation of the conformational transition of MBP from the HOLO to the APO state. The simulation is colored red, the HOLO state crystal structure (PDB: 3MP) is colored grey, and the APO state crystal structure (PDB:1OMB) is colored blue.

1. A high-throughput transition metal ion FRET (tmFRET) method is developed

2. tmFRET is used to map distances in Maltose Binding protein in the HOLO and APO states.

3. tmFRET accurately determines the structure and movements of MBP to within a few angstroms.

4. tmFRET-derived distances are used as constraints in molecular simulations.