Improving IMRT delivery efficiency with reweighted L1-minimization for inverse planning

Abstract

Purpose: This study presents an improved technique to further simplify the fluence-map in intensity modulated radiation therapy (IMRT) inverse planning, thereby reducing plan complexity and improving delivery efficiency, while maintaining the plan quality.

Methods: First-order total-variation (TV) minimization (min.) based on L1-norm has been proposed to reduce the complexity of fluence-map in IMRT by generating sparse fluence-map variations. However, with stronger dose sparing to the critical structures, the inevitable increase in the fluence-map complexity can lead to inefficient dose delivery. Theoretically, L0-min. is the ideal solution for the sparse signal recovery problem, yet practically intractable due to its nonconvexity of the objective function. As an alternative, the authors use the iteratively reweighted L1-min. technique to incorporate the benefits of the L0-norm into the tractability of L1-min. The weight multiplied to each element is inversely related to the magnitude of the corresponding element, which is iteratively updated by the reweighting process. The proposed penalizing process combined with TV min. further improves sparsity in the fluence-map variations, hence ultimately enhancing the delivery efficiency. To validate the proposed method, this work compares three treatment plans obtained from quadratic min. (generally used in clinic IMRT), conventional TV min., and our proposed reweighted TV min. techniques, implemented by a large-scale L1-solver (template for first-order conic solver), for five patient clinical data. Criteria such as conformation number (CN), modulation index (MI), and estimated treatment time are employed to assess the relationship between the plan quality and delivery efficiency.

Results: The proposed method yields simpler fluence-maps than the quadratic and conventional TV based techniques. To attain a given CN and dose sparing to the critical organs for 5 clinical cases, the proposed method reduces the number of segments by 10–15 and 30–35, relative to TV min. and quadratic min. based plans, while MIs decreases by about 20%–30% and 40%–60% over the plans by two existing techniques, respectively. With such conditions, the total treatment time of the plans obtained from our proposed method can be reduced by 12–30 s and 30–80 s mainly due to greatly shorter multileaf collimator (MLC) traveling time in IMRT step-and-shoot delivery.

Conclusions: The reweighted L1-minimization technique provides a promising solution to simplify the fluence-map variations in IMRT inverse planning. It improves the delivery efficiency by reducing the entire segments and treatment time, while maintaining the plan quality in terms of target conformity and critical structure sparing.

INTRODUCTION

The intensity modulated radiation therapy (IMRT; Refs. ^{1, 2, 3}) has been widely used for radiation therapy (RT) of various cancers as it ensures both high dose conformity to the target and reasonable dose distribution by intensity modulation. The current techniques of IMRT inverse planning can be divided into two types: direct aperture optimization (DAO; Refs. ^{4, 5, 6, 7}) and beamlet based optimization (BBO; Refs. ^{8, 9, 10, 11, 12}). DAO has the advantage of including the multileaf collimator (MLC) physical constraints into the plan optimization, but being computationally expensive due to the nonlinear relationship between the MLC shape and dose distribution. On the other hand, BBO first optimizes the fluence maps, which will then be converted to deliverable segments by a leaf-sequencing algorithm. Due to unconstrained level of beamlet intensities, the optimized fluence maps can be arbitrarily complex with BBO.

In order to reduce the complexity and constrain the intensities of fluence maps, various mathematical techniques have been proposed for fluence-map optimization such as L2-minimization (min.) for smoothing,^{13, 14, 15, 16, 17, 18, 19} and L1-min. for the (first-order) total-variation (TV) min.^{20, 21} In particular, several studies^{20, 21, 22, 23} have demonstrated that the TV form for the fluence-map optimization successfully reduces the complexity of the fluence-map by enhancing the sparsity of the fluence-map variations, and desirably facilitating the dose delivery, while maintaining similar plan quality. However, when stronger dose constraints are imposed on the critical structures, such as in complicated cases and hypofractionated radiotherapy, the fluence-map optimized by TV-min. may become too complicated, which will inevitably leads to inefficient dose delivery.

Theoretically, L0-min., which minimizes the number of nonzero elements, provides the ideal solution for sparse signal reconstruction. In practice, however, solving the L0-min. problem was computationally intractable because minimizing the number of the nonzero elements is a nonconvex optimization problem.²⁴ A couple of alternative methods to the L0-min. program have been proposed.^{25, 26, 27} Of those, the reweighted L1-min,²⁵ including the reweighted TV min. variant, has successfully demonstrated that iterating the convex L1-min. techniques by multiplication of a weight to each element becomes more effective for sparse signal reconstructions. The weight assigned to each element is inversely related to the magnitude of the corresponding element. By penalizing elements with small or near zero magnitude, sparsity in the fluence-map variations can be further improved. One unique advantage of this method is that existing L1-minimizing techniques can be used to obtain the solution.

In this paper, we use the reweighted TV min., derived from the reweighted L1-min., to further simplify the fluence-map and enhance the delivery efficiency for IMRT inverse planning. We will demonstrate that compared with the plans by the existing techniques (such as quadratic and TV min.), the plans obtained from the proposed method improve the delivery efficiency by reducing the fluence-map complexity, number of beam segments, and the actual treatment time required to attain the similar extent of the dose conformity to the target and dose sparing to the critical structures.

METHODS AND MATERIALS

Reducing the fluence-map complexity with L2-norm and L1-norm

In order to decrease the complexity of the fluence-map, constrained optimization has been applied for the fluence-map optimization in IMRT by adding a penalty term p(x) to the data fidelity term as described in Eq. 1,

$$\underset{x\in {\mathbb{R}}^n}{min}{\lambda }_i\Vert A_{i}x-d_i{\Vert }_2^2+\beta ·p\left(x\right)(x\ge 0),$$ (1)

where n is the entire number of beamlet elements (size of field multiplied by the number of beams), $x\in {\mathbb{R}}^n$ is the beamlet-intensity map to be optimized, $D\in {\mathbb{R}}^{2n\times n}$ is the 2D-difference matrix, and β is a user-supplied regularization parameter. $A_i\in {\mathbb{R}}^{m_i\times n}$ is the beamlet kernel or dose matrix acquired by voxel-based Monte Carlo (VMC; Ref. 28) simulations, d_i is the ideal prescribed dose distribution, and λ_i is the importance factor of structure i. Setting $p\left(x\right)={\Vert Dx\Vert }_2^2$, which is standard L2-min., smoothes intensities of fluence-map.^{13, 14, 15, 16, 17, 18, 19} Defining p(x) as ||Dx||₁ is called TV regularization based on L1-norm.^{20, 21, 22} Zhu et al.²⁰ have shown that TV regularization generates a simplified piecewise constant fluence-map. Kim et al.²³ demonstrate that the TV regularized approach can be solved in a memory efficient and computationally fast way using the large scale L1-solver, called template for first-order conic solver (TFOCS).²⁹ Their approach considers the variant with the constrained optimization as follows in Eq. 2,

$$\begin{array}{ccc}& & \underset{x\in {\mathbb{R}}^n}{min}{\Vert x\Vert }_{tv}={‖Dx‖}_1\hfill \\ & & \mathrm{subject}\mathrm{to}\Vert \sqrt{{\lambda }_i}(A_{i}x-d_i){\Vert }_2\le {\varepsilon }_i,x\ge 0,\hfill \end{array}$$ (2)

where ɛ_i represents the residue imposed on planning target volume (PTV) and the critical structures.

L0-norm characteristics differentiated from L1-norm

Simplifying the fluence-map can be done by finding the map with the least variations in neighboring beamlet-intensity components, namely, increasing the sparsity of the fluence-map variations. This brings the fluence-map optimization into the sparse signal reconstruction, which has been mostly performed by TV min. derived from L1-min. Even with TV min., however, the reconstructed solutions may not have sufficiently sparse variation in which (a) there are only a few samples acquired in order to reduce the scanning time in medical image processing, e.g., CT and MRI and/or (b) the extent of dose conformity to the structures gets far stronger, requiring the fluence-map to be more complicated in RT. In such cases, using the L0-norm as described in Eq. 3 results in a sparser signal reconstruction:

$$\begin{array}{ccc}& & \mathrm{General}\mathrm{form}:\underset{x\in {\mathbb{R}}^n}{min}{\Vert x\Vert }_0=\sum _{j}1\{j:x_j\ne 0\}\mathrm{subject}\mathrm{to}{‖(Ax-d)‖}_2\le \varepsilon \hfill \\ & & \mathrm{Difference}\mathrm{matrix}:\underset{x\in {\mathbb{R}}^n}{min}{\Vert Dx\Vert }_0=\sum _{j}1\{j:{\left(Dx\right)}_j\ne 0\}\mathrm{subject}\mathrm{to}{‖(Ax-d)‖}_2\le \varepsilon ,\hfill \end{array}$$ (3)

where A is the system or sensing matrix, and d is the raw or observation data in general. L1-min. is to sum the absolute values of the elements, which is convex and therefore easy to solve. Contrarily, the combinatorial problems in Eq. 3 represent that L0-norm is to compute the number of nonzeros elements or nonzero variations of the elements. In practice, the significant problem caused by the characteristic is that L0-norm is nearly impossible to implement as it is a particularly difficult nonconvex optimization problem.²⁴ Hence, it is essential to seek different approaches that combine the features of L0-min. for the sparse signal reconstruction with the tractability of L1-min.

Iteratively reweighted L1-min. to approximate L0-norm

Several techniques^{25, 26, 27} exist to approximate to L0-min. with the tractability of L1-min. Of these techniques, the iteratively reweighted L1-min., including the reweighted TV min. variant, proposed by Candès et al.²⁵ successfully demonstrates improved sparsity of reconstructed solutions, relative to the L1-min. The basic idea is to use a general L1-norm, which incorporates the multiplication of weight for each element, as presented in Eq. 4,

$$\begin{array}{ccc}& & \underset{x\in {\mathbb{R}}^n}{min}{\Vert W^{\left(k\right)}{x}^{\left(k\right)}\Vert }_1={\sum }_j{w}_j^{\left(k\right)}·\left|{x_j}^{\left(k\right)}\right|,\hfill \\ & & \mathrm{subject}\mathrm{to}\Vert A{x}^{\left(k\right)}-d\Vert \le \varepsilon \hfill \\ & & \left({w_j}^{\left(k\right)}=\frac{1}{|{x_j}^{\left(k\right)}|+{\delta }^{\left(k\right)}}({\delta }^{\left(k\right)}>0)\right),\hfill \end{array}$$ (4)

where W with elements w_j is the weight assigned to each element, δ is the positive coefficient, and the upper-index k is the order of iterates for the reweighting process. At the first iterate (k = 1), the weight equals 1 (w_j⁽¹⁾ = 1), which equals the standard L1-min. After computing the solution x⁽¹⁾, for the next iterate (k = 2), the weight is defined as the reciprocal of the addition of the positive coefficient δ and the solution x⁽¹⁾(w_j⁽²⁾ = 1/|x_j⁽¹⁾| + δ). Iteratively solving Eq. 4 can be seen as an approximation to L0-norm problem as shown in Eq. 5. As δ approaches zero, the weighted L1-norm exactly recovers the L0-norm. In practice, however, δ should be greater than 0 to prevent divergence when the elements of x go to zero, yet must not be too large to retain the approximation of the L0-norm. Candès et al.²⁵ recommend δ ≪ max (|x_j|). How to determine δ in this work will be discussed in a latter section,

$$\begin{array}{c}\hfill {\sum }_j{w_j}^{\left(k\right)}·\left|{x_j}^{\left(k\right)}\right|=\sum _j\frac{|{x_j}^{\left(k\right)}|}{|{x_j}^{\left(k\right)}|+{\delta }^{\left(k\right)}}\approx \sum _{j}1\{{x_j}^{\left(k\right)}\ne 0\}.\end{array}$$ (5)

If the process is repeated a few times, the computational time grows with each iteration, which is not computationally expensive. The greatest advantage from this approach is that each iteration can be solved using existing L1-norm techniques without additional memory costs, so no new algorithms need to be developed. Importantly, it produces solution with significantly more sparsity, which can enhance the sparse fluence-map variations in IMRT.

Iteratively reweighted TV for the fluence-map optimization

The principle explained in Secs. 2A, 2B, 2C is extended to the fluence-map optimization for IMRT inverse planning by incorporating the 2D-difference matrix D, the beamlet kernels (A_i), and the importance factors (λ_i) into the model as expressed in Eq. 6,

$$\begin{array}{ccc}& & \underset{x\in {\mathbb{R}}^n}{min}{\Vert W^{\left(k\right)}\left(D{x}^{\left(k\right)}\right)\Vert }_1={\sum }_{u,v,f}{w_{u,v,f}}^{\left(k\right)}·\left|{\left(D{x}^{\left(k\right)}\right)}_{u,v,f}\right|\hfill \\ & & \mathrm{subject}\mathrm{to}\Vert \sqrt{{\lambda }_i}(A_i{x}^{\left(k\right)}-d_i){\Vert }_2\le {\varepsilon }_i,x^{\left(k\right)}\ge 0\hfill \\ & & \left({w_{u,v,f}}^{\left(1\right)}=1,{w_{u,v,f}}^{\left(k\right)}=\frac{1}{|{\left(D{x}^{(k-1)}\right)}_{u,v,f}|+{\delta }_f^{\left(k\right)}}(k\ge 2)\right),\hfill \end{array}$$ (6)

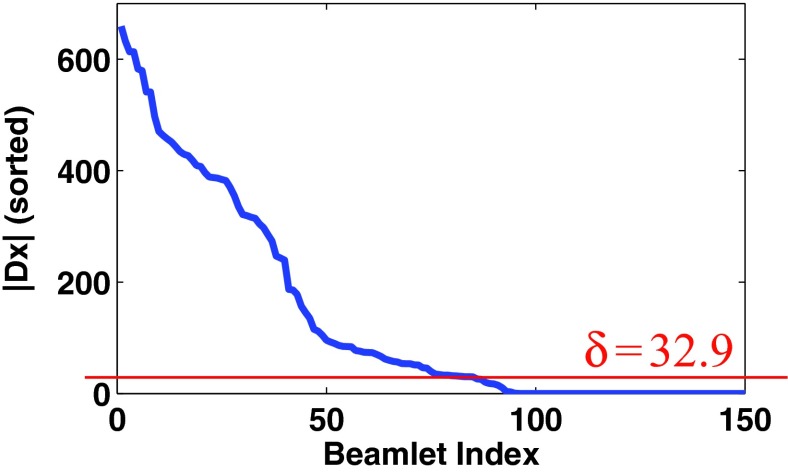
where the subindices denoted by u, v correspond to the beamlet components of fluence-map, x, while the subindex f represents the field order (n = u · v · f). The weight for each element is denoted by w_{u, v, f}, and the positive coefficient δ_f represents a field-specific constant in this work. The entire procedures, completed by two iterations, are summarized in Table 1. At the first iterate, the initial weight is defined as w_{u, v, f}⁽¹⁾ = 1, which is followed by solving the standard TV min. problem. Based on the results, we can update the weight with ${\delta }_f:{w_{u,v,f}}^{\left(2\right)}=1/\left(\right|{\left(D{x}^{\left(1\right)}\right)}_{u,v,f}|+{\delta }_f^{\left(2\right)})({\delta }_f^{\left(2\right)}>0)$. Finally, we perform the reweighted TV min. by one more iteration to improve the sparsity in the fluence-map variations. After the step 2 in Table 1, the variations in each voxel, |(Dx⁽¹⁾)_{u, v, f}|, can be computed and sorted at each field to determine the constant, ${\delta }_f^{\left(2\right)}$, as written in the following:

1. Sort the computed |(Dx⁽¹⁾)_{u, v, f}| in descending order at each field,

2. Determine the 5% of the smallest value of the sorted values as illustrated in Fig. 1.

Table 1.

The procedure to perform the reweighted TV min. for fluence-map optimization.

$\begin{array}{c}1.\mathrm{Define}\mathrm{the}\mathrm{initial}\mathrm{weights}\mathrm{to}\mathrm{be}1:w_{u,v,f}^{\left(1\right)}=1\hfill \\ 2.\mathrm{Implement}\mathrm{TVmin}.\mathrm{with}\mathrm{the}\mathrm{initial}\mathrm{weight}\hfill \\ \mathrm{Minimize}\sum _{u,v,f}{w}_{u,v,f}^{\left(1\right)}\left|{\left(D{x}^{\left(1\right)}\right)}_{u,v,f}\right|\hfill \\ \mathrm{subject}\mathrm{to}\sqrt{{\lambda }_i}·\Vert A_i{x}^{\left(1\right)}-d_i{\Vert }_2\le {\varepsilon }_i,x^{\left(1\right)}\ge 0\hfill \\ 3.\mathrm{Update}\mathrm{the}\mathrm{weight}\mathrm{from}\mathrm{the}\mathrm{fluence}-\mathrm{map}\mathrm{by}\mathrm{step}2\hfill \\ w_{u,v,f}^{\left(2\right)}=\frac{1}{|{\left(D{x}^{\left(1\right)}\right)}_{u,v,f}|+{\delta }_f^{\left(2\right)}}({{\delta }_f}^{\left(2\right)}>0)\hfill \\ 4.\mathrm{Implement}\mathrm{reweighted}\mathrm{TV}\mathrm{with}\mathrm{the}\mathrm{updated}\mathrm{weight}\hfill \\ \mathrm{Minimize}\sum _{u,v,f}{w}_{u,v,f}^{\left(2\right)}\left|{\left(D{x}^{\left(2\right)}\right)}_{u,v,f}\right|\hfill \\ \mathrm{subject}\mathrm{to}\sqrt{{\lambda }_i}·\Vert A_i{x}^{\left(2\right)}-d_i{\Vert }_2\le {\varepsilon }_i,x^{\left(2\right)}\ge 0\hfill \end{array}$

Figure 1.

This shows how to determine the field-specific constant δ_f in this work. The figure represents the sorted fluence-map variations (|(Dx)_{u, v, f}|) acquired at 4th field of Prostate1 data after fluence-map optimization with TV min. at the first iterate. The horizontal line corresponds to the 5% smallest value of the sorted fluence-map variation, which will be used to determine the weight for each element as a constant δ_f in the field.

Plan evaluations

To validate the proposed method, this work employed five treated patient datasets: two prostate (Prostate1 and Prostate2), two head-and-neck (HN1 and HN2), and a lung patient data. All plans were delivered in step-and-shoot IMRT mode. Table 2 presents the specified parameters of treatment plans for each case. In particular, due to the PTV location, the lung patient data has 6 beams with 180° range. For HN2 only, it was supposed that there are multitargets to be treated with 66 and 54 Gy.

Table 2.

The specifications of beam setting applied for the five clinical data used in this work.

Pretreated patient data	Number of beams	Field size (beamlet resolution)	PTV
Prostate1	7 (equispaced)	16 × 18 (5 mm)	78 Gy
Prostate2	7 (equispaced)	16 × 20 (5 mm)	78 Gy
Lung	6 (180° coverage)	18 × 14 (5 mm)	50 Gy
HN1	7 (equispaced)	18 × 22 (5 mm)	66 Gy
HN2	7 (equispaced)	16 × 18 (1 cm)	66/54 Gy
			(multiple targets)

Beamlet kernels denoted by A_i in Eq. 6 were acquired by voxel-based Monte Carlo simulation (VMC; Ref. 28) simulations. The patient CT images were down-sampled to 3.92× 3.92× 5.00 mm in HN1 and to 3.92 × 3.92× 2.50 mm in the other 4 clinical data. For all cases, to control the stiff dose reduction outside the PTV, besides the critical organs, the ring-shaped tuning structures nearby the PTV were incorporated into the fluence-map optimization. Also, to clearly demonstrate the benefits of the proposed method in improving delivery efficiency, all plans were obtained by strengthening the dose sparing to the critical organs, where the fluence-map optimized by the existing algorithms tends to be somewhat complicated.

For each dataset, this study compared three plans optimized by our proposed reweighted TV min., standard TV min., and quadratic min. to represent the regular, clinic IMRT plans, which minimizes the quadratic difference between the ideal and computed dose distributions without the penalized term added. We implemented the quadratic min. by the projected gradient descent method with backtracking line-search algorithm³⁰ based on the model as follows:

$$\begin{array}{c}\hfill {\min }_{x\in {\mathbb{R}}^n}{\lambda }_i\Vert A_{i}x-d_i{\Vert }_2^2(x\ge 0).\end{array}$$ (7)

For fair comparisons of plan quality, all three types of algorithms for each patient dataset yield similar dose sparing to the critical organs by adjusting the importance factors (λ_i) and the residue assigned to each structure, denoted by ɛ_i in Eq. 6. The resultant fluence-maps will be converted into the actual fluence-map by the same leaf-sequencing algorithm proposed by Zhu et al.²⁰

To evaluate the quality of all resultant treatment plans, various criteria were used. For assessing the dose conformity to the target, of a variety of conformality index (CI),^{31, 32, 33, 34, 35, 36} this work employed the conformation number (CN),^{31, 32, 33} consisting of PTV coverage (>95%) (CN1) and the healthy tissue protection (CN2),

$$\begin{array}{ccc}& & \mathrm{Conformation}\mathrm{Number}\left(\mathrm{CN}\right)\hfill \\ & & =\frac{V_{\tau ,\mathrm{ref}}}{V_{\tau }}·\frac{V_{\tau ,\mathrm{ref}}}{V_{\mathrm{ref}}}\genfrac{}{}{0pt}{}{\Delta }{=}\left(\mathrm{CN}1\right)·\left(\mathrm{CN}2\right),\hfill \end{array}$$ (8)

where V_τ is the volume of PTV, V_{τ, ref} represents the target volume receiving the dose greater than or equal to the reference (prescribed) dose, and V_ref is the total volume receiving the dose greater than or equal to the reference dose. In this study, CN1 is set up to be 0.95 for all plans, while trying to see the variations of CN, where higher CN implies better target dose conformity with healthy tissue protection. The delivery efficiency is closely associated with the fluence-map complexity, which was quantified by the entire number of segments and modulation index (MI; Ref. 37) as shown in Eq. 9,

$$\begin{array}{ccc}& & {\Delta }_u=\Vert x_{u,v,f}-x_{u-1,v,f}\Vert ,{\Delta }_v=\Vert x_{u,v,f}-x_{u,v-1,f}\Vert \hfill \\ & & N\left(f\right)=(\mathrm{Number}\mathrm{of}\mathrm{beamlets}\mathrm{such}\mathrm{that}\hfill \\ & & {\Delta }_u,{\Delta }_v>f·\sigma )(f=0.01,0.02,\cdots ,2)\hfill \\ & & z\left(f\right)=\frac{N\left(f\right)}{(N_u-1)N_v+N_u(N_v-1)}\to \mathrm{MI}={\int }_0^{0.5\sigma }z\left(f\right)df,\hfill \end{array}$$ (9)

where x is the resultant fluence-map, N_u and N_v are the size of beamlet, Δ_u and Δ_v are the intensity change between adjacent beamlets in perpendicular and horizontal directions, σ is the standard deviation of x, and N(f) is the number of elements meeting the condition above. The estimated dose delivery time (T_est) can explicitly represent the delivery efficiency of the plans by referring to Li et al.³⁸ as expressed in Eq. 10 for step-and-shoot IMRT delivery,

$$\begin{array}{c}\hfill T_{\mathrm{est}}=\frac{\mathrm{MU}}{\mathrm{DR}}+T_G\left(1-\frac{1}{N_f}\right)+\Delta T_G(1-N_f)+T_{\mathrm{MLC}},\end{array}$$ (10)

where MU is the monitor unit per fraction, DR represents the dose rate for plan delivery, which equals the 600 MU/min or 10 MU/s, and T_G is the time for a gantry rotation of 360°, which is 60 s. ΔT_G is the extra time caused by gantry control at a beam angle, which is about 0.6 s or 0.01 min, N_f is the number of beams applied, and T_MLC denotes the summation of MLC traveling time of all apertures applied, where MLC leaves travel at the maximum speed 3 cm/s. The monitor unit, MU, is calculated for each plan to make sure that 95% of the PTV receives 100% of the prescription dose (2 Gy). Finally, the dose sparing to the critical structures was evaluated by watching the dose volume histograms (DVHs) and dose distributions drawn, and by calculating the equivalent uniform dose (EUD),^{39, 40, 41} which is expressed as

$$\begin{array}{c}\hfill \mathrm{EUD}={\left(\frac{1}{n}{\sum }_{i=1}^n{d}_i^a\right)}^{1/a},\end{array}$$ (11)

where d_i is the dose at voxel i, and n is the total number of voxels of the structure. This work defines a to be −10, 6, and 1, which correspond to PTV, parallel structures (such as parotid), and serial structures (such as Rectum), respectively.

Algorithm implementation

In order to implement the proposed method with a general TV min. based on L1-norm, this work employs the large-scale L1-solver, TFOCS.²⁹ As specified in Kim et al.,²³ it demonstrates fast convergence speed with the minimal memory usage for RT applications. Our proposed algorithm is performed by one more iteration using the appropriate weight for each element with the TFOCS solver. The algorithm was implemented on a PC with 4 GB memory and Intel Core i5 CPU, 2.67 GHz in a MATLAB R2008a platform. The algorithmic details can be found in the released software package (http://tfocs.stanford.edu), which should be fitted to the RT applications in terms of the structures of the 2D-difference matrix for TV form. The maximum number of iterations for the fluence-map optimization is 2000, and it automatically stops when the difference in L2-norm between solutions at the next and the current iterate is less than 10⁻⁵, namely ‖x_{l + 1}^(k) − x_l^(k)‖₂ ⩽ 10⁻⁵, where subindex l is the order of iterations of computing kth reweighting process (x^(k)).

RESULTS

Figure 2 compares three resultant fluence-maps optimized by quadratic, conventional TV min., and the proposed reweighted TV min. for Prostate2 [Figs. 2a, 2b, 2c], Lung [Figs. 2d, 2e, 2f], and HN1 [Figs. 2g, 2h, 2i] cases. We see that the proposed method produces sparser fluence-map variations due to the reweighting process. Although the plans acquired by standard TV min. generates simpler fluence-map variations relative to the quadratic min. representing regular IMRT planning, the resultant fluence-maps are still complicated in order to meet stronger dose constraints, which can be overcome by reweighting process with more iteration. The computational time of the proposed method for the fluence-map optimization ranges from 6 to 10 min., which is about twice of the standard TV min. based approach due to the extra iteration, whereas its memory expenses (0.3–0.8 GB) remain unchanged in comparison with two existing algorithms.

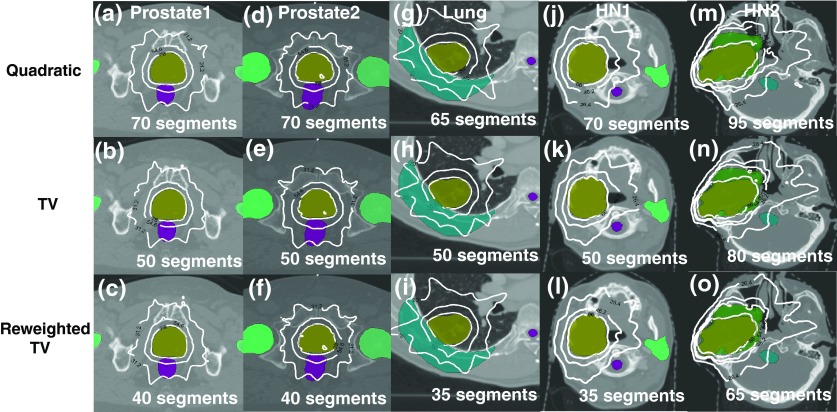
Figure 2.

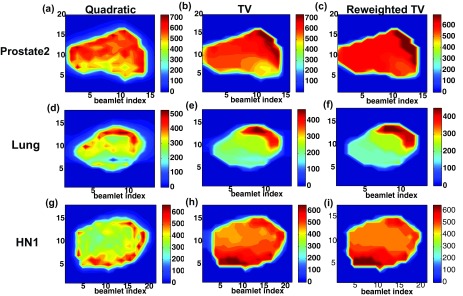
Fluence-maps acquired by quadratic min., TV min. and reweighted TV min. (proposed) for (a)–(c) Prostate2, (d)–(f) Lung, and (g)–(i) HN1 clinical data sets. The perpendicular bar in right-hand side for each figure represents the beamlet intensities. The proposed method successfully generates simplified fluence-maps than the other two techniques.

In order to see how the simplified fluence-maps can affect the delivery efficiency, we quantify the dose conformity to the target by CN, while varying the number of segments for all five cases, as illustrated in Figs. 3a, 3b, 3c, 3d, 3e. The solid (-), dashed (–), and dashed-dotted (-.) lines are matching the plans obtained from the quadratic, TV, and reweighted TV min. algorithms, respectively. This figure noticeably describes the benefits from the proposed method over the existing optimization techniques in terms of the dose conformity to the target (CN), since a similar CN can be achieved with much fewer segments applied by using the proposed method. As summarized in Table 3, to attain a similar CN, the number of entire segments of the plans by the proposed method was reduced by 10–15 segments relative to the plans by conventional TV min., and reduced by 30–35 segments compared with the quadratic min. based plans. Simultaneously, the plan complexity measured by MI can be decreased by about 20%–30% over TV min. and by about 40%–60% over quadratic min. based algorithm. Particularly, in the HN2 case with multiple targets (PTV66 and PTV54), a similar target dose conformity to PTV66 (CN = 0.75) was accomplished by the quadratic and TV min. based plans with more segments used. However, the dose conformity to PTV54 of those (CN = 0.73, 0.78) cannot get better than that of the plan by the proposed method (CN = 0.79) within the range of segments given. This result points out that the reduction in fluence-map complexity through reweighted TV min. can provide more secure controllability for multiple targets as well as single target than the existing algorithms.

Figure 3.

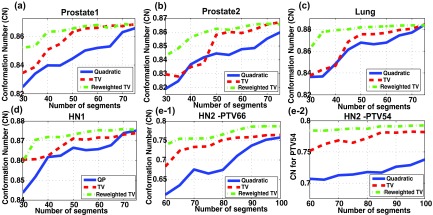
Comparing dose conformity to the target (CN) of the plans acquired by quadratic min. [solid (-)], TV min. [dashed (- -)], and reweighted TV min. [dashed-dotted (-.)] in (a) Prostate1, (b) Prostate2, (c) Lung, (d) HN1, (e-1) HN2 data for PTV66, and (e-2) HN2 data for PTV54, respectively. To achieve a similar CN, the reweighted TV min. required 10–15 fewer segments than TV min. and 30–35 fewer segments than quadratic min. based plans.

Table 3.

Comparison of the quality of the plans acquired by three different algorithms for five clinical data sets in dose conformity to the target (CN), and fluence-map complexity (number of segments and MI).The proposed method enables for attaining the similar CN with much fewer segments and simpler fluence-map complexity (MI) than the existing methods can do.

Patient case	Criterions	Algorithms
		QP	TV	Reweighted TV
Prostate1	Segments	70	50	40
	CN	0.8629	0.8671	0.8632
	MI	7.44	4.19	3.39
Prostate2	Segments	70	50	40
	CN	0.8753	0.8779	0.8731
	MI	7.88	4.26	3.28
Lung	Segments	65	50	35
	CN	0.8843	0.8854	0.8870
	MI	8.92	5.39	3.53
HN1	Segments	70	50	35
	CN	0.8739	0.8719	0.8710
	MI	6.71	3.37	2.47
HN2	Segments	95	80	65
	CN (PTV66)	0.7521	0.7522	0.7549
	CN (PTV54)	0.7286	0.7728	0.7878
	MI	7.33	5.75	4.63

To clarify the benefits of the proposed method in delivery efficiency, Table 4 specifies the estimated treatment time (T_est) and the MLC traveling time (T_MLC) of three treatment plans with MUs required for each case. The comparisons were made with different number of segments for three different plans that produce similar plan quality in CN as seen in Table 3. For instance, 70, 50, and 35 segments were applied to the plans by quadratic min., TV min. and reweighted TV min, respectively, in HN1 patient data as seen in Table 3. The plans with fewer segments achieved by the reweighted TV can lead to shorter treatment time, which mostly come from 25% to 30% reduced MLC traveling time (10–30 s) over TV min. based plans and from 50% to 60% reduced MLC traveling time (30–80 s) over quadratic min. based plans. Besides the great profits from the MLC traveling time, the MU levels required for achieving a similar plan quality affect the treatment time. The plans by the proposed method have about 3%–5% smaller MUs than conventional TV min. based plans, while those can lower MUs by up to 15% than the quadratic min. based plans. This reduction can further decrease the entire treatment time as well in such cases as Lung, HN1, and HN2, whereas the profit is relatively low in the prostate cases. Combining the two variable factors, the advantage in estimated delivery time obtained from the proposed method is about 12–30 s over the TV min., and 35–85 s over the quadratic min. based plans.

Table 4.

Estimated treatment time of the three plans by quadratic min., TV min., and the proposed method for the five clinical cases. The plans by the proposed method can save the estimated dose delivery time by about 10–30 s over the TV min. based plans, and about 30–80 s over the quadratic min. based plans.

Patient case	Criterions	Algorithms
		Quadratic	TV	Reweighted TV
Prostate1	Test(s)	173	148	135
	TMLC(s)	70	45	33
	MU	440	433	423
Prostate2	Test(s)	180	146	134
	TMLC(s)	73	43	32
	MU	473	432	425
Lung (180° coverage)	Test(s)	145	104	90
	TMLC(s)	75	38	25
	MU	360	320	312
HN1	Test(s)	227	190	165
	TMLC(s)	93	65	43
	MU	752	657	630
HN2	Test(s)	285	229	199
	TMLC(s)	150	103	74
	MU	758	672	656

To see the extent of the dose sparing to the organs-at-risk (OAR), DVHs and the dose distributions are employed as shown in Figs. 45. As in the delivery time estimations, with reference to Table 3, the different number of segments were applied for three plans that have a similar dose conformity to the target (CN) for each dataset. As illustrated in Fig. 4, with respect to the DVHs of the critical structures involved in the fluence-map optimization, the plans with fewer segments from the proposed method turned out to be similar to the plans from two existing techniques for five clinical data. This tendency can be also seen in Fig. 5, which describes the dose distributions acquired by three different methods for all clinical datasets. The dose of radiations from three different algorithms is distributed in an analogous fashion, which importantly implies that the plan acquired by the reweighted TV min. can preserve the critical structures at the similar extent even with fewer segments. The numerical results in Table 5 regarding EUDs of all structures involved in the fluence-map optimization support the consequences above. The three plans obtained from different algorithms yield similar EUDs of the critical organs although the plans by the reweighted TV min. have much fewer segments than the plans by the two existing algorithms. Additionally, the important fact to note is that in most cases, the EUDs of the PTV of the plans from the proposed method are lower than those by the existing techniques, which shows that reweighted TV min. makes the dose distribution inside the PTV more uniform due to further simplification of the resultant fluence-maps.

Figure 4.

DVHs of all structures involved in three plans acquired by quadratic min. [solid(-)], TV min. [dashed(–)], and reweighted TV min. [dashed-dotted(-.)] in (a) Prostate1, (b) Prostate2, (c) Lung, (d) HN1, and (e) HN2 data, respectively. The plans by the proposed method can maintain the similar dose sparing to the critical organs even with fewer segments applied.

Figure 5.

Dose distribtuions obtained from three different algorithms with the designated number of segments in (a)–(c) Prostate1, (d)–(f) Prostate2, (g)–(i) Lung, (j)–(l) HN1, and (m)–(o) HN2 clinical data. This claims that the proposed method even with much fewer segments does not harm the critical structures. (The iso-dose lines are 40%,70%, and 100% of the prescribed dose).

Table 5.

EUDs of all structures concerned in the fluence-map optimizations with three different methods. This shows that the reweighted TV can preserve the critical structures to similar extent to the existing techniques, even with fewer segments applied to the treatment planning.

Patient case	Structures	Algorithms
		Quadratic	TV	Reweighted TV
Prostate1	PTV	81.28	81.04	80.99
	Rectum	45.09	44.59	44.06
	Bladder	13.25	13.13	13.11
	Femoral heads (L,R)	16.05/14.83	15.81/15.33	15.91/15.21
Prostate2	PTV	81.41	81.07	81.02
	Rectum	46.97	46.55	46.80
	Bladder	13.21	12.89	12.79
	Femoral heads (L,R)	16.57/16.21	16.67/16.51	16.94/16.34
Lung	PTV	53.30	52.78	52.66
	Chest wall	6.51	6.40	6.18
	Spinal cord	28.72	29.15	29.29
HN1	PTV	69.99	69.55	69.52
	Spinal cord	16.90	16.00	15.83
	Brain stem	15.27	14.54	13.95
	Parotid (L)	11.97	11.30	11.49
HN2	PTV66	70.47	70.66	70.16
	PTV54	58.27	58.16	57.56
	Spinal cord	27.87	27.60	27.83
	Brain stem	26.23	25.63	25.76
	Parotid (L)	10.95	10.92	10.74

DISCUSSION

Fluence-map complexity is an important issue in IMRT inverse planning because it is directly related to delivery efficiency and treatment time. First-order TV min. based on L1-norm casts the inverse planning as a sparse signal reconstruction problem, hence offering a salient method for enhancing delivery efficiency by generating piecewise constant fluence maps. However, when the dose sparing to the critical structures gets stronger, the fluence-map will inevitably become more complicated to satisfy the dose constraints, which can negatively affect the delivery efficiency, i.e., dose delivery time. To further enhance the delivery efficiency by reducing the fluence-map complexity, we proposed the reweighted TV min. technique originated from the reweighted L1-min., in which the L1-min. program is iteratively executed by reweighting the elements at each iteration. The weight assigned to each element is inversely related to the magnitude of the corresponding element. By penalizing elements with small or near zero magnitude, the proposed technique ensures sparsity in the fluence map variations. The apparent advantage of this method is that existing L1-minimizing techniques can be used with only minor modifications in order to achieve the desired results.

In step-and-shoot delivery based IMRT inverse planning, we have demonstrated the benefits of the proposed method in terms of the delivery efficiency, while target dose conformity and dose sparing to the critical structures is maintained or strengthened. For five clinical cases (two prostate, one lung, and two HN data) with IMRT, the proposed method can produce simpler fluence-maps than the existing techniques (quadratic and standard TV min.). Notably, for all clinical cases, using reweighted TV min. helps achieve a similar dose conformity to the target (CN) with 10–15 fewer segments relative to the TV min. based plans and with 30–35 fewer segments compared with the quadratic min. based plans. With such conditions, the fluence-map complexity (MI) was decreased by about 20%–30% and about 40%–60% over TV min. and quadratic min. based algorithms, respectively. Ultimately, the reduction in the fluence-map complexity can lead to the greatly decreased MLC traveling time and slightly decreased MU levels, which save the entire estimated dose delivery time (T_est) by about 12–30 s over the TV min., and 35–85 s over the quadratic min. based plans.

There are several algorithmic parameters to be chosen as discussed in Sec. 2. The important parameter in the implementations of the proposed method is the positive coefficient (δ_f), which is recommended Candès et al.²⁵ to be lower than the maximum element or variation of elements. This work defines it as a field-specific constant. If it is too large, the reweighted L1-min. does not approximate L0-min., whereas too small coefficient will lead to oversimplified fluence-map and damage plan quality. Although the way to determine δ_f is empirical, the values used in this work should be close to the optimal one for IMRT inverse planning as verified by our clinical datasets.

Another consideration is the number of iterations for the reweighting process. The work proposed by Candès et al.²⁵ has suggested iterating the algorithm three to five times, while we propose to iterate just once. Unlike image processing problems with an image size typically ∼256 × 256 or larger, the “image” or fluence-map for inverse planning has smaller sizes, e.g., ∼16 × 18, and thus does not require a greater number of iterations for assuring the solution with sparser variations. Also, from our experimental observations, the additional iterations in inverse planning can oversimplify the fluence maps, which could make the target conformity and dose sparing to the certain critical structures worse. For these reasons, this work suggests iterating the reweighting process only once.

CONCLUSIONS

We have proposed a reweighted L1-minimization technique to simplify fluence maps in IMRT inverse planning and improve delivery efficiency. Results using clinical data in lung, prostate, and head and neck cases show that the proposed technique reduces the number of segments and fluence-map complexity compared with conventional L1-minimization technique, which in turn leads to shorter treatment time, while maintaining target conformity and dose sparing to critical structures.