Transmitter Release from Cochlear Hair Cells Is Phase Locked to Cyclic Stimuli of Different Intensities and Frequencies

Abstract

The auditory system processes time and intensity through separate brainstem pathways to derive spatial location as well as other salient features of sound. The independent coding of time and intensity begins in the cochlea, where afferent neurons can fire action potentials at constant phase throughout a wide range of stimulus intensities. We have investigated time and intensity coding by simultaneous presynaptic and postsynaptic recording at the hair cell-afferent synapse from rats. Trains of depolarizing steps to the hair cell were used to elicit postsynaptic currents that occurred at constant phase for a range of membrane potentials over which release probability varied significantly. To probe the underlying mechanisms, release was examined using single steps to various command voltages. As expected for vesicular release, first synaptic events occurred earlier as presynaptic calcium influx grew larger. However, synaptic depression produced smaller responses with longer first latencies. Thus, during repetitive hair cell stimulation, as the hair cell is more strongly depolarized, increased calcium channel gating hurries transmitter release, but the resulting vesicular depletion produces a compensatory slowing. Quantitative simulation of ribbon function shows that these two factors varied reciprocally with hair cell depolarization (stimulus intensity) to produce constant synaptic phase. Finally, we propose that the observed rapid vesicle replenishment would help maintain the vesicle pool, which in turn would equilibrate with the stimulus intensity (and therefore the number of open Ca²⁺ channels), so that for trains of different levels the average phase will be conserved.

Introduction

Among the acoustic features that the auditory system must represent, one of the most challenging is timing. Precise temporal processing is required for speech discrimination in humans and is also essential for the broadly conserved property of directional hearing (Ruggero, 1992; Yin, 2002).

It is well established that auditory nerve fibers are able to fire at a particular time within each cycle of a low-frequency periodic stimulus (Galambos and Davis, 1943; Kiang et al., 1965; Rose et al., 1967). Furthermore, this preferred phase can remain constant over a range of sound intensities at the characteristic frequency–phase constancy independent of intensity. Phase locking propagates throughout the auditory pathway supported by presynaptic and postsynaptic specializations such as calyciform synapses with large quantum contents and fast kinetics of postsynaptic receptors (Trussell, 1999; Schneggenburger and Forsythe, 2006).

The inner hair cell afferent synapse, the first synapse in the hearing pathway, is confronted with particular challenges. Synaptic contacts are small (Liberman, 1980), and while presynaptic ribbons may promote efficient vesicle resupply (Griesinger et al., 2005; Frank et al., 2010), nonetheless the readily releasable pool is several times smaller than that of calyceal terminals in the brainstem (Nouvian et al., 2006; Schneggenburger and Forsythe, 2006). Hair cell exocytosis is triggered not by temporally precise, invariant action potentials but rather by graded changes in membrane potential (Russell and Sellick, 1978), producing intracellular Ca²⁺ signals that vary continuously in amplitude and kinetics (Frank et al., 2009). As observed at other chemical synapses, transmitter release from the inner hair cell (IHC) ribbon synapse is Ca²⁺ dependent. Voltage-gated channels provide Ca²⁺ to drive a vesicular Ca²⁺ sensor that catalyzes fusion to the plasma membrane (Moser et al., 2006). Although the molecular identity of this Ca²⁺ sensor remains uncertain (Safieddine and Wenthold, 1999; Roux et al., 2006; Beurg et al., 2010; Johnson and Chapman, 2010; Pangrsic et al., 2010), it is highly cooperative, requiring the binding of five Ca²⁺ ions to trigger release, resulting in rate constants that are strongly Ca²⁺ dependent (Beutner et al., 2001). Thus, increasingly larger receptor potentials, driven by increasingly louder sounds, should cause more calcium influx and increasingly faster vesicular fusion (Fuchs, 2005). How then is phase constancy achieved at the hair cell ribbon synapse?

In this study, we made simultaneous recordings from IHCs and afferent boutons in an excised organ of Corti preparation and used numerical simulations to investigate the basis of transmitter release during cyclic stimuli. Using repetitive depolarizations to different frequencies and levels, we found intensity-independent, phase-locked transmitter release from the IHC ribbon synapse. However, in single-step experiments, synaptic latency shortened with greater presynaptic depolarization. This effect was offset by increased depletion of vesicular pools that slowed vesicular release at a given presynaptic depolarization. We propose that higher stimulation levels cause faster release kinetics through voltage-gated calcium influx, but also stronger depletion, which in turn reduces and thus slows transmitter release. The interplay of these two opposing actions confers phase constancy onto a given synapse. A corollary of this hypothesis is that the rate at which vesicular pools refill determines the mean quantum content during repetitive release, and therefore the firing probability of the postsynaptic afferent neuron.

Materials and Methods

Recordings of IHCs and afferent postsynaptic boutons.

Excised apical turns of 9- to 11-day-old rat cochleae (Sprague Dawley, either sex) were placed into a chamber under an upright microscope (Olympus BX51WI or Axioskop2 FS plus; Zeiss) and superfused with saline at 2–3 ml/min. IHCs and contacting postsynaptic terminals were visualized on a monitor via a water immersion objective (63× or 40×), additional magnification (2× or 4×), difference interference contrast optics, and a camera (a CCD Rolera XR from QImaging or a Newvicon from Dage MTI). For simultaneous, paired, whole-cell, patch-clamp recordings, the postsynaptic recording was established first and the IHC recording second.

Pipette solution for isolating IHC Ca²⁺-currents contained (in mm): 135 CsMeSO₃, 13 TEA Cl, 5 HEPES, 3.5 MgCl₂, 0.1 CaCl₂, 2.5 Na₂ATP, 1 EGTA, pH 7.2 (CsOH); liquid junction potential (LJP), 9 mV. Postsynaptic pipette solution contained (in mm): 135 KCl, 3.5 MgCl₂, 0.1 CaCl₂, 5 EGTA, 5 HEPES, 2.5 Na₂ATP, pH 7.2 (KOH); LJP, 4 mV. Extracellular solution contained (in mm): 5.8 KCl, 114 NaCl, 0.9 MgCl₂, 1.3 CaCl₂, 0.7 NaH₂PO₄, 5.6 d- glucose, 10 HEPES, 30 TEA Cl, pH 7.4 (NaOH), and 1–5 μm tetrodotoxin (Alomone Labs). All other chemicals were purchased from Sigma.

Recording pipettes were fabricated from 1 mm borosilicate glass (WPI), Sylgard coated, and fire polished with tip resistances of 9–12 (postsynaptic) and 6–8 (IHC) MΩ. Series resistance errors, 10–20 MΩ for IHC recordings, were compensated up to 70%. Holding potentials were not corrected for LJPs. Depolarizations in trains were sometimes modified from the indicated −40 and −30 (to −45 and to −34 mV, respectively) in order to obtain average Ca²⁺ currents amplitudes within the indicated values (Figs. 2–4 and 6). Experiments were done at 22–24°C. Recordings were performed with two 200B Axopatch amplifiers and Digidata 1440 board (Molecular Devices), filtered at 10 kHz, and digitized at 50 kHz. Data acquisition started 5–10 min after the IHC whole-cell recording. A ‘run-up’ of Ca²⁺-currents was typically observed during the first few minutes of recording. After ∼30 min of recording, run-down of synaptic activity was observed and therefore only data recorded within this time window were analyzed.

Figure 2.

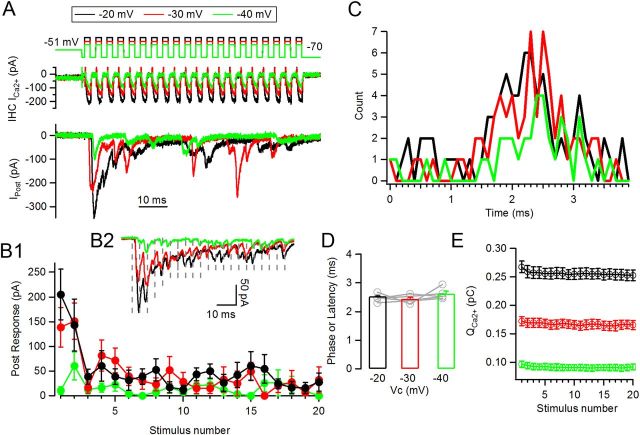
Responses to trains of pulses at different potentials are phase locked. A, Representative traces of synaptic responses at three different depolarization values: −20 mV (black), −30 mV (red), and −40 mV (green). Same panel distribution as Figure 1A. B1, Average peak postsynaptic responses per pulse for each level of stimulation. B2, Average traces (n = 8–12 repetitions) of synaptic responses for each train type (dashed lines indicate cycles). C, Phase (or latency) plot for EPSCs activated during any given cycle of the train (as indicated in Fig. 1D). D, Average preferred phase calculated for n = 5 cell pairs. E, IHC Q_Ca²⁺ at each pulse in the train for the three different levels.

Figure 3.

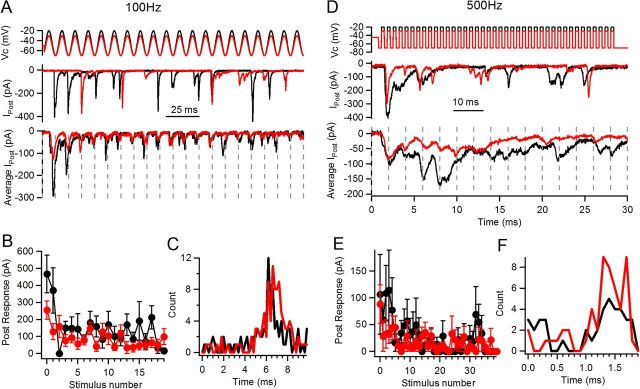
Phase locking at stimulation frequencies of 100 and 500 Hz. A, Representative postsynaptic responses to sinusoidal stimulation (20 cycles) of 100 Hz at −20 mV (black) and −30 mV (red). Top panel, Stimulation protocol; middle panel, individual postsynaptic responses to these two levels; bottom, average traces of n = 6 (−20 mV) and 12 (−30 mV) responses. Individual cycles are separated by dashed lines. Note local peaks within each cycle for both train levels. B, Average amplitude of postsynaptic responses per pulse at both depolarization levels. C, Phase (or latency) plot for recording shown in A and B. D, Representative responses to 500 Hz stimulation at −20 mV and −30 mV (40 pulses). Same panel distribution as in A, but a detail of the first 15 cycles in the train is shown on the bottom panel (dashed lines indicate cycles). E, Average postsynaptic response per pulse. Smaller average responses were observed per pulse. F, Phase (latency) plot for the recording shown in D and E.

Figure 4.

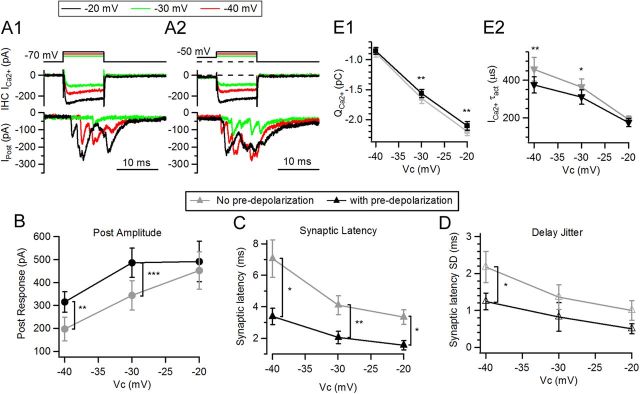
Timing of synaptic responses in single pulses at different potentials. A1, Synaptic responses at three different potentials, −40 (red), −30 (green), and −20 (black) mV, with no predepolarization. Presynaptic voltage protocol is on top, IHC Ca²⁺ currents are in the middle, and postsynaptic currents are in the bottom panels. A2, Same as A1 but using predepolarization to −50 mV for 50 ms. B, Average amplitude of postsynaptic responses as a function of depolarizing potential (with or without predepolarization). C, First synaptic latency for responses elicited with the protocol shown in A1 and A2. D, Jitter in synaptic latency. E1, IHC Ca²⁺ charge as the integral of the 10 ms current. E2, Activation τ of IHC Ca²⁺ currents (*p < 0.05, **p < 0.01, ***p < 0.001).

Figure 6.

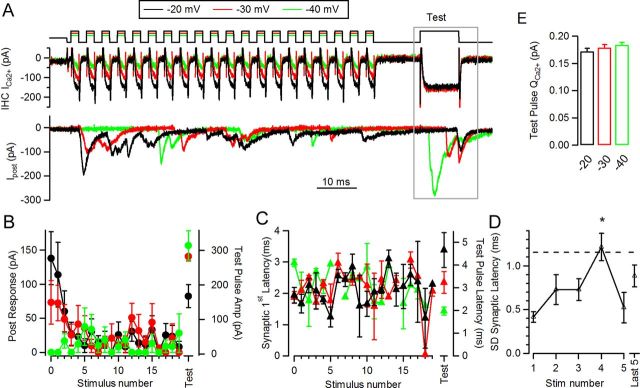
Testing vesicle pool state after trains of 250 Hz at different levels. A, Representative traces of responses to stimulation protocols at three different levels, followed by test pulse (10 ms depolarization to −20 mV, after 10 ms interval at the end of the train). B, Average postsynaptic response versus stimulus number (left axis), and test pulse amplitude (right axis). C, Average synaptic latency after every pulse in each train (left axis), and also to the test pulse (right axis). D, Jitter in latency (measured as standard deviation of the mean) for the first five pulses in the −20 mV trains and the events occurring in the ensemble's last five depolarizations. Dashed line indicates theoretical jitter for events occurring with equal probability at any point in time over the entire cycle (*p < 0.05). E, Ca²⁺ charge at test pulse.

Data analysis.

Data were analyzed off-line using MiniAnalysis (Synaptosoft) and custom routines implemented in Igor Pro (WaveMetrics). For leak subtraction of IHC currents, IHC membrane resistance was calculated from voltage steps between −80 and −60 mV. Ca²⁺ charge was calculated by the integral of the Ca²⁺ current from its onset time up to the end of the depolarizing pulse. Tail currents were excluded from the analysis because they were typically confounded by clamping artifacts. The onset time was in turn computed as the time point where the Ca²⁺ current trace crossed baseline (in the negative direction) after test depolarization started. Activation time constant (τ_act) was obtained by fitting the activation time course of the Ca²⁺ current from the onset time to the peak. Postsynaptic response amplitude was calculated as the sum of all EPSCs triggered by a given pulse (within a given cycle, in trains), including failures unless stated. Synaptic latency was computed from the onset of any given pulse until the onset of the EPSC (in case of first latencies, to the onset of the first EPSC activated by the stimulus). Phase plots (Figs. 1, 2, 3) were constructed using latencies of all EPSCs occurring in each cycle of trains (or first EPSC activated, as indicated) with a given stimulation protocol, and the characteristic phase and vector strength (synchronization index) were calculated as indicated (Goldberg and Brown, 1969).

Figure 1.

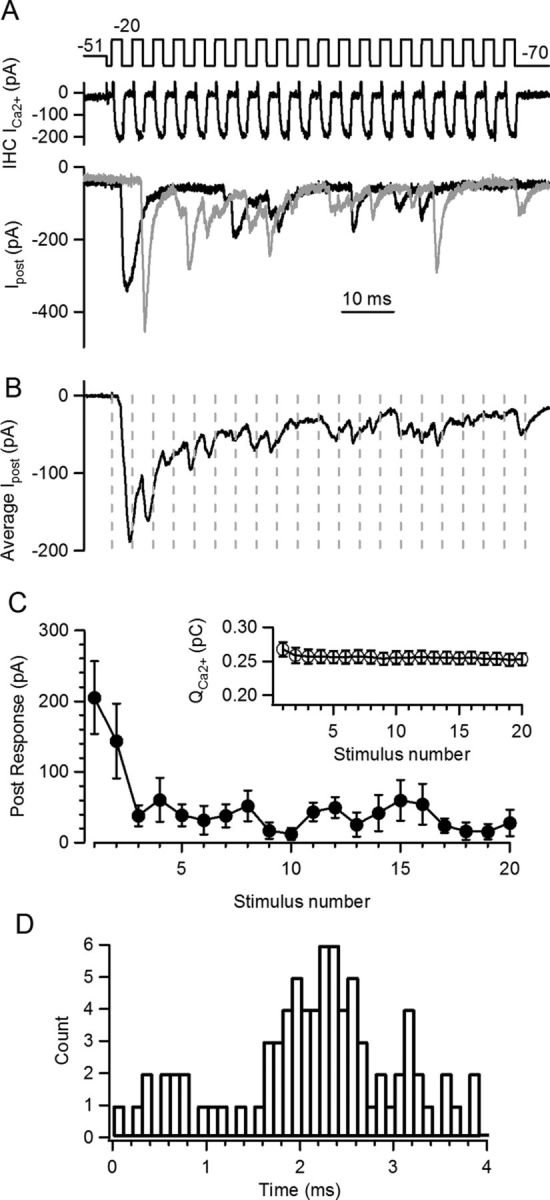
Periodic stimulation at the IHC ribbon synapse. A, Train of pulses to −20 mV (Vh = −70 mV, 2 ms + 2 ms, i.e., 250 Hz) following a predepolarization to −51 mV. Top panel: stimulation protocol, middle panel: IHC Ca²⁺ currents, bottom panels: two repetitions of the postsynaptic response. B, Average trace of n = 8 postsynaptic responses. Dashed lines indicate cycles' limit, where local peaks of the postsynaptic response can be observed. C, Average amplitude of postsynaptic responses at each pulse in the train. Note fast synaptic depression. Inset, Ca²⁺ charge produced by each pulse in the train at the IHC. Slight inactivation was observed during the train. D, Phase (or latency) plot for all EPSCs occurring during the train, regardless of their amplitudes or shapes. The histogram was constructed with latencies of all EPSC activated in each cycle, relative to the beginning of that cycle.

For statistical comparison, one-tailed or two-tailed Student's t test and one-way or two-way ANOVA were used. Tukey's post hoc test was used when one-way ANOVA analysis was significant, and Bonferroni's post hoc test was used in case of the two-way ANOVAs. Wilcoxon signed-rank test was used in case when normal distribution could not be assumed (ratios of response phases in 100 and 500 Hz stimuli; Fig. 3). Mean values are presented ± standard errors. Recovery of synaptic responses (Fig. 5) was fitted with a single exponential equation. In case of recovery of first latencies, average τ was calculated from individual recordings in which the fitting procedure converged properly.

Figure 5.

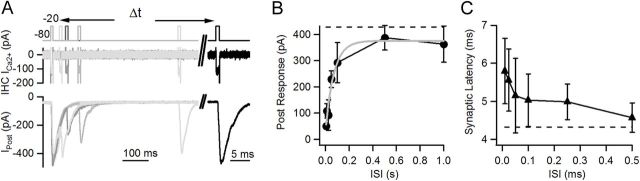
Fast synaptic recovery after partially depleting stimuli. A, An initial 10 ms − pulse was applied to elicit a partial depletion of the vesicle pool. Recovery after different intervals was assayed with a second 10 ms − pulse. Representative traces are shown; voltage protocol at the IHC is in the top panel, IHC Ca²⁺ current is in the middle, and postsynaptic response in the bottom. B, Average postsynaptic response as a function of recovery interval. Also, average response to first stimulus is included as dashed line. Gray line represents fit with exponential function C, Synaptic latency of second depolarization as a function of interval. Average latency of responses to first depolarization is indicated as horizontal dashed line.

Simulations.

The series of differential equations corresponding to a model of the IHC Ca²⁺ sensor (Beutner et al., 2001), with the addition of a vesicle recovery step, were solved numerically. Recovery was modeled as a single step with a rate constant that was proportional to 1/τ_rec as measured experimentally in Figure 5 and to the degree of emptiness of the pool (1 − sum of occupied states). Parameter values were the same as in Beutner et al., 2001: k_on = 27.6 (μm s)⁻¹, k_off = 2150 s⁻¹, γ = 1695 s⁻¹, and recovery rate = 27 s⁻¹.

Idealized Ca²⁺ transients were used to drive the kinetic model (Weis et al., 1999; Beutner et al., 2001). The on- and off- time constants for the Ca²⁺ transients corresponding to the three levels of depolarizations were implemented following the kinetics of the corresponding Ca²⁺ currents (τ_on: −20 mV, 270 μs; −30 mV, 370 μs; −40 mV, 430 μs; τ_off: 100 μs for all pulses). This approach was considered the most parsimonious provided the lack of information on the Ca²⁺ dynamics with periodic stimuli as used in this study. Intracellular Ca²⁺ signals as measured with low affinity dyes (Frank et al., 2009) show similar time courses, albeit slightly slower, possibly due to the characteristic filtering produced by this type of Ca²⁺ indicators (Fig. S1 in Frank et al., 2009 showed the estimated intracellular Ca²⁺ waveform). The amplitude of the transients for each stimulation intensity was fit so the ratios of peak and (quasi) steady-state in the trains, and also the proportionality among train levels, were similar to the experimental results (45 μm for the ‘−20 mV Train,’ 32 μm for the ‘−30 mV Train,’ and 23 μm for the ‘−40 mV Train’). These values were kept within the range of concentrations used in previous models (Beutner et al., 2001; Wittig and Parsons, 2008). Therefore, the three different levels differ in the amplitude of the Ca²⁺ transients, but also in its activation kinetics, as shown for Ca²⁺ currents in Figure 2. For each pulse in the train, the maximal release rate was calculated together with the latency to exocytosis of the first vesicle. Multivesicular release was not considered in this simulation, and an initial pool of 200 vesicles was implemented in analogy with the number of reported vesicles on the ribbon (Nouvian et al., 2006).

Results

Transmitter release during repetitive depolarization

To examine the mechanisms underlying phase locking at the IHC ribbon synapse, we used simultaneous recordings of an IHC and a postsynaptic afferent bouton. The IHC was repeatedly depolarized (20 times) from −70 (for 2 ms) to −20 mV for 2 ms, constituting a 250 Hz stimulus rate. Typical postsynaptic responses and IHC Ca²⁺ currents elicited by such protocols are illustrated in Figure 1A. As described previously (Moser and Beutner, 2000; Spassova et al., 2004; Johnson et al., 2005; Schnee et al., 2005; Goutman and Glowatzki, 2007; Li et al., 2009), synaptic depression is a prominent feature of this synapse as is evident in the average (n = 8) postsynaptic response (Fig. 1B,C). Synaptic depression occurred over the first 3–5 pulses (average τ = 2.2 ± 0.4 pulses), reaching a steady state (14.9 ± 0.7%; n = 6 paired recordings) of the initial response. Ca²⁺ currents activated during trains were also analyzed. The Ca²⁺ charge (Q_Ca²⁺), as the integral of the current elicited during the 2 ms pulses, was measured for each depolarization in the train (Fig. 1C, inset). A reduction was observed by the end of the train, 7 ± 2% (0.22 ± 0.03 pC for first stimulus), probably due to Ca²⁺-dependent inactivation of voltage-dependent Ca²⁺ channels (Grant and Fuchs, 2008), suggesting that part of the synaptic depression could be due to a reduced influx of Ca²⁺ to the cell.

EPSCs activated during trains, as shown in Figure 1A, regardless of their amplitudes or shape, were used to build a phase plot (Fig. 1D). This histogram represents the latencies of all EPSCs activated in each cycle, relative to the onset of that one cycle. The peak in this distribution indicates the time point within each cycle with the highest probability of EPSC occurrence. As the referential point to measure latency changes from cycle to cycle within the periodic waveform, latency in transmitter release should also be considered a phase of a periodic response. We will refer to this observation with both terms (latency and phase). The average phase (or latency) was calculated as suggested by Goldberg and Brown (1969) for the one recording shown in Figure 1D, obtaining a value of 2.1 ms, and for n = 6 IHC-afferent pairs, an average of 2.53 ± 0.07 ms (at 250 Hz, 5–12 repetitions each). For clarity, we will use the time scale to measure the average phase (as indicated above), although the corresponding value in radians would be 3.9 ± 0.8 and 223° ± 5° in degrees. The average phase parameter can also be constructed with solely latencies to the first EPSC in each cycle, but the resulting value was very similar to what described above (2.45 ± 0.07 ms, n = 6, t test p = 0.12).

Another important consideration is the level of synchronization of the events around the mean phase. This is quantified with the parameter r (vector strength or synchronization index) that provides a value of 0 in case of no phase-locking and 1 when events are perfectly synchronized (Goldberg and Brown, 1969). We obtained an average r of 0.38 ± 0.04 for n = 6 recordings that is significantly different from a theoretically non-phase-locked response (t test, one sample, p < 0.0001) (when computed with first EPSCs in each cycle, r = 0.37 ± 0.03).

Phase-locked responses were also obtained with stimulating frequencies of 100 and 500 Hz (see below, Phase constancy in trains with different levels of depolarizations and frequencies).

Phase constancy in trains with different levels of depolarizations and frequencies

Interestingly, auditory nerve fibers conserve a preferred phase regardless of the intensity of the stimulus (Kiang et al., 1965; Rose et al., 1967). Presynaptic hair cells were subjected to depolarizing trains at different voltage levels (−40, −30, and −20 mV) to mimic a range of sound intensities. These values span the range of potentials at which this synapse would operate in physiological conditions (Brandt et al., 2003; Johnson et al., 2005; Schnee et al., 2005; Keen and Hudspeth, 2006; Goutman and Glowatzki, 2007). Individual (Fig. 2A) and average (Fig. 2B2) postsynaptic responses during these three levels of hair cell depolarization are shown. In agreement with previous results, trains to −20 mV produced the largest average responses, followed by trains to −30 mV. As for −20 mV trains, the −30 mV ones showed synaptic depression over the first few pulses, whereas short-term facilitation occurred at the −40 mV trains presumably due to lower release probability during this stimulus. The average maximal response was 205 ± 51 pA for the −20 mV train, 139 ± 40 pA for the −30 mV train, and 61 ± 28 pA for the −40 mV train for recordings shown in Figure 2, and 140 ± 14 pA, 87 ± 15 pA, and 34 ± 7 pA for average of n = 6 cell pairs (6–12 repetitions each).

The last five pulses in each train were used to compute the (quasi-)steady-state level of the ensemble response at each depolarization level, with average values of −22 ± 3 pA for the train at −20 mV, 19 ± 4 pA for the train at −30 mV, and 9 ± 3 pA for the train at −40 mV (n = 6 cell pairs, 6–12 repetitions each, ANOVA p = 0.01). It is important to note that these values correspond to average responses per pulse, including release failures.

We also computed the average size of individual EPSCs for the three different depolarization levels (events in ‘successful’ cycles of the second half of each train). In the −20 mV trains the average EPSC was 82 ± 9 pA (n = 5 cells, 16–39 EPSCs per cell), 96 ± 10 pA (13–23 EPSCs) for the −30 mV trains, and for the −40 mV trains 90 ± 13 pA (3–18 EPSCs) (not shown). Thus, individual EPSCs were multivesicular, and the average size was constant across train intensities (ANOVA, p = 0.14), in agreement with previous results (Glowatzki and Fuchs, 2002; Goutman and Glowatzki, 2007).

The phase of synaptic responses (or latency) was measured within cycles of trains to different presynaptic membrane potentials. Phase plots are shown for one cell pair in Figure 2C, where it can be seen that the average phase was found at t = 2.30 ms, 2.38 ms, and 2.53 ms for the −20, −30 and −40 mV trains, respectively. This same parameter was calculated for n = 5 recordings (Fig. 2D), obtaining average phases of 2.53 ± 0.07, 2.44 ± 0.06, and 2.62 ± 0.09 ms for the same three depolarization levels and are not significantly different from each other (ANOVA, p = 0.23). The same parameters were computed solely with first latencies instead of all events in each cycle, but no significant differences were observed in this case either (data not shown).

These three distinct levels of stimulation expectedly produced presynaptic Ca²⁺ currents of different size and kinetics. Figure 2E shows Q_Ca²⁺ generated in each pulse by the three stimulation protocols. The −20 mV train produced a peak Q_Ca²⁺ at the first stimulus of 0.22 ± 0.03 pC as shown in Figure 1C (inset), whereas peak Q_Ca²⁺ for the −30 mV train was 0.12 ± 0.01 pC, and 0.06 ± 0.01 pC for the −40 mV train (ANOVA, p < 0.0001). Activation kinetics (single exponential) were strongly voltage dependent and averaged τ_act = 273 ± 28 μs for the −20 mV, 366 ± 42 μs for −30 mV, and 429 ± 66 μs for −40 mV (not shown, ANOVA, p < 0.0001).

Periodic stimuli at frequencies different from 250 Hz with maximal depolarizations of −20 and −30 mV were also applied. Both trains of square pulses and sinusoidal stimulation at 100 Hz produced synaptic depression with maximal responses of 404 ± 120 pA and 170 ± 42 pA at −20 and −30 mV, respectively (n = 4 cell pairs each, 5–27 repetitions each, t test, p = 0.08) and steady-state values of 81 ± 23 pA and 46 ± 9 pA for the same potentials (n = 4, t test, p = 0.09) (Fig. 3A,B). The maximal and steady-state responses of the −20 mV trains at 100 Hz are larger than the corresponding responses at 250 Hz (t test, p = 0.047), which is consistent with longer depolarizations in each cycle of the train. Synaptic responses at these low-frequency trains were also phase locked, and the average phase was not different when comparing the two evaluated levels. As different stimulation protocols (train of square pulses or sinusoidal waveform) were used in different recordings, and provided that the average phase could change depending on the shape of the stimulus, both absolute phase values and also ratios between −20 mV and −30 mV stimuli in each recording were calculated. For the recordings shown in Figure 3A–C, the average phase was 6.6 at −20 mV and 6.9 ms at −30 mV trains, and for n = 4 cell pairs the averages were 6.3 ± 0.7 ms at −20 mV and 6.7 ± 0.5 ms at −30 mV (n = 4, t test p = 0.18) (Fig. 3C). Calculating ratios between −30 mV and −20 mV phases, the average was 1.07 ± 0.05 (Wilcoxon signed-rank test, p > 0.05).

Increasing the frequency of stimulation produced a higher rate of failures per stimulus, consistent with shorter on-periods. Maximal responses of trains of square pulses or alternatively sinusoidal stimulation at 500 Hz with depolarizations to −20 mV were 113 ± 25 pA, and at −30 mV, 83 ± 27 pA (n = 4 cell pairs each, t test, p = 0.107) (Fig. 3D). Phase locking occurred also at this frequency, with average phases (or latencies) for the recording shown in Figure 3D of 1.65 ms at −20 mV and 1.49 ms at −30 mV trains, and mean ratios for these two potentials of 1.01 ± 0.07 (n = 4 cell pairs, Wilcoxon signed-rank test p > 0.05) (Fig. 3F).

Ratios for average phases at 250 Hz trains were computed as well, rendering close to 1 values for both −30/−20 mV trains and for −40/−20 mV trains (0.98 ± 0.04 and 1.03 ± 0.03, respectively).

In summary, these results show that transmitter release from the IHC ribbon synapse is phase locked to cyclic stimuli of different frequencies, and that the phase is conserved independently of stimulus strength (hair cell depolarization). IHC voltage-gated Ca²⁺ channels activate more extensively and faster as the membrane is progressively depolarized (Fig. 2C and (Moser and Beutner, 2000; Marcotti et al., 2003). This leads to the following question: why does the timing of repetitive EPSCs, which is strongly dependent on [Ca²⁺]_i, remain unchanged with hair cell depolarization (Figs. 2E,3C,F).

Timing of single postsynaptic responses is voltage (Ca²⁺) dependent

To probe the kinetics of transmitter release at the IHC ribbon synapse, single 10-ms-long depolarizations of varied amplitude were applied during paired recordings. Presynaptic steps to −20 mV produced EPSCs with an average amplitude of 462 ± 105 pA (n = 4 cell pairs, 3–5 repetitions each, Fig. 4A1,B). Smaller responses were obtained for smaller depolarizations, 314 ± 73 pA for presynaptic steps to −30 mV, and 201 ± 67 pA for steps to −40 mV (n = 4, Fig. 4B). Earlier work showed that short-term plasticity affects the size and timing of the synaptic response (Cho et al., 2011; Goutman and Glowatzki, 2011; Schnee et al., 2011). No significant changes in amplitude were obtained when saturating pulses to −20 mV were preceded by a predepolarization (491 ± 110 pA, n = 4, 2-way ANOVA, p > 0.05, Fig. 4A2) as described (Goutman and Glowatzki, 2011), but strong facilitation was observed for submaximal pulses; conditioning depolarizations facilitated responses at −40 mV by 98 ± 44% (315 ± 56 pA, n = 4 cell pairs, two-way ANOVA p < 0.01) and at −30 mV by 66 ± 19% (486 ± 81 pA, two-way ANOVA, p < 0.001).

Figure 4C shows synaptic latencies to the first EPSC after the pulse as a function of the command potential. As described for other synapses, there is a close relation between Ca²⁺ current size and postsynaptic response timing, as higher Ca²⁺ influx provokes larger and faster release (Llinás et al., 1981; Felmy et al., 2003). The IHC ribbon synapse behaves similarly. Synaptic latency for presynaptic pulses to −40 mV (without a conditioning predepolarization) was 7.07 ± 1.18 ms (n = 4 cell pairs, 3–5 repetitions) and 3.34 ± 0.45 ms at −20 mV (n = 4 cell pairs, two-way ANOVA, p < 0.05) (Fig. 4C). Interestingly, when the synapse was facilitated (after predepolarization), latency to all three potentials was shorter (−40 mV, 3.38 ± 0.53 ms; −30 mV, 2.05 ± 0.39 ms; −20 mV, 1.56 ± 0.30 ms; p < 0.001). It is important to note that a constant reduction of ∼50% was obtained across physiological potentials due to facilitation (49% for −40 mV, 50% for −30 mV, and 48% for −20 mV), but differences persisted when comparing between potentials (two-way ANOVA, p = 0.018). Jitter in synaptic latency underwent a reduction caused by predepolarizations (e.g., −40 mV SD of latency: 2.18 ± 0.42 ms to 1.24 ± 0.23 ms, two-way ANOVA, p < 0.05) (Fig. 4D). These results indicate that when the synapse is facilitated by a predepolarization, transmitter release occurs faster and with greater precision.

Ca²⁺ currents also showed higher amplitude and faster activation with pulses to more depolarized potentials (Fig. 4E1,E2). Predepolarizations also produced changes in these parameters, but only at −20 and −30 mV steps; Ca²⁺ influx decreased from 2.20 ± 0.07 pC to 2.10 ± 0.07 pC at −20 mV and from 1.65 ± 0.08 pC to 1.56 ± 0.07 pC at −30 mV steps (two-way ANOVA, p < 0.01). Presteps also produced faster activation of Ca²⁺ currents (e.g., at −40 mV steps τ_act: 0.46 ± 0.06 ms to 0.38 ± 0.04 ms, two-way ANOVA, p = 0.0004).

It can be argued that the duration of pulses in Figure 4 is different from the corresponding ones at the stimulating frequencies used in Figures 1–3 (2 ms for 250 Hz, 5 ms for 100 Hz, and 1 ms for 500 Hz) and that different results may arise. The duration of the pulse in Figure 4 (10 ms) was selected to maximize the release probability and so obtain a large number of events to analyze. One possibility is that tail currents of shorter pulses, or during trains, could set synaptic latency by the transient influx of Ca²⁺ that they produce. This was explicitly tested by performing similar experiments as shown in Figure 4, but with pulses of 2 ms. The two more positive presynaptic levels were exclusively tested, as many more failures are observed with the shorter pulses at less depolarized potentials. Similarly to the differences shown for the 10 ms pulses (where tail currents did not participate in triggering release), synaptic latency was shorter for the −20 mV pulses (2.39 ± 0.17 ms) than for the −30 mV ones (3.07 ± 0.20 ms) (n = 5, p = 0.022, t test).

Efficient recovery of the synaptic response is required for phase maintenance

Experimental and theoretical evidence suggests that precise timing at the IHC ribbon synapse depends on a large, readily releasable pool of vesicles (Wittig and Parsons, 2008; Trapani et al., 2009). Thus, phase locking during repetitive hair cell depolarization would also require efficient vesicular resupply. A 10 ms depolarization from −80 to −20 mV was sufficient to reach the peak of the ensemble postsynaptic response, consistent with deconvolution analysis indicating that the first component of release had a time constant of 2.1 ms (Goutman and Glowatzki, 2007). This stimulus was used to partially deplete the pool of synaptic vesicles and was then repeated at intervals out to 1 s (Fig. 5A). Due to the stochastic nature of release at the IHC ribbon synapse, recovery after every interval was tested 3–8 times, and the resulting EPSC was averaged (including failures). Recovery occurred quickly, with a monoexponential time course (τ_rec = 37 ± 9 ms; n = 5 cell pairs, both with or without cyclothiazide, Fig. 5B). The integral of the Ca²⁺ current generated during each pulse showed no significant change (ANOVA, p = 0.11, not shown).

It is of interest to note that the synaptic latency also correlated with the degree of recovery. Figure 5C shows average synaptic latencies for responses at different intervals after the depleting stimulus (average latency for S1 indicated by dashed line). As the response recovered, latency decreased (ANOVA, p = 0.03), following a time course similar to that indicated previously (τ_{rec, latency} = 54 ± 12 ms), consistent with the proposed dependence of release timing on pool size (Wittig and Parsons, 2008).

Interplay between depression and stimulus strength

The foregoing analysis demonstrates that vesicle pool depletion must occur during the standard stimulus train (20 stimuli at 250 Hz; total duration, 80 ms). However, the extent of this depression must depend on the initial probability of release, varying with presynaptic depolarization. These two effects will combine to provide a level of depression at the end of each train, which was tested explicitly by applying an additional 10 ms step to −20 mV. This ‘test pulse’ was designed to release any remaining vesicles and, therefore, to reveal the degree of depression occurring during stimulus trains to different presynaptic voltages (Fig. 6).

Average postsynaptic responses during the 20 stimuli trains, before the test pulse, were similar to those shown in Figure 2. The test pulse at the end of a train to −20 mV elicited a response with an average amplitude of 227 ± 29 pA (n = 4 cell pairs, 3–10 repetitions each) (Fig. 6A,B). The average response at the end of the −40 mV train was significantly larger, 413 ± 35 pA (ANOVA, p = 0.0005), and an intermediate result was obtained in the case of the −30 mV train (335 ± 20 pA, ANOVA p < 0.005). Synaptic latency of the test EPSC was longer after more intense trains (Fig. 6C) (−20 mV, latency 5.0 ± 0.7 ms in average of n = 4 cell pairs) and shorter after less demanding trains (−40 mV train, 2.1 ± 0.1 ms, ANOVA, p = 0.0011). This result contrasts with the overall constant synaptic phases (or latencies) across trains of different intensities (Figs. 2C,E). Ca²⁺ currents at the test pulse (Fig. 6E) were not significantly different among the three different protocols (Q_Ca²⁺ for the −20 mV train was 0.18 ± 0.02 pC, for the −30 mV train it was 0.18 ± 0.02 pC, and for the −40 mV it was 0.19 ± 0.03 pC, ANOVA p = 0.6). Jitter in synaptic latency was also computed, but due to the scarce number of events, it was done only for the −20 mV trains at each of the first five depolarizations and the ensemble of the last five pulses (Fig. 6D). The standard deviation (jitter) for n = 4 recordings was fairly constant throughout the train, except for stimulus number 4 (1.22 ± 0.16 ms, ANOVA, p < 0.05), which was over the critical value of ∼1.2 ms, corresponding to a random temporal distribution of events within a cycle (Fig. 6D, dashed line; see Materials and Methods). This observation resembles the unchanged spike-timing precision observed after adaptation in the auditory nerve (Avissar et al., 2007).

Thus, during repeated stimulus trains, transmitter release is enhanced by stronger depolarization, but at the same time diminished by greater depletion of the available pool of vesicles. These two processes would reach a steady state dependent on the rate of pool replenishment. These assumptions were tested with a simple model of transmitter release, incorporating available data on the function of IHC release machinery (Beutner et al., 2001), a simplified pattern of Ca²⁺ influx based on the kinetics of Ca²⁺ currents (Fig. 2), and a recovery rate as measured in Figure 5.

Simulating transmitter release during stimulus trains

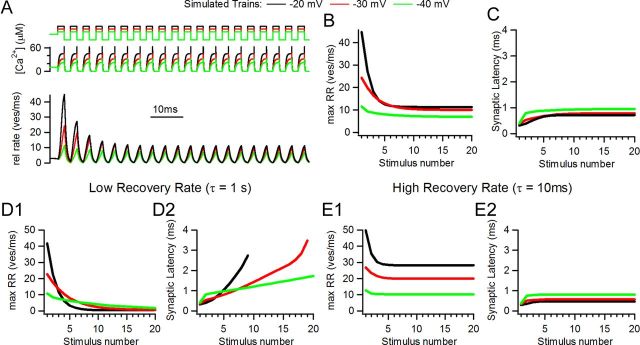
Transmitter release was driven by a highly cooperative model with five binding steps for Ca²⁺ (Beutner et al., 2001). The intracellular Ca²⁺ concentration used for driving release was implemented as idealized waveforms following the activation and deactivation time courses of Ca²⁺ currents as in Figure 2 (see Materials and Methods for details on the model). Simulations of 20 pulse trains with three different levels of stimulation are shown in Figure 7, where two main parameters were tracked: maximum release (as release rate, Fig. 7B) and synaptic latency per pulse (Fig. 7C). A scheme of the stimulus protocol, [Ca²⁺]_i, and release rate are shown in the top, middle and bottom panels of Figure 7A. Three stimulation patterns were used to drive the model: ‘−20 mV,’ ‘−30 mV,’ and ‘−40 mV’ by analogy to the experimental values. Trains at −40 mV and −30 mV had maximal release of ∼25% and 54%, respectively, that of the −20 mV train (11.4 vesicles (ves)/ms, 24.3 ves/ms, and 44.8 ves/ms, for the three train levels). At (quasi)steady state the rates were 6.9, 10.0 and 11.3 ves/ms, respectively. Average latency to the first exocytosed vesicle per pulse showed convergence between trains (Fig. 7C) (0.72 ms, 0.79 ms, and 0.96 ms for the −20 mV, −30 mV, and −40 mV trains, respectively) although the absolute values were smaller than in the experimental data (compare Figs. 2 and 6; see Discussion for possible reasons). These values differed maximally by 33% with stimulus intensities (−20 mV vs −40 mV) that drive release at five-fold different rates (see peak rate in first pulse, Fig. 7A,B).

Figure 7.

Computer simulations with a model of synaptic transmission at the IHC ribbon synapse. A, Simulated traces of release rate (bottom), idealized [Ca²⁺]_i waveform (middle), and stimulation protocol (top). Three different levels of stimulation were used and illustrated in different colors. B, Peak release rate for each stimulus showing synaptic depression. C, Synaptic latency for each pulse in the train (calculated from the onset of each pulse to the release of first vesicle). Model used for panels A, B, and C include a recovery step with a time constant of 37 ms. D1, D2, Peak release rate and synaptic latency in a model with slow recovery rate (τ = 1 s). E1, E2, Same as before but with an overly high recovery rate (τ = 10 ms).

The rate of vesicle pool replenishment should be important in determining the dynamics of release during stimulus trains. This was examined in the model by reducing (τ = 1 s, Fig. 7D1,D2) or increasing (τ = 10 ms, Fig. 7E1,E2) the recovery rate. With slower pool recovery, release dropped to values close to zero in all conditions (0.5 vesicle/ms for −20 mV, 0.6 vesicle/ms for −30 mV, 1.8 ves/ms for −40 mV). Latency per pulse underwent a constant increase during the course of the 20 stimuli train, reaching maximum values of: 2.7 ms for the −20 mV, 3.5 ms for the −30 mV, and 1.7 ms for the −40 mV trains (measurements were interrupted before the end of the train at −20 and −30 mV because release rate dropped below threshold criteria). This behavior would degrade phase constancy. On the other hand, the rapid pool recovery rate model showed relatively constant latencies (Fig. 7E2), but steady-state release (28.4 ves/ms for the −20 mV, 20.0 ves/ms for the −30 mV, and 10.3 ves/ms for the −40 mV trains) was significantly larger than that found experimentally. Since models with altered pool recovery rates diverged significantly from experimental observations, additional work was restricted to the model parameters illustrated in Figure 7A–C. This simple model, which can be driven with stimuli of different intensities and includes a vesicle recovery mechanism, was able to capture the main features of the experimental results. including fairly constant synaptic latencies throughout the train.

Mixed trains

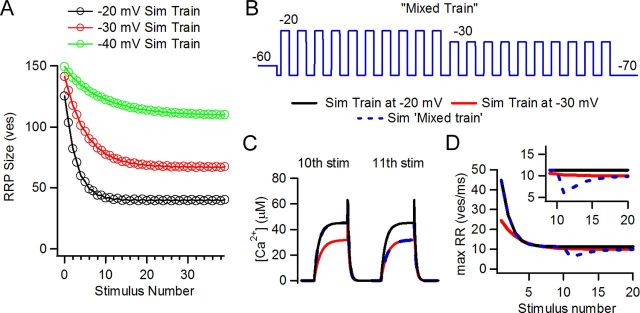
Figure 8A shows the estimated size of the readily releasable pool at the end of each pulse in simulated trains at three depolarization levels. It can be clearly noted that the higher the intensity of the stimulus, the fewer vesicles were left for release after each pulse. At steady state, the −20 mV train operated with the smallest pool size but still released more vesicles than the other two trains (Fig. 7A,B). The strength of the stimulus compensated for the smaller pool size.

Figure 8.

Equilibrium between recovery and release rate was unbalanced after changing stimulus pattern in simulations (Sim) of synaptic activity. A, Vesicle pool size at the end of each stimulus for the three levels. B, Mixed train protocol. C, Detail of 10th and 11th pulses in the simulated trains. In the mixed train, Ca²⁺ transients changed from a −20 mV regime to a −30 mV regime. D, Peak release rate for the −20 and −30 mV trains (acting as controls) and the mixed trains. Note the transient dip in the mixed train upon switching to the −30 mV regime on the 11th pulse due to alteration of the equilibrium between release drive and depression level.

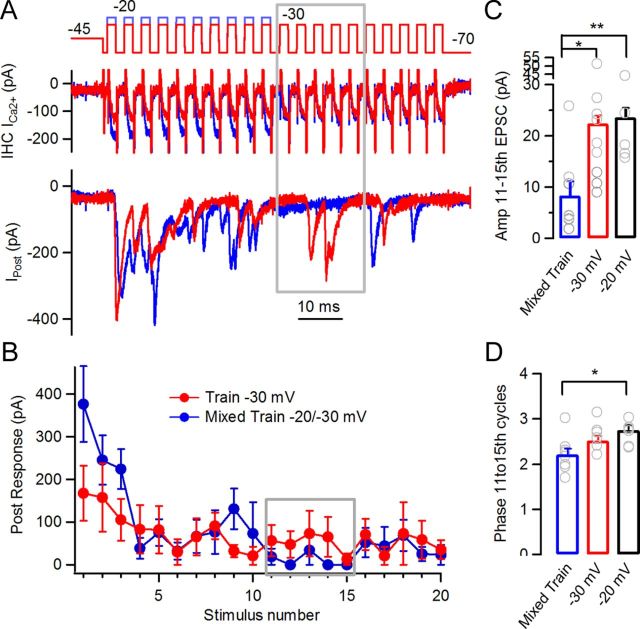
If in steady state a balance was reached between depletion and Ca²⁺ channel gating probability, it would be insightful to investigate the consequence of altering this equilibrium. The model was used to predict this effect by using ‘mixed trains’ in which the first 10 steps were to −20 mV and the last 10 were to −30 mV (Figs. 8A,B). Stronger depletion (at −20 mV) combined with weaker calcium channel gating (at −30 mV) would be expected to produce diminished vesicular release, as indeed was found (Fig. 8D). At the transition point, the release rate fell transiently before gradually rising and finally converging to that of a control (‘unmixed’) train at −30 mV. Latency to release underwent a transient increase in the same time window that also recovered to control values in the following stimuli. The mixed train protocol was repeated on paired recordings from IHCs and afferent boutons. Transmitter release during mixed trains was compared to control unmixed trains at −30 mV and −20 mV (Fig. 9). EPSCs evoked during the 11th to 15th pulses in the mixed train were compared to EPSCs in the unmixed trains (Fig. 9A,B, gray boxes). The average response to these five stimuli in the unmixed train was 22 ± 2 pA, whereas in the mixed train it was 8 ± 3 pA (n = 5 and 8 cell pairs respectively, 6–58 repetitions), showing a strong reduction in the average response (ANOVA, p = 0.003) (Fig. 9C). The phase of the synaptic events occurring at the transition point between the two levels was calculated. The mixed trains showed an out of phase average compared with the control −20 mV trains, but not with the −30 mV (Fig. 9D) (2.21 ± 0.12 ms, 2.75 ± 0.11 ms, 2.52 ± 0.10 ms, respectively. ANOVA, p = 0.0178). Ca²⁺ currents in the mixed train were similar to those of the unmixed trains (not shown).

Figure 9.

Synaptic responses with mixed trains. A, Synaptic responses to mixed trains. Voltage protocols for the −30 mV train (red) and the mixed train (blue, first half pulses to −20 mV, second half to −30 mV) are included. Gray box indicates period where ‘equilibrium’ between strength of stimuli and depression is lost by sudden change in stimulus intensity. B, Average postsynaptic amplitude per stimulus in the −30 mV and mixed trains (gray box, same as in A). C, Average responses to 11th–15th pulses in mixed (blue), −30 mV (red), and −20 mV (black) trains. D, Phase of synaptic events activated between the 11th and 15th pulses in the mixed trains and the −20 mV and −30 mV trains (*p < 0.05, **p < 0.01).

The transient dip in synaptic response amplitude (release rate in the stimulations) would indicate that the proposed equilibrium between release drive and size of vesicle pool was unique for each stimulation regime favoring phase-locked responses to periodic stimuli.

Discussion

Auditory timing and Ca²⁺ dependence

The auditory system shows several synaptic adaptations that contribute to maintaining accurate and precise neurotransmission. Fast kinetics of postsynaptic AMPA receptors and short membrane time constants (generally influenced by resting potassium conductances) help to abbreviate synaptic events and are therefore capable of maintaining high-frequency signaling (Trussell, 1999). On the other hand, large amplitude synaptic potentials ensure fast transitions to threshold, and with low variability.

It has been clear since early work by Bernard Katz that transmitter release is highly dependent on extracellular calcium (Katz and Miledi, 1965). Later, it was shown that postsynaptic responses are preceded by voltage-dependent Ca²⁺ currents and that synaptic latency is voltage (and thus Ca²⁺) dependent (Llinás et al., 1981; Felmy et al., 2003; Bollmann and Sakmann, 2005). The IHC ribbon synapse is driven by continuously varying receptor potentials, rather than action potentials, and has rate constants for vesicular release that are Ca²⁺ dependent (Beutner et al., 2001). Thus, it seems somewhat paradoxical that tone bursts at a fixed frequency (typically at best or characteristic frequency) evoke action potentials in auditory afferent neurons with a constant phase throughout a wide range of stimulus intensities (Galambos and Davis, 1943; Kiang et al., 1965; Rose et al., 1967; Ruggero, 1992). Since action potentials in the auditory nerve are driven by the release of neurotransmitter from the IHC (Robertson and Paki, 2002), a louder sound, producing greater hair cell depolarization and more calcium influx, should evoke more and earlier transmitter release.

Phase-locking at the IHC ribbon synapse

Considering the differences in experimental paradigms between explants of the organ of Corti (from neonatal rats) and auditory nerve recordings from anesthetized animals, we set out to investigate phase locking of neurotransmission occurring at the IHC ribbon synapse. We first observed that transmitter released from the IHC is indeed phase locked to a periodic stimulus and remains constant even as release probability changes. EPSCs from IHCs were elicited at a constant phase (or latency) by trains of square pulses or sinusoidal stimulation to different levels of depolarization (Figs. 2, 3). To our knowledge, this work shows for first time that phase constancy is a fundamental property of the IHC ribbon synapse.

We also extended recent observations indicating that this synapse would operate in a steady facilitated mode (Cho et al., 2011; Goutman and Glowatzki, 2011; Schnee et al., 2011), and we now show that facilitation produces a significant increase in accuracy and precision throughout the operating range of the synapse (Fig. 4). Responses to single steps at different potentials (−40, −30, or −20 mV) still showed differences in latency (Fig. 4C, black symbols), which is consistent with a Ca²⁺-dependent process as shown in ribbon (Heidelberger et al., 1994; Beutner et al., 2001) and regular chemical synapses (Neher and Sakaba, 2008).

The single pulse data may also depart from the nanodomain model in which the IHC ribbon synapse would operate (Brandt et al., 2005; Graydon et al., 2011). According to this model, the opening of a single Ca²⁺ channel is sufficient to trigger the release of a tightly colocalized vesicle(s). Under this scenario, the Ca²⁺ concentration at the vesicular sensor would be saturating, and release latency (and probability) would be highly determined by the gating properties of the Ca²⁺ channels. However, whereas Ca²⁺ currents activated by pulses to −20 and −40 mV differed in activation kinetics by ∼200 μs (Fig. 4E2), release latencies to the same pulses were 1.55 or 3.70 ms apart (with or without predepolarization, respectively, Fig. 4C). It is still possible that the opening of few channels (not strictly one) are necessary to trigger release (Brandt et al., 2005), but future investigations will help determine precisely the release mechanism at this synapse.

We also observed that at the end of a train of stimuli, an additional depolarization revealed the level of depression that was reached by the train (Fig. 6). With this protocol, trains of higher intensity produced more profound levels of depression and, consistently, weaker trains presented higher responsiveness. How might this behavior affect response timing during a train? It is reasonable to think that a given stimulus in a train promotes and accelerates release by allowing Ca²⁺ into the cell, but at the same time it provokes partial vesicle depletion. It has been shown recently that latency to the first exocytotic event is inversely correlated with vesicle pool size (also between jitter and size) (Wittig and Parsons, 2008). Therefore, we propose that the partial depletion provoked by a given pulse slows release to the following stimuli. As a consequence, a competing dynamic would be established in which larger depolarization produces faster release due to larger Ca²⁺ influx, but simultaneously delays subsequent release by depleting the available vesicle pool. It is still necessary to determine the linkage between recovery and different phases of synaptic adaptation (Relkin and Doucet, 1991; Ruggero, 1992) and also whether depression at this synapse is produced by simple vesicle depletion, clearance of release sites, or some other mechanism (Neher, 2010).

Finally, we would like to propose that an equilibrium would be established between the level of depolarization in a train and the average size of the vesicle pool on which stimuli operate. In an ongoing train with large depolarizations, release would operate on a relatively smaller pool (due to stronger depression produced by the stimulus), whereas trains with weaker depolarizations would function on a larger one. Simulations allow us to track the size of the pool during a given stimulation protocol, and differences in number of vesicles were actually observed (Fig. 8A). Moreover, results in Figures 8 and 9 confirm this hypothesis; when a low intensity train operates in a context of a small vesicle pool due to strong depletion (the transition point in the mixed train), the synapse departs from equilibrium and shows a significant drop in release rate. It is important to note that auditory nerve responses to decrements in tonal intensity show very similar transient dips in firing rate (Smith et al., 1985). In simulations, a concomitant transient increase in latency at the transition point, followed by return to control unmixed values, was also observed. This modeling prediction was only partially observed experimentally, as a significant difference was observed in the phase of synaptic responses in the mixed train compared with the −20 mV trains but not with the −30 mV ones. As release dropped so dramatically at the transition point (Fig. 9B,C), it is possible that the few events left for analysis were insufficient for a complete comparison (2–22 events in the 11th to 15th cycles, n = 8 recordings). It is important to note that an ahead phase as observed in the mixed train (Fig. 9D) does not mean that release is faster but rather that latencies are changed and phase is not conserved.

Simulations

Several studies have presented models of synaptic transmission that successfully represented experimental results at central synapses (Dittman and Regehr, 1998; Weis et al., 1999; Saviane and Silver, 2006; Hosoi et al., 2007). Recovery in all these studies is critical for determining the strength of the synapse and has been repeatedly modeled as a Ca²⁺-dependent process. Modeling efforts were also undertaken to investigate the dynamics of vesicle pools and transmission timing at the hair cell ribbon synapse (Beutner et al., 2001; Schnee et al., 2005; Wittig and Parsons, 2008). The present model shows features that are shared with those studies, including a Ca²⁺ sensor model derived from Ca²⁺-uncaging experiments to drive release (Beutner et al., 2001), idealized intracellular Ca²⁺ transients following the kinetics of the currents measured in Figures 2 and 6 (Weis et al., 1999; Beutner et al., 2001), and a recovery process as studied in Figure 5 (see Materials and Methods for details on the model). The latter feature assumes that only a partial depletion of the vesicle pool was produced during the trains.

Simulations in Figure 7 show that this simple model is able to capture the basic characteristics of IHC ribbon function during trains of stimuli, such as intensity coding, phase locking, and the tight relation between timing precision and efficient recovery. As shown in the model, a low recovery rate produces increasing synaptic latency during the train. In contrast, fast recovery provides good timing but excessive sustained release that does not match the results obtained in these recordings from the immature cochlea.

Discrepancies in the absolute values of latency between simulations and experimental results may arise from processes that are not contemplated in the model, such as diffusion of Ca²⁺ in the cytosol, other putative Ca²⁺-dependent processes, vesicle translocation, vesicle fusion to the plasma membrane, diffusion of glutamate, and activation of postsynaptic receptors.

Finally, this model strengthens the idea that phase locking is primarily determined by an equilibrium between release drive and pool size, conferring a constant synaptic latency throughout the train. It cannot be precluded, though, that additional mechanism(s) not taken into account in this model might contribute as well to improve phase locking. This issue deserves special attention, as for instance some differences in latency persisted when comparing different train levels (Fig. 7C).

Functional consequences

Phase locking has been extensively shown in different species with diverse hearing frequency ranges. In every case, this property degrades as the stimulation frequency increases above 1–5 kHz (Kiang et al., 1965; Rose et al., 1967; Taberner and Liberman, 2005). In species with poor low-frequency sensitivity, such as mice and rats, few auditory nerve neurons respond to pure tones below or within this range (Taberner and Liberman, 2005). However, it has also been shown that phase locking occurs when high-frequency sounds are modulated in amplitude by a low-frequency envelope (Buran et al., 2010) with several common characteristics (Yin, 2002).

It is useful to compare the degree of phase locking (or synchronization) that was reached in synaptic responses with that of auditory nerve recordings in vivo. It has been reported in auditory nerve recordings from rats that vector strength (a measure of synchronization that ranges from 0 to 1) decreases with frequency and also that it is larger at higher intensities of stimulation (Paolini et al., 2001). The value of vector strength calculated in the current study, ∼0.4, is in the range of values reported for auditory nerves, but it is also important to consider that few fibers with characteristic frequency (or best frequency) below 1 kHz are found in rats. In low-frequency hearing animals such as cats, auditory nerves present higher synchronization values (Johnson, 1980). Provided that the experiments in the current study were done at room temperature and with an immature organ of Corti, it is expected that better synchronization would be obtained in more physiological conditions.

The mechanism proposed in the current study is based on general phenomena such as the dynamics of vesicle pools, synaptic plasticity, and the characteristics of the receptor potential with variable amplitudes at the hair cells. However, these experiments were performed in the apical coil of neonatal rats, and thus the conclusions should not be immediately extrapolated to the in vivo situation. Future studies on mature endorgans and/or in species with higher sensitivity to low-frequency components (<1 kHz) should be done to confirm whether our model can be generalized to other synapses.