Probing the transient dark state of substrate binding to GroEL by relaxation-based solution NMR

Abstract

The mechanism whereby the prototypical chaperonin GroEL performs work on substrate proteins has not yet been fully elucidated, hindered by lack of detailed structural and dynamic information on the bound substrate. Previous investigations have produced conflicting reports on the state of GroEL-bound polypeptides, largely due to the transient and dynamic nature of these complexes. Here, we present a unique approach, based on combined analysis of four complementary relaxation-based NMR experiments, to probe directly the “dark” NMR-invisible state of the model, intrinsically disordered, polypeptide amyloid β (Aβ40) bound to GroEL. The four NMR experiments, lifetime line-broadening, dark-state exchange saturation transfer, relaxation dispersion, and small exchange-induced chemical shifts, are dependent in different ways on the overall exchange rates and populations of the free and bound states of the substrate, as well as on residue-specific dynamics and structure within the bound state as reported by transverse magnetization relaxation rates and backbone chemical shifts, respectively. Global fitting of all the NMR data shows that the complex is transient with a lifetime of <1 ms, that binding involves two predominantly hydrophobic segments corresponding to predicted GroEL consensus binding sequences, and that the structure of the bound polypeptide remains intrinsically and dynamically disordered with minimal changes in secondary structure propensity relative to the free state. Our results establish a unique method to observe NMR-invisible dynamic states of GroEL-bound substrates and to describe at atomic resolution the events between substrate binding and encapsulation that are crucial for understanding the normal and stress-related metabolic function of chaperonins.

Molecular chaperones are proteins that are ubiquitous to all three domains of life and assist native cellular proteins to reach their correct fate in vivo by facilitating folding, transport, oligomeric assembly, and controlled conformational switching (1–3). The chaperone system comprises a network of interconnected and redundant, yet unrelated, proteins that function via a broad range of mechanisms and under various physiological contexts. In addition to assisting in basal protein function, the chaperone system functions as a cellular quality control network tuned to mitigate the deleterious and toxic effects of environmental and pathological stress on proteins by preventing and, in some cases, reversing macromolecular aggregation (4). The energy barrier separating the folded and unfolded states is small for most proteins; consequently, many proteins are under continual risk of unfolding and aggregating, a risk that becomes particularly acute in response to extracellular stress. To carry out their protective role, chaperones have to interact transiently with myriad nonnative protein substrates to promote correct folding or assembly without the aid of stereospecific information on the native structure of the substrates. Generally, chaperones achieve this by presenting a hydrophobic surface that is able to bind exposed hydrophobic patches on partially folded or misfolded proteins (2, 3).

Chaperonins are a subclass of molecular chaperones characterized by cylindrical, stacked ring structures that form interior cavities large enough to encapsulate substrate proteins. The most studied and best understood chaperonin, both mechanistically and structurally, is GroEL, a 780-kDa supramolecular machine comprising seven identical 56-kDa subunits per cylindrical ring that assists protein folding through a multistep reaction cycle (2, 3). GroEL initially binds substrate proteins on exposed hydrophobic patches facing the inside of the cavity. Through a series of ATP-driven conformational rearrangements of the GroEL subunits and recruitment of the cochaperone GroES, GroEL encapsulates the substrate within the central chamber (2, 3). However, the structure and dynamics of substrate interactions with GroEL, as well as exactly how GroEL assists substrates to attain their native state (5–7), remain poorly understood, because the bound substrate, except under special circumstances, is generally invisible to conventional biophysical and structural techniques.

Previous investigations of GroEL have provided conflicting reports on the state of GroEL-bound peptides and proteins. Well-ordered β-hairpin and extended conformations have been observed by crystallography (8, 9), but these conformations were likely selected preferentially during crystallization. NMR-based transferred nuclear Overhauser enhancement studies have reported both helical and hairpin conformations (10–12), but interpretation is complicated by extensive spin diffusion (13) within GroEL. Conversely, hydrogen–deuterium exchange experiments (14, 15) imply that the secondary structure is sufficiently destabilized or disrupted upon binding to GroEL to allow substantial backbone amide hydrogen–deuterium exchange to occur. Likewise, ¹H-¹⁵N correlation experiments, designed specifically for large (>>100 kDa) protein assemblies, suggest that bound protein substrates are dynamic and largely unfolded, because the few cross-peaks observed are located at characteristic random coil positions (16, 17).

The majority of physical studies on GroEL–substrate interactions have been carried out on heterologous systems, an approach validated by the high degree of conservation of chaperonins across evolution (2, 3). To address the conformational preferences and dynamics of a GroEL-bound substrate directly at atomic resolution, we have made use of four complementary relaxation-based NMR experiments (18–22) to probe directly and quantitatively the “dark” NMR-invisible state of the model, intrinsically disordered, polypeptide amyloid β (Aβ40) bound to GroEL. Although we use Aβ40 as a model system here to probe the interaction of intrinsically disordered, aggregation-prone proteins with GroEL, we note that the interaction of Aβ with the human homolog of GroEL, heat shock protein 60 (51% sequence identity), is involved in the translocation of Aβ to the mitochondria, where accumulation of Aβ plaques is thought to lead to mitochondrial dysfunction and to represent an important component of Alzheimer’s disease (23).

Results and Discussion

We used a unique multipronged approach, based on the combined analysis of four relaxation-based NMR experiments, to study the dynamic interaction of Aβ40 with GroEL at atomic resolution. Specifically, lifetime line-broadening (20), dark-state exchange saturation transfer (DEST) spectroscopy (21, 22), Carr–Purcell–Meinboom–Gill (CPMG) relaxation dispersion spectroscopy (18, 24), and quantitative interpretation of very small exchange-induced chemical shifts (19) report in different ways on the overall exchange rates and populations of the free and bound states of Aβ40, as well as on residue-specific dynamics and structure within the bound state as reported by transverse magnetization relaxation rate constants (R₂) and backbone chemical shift values, respectively.

ΔR₂ Measurements.

Fig. 1A displays the difference in ¹⁵N-R₂ values (¹⁵N-ΔR₂) of 50 μM monomeric Aβ40 (21) in the presence and absence of GroEL. Line-broadening can arise from two sources: differences in chemical shifts between the free and bound states giving rise to chemical exchange line-broadening and lifetime line-broadening due to large R₂ values in the bound state, leading to rapid decay of magnetization (20). At a CPMG field of 550 Hz, exchange-induced line-broadening is virtually completely suppressed and the observed increases in ¹⁵N-R₂ values arise almost exclusively from lifetime line-broadening. This is evident from the absence of any correlation between ¹⁵N-ΔR₂ values and ¹⁵N exchange-induced shifts (Fig. 2E), as well as from analysis of the CPMG relaxation dispersion data (see below), which indicate that the largest contribution of exchange line-broadening to the measured ¹⁵N-ΔR₂ values is less than 0.5 s⁻¹ (Fig. S1). The ¹⁵N-ΔR₂ values are linearly dependent on the concentration of GroEL (up to the highest concentration of GroEL used in the study, 40 μM in subunits) (Fig. S2 C and D), reflecting the linear dependence of ¹⁵N-ΔR₂ on the pseudo–first-order association rate constant, , given by , where k_on is the second order association rate constant and K_A is the equilibrium association constant. In contrast to our previous work on the interaction of monomeric Aβ40 on the surface of Aβ40 protofibrils, where ΔR₂ was found to be independent of the nucleus and magnetic field (20), the observed ΔR₂ profiles in the current study are dependent on the field (Fig. 1A and Fig. S2B) and nucleus (compare Fig. S2 E and F, which show that the ΔR₂ values for backbone amide protons are just over 50% larger than for ¹⁵N). This immediately suggests that the dissociation rate constant, k_off, is of the same order of magnitude or larger than the R₂ values in the bound state (predicted to be ∼1,000 s⁻¹ for ¹⁵N at 5 °C and 900 MHz for a rigid N-H bond vector in a globular molecule the size of GroEL) and that must be greater than ; otherwise, there would be no mechanism to create the observed residue-specific R₂ relaxation enhancement. Addition of acid-denatured ribulose-1,5-bisphosphate carboxylase (Rubisco) (25), a protein known to bind with high affinity specifically to the hydrophobic patches on the interior surface of the GroEL cavity, to a sample containing Aβ40 and GroEL reduces ¹⁵N-ΔR₂ to values very close to zero (Fig. 1A), indicating that Rubisco and Aβ40 compete for the same binding site(s) on GroEL and that the lifetime line-broadening effect arises from a specific interaction of Aβ40 with GroEL.

Fig. 1.

¹⁵N-ΔR₂, ¹⁵N-DEST, and ¹⁵N relaxation dispersion profiles of Aβ40 in the presence of GroEL. (A) ¹⁵N-ΔR₂ (CPMG field = 550 Hz) for 50 μM ¹⁵N-labeled Aβ40 in the presence of 20 (circles) and 40 (diamonds) μM (in subunits) GroEL at spectrometer frequencies of 600 (blue) and 900 (red) MHz. ¹⁵N-ΔR₂ at 600 MHz for a control sample (green squares) containing 50 μM ¹⁵N-labeled Aβ40, 2.9 μM acid-denatured Rubisco, and 20 μM GroEL [in subunits, corresponding to 2.9 μM in Rubisco binding sites (i.e., one binding site per GroEL cavity)] demonstrates that acid-denatured Rubisco displaces GroEL-bound Aβ40. (B) Comparison of observed (obs) ¹⁵N-ΔR₂ values with the calculated (calc) values obtained from global fitting of all experimental data to a two-state exchange model. (C) Examples of ¹⁵N-DEST profiles (plotted as normalized cross-peak intensities as a function of frequency offset from the ¹⁵N carrier at 118.5 ppm) obtained with rf (RF) field strengths of 250 (open circles) and 500 (closed circles) Hz for the ¹⁵N continuous wave saturation pulse recorded at a spectrometer frequency of 900 MHz on a sample containing 50 μM ¹⁵N-labeled Aβ40 in the presence of 20 μM (in subunits) GroEL. (D) ¹⁵N-CPMG relaxation dispersion curves at spectrometer frequencies of 600 (blue) and 900 (red) MHz observed for 50 μM ¹⁵N-labeled Aβ40 in the presence of 20 μM (in subunits) GroEL. Reference dispersion curves at 600 MHz for ¹⁵N-labeled Aβ40 in the absence of GroEL are shown in green. The red and blue dashed and solid lines in A and D are the best-fit curves obtained by simultaneously fitting all the experimental data to a two-state exchange model. The green lines in A and D serve to guide the eye. The sequence of Aβ40 is shown at the top of the figure with hydrophobic residues highlighted in green and the GroEL substrate consensus sequences (where P stands for polar residues and H stands for hydrophobic residues) (28) aligned above the Aβ40 sequence for reference. All experiments were conducted at 5 °C. Error bars = 1 SD.

Fig. 2.

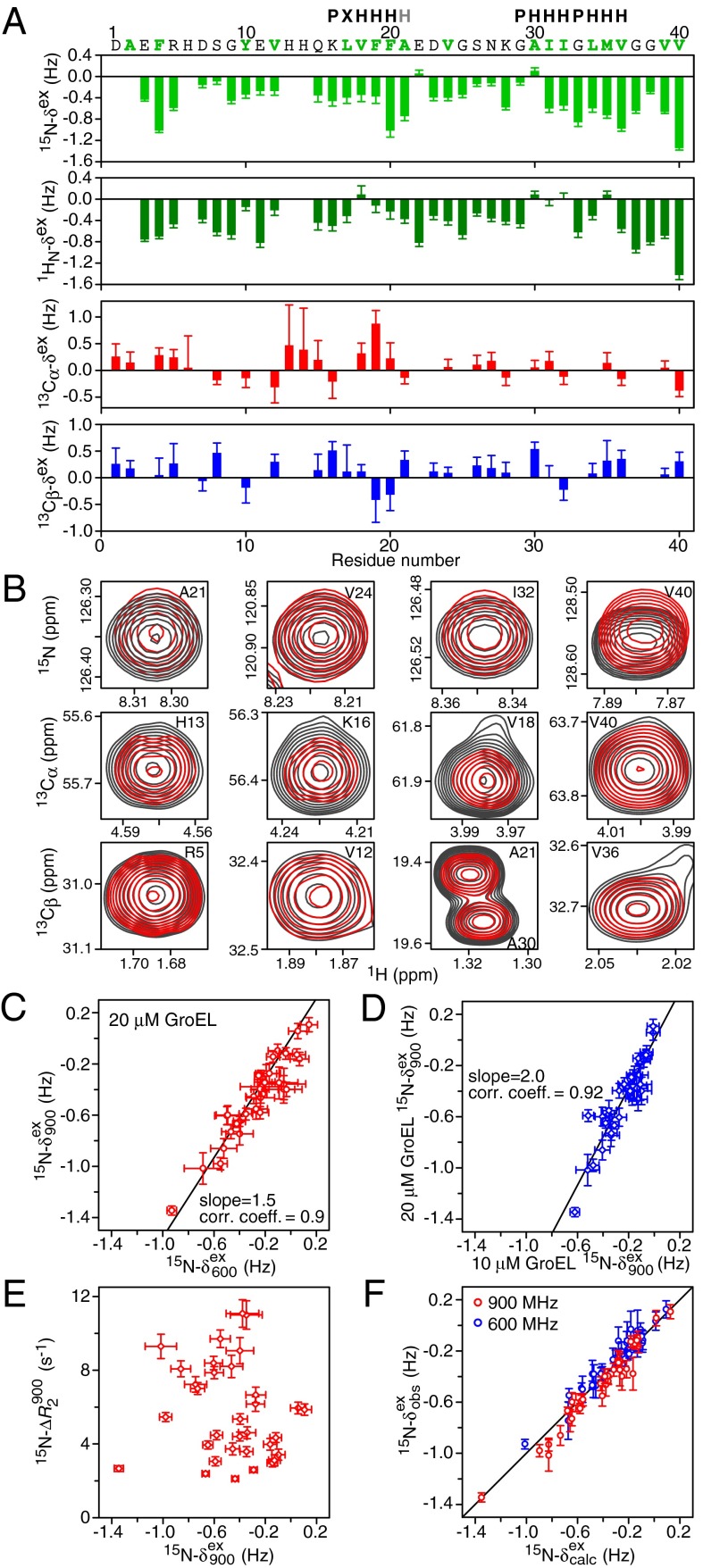
Observed exchange-induced chemical shifts for Aβ40 in the presence of GroEL. (A) ¹⁵N, ¹H_N, ¹³Cα, and ¹³Cβ chemical shift differences (in hertz) between 50 μM ¹⁵N-labeled Aβ40 samples containing 20 and 0 μM GroEL at a spectrometer frequency of 900 MHz. (B) Expansions of selected regions of the ¹H-¹⁵N HSQC spectra and ¹H-¹³C constant time HSQC spectra of 50 μM ¹⁵N-labeled Aβ40 in the absence (black contours) and presence (red contours) of 20 μM GroEL. Correlation of ¹⁵N exchange-induced chemical shifts of ¹⁵N-labeled Aβ40 at two spectrometer frequencies (C) and two GroEL concentrations (D) is shown. corr. coeff., correlation coefficient. (E) ¹⁵N-ΔR₂ values are not correlated to the ¹⁵N exchange-induced chemical shifts. (F) Comparison of observed ¹⁵N exchange-induced shifts with the calculated values obtained by simultaneously fitting all the experimental data to a two-state exchange model. Error bars = 1 SD.

¹⁵N-DEST.

Fig. 1C displays examples of ¹⁵N-DEST profiles created by applying a weak ¹⁵N saturation pulse at intervals from −21 to +21 kHz off-resonance of the spectrum of free Aβ40, thereby imprinting with single residue resolution dynamic information on the Aβ40 GroEL-bound species onto the easily observed ¹H-¹⁵N correlation spectrum of free Aβ40 (21). When Aβ40 is bound to GroEL, reorientational motions within the peptide backbone of Aβ40 are dramatically slowed, resulting in ¹⁵N-R₂ values that are several orders of magnitude larger than in the free state. Although these large ¹⁵N-R₂ values preclude direct observation of the bound state, they allow for efficient partial saturation by a weak rf field even at large offsets, where the magnetization in the free state is completely unaffected, that is subsequently transferred back to the free state via chemical exchange and observed as a decrease in cross-peak intensity (21, 22). The profiles are dependent on k_off, and variations in width reflect residue-specific variations in ¹⁵N-R₂ values in the bound state.

¹⁵N-CPMG Relaxation Dispersion and Exchange-Induced Chemical Shifts.

Fig. 1D provides some examples of ¹⁵N-CPMG relaxation dispersion curves. Although no relaxation dispersion is observed in the absence of GroEL, small but clear-cut relaxation dispersion effects for some residues are apparent in the presence of GroEL. Relaxation dispersion is dependent on chemical shift differences between the free and bound states (24), and, interestingly, the largest dispersion is observed for the C-terminal residue Val40. Very small (≤1 Hz) but measurable exchange-induced chemical shifts are also observed for ¹⁵N, ¹H_N, ¹³Cα, and ¹³Cβ resonances (Fig. 2 A and B). The exchange-induced shifts are field-dependent (Fig. 2C) and directly proportional to the concentration of GroEL (Fig. 2D).

Global Analysis of Relaxation-Based NMR Experiments.

The data for all four relaxation-based NMR experiments at two fields (600 and 900 MHz) and several concentrations of GroEL were analyzed simultaneously using a simple two-state exchange model (Fig. 3A). All the experimental observables can be described by solutions to the McConnell equations (26) (SI Materials and Methods). The ¹⁵N DEST profiles and ¹⁵N-ΔR₂ values were calculated numerically (Eqs. S2 and S3), whereas analytical solutions were used for the ¹⁵N relaxation dispersion data (Eqs. S4 and S5) and exchange-induced chemical shifts (¹⁵N-δ^ex) (Eq. S6). Global nonlinear least-squares fitting (Eq. S7) was carried out by optimizing the values of two global parameters (whose values are determined by the data for all residues), namely, the pseudo–first-order association rate constant and the fraction p_A of free Aβ40 [where the dissociation rate constant k_off is given by , and the fraction p_B of GroEL-bound Aβ40 is given by (1− p_A)]; and two sets of residue-specific parameters, namely, values in the bound state and the differences in ¹⁵N chemical shift values, ¹⁵N-Δδ(i), between the bound and free states, whose values are determined by the data for each individual residue. Comparisons of observed and calculated values for the ¹⁵N-ΔR₂, ¹⁵N-DEST, and ¹⁵N relaxation dispersion curves are shown in Fig. 1 A, C, and D, respectively, and correlation plots between observed and calculated values for ¹⁵N-ΔR₂ and ¹⁵N-δ^ex are shown in Fig. 1B (also Fig. S2A) and Fig. 2F, respectively.

Fig. 3.

Kinetic scheme for Aβ40 binding to GroEL. (A) Two-state exchange model describing the association of Aβ40 with GroEL. The values listed for and the populations of free (p_A) and GroEL-bound (p_B) Aβ40 are those obtained in the presence of 20 μM GroEL. The equilibrium dissociation constant K_d and the second-order association rate constant k_on are calculated assuming each GroEL cavity only accommodates a single molecule of Aβ40 with numerous available binding modes. (B) Rapid interconversion (with a rate constant >k_off) between different GroEL-bound configurations of Aβ40 consisting of the central hydrophobic, C-terminal hydrophobic, or both hydrophobic regions in contact with GroEL is possible.

It is important to note that the combined use of all experiments is critical to finding the unique solution for the global kinetic parameters as well as the residue-specific and ¹⁵N-Δδ(i) values (SI Materials and Methods). The observables in each experiment have a unique dependence on the global and residue-specific parameters (compare Eqs. S2–S6). Thus, global fitting to a combination of observables using several orthogonal experiments not only results in a deeper minimum on the optimization landscape (critical in the presence of inevitable experimental uncertainty in the data) but, equally importantly, circumvents correlations in the values of the optimized parameters present in any one experiment (27) (further discussion is provided in SI Materials and Methods). Further, because there are only two global parameters, with the remaining parameters being entirely local to each residue position (and therefore uncorrelated from one residue to the next), the range of possible solutions in multidimensional parameter space is readily sampled.

The exchange model and global best-fit kinetic parameters are provided in Fig. 3A. At 20 μM (in subunits) GroEL, the population p_B of bound Aβ40 is 2.3 ± 0.1%, has a value of 34.8 ± 0.8 s⁻¹, and k_off has a value of 1,440 ± 83 s⁻¹. Convergence of the solution was confirmed by varying initial values for all optimized parameters and obtaining the same solution within reported uncertainties. Assuming that one Aβ40 molecule binds per GroEL cavity, the value of the second-order association rate constant (k_on) is computed to be ∼2 × 10⁷ M⁻¹⋅s⁻¹ and the value of the equilibrium dissociation constant (K_d) is ∼70 μM. Alternatively, if we assume that it takes three Aβ40 molecules to saturate each cavity instead of one, and that the three Aβ40 molecules bind to each GroEL cavity completely independently from one another, the values of k_on and K_d are computed to be 4.7 × 10⁶ M⁻¹⋅s⁻¹ and 307 μM, respectively.

Residue-Specific ¹⁵N-R₂ Values of Aβ40 in the GroEL-Bound State.

The optimized values of for Aβ40 bound to GroEL are shown in Fig. 4A. There are two regions that show particularly large values (350–650 s⁻¹ at 900 MHz), namely, the central (residues 16–21) and C-terminal (residues 30–36) hydrophobic regions, which correspond to the GroEL-binding consensus sequences (28). With eight residues spanning the two hydrophobic regions, one would anticipate that the latter two segments of the polypeptide chain bind to adjacent subunits on GroEL. Thus, even if a single GroEL cavity can only accommodate one Aβ40 molecule, there are numerous potential binding modes: If we consider the central hydrophobic patch of Aβ40 first, each GroEL cavity has seven potential binding sites available, each with two adjacent sites available to bind the C-terminal hydrophobic patch (Fig. 3B). (Thus, the overall affinity can reach the micromolar range even if the individual contacts are much lower in affinity). The observation that the maximum value at 900 MHz is about 60–70% of the expected value for a rigid N-H group suggests that the two hydrophobic regions retain significant internal mobility on the nanosecond time scale when bound to GroEL and/or that the two hydrophobic regions bind to GroEL independently of one another. In the latter case, there would be two hemiassociated states in which only one hydrophobic region is in direct contact with GroEL at a given time, in addition to the fully bound state in which both hydrophobic regions are bound simultaneously. A third partially hydrophobic segment (Tyr-Glu-Val) from residues 10–12 displays intermediate values (∼300 s⁻¹ at 900 MHz), suggesting that this region may also transiently interact with GroEL, although to a lesser degree than the two main hydrophobic regions. The relatively low for the N and C termini (100–200 s⁻¹) suggests that these regions are significantly more mobile, and hence not in direct contact with GroEL but rather tethered to the surface of GroEL via the direct interactions between GroEL and the hydrophobic regions.

Fig. 4.

Calculated residue-specific parameters for Aβ40 in the dark GroEL-bound state. (A) Optimized values of the residue-specific backbone ¹⁵N-R₂ rates, , for GroEL-bound Aβ40 at spectrometer frequencies of 600 (blue) and 900 (red) MHz. (B) Residue-specific ¹⁵N, ¹H_N, ¹³Cα, and ¹³Cβ chemical shift differences between GroEL-bound and free Aβ40. The ¹⁵N chemical shift differences (¹⁵N-Δδ) are optimized in the fitting procedure, whereas the other chemical shift differences are calculated from the ΔR₂ values and fitted global kinetic parameters (SI Materials and Methods). (C) Secondary structure populations (top, coil; middle, β and polyproline II; bottom, α) for free (blue line) and GroEL-bound (red circles) Aβ40 (Left, y axis) obtained using the δ2D method (29) and the difference in secondary structure populations between bound and free Aβ40 (gray bars; Right, y axis). Error bars = 1 SD.

In contrast to the interaction of monomeric Aβ40 on the surface of Aβ40 protofibrils, where the bound state for each residue had to be kinetically partitioned between direct contact and tethered states (21), the current data are fully described by a simple two-state exchange model in which Aβ40 is either free or bound to GroEL. This implies that the interconversion rates between hemiassociated and fully associated states, as well as those between direct contact and tethered states for any given residue, are significantly faster than k_off (∼1,400 s⁻¹).

Chemical Shifts and Structural Characteristics of Aβ40 in the GroEL-Bound State.

The calculated differences in ¹⁵N shifts (¹⁵N-Δδ) between bound and free Aβ40 are shown in the upper first panel of Fig. 4B. With only two exceptions (residues 21 and 30), all ¹⁵N resonances are upfield-shifted in the bound state. The largest differences in ¹⁵N shifts (−0.5 to −0.8 ppm) are observed for Phe20 and Ala21 in the central hydrophobic region; residues 31–36 (IIGLMV) within the C-terminal hydrophobic region; and, interestingly enough, three residues (Gly37, Val39, and Val40) at the C terminus. Indeed, the ¹⁵N resonance of Val40 exhibits the largest chemical shift difference (∼−0.8 ppm) between the bound and free states, as well as the largest relaxation dispersion (Fig. 1D, Right). Because the value for Val40 is low (∼100 s⁻¹; Fig. 4A), this shift presumably arises through a secondary effect (e.g., through proximity to the bound C-terminal hydrophobic region).

Given the global exchange rate constants and the R₂ values in the GroEL-bound state, the ¹H_N, ¹³Cα, and ¹³Cβ chemical shift differences (Δδ) between the bound and free states can be computed from the observed exchange-induced shifts (δ^ex) using Eq. S6. The results are displayed in the lower three panels of Fig. 4B. These backbone shifts allow one to ascertain quantitatively the structural characteristics of Aβ40 bound to GroEL. Although access to the chemical shifts of “invisible” bound states has been previously accessible from relaxation dispersion experiments alone (18, 24), it is important to note that incorporating quantitative interpretation of exchange-induced chemical shifts into the analysis provides the chemical shift difference (including the sign) at every observed position.

Free Aβ40 is largely random coil with only small β/polyproline II and α-helical propensities, as evidenced by the small deviations from the most recently published backbone chemical shift library for random coils (29) (Fig. S3) and the low values of the secondary structure propensities calculated from the backbone chemical shifts using the program δ2D (30) (Fig. 4C). The backbone ¹³C chemical shifts induced on binding to GroEL are very small, with only the ¹³Cα of Phe19 exhibiting a shift of greater than 0.4 ppm. The δ2D shift-based calculations indicate that the GroEL-bound state of Aβ40 is dynamically disordered, differing minimally from the intrinsically disordered free state. The GroEL-bound state exhibits a very small increase in helical propensity from residues 18–20 relative to the free state, consistent with the downfield ¹³Cα and upfield ¹³Cβ shifts for residues 19–20, perhaps indicative of a transient kink in the direction of the polypeptide chain. In addition, there appears to be a small overall increase in the coil population and a corresponding decrease in the β/polyproline II population on GroEL binding that is most marked in the C-terminal hydrophobic region, followed by residues 24–27 in the linker region and residues 17–21 in the central hydrophobic region.

Concluding Remarks.

In summary, we have made combined use of four complementary relaxation-based NMR experiments, including a generally applicable method for extracting invisible state chemical shifts from quantitative interpretation of very small observed exchange-induced shifts, that, together, provide direct information at atomic resolution on the sparsely populated (∼2%), NMR-invisible dark state of Aβ40 bound to GroEL. The data reveal that the primary sites of interaction with GroEL are located in two hydrophobic segments that coincide with the predicted GroEL consensus sequences (28) and indicate that Aβ40 remains intrinsically and dynamically disordered on binding to GroEL. We note that these two hydrophobic segments comprise the β-strand core of amyloid fibrils (31) and protofibrils (32), and are thus capable of forming a stable secondary structure (33). However, for the reasons discussed below, it is advantageous for GroEL function that substrates do not become ordered on binding.

The spacing between the two main hydrophobic regions suggests that these two segments bind to adjacent subunits of GroEL, and the values are suggestive of the existence of hemiassociated states in which only one of the two hydrophobic regions is in contact at a given time, as well as a state in which both segments are bound. Given the transient nature of the interaction, it is likely that Aβ40 exchanges between multiple pairs of sites within the cavity and that this exchange process occurs on a time scale that is faster (<700 μs) than the lifetime of the bound state.

The findings reported here provide a more complete description of GroEL–substrate interactions than was available from previous studies. Directly observed ¹H-¹⁵N correlation methods were suggestive (but not conclusive) of protein substrates being disordered and dynamic while bound to GroEL, because all observable cross-peaks had chemical shifts characteristic of random coil and significant portions of the bound proteins were NMR-invisible because the cross-peaks for every residue type were underrepresented (16, 17). This conclusion, which was essentially one of exclusion because the portion of the protein substrates directly bound to GroEL could not be observed, is confirmed by the current work, which directly probes the NMR-invisible dark state of the bound substrate at every residue position. Further, conformational exchange of Aβ40 while bound to GroEL is also consistent with recent EM studies in which the substrate malate dehydrogenase was observed to adopt several binding topologies within the GroEL cavity (34).

The absence of structural ordering of Aβ40 on interaction with GroEL has important implications for the mechanism of substrate capture and release, because binding to GroEL likely entails minimal loss of entropy and extensive conformational plasticity that facilitates binding to essentially any solvent-exposed, 5- to 10-residue nonpolar sequence. Although binding to any individual hydrophobic segment may be very weak, the fact that multiple segments of a disordered polypeptide chain can bind to adjacent subunits of GroEL will result in a large increase in binding avidity, although still allowing for rapid dissociation. Further, the independent binding of multiple segments of Aβ40 may be indicative of a GroEL substrate selectivity mechanism for individual segments within a partially folded or misfolded ensemble. In the context of a kinetically trapped, partially folded or misfolded protein, it seems likely that initial binding of exposed hydrophobic segments will promote destabilization of the substrate, allowing the buried segments to become accessible for GroEL binding, and thereby rapidly propagating the unfolding process. Moreover, binding to adjacent subunits within the cavity is likely to promote stretch-induced unfolding (35), followed by dissociation into the cavity, as the distance between binding sites on the apical domains of adjacent subunits is increased from ∼25 to ∼33 Å on transition from the closed state to ATP-bound open state (2). In the case of Aβ40, for example, the two GroEL-binding regions are separated by 14 residues center-to-center (Fig. 4A), which corresponds to an average end-to-end distance of 32–38 Å for a random coil calculated using well-established standard polymer theory (36) (SI Materials and Methods). Hence, the probability of the two hydrophobic regions of Aβ40 being bound to adjacent GroEL subunits simultaneously, and therefore the avidity of Aβ40 for GroEL, would be predicted to be higher in the closed state than in the open state.

In conclusion, the results presented here expand current paradigms of GroEL–substrate interactions by providing previously unobservable, residue-specific details of exchange kinetics, structure, and dynamics of polypeptides in the GroEL-bound dark state.

Materials and Methods

Uniformly ¹⁵N-labeled Aβ40 was prepared from NaOH-treated stocks as described (20). Escherichia coli GroEL (37) and acid-denatured Rubisco (25) at natural isotopic abundance were purified as described previously and were a gift from George Lorimer and Don Yang (University of Maryland, College Park, MD). Aβ40 (50 μM) was combined with GroEL at 40, 20, 10, and 0 (reference sample) μM (in monomer units). An additional control sample was also prepared comprising Aβ40 (50 μM), GroEL (20 μM in monomer subunits), and Rubisco (2.9 μM). Sample conditions were 50 mM Hepes (pH 6.6) and 92% H₂O/8% D₂O. All samples were prepared and maintained at 5 °C at all times. Under these conditions, Aβ40 remains essentially entirely monomeric (>95%) for several weeks (21) (Fig. S4). NMR experiments were conducted at 5 °C on Bruker 900-MHz and 600-MHz spectrometers, each equipped with a triple-resonance, z-gradient cryoprobe.

The ¹⁵N-R₂ (with a relaxation-compensated CPMG scheme at a CPMG field of 550 Hz to eliminate virtually all chemical exchange line-broadening) (20), ¹⁵N-longitudinal magnetization relaxation rate R₁ (Fig. S5) (21), ¹⁵N-R_1ρ (Fig. S6) (38), ¹⁵N-DEST (Fig. S7) (21), and ¹⁵N-CPMG (single quantum) relaxation dispersion (39) experiments were carried out as described previously. ¹⁵N and ¹H_N, as well as ¹³Cα and ¹³Cβ, exchange-induced shifts were measured from high-resolution ¹H-¹⁵N heteronuclear single quantum coherence (HSQC) experiments and constant-time ¹H-¹³C HSQC experiments, respectively (further details are provided in SI Materials and Methods).

All the DEST, ΔR₂, CPMG relaxation dispersion, and exchange-induced chemical shift data for ¹⁵N were simultaneously fit to a two-state (free/bound) model (see Fig. 3) using a combination of numerical and analytical solutions to the McConnell equations (26) to determine the global kinetic parameters and the GroEL-bound ¹⁵N-R₂ values and ¹⁵N chemical shifts at each residue as described in SI Materials and Methods (Eqs. S2–S7). The GroEL-bound ¹H_N and ¹³Cα/β shifts were determined from the corresponding exchange-induced shifts in conjunction with the R₂ rates and global kinetic parameters as described in SI Materials and Methods.