Transformation of the neural code for tactile detection from thalamus to cortex

Significance

Place a hand on the hood of a car and ask, is it running or not? Answering this involves the sequential activation of many neurons, from mechanoreceptors under the skin to cortical neurons whose activity is closely related to the evoked internal sensation. We investigate how vibratory stimuli are represented in two steps along this processing chain during a detection task. We find that activity changes from a “literal” code, in which neural responses faithfully track the stimulus, to a more abstract and robust one, from which other neurons can more easily infer whether a stimulus was presented or not.

Abstract

To understand how sensory-driven neural activity gives rise to perception, it is essential to characterize how various relay stations in the brain encode stimulus presence. Neurons in the ventral posterior lateral (VPL) nucleus of the somatosensory thalamus and in primary somatosensory cortex (S1) respond to vibrotactile stimulation with relatively slow modulations (∼100 ms) of their firing rate. In addition, faster modulations (∼10 ms) time-locked to the stimulus waveform are observed in both areas, but their contribution to stimulus detection is unknown. Furthermore, it is unclear whether VPL and S1 neurons encode stimulus presence with similar accuracy and via the same response features. To address these questions, we recorded single neurons while trained monkeys judged the presence or absence of a vibrotactile stimulus of variable amplitude, and their activity was analyzed with a unique decoding method that is sensitive to the time scale of the firing rate fluctuations. We found that the maximum detection accuracy of single neurons is similar in VPL and S1. However, VPL relies more heavily on fast rate modulations than S1, and as a consequence, the neural code in S1 is more tolerant: its performance degrades less when the readout method or the time scale of integration is suboptimal. Therefore, S1 neurons implement a more robust code, one less sensitive to the temporal integration window used to infer stimulus presence downstream. The differences between VPL and S1 responses signaling the appearance of a stimulus suggest a transformation of the neural code from thalamus to cortex.

Detecting a stimulus involves the activation of multiple areas extending from the sensory receptors to subcortical and cortical structures (1–4), and as the signal is relayed from one layer to the next, its representation in spatiotemporal patterns of activity may change (1). Previous studies have shown that, when a tactile vibratory stimulus is presented, neurons in the ventral posterior lateral (VPL) nucleus in the somatosensory thalamus and primary somatosensory cortex (S1, areas 3b and 1) respond by modulating their firing rates computed over a time scale of hundreds of milliseconds (5–9). Because these slow firing rate modulations occurring within relatively long time windows depend on amplitude and vibration frequency, they encode these key stimulus features. In addition, to varying degrees, evoked spikes in both areas also tend to be synchronized to the waveform of the applied mechanical stimulus, which, for frequencies <40 Hz, varies on a time scale of tens of milliseconds. This entrainment, which corresponds to fast firing rate modulations, also depends on stimulus amplitude (9), and so it too carries information about stimulus presence. However, it is unknown whether both the slow (∼100 ms) and fast (∼10 ms) modulations in firing rate contribute to perceptual performance during stimulus detection. Moreover, it is not clear whether the two time scales are equally important in VPL and S1, nor whether the capacity to signal stimulus presence changes from one area to the next.

To investigate these issues, we recorded activity from single neurons in the VPL nucleus and S1 cortex in monkeys trained to report the presence of a 20-Hz vibrotactile stimulus of variable amplitude. The responses were then analyzed from the point of view of an ideal observer that, based on an evoked spike train, determines whether a stimulus was presented or not in a trial; crucially, however, the observer's performance is optimized according to a specific time scale of integration. We found that, in general, fast rate modulations are more prominent in VPL than in S1 neurons, and vice versa, slow modulations are stronger in S1 than in VPL, but despite these differences, on average, the detection accuracy of single neurons was statistically the same in both areas. Importantly, however, the neural code in S1 was more resilient than in VPL, in the sense that S1 neurons were less sensitive to the readout method and time scale of integration used to infer stimulus presence. Therefore, information is transformed—but not lost—between thalamus and S1, such that fast rate modulations closely tied to the physical stimulus are progressively discarded in favor of a slower, more tolerant rate code.

Results

Two monkeys (Macaca mulatta) were trained to perform a vibrotactile detection task (6). In each trial, the animal had to report whether the tip of a mechanical stimulator vibrated or not by pressing one of two push buttons with the left, free hand. The vibrotactile stimulus, a sinusoidal wave of 20-Hz frequency and 0.5-s duration, was delivered to the glabrous skin of one fingertip of the restrained, right hand. Half of the trials contained a stimulus (stimulus-present trials) and the other half did not (stimulus-absent trials). The two trial types were randomly interleaved (Fig. 1A). Stimulus amplitudes in stimulus-present trials varied between subthreshold and suprathreshold. Thus, the task produced four behavioral outcomes: hits or misses in stimulus-present trials and correct rejections or false alarms in stimulus-absent trials (Fig. 1B). While the monkey performed the detection task, activity was recorded simultaneously from single neurons in the VPL nucleus and S1 (areas 1 and 3b; Fig. 1C) that shared the same cutaneous receptive field. In the following sections, we analyze how the responses of these neurons encode the presence of a stimulus and how the neural codes vary between the two areas.

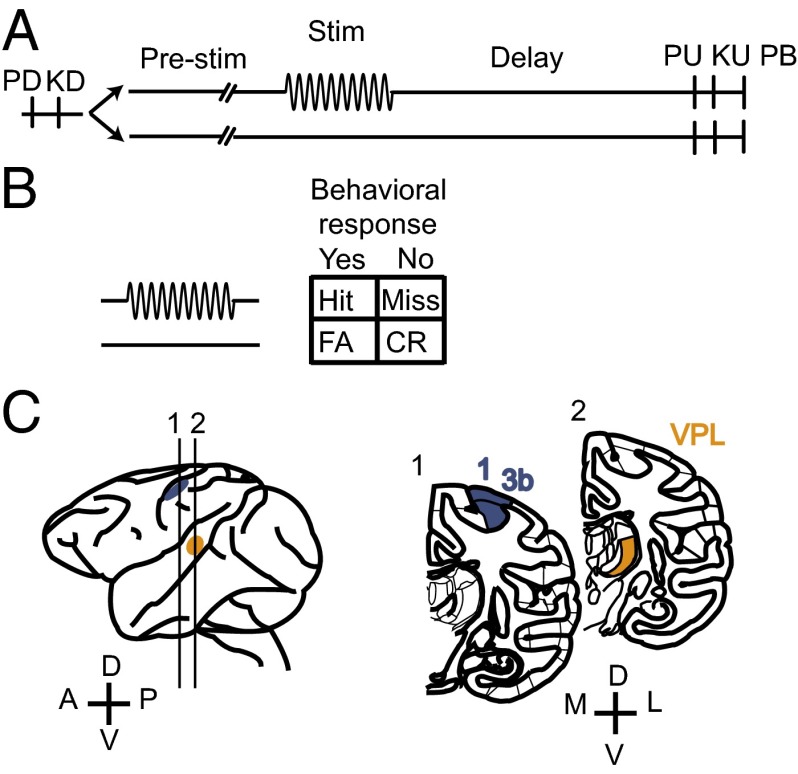
Fig. 1.

Behavioral task and recording sites. (A) Detection task. Trials began when the stimulator probe tip indented the skin of one fingertip of the monkey’s restrained right hand [probe down (PD)]; the monkey reacted by placing its left, free hand on an immovable key [key down (KD)]. After a variable prestimulus period (1.5–3 s), a vibratory stimulus of variable amplitude (1–34 μm, 20 Hz, 0.5-s duration) was presented on one-half of the trials; no stimulus was presented on the other half of the trials. Following the stimulus presentation period or a period where no stimulus was delivered, the monkey waited for 3 s until the probe was retracted [probe up (PU)]; the animal removed its free hand from the key [key up (KU)] and pressed one of two push buttons (PBs) to report whether the stimulus was present or absent. Lateral and medial buttons were used for reporting stimulus presence and stimulus absence, respectively. Stimulus-present and stimulus-absent trials were randomly interleaved in a run. (B) Behavioral responses in the detection task. CR, correct rejections; FA, false alarms. (C) Recording sites in the VPL nucleus (orange) and areas 1 and 3b of S1 (blue).

Basic Response Properties of VPL and S1 Neurons.

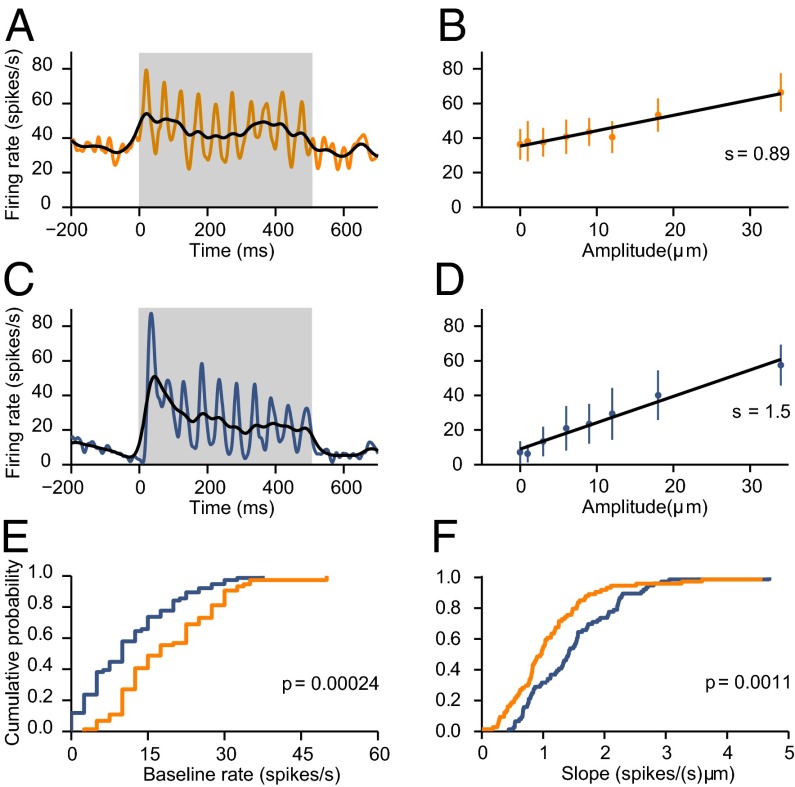
We recorded 74 VPL and 76 S1 responsive neurons with quickly (QA) or slowly adapting (SA) properties (10). In all figures, results shown in orange and blue correspond to data from VPL and S1, respectively. We confirmed that VPL neurons had higher spontaneous firing rates than S1 neurons (VPL: 17.5 ± 1.2 spikes/s, median ± SE; S1: 10 ± 1.04 spikes/s; P = 0.00024; Fig. 2E) and that in the two areas, two quantities increase as functions of stimulus amplitude: the mean firing rate computed during the full stimulation period and the synchronization of the spikes to the stimulus waveform (6–9) (Fig. 2 A–D). These dependencies were quantified via linear regression analyses (Materials and Methods). In both areas, the slopes of the linear fits, which indicate the sensitivity to stimulus amplitude, were significantly positive for the majority of the neurons (F-test, P < 0.05; Fig. 2 B and D). For modulations in the mean rate, S1 neurons had significantly higher slopes than VPL neurons (VPL: 0.96 ± 0.08 Hz/µm, mean ± SE; S1: 1.41 ± 0.08 Hz/µm; P = 0.0011; Fig. 2F), whereas for synchronization, there was a trend toward higher slopes in VPL, but it was not significant (VPL: 1.17 × 10⁻⁴ ± 0.09 × 10⁻⁴ AU/µm; S1: 0.92 × 10⁻⁴ ± 0.10 × 10⁻⁴ AU/µm; P = 0.12).

Fig. 2.

Response properties of VPL and S1 neurons. In all panels, results for VPL and S1 are shown in orange and blue, respectively. (A) Spike density function of a VPL neuron that responded to the sinusoidal stimulus (gray bar). The width of the Gaussian filter used to smooth the cell's spike trains was 5 (orange) or 20 ms (black). (B) Firing rate (mean ± SD) as a function of stimulus amplitude for the VPL neuron in A. Points correspond to the average firing rate evoked during the stimulation period. Black lines are linear fits. Slope (s) values are indicated. (C) Spike density function for an S1 neuron that responded to the sinusoidal stimulus (gray bar). The width of the Gaussian filter used to smooth the cell's spike trains was 5 (blue) or 20 ms (black). (D) Firing rate (mean ± SD) as a function of stimulus amplitude for the S1 neuron in C. Points correspond to the average firing rate evoked during the stimulation period. Black lines are linear fits. Slope (s) values are indicated. (E) Cumulative distributions of baseline firing rates for VPL and S1 populations. The median baseline rate was significantly higher in VPL than in S1 (VPL: 17.5 ± 1.2 spikes/s, n = 74; S1: 10 ± 1.04 spikes/s, n = 76; P = 0.00024). (F) Cumulative distributions of slope values for VPL and S1 neurons. Slopes were obtained from plots like those in B and D. The median slope was significantly higher in S1 than in VPL [VPL: 0.96 ± 0.08 spikes/(s μm), n = 74; S1: 1.41 ± 0.08 spikes/(s μm), n = 76; P = 0.0011].

What Response Features Are Relevant for Stimulus Detection?

Previous studies have shown that VPL (9) and S1 (6) neuronal responses may account for behavioral performance in the detection task. Both fast and slow modulations in the firing rate are seen, the former evidenced by high periodicity at the stimulus frequency (20 Hz) and the latter by changes in the mean rate computed over the full stimulation period. However, their relative contributions to psychophysical performance are unknown. Does the detection of a vibrotactile stimulus rely exclusively on response modulations that vary relatively slowly (∼100 ms) or do fast modulations (∼10 ms) contribute to it also? Importantly, the relevant timescale might be different for S1 and VPL; the two areas could exploit different temporal features to encode the presence of a vibrotactile stimulus in different ways, in effect transforming the neural code. A related question is whether the two areas encode stimulus presence with the same accuracy.

To distinguish between these possibilities as information flows from VPL to S1, we developed the Poisson spike train classifier (PSTC) to quantify how accurately the presence of a stimulus can be inferred at a given timescale of integration. The PSTC is a decoding method with a free parameter, w, that determines the timescale under consideration. The PSTC takes as input the neural responses recorded during task performance; some trials are used for training and the rest for testing the classifier. Once trained, the PSTC classifies each test spike train as corresponding to a stimulus-present or a stimulus-absent trial. Within the PSTC algorithm, firing rate template functions for stimulus-present and stimulus-absent classes are generated internally after convolving all spike trains with a Gaussian filter of width w (Materials and Methods). Narrow filters resolve fine temporal modulations (Fig. 2 A and C, colored traces), whereas broad filters blur them, reflecting instead the spike count over longer timescales (Fig. 2 A and C, black traces). Because all this is done for a given value of w, the fraction of correct classifications for the neuron under study can be plotted as a function of w. This plot, the PSTC performance curve, reveals how informative the neuron is about stimulus presence and what is the timescale at which it is most informative. The PSTC is simply a convenient and efficient way to characterize how stimulus amplitude is represented in spike trains in our experiments; it is not meant as a model for how circuits downstream from S1 may reach a decision about stimulus presence or absence.

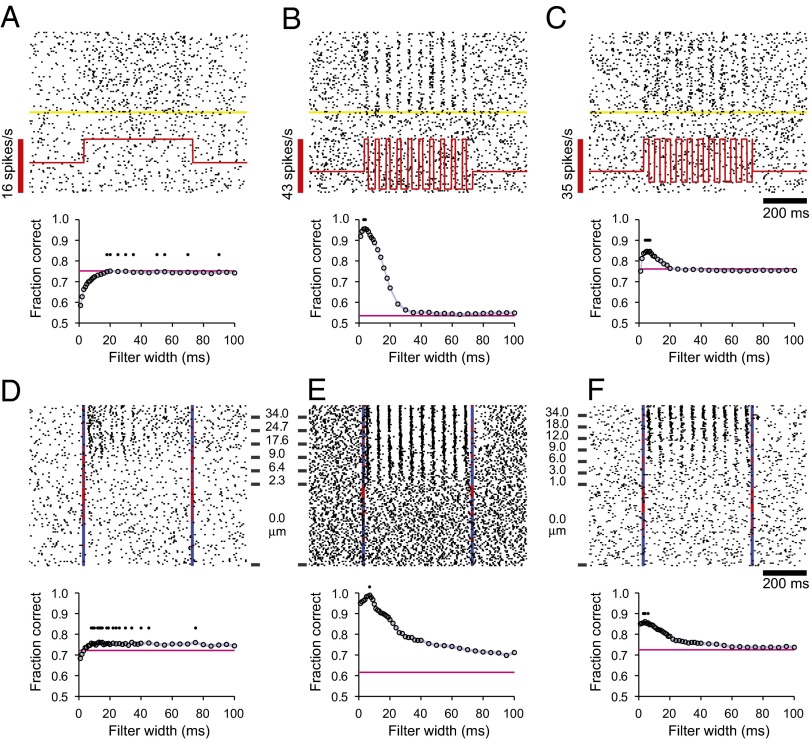
To provide some intuition about the PSTC performance curve and how it characterizes the neural data, we first use it to analyze the responses of three simulated neurons that capture the main properties of the real, recorded neurons. The first simulated neuron responded to the stimulus by increasing its firing rate uniformly through the stimulation period, and its spikes had no temporal structure whatsoever (Fig. 3A, Upper). The second simulated neuron responded to the stimulus by synchronizing its spikes to the 20-Hz stimulus waveform, but its average firing rate over the stimulation period was the same as its baseline rate (Fig. 3B, Upper). Finally, the third simulated neuron combined both effects: it fired more spikes in stimulus-present trials and these were synchronized to the stimulus waveform (Fig. 3C, Upper).

Fig. 3.

Classification performance based on fast and slow firing modulations. (A–C) (Upper) Rasters of three simulated neurons. The first (A) simply increases its overall firing rate during the stimulation period; the second (B) maintains the same overall firing rate but synchronizes its spikes to the individual stimulation pulses; and the third (C) shows a mixture of the two effects. In each raster plot, the yellow line divides stimulus-present and stimulus-absent trials, and the red trace indicates the underlying firing rate of the idealized neuron in stimulus-present trials. Stimulus amplitude was considered constant across all stimulus-present trials. Spikes were produced by feeding the underlying firing rate value to a Poisson process in each 1-ms time step. (Lower) Mean fraction of correct classifications achieved by the PSTC as a function of the Gaussian filter width used to smooth the spikes. Pink horizontal lines in the lower panels in A–C indicate the mean fraction of correct classifications based on the total number of spikes counted during the stimulation window. Small black dots indicate filter widths that achieved maximum classification performance. (D–F) As in A–C, but for three recorded neurons: two from S1 (D and F) and one from the VPL nucleus (E). Vertical lines indicate stimulus onset and offset; blue marks indicate correct responses (hits and correct rejections); and red marks indicate incorrect responses (misses and false alarms). Stimulus amplitudes are indicated beside each raster plot. Lower panels in D–F show results obtained with the PSTC for the three recorded neurons. Same notation as in lower panels in A–C.

The PSTC was trained to classify the responses of these three ideal neurons as either stimulus-present or stimulus-absent, and its performance was indicative of both the slow and fast modulations in firing rate. For the first simulated neuron, the fraction of correct classifications increased steadily as a function of filter width, saturating after w = 20 ms (Fig. 3A, Lower, circles). The saturation value was equal to the fraction correct elicited by a simpler classifier (Materials and Methods) that only keeps track of the spike count accrued during the stimulation interval in each trial (Fig. 3A, Lower, pink horizontal line). Because the firing rate remains constant throughout the stimulation period, the spike count of this simulated neuron provides the maximum amount of information, and therefore, as long as the integration time is not too short (>20 ms), the PSTC determines the presence of a stimulus as accurately as possible. In contrast, for the second simulated neuron, the fraction of correct classifications was close to chance both for the PSTC at long w (>30 ms) and for the spike-count classifier (Fig. 3B, Lower). This drop in performance occurs because the number of spikes fired during stimulus-present and stimulus-absent trials were nearly the same. In this case the optimal filter width was short, w = 7 ms, and with it the PSTC was able to classify correctly more than 95% of the test trials. Therefore, with the appropriate timescale of integration, the PSTC was highly sensitive to the fast fluctuations in firing probability that were time locked to the vibratory stimulus. Finally, for the third simulated neuron, the PSTC performance curve reflected both the fast modulations (evidenced by a peak in performance at w = 5 ms) and the slower, overall increase in firing rate (evidenced by performance well above chance for w > 30 ms) induced by the stimulus (Fig. 3C, Lower). Therefore, the PSTC extracts information about stimulus presence from fast or slow modulations in firing activity. When the modulations are fast, the fraction of correct classifications can be very high, but integrating over a short timescale (w < 15 ms) is crucial because broad filters produce a dramatic drop in performance (Fig. 3B, Lower). By contrast, when the modulations are slow, accurate performance is achieved with a wider range of filters (Fig. 3A, Lower); any filter that is not too narrow (w > 20 ms) will work. When the neural responses include both fast and slow components, the optimal filter is again narrow, but a near-maximal fraction of correct classifications is obtained with any filter width (Fig. 3C, Lower); the timescale of integration becomes less critical in this case.

Given these insights, we used the PSTC analysis to ask (i) how do real, single somatosensory neurons encode stimulus presence; (ii) what is their relevant timescale of integration; (iii) how accurately do they encode stimulus presence; and (iv) how do the results differ between VPL and S1?

Neural Detection in VPL and S1 Through Fast and Slow Modulations in Firing.

The PSTC performance curves of single VPL and S1 neurons were similar to those of the idealized neurons. Some VPL neurons were strongly synchronized to the stimulus waveform and varied their overall mean firing rate weakly during stimulation, so their best performance required a short filter width (Fig. 3E). The reverse situation was more common in S1: there, neurons often modulated the number of spikes emitted during stimulation, and these were loosely aligned with the stimulus waveform (Fig. 3D); hence, the detection performance of the PSTC was optimal with a wide range of filter widths (Fig. 3D, Lower, small dots), and the maximum fraction of correct classifications was similar to that obtained with the spike count classifier. Neurons with mixed properties, with fast and slow modulations, were found in both areas (Fig. 3F). To quantify the prevalence of these cell types, we generated PSTC performance curves for all of the recorded VPL and S1 neurons and analyzed the optimal widths and performance levels across the two populations.

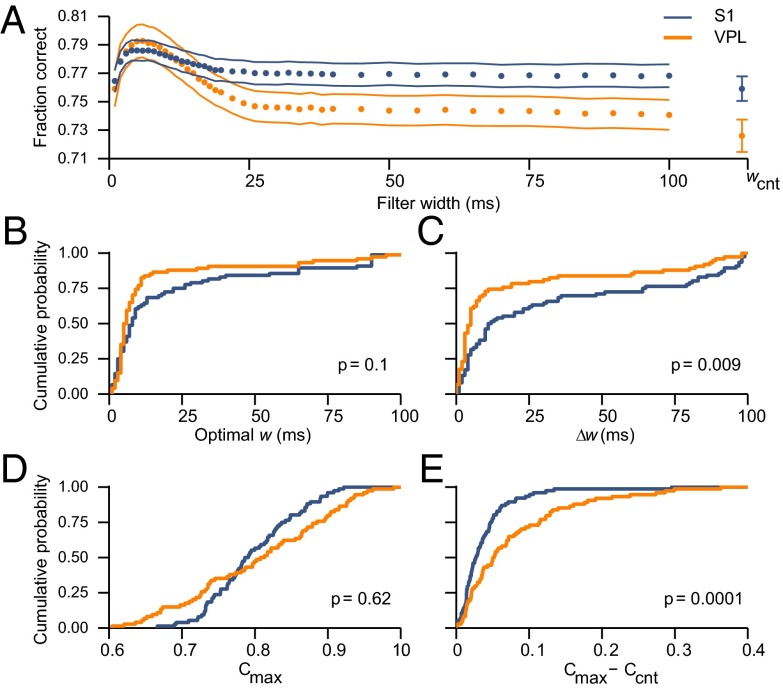
Fig. 4A shows the mean PSTC performance curves obtained by averaging the results over the VPL and S1 populations. Both curves peaked at w ∼ 6 ms, with maximum performance around 79% correct. For long filter widths (w > 25 ms), the fraction of correct classifications was lower than the maximum but still well above chance (which corresponds to a fraction correct of 0.5). In this range, and including the spike count classifier (w_cnt), performance was always higher for S1, so the relative size of the peak was larger for VPL than for S1. Hence, fast modulations were more dominant in VPL and slow modulations more dominant in S1.

Fig. 4.

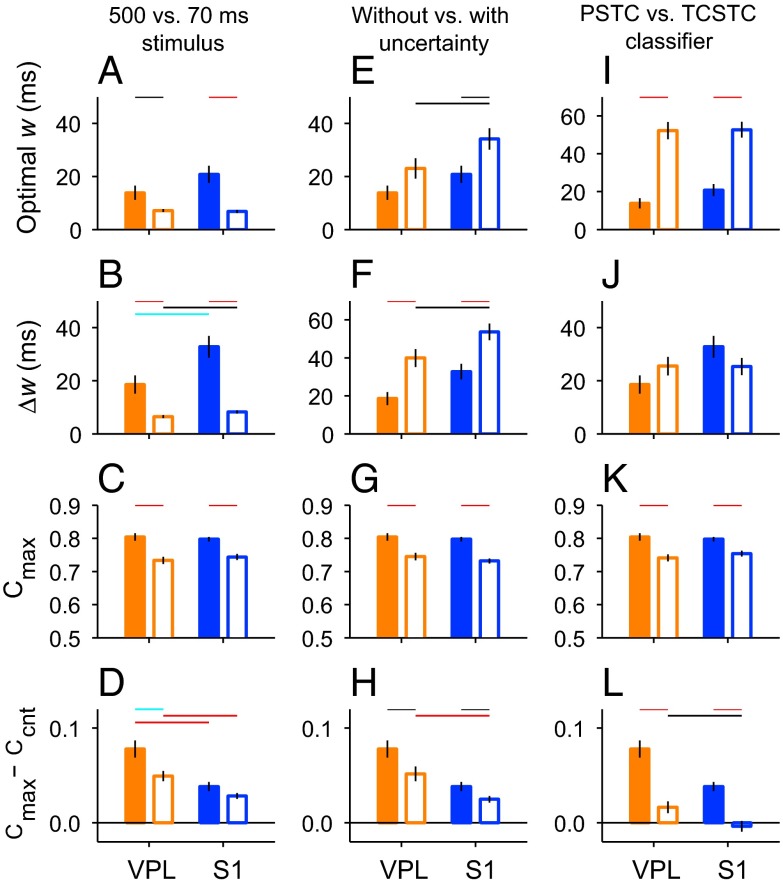
Performance of the PSTC based on VPL and S1 responses. In all panels, results for VPL and S1 are shown in orange and blue, respectively. (A) Fraction of correct classifications (±SE), averaged across neurons, as a function of the filter width used by the PSTC. For comparison, w_cnt indicates performance based only on the spike count during the full stimulation period (C_cnt). (B) Cumulative distributions of optimal w values. Optimal widths tended to be smaller for VPL than for S1 neurons, although the difference was not significant (VPL: 13.86 ± 2.67 ms, n = 74; S1: 20.82 ± 3.22 ms, n = 76; P = 0.1). (C) Cumulative distributions of Δw values. The range of optimal filter widths was significantly smaller in VPL than in S1 (VPL: 18.54 ± 3.44 ms, n = 74; S1: 32.73 ± 4.12 ms, n = 76; P = 0.009). (D) Cumulative distributions of C_max values. The maximum fraction of correct classifications was the same in the two areas (VPL: 0.80 ± 0.01, n = 74; S1: 0.79 ± 0.01, n = 76; P = 0.62). (E) Cumulative distributions of C_max – C_cnt values. The difference in performance was significantly larger in VPL than in S1 (VPL: 0.077 ± 0.009, n = 74; S1: 0.038 ± 0.004, n = 76; P = 0.0001).

For each neuron, the optimal width was the value of w for which the PSTC achieved the highest fraction of correct classifications. On average, optimal widths were short in both areas but tended to be shorter for VPL than for S1 neurons, although the difference was not significant (Fig. 4B; P = 0.1). More tellingly, however, the range of optimal filter widths, ∆w, was significantly narrower in VPL than in S1 (Fig. 4C; P = 0.009). ∆w stands for the difference between the maximum and minimum filter widths that, for each neuron, were statistically equivalent to its optimal. A large Δw indicates that a neuron has a wide range of filter widths over which its detection performance is statistically equal to the highest (Fig. 3D), whereas a small Δw corresponds to a neuron for which performance is a strongly peaked function of filter width (Fig. 3E). In S1, more than 30% of the neurons had a range Δw > 50 ms, whereas in VPL the number was just above 10% (Fig. 4C). Therefore, in both areas, the highest performance was achieved when the neural detection was based on narrow filters, exploiting the fast periodic modulations, but the drop in performance as a function of filter width was more pronounced in VPL than in S1. The responses of S1 neurons contained more slow modulations and were less sensitive to the exact filter width used for determining stimulus presence.

The conclusions were similar when the distributions of performance levels were compared. On average, the maximum fraction correct C_max, i.e., the fraction of correct PSTC classifications obtained with the optimal filter width, was the same in VPL and S1 (Fig. 4D; P = 0.62). However, for S1, the difference between C_max and the performance obtained with the spike count classifier C_cnt (for each cell) was significantly smaller than for VPL (Fig. 4E, P = 0.0001). Therefore, S1 neurons were more tolerant with respect to the timescale of integration.

In summary, when the classification was based on narrow filters (i.e., fast modulations), VPL and S1 neurons attained similar performance levels overall, and detection performance was accurate. However, if only slow modulations were taken into account, or if the timescale of integration was not the optimal one for each neuron, then S1 neurons were better detectors than VPL neurons because their fraction correct deviated significantly less from the maximum.

Earlier we found that, for each neuron, both the mean firing rate during the stimulation period and the synchronization of its spikes to the stimulus waveform change as functions of stimulus amplitude (Fig. 2 B and D) (9). These two quantities correspond to slow and fast modulations in firing probability, respectively, and it is important to note that their differences across the VPL and S1 populations are consistent with the results of the PSTC analysis: when judged by the distributions of slopes obtained from linear regression, the mean rates are more informative in S1 (Fig. 2F), and the synchronization is equally informative in both areas, although there is a tendency for stronger synchronization in VPL. Thus, similar conclusions are reached through very different methods.

The following section describes additional analyses showing that the neural code in S1 remained more robust than that in VPL under a variety of conditions. We tested different stimulus lengths, amounts of uncertainty, and classification methods.

Neural Detection Based on the First Evoked Spikes.

Thus far, the analysis considered the full stimulus, which consisted of 10 sinusoidal pulses within 500 ms. However, it is possible that the monkeys did not use all 10 pulses to detect the stimulus. If, for instance, the first pulse provides a strong enough signal, the subsequent periodic modulations in firing could be ignored and thus be irrelevant for the detection process. To assess this possibility, we repeated the PSTC analysis using only the first 70 ms after stimulus onset. Assuming a neuronal latency of ∼20 ms (9), this constrained the analysis to the spikes evoked by a single 50-ms stimulation pulse. Except for the shortened time window, the classifier was trained and tested exactly as before.

The fraction of correct classifications was generally lower in this case than with the full stimulus, but the main differences between VPL and S1 were still evident (Fig. S1). These results are summarized in Fig. 5 A–D, which depicts the means for the optimal width, ∆w, C_max, and C_max – C_cnt, based on the 70-ms stimulus (open bars), and compares them with the means obtained in the standard condition (full stimulus, filled bars). When a short stimulus was used, there was no obvious peak in the mean PSTC performance curves (Fig. S1A), and the optimal filter widths were the same in both areas (Fig. 5A, open bars; Fig. S1B). Nevertheless, the range of filter widths that produced maximum performance (∆w) was slightly narrower for VPL than for S1 (Fig. 5B, open bars, P = 0.037; Fig. S1C), suggesting that S1 was again more tolerant of deviations from the optimal filter width. Also, on average, S1 neurons had a slightly higher fraction of correct detections than VPL neurons at all filter widths, although the difference was not significant (Fig. 5C, open bars; Fig. S1 A and D). Finally, the difference between C_max and C_cnt was significantly larger in VPL than in S1 (Fig. 5D, open bars, P = 0.0011; Fig. S1E). In essence, then, these results were analogous to those obtained with the full 10-pulse stimulus (compare pairs of filled and open bars in Fig. 5 A–D).

Fig. 5.

Detection performance in VPL and S1 under alternative conditions. In all panels, bars and vertical lines indicate mean ± SEM, respectively, of the quantities indicated on the y axes, i.e., optimal width, range of optimal widths (∆w), maximum fraction of correct classifications (C_max), and the difference between C_max and C_cnt. Horizontal colored lines indicate significance levels for each comparison (black: P < 0.05, cyan: P < 0.01, red: P < 0.001). Orange and blue bars are for VPL and S1 data, respectively. Filled bars correspond to the standard condition, in which spike trains elicited during the full stimulation period (500 ms) were analyzed by the PSTC and the stimulus onset was known to the classifier (no temporal uncertainty). (A–D) Results in the standard condition and when only the spikes in the first 70 ms of stimulation were used by the PSTC (open bars). (E–H) Results in the standard condition and when the stimulus onset time was unknown to the PSTC (temporal uncertainty, open bars). (I–L) Results in the standard condition and when performance was assessed by a suboptimal classifier, the TCSTC (open bars). To avoid clutter, significant differences between VPL and S1 neurons in the standard condition (filled bars) are indicated only in A–D.

Effect of Temporal Uncertainty.

In the analyses described above, in any given trial, the stimulus is either present or absent, but if it is present, its onset time is always the same (t = 0 ms). However, when the monkey performs the task, the prestimulus interval varies across trials (Fig. 1A), making the time of stimulus onset uncertain for the monkey. To investigate the impact of such temporal uncertainty, we modified the neural classification procedure such that the test spike trains included not only the relevant stimulation period but also additional time before it. Thus, the PSTC had to search for the time of stimulus onset (Materials and Methods). When the PSTC analyses were repeated with such temporal uncertainty, the performance levels declined across the board, but the differences between S1 and VPL remained (Fig. 5 E–H, open bars). In particular, optimal filter widths were larger for S1 than for VPL neurons (Fig. 5E, open bars, P = 0.04), and so were the ∆w values (Fig. 5F, open bars, P = 0.037). The performance achieved with the optimal filters remained similar in the two areas (Fig. 5G, open bars), but the difference between C_max and C_cnt was still smaller for S1 than for VPL (Fig. 5H, open bars, P = 0.0007). Thus, temporal uncertainty makes the stimulus detection process more difficult overall, but does not change the relative efficacies of the neural codes for stimulus presence in S1 and VPL (compare pairs of filled and open bars in Fig. 5 E–H).

Neural Performance Based on a Simpler Detection Algorithm.

Up to this point, all analyses have been based on the PSTC, a decoding method that is optimal under relatively mild assumptions (Poisson statistics and stationarity within stimulus-present and stimulus-absent conditions). It is possible, however, that sensory systems implement a less accurate algorithm for detecting stimuli, for instance, to trade off accuracy for speed. The space of such possible algorithms is large, but to obtain a rudimentary understanding of how the results might change if stimulus detection were based on a suboptimal procedure, we designed a simpler classification scheme based on a plausible neural operation: firing rate threshold crossing (6) (Materials and Methods). This simpler classifier, the threshold-crossing spike train classifier (TCSTC), was also evaluated with a range of filter widths. The contrast between the PSTC and TCSTC methods provided further indication that, in general, fast modulations in firing do contain useful information that improves stimulus detection.

Before presenting the results of the TCSTC analysis, we first give a brief description of the method and an intuitive example illustrating how it differs from the PSTC. In the TCSTC, the spikes in each trial are convolved with a Gaussian filter of width w, and the maximum firing rate of the resulting spike density function is calculated. This maximum rate (r_max) is then compared with a threshold θ: if r_max > θ, the trial is classified as stimulus-present, and if r_max < θ, the trial is classified as stimulus-absent. This procedure is sensitive to spike timing, but in a limited way. To see this, consider the following hypothetical scenario. Suppose that a neuron responded to the vibratory stimulus by emitting just a single burst of three spikes within 20 ms. In that case, the optimal w for both classifiers would be short (∼10 ms), and the performance of the TCSTC would be comparable to that of the PSTC, because the maximum rate in each trial would be a reliable indicator of the presence of a burst (and thus of a stimulus). However, now suppose that the neuron responded instead by firing two such bursts separated by 50 ms. The PSTC would still use a filter width of ∼10 ms and would perform much better, because it would use essentially twice as much information as with a single burst. In contrast, because the TCSTC computes a single maximum rate, it might use one of two strategies: (i) it could still use a 10-ms filter width, which would, in essence, produce almost the same result as with only one burst, or (ii) it could use a much longer w of about 50 ms to try to generate an r_max based on both bursts. Either way, the performance of the TCSTC would be suboptimal because it has difficulty resolving multiple short-duration events (∼10 ms) and integrating them over relatively long times (∼50 ms) with a single time constant.

With this in mind, consider the results of the TCSTC analysis: no significant differences were found among areas, neither for the optimal width, which on average was relatively large (>40 ms), nor for the range of optimal widths (Fig. 5 I and J, open bars); the maximum performance achieved (C_max) was lower than with the PSTC, as expected, and approximately the same for the VPL and S1 populations (Fig. 5K). Also, for the VPL neurons, the maximum performance with the TCSTC was just slightly higher than that with the spike count classifier, C_cnt, whereas for the S1 population there was essentially no difference (Fig. 5L). The TCSTC was able to extract a small amount of information from the synchronous responses in VPL but not in S1.

Therefore, the TCSTC is clearly suboptimal because, as stated above, this decoding method simply cannot combine very effectively multiple short-duration events (spikes or spike bursts) that can only be resolved via a small filter width if they are spread over a much longer stimulation period. Nevertheless, the results are interesting for two reasons. First, the classifier was still useful: although the maximum performance was clearly below that achieved with the optimal method (Fig. 5K), it remained significantly above chance for all of the neurons. Second, the contrast between the PSTC and TCSTC is another indication that fast modulations in firing do contain useful information that improves stimulus detection, and at least judging by the difference between C_max and C_cnt, these were still slightly more prominent in VPL than in S1 (Fig. 5L).

Neural Detection Performance Relative to Behavioral Performance.

In the previous sections we demonstrated that fast modulations in spiking activity contribute information that is useful for stimulus detection and that their contribution is more important in VPL than in S1. To relate these modulations to the monkey’s sensitivity to stimulus amplitude, we constructed neurometric curves based on PSTC performance at each stimulus amplitude and compared them with the monkey’s psychometric curves based on behavioral responses. To distinguish the potential contributions of fast and slow firing rate modulations to performance, two neurometric curves were generated for each neuron: one based on a narrow filter (w = 5 ms; Fig. 6A) and another based on a wide filter (w = w_cnt; Fig. 6B). All such curves show the probability of reporting that yes, a stimulus was presented, as a function of stimulus amplitude.

Fig. 6.

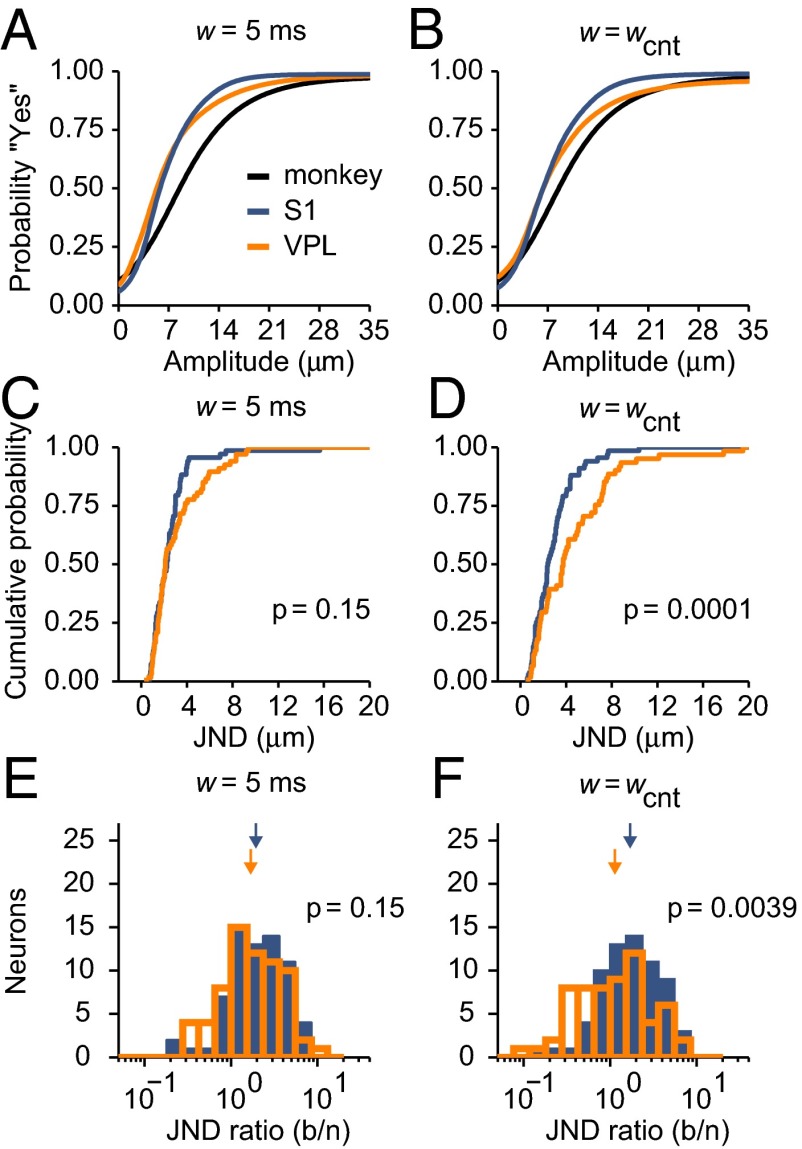
Probability of detection in monkeys and neurons. (A and B) Black curves are psychometric curves showing the mean probability of the monkey reporting the detection of a stimulus (“yes”) as a function of stimulus amplitude (monkey JND: 4.7 µm). Orange and blue curves show mean neurometric curves averaged across VPL and S1 neurons, respectively, obtained either with the PSTC and a filter width of 5 ms (A) or with the spike-count classifier (w = w_cnt; B). (C) Cumulative distributions of JNDs from neurometric curves based on the PSTC (w = 5 ms). The means were not significantly different across areas (VPL: 3.04 ± 0.27 µm, n = 67; S1: 2.5 ± 0.24 µm, n = 68; P = 0.15). (D) Cumulative distributions of JNDs from neurometric curves based on the spike-count classifier (w = w_cnt). JNDs in S1 were significantly smaller than in VPL (VPL: 4.61 ± 0.47 µm, n = 61; S1: 2.86 ± 0.22 µm, n = 67; P = 0.0001). (E) Histograms of JND ratios (behavior/neuron) for the same condition in C. Mean JND ratios for VPL and S1 are indicated by orange and blue arrows, respectively; they were not significantly different (VPL: 1.69 ± 0.043; S1: 1.94 ± 0.039; P = 0.15). (F) Histograms of JND ratios for the same condition in D. Ratios were significantly larger in S1 than in VPL (VPL: 1.13 ± 0.052; S1: 1.69 ± 0.041; P = 0.0039).

The two mean neurometric curves averaged across VPL and S1 populations were generally steeper than the mean psychometric curves (Fig. 6 A and B). This result was confirmed quantitatively by calculating the just noticeable difference (JND) of each curve, which is a measure of its width (Materials and Methods). The JNDs from individual neurometric curves based on fast modulations (w = 5 ms) were similar for VPL and S1 neurons (Fig. 6C; P = 0.15), indicating that the sensitivity to stimulus amplitude derived from fast modulations did not differ across areas. In contrast, when based on slow firing rate modulations, the neurometric JNDs were significantly smaller for S1 than for VPL neurons (Fig. 6D; P = 0.0001). So, again, S1 neurons are better detectors—they have a higher sensitivity to stimulus amplitude—when spike counts are used to infer the presence of a stimulus.

To compare these results directly with the monkey's psychophysical performance, for each neuron we calculated a JND ratio, with the neuron's JND (from the neurometric curve) in the denominator and the monkey’s JND (from the psychometric curve in the corresponding recording session) in the numerator. In this way, a ratio larger than 1 indicates better neuronal performance than behavioral performance. The mean VPL and S1 JND ratios based on fast modulations (w = 5 ms) were statistically the same (Fig. 6E; P = 0.15), but the JND ratios based on slow modulations (w = w_cnt) were significantly larger for S1 than for VPL neurons (Fig. 6F; P = 0.0039). These results recapitulate the findings described above, but with performance measured in terms of the monkey's perceptual sensitivity: VPL and S1 neurons are approximately equivalent when only fast modulations are taken into account, but because slow modulations are stronger in S1, classification performance in S1 varies more sharply with stimulus amplitude; as a result, the spike counts in this area are significantly more informative about stimulus presence.

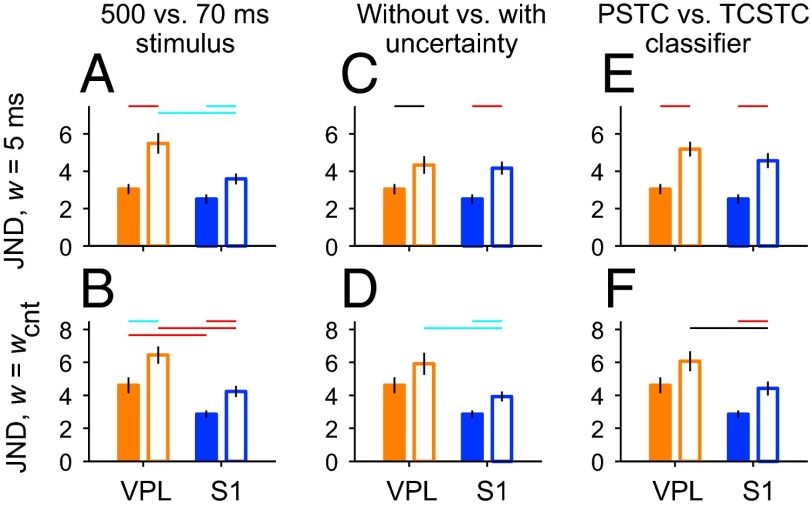
Fig. 7 extends the analysis just discussed to the wider set of conditions explored earlier (Fig. 5), in which different stimulus lengths, amounts of uncertainty, and classification methods were compared. All of the manipulations made the detection of the stimulus more difficult relative to the original condition; the neurometric JNDs obtained with both narrow (w = 5 ms) and wide (w = w_cnt) filters increased, both for VPL and S1 (Fig. 7, compare pairs of filled and open bars). However, the increases largely respected the original differences between VPL and S1. When a narrow filter was used, the JNDs for the two areas were similar when temporal uncertainty was included (Fig. 7C, open bars) and when a suboptimal classifier was used (Fig. 7E, open bars), but there was a significant difference among the two areas, favoring S1, when a shorter stimulus length (70 ms) was considered (Fig. 7A, open bars). On the other hand, when the spike count (w = w_cnt) was used, the differences between JNDs across areas remained significant in all cases, with S1 neurons displaying, on average, a higher sensitivity to stimulus amplitude, i.e., smaller JNDs (Fig. 7 B, D, and F, open bars). Thus, overall, our analyses are generally quite consistent and point to the same conclusion: the firing rates of S1 neurons carry information about stimulus presence over a wider range of timescales than the rates of VPL neurons.

Fig. 7.

Neurometric detection under alternative conditions. The format is identical to that of Fig. 5. In all panels, bars and vertical lines indicate mean values ± SEM, respectively, of the quantities indicated on the y axes, i.e., neurometric JND obtained with a filter width of 5 ms (w = 5 ms) or with the spike-count classifier (w = w_cnt). Horizontal colored lines indicate significance levels for each comparison (black: P < 0.05, cyan: P < 0.01, red: P < 0.001). Orange and blue bars are for VPL and S1 data, respectively. Filled bars correspond to mean JNDs obtained in the standard condition, in which spike trains elicited during the full stimulation period (500 ms) were analyzed by the PSTC and the stimulus onset was known to the classifier (no temporal uncertainty). (A and B) Results in the standard condition and when only the spikes in the first 70 ms of stimulation were used by the PSTC (open bars). (C and D) Results in the standard condition and when the stimulus onset was unknown (temporal uncertainty, open bars). (E and F) Results in the standard condition and when classification performance was assessed by a suboptimal classifier: the TCSTC (open bars). Significant differences between VPL and S1 in the standard condition are depicted only in A and B.

Discussion

To understand the development of a perceptual decision associated with the detection of a stimulus, it is fundamental to determine how the signal indicating stimulus presence is encoded and relayed from the periphery to central brain areas (11). Here, neurons from the VPL nucleus and S1 were simultaneously recorded while monkeys performed a vibrotactile detection task (6, 9). We used a unique decoding method to determine (i) the features in the evoked spike trains that covary with the vibrotactile stimuli; (ii) the timescale that is optimal for decoding stimulus presence from single neurons in both areas; (iii) how accurate such decoding can be; and (iv) how neuronal detection performance relates to the subject's perceptual decision report. The results show that fast, stimulus-linked variations in firing probability occurring within tens of milliseconds do provide significant information about stimulus presence, not only in VPL, where they are more evident, but also in S1. However, the optimal timescale of integration varies widely among neurons in both areas, and notably, stimulus presence is also strongly encoded through slower modulations in firing rate in S1 cells. Therefore, S1 neurons are better detectors than VPL neurons in the sense that their timescale of integration does not need to be set as precisely to produce accurate performance. These findings suggest a potential rationale for the progressive changes in response properties observed from thalamus to cortex: in comparison with the VPL, inferring stimulus presence from S1 may require less fine tuning of the neural circuits downstream [e.g., secondary somatosensory cortex (S2)].

Here, the behaviorally relevant stimulus feature was amplitude, but a similar transformation in the neural code has been documented, also with mechanical vibrations, when the relevant dimension is stimulus frequency (8). In that case, a large change occurs between S1 and S2 and relates to performance in a different psychophysical task: frequency discrimination. In S1, the neurons that modulate their mean firing rates (computed over a stimulation period of several hundred milliseconds) as functions of stimulus frequency almost always display a positive monotonic dependence, such that the mean firing rates are typically higher for higher stimulus frequencies. In contrast, in S2 and areas downstream (8, 12–14), neurons with negative monotonic dependencies (42%) are about as common as those with positive monotonic dependencies (58%). In addition to the appearance of such negative monotonic tuning, i.e., of neurons that fire most intensely for low stimulus frequencies, the information about vibration frequency conveyed by the periodicity of the evoked spike trains decreases by a factor of 10 from S1 to S2 (8); this is because S2 neurons show extremely weak phase-locking to the stimulus waveform in comparison with S1. Notably, a nearly identical progression in the coding of stimulus frequency is observed along the caudal-to-rostral axis in the auditory cortex (A1) of marmoset monkeys in the same frequency range (5–50 Hz), but in the case of sounds (15). This dual temporal/rate representation of acoustic flutter stimuli in A1 results from a progressive transformation that begins in the auditory thalamus [in the medial geniculate body (MGB)], because in the previous relay station, the inferior colliculus, most neurons synchronize their spikes but do not vary their overall firing rate as a function of sound frequency (16, 17). Thus, in both modalities, the more central area displays weaker phase-locking to the stimulus waveform and more robust slow modulations in firing rate than the more peripheral area.

The transformation of a neural code may be strongly influenced by how the encoded sensory stimulus is used to direct behavior (8, 18), and the results of two studies using vibrotactile stimuli are consistent with this idea. Work by Mackevicius and colleagues showed that the timing of spikes in primary mechanoreceptive afferents is crucial for discriminating complex vibratory stimuli (19). In their analyses, they used a decoding method that, although conceptually very different from the PSTC, also takes into consideration the fine temporal structure of spike trains. They found, first, that primary afferents convey more information about the frequency composition of vibrotactile stimuli when the temporal resolution of the decoder is high (on the order of 1–10 ms), and second, that the performance of human subjects in making dissimilarity judgments was better predicted by the afferent responses when their temporal structure was taken into account. In contrast, Muniak et al. investigated how the primary afferent responses related specifically to the subjective sensation of stimulus intensity reported by human subjects (20). They found that stimulus intensity ratings were fully accounted for by the summed mean firing rates of all of the responding afferents located under or near the stimulation probe, weighted by afferent type. These studies suggest that fine temporal information may be discarded early on when stimulus amplitude is the behaviorally relevant quantity, as it is for detection, but not when stimulus frequency is important.

More generally, several studies point toward a transformation from a faithful representation in the primary afferents, which follow the temporal fluctuations of vibrotactile stimuli extremely tightly, to a more abstract representation in downstream cortices, which is ultimately correlated with the perceptual report. Recordings of neural responses evoked by sinusoidal stimuli in primary afferents (4), cuneate nucleus (2), VPL (9), and S1 (8, 21) show periodic responses that are phase-locked to the sinusoidal wave, whereas in S2 and frontal lobe cortices the fraction of neurons presenting phase-locked responses decreases until it is minimal or nonexistent (1, 8, 12, 14, 22, 23). Such progression may reflect a general property of cortical circuits regardless of sensory modality, because similar findings have also been reported in the auditory system, at least for the first relay stations (17). Additionally, the information encoded within early areas does not entirely determine behavioral output in the detection task; on the contrary, the perceptual decision about whether a stimulus is present or absent seems to build up across brain areas (6, 12, 24).

According to our results, detection performance should be somewhat worse when based on a very short stimulus (i.e., a single sinusoidal pulse) compared with performance based on the full, 10-pulse, 500-ms stimulus (Figs. 5C and 7 A and B). With the 70-ms stimulus, all differences based on fast modulations were much smaller, likely because the location of the spikes within such a small window is much less consistent across trials; i.e., the periodic structure that is evident with a 10-pulse stimulus is largely absent within a single stimulation pulse. The result raises the issue of what is the actual amount of stimulation time that is relevant for behavior. When the task involves the comparison between two stimulus frequencies (i.e., discrimination), the effective integration window for neurons in S1 is ∼250 ms (7). However, shorter integration times may suffice to produce fast and accurate detection. Previous findings in humans and rats (25, 26) suggest that monkeys may be capable of detecting a stimulus that consists of a single sinusoidal pulse. If so, it will be interesting to test whether their accuracy drops relative to that with 10-pulse stimuli, as predicted from the neurometric curves obtained here. A comparable drop would suggest that when the stimulus is long (500 ms), all of it is used to determine its presence, whereas a smaller or negligible drop would suggest that only a short segment (e.g., 70 ms) is used, regardless of whether more information is available or not. An intermediate scenario in which the first 200–300 ms are relevant is plausible because, in general, the time dedicated to sampling a stimulus should be limited to optimally balance speed and accuracy (27).

Two neural features that impact how VPL and S1 neurons encode stimulus presence are the spontaneous firing rate and the slope of the mean firing rate as a function of stimulus amplitude, and we found that both differ significantly across areas. VPL neurons have significantly higher spontaneous firing rates in comparison with S1 by a factor of 1.75 (Fig. 2E). Similar findings have been documented in rats and cats (28, 29). The difference can be attributed both to differential inputs and to local circuit properties (30, 31). For example, it is likely that modulatory signals, such as cholinergic inputs from the brainstem, which are highly active when the animal is awake, contribute to maintaining a high firing rate in VPL (32, 33). In contrast, it is known that cortical neurons receive the majority (∼85%) of their inputs from other cortical neurons (31), such that both recurrent excitation and inhibition are strong (34), and allowing for periods of low spiking activity (31). Also, inhibitory conductances within intracortical circuits are more active when a subject is awake (35) and could play an important role in maintaining S1 low spontaneous rates and thus in shaping the stimulus-evoked responses.

Our results suggest that fast modulations (∼10 ms) in the firing of VPL neurons are exploited by S1 to generate more robust firing rate modulations in a slower range (∼100 ms). Another possibility, however, is that the fast modulations are relatively inconsequential and that the circuitry simply attempts to enhance the slower modulations already present in VPL independently of the fast ones, perhaps through convergence of selected thalamic inputs or other integration mechanisms. Although this scenario is conceivable, we think it is somewhat unlikely for three reasons. First, at least under some conditions, primary mechanoreceptors convey stimulus information almost exclusively through spike timing (4, 19, 20), so the circuitry downstream must be capable of converting highly structured spike patterns into slow firing rate modulations. Second, it is known that several convergent and synchronous thalamic inputs are necessary to elicit a single action potential in S1 (36), so mechanisms for detecting synchrony must be ubiquitous. Third, the changes that we observed between VPL and S1 can, to a first approximation, be explained by relatively simple computational operations, such as thresholding and rectification (Fig. S2), so exploiting the fast, synchronous responses should not be particularly difficult for neural circuits. S1 neurons were 1.46 times more sensitive than VPL neurons in terms of the slopes relating mean firing rate to stimulus amplitude (Fig. 2F). This “gain factor” might also be explained in part by other gain control mechanisms that produce selective amplification through intracortical dynamics (37–39). Notably, in rats, microstimulation of single neurons in the VPM nucleus leads to no perceptual effects, whereas in cortex it does (40). These facts, in conjunction with our results, suggest that, in general, neural representations of stimuli in the thalamus are different from those in cortex and that the transformation of the neural code from thalamus to cortex has a direct impact on stimulus perception.

Materials and Methods

Detection Task.

Two macaque monkeys were trained to perform a vibrotactile detection task described earlier (6, 9). Monkeys were handled according to the institutional standards of the National Institutes of Health and Society for Neuroscience. All protocols were approved by the Institutional Animal Care and Use Committee of the Instituto de Fisiología Celular.

Recording Sessions and Sites.

Neuronal recordings were obtained with two arrays of seven independent, movable microelectrodes (2–3 MΩ) (13) inserted into S1: one microelectrode array in the cutaneous representation of the fingers and the other medial to the hand representation, in a way that allowed us to lower the microelectrodes into the VPL nucleus. Single neurons were recorded contralateral to the stimulated hand while animals performed the vibrotactile detection task. Each recording session began with a mapping procedure to find the cutaneous representation of the fingers in the VPL and S1 (areas 1 and 3b). Neurons in both structures had small cutaneous receptive fields located in the distal segment of one digit (fingertips 2, 3, 4, or 5) and displayed QA or SA properties. Stimuli were delivered at the receptive field center. Locations of electrode penetrations in both areas were confirmed using standard histological techniques.

Neurons were classified as QA or SA according to their responses when the stimulation probe was lowered at the beginning of each trial, as described in ref. 9. The majority of the neurons recorded were QA (65 in VPL, 71 in S1); only a minority were SA (9 in VPL, 4 in S1).

Statistical Analyses.

We analyzed the responses of 74 VPL and 76 S1 neurons with 120–360 detection trials collected per neuron. All analyses were performed via customized programs run in Matlab (MathWorks).

Neurons were considered responsive if the distribution of firing rates during the stimulation period (500 ms) for the highest amplitude was statistically different from that in a period immediately before stimulus onset [500 ms, receiver operating characteristic curve (ROC) test, α = 0.01 (41)]. The relation between stimulus amplitude and neural activity was first quantified using linear regression; the independent variable was stimulus amplitude and the dependent variable was either the firing rate computed over the full stimulation interval (500 ms) or the power at 20 Hz, as a measure of stimulus-driven periodicity (8, 9). Differences in spontaneous rate and in fitted slopes across areas were assessed using the Kolmogorov–Smirnov test. For all other measured quantities, means and SEM are reported, and differences between VPL and S1 populations were assessed using a permutation test for unpaired samples (n = 10,000 permutations).

Simulation of Ideal Neurons.

We simulated the responses of ideal neurons to determine the sensitivity of the neural detection method described below and to gain intuition about the recorded data. Three prototypical neurons were considered: (i) a neuron that simply increased its mean firing rate during stimulation and was completely insensitive to the temporal structure of the stimulus; (ii) a neuron that maintained the same overall firing rate with and without stimulation but synchronized its spikes to the individual stimulation pulses; and (iii) a neuron that showed a mixture of the two effects, i.e., it fired more spikes during stimulation and these were synchronized to the stimulus waveform. For each case, we first defined the firing rate as a function of time, r(t) (Fig. 3 A–C, red traces). This function lasted a total of 1,000 ms; in the first and last 250 ms (no stimulation), r(t) was equal to a constant, baseline rate, whereas in the middle 500 ms (yes stimulation), it described the stimulus-related response. The stimulus-evoked modulations for types 2 and 3 were modeled using 20-Hz square waves of varying amplitudes and duty cycles. Spikes were then generated by first converting the rate function into a firing probability in each time step of 1 ms and then using a random number generator to determine whether one spike or no spike was fired in each time step. In this way, Poisson spike trains with variable underlying rate r(t) were produced. For each neuron type, 60 stimulus-present and 60 stimulus-absent trials were simulated. In stimulus-absent trials, r(t) remained equal to the baseline rate throughout the 1,000-ms period. A single stimulus amplitude was considered in these simulations. For all simulations and analyses, time was discretized in steps of 1 ms.

PSTC.

Simulated or recorded neuronal responses in individual trials were used to infer whether a stimulus was presented or not. Such decoding was done using a PSTC with cross-validation, which we developed specifically to analyze the current data. Trials were randomly divided into two groups, one for training the classifier (80 trials: 40 stimulus-present and 40 stimulus-absent) and another for testing it (all remaining trials), and the fraction of correctly classified test trials was saved. A test trial was deemed correct if the PSTC identified it correctly as a stimulus-present or stimulus-absent trial. For each neuron, this whole process was repeated 300 times; each one with different, with randomly split groups of training and testing trials, to obtain the mean fraction correct and its spread (standard error, SE). The PSTC has a free parameter, the filter width w, and the mean fraction of correct classifications was plotted as a function of w for each recorded neuron (Fig. 3 A–C, Lower). The optimal filter width of each neuron was defined as the value of w that produced the highest mean fraction of correct classifications (C_max). Classification performance was considered indistinguishable from optimal for all those points that were less than 2 SE away from C_max. Based on this criterion, the range of optimal filters for each neuron, Δw, was defined as the difference between the maximum and minimum filter widths for which performance was statistically indistinguishable from optimal.

The PSTC assumes that the responses of a given neuron are based on two elements: a spike-generation mechanism that follows simple Poisson statistics and a time-varying rate function that depends on whether a stimulus was presented or not. Notably, the firing rate function is assumed to be the same from one trial to another within the same class: stimulus-present or stimulus-absent. Thus, during training, the PSTC constructs two firing rate functions or templates, r_SP(t) and r_SA(t), that characterize the cell's responses. For this, all of the spike trains from training trials are convolved with a Gaussian function, or filter, of SD w, and the results are averaged separately across stimulus-present trials [to produce r_SP(t)] and across stimulus-absent trials [to produce r_SA(t)]. Here, it is important to recall that time is divided into a finite number of 1-ms steps. Then, during testing, the PSTC computes two quantities: one that is proportional to the probability of observing the probe spike train given the rate function r_SP(t) and another that is proportional to the probability of observing the probe spike train given the rate function r_SA(t):

and

where the index j identifies all of the time points in the probe spike train in which there was a spike, the index k identifies all of the time points in which there was no spike, and c is a constant (1/1,000) that converts the firing rate (in spikes per second) into a probability of firing a spike in a 1-ms step. These expressions are based on the binomial distribution, which underlies the Poisson model. They basically assume (i) that at any given time step a biased coin was flipped and the outcome determined whether a spike was produced or not and (ii) that the bias was given by either r_SP(t) or r_SA(t). Thus, unlike other time-sensitive measures, such as the vector strength or the Fourier power at a given frequency, the PSTC requires no information about the stimulus (e.g., its frequency) and does not rely on periodicity per se but rather just on the repeatability of a response given a particular stimulus. If Q_SP > Q_SA, then the pattern of spikes in the probe spike train is more likely to have been produced by r_SP(t) than by r_SA(t), and the spike train is considered to belong to the stimulus-present class. Conversely, if Q_SA > Q_SP, then the spike train is assigned to the stimulus-absent class. All test trials are similarly classified based on the same r_SP(t) and r_SA(t) template functions derived from the training trials. In the current PSTC implementation, stimulus-present and stimulus-absent trials are assumed to be equally likely.

As a part of the PSTC performance curve (fraction of correct classifications vs. filter width w), we included one additional point: the fraction of correct classifications achieved (C_cnt) when the classifier bases its output only on the total number of spikes counted in the full analysis window (500 or 70 ms). This point corresponds to the expected performance of the PSTC in the limit when w becomes large. This spike count classifier compared the probability of observing n spikes in a test trial given either the mean number of spikes in stimulus-absent (training) trials, m_SA, or given the mean number of spikes in stimulus-present (training) trials, m_SP, all counted during the full analysis period. Thus, in keeping with the assumption of Poisson statistics, it compared (m_SA)ⁿ exp(–m_SA)/n! vs. (m_SP)ⁿ exp(–m_SP)/n! with the largest probability determining whether the trial was considered as stimulus-present or stimulus-absent.

In constructing the PSTC performance curves, we first considered exclusively the time window of stimulation, so all spike trains used for training and testing were 500 ms long (or, for the short-window analysis, 70 ms long). In this case the PSTC had to infer whether there was a stimulus or not, but the time of its occurrence was certain. We also implemented a variant of the PSTC analysis in which, during testing, there was uncertainty about when the stimulus might have occurred. In this case, the training phase proceeded exactly as before—in fact, the classifier generated the exact same r_SP(t) and r_SA(t) functions—but the spike trains use for testing were lengthened by adding the 500 ms before stimulus onset and 500 ms after its offset. Now the PSTC considered multiple temporal locations of the spike train to be classified relative to the r_SP(t) and r_SA(t) functions and made a decision according to the following rules: (i) the likelihood of stimulus present, L_SP, was the maximum value of Q_SP/(Q_SP + Q_SA) across all of the possible temporal locations; (ii) the trial was classified as stimulus-present if L_SP > α; and (iii) the threshold α was set so that, across all tested trials, stimulus-present and stimulus-absent classifications were equally likely.

As with any neural decoding method, the PSTC can be used to benchmark coding capacity to the degree that it is optimal. Thus, it may not generalize to different experimental conditions (e.g., if the stimuli to be detected varied in both amplitude and frequency) unless it is appropriately modified.

TCSTC.

Like the PSTC, the TCSTC assigns test spike trains to stimulus-present and stimulus-absent classes. Each test spike train is convolved with a Gaussian filter of SD w. The classifier then finds the maximum value of the resulting firing rate function, r_max, and compares its value to a threshold ɵ: if r_max > ɵ, the trial is classified as stimulus-present, and otherwise it is classified as stimulus-absent. The value of ɵ is set during training; it is chosen so that the resulting fraction of correct classifications for the training trials is maximized. Additional variants of the TCSTC were explored in which the classification was based on trial-specific statistics other than the maximum of the firing rate function, r_max (e.g., the SD or the skewness of the distribution of firing rate values or the rate marking a particular quantile in the distribution), and the results were essentially the same as with r_max, in the sense that all of those classifiers could only extract a limited amount of information from the fast modulations. Their performance reflected primarily the overall differences in mean firing rate across conditions.

Psychometric and neurometric curves.

Psychometric and neurometric curves both refer to the probability p_Y, varying as a function of stimulus amplitude, of reporting that yes, a stimulus was presented. They characterize a monkey's or a neuron’s sensitivity to stimulus amplitude. The psychometric curve was based on behavioral responses, whereas the neurometric curve was based on the performance of the PSTC or TCSTC. The classifiers were not retrained to generate the neurometric curve; rather, the test trials were simply sorted by amplitude during the testing phase of the classification analysis described above. Two neurometric curves were computed for each neuron: one with w = 5 ms and another based on the total spike count (w = w_cnt) inside the analysis window (500 or 70 ms).

Each curve, psychometric or neurometric, was fitted with a continuous Boltzmann curve:

where A is the stimulus amplitude and C₁, C₂, and b are free parameters. Best-fitting parameter values were obtained using the nlinfit function in Matlab and were fixed given the behavioral or neural data in a given session. Only curves with significant goodness of fit were considered. Neurometric curves where the false alarm rate (i.e., the probability of detection at A = 0) was ≥0.4 and the hit rate (i.e., the mean probability of detection for A > 0) was ≤0.6 were discarded because they contained virtually no information about stimulus amplitude. For each neurometric and psychometric curve, the detection JND was equal to one-half of the difference in amplitude needed to go from a probability of detection of 0.25 to one of 0.75. The JND for a monkey or a neuron was calculated from the corresponding Boltzmann curve fitted to the data. Threshold ratios were calculated by dividing the behavioral JND by the neurometric JND (b/n). Ratios <1 imply that neural sensitivity is smaller than the monkey’s, whereas ratios >1 imply the opposite.