Abstract
Various insects and small animals can navigate in turbulent streams to find their mates (or food) from sparse pheromone (odor) detections. Their access to internal space perception and use of cognitive maps still are heavily debated, but for some of them, limited space perception seems to be the rule. However, this poor space perception does not prevent them from impressive search capacities. Here, as an attempt to model these behaviors, we propose a scheme that can perform, even without a detailed internal space map, searches in turbulent streams. The algorithm is based on a standardized projection of the probability of the source position to remove space perception and on the evaluation of a free energy, whose minimization along the path gives direction to the searcher. An internal “temperature” allows active control of the exploration/exploitation balance during the search. We demonstrate the efficiency of the scheme numerically, with a computational model of odor plume propagation, and experimentally, with robotic searches of thermal sources in turbulent streams. In addition to being a model to describe animals’ searches, this scheme may be applied to robotic searches in complex varying media without odometry error corrections and in problems in which active control of the exploration/exploitation balance is profitable.
Keywords: biological search, plume tracking, search algorithm
The survival of insects and animals depends on their ability to search and reach for food and mate from the various emitted chemicals in complex varying environments. It is very likely that evolution, regarding search strategies, acted not only on the statistics of different modes of space exploration (1–6) (e.g., generalized levy processes) but also actively on the decision process in relation to the time evolving detected signals. However, a limited number of models tackle with deciphering the information of the signal transported in the environment.
Considering search schemes from the signal deciphering point of view shifts the modeling process toward a mix of information, game, and optimal control theory. Hence, a key part of the reasoning is focused on how evolution selected a balance between exploitation of the information accumulated during the search and exploration of the environment (7, 8). Among the schemes that are intended to deal with the randomness induced by turbulence and that directly address the exploration/exploitation balance, infotaxis is the most efficient (9–11), i.e., the one exhibiting the lowest average search time and the highest reliability in source reaching. The two key elements of infotaxis are the knowledge by the searcher of both the rate of detection function and the statistics of detection, to infer the probability map of the source position, and the use of entropy as a function to be greedily minimized along the path chosen by the searcher. Infotaxis is robust to various sources of noise, with optimal search efficiency when the model in infotaxis matches the environmental dynamics. However, for an animal, the probability building process requires both an advance space perception (SI Appendix, section A.1) and the knowledge of its position relative to this map. An appropriate modeling or knowledge of the dynamics of the environment is needed to achieve the best search efficiency (SI Appendix, section A.3). Finally, to “know” its position and correct its odometry errors, the animal should be able by one or multiple processes to access environmental cues (SI Appendix, section A.2).
Since Tolman (12) suggested in the 1930s the existence, mostly in mammals, of “cognitive maps” for navigational purposes, debates about animal spatial behaviors have flourished. O’Keefe and Nadel’s book (13) published in 1978 suggested that the cognitive map is located (and/or built) in the hippocampus. Since then, numerous experiments have studied map-like processes happening in the hippocampus and the entorhinal cortex (14–17). Even today, the debate about cognitive maps is still active for many reasons, the lack of consensus regarding the definition of cognitive maps (18) and a clear way to test their existence being the most obvious ones.
Insects can direct themselves over large distances (19–22) and find sources of pheromone (23–28) or food from the rare cues transported by wind-induced turbulent flow (29, 30). There is great variability in the search capacities of different insects depending on the typical distances they have to travel, the physical and ecological characteristics of their environments, the amount of information they can extract from visual cues, the need to go back to a nest, and so on. It seems unlikely, although not impossible (31, 32), that (some) insects have access to space perception similar to that of rodents (33). Hence, when butterflies or other insects navigate among pheromone plumes (23–28), they can perform the search without full access to their positions with respect to their environments. However, they can find their mates or specific vegetal compounds without advanced space perception. It is worth mentioning that there is a lack of knowledge in the success rate of insect searches; i.e., if N butterflies are freed at a defined distance from a pheromone source in a turbulent stream, how many of them will reach the source?
However, insects’ access to space is not necessarily inefficient. Path integration (14, 34–38), with and without external cues, allows the insect to know its position with respect to its previous positions, by integration of its body motion and, for some insects, by the relative motion of external cues (39). Other processes, such as navigation in familiar spaces, may give partial access to space perception (40–43) (see SI Appendix, section A.1 for more comments). The two goals of the present work are to show that (i) efficient searches are possible for a searcher with limited space-processing capacities, evolving in complex varying environments with limited access to cues that would allow odometry error correction, and (ii) the scheme designed to accomplish this task leads to a potential framework to describe some animal search strategies.
The bottom line is the projection of the probability distribution of the source into a form allowing computation without advanced space perception and the design of a free energy whose minimization along the path gives direction to the searcher. The introduction of an “internal temperature” term allows active control of the balance between exploration and exploitation of information. In the following text, we introduce the Mapless search scheme, show its efficiency, quantify its performance with numerical simulations, and finally experimentally test its efficiency with thermal source robotic searches.
Results
The Mapless Search Scheme.
To investigate searches in conditions matching those of a space perception-limited animal evolving in a complex varying environment, the searcher moves along a self-generated path,  , and has to choose a direction based on the events experienced along
, and has to choose a direction based on the events experienced along  . The searcher accesses its position from uncorrected path integration and is considered to evolve in a cue-limited environment, preventing an accurate correction of its position. Information-bearing events are either detections (rare local events) or the absence of detection (frequent, less localized events). The environment is characterized by a rate of detection function,
. The searcher accesses its position from uncorrected path integration and is considered to evolve in a cue-limited environment, preventing an accurate correction of its position. Information-bearing events are either detections (rare local events) or the absence of detection (frequent, less localized events). The environment is characterized by a rate of detection function, 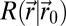 , which gives the rate of detection of a searcher in
, which gives the rate of detection of a searcher in 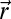 when the source is in
when the source is in 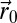 (SI Appendix, section B.2). A correlation length, λ, is associated with
(SI Appendix, section B.2). A correlation length, λ, is associated with 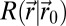 (9). The absence of complex space perception prevents the direct decoding (SI Appendix, section B.3) of the information stored in path
(9). The absence of complex space perception prevents the direct decoding (SI Appendix, section B.3) of the information stored in path 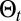 using Bayesian inference (8, 9) (SI Appendix, sections B.4 and B.5). Hence, to implement the scheme, the first necessary element is an approximate expression of the inferred position of the source:
using Bayesian inference (8, 9) (SI Appendix, sections B.4 and B.5). Hence, to implement the scheme, the first necessary element is an approximate expression of the inferred position of the source: 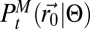 . The searcher will neither evaluate nor directly update
. The searcher will neither evaluate nor directly update 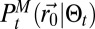 but will use it to compute the various variables necessary for the decision process. It was found that no moment-based approximation could gather enough information to be used in a search scheme. Similarly, saddle point-based approximations failed to give an appropriate description of the source position probability, and finally, attempts to fit the distribution through simple characteristic functions failed because updates and computation of variables were impossible without either space perception or a significant amount of calculi (SI Appendix, section B.6). An essential element, which the source position probability map needs to bear, is the reduction of probability around the searcher, as it receives no detection. Hence, the way chosen to catch as much information as possible was to separate the detection terms from the nondetection terms, and to approximate the former by its main component and the latter by a mean field approximation (SI Appendix, section B.7). These approximations lead to
but will use it to compute the various variables necessary for the decision process. It was found that no moment-based approximation could gather enough information to be used in a search scheme. Similarly, saddle point-based approximations failed to give an appropriate description of the source position probability, and finally, attempts to fit the distribution through simple characteristic functions failed because updates and computation of variables were impossible without either space perception or a significant amount of calculi (SI Appendix, section B.6). An essential element, which the source position probability map needs to bear, is the reduction of probability around the searcher, as it receives no detection. Hence, the way chosen to catch as much information as possible was to separate the detection terms from the nondetection terms, and to approximate the former by its main component and the latter by a mean field approximation (SI Appendix, section B.7). These approximations lead to
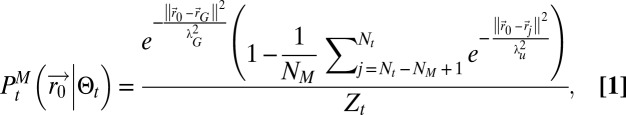 |
where  is the damped center of mass of detections,
is the damped center of mass of detections, 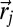 the positions of the searcher where there has been no detections,
the positions of the searcher where there has been no detections, 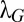 the scale associated with the Gaussian term approximating the detection terms,
the scale associated with the Gaussian term approximating the detection terms, 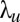 the scale associated with the Gaussian term approximating the nondetection terms,
the scale associated with the Gaussian term approximating the nondetection terms,  the number of visited points stored in memory, and
the number of visited points stored in memory, and 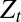 the normalization constant. The lack of space perception, coupled with the accumulation of positioning errors, leads to precautions in the “memory” that the searcher should keep from its past. Hence, the damped center of mass reads
the normalization constant. The lack of space perception, coupled with the accumulation of positioning errors, leads to precautions in the “memory” that the searcher should keep from its past. Hence, the damped center of mass reads 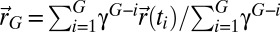 , where
, where 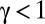 and
and  are the times of the detections. The second necessary element to decide the direction to be taken after experiencing the self-generated path
are the times of the detections. The second necessary element to decide the direction to be taken after experiencing the self-generated path  is the choice of a function of
is the choice of a function of 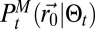 that the searcher has to minimize. Entropy is known from infotaxis (9) to be efficient, yet it works for a distribution precisely modeling the dynamics of the environment. Furthermore, we already noticed that entropy tends to shift the exploration/exploitation balance toward exploration, hence another term should be added to reinforce maximum likelihood behavior and so shift the balance toward exploitation. We introduce a free energy that reads
that the searcher has to minimize. Entropy is known from infotaxis (9) to be efficient, yet it works for a distribution precisely modeling the dynamics of the environment. Furthermore, we already noticed that entropy tends to shift the exploration/exploitation balance toward exploration, hence another term should be added to reinforce maximum likelihood behavior and so shift the balance toward exploitation. We introduce a free energy that reads
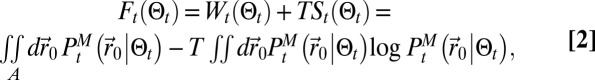 |
where 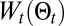 is the working energy, A the integration domain defined as
is the working energy, A the integration domain defined as 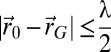 ,
, 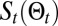 the Shannon entropy, and T the temperature that controls the relative value between the two previous terms. When moving from the position at time t,
the Shannon entropy, and T the temperature that controls the relative value between the two previous terms. When moving from the position at time t, 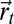 , to a neighboring position,
, to a neighboring position, 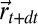 , the expected variation of the free energy will be the sum of two terms, one accounting for the discovery of the source and the other one for its absence. This variation reads
, the expected variation of the free energy will be the sum of two terms, one accounting for the discovery of the source and the other one for its absence. This variation reads
 |
where the dependency of 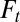 with
with  was not shown for display purposes,
was not shown for display purposes, 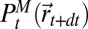 is the probability that the source is at
is the probability that the source is at 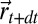 ,
, 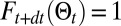 is the free energy if the source has been found (SI Appendix, section B.9),
is the free energy if the source has been found (SI Appendix, section B.9), 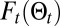 is the free energy of the searcher at time t,
is the free energy of the searcher at time t, 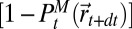 is the probability that the source is not at
is the probability that the source is not at 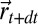 ,
, 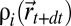 is the expected probability of having i detections, and
is the expected probability of having i detections, and 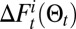 is the expected variation of the free energy if there were i detections. The Poisson detection model gives
is the expected variation of the free energy if there were i detections. The Poisson detection model gives 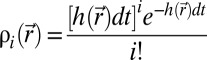 , where
, where 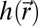 is the expected average hit rate and reads
is the expected average hit rate and reads 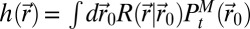 and
and 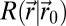 is the rate of detection of the searcher if it is at the position
is the rate of detection of the searcher if it is at the position  and the source is at
and the source is at 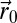 .
. 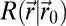 is approximated by a Gaussian function. All terms involved in the search,
is approximated by a Gaussian function. All terms involved in the search, 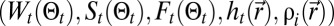 , are expressed in Materials and Methods (SI Appendix, section B.8), where it can be seen that the actual expression of
, are expressed in Materials and Methods (SI Appendix, section B.8), where it can be seen that the actual expression of 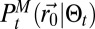 is not used.
is not used.
Analysis and Numerical Investigation of the Mapless Searches.
With and without wind.
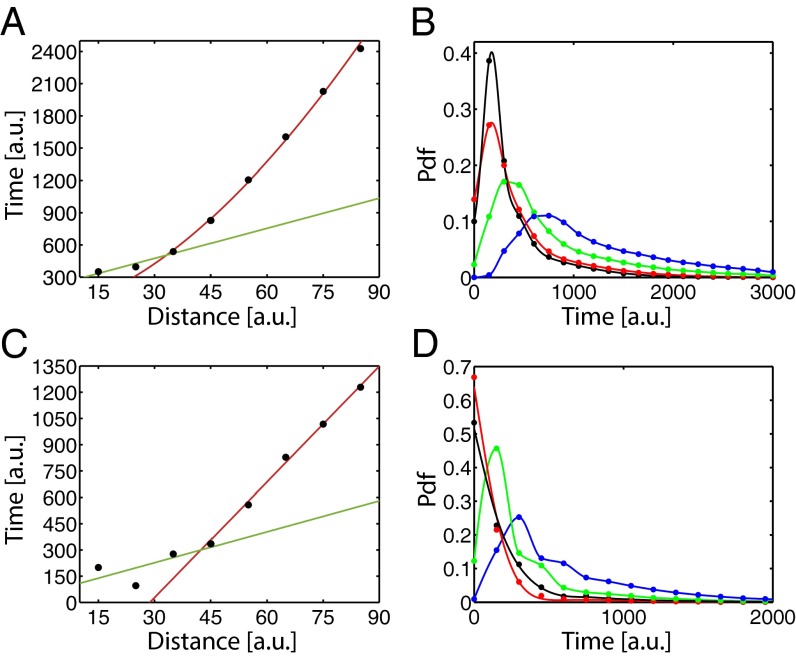
Animals such as insects show an incredible capacity to reach a target in complex medium. To be a relevant model, Mapless should be able to reach its target efficiently and to have a nonexponential search time dependency with distance (9). In Fig. 1, we show the evolution of the average search time with distance, with (Fig. 1C) and without wind (Fig. 1A), combined with time search statistics for various initial distances (Fig. 1 D and B, respectively). Mapless exhibits fast source-reaching dynamics and fast decreasing search time statistics for large times (no heavy tails; SI Appendix, section B.10). It also exhibits a subquadratic average search time dependency with initial distances, for searchers starting from distances less than 3λ.
Fig. 1.
(A and C) Evolution of the average search time with initial distance from the source. (B and D) Evolution of the statistics of searching time with initial distances. In A and B, simulations were performed with the windless scheme, with λ = 30 a.u, V = 0 a.u., γ = 0.8, NM = 750, and T = 1. V is the velocity of the wind. In C and D, simulations were performed with the wind scheme, with λ = 30 a.u, V = 0.5 a.u., γ = 0.25, NM = 750, and T = 1, and with the initial position of the searcher uniformly drawn within a 30° angle from a line starting at the source and extending in the direction of the wind. In A and C, the color lines are approximating fits. The green lines are linear fits for short distances; the red lines are a 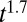 fit for A and a linear fit for C. Points are the results of simulations (20,000 simulations per point). In B and D, the colors are associated with initial distances: black,
fit for A and a linear fit for C. Points are the results of simulations (20,000 simulations per point). In B and D, the colors are associated with initial distances: black, 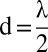 ; red, d = λ; green,
; red, d = λ; green, 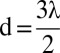 ; and blue, d = 2λ. Note the difference in scale between A and C.
; and blue, d = 2λ. Note the difference in scale between A and C.
Exploration/exploitation balance.
During the search, two processes should be balanced: exploration of the environment, to get more information on the source, and exploitation of the information already accumulated (7–11). In infotaxis, the entropy was used to balance exploration and exploitation. Based on the reliable inference of the source position distribution 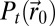 , the balance was managed efficiently with an advantage toward exploration. Here, information accessible from
, the balance was managed efficiently with an advantage toward exploration. Here, information accessible from 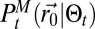 is only partially reliable. The searcher has no exact access to its position, and the detection process may not correspond to the one used in the scheme (e.g., the experiments). By adding
is only partially reliable. The searcher has no exact access to its position, and the detection process may not correspond to the one used in the scheme (e.g., the experiments). By adding 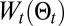 , we can reinforce maximum likelihood behavior. Furthermore, the temperature, T, allows shifting the balance between exploration and exploitation. Note that both exploration and exploitation are present in the entropy, where mostly exploitation is present in
, we can reinforce maximum likelihood behavior. Furthermore, the temperature, T, allows shifting the balance between exploration and exploitation. Note that both exploration and exploitation are present in the entropy, where mostly exploitation is present in 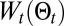 . This allows the temperature to actively control the balance. Furthermore,
. This allows the temperature to actively control the balance. Furthermore, 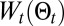 prevents the self-trapping behavior noticed for simulations performed at high temperatures (T > 5), when large numbers of detections have been made far from or close to the source.
prevents the self-trapping behavior noticed for simulations performed at high temperatures (T > 5), when large numbers of detections have been made far from or close to the source.
Improvements of the numerical scheme.
After the first trial simulations of the scheme, we added a few improvements along with the constraint that to evaluate the scheme, a “no-lost-searcher” policy should be implemented (SI Appendix, section B.14). This policy consisted of ensuring that if at least two detections were made, the searcher should find the source. After the initial detection (that started the search), it was noticed that there was a spontaneous symmetry breaking of the initial spiral, which induced slower searches. Hence, until a second detection was made, the Archimedean spiral was maintained (9). Furthermore, when the scheme decided to stop moving for a step, it was replaced by linear motion in a random direction. Finally, when numerous detections were made, the memory of the searcher was cleaned after a user-defined time. This improvement was useful mostly in cases in which the searcher began the search far from the source and hence reached the vicinity of the source with numerous detections. Memory removal allows the balance of exploration/exploitation to shift back to exploration. Including wind information in the scheme is achieved by imposing the same no-lost-searcher constrains. Hence, the projected probability keeps the same analytical expression, but all the parameter values  , the updating procedure for
, the updating procedure for 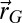 , and the choice of temperature are modified (SI Appendix, section B.8). Obviously, keeping a symmetrical expression of the projected probability leads to underuse of the wind information but ensures the possibility, for the searcher, of going in the wind direction if it travels beyond the source position. Finally, initial spiraling is performed asymmetrically, with larger motion in the opposite direction of the wind than in the same direction.
, and the choice of temperature are modified (SI Appendix, section B.8). Obviously, keeping a symmetrical expression of the projected probability leads to underuse of the wind information but ensures the possibility, for the searcher, of going in the wind direction if it travels beyond the source position. Finally, initial spiraling is performed asymmetrically, with larger motion in the opposite direction of the wind than in the same direction.
Characteristics of the searches.
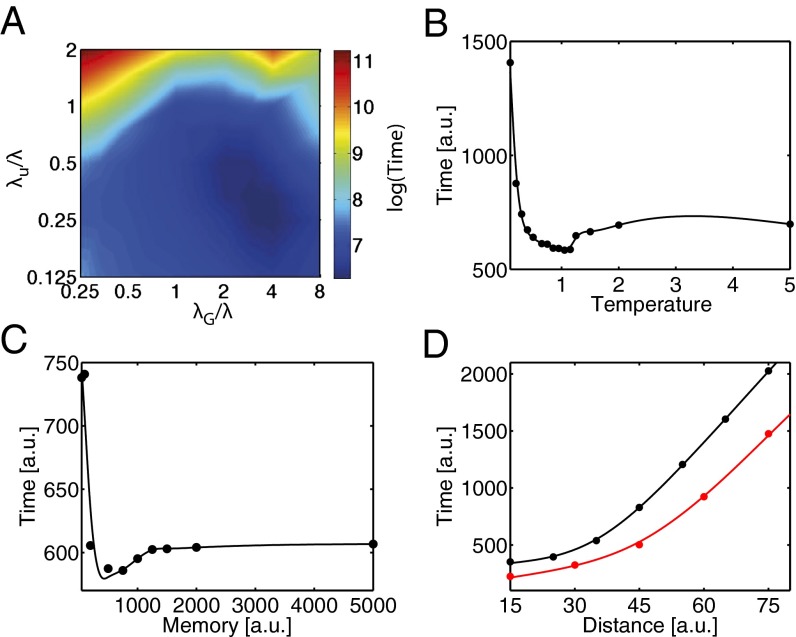
We studied the evolution of the search times for various parameters of the model to investigate their role in the properties of the searches. The balance between exploration and exploitation is controlled primarily by the temperature; the evolution of the average search time with the temperature is shown in Fig. 2A (see also SI Appendix, section B.13). At short initial distances, low-temperature search schemes are more efficient because 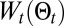 , which favors maximum likelihood behavior, has more influence on the decision process than it does at high temperatures. As the initial distance increases, the optimal temperature rises with a flattening of the mean search time–temperature curve. Two terms,
, which favors maximum likelihood behavior, has more influence on the decision process than it does at high temperatures. As the initial distance increases, the optimal temperature rises with a flattening of the mean search time–temperature curve. Two terms, 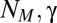 , act on the memory of the searcher; their evolutions are shown in Fig. 2 B and C. Interestingly, there are optimal values of memory for which it might have been expected that the longer the memory, the more efficient the research. However, the larger
, act on the memory of the searcher; their evolutions are shown in Fig. 2 B and C. Interestingly, there are optimal values of memory for which it might have been expected that the longer the memory, the more efficient the research. However, the larger 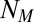 , the lesser the diminution of probability of the visited sites, which is necessary to induce an efficient exploration of space. A γ close to 1 weighs all the detections in the same fashion; thus, if detections are made far from the source, numerous other detections closer to the source would be necessary to shift
, the lesser the diminution of probability of the visited sites, which is necessary to induce an efficient exploration of space. A γ close to 1 weighs all the detections in the same fashion; thus, if detections are made far from the source, numerous other detections closer to the source would be necessary to shift 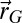 closer to the source. Finally, the resistivity of the scheme to odometry errors is shown in Fig. 2D. The scheme begins to lose efficiency when the positioning noise for each step is equal to the step size (SI Appendix, section B.12).
closer to the source. Finally, the resistivity of the scheme to odometry errors is shown in Fig. 2D. The scheme begins to lose efficiency when the positioning noise for each step is equal to the step size (SI Appendix, section B.12).
Fig. 2.
Evolution of the average search time with the temperature (A), the memory of the searcher (B), the damping factor (C), and the odometry errors (D). Points are the results of the simulations (20,000 simulations per point), and lines are visual aids. (A–C) Colors are associated with the initial distance from the source: black, 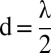 ; red, d = λ; green,
; red, d = λ; green,  ; and blue, d = 2λ. Simulations were performed with λ = 30 a.u., V = 0 a.u., with (A) NM = 750 and γ = 0.8, (B) T = 1 and γ = 0.8, (C) T = 1 and NM = 750, and (D) NM = 750, γ = 0.8, T = 1, an initial radius from the source equal to
; and blue, d = 2λ. Simulations were performed with λ = 30 a.u., V = 0 a.u., with (A) NM = 750 and γ = 0.8, (B) T = 1 and γ = 0.8, (C) T = 1 and NM = 750, and (D) NM = 750, γ = 0.8, T = 1, an initial radius from the source equal to 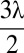 , and with an odometry error modeled as a Gaussian noise of defined deviation σ added to the searcher’s true position
, and with an odometry error modeled as a Gaussian noise of defined deviation σ added to the searcher’s true position
Choice of the parameters.
An important aspect of the search is how the parameters are chosen, either by evolution for animals’ searches or by design for robotic searches. Furthermore, robustness to parameter variation also was investigated to ensure that small departures from the optimal parameters did not reduce the efficiency of the searches significantly. Searchers, by nature, start at various distances from the source; hence, parameters must be chosen to incorporate this variability in initial distances. In Fig. 3, we display the evolution of the average search time with the correlation lengths 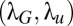 of the Mapless scheme (Fig. 3A), the temperature (Fig. 3B), and the memory time (Fig. 3C) for searchers randomly starting inside a radius 2λ from the source. In SI Appendix, section B.12, we also discuss Mapless searches in relation to the first and last arrivals at the source. Similar results are found for searchers starting inside a circle of 3λ.
of the Mapless scheme (Fig. 3A), the temperature (Fig. 3B), and the memory time (Fig. 3C) for searchers randomly starting inside a radius 2λ from the source. In SI Appendix, section B.12, we also discuss Mapless searches in relation to the first and last arrivals at the source. Similar results are found for searchers starting inside a circle of 3λ.
Fig. 3.
(A) Evolution of the log (for display purposes) of the average search time with the two normalized scales of the Mapless search scheme 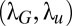 . The minimal average search time is 534 a.u. (B and C) Evolution of the average search times with temperature (B) and memory time (C). (A–C) Searchers start randomly inside a circle of 2λ radius, i.e., searchers may start at any radius between 0 and 2λ. Note that for a memory of 25 a.u., the average search time is 5,616 a.u. (D) Comparison of the evolution of the average search time with distance for one source (black) and for two sources (red). (B–D) The points are the results of the simulations, and the lines are visual aids.
. The minimal average search time is 534 a.u. (B and C) Evolution of the average search times with temperature (B) and memory time (C). (A–C) Searchers start randomly inside a circle of 2λ radius, i.e., searchers may start at any radius between 0 and 2λ. Note that for a memory of 25 a.u., the average search time is 5,616 a.u. (D) Comparison of the evolution of the average search time with distance for one source (black) and for two sources (red). (B–D) The points are the results of the simulations, and the lines are visual aids.
Multisources.
Insects often emit pheromones at a specific time of day, with females emitting pheromones at the same time, usually from similar host plants. Hence, the sources of pheromone are close to one another. Mapless should be able to be applied to multiple source searches without modification and still be able to reach one of the emitting sources efficiently. The issue with multiple sources is that when detections are made, their sources are unknown and the underlying 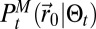 stores only the position of one source. When infotaxis is used, this leads to the overexploration of the areas between the sources. (11) (SI Appendix, section B.11). We display in Fig. 3D the evolution of the average search time with distance for two emitting sources. Interestingly, the average search time diminishes compared with the single source searches. Here, because
stores only the position of one source. When infotaxis is used, this leads to the overexploration of the areas between the sources. (11) (SI Appendix, section B.11). We display in Fig. 3D the evolution of the average search time with distance for two emitting sources. Interestingly, the average search time diminishes compared with the single source searches. Here, because 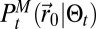 catches only some the characteristics of the environment, the multiple sources help the searcher reach the vicinity of these sources, then the free energy helps lock the searcher to one source.
catches only some the characteristics of the environment, the multiple sources help the searcher reach the vicinity of these sources, then the free energy helps lock the searcher to one source.
Experimental Implementation.
The Mapless search scheme was implemented experimentally to test its effectiveness and robustness in a complex varying environment, with a source emission not corresponding to the one used in the model and with significant uncorrected odometry errors (Fig. 4). A small robot (K-Team, www.k-team.com; SI Appendix, section C) equipped with a thermocouple detector had to search a thermal source from the transported thermal plumes. The thermal transport was used as an approximation of pheromone transport in a turbulent flow (44). We took advantage of the differences between the model and reality, as a result of the necessity of significant thermal heating for detection purposes, to test the robustness of the Mapless search scheme to strong deviation from the model. Furthermore, the detection process of the thermocouple was not a Poisson law, but the scheme was designed to resist this kind of mismatch. The thermal source consisted of a heater near a fan to disperse the thermal plumes. The thermal sources did not generate a thermal gradient profile, hence could not be found by a gradient climbing algorithm. Typical temporal evolution of the temperature at various distances from the source is given in SI Appendix, Fig. 11. Detections were defined as quantified events corresponding to a local variation (six or more digits, +0.25 °C) of temperature.
Fig. 4.
Two examples of experimental Mapless searches. The two chosen examples are efficient searches for display purposes. Five movies (Movies S1, S2, S3, S4, and S5) of experimental searches (including these two examples) are accessible in SI Appendix. Images are made of a mosaic of image captions from the recorded movie using an ImageJ plugin (45), leading to a semitransparent appearance of the robot positions. Contrast around the robot was enhanced locally to allow better visibility in the final composite images. This contrast enhancement appears as rectangles around the robot positions. To help visualization further, black arrows are positioned above the robot positions. (A) Mapless search without wind information (Movie S1). (B) Mapless search with wind information (Movie S5). The image is deformed as the result of changes in the camera angle that were not taken into account in the mosaic-building process. The distances can be appreciated better by viewing the movie of the search. In both A and B, a rotating fan and a heater are present. The temporal evolution of the robot-measured temperature along the path explored in A is shown in C, and the one explored in B is shown in D. In C and D, the black line is the measured temperature with 0.1-s time resolution; red dots are the detection events. Only the detections are used in the information processing. Note that the detections are discontinuous and that during long periods, there are no detections.
Five movies of search processes, three of which do not exploit wind information, are provided in SI Appendix and Movies S1, S2, S3, S4, and S5. They sample a large variety of behaviors, from very efficient searches to longer searches in which the robot had sufficient time to accumulate significant odometry errors and in which the detection pattern revealed a source very different from the one inserted in the model. However, in all situations, the Mapless searches could reach the source efficiently. The combination of the fan and the temperature of the heater led to a burst of detections that induced persistent, but limited, searches in the local environment where these bursts were detected. Interestingly, however, the searchers were not trapped by these abnormal bursts and were able to escape these local space explorations to resume the exploration part of the search. The large exploratory paths observed in simulations were not observed experimentally, mostly because of the bursts of detection themselves, which reduced the probability that the sources were far from these bursts. Furthermore, long searches confirmed that Mapless searches are resistant to odometry error. It may be seen from the long search in Movie S3, in which the accumulation of odometry errors can be seen by the progressive reorientation of the robot (it is supposed to turn 90o), that positioning errors did not prevent the source-reaching process.
Experimental searches have confirmed the efficiency of the Mapless scheme. The structure of 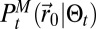 is sufficiently unspecific to catch enough of the plume dynamics to allow successful searches. Furthermore, the free energy used to decide the direction allows an efficient balance of the exploration/exploitation dynamics. Experimentally, we also varied the parameters of the model to investigate the behavior of the robot (see also SI Appendix, section C.7). Obviously, the actual duration of experimental searches prevents the accurate evaluation of average search times. However, variations of some parameters lead to directly observable effects. Reducing the temperature leads to very efficient searches for small initial distances but, for some searches, long self-trapping in local searches induced by a burst of detections (overexploitation). High temperatures were more difficult to test, as they tend to induce large exploration, which the finite size of the room prevented. Temperatures between 0.5 and 1.5 led to efficient searches. Variations of
is sufficiently unspecific to catch enough of the plume dynamics to allow successful searches. Furthermore, the free energy used to decide the direction allows an efficient balance of the exploration/exploitation dynamics. Experimentally, we also varied the parameters of the model to investigate the behavior of the robot (see also SI Appendix, section C.7). Obviously, the actual duration of experimental searches prevents the accurate evaluation of average search times. However, variations of some parameters lead to directly observable effects. Reducing the temperature leads to very efficient searches for small initial distances but, for some searches, long self-trapping in local searches induced by a burst of detections (overexploitation). High temperatures were more difficult to test, as they tend to induce large exploration, which the finite size of the room prevented. Temperatures between 0.5 and 1.5 led to efficient searches. Variations of  led to no significant change in the search times or in the characteristics of the trajectories, in good agreement with Fig. 3A. Finally, low values of
led to no significant change in the search times or in the characteristics of the trajectories, in good agreement with Fig. 3A. Finally, low values of  (short memory) led to significantly longer searches, with reexploration of the same part of space.
(short memory) led to significantly longer searches, with reexploration of the same part of space.
Discussion
We have introduced the Mapless scheme, which allows a searcher with minimal space perception, with limited access to positional cues preventing the correction of odometry errors, and evolving in complex varying environments, to perform efficient searches. The scheme is based on the combined use of a projected probability distribution of the source, whose description of the environmental dynamics is sufficiently rough to allow space computation removal but catches enough of the search dynamics to allow efficient searches, and on a greedy decision process built on the minimization, along the path, of a free energy. The scheme performs very efficiently with and without wind and was tested experimentally in a complex varying environment. The scheme also is experimentally robust to odometry errors. Hence, this model offers a framework to model animal search strategies and shows that efficient searches can be performed with minimal access to space information or cognitive maps.
Balance between exploration and exploitation of information is a key element of any search problem in which the signal-deciphering dynamics are the principal source of the dynamical decision process. Here, by controlling the internal temperature, we could shift the balance in either direction. The temperature was kept constant during the search, yet it was possible to change its value as the detection accumulated. A possible implementation of the changing temperature scheme would be to reduce the temperature when the time between detections is found to be below a user-defined threshold. The temperature reduction would shift the balance to the exploitation side. Interestingly, this specific dynamical change does not reduce the average search time significantly; rather, it leads to a faster decrease of the search time statistic tail.
The scheme that included wind information underused this information. This underexploitation was the consequence of ensuring that all searchers reached the source. Obviously, if this constraint were removed, more efficient searches would be possible for the searchers reaching the source. For example, adding a drift velocity in the opposite direction of the wind and biasing the accessible positions in the same direction may improve the search time. This raises the issue of displacement of the exploration/exploitation equilibrium when additional external information is accessible. Here, the reliability and robustness of the searches were the limiting parameters (SI Appendix, section B.14). Further reflections on this subject would benefit from reliable quantitative experimental data on the successfulness of searches in random media for different animal species.
Space-processing capacities, variability of the environments, and access to self-position of the searcher are the key problems that led to the development of Mapless as a scheme to model the search dynamics of some animals. The capacity to deal with these key problems also draws the line between the use of infotaxis and the use of Mapless. If the searcher has the capacity to build probability maps, has an accurate modeling of its environment, and can correct its odometry errors (at least partially) using external cues, then infotaxis is a good searching scheme. Conversely, a searcher with limited access to space perception, evolving either in complex varying environments or without proper modeling of its environment, and unable to reliably correct its odometry error from external cues could not use infotaxis to perform an efficient search and would be able to use Mapless as a source-reaching scheme. Infotaxis (-like) schemes likely may apply to rodents and other “higher” mammals and Mapless (-like) schemes likely may apply to insects.
To conclude, experiments are necessary to investigate animal search strategies in turbulent flow (SI Appendix, section A.4). The first set of experiments might investigate the success rate of insect searches, trajectories, and various search time statistics from various initial distances. Results may indicate whether the various schemes designed to model these strategies are compatible with the results. However, to study the direction decision process, experiments in which simultaneous recordings of animals’ trajectories with the signal they detect (e.g., ElectroAntennoGram in insects) are necessary, as the “input” signal—to borrow from engineering language—must be known. During the search process, access to the full neural pathways involved in the search seems, at the moment, technically out of reach.
Materials and Methods
Here, we briefly introduce the terms used in the computation of the scheme. More explanations are given in SI Appendix, section B.8. The normalization in Eq. 1 reads 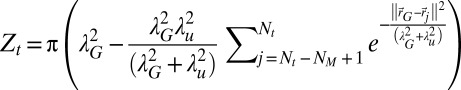 , the work energy in Eq. 2 reads
, the work energy in Eq. 2 reads 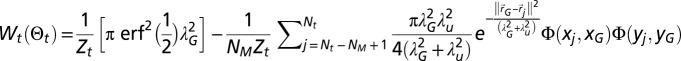 with
with  and the entropy in Eq. 2 reads
and the entropy in Eq. 2 reads  . Finally, the average hit rate reads
. Finally, the average hit rate reads 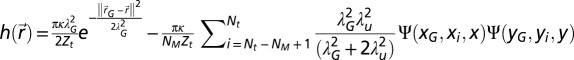 with
with 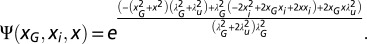
Supplementary Material
Acknowledgments
We thank Thomas Lochmatter, Philippe Lucas, Dominique Martinez, Didier Rochat, Philippe Rospars, Massimo Vergassola, and Jerome Wong-Ng for helpful discussions. We also thank the reviewers, whose remarks allowed important improvements to the paper. This work was funded by the state program “Investissements d’avenir,” managed by Agence Nationale de la Recherche (Grant ANR-10-BINF-05 “Pherotaxis”).
Footnotes
The author declares no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1221091110/-/DCSupplemental.
References
- 1.Oshanin G, Lindenberg K, Wio HS, Burlatski S. Efficient search by optimized intermittent random walks. J Phys A Math Theor. 2009;42:434008. 1–14. [Google Scholar]
- 2.Revelli JA, Rojo F, Budde CE, Wio HS. Optimal intermittent search strategies: Smelling the prey. J Phys Math A Math. Theor. 2010;43:195001. 1–11. [Google Scholar]
- 3.Edwards AM, et al. Revisiting Lévy flight search patterns of wandering albatrosses, bumblebees and deer. Nature. 2007;449(7165):1044–1048. doi: 10.1038/nature06199. [DOI] [PubMed] [Google Scholar]
- 4.Gelenbe E. Search in unknown random environments. Phys Rev E Stat Nonlin Soft Matter Phys. 2010;82(6 Pt 1):061112. doi: 10.1103/PhysRevE.82.061112. 1–8. [DOI] [PubMed] [Google Scholar]
- 5.Bénichou O, Coppey M, Moreau M, Suet PH, Voituriez R. Optimal search strategies for hidden targets. Phys Rev Lett. 2005;94(19):198101. doi: 10.1103/PhysRevLett.94.198101. [DOI] [PubMed] [Google Scholar]
- 6.Lomholt MA, Tal K, Metzler R, Klafter J. Levy strategies in intermittent search processes are advantageous. Proc Natl Acad Sci USA. 2008;105(32):11055–11059. [Google Scholar]
- 7.Sutton RS, Barto AG. Reinforcement Learning: An Introduction. Cambridge, MA: MIT Press; 1998. [Google Scholar]
- 8.MacKay D. Information Theory, Inference, and Learning Algorithms. Cambridge, UK: Cambridge Univ Press; 2003. [Google Scholar]
- 9.Vergassola M, Villermaux E, Shraiman BI. ‘Infotaxis’ as a strategy for searching without gradients. Nature. 2007;445(7126):406–409. doi: 10.1038/nature05464. [DOI] [PubMed] [Google Scholar]
- 10.Barbieri C, Cocco S, Monasson R. On the trajectories and performance of Infotaxis, an information-based greedy search algorithm. Europhys Lett. 2011;94(2):20005. [Google Scholar]
- 11.Masson J-B, Bailly-Bechet M, Vergassola M. Chasing information to search in random Environments. J Phys A Math Theor. 2009;42:434009. 1–14. [Google Scholar]
- 12.Tolman EC. Cognitive maps in rats and men. Psychol Rev. 1948;55(4):189–208. doi: 10.1037/h0061626. [DOI] [PubMed] [Google Scholar]
- 13.O’Keefe J, Nadel L. The Hippocampus as a Cognitive Map. Oxford: Clarendon; 1978. [Google Scholar]
- 14.Jefferey J. The Neurobiology of Spatial Behaviour. New York: Oxford Univ Press; 2003. [Google Scholar]
- 15.Fyhn M, Hafting T, Treves A, Moser M-B, Moser EI. Hippocampal remapping and grid realignment in entorhinal cortex. Nature. 2007;446(7132):190–194. doi: 10.1038/nature05601. [DOI] [PubMed] [Google Scholar]
- 16.Langston RF, et al. Development of the spatial representation system in the rat. Science. 2010;328(5985):1576–1580. doi: 10.1126/science.1188210. [DOI] [PubMed] [Google Scholar]
- 17.Yartsev MM, Witter MP, Ulanovsky N. Grid cells without theta oscillations in the entorhinal cortex of bats. Nature. 2011;479(7371):103–107. doi: 10.1038/nature10583. [DOI] [PubMed] [Google Scholar]
- 18.Bennett AT. Do animals have cognitive maps? J Exp Biol. 1996;199(Pt 1):219–224. doi: 10.1242/jeb.199.1.219. [DOI] [PubMed] [Google Scholar]
- 19.Wehner R. Spatial organisation of foraging behaviour in individually searching desert ants, Cataglyphys (Sahara Desert) and Ocymyrmex (Namib Desert) In: Pasteels JM, Deneubourg J-L, editors. From Individual to Collective Behaviour in Social Insects. Basel: Birkhauser; 1987. pp. 15–42. [Google Scholar]
- 20.Visscher PK, Seeley TD. Foraging strategy of honeybee colonies in a temperate deciduous forest. Ecology. 1982;63:1790–1801. [Google Scholar]
- 21.Collett M, Collett TS, Bisch S, Wehner R. Local and global vectors in desert ant navigation. Nature. 1998;394:269–272. [Google Scholar]
- 22.Lihoreau M, Chittka L, Raine NE. Travel optimization by foraging bumblebees through readjustments of traplines after discovery of new feeding locations. Am Nat. 2010;176(6):744–757. doi: 10.1086/657042. [DOI] [PubMed] [Google Scholar]
- 23.Murlis J, Elkinton JS, Carde RT. Odor plumes and how insects use them. Annu Rev Entomol. 1992;37:505–532. [Google Scholar]
- 24.Mafra-Neto A, Carde RT. Fine-scale structure of pheromone plumes modulates upwind orientation of flying moths. Nature. 1994;369:142–144. [Google Scholar]
- 25.Kennedy JS. Zigzagging and casting as a preprogrammed response to wind-borne odour: A review. Physiol Entomol. 1983;27:58–66. [Google Scholar]
- 26.Vickers NJ, Christensen TA, Baker TC, Hildebrand JG. Odour-plume dynamics influence the brain’s olfactory code. Nature. 2001;410(6827):466–470. doi: 10.1038/35068559. [DOI] [PubMed] [Google Scholar]
- 27.Vickers NJ. Mechanisms of animal navigation in odor plumes. Biol Bull. 2000;198(2):203–212. doi: 10.2307/1542524. [DOI] [PubMed] [Google Scholar]
- 28.Willis MA, Avondet JL, Zheng E. The role of vision in odor-plume tracking by walking and flying insects. J Exp Biol. 2011;214(Pt 24):4121–4132. doi: 10.1242/jeb.036954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hansson BS. Insect Olfaction. Berlin: Springer; 1999. [Google Scholar]
- 30.Payne TL, Birch MC, Kennedy MC, editors. Mechanisms in Insect Olfaction. Oxford: Clarendon; 1986. [Google Scholar]
- 31.Mizunami M, Okada R, Li Y, Strausfeld NJ. Mushroom bodies of the cockroach: activity and identities of neurons recorded in freely moving animals. J Comp Neurol. 1998;402(4):501–519. [PubMed] [Google Scholar]
- 32.Mizunami M, Weibrecht JM, Strausfeld NJ. Mushroom bodies of the cockroach: Their participation in place memory. J Comp Neurol. 1998;402(4):520–537. [PubMed] [Google Scholar]
- 33.Wehner R, Menzel R. Do insects have cognitive maps? Annu Rev Neurosci. 1990;13:403–414. doi: 10.1146/annurev.ne.13.030190.002155. [DOI] [PubMed] [Google Scholar]
- 34.Narendra A. Homing strategies of the Australian desert ant Melophorus bagoti. II. Interaction of the path integrator with visual cue information. J Exp Biol. 2007;210(Pt 10):1804–1812. doi: 10.1242/jeb.02769. [DOI] [PubMed] [Google Scholar]
- 35.Kohler M, Wehner R. Idiosyncratic route-based memories in desert ants, Melophorus bagoti: How do they interact with path-integration vectors? Neurobiol Learn Mem. 2005;83(1):1–12. doi: 10.1016/j.nlm.2004.05.011. [DOI] [PubMed] [Google Scholar]
- 36.Andel D, Wehner R. Path integration in desert ants, Cataglyphis: How to make a homing ant run away from home. Proc Biol Sci. 2004;271(1547):1485–1489. doi: 10.1098/rspb.2004.2749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Menzel R, Giurfa M. Cognitive architecture of a mini-brain: The honeybee. Trends Cogn Sci. 2001;5(2):62–71. doi: 10.1016/s1364-6613(00)01601-6. [DOI] [PubMed] [Google Scholar]
- 38.Prabhakar B, Dektar KN, Gordon DM. The regulation of ant colony foraging activity without spatial information. PLOS Comput Biol. 2012;8(8):e1002670. doi: 10.1371/journal.pcbi.1002670. 1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Wehner R, Michel B, Antonsen P. Visual navigation in insects: Coupling of egocentric and geocentric information. J Exp Biol. 1996;199:129–140. doi: 10.1242/jeb.199.1.129. [DOI] [PubMed] [Google Scholar]
- 40.Cartwright BA, Collett TS. Landmark learning in bees. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 1983;151:521–543. [Google Scholar]
- 41.Harrison JF, Fewell JH, Stiller FM, Breed MD. Effects of experience on use of orientation cues in the giant tropical ant. Anim Behav. 1989;37:869–871. [Google Scholar]
- 42.Menzel R, et al. Honey bees navigate according to a map-like spatial memory. Proc Natl Acad Sci USA. 2005;102(8):3040–3045. doi: 10.1073/pnas.0408550102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Ofstad TA, Zuker CS, Reiser MB. Visual place learning in Drosophila melanogaster. Nature. 2011;474(7350):204–207. doi: 10.1038/nature10131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Falkovich G, Gawedzki K, Vergassola M. Particles and fields in fluid turbulence. Rev Mod Phys. 2001;73:913–975. [Google Scholar]
- 45.Thévenaz P, Unser M. User-friendly semiautomated assembly of accurate image mosaics in microscopy. Microsc Res Tech. 2007;70(2):135–146. doi: 10.1002/jemt.20393. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.