Cognitive relevance of the community structure of the human brain functional coactivation network

Abstract

There is growing interest in the complex topology of human brain functional networks, often measured using resting-state functional MRI (fMRI). Here, we used a meta-analysis of the large primary literature that used fMRI or PET to measure task-related activation (>1,600 studies; 1985–2010). We estimated the similarity (Jaccard index) of the activation patterns across experimental tasks between each pair of 638 brain regions. This continuous coactivation matrix was used to build a weighted graph to characterize network topology. The coactivation network was modular, with occipital, central, and default-mode modules predominantly coactivated by specific cognitive domains (perception, action, and emotion, respectively). It also included a rich club of hub nodes, located in parietal and prefrontal cortex and often connected over long distances, which were coactivated by a diverse range of experimental tasks. Investigating the topological role of edges between a deactivated and an activated node, we found that such competitive interactions were most frequent between nodes in different modules or between an activated rich-club node and a deactivated peripheral node. Many aspects of the coactivation network were convergent with a connectivity network derived from resting state fMRI data (n = 27, healthy volunteers); although the connectivity network was more parsimoniously connected and differed in the anatomical locations of some hubs. We conclude that the community structure of human brain networks is relevant to cognitive function. Deactivations may play a role in flexible reconfiguration of the network according to cognitive demand, varying the integration between modules, and between the periphery and a central rich club.

Our understanding of human brain network organization has advanced considerably in the last decade (1). Graph theory has been increasingly used to describe the topological properties of anatomical and functional networks, typically based on estimates of structural or functional brain connectivity from MRI data (2). Several studies have confirmed that human brain networks have complex topological properties (3)—including small worldness; high-degree hub nodes; and a community structure that can be decomposed as a set of modules (4), or as a small rich club and a large periphery (5).

It remains an open question how the complex topological properties of human brain networks are related to their capacity for information processing or for adapting to changing cognitive demands. It has been shown that higher intelligence quotient is correlated with shorter topological path length of structural and functional networks, which would facilitate globally efficient, integrative processing (6, 7). Other studies have shown network changes under contrasting experimental conditions (8–10). However, the reliance on resting-state functional MRI (fMRI) as the experimental basis for most work on functional networks has limited the extent to which the topology of brain graphs has been related to cognitive tasks, or to other aspects of brain function, such as local deactivations, which are well-established findings in task-related fMRI studies (11).

Meta-analysis is a powerful way of combining data from functional neuroimaging studies that have located task-related brain activations and deactivations. For example, it has been shown meta-analytically that deactivations elicited by a wide range of tasks are frequently located in the “default-mode network” (12, 13). Meta-analyses of task-related fMRI data have also estimated the frequency with which two brain regions are consistently activated across different tasks. This provides an alternative measure of functional connectivity between regions, without describing a possible direction of the influence (unlike causal or effective connectivity) (14). Such meta-analytic measures of task-related coactivation have been explored using “seed-based” analysis (identifying which other regions are coactivated with an arbitrary region or “seed”) (15, 16) and by independent component analysis (ICA) (identifying a set of components or systems of regions that are consistently coactivated with each other) (17). Thus, it has been shown that brain coactivation components can be meta-analytically linked to specific cognitive domains (18) and that they are anatomically similar to the systems identified by ICA of resting-state fMRI data (17).

Here, we combined a meta-analysis of cognitive task-related regional coactivation with a graph theoretical analysis of the topological properties of weighted functional coactivation networks. The strength of functional coactivation was estimated by the Jaccard index (range [0,1]), a measure of similarity between the patterns of activation of two regions reported across a large number of experimental contrasts in the primary literature of 1,641 task-related fMRI or PET studies published between 1985 and 2010, and collated in the BrainMap database (19, 20). From these data, we estimated the Jaccard index between each pair of 638 regional nodes covering the whole brain, collated these pairwise association measures in a continuous association matrix, and then built a weighted graph to investigate topological and spatial network properties in relation to the various cognitive tasks studied in the primary experiments. This method also allowed us to analyze the network position or topological role of cognitively deactivated nodes. We additionally compared the results to a functional connectivity network constructed from correlations between regional fMRI times series, measured at the same 638 nodal locations as in the coactivation analysis, from 27 healthy volunteers scanned in the resting state.

Results

Global and Nodal Properties of Coactivation and Connectivity Networks.

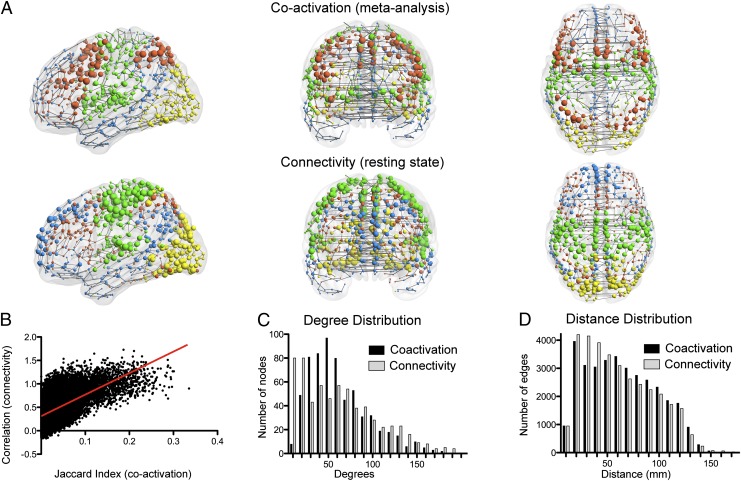
The coactivation network was topologically complex in several ways. The nodal degree distribution was fat-tailed with high-degree hub nodes located in: thalamus; putamen; insula; prefrontal, premotor, and precentral cortex; inferior parietal cortex; and ventral occipital cortex (Fig. 1 A and C). Physically, this topology was embedded parsimoniously, in terms of the connection distance between coactivated nodes (Fig. 1D). Most connections or edges were short distance (median length of 57 mm; significantly shorter than random networks; P < 10⁻³, permutation test). Relatively few edges were long distance, and these were often interhemispheric projections between bilaterally homotopic regions [14% of longest connections (defined as top 10 percentile) were homotopic; significantly more than random; P < 10⁻³, permutation test]. Although the network cost was overall low, as measured by the distance of connections, the network topology still managed to balance integration and segregation between all brain regions: the clustering of the network thresholded at sparse levels was much higher than random, while retaining a similar path length, i.e., it was small world (21) (Fig. S1).

Fig. 1.

The functional coactivation network based on meta-analysis of task-related fMRI studies has similar modularity and other properties to a functional connectivity network based on resting-state fMRI data. (A) Coactivation and connectivity networks plotted in anatomical space. The edges are defined by the minimum spanning tree for illustrative purposes. The size of the nodes is proportional to their weighted degree (strength), and their color corresponds to module membership. (B) Relationship between the coactivation metric (Jaccard index) and the connectivity metric (resting-state fMRI time series correlations) for every pair of regions. (C) Degree and (D) distance distributions of the coactivation network and a resting-state fMRI connectivity network.

In all these respects, the organization of the coactivation network was convergent with properties of a comparable functional connectivity network generated from resting-state fMRI data. As known from prior studies (22, 23), and reproduced here, resting-state fMRI networks are small world, with fat-tailed degree distributions and parsimonious distance distributions (Fig. 1 C and D, and Fig. S1).

The correspondence between coactivation and connectivity networks was confirmed more quantitatively. The measure of functional coactivation (Jaccard index) was positively correlated with the functional connectivity measure (Z-normalized Pearson’s correlation): strongly connected regions in the resting-state data tended to be strongly coactivated in the meta-analysis (r = 0.49; Fig. 1B). Both networks had fat-tailed degree distributions. The nodal degrees were significantly correlated between the two networks (Spearman’s ρ = 0.27 for degree; ρ = 0.3 for weighted degree). These results indicate that nodes that were high-degree hubs in one network tended also to be hubs in the other, although the correspondence was not perfect. There were also differences in the length of connections, with the coactivation network having more long-range edges (Fig. 1D), particularly when considering the most strongly coactivated pairs of nodes (Fig. S2).

Modularity of Coactivation and Connectivity Networks.

By a classical Newman decomposition (24), the coactivation network was found to be modular (Q = 0.47). It comprised four large modules, labeled anatomically: occipital, central (including sensorimotor areas), frontoparietal, and default mode (including medial frontal cortex, precuneus and posterior cingulate cortex, lateral parietal and temporal cortex, amygdala, and hippocampus) (25). The connectivity network derived from resting-state data were also modular (Q = 0.49), with four modules that approximated anatomically to the modules of the coactivation network (Fig. 1A and Fig. S3). The correspondence between coactivation and connectivity network modular decompositions was high, with a Rand index of 0.78 (significantly greater than the correspondence between modules of the connectivity network and randomly reassigned modules of the coactivation network; P < 10⁻⁴, permutation test).

For the coactivation network, it was possible to assign functional as well as anatomical labels to the modules. To do this, we considered the five high-level behavioral domains used by the BrainMap database to describe each contrast in the primary literature (26): action, cognition, emotion, perception, and interoception. We then labeled each edge according to the domain most frequently causing coactivation of the corresponding pair of regions (Fig. S4). In the occipital module, the highest proportion of intramodular edges corresponded to coactivation by perception (39%) and the other domains coactivated less than 20% each; similarly, in the default-mode module, 37% of edges were coactivated by emotion and the other domains each accounted for less than 21%; whereas, in the central module, 62% of intramodular edges were coactivated by action. Thus, it seems reasonable to say that the central module is relatively specialized for action, the occipital module for perception, and the default-mode module for emotion. Action and cognition tasks accounted for approximately the same proportion of intramodular edges in the frontoparietal module (34% and 38%, respectively), and therefore we described it as specialized for executive functions.

Rich Clubs of Coactivation and Connectivity Networks.

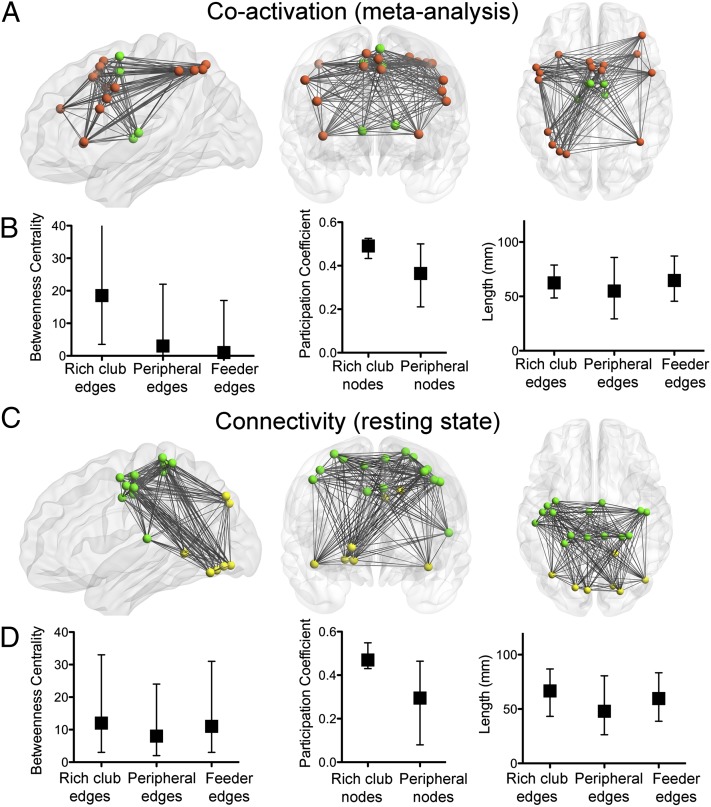
Rich-club analysis provides another perspective on the community structure of complex networks, describing networks that have an elite minority of highly interconnected hub nodes (the rich club) and a majority of less well-connected nodes (the poor periphery). The coactivation network had a rich club (Fig. S5A), comprising 21 nodes located topologically in frontoparietal and central modules; or anatomically in prefrontal, premotor, precentral, and inferior parietal cortex, thalamus, and insula (Figs. 2A and 3A). The connections between rich-club nodes had significantly greater betweenness centrality than the connections between other nodes (P < 10⁻⁴, permutation tests; Fig. 2B). In other words, more of the shortest paths between any pair of nodes passed through a connection between two rich-club nodes than through a feeder connection (between a peripheral node and a rich-club node) or a peripheral connection (between two peripheral nodes). Rich-club nodes were also important in mediating connections between modules, as indicated by their higher mean participation coefficient compared with the periphery (P < 0.008, permutation test). This central component of the network was costly for the system: the connections between rich-club regions, and the “feeder” connections between a peripheral and a rich-club node, were longer distance than the connections between peripheral nodes (P < 0.005, permutation tests).

Fig. 2.

The rich club of the functional coactivation network and of the functional connectivity network. (A and C) Anatomical location of rich-club nodes and connections for the (A) coactivation and (C) connectivity networks. Color of nodes corresponds to their module as in Fig. 1. Note that, in both networks, the rich club formed one connected component. (B and D) Betweenness centrality of edges, participation coefficient of nodes, and connection distance of edges defined according to their relationship to the rich club in (B) the coactivation and (D) the connectivity network. In both networks, the rich club is highly central, important for intermodular connections, and the edges connecting rich-club nodes to each other or to peripheral nodes are longer distance than the edges between peripheral (nonrich) nodes. Median and interquartile range are shown.

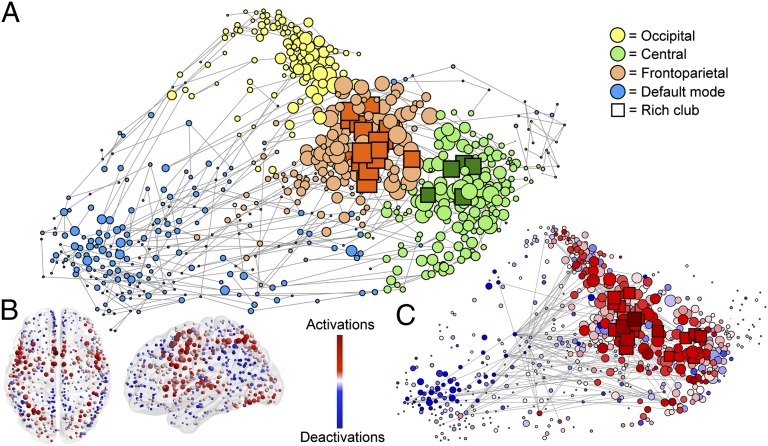
Fig. 3.

Topological representation of the functional coactivation network. (A) Force-based layout of the minimum spanning tree is used to locate nodes in relation to their topological (rather than anatomical) proximity to each other. Different modules are coded by color, and rich-club nodes are represented by squares, with the size of all nodes proportional to their weighted degree (strength). (B) Nodes in anatomical space, colored according to proportion of times they present activations and deactivations. (C) Nodes arranged in the same layout as A, and colored as in B (see Movie S1 for a dynamic perspective on this). Note that the rich club concentrates most of the activations, whereas the periphery and particularly the default-mode network concentrates the deactivations. Edges represent the top 1 percentile of most consistently reported activation and deactivations (no directions shown for clarity purposes). Edges can be seen spanning across different modules.

Likewise, the functional connectivity network derived from resting-state fMRI had a rich-club configuration (Fig. S5B). We first defined the rich club as the subset of the top 21 most highly connected nodes in the functional connectivity network. This size of club was chosen to facilitate comparison with the 21-node rich club of the coactivation network; for completeness, we also explored the rich-club organization of a larger subset of nodes in the fMRI connectivity network, but this did not substantively affect the results (SI Results and Fig. S6). The rich club (n = 21) was located in the central and occipital modules (Fig. 2C). Their edges also occupied a central position in the network (edge betweenness centrality greater than peripheral connections; P < 10⁻³, permutation test; Fig. 2D); they were also important for intermodular connections (higher participation coefficient in rich-club nodes than peripheral; P < 10⁻⁴, permutation test), and they were more costly in the sense that the connection distance between rich-club nodes, and the distance of feeder connections, was greater than the distance of peripheral connections (both P < 10⁻⁴, permutation tests).

For the coactivation network, we investigated the functional role of the rich club by analyzing the task-related contrasts that had generated edges between rich-club nodes. Rich-club nodes were most frequently coactivated by action (59%) or cognition tasks (30%), much less frequently by the other domains (Fig. S7A). It was also notable that the edges between rich-club nodes represented coactivation of pairs of regions by a more diverse range of task-related contrasts, whereas feeder or peripheral edges typically represented coactivations by experimental contrasts from a more restricted range of similar behavioral domains. The cognitive diversity of coactivation was quantified in the range [0,1], such that edges coactivated by only one behavioral domain scored 0 and edges diversely coactivated with equal frequency by all domains scored 1. We found that diversity was higher for rich-club connections (0.74) than for feeder (0.72) or peripheral connections (0.7; P < 10⁻³ for both comparisons, permutation tests; Fig. S7B).

The Topological Role of Deactivations.

We first looked at the role of deactivations (defined as fMRI signal greater during rest than during a task condition) by examining where they appeared in the coactivation network. In line with prior meta-analyses (12, 13), deactivations were most often located in nodes of the default-mode module (Fig. 3B).

Although coactivation of two regions indicates that they act “cooperatively” to perform a task, concomitant activation and deactivation of two regions could be described as a “competitive” interaction. To explore further the role of deactivations, we examined their relationship to those regions activated by the same task, and mapped these “competitive” activation/deactivation pairs to the coactivation network. Competitive interactions were significantly more likely to appear between nodes in different modules than nodes in the same module (odds ratio of 2.02; P < 0.001, permutation test). They were also much more likely to mediate a connection between an activated rich-club node and a deactivated peripheral node, than they were to mediate a connection between two peripheral or two rich-club nodes, or an activated peripheral node and a deactivated rich-club node (odds ratios of 4.4, 5.2, and 9.8, respectively; all P < 0.01, permutation tests, Bonferroni corrected; Fig. 3C).

Robustness Analysis.

We considered the effects of various possible confounding or methodological factors on these results (SI Materials and Methods). Main findings were robust to variation in the brain template used, assumptions when modeling activations from peak coordinates, and to controlling the estimation of coactivation for possible biases due to the uneven number of primary studies across behavioral domains (Table S1).

Discussion

This analysis of the human brain functional coactivation network revealed a community structure that was similar (but not identical) to that of the functional connectivity network derived from resting-state fMRI. Moreover, the meta-analytic network provided insight into the cognitive specialization (or generalization) of the modules and the rich club of human brain functional networks, as well as suggesting a network role for cognitive deactivations.

Relatively specialist roles in cognitive processing could be assigned to most modules. The occipital module was mostly coactivated by tasks involving perception, the central module by action, the default-mode module by emotion, and the frontoparietal module by executive tasks demanding action or cognition. These results are broadly in agreement with those obtained by previous studies using ICA (17, 18). For example, each of the four modules defined by our analysis corresponds closely to one or more of the 10 independent components reported by Smith et al. (17) on a nearly identical sample of the BrainMap database (Fig. S8). (The methodological and substantive commonalities and differences between ICA and graph analysis of the functional coactivation and connectivity networks are detailed more extensively in SI Discussion.) Thus, the modularity results are not surprising discoveries, but they provide support for the cognitive relevance of the graphical analysis of the coactivation network and, by extension, of the fMRI connectivity network.

The use of graph analysis also provided us with opportunities to go beyond the description of these basic building blocks of the functional brain network as explored with modularity analysis or ICA. For example, in addition to the highly segregated modules, we discovered the existence of a rich club that represented a key integrative element of both coactivation and connectivity networks [as has been suggested previously by analysis of anatomical networks (5, 27, 28)]. We were also able to demonstrate that local activation or deactivation of brain regions in response to task/rest contrasts could be related to the topology of the networks, with many competitive edges linking an activated node of the rich club to a deactivated node in the periphery. In short, the community structure of human brain functional networks can be rendered as a set of functionally specialized and topologically peripheral modules ranged around a functionally generalized and topologically central rich club (Fig. 3A).

Because topological modules in brain networks are often anatomically colocalized, i.e., topologically neighboring nodes tend to be anatomical neighbors, this result is consistent with theoretical expectations that specialized functions should be concentrated in anatomical space (29). It is also consistent with a prediction of workspace theory (30), and prior meta-analytic results (31), that integrative and general intelligence functions depend on efficient communication between a large number of anatomically dispersed processing nodes. The rich club has a cognitively valuable (executive) role, but it is also costly as demonstrated by the longer distance connections between rich-club nodes, and between rich and peripheral nodes, than between a pair of peripheral nodes. This combination of high functional capacity and high cost echoes analogous results on the rich club of the human brain anatomical network measured using diffusion tensor imaging (32) and on the rich club of the nervous system of the nematode worm Caenorhabditis elegans described at a cellular level by electron microscopy (33).

However, it is important in considering these results not to rigidify the decomposition of human brain functional networks unduly. The possible configurations of a brain functional network will dynamically change over time, either in response to changing external contingencies or endogenously (34, 35). Some aspects of such processes of functional network reconfiguration can be inferred from these data.

When a task is presented experimentally in contrast to rest in fMRI studies, the signal increases in some brain regions (activations) while it decreases in others (deactivations). Here, we found that activations were likely to appear in a rich-club node, whereas the accompanying deactivation appeared in a peripheral node, and that activation and deactivations often occurred in different modules. There are various possible interpretations of this observation. Rich-club activation could switch off certain peripheral modules under certain task conditions, or an active module could suppress activity in an inactive one (36, 37). Alternatively, there may be a finite resource for coactivation, such that all modules cannot be coactivated simultaneously; central coactivation resource is therefore distributed economically by competition between modules (38). Our data cannot resolve the choice between these and other possible models for the topological role of deactivations. However, the economical model has the advantage that it does not assume the rich club has a homunculus-like agency to direct activity elsewhere in the network.

A related aspect of functional network reconfiguration was revealed by a comparison of the meta-analytic network (derived from measurements under some experimentally controlled condition of cognitive demand) and the resting-state network (derived from measurements while people lie idly in the scanner). Although the two networks were topologically similar in many ways, there were also some differences. For example, although high-degree nodes in one network tended to be also hubs in the other network, this correspondence in the anatomical location of hubs was not perfect. Hubs of the resting-state connectivity network were located in occipital and central modules, arguably as expected from the observation of synchronized EEG oscillations in occipital and central recordings at rest, whereas frontoparietal nodes particularly appeared more prominent in the coactivation network, i.e., during cognitive effort. It was also notable that although both networks had a rich club, the anatomical locations of the rich-club nodes did not overlap between the two networks. We hypothesize that the anatomical locations of high-degree hubs (and rich clubs) can change dynamically in parallel to changes in type and levels of cognitive processing, whereas the global network topological properties of the brain functional network are relatively conserved under different cognitive conditions (39). During cognitive effort, nodes such as those classically described as part of attention networks become highly connected, whereas nodes that are more highly connected during rest, such as regions of the default-mode network, become less hub-like under conditions of cognitive stress. There were spatial as well as topological differences between the networks. The coactivation network had more long-range connections. This is also compatible with an economical interpretation: integrative network features, such as long-range connections, incur a premium in terms of connection cost, emerging only under conditions where they can add value behaviorally in response to a cognitively challenging environment (10, 40).

Materials and Methods

Network Construction.

To build weighted functional networks from meta-analytic data on task-related activation, we used bipartite graphs. These comprise two disjoint sets of nodes, which can model interactions between nodes on one level that are determined by their individual interactions with nodes on another level [for example, actors and the films they have starred in (41)]. Here, we defined the coactivations between brain regions (level 1) in relation to the cognitive tasks or contrasts (level 2) deployed experimentally in the primary literature. All functional metadata were extracted from the BrainMap database [brainmap.org (19, 20, 26)]. We included 6,884 task-related contrasts from 1,641 nonpharmacological neuroimaging studies including more than five healthy adult subjects, irrespective of the tasks. Each activation from each contrast was modeled as a 1-cm³ sphere centered around its reported coordinates (15) in a standard stereotactic space (42, 43). We subdivided or parcellated the gray matter of the brain (excluding the cerebellum) into 638 similarly sized regions that respected anatomical landmarks (44, 45). For the purposes of building the bipartite graph, the activation loci reported for each contrast were linked to brain regions if 20% or more of the modeled activation sphere overlapped with the regional volume defined by the parcellation template. Main results were unchanged when using only the locus of the peak activation rather than modeling it as a sphere (Table S1). The bipartite graph relating cognitive contrasts to brain regions was then transposed to a one-mode graph where regions were linked to each other if they were frequently coactivated. We used the Jaccard index as the metric of coactivation strength, defined for each pair of regions as the number of contrasts activating both regions X and Y divided by the union of contrasts activating region X and activating region Y. We therefore focused on the frequency of coactivation of each pair of regions, accounting for the combined frequencies of activation of each region independently. This metric was chosen to control the frequency of coactivation for the variable frequency of activations in certain brain regions elicited by popular behavioral tasks in the primary literature. Further controls for a possible publication bias in the primary reporting of the activation data are described in Table S1 (balancing the number of contrasts in each of the five behavioral domains) and Fig. S9 [demonstrating that rich-club nodes are not selectively reported in high-impact factor journals (46)]. The coactivation matrix was probabilistically thresholded (15) such that if the Jaccard index between a pair of regions was not significantly greater than expected under the null hypothesis, then no edge was drawn between the corresponding nodes of the coactivation network; whereas if it was significantly greater, then an edge was drawn between the corresponding nodes and weighted by the Jaccard index (SI Materials and Methods). Setting the probabilistic threshold at P < 0.01 false discovery rate corrected, resulted in a sparse graph with a connection density of 9.2% and at least one edge connecting each node to the rest of the network. Further details on graph construction are provided in SI Materials and Methods, Fig. S10A, and a schematic summary in Movie S2. Several topological and spatial metrics were calculated for the coactivation network, detailed in SI Materials and Methods. Measures on the coactivation network were compared with the same measures estimated on random graphs matched for number of nodes, connection density, degree and weight distributions (47), and on graphs constructed from random permutations of the BrainMap database (48) (SI Materials and Methods and Fig. S11).

Characterizing Links of the Network According to Behavioral Domains.

For each edge of the coactivation network, we counted the number of contrasts in each of five major behavioral domains (action, cognition, emotion, perception, and interoception) that reported coactivation of the corresponding pair of regions. The frequency of coactivation by each domain was normalized by the total number of contrasts reported in each domain, to mitigate possible bias due to the uneven number of contrasts reported across different domains in the primary literature. Each edge was categorized functionally by the behavioral domain that was most frequently reported to cause coactivation of the corresponding pair of nodes. We also estimated the diversity of contrasts coactivating a pair of regions (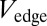), where values near zero mean that the edge is only coactivated by contrasts in one domain, whereas values near 1 describe edges that are coactivated by contrasts in several domains (SI Materials and Methods).

Defining Competitive Edges of the Network.

We identified a subset of 110 contrasts from 67 studies that used rest or fixation as task control, and that reported both activations (task > rest) and deactivations (rest > task) for the same contrast. Each pair of regions activated and deactivated by a contrast in the primary literature was linked by a competitive edge and the topological and functional roles of the competitive edges were defined in relation to the topology of the corresponding nodes in the coactivation network (SI Materials and Methods and Fig. S10B).

fMRI Data Acquisition and Analysis.

fMRI data were acquired from 27 healthy volunteers (mean age, 24 y) using a 3T Siemens Tim Trio system while they lay quietly at rest in the scanner with eyes closed. Gradient-echo echo-planar imaging data sensitive to blood oxygenation level-dependent contrast were recorded for 5 min, 6 s with the following parameters: relaxation time of 2 s; echo times, 13 and 31 ms; flip angle, 80°; voxel size, 3.5 × 3.5 × 3 mm; in-plane field of view, 22.5 cm; 36 interleaved slices. Images were slice-time corrected, realigned, and normalized. Regional mean time series were estimated for each of 638 gray matter regions, corrected by regression for head movement parameters (rotations and translations in three dimensions and their first derivatives) and the mean ventricular cerebrospinal fluid time series, and bandpassed (0.01–0.1Hz). There was no evidence for residual effects of head movement on these corrected regional mean time series (49) (SI Materials and Methods and Fig. S12). Pearson’s correlations between each pair of time series in each individual were estimated, and normalized by the Fisher transform before averaging over individuals to estimate the group mean functional connectivity matrix. We then used a global thresholding rule to build a weighted network of the same connection density as the coactivation network.

Data Availability.

The functional coactivation matrix, the group functional connectivity matrix, and the stereotactically coordinated template used for brain parcellation, are all freely available for download from the Brain Connectivity Toolbox (50).