Instructional Review: An Introduction to Optical Methods for Characterizing Liquid Crystals at Interfaces

Abstract

This Instructional Review describes methods and underlying principles that can be used to characterize both the orientations assumed spontaneously by liquid crystals (LCs) at interfaces and the strength with which the LCs are held in those orientations (so-called anchoring energies). The application of these methods to several different classes of LC interfaces is described, including solid and aqueous interfaces as well as planar and non-planar interfaces (such as those that define a LC-in-water emulsion droplet). These methods, which enable fundamental studies of the ordering of LCs at polymeric, chemically-functionalized and biomolecular interfaces, are described in this article at a level that can be easily understood by a non-expert reader such as an undergraduate or graduate student. We focus on optical methods because they are based on instrumentation that is found widely in research and teaching laboratories.

1. Introduction

Measurements of the orientational ordering of liquid crystals (LCs) near interfaces enable fundamental studies of biological materials (e.g., lipid droplets found in certain types of mammalian cells),^{1, 2} the design of electro-optical devices (such as liquid crystal displays),³ strategies for the hierarchical design of nano-scale materials (e.g., semiconducting nanorods),^{4, 5} and the creation of LC-based materials that respond to specific chemical and biological cues.^6–8 The intent of this Instructional Review is not to dig deeply into fundamental questions specific to any one of these contexts, but rather, this article seeks to enable new researchers to study interfacial phenomena involving LCs by providing instruction in key experimental methods. We focus, in particular, on the use of optical methods as these are accessible in many research and teaching laboratories and they can provide broadly useful information on both the average orientations of LCs and the strengths with which LCs are held in preferred orientations at interfaces. In this review, we also avoid providing extensive details regarding the preparation of experimental systems as they tend to be specific to a particular line of investigation and are described elsewhere.^6–26

2. Organization of this review

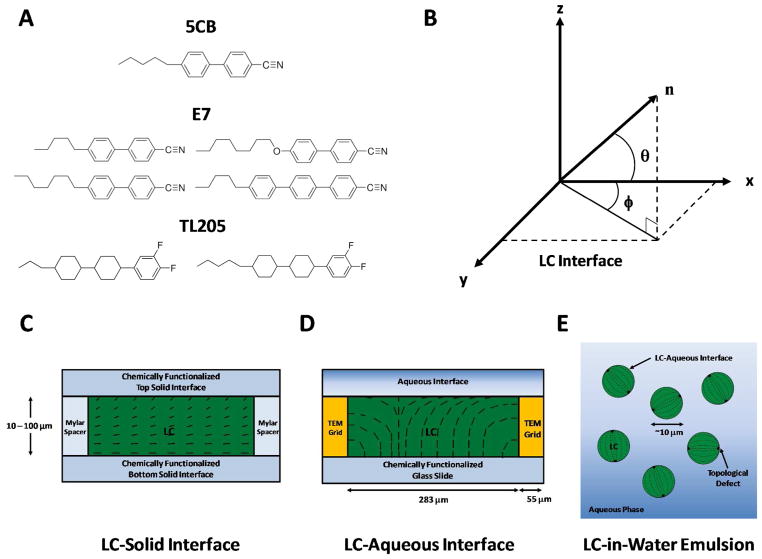
This review covers three classes of LC interfaces (where the LCs are formed from molecules such as those shown in Figure 1A). We briefly describe these LC interfaces below and refer back to them in subsequent sections of this review.

Figure 1.

(A) Molecular structures of three common mesogens that form room-temperature nematic LC phases: 4-cyano-4′-pentylbiphenyl (5CB), E7 and TL205. Physical properties of these LCs are shown in Table S1 of the SI. (B) Definition of angles used to characterize the average orientation of a LC (director, n) near a flat interface. The azimuthal orientation is characterized by the azimuthal angle (φ) and the zenithal orientation is characterized by the zenithal angle (θ). (C–E) Schematic illustrations of three classes of LC interfaces that are discussed in this review. (C) LC-solid interface: LC is sandwiched between two chemically functionalized solid surfaces, each of which anchoring the LC in a preferred orientation. (D) LC-aqueous interface: LC is hosted within the pores of a grid supported on a chemically functionalized glass-slide and submerged under an aqueous solution to create a stable LC-aqueous interface. (E) LC-in-water emulsion: LC droplets are dispersed in an aqueous phase. Dashed lines indicate the director of the LC. Modified and reproduced with permission.¹⁷

The first class of LC interfaces is formed between a LC and solid (Figure 1C). This is the most widely explored class of LC interfaces because of its use in electro-optical devices (the planar solid surface typically comprises an electrode that is used to switch the orientation of the LC). Materials that are commonly used to prepare such solid interfaces include polymers (e.g., sheared mechanically to align the polymer such that it serves as a molecular template that directs the orientation of the LC)^{27, 28} and inorganic compounds prepared by physical vapor deposition (such as silicon oxide or gold).^{29, 30} In the case of gold, the surface can be chemically functionalized using organosulfur compounds to generate a wide-range of intermolecular interactions between the LC and the solid interface.^{14, 23, 24, 31, 32} This latter system is particularly versatile and suitable for fundamental studies of the ordering of LCs at solid surfaces. At solid surfaces, the preferred orientation of the LC (easy axis) is defined by an azimuthal angle and a zenithal angle (Figure 1B). Typically, the azimuthal angle, φ, is defined with respect to a symmetry axis within the solid surface (e.g., the direction of deposition of an inorganic layer deposited by physical vapor deposition at an oblique angle of incidence). The zenithal angle, θ, is reported with respect to the surface normal.

We note that a common occurrence in an experiment involving a film of LC confined between two solid surfaces is that the easy axes of the LC differ at the two surfaces. In this situation (often referred to as a “hybrid” LC system), the orientation of the LC between the two surfaces is determined by minimization of the anchoring and elastic energies of the film of LC (Figure 1C). The strains experienced by a LC include splay, bend and twist, and an elastic constant (K) for each mode of deformation connects the strain to the free energy density (see Equation 2 and associated text below for additional detail).^{3, 33, 34} In this situation, it is common to consider a so-called “extrapolation length”, defined as L ~ K/W for the case of planar films, where W is the orientation-dependent surface energy or “anchoring energy” per unit area.³⁴ In a planar film of LC, the extent to which the LC departs from the orientation of the easy axis depends on the ratio of the extrapolation length to the thickness of the LC film (d). For sufficiently thick films (L/d ≪ 1), the orientation of the LC near an interface is close to the easy axis. Unless indicated otherwise, the planar films of LC discussed in this review satisfy this criterion.

The second class of planar interfaces involving LCs that can be characterized using the methods described in this review are those formed between LCs and aqueous phases.⁷ As depicted in Figure 1D, stabilization of this type of LC interface has to date been commonly achieved by using capillary forces generated by placement of a grid onto a solid surface.¹⁰ Within the pores of the grid, which have a width (typically ~ 300 μm) much larger than the thickness of the LC film (5 – 50 μm), an approximately planar interface can be formed between the LC and the aqueous phase. Particular experimental protocols must be followed, however, to obtain an approximately planar interface. For example, if an excess of LC is deposited within the pores of the grid, the resulting LC interface will be curved (meniscus), which will impact optical characterization of the interface (see below). Similar to the case of a LC-solid interface, the orientation of the LC at the aqueous interface is defined by azimuthal and zenithal angles (see above).

Finally, we comment that this review also addresses the characterization of LC droplets (Figure 1E), including LC droplets dispersed in an aqueous phase. This spherical geometry has particular relevance to the development of stimuli-responsive LC materials, as confinement can lead to configurations of LC within the droplet that reflect a delicate balance of interfacial and elastic contributions to the free energy. One additional common feature of the droplet geometry is the formation of so-called topological defects in the LC. In brief, when LCs are confined within the approximately spherical volume of a droplet, in many instances, it is not possible for the LC to satisfy the anchoring conditions at the droplet interface through continuous strain of the LC (such as by some combination of twist, splay and bend). In these situations, localized regions of the LC partially “melt” (i.e., exhibit low levels of orientational order relative to the bulk LC) to generate defects in the LC. The “cores” of the defects, although nanoscopic in size, possess refractive indices that differ substantially from the surrounding LC and thus can be characterized using optical methods. Common defects encountered in the droplet geometry include “point defects” and “line defects”, where the latter are frequently referred to as “disclination lines”. Additional discussion regarding defects in LCs can be found later in this Instructional Review.

The remainder of this Instructional Review is organized into four sections. First, we briefly outline procedures that can be used to prepare of each of the three classes of experimental systems mentioned above. For details, we refer the reader to past publications.^6–26 Second, we describe the use of polarized light microscopy to provide qualitative information regarding the orientations of LCs near interfaces. Third, we report optical methods that permit quantitation of optical properties of LCs that in turn provide quantitative measurement of, for example, the zenithal angle assumed by a LC at an interface. Fourth, we describe methods that permit measurement of the anchoring energies of LCs. Finally, we briefly describe some unresolved challenges related to the preparation and characterization of LC interfaces. In each of these sections, we address characterization of the three classes of experimental systems shown in Figure 1C–E.

3. Preparation of experimental systems

3.1. LC-solid interfaces

To study the orientation of a LC at a solid surface, it is common to form an optical cell within which the LC is confined between two solid surfaces (as shown in Figure 1C). Preparation of the system typically begins by placement of thin sheets of a polymer film, often Mylar, of known thickness along two edges of the bottom solid surface. Next, the top surface is inverted, aligned with the bottom surface, and placed on the spacers in a manner such that a cavity is defined between the two surfaces of interest. The edges that have the spacers are then clipped together (we use “bulldog” or “binder” clips); alternatively, the cell can be sealed and held together using epoxy after the introduction of the LC. Next, both the LC in a glass syringe and the sample cell are heated above the isotropic transition temperature of the LC, which can be achieved, for example, by placement of the sample on a hot plate. The LC is then introduced into the cell by capillary action. We note that it is generally preferred to introduce the LC into an optical cell after heating it above the clearing temperature to avoid flow-induced alignment and “surface-memory” effects that occur if the material is introduced in the LC phase. If using labile organic interfaces (e.g., self-assembled monolayers formed on gold films), however, one also has to be careful that the heating of the system does not cause thermal degradation. Finally, the sample is moved to an optical microscope for characterization.

3.2. LC-aqueous interfaces

The preparation of an interface between an aqueous phase and LC can be achieved by first adding a small amount (~0.2 μL) of a nematic LC into the pores of a copper or gold-coated transmission electron microscopy (TEM) grid supported on a glass substrate.¹⁰ The glass substrate is usually chemically functionalized to induce a preferential zenithal orientation of the contacting LC. Common treatments of the glass employ the silanes, octadecyltrichlorosilane (OTS) or dimethyloctadecyl[3-(trimethoxysilyl)propyl]ammonium chloride (DMOAP), both of which cause perpendicular (homeotropic) anchoring of most nematic LCs.^{7, 10, 35} As mentioned above, the grids are used to generate capillary forces that lead to the formation of stable LC-aqueous interfaces. A typical grid used in such an experiment will have a lateral pore size of ~ 300 μm and a thickness ranging from 5 μm to 50 μm. Prior to use, the grids should be rinsed sequentially with ethanol, methanol and chloroform and dried overnight in an oven. After placing a grid onto the glass substrate, it is filled with LC to form a film with approximately the same thickness as the grid. Excess LC (which will create a curved interface) can be removed from the grid by touching the LC with an empty capillary tube. The LC-filled grid is then held at a slight angle from the horizontal and immersed into an aqueous solution to form the interface between the LC and the aqueous solution. As noted above, curved LC-aqueous interfaces will be generated if the grid is significantly over-filled or under-filled with LC. These situations are easily recognized by rings of interference colors that are observed upon imaging of the sample between crossed polarizers using white light (described below). Finally, we note that the gold- and copper-coated surfaces of the TEM grids cause a homeotropic orientation of the LCs. However, the extent of this alignment (~10 μm) is small compared to the lateral size of the grid pores typically used in these experiments (~ 300 μm).

3.3. LC-in-water emulsions

The simplest method for preparing a LC-in-water emulsion involves the use of sonication and vortex mixing to disperse LC added to a bulk aqueous phase (i.e., 2 μL of LC in 1 mL of water).^{21, 25} When using conditions detailed in our past publication, this simple procedure results in a polydisperse population of LC droplets with diameters ranging from 1 to 20 μm.²⁵ A measurement of turbidity (using a UV-Vis spectrophotometer) is a useful way to assess the end point of the sonication because, for a given volume of LC added to the bulk aqueous phase, emulsions with similar turbidities will possess similar size distributions of LC droplets. If precise control over the size of the LC droplets in the LC-in-water emulsion is desired, one of several alternative methods of preparation can be employed. For example, monodispersed LC-in-water emulsions have been prepared by using polyelectrolyte multilayer capsules as templates²⁶ or by using microfluidics.¹⁹ Finally, for optical characterization of a LC-in-water emulsion, a small volume of the emulsion (several μL is usually sufficient) can be dispersed onto a supporting substrate (e.g., a glass microscope slide) and the sample placed onto the stage of a microscope. We note that glycerol is often added to the aqueous phase of LC-in-water emulsions in order to increase the viscosity of the aqueous phase and thereby slow the diffusion of the LC droplets (for ease of observation by microscopy).

4. Qualitative optical characterization of LCs at interfaces

Most LCs possess anisotropic optical properties, and thus many methods used to characterize the orientations of LCs revolve around the interaction of polarized light with the LCs. As detailed below, measurements of the polarization of light transmitted through LCs are commonly performed by placing a polarizer before and after a LC sample in the optical path of a microscope (Figure 2). To enable a discussion of polarized light microscopy, below we briefly describe how polarized light interacts with (uniaxial) LCs.

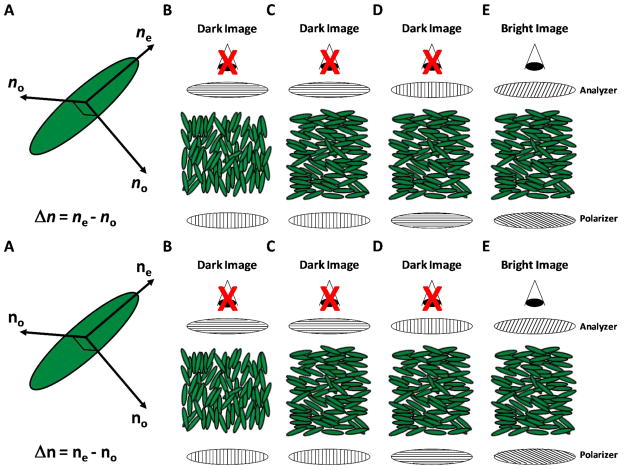
Figure 2.

Polarized light microscopy of nematic LCs using orthoscopic illumination. (A) Schematic illustration of the index ellipsoid of a uniaxial nematic LC. Two distinct refractive indices are evident - a refractive index parallel to the nematic director (n_e) and a refractive index perpendicular to the director (n_o). The difference between these refractive indices is known as birefringence (Δn = n_e−n_o). (B–D) Examples of orientations of LCs that, when viewed between crossed polarizers, exhibit a dark optical appearance. In B, the director of the LC is oriented parallel to the direction of propagation of the light through the LC. In C and D, the director of the LC is oriented in the plane of the sample with an azimuthal alignment that is either perpendicular (C) or parallel (D) to the incident polarizer. (E) When the director of the LC is oriented in the plane of the sample but with an azimuthal orientation that lies between the polarizer and analyzer, the light transmitted through the LC gains an elliptical polarization leading. This leads to a bright optical appearance of the LC.

Polarized light propagating through a LC in a uniaxial nematic phase can experience two distinct refractive indices depending on the polarization of the light relative to the director of the LC (the direction the molecules tend of the LC to align on average) – a refractive index parallel to the nematic director (n_e, extraordinary refractive index) and a refractive index perpendicular to the director (n_o, ordinary refractive index) (Figure 2A).³³ The difference between these direction-dependent refractive indices is known as birefringence (Δ n = n_e − n_o), and leads to two possible scenarios when a nematic LC is placed between a polarizer and an analyzer (oriented 90° with respect to the polarizer; crossed polarizers) and viewed in transmission mode using white light (Figure 2B–E). First, if the LC is oriented perpendicular to the bottom surface of the sample (Figure 2B), or if the azimuthal orientation of the LC is either 90° (Figure 2C) or 0° (Figure 2D) relative to the plane of polarization of the light passing through the bottom polarizer, the light propagating through the LC will experience only one index of refraction (n_e or n_o), and the polarization of the light passing through the LC will remain unchanged. Thus, upon exiting the LC, light will not pass through the crossed analyzer, resulting in a dark optical appearance of the material (Figures 2B–D). Second, if the azimuthal orientation of the LC is neither parallel nor perpendicular to the bottom polarizer (Figure 2E), the light propagating through the LC will experience two indices of refraction and split into so-called ordinary and extraordinary rays with electric field vectors vibrating in different planes. The different refractive indices experienced by the two rays causes them to travel at different velocities, inducing a phase shift. In general, the rays are phase shifted such that the light emerges from the LC with an elliptical polarization. Thus, some light will pass through the analyzer, resulting in a bright optical appearance of the LC (Figure 2E). As will be discussed in detail below, the specific orientations of the LCs in the second scenario can give rise to a range of optical appearances of the LC samples.

4.1. Orthoscopic polarized light microscopy of LCs

4.1.1. Orthoscopic polarized light microscopy of planar films of LC

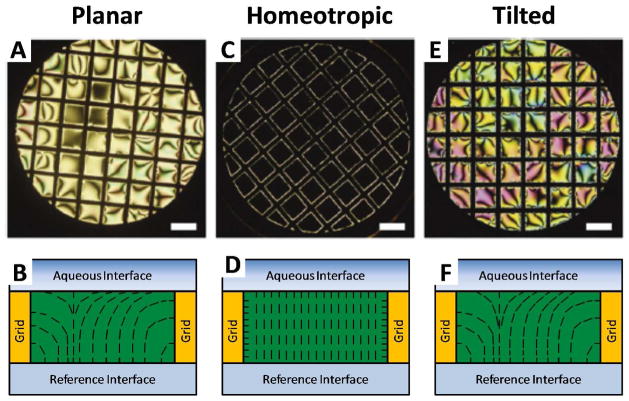
An important consequence of the above-described birefringence of nematic LCs is that orthoscopic polarized light microscopy can be employed to characterize the orientational ordering of nematic LCs at interfaces.^{6, 7} This technique probes a LC sample with a beam of near-parallel rays of polarized light. To illustrate its utility in characterizing the orientational ordering of nematic LCs at interfaces, we focus on a system in which a thin planar film (slab geometry) of LC, tens of micrometers in thickness, is confined between a solid substrate and an aqueous phase (Figure 3). At the LC-aqueous interface, the zenithal orientation of the LC can be either homeotropic (perpendicular to the interface), planar (parallel to the interface), or tilted (at an acute angle to the interface). The bottom interface in Figure 3 is a reference interface, where the zenithal orientation of the LC is homeotropic (caused by treatment of a glass surface with a silane – see above). Each of the three zenithal orientations of the LC at the top interface will lead to distinct optical appearances of the LC film when viewed using polarized light microscopy. Below, we describe the optical appearance of the film for each of these zenithal orientations. We also comment that this discussion, while presented in the context of LC-aqueous interfaces, applies also to analysis of LCs between two solid surfaces.

Figure 3.

Polarized light micrographs (orthoscopic illumination) of micrometer-thick films of nematic 5CB anchored in three distinct orientations at LC-aqueous interfaces. Optical images (crossed polarizers; A, C and E) and schematic illustrations of the director profiles (B, D and F) are shown. A and B correspond to planar anchoring, C and D correspond to homeotropic anchoring, and E and F correspond to tilted anchoring of the LC at the LC-aqueous interface. Scale bars are 300 μm. Reproduced with permission.⁷

When the zenithal orientation of the LC is parallel at the aqueous interface (so-called planar anchoring), the LC confined in the film will undergo splay and bend distortions (Figure 3B) to accommodate the competing anchoring conditions at opposing interfaces. This configuration of the LC leads to a bright optical appearance of the film as a result of the in-plane birefringence of the LC (Figure 3A). It is important to note that, while the zenithal orientation of the LC is well-defined at the LC-aqueous interface in Figure 3A, the azimuthal orientation (preferred orientation of the LC in the plane of the interface) of the LC is influenced interactions with the vertical surfaces of the TEM grid. As a result of the anchoring on the TEM grid, dark brushes that emanate from the edges of the film as well as defects (described in further detail below) are evident in the optical appearance of the LC film. The LC appears dark when the azimuthal orientation of the LC is locally parallel to either the polarizer or analyzer, and bright when the LC adopts an intermediate azimuthal orientation. When the azimuthal orientation of a LC is degenerate, the appearance of the LC is often called a “Schlieren texture”.^{33, 36, 37} Outside of the dark brushes, if the sample is illuminated using white light, the colors of the film of LC are typically faint yellow, pink, or green (Figure 3A). These colors depend on the optical retardance of the LC film, which in turn is a function of thickness of the film of LC as well as its orientation (also discussed in more detail below).

In contrast to the case of a planar orientation at the LC-aqueous interface, when the zenithal orientation of the LC is homeotropic, the orientation of the LC is uniformly perpendicular except near the vertical surfaces of the grid (Figure 3D). The perpendicular configuration of the majority of the LC leads to a dark optical appearance when the LC film is viewed between crossed polarizers (Figure 3C). The sample appears dark because, as described above, polarized light transmitted through the LC only experiences one index of refraction of the LC (the so-called ordinary refractive index). Thus, the polarization of the incident light will be preserved upon transmission through the sample and the light will not be able to pass through the crossed analyzer. As noted above, the bright regions of the LC evident near the surfaces of the grid are caused by a homeotropic orientation of the LC on the vertical surfaces of the grid. The influence of the grid on the LC extends a distance horizontally from the grid surface that is comparable to the thickness of the LC film (~ 10 μm in Figure 3C).

Finally, similar to the case of a planar orientation, when the orientation of the LC is tilted at the LC-aqueous interface, both splay and bend distortions will be present in the LC film (Figure 3F). In the regions of the LC where the azimuthal orientation of the LC is not influenced by the grid, the LC exhibits an appearance that is similar to a Schlieren texture (Figure 3E). However, as compared to the case of a planar orientation, a tilted orientation at the top interface leads to a lower optical retardance. This lower retardance leads to intense coloration in regions outside of the dark brushes (Figure 3E). Analysis of the interference colors can provide quantitative information regarding the tilt angles of the LC at the interface (see below).

The experimental situation addressed in Figure 3 did not involve a twist deformation of the thin film of LC. If a sample, when viewed between crossed polarizers, does not appear dark at some orientation between crossed polarizers, it is likely that a twist distortion is present in the sample. This situation can occur if the orientation of the LC is parallel to both the top and bottom interface, yet the azimuthal orientation of the LC is different at both interfaces (Figure 9). In this situation, if the azimuthal orientation of the LC at the bottom surface is aligned with the plane of polarization of the light passing through the bottom polarizer, the LC will serve as a waveguide where the polarization of the light follows the twist of the nematic director. In later sections, we describe in detail how the rotation of a sample cell with a twist distortion can be used to quantify the azimuthal orientation of the LC at each interface (and thus also the twist angle of the LC in the sample).

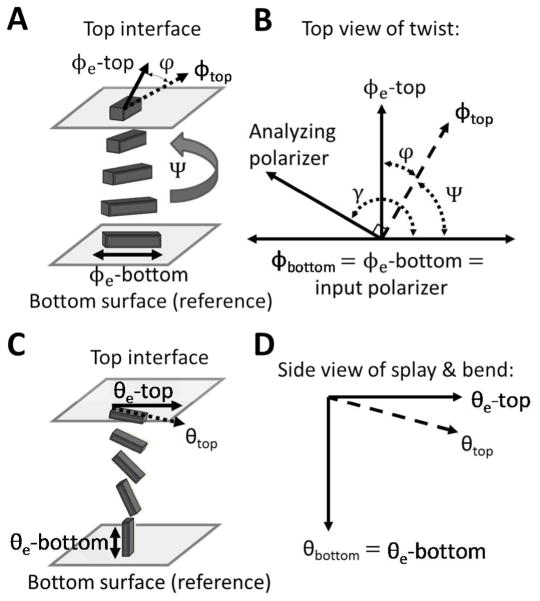
Figure 9.

Experimental set-ups and angle diagrams used to determine azimuthal (A and B) and zenithal (C and D) anchoring energies. (A) Schematic illustration of a twisted nematic LC (TNLC). (B) Diagram depicting the angles used to characterize the TNLC between two polarizers. The azimuthal orientation of the easy axis of the LC (defined by φ ₃) and the azimuthal orientation of the LC director (defined by φ) are shown for both the top and bottom surfaces. Modified and reproduced with permission.¹⁴ (C–D) Schematic illustrations and corresponding definitions of angular displacements of the director in a LC film with planar-homeotropic hybrid anchoring conditions. The bottom surface is assumed to cause strong homeotropic anchoring and is used as a reference surface. The orientation of the easy axis of the LC at the top surface is characterized by the zenithal angle θ₃, and the orientation of the LC director is characterized by θ.

As briefly mentioned above, the optical texture of a thin film of LC between crossed polarizers often possesses dark brush-like features (see Figure 3A and E). These brushes typically emanate from defects present in the film. The defects can be either line defects (disclinations) extending throughout the bulk of the film of LC, or isolated point defects confined to the plane of observation. Under conditions that lead to a degenerate azimuthal orientation at the top interface of a thin film of LC, (Figure 4A), two dark brushes emanate from the cores of disclinations whereas four dark brushes will emanate from the cores of isolated point defects.³⁶ The presence of disclinations in areas where two brushes originate can be confirmed by displacing either the top or bottom confining surface of the LC film. When either of the surfaces is shifted, the centers with two brushes will leave a clear singular trace, while the centers with four brushes will not.³⁶

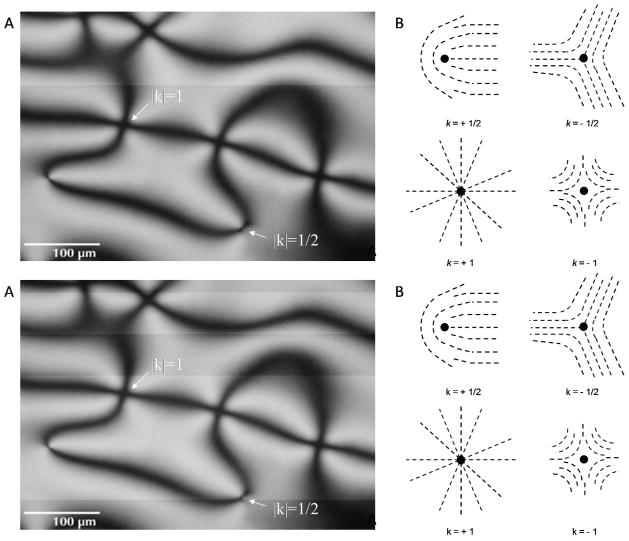
Figure 4.

Topological defects in LCs. (A) Polarized light micrograph of a Schlieren texture characteristic of a micrometer-thick film of LC with a degenerate planar alignment. Arrows indicate the positions of topological defects. (B) Schematic illustrations of director profiles around topological defects of indicated strength (k). (A) Modified and reproduced with permission.⁵⁰

The number of brushes (B) emanating from the core of a defect can be used to assign the magnitude of the strength of a defect (|k|) according to the relationship |k|=B/4.³⁶ Physically, |k| defines the number of times the orientation of the nematic director rotates by ± 2 π around the core of the defect (Figure 4B). In addition, the direction that the brushes rotate around a defect during an in-plane rotation of the film of LC can be used to define the sign of the defect. Clockwise rotation of the brushes around a defect corresponds to a positive defect, and counterclockwise rotation of the brushes corresponds to a negative defect. Figure 4B shows the director profiles around defects with different strengths. Finally, we note that the type of defect can provide insight into the orientation of the LC at an interface. For example, in a film formed by spreading LC onto a solid substrate in air (with a perpendicular orientation of the LC at the LC-air interface), the observation of a disclination line running through the central region of the film indicates that the zenithal orientation at the LC-solid interface is planar and the azimuthal orientation is uniform.³⁸ Furthermore, the direction that the disclination traverses the film is perpendicular to the azimuthal orientation of the LC at the LC-solid interface.

4.1.2. Orthoscopic polarized light microscopy of LC-in-water emulsions

The example presented above illustrates how orthoscopic polarized light microscopy can be used to make qualitative statements regarding the orientational ordering of nematic LCs at the flat interface of a micrometer-thick film. While the orientational ordering of LCs at the interface of micrometer-sized droplets in a LC-in-water emulsion can also be elucidated through the use of orthoscopic polarized light microscopy,^{3, 6, 7, 18, 21, 25, 33} key differences exist between the approaches typically used to determine the orientations of LCs at the interfaces of droplets as compared to planar films. In particular, confinement of LCs to micrometer-sized droplets generates well-defined patterns of topological defects within LCs.^{3, 39} Observation of these defects can be very useful when determining the orientations of LC within droplets with light microscopy. As shown in Figure 5, the positions of topological defects in LC droplets and the organizations of the LCs around these defects (so-called “director configurations”) result in distinct optical signatures when the LC droplets are viewed between crossed polarizers.

Figure 5.

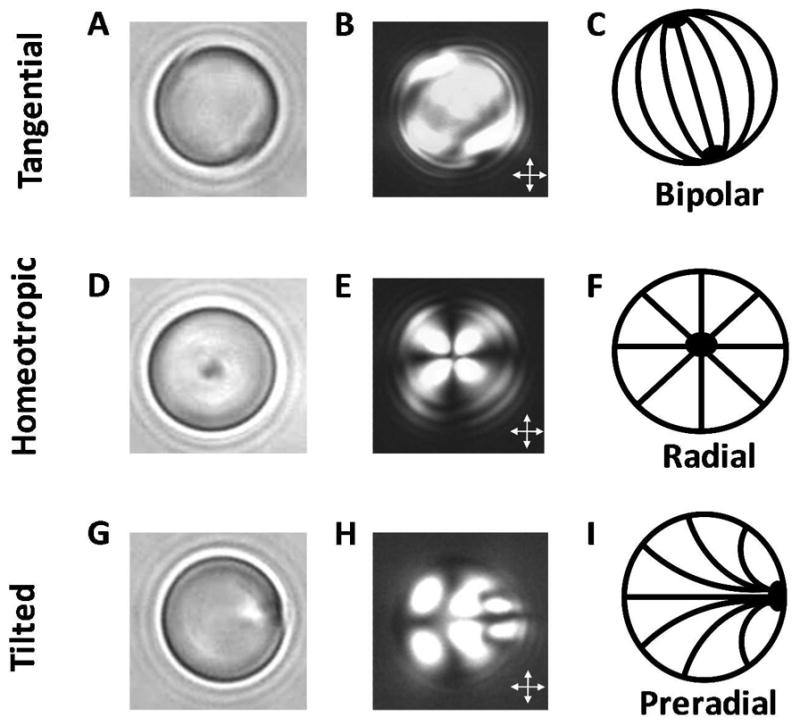
Orthoscopic bright field and polarized light micrographs of 8-μm-diameter droplets of nematic 5CB, shown as a function of the anchoring of the LC at the droplet interface. Bright field micrographs (A, D, G), polarized light micrographs (crossed polarizer, B, E, H) and schematic illustrations of the director configurations (C, F, I) are shown, for tangential (A–C), homeotropic (D–F), and tilted (G–I) anchoring of the LC at the droplet interface. Reproduced with permission.²¹

The positions of topological defects within the bulk or at the interfaces of LC droplets are governed by a subtle balance of surface anchoring and bulk elastic energies of the LC.^{3, 16, 39} The relative importance of the two contributions to the droplet free energy is size-dependent, with the anchoring energy scaling with the square of the droplet radius and the elastic energy scaling in proportion to the droplet radius. For the purpose of this review, we focus on characterization of large LC droplets (>1 μm) with “strong anchoring”. The term strong anchoring implies that the surface chemistry at the droplet interface sets the orientation of the LC at this interface and the LC within the bulk of the droplet relaxes to a director configuration that minimizes the elastic energy of the LC. For a discussion of the influence of droplet size and “weak anchoring” on defect structures encountered in LC droplets, the reader is directed elsewhere.^{3, 16, 39}

In contrast to systems containing flat films of LC, LC-in-water emulsions contain LC droplets that are diffusing (translating and rotating), resulting in time-varying optical appearances of LC droplets. When characterizing LC droplets, it is useful, therefore, to obtain multiple images of each LC droplet by using video microscopy. By imaging LC droplets in many different orientations, the full director profile of the LC confined within the droplet can be determined. In addition to diffusion, when the LC is denser than the confining aqueous medium (such as in the case of nematic 5CB), a second complication is that the LC droplets undergo sedimentation. Our past studies have established that sedimentation of LC droplets onto solid surfaces (e.g., a glass microscope slide) can result in changes in the orientational ordering of the LC within the droplets.²⁰ Imaging of LC droplets should, therefore, be performed before a majority of the LC droplets contained in the emulsion have sedimented onto the supporting substrate (this often occurs within a few minutes of preparing a sample for observation). Finally, to ensure that the LC droplets were not perturbed by the supporting substrate, LC droplets that were at least 50 μm above the surface of the substrate and translating with velocities greater than 1 μm s⁻¹ were selected for characterization in our past experiments. This distance (50 μm) is a conservative estimate based on our experimental observations and knowledge of the sizes of the LC droplets in the LC-in-water emulsions used in our studies (diameters of 1 to 20 μm).^{20, 21, 25} Hydrodynamic interactions between diffusing LC droplets and surfaces have not been studied in detail, although it is likely that the distance over which interactions occur will depend on the sizes of the droplets. As noted above, glycerol can also be added to the aqueous phases to increase the viscosity and slow sedimentation.

If the orientation of the LC at a droplet interface is tangential (i.e., locally planar), the director may exhibit a so-called “bipolar” configuration within the droplet (Figure 5A–C). In a bipolar configuration, the droplet possesses two diametrically opposed point defects (called boojums; Figure 5A and B).³ These point defects can be identified by their dark appearance in polarized light images (Figure 5B), but are more readily identified when the droplets are viewed using bright field microcopy because they scatter light, resulting in areas of high contrast compared to defect-free regions (Figure 5A).¹⁸ Therefore, bright field microscopy is a useful and complimentary tool to polarized light microscopy when characterizing the orientational ordering of LCs confined within micrometer-sized droplets. In brief, bright field microscopy is performed by imaging the sample following removal of the analyzer in a polarized light microscope.

In regions of a droplet where the projected orientation of the LC is uniform along the optical path and either parallel or perpendicular to the polarizer or analyzer (crossed polarizers), the LC will appear dark. In other regions of the LC droplet, the LC will appear bright. Thus, in the polarized light micrograph of the bipolar droplet shown in Figure 5B, the majority of the LC within the droplet appears bright. However, Figure 5B is only one of many appearances that a bipolar droplet can exhibit between crossed polarizers because the ordering of the LC within the bipolar configuration is not spherically symmetric. Polarized light micrographs of bipolar droplets viewed in many different orientations can be found in Liquid Crystal Dispersions written by Drzaic.³

When the orientation at a LC droplet interface is homeotropic, one possible director configuration is a so-called “radial” configuration (Figure 5D–F). The radial configuration is characterized by a single point defect (or a very small disclination line in the shape of a ring) located at the center of the droplet.³ A radial droplet possesses spherical symmetry, and thus its optical appearance is invariant upon rotation of the droplet. Finally, a polarized light micrograph of a radial droplet is characterized by a dark cross-like pattern, as generated by the regions of the LC that are oriented either parallel or perpendicular to a polarizer (Figure 5E).

When the orientation of the LC at a droplet interface is tilted, one possible director configuration is the so-called “preradial” configuration (Figure 5G–I). Similar to a radial configuration, the preradial configuration possesses a single point defect. However, this defect is located at the surface of the droplet rather than in the core of the droplet. Similar to a bipolar droplet, a preradial droplet does not possess the spherical symmetry characteristic of a droplet in a radial configuration, and thus many possible optical appearances are exhibited by preradial droplets, dependent on the plane of rotation of the droplets. Again, by imaging preradial droplets oriented in many different planes of rotation, the full director profile within the droplet can be characterized (Figure 5I).

Finally, we note that the LC droplet configurations described above each represent one of many possible director configurations induced by a tangential, homeotropic or tilted orientation of a LC at a droplet interface. The most stable director configuration for a given preferred orientation is dictated by the relative magnitudes of the elastic constants that characterize the different modes of strain within the LC droplets. The elastic constant for twist is typically smaller than the other elastic constants (for splay and bend), and thus twisted configurations of LCs droplets are not uncommon. For an extensive catalog of possible director configurations for each anchoring condition, the reader is directed elsewhere.³ Finally, in contrast to defects in planar films of LC, defects present in LC droplets are typically classified by a topological charge. This classification is somewhat more complex than assigning a strength to a defect.³⁹

4.2. Conoscopic polarized light microscopy of planar films of LCs

The above sections describe how orthoscopic polarized light microscopy can be used to characterize the orientational ordering of nematic LCs at interfaces. Oftentimes, however, a complimentary technique is necessary to provide an unambiguous determination of the orientation of the LC. For example, in the slab geometry, either a LC film with a uniform homeotropic orientation between confining interfaces (Figure 3D) or a film containing an isotropic phase of mesogens, will appear dark when viewed using orthoscopic polarized light microscopy (Figure 6C and E). If the LC film is formed within the pores of a TEM grid, a simple method to distinguish between these two states of a LC film is to observe the regions near the grid. As discussed in Section 4.1.1., the regions of the LC films near the surfaces of the grids will appear bright (Figure 6C). In contrast to LC films with a uniform homeotropic alignment, an isotropic phase of mesogens will appear dark near the surfaces of the grids. More generally, however, conoscopic polarized light microscopy can be performed in conjunction with the orthoscopic examination to distinguish between homeotropic and isotropic states of the LC film.

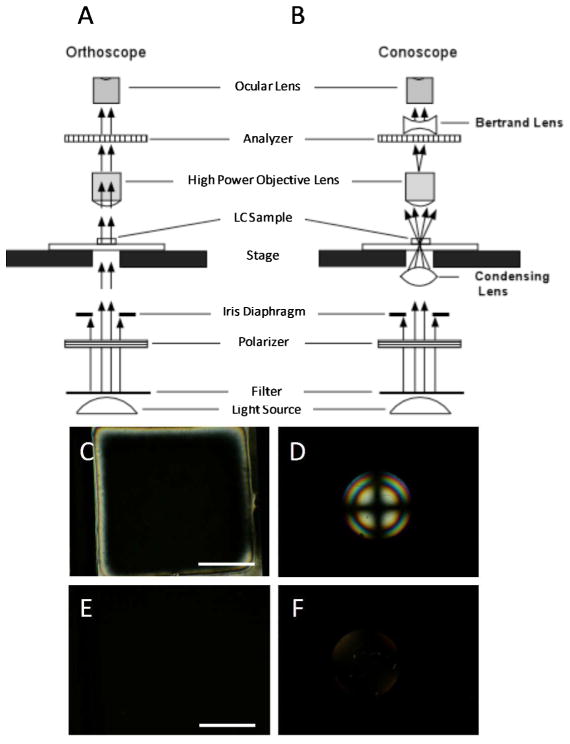
Figure 6.

Schematic illustrations (cross-sectional view) of the optical elements in a polarized light microscope when using (A) orthoscopic and (B) conoscopic illumination. (C) Orthoscopic and (D) conoscopic polarized light micrographs (crossed polarizers) of a LC film with a uniform homeotropic orientation. (E) Orthoscopic and (F) conoscopic polarized light micrographs (crossed polarizers) of a film of an isotropic phase of mesogens. Scale bars are 100 μm. (A) and (B) modified and reproduced with permission.⁵¹

Figures 6A and B show schematic illustrations of a polarized light microscope configured for orthoscopic and conoscopic observations, respectively. In contrast to orthoscopic examination, conoscopic examination requires, in addition to crossed polarizers, insertion of a sub-stage condensing lens and a Bertrand lens.⁴⁰ The sub-stage condenser causes the sample to be illuminated by a cone of light rather than a column of light, while the Bertrand lens brings interference patterns resulting from the interaction of this cone of light with the LC film into the focal plane of the ocular lens of the microscope. Conoscopic examination of a thin film of LC in a uniform homeotropic alignment between confining interfaces will lead to an interference pattern consisting of a dark cross overlying concentric rings (Figure 6D). In contrast, conoscopic examination of an isotropic phase of mesogens will not generate an interference figure, but rather will give rise to a dark optical appearance of the LC film (Figure 6F) because the polarization of the light transmitted though the LC film remains unchanged. If the LC is tilted slightly away from homeotropic, the cross shown in Figure 6D will be displaced from the center of the image. Below we return to the analysis of conoscopic figures to provide quantitative information regarding the tilt of a LC away from the surface normal.

We conclude this section by reminding the reader that a film of LC oriented in a uniform planar alignment between confining interfaces can also give rise to a dark optical appearance during orthoscopic examination with crossed polarizers. However, conoscopic examination is not necessary to distinguish between this situation and the previous two scenarios described above. Instead, if the film of LC is rotated at an angle between 0° and 90° relative to the polarizer, the LC will exhibit a bright optical appearance (brightest at 45°). In contrast to a film containing LC in a uniform planar alignment, both a film with a uniform homeotropic alignment of the LC and a film of an isotropic material will remain dark at all angles of rotation of the sample.

5. Quantitation of the orientations of LCs at planar interfaces

The experimental methods described above lead to qualitative information regarding the orientations of LCs at interfaces (for example, they can indicate the presence of a tilt, but do not provide the tilt angle). In this section, we discuss optical methods that permit quantitation of the orientations of LCs at interfaces. Obtaining quantitative information regarding the orientation of a LC at a surface, in general, requires consideration of the director profile in a sample (that is, a description of the variation of the nematic director as a function of position throughout the sample). In this section, we will discuss the experimental methods that are used to infer both the zenithal and azimuthal orientations of LCs in thin films.

5.1. Quantitation of the zenithal orientations of LCs

First we consider the case of a LC film that exhibits a homeotropic orientation at a bottom (reference) surface. In this situation, as was shown in Section 4.1.1., the zenithal orientation of the LC at the opposing top interface (i.e., planar, homeotropic, or tilted) determines the optical appearance of the LC film (Figure 3). To quantify the orientation of the LC at the top interface of the LC film (θ_top, zenithal tilt angle), it is necessary to first determine both the thickness, d, as well as the optical retardance, Δr, of the LC film. Methods used to measure these two quantities are described below.

5.1.1 Measurement of LC film thickness, d

In some circumstances, where precise measurement of θ_top is not required, it may be sufficient to approximate the thickness of a LC film by, for example, the thickness of a Mylar spacer⁴¹ (slab geometry) or by the thickness of a TEM grid (LC-aqueous interface).¹⁰ To obtain a precise measurement of the tilt angle of the LC, however, a measurement of LC film thickness will likely be required. As described below, the thickness of the LC film within a LC optical cell can be obtained through the use of a UV-Vis spectrophotometer.

In the situation where a LC film is to be confined between two semi-reflective solid surfaces, the thickness can be measured using the interferogram generated when the cell is inserted into the light path in a UV-Vis spectrophotometer (before the cell is filled with the LC or when the LC is heated into an isotropic phase). Once within the light path, constructive and destructive interference of light partially reflected from the internal surfaces of the optical cell leads to the formation of a pattern of interference fringes. Specifically, the thickness is calculated by identifying the wavelengths of adjacent peaks (λ _i) in the interference pattern using the following equation:

$$d=\frac{1}{2n}\left(\frac{1}{\frac{1}{{\lambda }_2}-\frac{1}{{\lambda }_1}}\right)$$ (1)

where n is the index of refraction of the medium in the optical cell (for the case of an air-filled cell, n = 1).

When a LC film has a free interface (e.g., a LC-aqueous interface), measuring the thickness of the LC film is not as straightforward as in the case of a LC film confined between two solid surfaces. In the former situation, one approach is to measure the LC film thickness by decorating the aqueous interface of the LC with a few micro-particles and by scratching the surface of the supporting solid surface (before contacting the LC with the surface).²¹ By locating the focal plane of the microscope on the features on both interfaces of the LC, and by calibrating the notches on the fine focus knob of the microscope, the distance between the two interfaces of the LC can be determined by moving the focus from the bottom surface to the top interface of the LC film. The theoretical accuracy of this method is limited by the numerical aperture (NA) of the objective used (the limit of the out-of-plane resolution of a microscope objective is proportional to 1/NA²). We estimate, in practice, that this method permits determination of the LC film thickness within ± 1 μm when using a 50x objective with NA = 0.5 (on an Olympus BX60 microscope).

5.1.2. Measurement of LC film optical retardance, Δr

The optical retardance, Δr, of a LC film is the integrated effect of the LC birefringence and the optical pathlength experienced by light transmitted through the film. As described in Section 4.1.1., upon entering a LC film with hybrid boundary conditions, light refracts into two components (ordinary and extraordinary rays) that travel at different velocities through the film. The relative phase shift between these two rays upon exiting the LC medium is referred to as the optical retardance. As described below, this quantity can be measured through the use of a compensator, a Polscope, or it may also be estimated through the use of a Michel-Levy chart.

Compensators are instruments that shift the phase of light to exactly offset, or compensate for, the retardance of a birefringent sample. Although many different types of compensators exist and can be used to determine the retardance of a sample, here we discuss the Berek U-CTB compensator, as it is a commonly used compensator. A Berek compensator consists of a birefringent calcite plate that can be precisely tilted to generate a desired (compensating) optical retardance (Figure 7). To use this instrument to determine the retardance of a LC film, one must first place the sample on a circular stage and examine the film between crossed polarizers using a polarized light microscope. It is then necessary to identify and focus on a region of the film where the LCs exhibit locally a uniform azimuthal orientation. The stage is then rotated until the observed region of the film attains extinction. Note that if the confining interface does not give rise to an overall preferred azimuthal orientation, as is the case for the interface between a LC and water, regions of local uniform azimuthal alignment can be conveniently identified by the location of dark brushes. Next, the stage is rotated clockwise 45° and clamped into place (Figure 7C). The Berek compensator crystal is then inserted into the optical path above the sample but beneath the analyzer with its drum initially set to 30°. Subsequently, the angle adjustment dial of the compensator is slowly rotated in one direction, which leads to the appearance of a number of brightly colored fringes passing through the sample. The dial should continue to be rotated until a single black fringe intersects the center of the field of view (Figure 7D). This angle (θ₁) is recorded from the compensator. The dial is then rotated in the opposite direction, past 30°, until a second black fringe appears at θ₂ (Figure 7E). If no colored fringes are observed during this process, rotate the stage counterclockwise 90°, reclamp it, and then repeat the procedure described above. If a black fringe still is not observed to intersect the center of the field of view, it is possible that the retardation of the LC film exceeds that which is measurable by the Berek compensator. After measurement of these angles, the angle θ = |θ₁− θ₂|/2 is computed and used to determine the retardance of the LC film (each compensator is accompanied by a reference table that reports retardance as a function of this angle).

Figure 7.

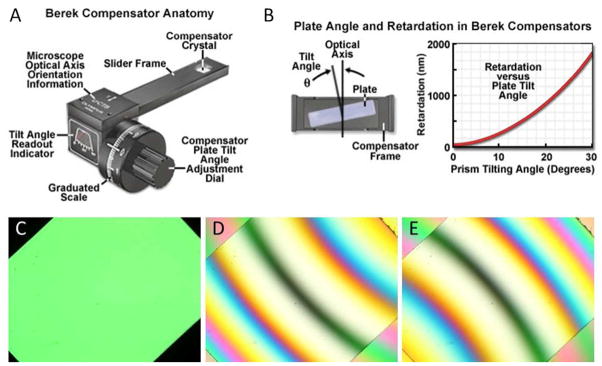
Measurement of optical retardance using a Berek compensator. (A) Schematic illustration of a Berek compensator. (B) Illustration of the calcite crystal within a Berek compensator, and the tilting of the crystal to introduce compensating retardance into the optical path. (C) Polarized white light micrograph of a birefringent LC sample viewed between crossed polarizers when rotated by 45° from extinction. (D, E) Optical images following insertion of a Berek compensator into the optical path and subsequent rotation of the compensator dial, both forward (D) and backward (E), to locate a black fringe in the middle of the image. (A) and (B) reproduced with permission.⁵²

An alternative way to measure the optical retardance of a LC film is through the use of a retardance mapping instrument such as the CRI PolScope.¹⁵ This instrument operates by illuminating a sample with circularly polarized light (λ = 546.5 nm). After passing through the sample, the light is collected by a LC compensator and imaged through use of a CCD camera. This instrument is capable of mapping the retardance of a sample over a large spatial area and can determine retardance values between 0 and 273 nm (i.e., λ/2) to a precision of 0.02 nm. A limitation of this technique is that it cannot be used to measure the absolute value of the retardance of a sample when the retardance exceeds 273 nm (the Polscope reports retardances above 273 nm with an ambiguity in the order of the retardation). The Polscope is best utilized either for analyzing small spatial variations in the retardance of a sample or for calculating exact retardance values in cases when the approximate retardance of the sample is already known.

Finally, we comment that a comparison of the interference colors observed in a LC sample (when imaged between crossed polarizers using white light) with those found in a Michel-Levy chart (Figure 8) can be used to estimate the retardance of a thin film of LC. However, the precision of this method can be low, especially for high optical retardances (> 1500 nm), as individual interference colors can correspond to broad ranges (~300 nm) of retardance values. The interference colors also become increasingly washed out at high orders. We note that the Michel-Levy chart can also be utilized to estimate the thickness of a LC film when the orientation of the LC is known.

Figure 8.

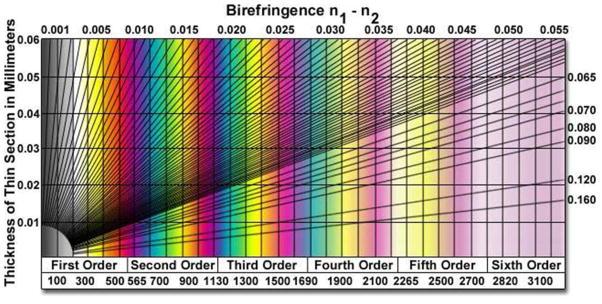
Michel-Levy color chart. The chart relates sample thickness, optical retardance and effective birefringence of optically anisotropic materials to colors observed when using crossed polarizers and white light illumination. Optical retardance (in nm) is given at the bottom of the chart. Reproduced with permission.⁵³

5.1.3. Determination of the zenithal (tilt) angle

As mentioned above, the zenithal orientation of a LC (θ_top) at the upper interface of a LC film can be determined from the measurements of the retardance and film thickness. The evaluation of θ_top is based on a model of the director profile across the thickness of the LC film, which is typically determined by minimization of an expression for the elastic free energy of the thin LC film.^{7, 11, 15} The elastic free energy density of a LC, as described by the Frank-Oseen expression, is

$$F_{\text{Elastic}}=\frac{1}{2}\left[K_{11}{(\nabla ·n)}^2+K_{22}{(n·\nabla \times n)}^2+K_{33}{(n\times \nabla \times n)}^2-K_{24}\nabla ·\left(n\times \nabla \times n+n(\nabla ·n)\right)\right]$$ (2)

where n is the director of the LC, and K₁₁, K₂₂, K₃₃ and K₂₄ are the elastic constants for splay, twist, bend, and saddle-splay deformations, respectively.³⁴ An additional term containing K₁₃, the splay-bend elastic constant, is not included in equation 2 since it contains higher order derivatives of n.^{42, 43} The term containing K₂₄ is also often neglected, although it clearly plays an important role in some geometries, including spherical LC droplets.^{3, 16, 21, 25} Finally, a one elastic constant approximation (K11 = K22 = K33) of the full Frank-Oseen expression3, 34 is often used to simplify further equation 2, although we note that there are instances where this simplification does not capture the experimental behavior of the LC.^{16, 25} Use of the one-constant approximation reduces the expression for the elastic free energy density of the film to

$$f_{\text{b}}(\theta ,\stackrel{.}{\theta })=\frac{1}{2}K{\stackrel{.}{\theta }}^2$$ (3)

Minimization of the elastic free energy of the LC slab geometry leads to the result that the tilt of the LC varies linearly with position across the film

$$\theta (z)=\frac{z}{d}({\theta }_{\text{top}}-{\theta }_{\text{bottom}})+{\theta }_{\text{ref}}$$ (4)

For the situation where the orientation of the LC on the bottom substrate is strong and homeotropic (θ_bottom =0°), the relationship between the optical retardance of the LC film of thickness d, and the tilt angle at the top interface (θ_top, measured from the surface normal) is given by

$$\mathrm{\Delta }r\approx {\int }_0^d\left(\frac{n_{\text{o}}{n}_{\text{e}}}{\sqrt{n_{\text{o}}^2{\text{sin}}^2({\theta }_{\text{top}})+n_{\text{e}}^2{\text{cos}}^2({\theta }_{\text{top}})}}-n_{\text{o}}\right)dz$$ (5)

in which n_o and n_e are the indices of refraction perpendicular (ordinary refractive index) and parallel (extraordinary refractive index) to the optical axis of the LC, respectively.^{7, 11, 15} Solution of this equation to obtain the experimentally measured value of Δr yields θ_top. The interested reader is referred elsewhere for a detailed derivation of the equations for Δr and θ(z).⁷

To illustrate the relative precision of estimates of θ_top obtained using a compensator versus the Michel-Levy chart, we consider the following example. The retardance of a sample composed of a 20 μm-thick film of nematic 5CB (n_e=1.711 and n_o=1.5296)²² with strong homeotropic orientation at the bottom reference surface was measured using a compensator in our laboratory to be Δr = 1055±14 nm. Solution of equation 5 for θ_top yields θ_top =63.0°±0.5°. For comparison, from the Michel-Levy chart (Figure 8), it can be seen that such a film would possess pink interference colors when imaged between crossed polarizers using white light. However, the chart also shows that the pink interference color will be observed for all Δr values between ~1020–1100 nm. Therefore, if the Michel-Levy chart only was used to estimate θ_top in this particular sample, θ_top would be determined to lie between 61.7°–64.6°.

Finally, we note that conoscopy can also be used to determine θ_top, particularly when the director is tilted only slightly from a homeotropic orientation. As noted above, conoscopic examination of a thin LC film with uniform homeotropic alignment yields an interference figure consisting of a dark extinction cross overlying concentric rings in the center of the field of view. In the case of a LC film that tilts slightly from the homeotropic orientation, the dark cross will be shifted from the center of the field of view. Measurement of the position of the cross, when combined with knowledge of the refractive indices of the LC, can be used to obtain α_o, the angle between the surface normal and the center of the interference figure through use of Mallard’s equation

$$\frac{r}{R}NA=\langle n\rangle sin{\alpha }_{\text{o}}$$ (6)

where r is the distance between the center of the field of view and the center of the cross, R is the radius of the field of view, NA is the numerical aperture of the objective, and 〈n〉 is the average refractive index of the sample⁴⁴. The tilt angle is then given by

$${\theta }_{\text{top}}=90°-{\alpha }_{\text{o}}.$$ (7)

We refer the reader to a prior publication for a complete description of this method.⁴⁴

5.2. Quantitation of azimuthal orientations of LCs

In this section, we describe how the azimuthal orientation of a LC can be quantified for the experimental situation in which the LC film is sandwiched between two contacting solid surfaces, each of which induces different azimuthal orientations in the LC. The distinct azimuthal orientation of the nematic LC at each of the two confining surfaces will lead, in general, to formation of a twist distortion within the LC (Figure 9A). Depending on the azimuthal anchoring energy (W_a) at each of the confining surfaces, as well as the elastic energy stored in the bulk due to the twist deformation, the LC director at one or both of the surfaces may depart from the easy axis.¹⁴ Figure 9A depicts a case in which the easy axes of the LC at the two confining surfaces are aligned orthogonal to one another and where a strong azimuthal orientation of the LC at the bottom reference surface prevents the LC director from deviating from the easy axis at the bottom surface.⁶ However, weak anchoring of the director at the top surface allows the LC director to deviate from the top easy axis, decreasing the twist distortion across the film (characterized by the twist angle, Ψ).

The twisted nematic LC (TNLC) described above acts as a waveguide. Thus, polarized light propagating through the LC film follows the twist of the LC director provided the Mauguin condition, λ ≪ (n_e− n_o) is satisfied,³⁴ where P, the pitch of the LC, is equivalent to 4d, where d is the thickness of the film, for a 90° twist.³⁴ This condition is satisfied in LC films which are tens of micrometers in thickness.

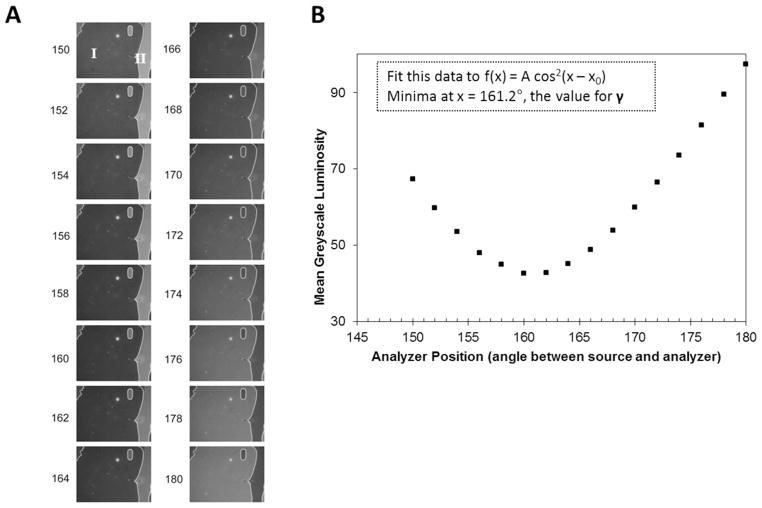
With reference to Figure 9B, in order to determine Ψ, it is necessary to first determine the angle between the analyzer and source polarizer corresponding to minimal transmission of polarized light (angle γ). Determination of γ requires that the easy axis of the LC on the bottom reference surface be aligned parallel to the input polarizer. This can be accomplished by the use of “reference regions” within the TNLC cell, corresponding to regions of the upper substrate that have been patterned such that the easy axis is parallel to that of the reference surface.²⁴ Within these regions, the LC film will have a uniform zenithal and azimuthal alignment. However, even in the absence of these reference regions, the reference surface of a TNLC cell can be properly aligned since complete extinction of transmitted light will be observed upon rotation of the analyzer only when the easy axis of the reference surface is aligned parallel to the input polarizer. In this situation, the TNLC cell is placed on a microscope stage between crossed polarizers with the input polarizer facing the reference surface and the sample is subsequently rotated between the stationary polarizers to minimize light transmitted through the sample. Subsequently, the analyzer is rotated to further minimize the light transmitted through the sample. Three iterations of this procedure are typically sufficient to obtain extinction.²⁴ This procedure can be conveniently performed by capturing optical images of the TNLC at regularly spaced intervals of the sample or analyzer orientation (Figure 10A). Image processing is then used to determine the mean luminosity of the LC in each image and this data can be plotted as a function of analyzer position (Figure 10B). The magnitude of light transmitted through the twisted LC film can be fit to a function of the form^{14, 45}

Figure 10.

Measurement and analysis of the intensity of light transmitted through a twisted LC to determine the angle γ (see text for definition) (A) Optical images (polarized white light) captured for the TNLC cell as a function of analyzer position (i.e., “crossed polarizers” correspond to 90°). (B) Mean luminosity of a domain within the LC sample, plotted as a function of analyzer position. The data was fit to a cosine squared function (inset) to provide an accurate determination of the minimum. The angle at which the minimum occurs corresponds to γ. Reproduced with permission.¹⁴

$$f(x)=A{\text{cos}}^2(x-x_{\text{o}})$$ (8)

to determine γ. The twist angle, Ψ, can then be obtained from γ using the angle diagram depicted in Figure 9B. For the case of interest, when the easy axes of the two confining substrates are orthogonal to one another, the relationship is

$$\psi =\gamma -90°$$ (9)

where Ψ is constrained to be between −90°and +90°.^{14, 45} Generalization of this expression for TNLC cells in which the easy axes are not orthogonal can be found elsewhere.^{14, 45}

Finally, we note that pixel-by-pixel quantitation of the twist angle within a TNLC cell (i.e., azimuthal orientation of LC at the top surface relative to the bottom surface) can also be performed using methods adapted from those described above.²³ For example, Figure 11 shows a high-resolution map of the twist angle within a TNLC cell.²³ We also note that quantification of the orientations of LCs in spherical geometries (i.e., LC-in-water emulsions) is more difficult than the slab geometry described above. In general, quantitative information about the orientations of LCs at the interfaces of LC droplets is obtained by comparing optical textures of droplets calculated from simulations to experimentally obtained polarized light micrographs.³ We caution that the procedure is laborious and can be ambiguous.

Figure 11.

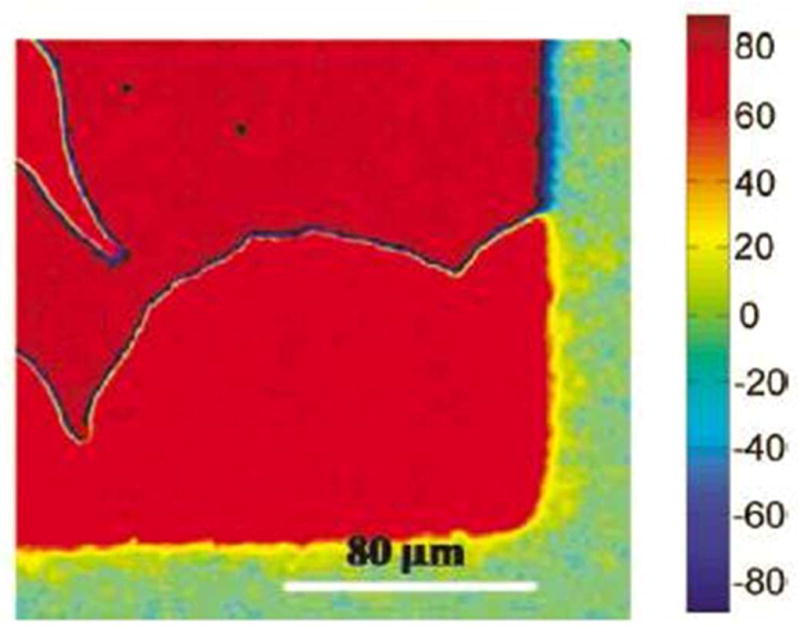
Optical map depicting spatial variation of the twist angle within a LC that is anchored on a chemically patterned surface. The color chart shown at the right side of the figure indicates the twist angle. Measurement of the position-dependent twist angle of the LC can be used to image chemical patterns on surfaces (see text for details). Reproduced with permission.²³

6. Measurements of anchoring energies

Measurement of the anchoring energy of a LC can provide fundamental insight into the intermolecular interactions responsible for the orientations of a LC at a particular interface, and it is also a technologically important quantity as it often determines the response of a LC to a stimulus (e.g., electric field) or adsorbate. In the context of using LCs to report interfacial phenomena, measurements of changes in anchoring energy can be substantially more sensitive than measurements of changes in the easy axis.^{9, 14, 23} Below, we describe methods that permit measurement of anchoring energies at a variety of LC interfaces.

6.1. Quantification of anchoring energies of LCs at planar interfaces

A number of methods exist to measure the anchoring energy of a LC at an interface.^{3, 7, 14, 21, 23–25, 34} In general, the methods involve application of a perturbation to the LC and measurement of a response that is dictated by the anchoring energy. One common approach is to design the LC to be elastically strained (deformed in the bulk), such that the torque generated by the strain in the LC causes the LC to deviate from the easy axis at the surface of interest. The magnitude of the angular deviation of the LC from the easy axis permits evaluation of the anchoring energy. We note that this approach requires knowledge of the orientation of the easy axis of the LC. When characterizing LCs in slab geometries, the torque generated by a thick film will be small, and thus experiments performed with thick LC films (i.e., d ~ 50 μm) are typically used to determine the orientation of the easy axis of the LC. Conversely, measurements using thin films of LC will yield orientations of the LC at the confining surfaces that deviate from the easy axes (due to the torque associated with the strain of the LC), and thus provide access to anchoring energies of LCs.

6.1.1. Governing equations used to determine anchoring energies

The orientation-dependent interfacial energy, γ_aniso, of a LC is often described by the so-called Rapini-Papoular expression,^{7, 46} namely,

$${\gamma }_{\text{aniso}}=\frac{1}{2}{W}_{\text{z}}{sin}^2(\theta -{\theta }_{\text{e}})+\frac{1}{2}{W}_{\text{a}}{sin}^2(\phi -{\phi }_{\text{e}})$$ (10)

where the subscripts z and a denote zenithal and azimuthal quantities, respectively. We consider first an experiment performed in a thin film geometry that is designed to provide values for W_z (we then generalize the result to allow determination of W_a). For simplicity, we assume that the magnitude of the elastic constants for splay, bend and twist are equal (the so-called “one constant approximation” discussed above). The experimental system comprises a bottom confining surface (reference surface with strong anchoring), and a top surface at which the anchoring energy is to be determined. As described below, minimization of the free energy of the system using the one elastic constant expression for the elastic energy and the Rapini-Papoular expression for the interfacial energy at the top surface, results in a simple expression for W at the top surface. In brief, equations 3, 4, and 10 are inserted into the expression for the free energy of the LC film

$$F={\int }_0^d\underset{F_{\text{Elastic}}}{\underbrace{f_{\text{b}}(\theta ,\stackrel{.}{\theta })}}dz+\underset{F_{\text{Surface}}}{\underbrace{f_{\text{S}1}+f_{\text{S}2}}}$$ (11)

to yield

$$F({\theta }_{\text{top}})={\int }_0^d\frac{K}{2}{\left(\frac{{\theta }_{\text{top}}-{\theta }_{\text{bottom}}}{d}\right)}^{2}dz+\frac{1}{2}{W}_{\text{z}}{sin}^2({\theta }_{\text{top}}-{\theta }_{\text{e}})+f_{\text{S}2}$$ (12)

where θ_top and θ_bottom are the zenithal angles defined by the director at the top and bottom interfaces, respectively (Figure 9), and θ_e defines the orientation of the easy axis of the LC at the top interface. Minimization of this free energy with respect to the orientation of the LC at the top interface yields the expression

$$W_{\text{z}}=\frac{2K({\theta }_{\text{top}}-{\theta }_{\text{bottom}})}{dsin\left(2({\theta }_{\text{top}}-{\theta }_{\text{e}})\right)}$$ (13)

For measurement of the azimuthal anchoring energy, a twisted nematic LC cell is used. By using the twist elastic constant (i.e., K = K₂₂) and by re-defining the angles in the system, we reach the commonly used torque balance expression (φ_top − φ_bottom = ψ; and φ_e − φ_top = ϕ; see Figure 9)^{14, 23}:

$$W_{\text{a}}=\frac{2K_{22}\psi }{dsin(2\varphi )}$$ (14)

6.1.2. Measurement technique

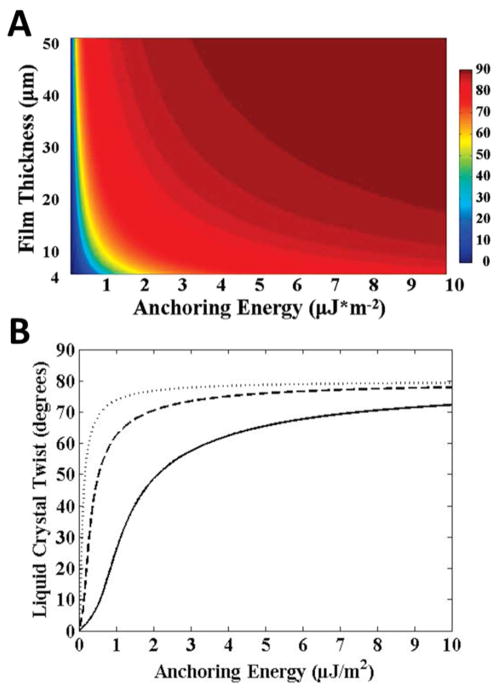
To use equation 14 to determine the azimuthal anchoring energy at a LC-solid interface, the thickness of the LC film (see Section 5.1.1) and the twist angle of the LC (see Section 5.2) are measured. Figure 12 shows the relationship between LC film thickness, twist angle, and anchoring energy calculated using equation 14 (using K₂₂ ≈ 3.8 pN).^{24, 47} From Figure 12, we make a couple of observations. First, the twist angle varies significantly with anchoring energy for values of W that are less than ~ 0.5 μJ/m² for thick films (d = 50 μm), and less than ~2 μJ/m² for thin films (d = 4 μm). For larger values of the anchoring energy, the torque generated by the elastic energy stored in the LC film is insufficient to cause easily measured deviations of the LC orientation from the easy axis at the interface. The range of anchoring energies that can be measured by this method is, therefore, relatively limited (0.5 – 2.0 μJ/m²). Outside of this range of anchoring energies, the uncertainty associated with the measured anchoring energies will be larger because small changes in the twist angle correspond to large changes in the anchoring energy (Figure 12B).²⁴ Specifically, for a surface with an anchoring energy of 5 μJ/m², if characterized with a LC film with thickness of 50 μm and LC orientation measured with a precision of ± 0.5°, the uncertainty in the anchoring energy would be approximately ± 2 μJ/m².

Figure 12.

Twist angles of LCs calculated from the torque-balance equation (see text for details). Results shown are for 5CB and assume that the orientations of the easy axes (in plane of surface) at the confining surfaces are separated by 80°. (A) LC twist angles plotted as a function of anchoring energy and LC film thickness. (B) Plots of LC twist versus azimuthal anchoring energy for LC films thicknesses of 50 μm (dotted line), 16 μm (dashed line), and 4 μm (solid line). Reproduced with permission.²⁴

An alternative implementation of equation 13 forms the basis of a measurement of the zenithal anchoring energy. To illustrate this method, we describe measurement of the zenithal anchoring energy at a free interface of a LC film, such as the LC-aqueous interface. Here we assume that the anchoring of the LC at the bottom reference surface is strong and homeotropic. As with the example described above, it is necessary to first determine the thickness of the LC film (see Section 5.1.1. for details). Next, measurement of the retardance of the LC film is performed using a compensator (see Section 5.1.2.). By solving equation 5, it is possible to determine the tilt of the LC at the LC-aqueous interface, and subsequently, using equation 13, to determine the zenithal anchoring energy. The challenges associated with this method include measurement of the thicknesses of LC films with free interfaces (such as a LC-aqueous interface). For example, a LC film of thickness 7 ± 1 μm and measured retardance 475 ± 10 nm leads to an estimate of W that lies between 2 to 16 μJ/m² (using K = 6 pN). When performing measurements of the anchoring energies of LCs at LC-aqueous interfaces, it is also important to understand that the pH and the ionic content of the aqueous phase play an important role in determining the anchoring energy.^{12, 13}

We end this section by commenting that the above analysis assumes that the film thickness (d) is large compared to the extrapolation length (L/d ≪ 1, where L is the extrapolation length, defined in Section 2, at the top surface). As described earlier, this means that the LC film thickness is sufficiently large that it leads to relatively small deviations of the director from the easy axis. In experiments for which the LC film thickness is comparable to the extrapolation length at the top surface (L/d ~ 1), and the anchoring of the LC at the bottom surface is strong and homeotropic, determination of the film thickness at which the entire film becomes homeotropic provides the basis of another method to estimate the anchoring energy of the LC at the top surface.

6.2. Anchoring energies in LC-in-water emulsions

Determination of the anchoring energy of a LC at the aqueous interface of a LC droplet can be achieved by exploiting the elastic energies generated by confinement of the LCs to the droplets. As mentioned in Section 4.1.2., the relative importance of surface and elastic contributions to the free energy of a LC droplet is dependent on the size of the LC droplet. This scaling can be used to determine anchoring energies based on observations of size-dependent ordering in LC droplets. For large droplets dispersed in an aqueous medium where the easy axis is tangential to the droplet interface, the surface energy will be dominant and LC droplets will assume a bipolar configuration. In contrast, for small droplets, the elastic energy of the LC in the volume of the droplet becomes dominant and causes a transition to a radial configuration (Figure 13).¹⁶ By observing the size at which droplets spontaneously transition to a radial orientation, one can estimate the anchoring energy at the LC-aqueous interface for the LC emulsion system. Specifically, as described elsewhere, the free energies of a bipolar droplet and a radial droplet (both with an easy axis tangential to the LC interface) can be approximated as²⁵

Figure 13.

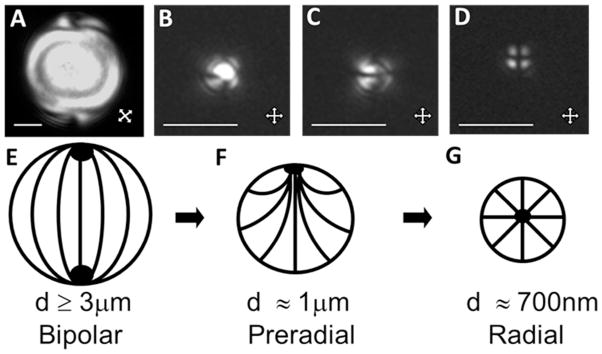
Optical micrographs and schematic illustrations of the configurations of LCs within LC droplets, shown as a function of LC droplet size (with constant surface chemistry). (A–D) Polarized light micrographs (crossed polarizers) of 5CB droplets hosted within polymer capsules with diameters of (A) 8.0 ± 0.2 μm, (B, C) 1.0 ± 0.2 μm, or (D) 0.70 ± 0.08 μm. (E–G) Schematic illustrations of bipolar (E), preradial (F) and radial configurations (G) of LCs, corresponding to the micrographs in A, B and C, and D, respectively. Scale bars are 2 μm in AC and 1 μm in D. Modified and reproduced with permission.¹⁶

$$F_{\text{Bp}}=5\pi K_{11}R-2\pi K_{24}R$$ (15)

$$F_{\text{R}}=8\pi K_{11}R-4\pi K_{24}R+2\pi {WR}^2$$ (16)

Equating (15) and (16), the anchoring energy can be written as

$$W=\frac{K_{24}-\frac{3}{2}{K}_{11}}{R_{\text{c}}}$$ (17)

where R_c is the size of the LC droplets at which the transition from radial to bipolar configurations takes place. While this method appears straightforward to implement, we make three comments regarding its use. First, equations 15 and 16 are approximate, and thus equation 17 only provides an estimate of the anchoring energy. Second, it relies on knowledge of K₂₄, and there is substantial variation in the estimates of this elastic constant in the literature. Third, for LC-aqueous interfaces, commonly encountered anchoring energies lead to values of R_c that can be below the resolution of an optical microscope. For example, we measured R_c to be 400 nm (using a 100x objective) for droplets of nematic 5CB in contact with aqueous solutions. By using K₁₁ = 6.4 pN and K₂₄ = 1.53K₁₁, we arrived at an estimate of W of ~0.5 μJ/m^{2.16, 25} Values of W higher than ~1 μJ/m² will involve even small values of R_c.

7. Unresolved challenges and cautions

Before concluding this review, we briefly discuss some unresolved challenges and cautions related to optical characterization of LC interfaces. We present the challenges with the hope that they might define topics of research for new researchers entering the field. The cautions are presented with the goal of alerting new researchers to some of the potential pitfalls when characterizing LC interfaces.

Our first comments involve characterization of LC droplets. As discussed above, this area of research is a fertile one (for example, as the basis of biological sensors) yet characterization of the interfaces of LC droplets remains relatively difficult. As noted in Section 4.1.2., micrometer-sized LC droplets in LC-in-water emulsions typically translate with velocities greater than 1 μm s⁻¹ both in and out of the focal plane of a microscope. This makes imaging of LC droplets a challenge.^{20, 21, 25} Past attempts by us and others to address this issue include “immobilization” LC droplets on chemically tailored solid surfaces. ²⁰ Immobilization of the LC droplets, however, perturbs the ordering of the LC within the droplets.²⁰ An alternative approach (as described above) is to add glycerol to the aqueous phase to increase the viscosity of the aqueous phase and thus slow the motion of the LC droplets. While this approach does decrease the velocity of the droplets, it also has the potential to substantially change interfacial phenomena occurring in LC-in-water emulsion systems (e.g., adsorbate-induced ordering transitions involving biological molecules). In addition, we emphasize that it is, in general, particularly difficult to obtain quantitative information about the orientations of LCs at the interfaces of droplets. Current procedures typically involve calculations of the optical appearances of droplets from the results of simulations, and comparisons of the calculated optical appearances to experimentally determined polarized light micrographs. These procedures are laborious and can be ambiguous.³ Overall, there exists an unmet need for the development of general and facile optical methods that permit quantitative characterization of LC-in-water droplets. Advances in microfluidic technologies and associated single-particle optical techniques (e.g., flow cytometry) might form the basis of such techniques.

We also offer a few cautions for new researchers working in this field. The first caution relates to the purity (and stability) of LCs. LCs, while often provided by manufacturers at high purity, can degrade if not handled correctly (e.g., exposed to sunlight from a window).⁴⁹ Degradation of a small fraction of the molecules within a LC sample can quickly change the interfacial ordering of the LC if the degradation products are surface-active. Therefore, care must be taken to avoid degradation of the LC or the introduction of impurities from materials that contact the LC (e.g., water that forms the basis of a LC-aqueous interface). A second caution that we offer here relates to characterization of aqueous-LC interfaces. This is a so-called “buried” interface that is relatively difficult to characterize when decorated, for example, by a biological analyte such as a lipid that triggers an anchoring transition within the LC. A common approach is to add to the adsorbate a small amount of a fluorescent marker and perform fluorescence microscopy in parallel with both bright field and polarized light optical microscopy.^{6, 7, 18, 20, 21} We and others have observed that the presence of fluorophores at the LC interface can substantially change the ordering of the LC.²¹ The development of spectroscopic methods that do not require the use of labels and can be used to characterize buried interfaces (e.g., non-linear optical methods) is a promising area of ongoing research.

8. Conclusion

In summary, this review presents an introductory-level description of widely accessible optical methods that can be used to characterize the orientations of LCs at interfaces. These methods can be used to characterize the orientations of LCs at planar interfaces (LC-solid and LC-aqueous) as well as LC-in-water emulsion droplets. All of the methods described in this review can be performed on a standard polarized light microscope with white-light illumination and a Bertrand lens. In addition, we describe optical methods that permit measurement of the anchoring energies of LCs at interfaces. Such measurements can provide important insights into interfacial phenomena occurring at LC interfaces that do not give rise to changes in the easy axes of LCs. Overall, the methods described in this paper enable studies of LC interfaces relevant to electro-optical devices, materials synthesis, biological liquid crystals, or the design of stimuli-responsive LC systems suitable for chemical and biological sensing.