Abstract
In this paper we consider the Hopf bifurcation and synchronization in the two coupled Hindmarsh–Rose excitable systems with chemical coupling and time-delay. We surveyed the conditions for Hopf bifurcations by means of dynamical bifurcation analysis and numerical simulation. The results show that the coupled excitable systems with no delay have supercritical Hopf bifurcation, while the delayed system undergoes Hopf bifurcations at critical time delays when coupling strength lies in a particular region. We also investigated the effect of the delay on the transition of bursting synchronization in the coupled system. The results are helpful for us to better understand the dynamical properties of excitable systems and the biological mechanism of information encoding and cognitive activity.
Keywords: Delay, Chemical coupling, Excitability, Hopf bifurcation, Synchronization
Introduction
Excitability is a character common to many biological systems. For example, we have found some isolated or coupled neurons typically exhibit excitable behavior. From a dynamical system point of view we might paraphrase this as follows: A slight perturbation of the single stable stationary state would lead to a large and long lasting excursion away from stationary point before the system asymptotically returning back to equilibrium. Two general types of synaptic connection between neurons are electrical and chemical, and the chemical synapses are much more common. The time-delay is well known in the information transition between neurons because of the gap junctions. Researchers show that time-delay can change qualitatively the dynamical features of the system (Burić and Ranković 2007; Faria 2000).
The studies related to neural systems are mainly focused on the following two aspects. On the one hand, a lot of researches have been made on the synchronous transition and its application in the coupled neural system and network with no delay. For example, Shi and Lu (2004) studied the complete synchronization of coupled Hindmarsh–Rose (HR) neural network with the ring structure. Wang et al. (2007) gave the types of bursting and synchronous transition in the coupled modified Morris–Lecar (ML) neurons systems. And Yuan et al. (2005) analyzed synchronization and asynchronization in two coupled excitable systems, and so on. On the other hand, time-delay can change qualitatively the dynamical features of the system and consequently will influence the neuron’s biological behavior. Recently, the coupled systems with delay have attracted much attention of researchers in different research fields. Burić and Todorović (2003), Ranković (2011) investigated Hopf bifurcation of coupled excitable FitzHugh–Nagumo (FHN) neurons with delayed coupling and concluded that the time delay can induce the Hopf bifurcation. Wang et al. (2009) elaborated the bifurcation and synchronization of synaptically coupled FHN models with time delay and they confirmed that rich bifurcation behavior can be exhibited with variation of the coupling strength and time delay, as well as the synchronization of the coupled neurons can be achieved in some parameter ranges. Burić et al. (2005) observed different synchronization states in a coupled FHN system with delay with the variation of the coupling strength and delay. Dhamala et al. (2004) studied in detail the effect of the delay on the complete synchronization of the coupled HR systems. Zhen and Xu (2010), Neefs et al. (2010) touched respectively on the stability of the stationary point in a non-chemical coupled FHN and HR neural system with delay. All works but not limited to the mentioned above have promoted better understanding of the dynamics of coupled systems with delay.
Synchronous firing behavior could be widely found during the neural activity in the brain. The observation of synchronous neural activity in the central nervous system suggest that neural activity is a cooperative process of neurons and synchronization plays a vital role in information processing in the brain. On the other hand, bifurcations led by the coupling strength and time-delay can induce different dynamical synchronous behaviors and hence form different synchronization regions. As is known, different synchronization areas imply different neurocognitive function and pathological state. So the investigation of the bifurcation and synchronization is still of vital importance for us to understand the mechanism of how the information is encoded and the cognitive activity happens.
Particularly, excitable systems with delay are very important in theoretical study and application. Hence, bifurcation and synchronization of coupled excitable systems with delay is interesting and necessary to be investigated. To explore the general rule of the effect of delay for the excitable neural system and offer a more sufficient theoretical basis for diagnosing or curing these diseases connected with neural system, we must deeply and extensively analyze the dynamic nature of different systems, especially the excitable neural systems with delay. Most of the papers focus on Hopf bifurcation and synchronization of the electrical coupled general HR neural systems with delay. However, the effects of the coupled strength and delay on the bifurcations and synchronization in chemical coupled excitable HR systems are still important in understanding information processing in the brain. In this paper, motivated by Ranković (2011), Burić et al. (2008), Vasović et al. (2012), we focus on the excitable HR system with chemical couple and time delay. Our studies are mainly about the stability of the stationary point, the bifurcation with one or two parameters and the effect of delay on the synchronization transition of the excitable system.
This paper is organized as follows. In “Main results” section, we discuss the stability of the stationary point, give the conditions for Hopf bifurcations happening of the coupled excitable HR system with no or with time-delay and graphically reveal the effect of the delay on the synchronization transition in the excitable HR system. We conclude the paper in last section.
Main results
The model of two chemical coupled HR excitable neurons with delay is given as follows:
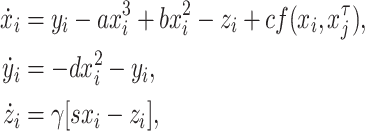 |
1 |
where 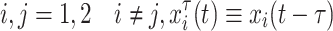 , x is the synaptic membrane potential, y is a recovery variable and z is a slow adaptation current. The variable parameter τ represents the time delay in signal transmission and the variable parameter c is the coupling strength between the first neuron at time t and its neighbor at some previous time t − τ, so they are real and positive. The coupling term that we shall use, is the form of the FTM (Belykh et al. 2005; Somers and Kopell 1993) coupling:
, x is the synaptic membrane potential, y is a recovery variable and z is a slow adaptation current. The variable parameter τ represents the time delay in signal transmission and the variable parameter c is the coupling strength between the first neuron at time t and its neighbor at some previous time t − τ, so they are real and positive. The coupling term that we shall use, is the form of the FTM (Belykh et al. 2005; Somers and Kopell 1993) coupling:
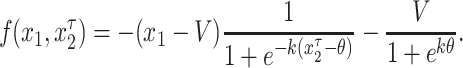 |
In this paper, the values of the parameters θ, V, and k will be fixed as θ = 0.25, V = 2, k = 10.
The dynamics of the coupled system depends on the properties of each of the units and their interactions. Both the neurons in the two coupled HR excitable system display the excitable behaviors. The single HR excitable neuron model is described as the following equations:
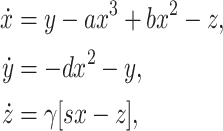 |
2 |
where 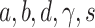 are positive parameters,
are positive parameters, 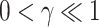 and usually
and usually 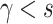 is satisfied.
is satisfied.
It is easy to verify that point  is the only one stable stationary solution of system (2) when
is the only one stable stationary solution of system (2) when 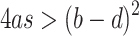 . The eigenvalues of the linearized system of (2) are
. The eigenvalues of the linearized system of (2) are 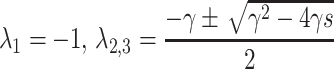 , of which one is real and the others are complex. Therefore, system (2) has a stable focus·node attractor when
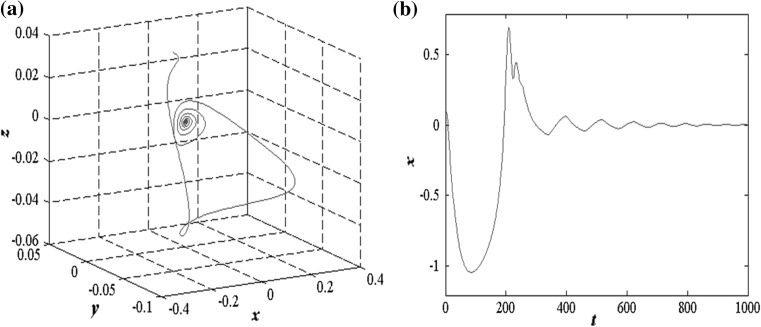
, of which one is real and the others are complex. Therefore, system (2) has a stable focus·node attractor when 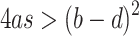 . The phase trajectory and firing pattern of system (2) for parameters
. The phase trajectory and firing pattern of system (2) for parameters 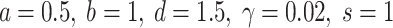 are intuitively shown in Fig. 1. The steady state is stable focus·node.
are intuitively shown in Fig. 1. The steady state is stable focus·node.
Fig. 1.
The phase trajectory and firing pattern of single HR excitable system for parameters 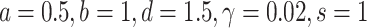 . a Stable focus·node in 3-D space, b the time series of membrane potential
. a Stable focus·node in 3-D space, b the time series of membrane potential
Local stability and bifurcations of the stationary solution
In this section we study the stability and bifurcations of the stationary solution 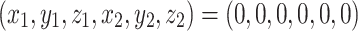 of the system (1) for varying parameters c > 0 and
of the system (1) for varying parameters c > 0 and 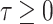 . Parameters a, b, d, s meet the condition
. Parameters a, b, d, s meet the condition 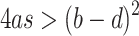 such that each of the units displays the excitable behavior.
such that each of the units displays the excitable behavior.
Instantaneous coupling τ = 0
Consider the system (1) in the case of instantaneous coupling
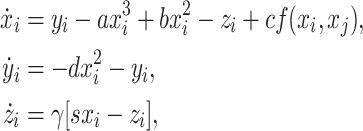 |
3 |
where 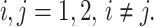
Theorem 2.1.1
Stationary solution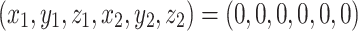 of the system (3):
of the system (3):
-
(i)
is stable attractor for every
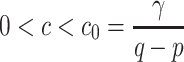 ;
; -
(ii)
is stablefocus·node–focus·node for
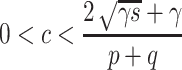 and stablefocus·node–nodefor
and stablefocus·node–nodefor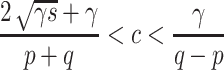 ;
; -
(iii)
has supercritical Hopf bifurcation when parameter
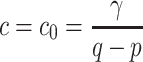 .
.
Proof
Local stability of the stationary solution is determined by analyzing the linearized system at 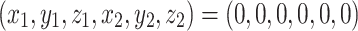 :
:
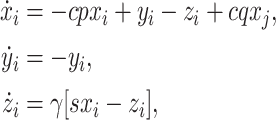 |
4 |
where 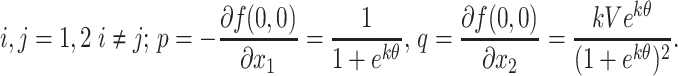 Linear part of (4)
Linear part of (4)
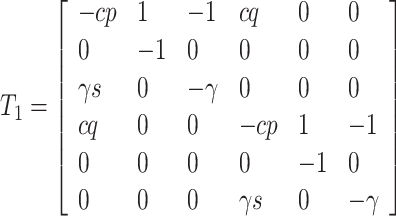 |
implies the following characteristic equation:
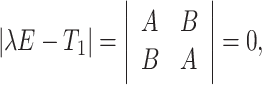 |
where
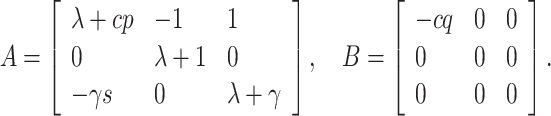 |
Then
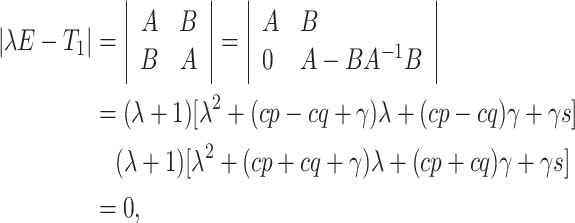 |
hence
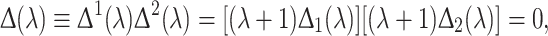 |
where
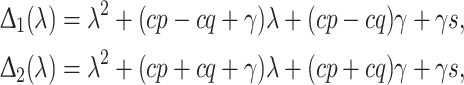 |
with solutions
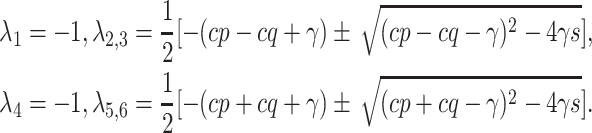 |
-
(i)
The sign of the real parts of the six eigenvalues determines the stability type of the trivial stationary point. Obviously, the real part of
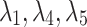 and
and 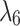 is negative for any value of the parameter c, but
is negative for any value of the parameter c, but 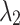 and
and 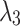 becomes pure imaginary for
becomes pure imaginary for 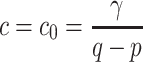 . Furthermore,
. Furthermore, 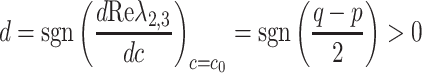 , so the real parts of
, so the real parts of  and
and  are also negative for
are also negative for 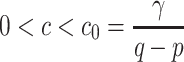 . As a result, the real parts of six eigenvalues are all negative for
. As a result, the real parts of six eigenvalues are all negative for 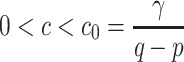 , namely the stationary solution is a stable attractor.
, namely the stationary solution is a stable attractor. -
(ii)
We can know from (i) that
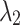 and
and 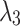 is a pair of complex conjugated eigenvalues for
is a pair of complex conjugated eigenvalues for 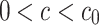 , i.e.,
, i.e., 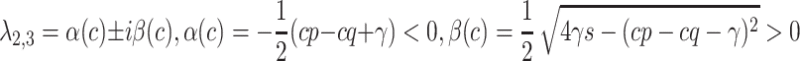 ; while
; while 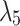 and
and 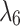 is a pair of complex-conjugate eigenvalues with negative real part for
is a pair of complex-conjugate eigenvalues with negative real part for 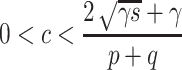 , and they become real when
, and they become real when 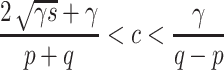 . Accordingly, the stationary solution is stable focus·node–focus·node and stable focus·node–node, respectively.
. Accordingly, the stationary solution is stable focus·node–focus·node and stable focus·node–node, respectively. -
(iii)When
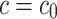 ,
, 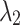 and
and 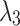 are pure imaginary
are pure imaginary 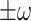 , where
, where 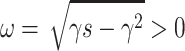 . The real parts of the other four eigenvalues are negative. The type of bifurcation at
. The real parts of the other four eigenvalues are negative. The type of bifurcation at  can be obtained by reducing the system (3) on the corresponding center manifold. Applying the center manifold theorem (Lu 2010) to system (3) and by logical deduction, step after step, we come to the dynamical system on the center manifold with parameter
can be obtained by reducing the system (3) on the corresponding center manifold. Applying the center manifold theorem (Lu 2010) to system (3) and by logical deduction, step after step, we come to the dynamical system on the center manifold with parameter  :
:
After using the normal form method (Lu 2010) and the conversion of coordinates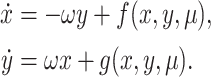
5 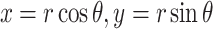 , we can get the normal form with the small
, we can get the normal form with the small 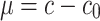 of Hopf bifurcation
of Hopf bifurcation
where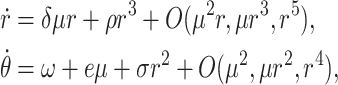
6 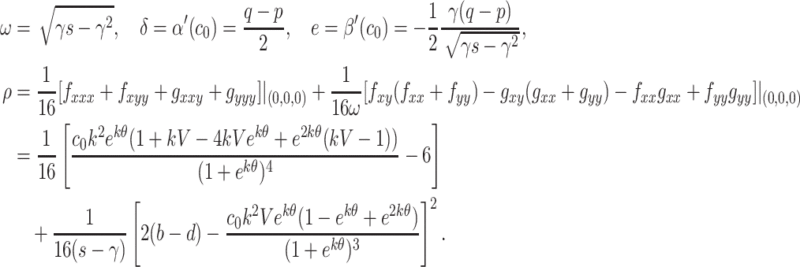
Since 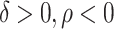 , stationary point for
, stationary point for 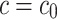 has supercritical Hopf bifurcation and that completes the proof of the theorem.
has supercritical Hopf bifurcation and that completes the proof of the theorem.
Now we consider an example to illustrate our conclusion. Let 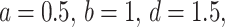
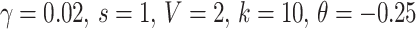 in system (3), then we have
in system (3), then we have 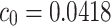 . Then, the Theorem 2.1.1 has supercritical Hopf bifurcation at
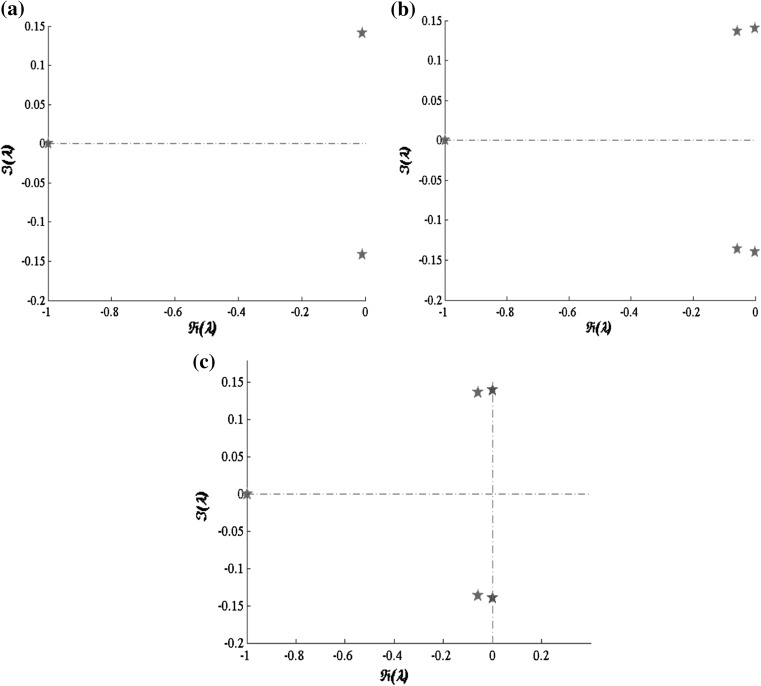
. Then, the Theorem 2.1.1 has supercritical Hopf bifurcation at 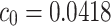 . The stability of the stationary point for the system (3) in Theorem 2.1.1 with parameters
. The stability of the stationary point for the system (3) in Theorem 2.1.1 with parameters 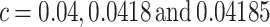 is shown in Fig. 2, in which we can clearly observe the change of the six eigenvalues’ real parts with the variation of the coupling strength in the complex plane.
is shown in Fig. 2, in which we can clearly observe the change of the six eigenvalues’ real parts with the variation of the coupling strength in the complex plane.
Fig. 2.
Computing and plotting stability of the stationary point of the system (3) for parameter a c = 0.04, b c = 0.0418, c c = 0.4185. The five-pointed stars denote the positions of the six eigenvalues of (3) in the complex plane, of which the green/red stars are those eigenvalues with negative/positive real part
Delayed coupling τ > 0
Consider the system (1) in the case of delayed coupling. As in the previous case, local stability of stationary solution is determined by analyzing the system linearized at 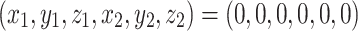 .
.
Theorem 2.1.2
The system (1) undergoes a codim-1 Hopf bifurcation at equilibrium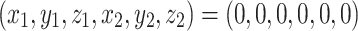 for critical time delays given by:
for critical time delays given by:
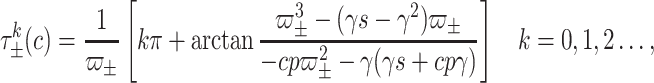 |
where
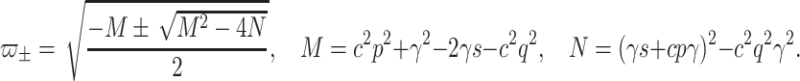 |
Proof
Linearization of the system (1) at 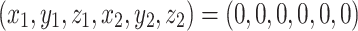
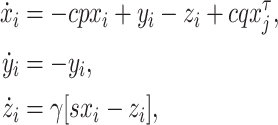 |
7 |
where
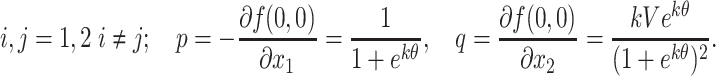 |
Because of the existence of delay, system (9) can be written as the form
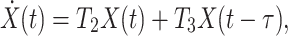 |
where
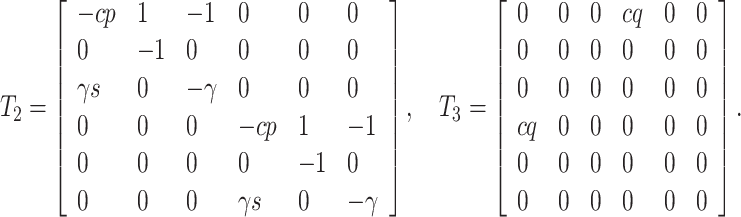 |
The equation 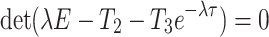 implies
implies
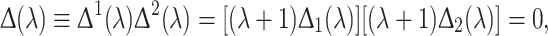 |
where
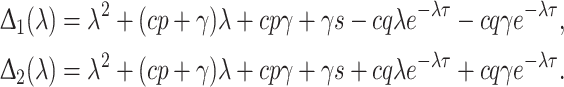 |
Bifurcations due to a nonzero time lag occur when some of the roots of equation above across the imaginary axes. Let us first discuss the nonzero pure imaginary roots. Substitution 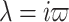 into
into 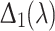 gives
gives
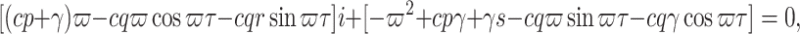 |
hence
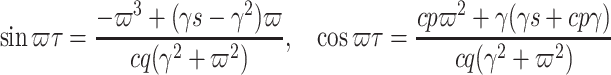 |
or into 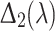 gives
gives
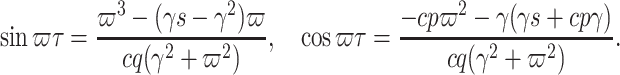 |
From the identities 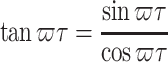 and
and 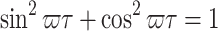 , we can obtain
, we can obtain
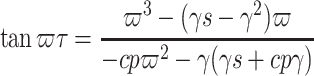 |
8 |
and
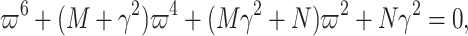 |
9 |
where
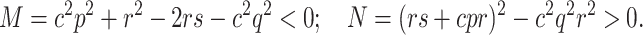 |
Since 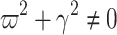 , the term
, the term 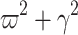 can be factored out from (9) to obtain
can be factored out from (9) to obtain
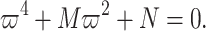 |
10 |
Hence
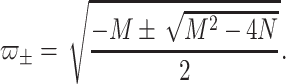 |
Substitution of 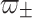 into (10) gives
into (10) gives
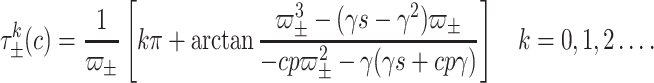 |
Differentiation of the characteristic equation
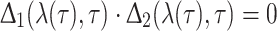 |
gives
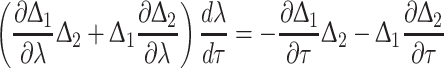 |
and
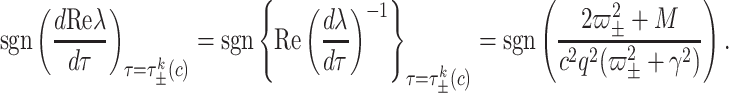 |
Substitution of 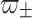 finally gives
finally gives
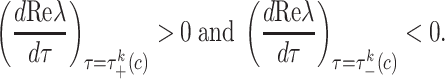 |
□
The expressions for 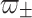 in Theorem 2.1.2 are valid if coupling constant c satisfies
in Theorem 2.1.2 are valid if coupling constant c satisfies 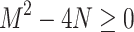 , i.e.
, i.e. 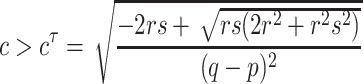 . For this reason, Theorem 2.1.2 is valid for
. For this reason, Theorem 2.1.2 is valid for 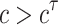 and for
and for 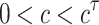 , the stationary point is stable for any τ.
, the stationary point is stable for any τ.
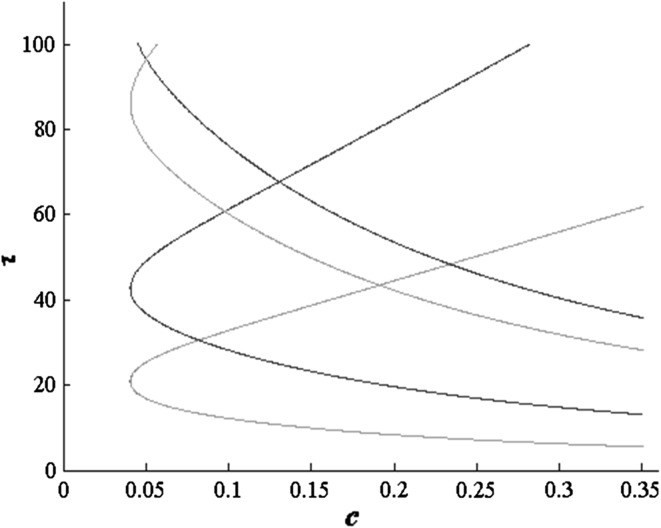
Below we use the DDE-BIFTOOL (Engelborghs et al. 2007), a Matlab package for bifurcation analysis of delay differential equations, to simulate the results of Theorem 2.1.2. Parameters in system (1) are the same as in Fig. 2 and then we have 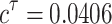 , i.e., the Theorem 2.1.2 is valid for
, i.e., the Theorem 2.1.2 is valid for 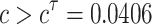 . The first few branches of the Hopf bifurcation curves
. The first few branches of the Hopf bifurcation curves 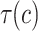 given by Theorem 2.1.2 is shown in Fig. 3, from which we can see that the system (1) has a good robustness for any delay when
given by Theorem 2.1.2 is shown in Fig. 3, from which we can see that the system (1) has a good robustness for any delay when  ; while for
; while for  , it is very sensitive for delay, namely for any fixed value of
, it is very sensitive for delay, namely for any fixed value of 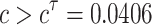 , the system will undergo a series of supercritical or subcritical Hopf bifurcations as the delay increasing.
, the system will undergo a series of supercritical or subcritical Hopf bifurcations as the delay increasing.
Fig. 3.
First few branches of the Hopf bifurcation curves 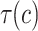 given by Theorem 2.1.2. Parameters as in Fig. 2. Cyan/blue curves correspond to supercritical/subcritical Hopf bifurcations. (Color figure online)
given by Theorem 2.1.2. Parameters as in Fig. 2. Cyan/blue curves correspond to supercritical/subcritical Hopf bifurcations. (Color figure online)
Synchronization transition of the firing patterns
In this section, corresponding to the different regions of Fig. 3 we mainly numerically investigate when the excitability of coupled system switches on or off and how the synchronous states transit with the changing of coupling strength and time-delays. So in what follows, we still focus on synchronization transitions of two excitable HR neurons coupled by delayed chemical coupling (1), and study the influence of coupling strength and delay on synchronization and neural firing.
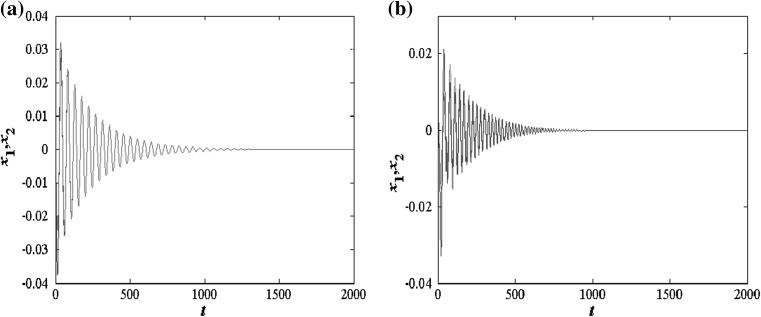
As is shown in Fig. 4a, b, when the coupling strength is less than the critical value for Hopf bifurcation (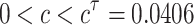 ), the system (1) will go to stable state for any delay. When coupling strength c = 0.03, the system (1) slows down to a stable state after going through an attenuated-oscillation for
), the system (1) will go to stable state for any delay. When coupling strength c = 0.03, the system (1) slows down to a stable state after going through an attenuated-oscillation for 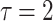 and
and 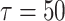 . The coupled neurons can’t fire in this case.
. The coupled neurons can’t fire in this case.
Fig. 4.
The firing patterns of the chemically coupled HR neurons for parameters c = 0.03 and a , b
, b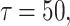 where the red and blue lines represent neuron 1 and neuron 2, respectively. (Color figure online)
where the red and blue lines represent neuron 1 and neuron 2, respectively. (Color figure online)
When the coupling strength is more than the critical value for Hopf bifurcation (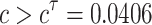 ), the coupled neurons begin to fire. To study the synchronous firing of the two neurons with delayed coupling, we introduce a statistic—similarity function:
), the coupled neurons begin to fire. To study the synchronous firing of the two neurons with delayed coupling, we introduce a statistic—similarity function: 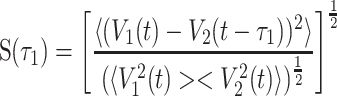 , where
, where 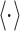 represents the mean with respect to time. Similarity function measures the time relatedness of the two signals
represents the mean with respect to time. Similarity function measures the time relatedness of the two signals 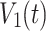 and
and 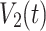 . The smaller the
. The smaller the 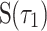 is, the lager the relatedness between
is, the lager the relatedness between 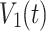 and
and 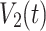 is, i.e., in-phase synchronization of the two coupled system becoming stronger from the synchronization point of view. Especially, when the coupled systems are complete synchronization,
is, i.e., in-phase synchronization of the two coupled system becoming stronger from the synchronization point of view. Especially, when the coupled systems are complete synchronization, 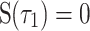 at
at 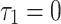 .
.
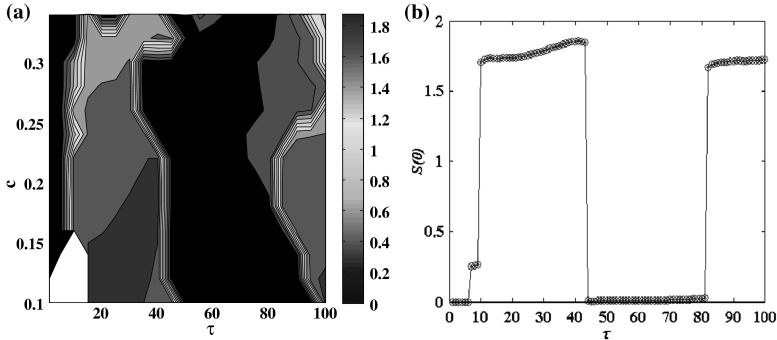
We give the change of 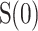 in the plane
in the plane 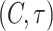 , as shown in Fig. 5a. Obviously, there are some areas in the plane
, as shown in Fig. 5a. Obviously, there are some areas in the plane 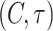 where
where 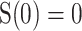 . So by numerical calculation, the coupled systems arrive at complete synchronization in some delay areas when
. So by numerical calculation, the coupled systems arrive at complete synchronization in some delay areas when 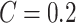 (see Fig. 5b). Meanwhile, in other delay areas the coupled systems reach to the inverse synchronization, see Figs. 6 and 7.
(see Fig. 5b). Meanwhile, in other delay areas the coupled systems reach to the inverse synchronization, see Figs. 6 and 7.
Fig. 5.
The change graph of the similarity functions for the chemically coupled HR neurons. a The variation of 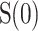 in the plane
in the plane 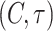 , b the variation of
, b the variation of 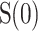 with
with 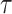 increasing when
increasing when 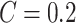
Fig. 6.
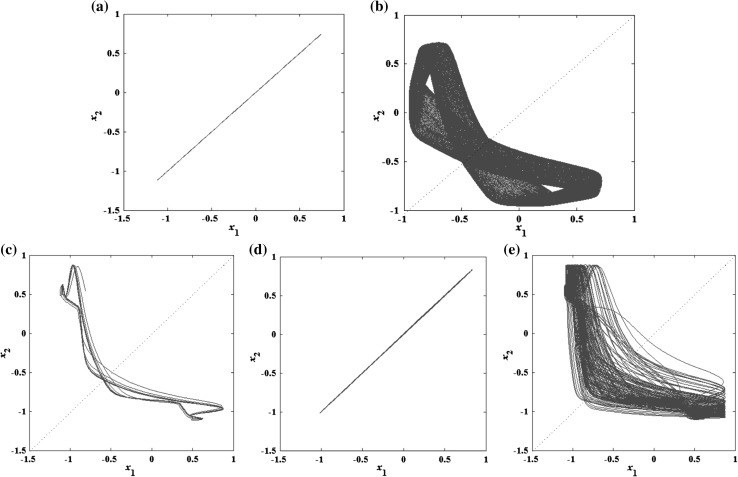
The phase graph in the plane 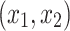 of the chemically coupled HR neurons with parameters C = 0.2 and τ = 5, 10, 30, 45, 90 from a to e
of the chemically coupled HR neurons with parameters C = 0.2 and τ = 5, 10, 30, 45, 90 from a to e
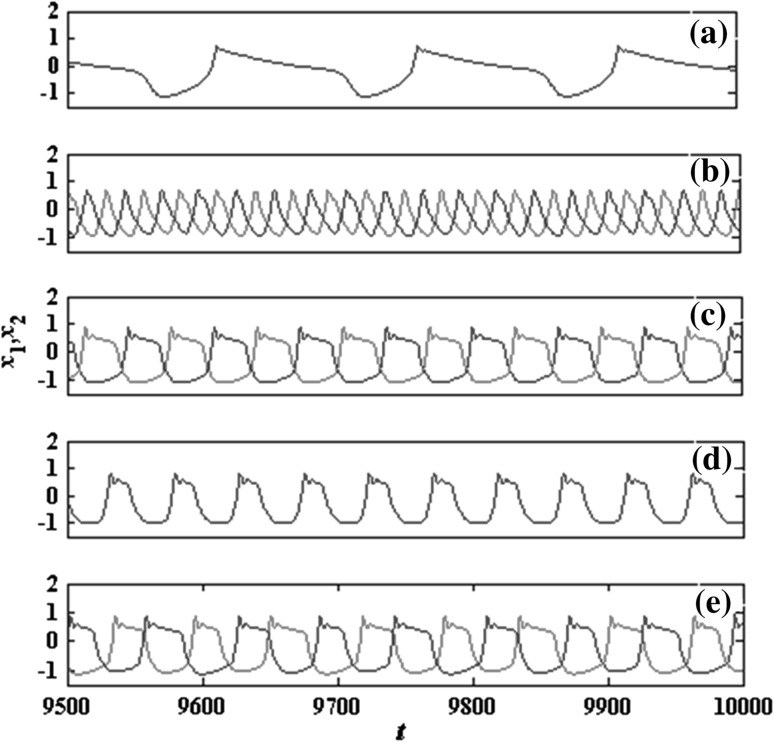
Fig. 7.
The transition of the synchronous firing patterns of system (1) with different delay τ from top to bottom being a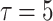 , complete bursting synchronization, b
, complete bursting synchronization, b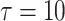 , inverse spiking synchronization, c
, inverse spiking synchronization, c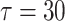 , inverse bursting synchronization, d
, inverse bursting synchronization, d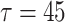 , complete bursting synchronization; e
, complete bursting synchronization; e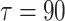 , inverse bursting synchronization
, inverse bursting synchronization
Figure 6a, d show that the membrane potentials of the two coupled neurons are completely linear correlated, indicating complete synchronization happens. Whereas, Fig. 6b, c, e show the two coupled neurons reach to inverse synchronization.
Figure 7 shows the synchronous firing patterns for coupling strength 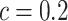 . The system (1) becomes oscillating when the coupling strength above the critical value for Hopf bifurcation (
. The system (1) becomes oscillating when the coupling strength above the critical value for Hopf bifurcation (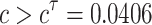 ). Taking some values of delay, the transition of synchronization can be shown in Fig. 5. It is observed that when the delay
). Taking some values of delay, the transition of synchronization can be shown in Fig. 5. It is observed that when the delay 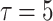 , the coupled neurons reach to complete bursting synchronization, as shown in Fig. 7a. When the delay increases to
, the coupled neurons reach to complete bursting synchronization, as shown in Fig. 7a. When the delay increases to 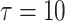 , the complete bursting synchronization transits to inverse spiking synchronization, as shown in Fig. 7b. As the delay increased to
, the complete bursting synchronization transits to inverse spiking synchronization, as shown in Fig. 7b. As the delay increased to 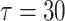 , the inverse spiking synchronization transits to inverse bursting synchronization as shown in Fig. 7c. When the delay further increased to
, the inverse spiking synchronization transits to inverse bursting synchronization as shown in Fig. 7c. When the delay further increased to 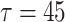 , the coupled neurons reach to complete bursting synchronization again, as shown in Fig. 7d. And in the Fig. 7e, i.e., when the delay is as large as
, the coupled neurons reach to complete bursting synchronization again, as shown in Fig. 7d. And in the Fig. 7e, i.e., when the delay is as large as 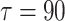 , the coupled system returns to inverse bursting synchronization once more. Therefore, the increasing of delay alternatively and regularly switches the synchronous patterns of system (1) between the complete bursting synchronization and the inverse synchronization.
, the coupled system returns to inverse bursting synchronization once more. Therefore, the increasing of delay alternatively and regularly switches the synchronous patterns of system (1) between the complete bursting synchronization and the inverse synchronization.
As above, firstly, we can know when the coupling strength is lower than the critical value the coupled systems always retain to be stable no matter how large the delay is, but the opposite hold false when the coupling strength is larger than the critical value, i.e., at this time, the coupled systems are always excitable. Secondly, when the neurons are coupling, the synaptic strength between actual neurons will increase to tend a stable value, which will keep its stability under certain conditions without drastic changes of the environment. Otherwise, great numbers of synchronous phenomena such as the spread of the virus in epidemiological network and congestions in the transmission of the signals are all influenced by time-delay. Therefore we mainly discuss the effect of time-delay in the synchronization.
Conclusion
In this paper, based on the excitable HR systems with chemical delayed coupling,we analytically investigated the conditions for the Hopf bifurcations by means of bifurcation theory. We numerically gave the supercritical and subcritical Hopf bifurcations which agree with the analytical ones. We also numerically investigated the synchronization transition of the firing patterns and found the complete synchronization and the inverse synchronization changed alternatively with the delay increasing. The reason for the synchronization transition of the firing pattern maybe relate to the supercritical and subcritical Hopf bifurcations which also occur alternatively as the delay increasing. We will give detailed research in the future work.
A certain delay can destroy the complete synchronization of coupled excitable neurons, and as the delay increasing, it can prohibit the inverse synchronization from arising in some particular time region. Moreover, we can control the c varying in a small region to inhibit the system’s excitability. As we know that phase synchronization and synchronization transitions have become more and more important because of their physiological and pathological significance, so the results may be helpful for us to forecast the dynamical behavior of coupled excitable neurons and provide a theoretical direction for developing medical treatment of restraining the synchronization of neurons, and further understand the essence of encoding and decoding of information.
Acknowledgments
The Project was supported by the NSFC (Grant No.10902001 and 11072013).
References
- Belykh I, Lange E, Hasler M. Synchronization of bursting neurons: what matters in the network topology. Phys Rev Lett. 2005;94(18):188101. doi: 10.1103/PhysRevLett.94.188101. [DOI] [PubMed] [Google Scholar]
- Burić N, Ranković D. Bursting neurons with coupling delays. J Phys Lett. 2007;363(4):282–289. doi: 10.1016/j.physleta.2006.11.032. [DOI] [Google Scholar]
- Burić N, Todorović D. Dynamics of FitzHugh–Nagumo excitable systems with delayed coupling. Phys Rev E. 2003;67(6):066222. doi: 10.1103/PhysRevE.67.066222. [DOI] [PubMed] [Google Scholar]
- Burić N, Grozdanović I, Vasović N. Type I vs. type II excitable systems with delayed coupling. Chaos, Solitons Fractals. 2005;23(4):1221–1233. [Google Scholar]
- Burić N, Todorović K, Vasović N. Synchronization of bursting neurons with delayed chemical synapses. Phys Rev E. 2008;78(3):036211. doi: 10.1103/PhysRevE.78.036211. [DOI] [PubMed] [Google Scholar]
- Dhamala M, Jirsa VK, Ding MZ. Enhancement of neural synchrony by time delay. Phys Rev Lett. 2004;92(7):74104. doi: 10.1103/PhysRevLett.92.074104. [DOI] [PubMed] [Google Scholar]
- Engelborghs K, Luzyanina T, Samaey G (2007) DDE-BIFTOOL: a Matlab package for bifurcation analysis of delay differential equations. http://twr.cs.kuleuven.be/research/software/delay/ddebiftool.shtml
- Faria T. On a planer system modelling a neuron network with memory. J Differ Equ. 2000;168(1):129–149. doi: 10.1006/jdeq.2000.3881. [DOI] [Google Scholar]
- Lu QS. Ordinary differential equation and dynamical system. Beijing: Beijing Aerospace University Press; 2010. [Google Scholar]
- Neefs PJ, Steur E, Nijmeijer H. Network complexity and synchronous behavior—an experimental approach. Int J Neural Syst. 2010;20(3):233–247. doi: 10.1142/S0129065710002395. [DOI] [PubMed] [Google Scholar]
- Ranković D. Bifurcations of Fitzhugh–Nagumo excitable systems with chemical delayed coupling. Matematiqki Vesnik. 2011;63:103–114. [Google Scholar]
- Shi X, Lu QS. Complete synchronization of coupled Hindmarsh–Rose neurons with ring structure. Chin Phys Lett. 2004;21(9):1695–1698. doi: 10.1088/0256-307X/21/9/005. [DOI] [Google Scholar]
- Somers D, Kopell N. Rapid synchronization through fast threshold modulation. J Biol Cybern. 1993;68(5):393–407. doi: 10.1007/BF00198772. [DOI] [PubMed] [Google Scholar]
- Vasović N, Burić N, Todorović K, Grozdanović I. Synchronization of the minimal models of bursting neurons coupled by delayed chemical or electrical synapses. J Chin Phys. 2012;21(1):10203. doi: 10.1088/1674-1056/21/1/010203. [DOI] [Google Scholar]
- Wang HX, Lu QS, Wang QY. Bursting and synchronization transition in the coupled modified ML neurons. J Commun Nonlinear Sci Numer Simul. 2007;13(8):1668–1675. doi: 10.1016/j.cnsns.2007.03.001. [DOI] [Google Scholar]
- Wang QY, Lu QS, Chen GR, Duan LX. Bifurcation and synchronization of synaptically coupled FHN models with time delay. Chaos, Solitons Fractals. 2009;39(2):918–925. doi: 10.1016/j.chaos.2007.01.061. [DOI] [Google Scholar]
- Yuan GY, Zhang GC, Wang GR, Chen SG. Synchronization and asynchronization in two coupled excitable systems. Commun Theor Phys. 2005;43(3):459–465. doi: 10.1088/0253-6102/43/3/017. [DOI] [Google Scholar]
- Zhen B, Xu J. Simple zero singularity analysis in a coupled FitzHugh–Nagumo neural system with delay. Neurocomputing. 2010;73(4–6):874–882. doi: 10.1016/j.neucom.2009.09.015. [DOI] [Google Scholar]