Platelet Transport Rates and Binding Kinetics at High Shear over a Thrombus

Abstract

Thrombus formation over a ruptured atherosclerotic plaque cap can occlude an artery with fatal consequences. We describe a computational model of platelet transport and binding to interpret rate-limiting steps seen in experimental thrombus formation over a collagen-coated stenosis. The model is used to compute shear rates in stenoses with growing boundaries. In the model, moving erythrocytes influence platelet transport based on shear-dependent enhanced diffusivity and a nonuniform platelet distribution. Adhesion is modeled as platelet-platelet binding kinetics. The results indicate that observed thrombus growth rates are limited by platelet transport to the wall for shear rates up to 6000 s⁻¹. Above 7000 s⁻¹, the thrombus growth rate is likely limited by binding kinetics (10⁻⁴ m/s). Thrombus growth computed from these rate-limiting steps match the thrombus location and occlusion times for experimental conditions if a lag time for platelet activation is included. Using fitted parameters, the model is then used to predict thrombus size and shape at a higher Reynolds number flow consistent with coronary artery disease.

Introduction

Arterial thrombosis leads to the vast majority of acute myocardial infarction and stroke cases (1–4). Recent studies have identified the importance of high shear rates on platelet adhesion and aggregation (5–17). Although shear-induced platelet accumulation has often been observed in experiments, the physical basis for this shear-dependence is not clear. For platelets to stick to the subendothelium, the platelet must be first transported to the wall and then must adhere. It is possible that the transport of platelets confers the shear rate dependence separately from the binding, which may or may not be shear stress-dependent.

The movement of platelets in whole blood is strongly affected by the motion of the red blood cells (RBCs) in arterial flow. For flowing blood, the semisolid RBCs collide and rotate at a rate that depends on local shear rates and the local concentration of particles (18–23). The additional particulate motion creates an enhanced diffusivity relative to the thermal motion predicted to occur in a dilute suspension and may play an important role in shear-induced platelet accumulation (24,25).

Platelet transport is further affected by nonuniform particulate concentration profiles. RBCs move toward the center of a vessel and platelets move toward the periphery, which is commonly called platelet margination. Platelet margination can create a large concentration of platelets near the surface of a vessel, reaching up to 17 times the average platelet concentration (26–28). Because binding kinetics are directly affected by the local species concentration, margination of platelets could play a major role in thrombus growth. The relative contributions of margination and enhanced diffusivity versus binding kinetics on thrombosis at a given shear rate remains unknown.

The hemodynamic transport of platelets can be modeled several ways. Some transport models have been used in an attempt to characterize RBC motion on a microscale (29–31), whereas others have modeled motion on a macroscale (32–34). Direct numerical simulations of particulate RBC and platelet motion are too computationally expensive for our study of large-scale thrombosis. Alternatively, the convection-diffusion equation can be used to model concentrated suspensions through the use of a potential function in the species flux constitutive equation, an enhanced diffusivity term, and a drift function for RBCs (24,35,36). This approach allows for more exploration of relative shear effects with standard computational resources. We then compare platelet flux to the wall relative to the observed experimental thrombus growth rate to determine if flux due to transport is rate-limiting.

If the platelet-surface flux far exceeds thrombus growth rates, then growth is taken to be limited by binding kinetics or embolization. Platelet on-/off-rate kinetics are dependent on their activation state, glycoprotein efficacy, and binding protein presence, which all have been shown to be shear- dependent, with little delineation between shear stress relative to shear rate effects. However, the combined influence of these factors on platelet binding is largely unknown. Lastly, thrombus embolization and removal may occur (37). This process has been observed experimentally, but little data exist as to the incidence or rate of this process. We neglect embolization from lack of information.

Atherosclerosis produces a lesion that narrows the arterial lumen over time, creating a stenosis. High shear rates exist near the stenosis apex, which is where rapid platelet accumulation can occur (5–11). The hemodynamics around a stenosis are pathophysiological with large changes in shear rate and the potential for flow separation, providing a rich, complex environment in which to compare a model with experimental thrombus growth. We have previously reported on the experimental creation of thrombus under high shear, near a stenosis, that grows to full occlusion and is consistent with clinical disease (11,38,39). These thrombi grow very rapidly and are platelet-rich, with platelets comprised of ∼80% of the thrombus. We use the thrombus growth data from these experiments to fit variables in a computational model. Selective variation in the models can provide insight into the separate mechanisms of shear-dependent growth from transport and binding.

In this study, we investigate the transport of platelets for stenotic blood flow by developing a computational model of convection-diffusion, accounting for RBC effects on platelet transport. This model includes the ability to model dynamic thrombus growth as a solid mass with updated hemodynamic variables in an iterative process until the vessel is nearly occluded. We investigate rate-limiting processes in thrombus growth for shear rates ranging from 100 to 100,000 s⁻¹. These computational results are first compared with experimental in vitro thrombus growth over a stenosis with collagen coating under the same hemodynamic conditions (38). We extend the model to predict occlusion times for 40–80% stenoses in a coronary artery to illustrate how hemodynamic computations can be used with other studies to begin describing the risk of thrombosis in a clinically relevant setting with patient-specific parameters.

Methods

The transport of platelets in blood flow consists of convection due to the fluid motion, diffusion of platelets across streamlines caused by RBCs, and platelet depletion from the blood. The constitutive equation used in the model that describes species flux in the convection-diffusion equation is

$${\overrightarrow{N}}_j=-\overrightarrow{v}{c}_j-D_j\nabla {\psi }_j,$$ (1)

where c_j is the concentration of species, j, D_j is the diffusivity of the species, ψ_j is the field potential, and $\overrightarrow{v}$ is the velocity vector. The velocity is determined by solving for the incompressible conservation of mass and momentum in the Navier-Stokes equations. Constants used in the transport methods are provided in Table 1.

Table 1.

Constants used in the model based on the references noted below

Nomenclature	Constant	Description
a	4 μm	Scale for particle collisions on the order of a RBC
β	−7.87	Constant in tanh function for the CRBC,eq profilea
k	0.15	Constant for enhanced diffusivityb
Dth,platelet	3.1 × 10−14 m2/s	Thermal diffusivity of a platelet
Dth,RBC	1.4 × 10−14 m2/s	Thermal diffusivity of a RBC
δ	0.77	Constant in tanh function for the CRBC,eq profilea
kb	1.38 × 10−23 m2 kg/s2	Boltzmann constant
kt	10−3, 10−4, 10−5 m/s	Binding rate constant
η	0.0038 kg/m/s	Kinematic viscosity of blood at high shear rates
n	0.8	Constant for enhanced diffusivityb
Q0	120 mL/min	Average flow through the coronary artery
R	0.75 mm, 1.5 mm	Radius of the vessel for the experimental-based studies and for the extension to a coronary artery, respectively
Req,j	4.2 μm, 1.9 μm	Equivalent radius of a sphere for a RBC and platelet, respectivelyc
T	310 K	Temperature
z	2.25 mm	Axial location of simplified model measurements (stenosis apex)c

^aAarts et al. (26).

^bZydney and Colton (24).

^cBark et al. (38).

Enhanced diffusivity, D_j

The diffusivity term in the transport equation is set as a constitutive relation, a property of the species j in the fluid. We estimate thermal diffusivity, D_th, from the Stokes-Einstein equation for dilute suspensions,

$$D_{th}=\frac{k_{\text{B}}T}{6\pi \mu R_{\text{eq}}},$$ (2)

where k_B is the Boltzmann constant, T is the temperature (310 K), μ is the kinematic viscosity of the fluid, and R_eq is the equivalent radius of a sphere (∼4 μm for a RBC and ∼2 μm for a platelet). The choice for RBCs is based on the average volume of an undeformed RBC, despite reorientation and stretch under flow, resulting in a shear-dependent increase in cell diameter (40).

In blood, thermal diffusivity is not sufficient to describe lateral migration because blood is a concentrated suspension. RBC motion exhibits a random walk similar to diffusion. To model the enhanced motion, the diffusivity term can be augmented. Zydney and Colton (24) describe an augmentation based on an earlier model (25), which they denote as enhanced diffusivity, and is expressed as

$$D_j=k{a}^2\varphi {\left(1-\varphi \right)}^n\dot{\gamma }+D_{th},$$ (3)

where k is a constant at 0.15; a is a scale for particle collisions and is taken as the approximate radius of a RBC, 4 μm; ϕ is the local hematocrit; n is a constant at 0.8 ± 0.3; and $\dot{\gamma }$ is the local shear rate.

Field potential, ψ_j, for mass transport

The gradient in the field potential, Eq. 1, is described with a modified equation similar to one developed by Hund and Antaki (35). A field potential acts as a driving force for particles, where Fick’s first law is used to describe species flux for RBCs. For platelets, the potential excludes platelets from regions of high hematocrit, which we model as

$$\begin{array}{c}\nabla {\psi }_{\text{RBC}}=\nabla \left(c_{\text{RBC}}\right),\\ \nabla {\psi }_{\text{platelet}}=\nabla \left(\varphi c_{\text{platelet}}\right).\end{array}$$ (4)

Nonuniform cell concentration, margination

We create a nonuniform concentration of RBCs a priori by utilizing a drift term, similar to the platelet drift term used by Eckstein and Belgacem (36). The flux of RBCs, Eq. 1, is augmented with an additional drift term

$$J_{\text{RBC}}\hat{r}=\left[{\zeta }_{\text{RBC}}^{\prime }{c}_{\text{RBC}}-v_r{c}_{\text{RBC}}-D_{\text{RBC}}\frac{d}{dr}{\psi }_{\text{RBC}}\right]\hat{r},$$ (5)

where ζ′ is the drift term that is equal to 0 for a uniform equilibrium concentration profile. In cylindrical fully developed flow, the drift term is

$${\zeta }_{\text{RBC}}^{\prime }=D_{\text{RBC}}\frac{1}{c_{\text{RBC},\text{eq}}}\frac{d}{dr}{c}_{\text{RBC},\text{eq}},$$ (6)

where c_RBC,eq is the equilibrium RBC concentration profile. When RBC profiles are disturbed, they return to equilibrium at a rate proportional to the diffusivity.

The equilibrium RBC profile is taken from experiments of Aarts et al. (26) for flow through a 3 mm cylindrical vessel, which we describe using a hyperbolic tangent function, similar to Hund and Antaki (35):

$$c_{\text{RBC},eq}=\frac{{\overline{c}}_{\text{RBC}}{R}^2\left(1+\tanh \left[\beta \left(r/R-\delta \right)\right]\right)}{2\underset{0}{\overset{R}{\int }}r\left(1+\tanh \left[\beta \left(r/R-\delta \right)\right]\right)dr}.$$ (7)

Here, ${\overline{c}}_{\text{RBC}}$ is the mean RBC concentration across the vessel, whereas β and δ are used to shape the hyperbolic tangent, corresponding to −7.87 and 0.77. A more detailed description of this development is listed in the Supporting Material. The flux of platelets is assumed to react passively to the RBC distribution through Eq. 4. The value R is updated during the simulation to account for a growing thrombus, and therefore Eq. 7 is assumed to scale smaller with the local vessel radius. A cubic spline is fit to R as a function of axial location to avoid discontinuities.

Computational regions

A growing boundary is modeled to simulate platelet deposition resulting in thrombus growth. However, a moving boundary presents issues in user-defined functions within the commercial code used in this study and, therefore, three different spatial regions are modeled to simulate an impenetrable thrombus, including the thrombus, the border, and normal computational cells. The thrombus is assumed to be impenetrable by plasma and effectively acts as a solid. The border is a region where platelets are allowed to react with thrombus and deposit on the thrombus surface. The normal region depicts a region where blood flows freely. The regions are depicted in Fig. 1 A. The mass and momentum governing equations are solved in all regions with a −10⁵⁰$\left(\mu \overrightarrow{v}\right)$ viscous resistance used in the thrombus. The flow field is determined in the normal and border cells by the Navier-Stokes equations. A no-slip condition is applied at the vessel wall.

Figure 1.

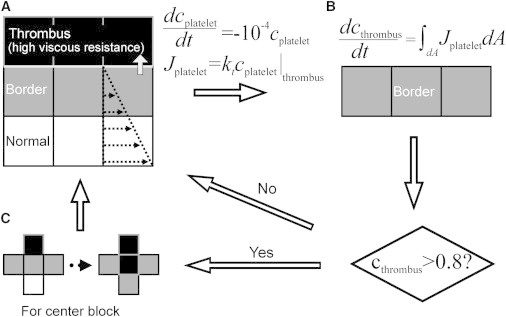
Schematic of the algorithm used to model thrombus growth. (A) Three different regions exist, including normal, thrombus border, and thrombus. The flow field is determined in all computational cells. Thrombus acts as a solid region, impenetrable to flow and RBC’s. Species transport is computed for platelets with a sink term in the thrombus and a flux term acting as a boundary condition between a thrombus border and thrombus to simulate deposition of platelets. (B) The rate of change of the thrombus volume fraction in the thrombus border is determined by integrating the flux of platelets out of the thrombus border. After the volume fraction of a thrombus border is >0.8 platelets, the cell is converted to thrombus. (C) All computational cells adjacent to a new thrombus are converted to a thrombus border.

After flow variables are updated, transport is determined through the convection-diffusion equation. A Neumann boundary condition of 0 species flux is applied at the vessel wall for RBCs and platelets. The same condition is applied at the border/thrombus interface for RBCs. Alternatively, for platelets, the flux at the border/thrombus interface is

$$J_{\text{platelet}}=k_t{c_{\text{platelet}}|}_{\text{thrombus/thrombus}\text{-}\text{border}},$$ (8)

where k_t is the reaction rate of platelets at a thrombus surface. The reaction rate represents the net rate of adhesion, incorporating both attachment and detachment. To implement this in the software FLUENT 6.3.26 (ANSYS, Santa Clara, CA), we adopted user-defined functions where platelets are consumed from a border based on Eq. 8 and correspondingly the volume fractions of the consumed platelets are recorded for each time step in each border cell. However, platelets computationally enter the thrombus, which are eliminated by a sink (dc_platelet/dt = −10⁴ c_platelet); see Fig. 1 B. Once the volume fraction recorded in the border cells exceeds 80%, it becomes thrombus and the surrounding normal cells are converted to border cells. 80% is chosen as a threshold because the platelet packing factor is experimentally found to be 0.8 (39,41); see Fig. 1 C. Added complexities of platelet spreading are neglected, and we assume the conservation of cell volume.

Computational implementation

Computational fluid dynamics were used to solve the mass transport and Navier-Stokes equations through the software FLUENT 6.3.26 (ANSYS). First-order upwind discretization schemes are used to solve the Navier-Stokes and convection-diffusion equations. Because sudden changes are temporally made in the flow region of the simulations due to converting cells into different computational regions, a second-order scheme is not used for stability purposes. A coupled method is used for pressure-velocity coupling. Fluid density is set at 1025 kg/m³ and fluid kinematic viscosity is set at 0.0038 kg/m^−s. An unsteady solver was used for the simulation time required for thrombus boundary growth. Atmospheric pressure is applied as an outlet boundary condition. User-defined functions are used to create the model described above.

The software GAMBIT (ANSYS) was used to generate and mesh a two-dimensional axisymmetric vessel. A structured mesh was created with high resolution near the region where thrombus was expected to grow, and a lower resolution mesh was created elsewhere. Mesh independence was verified, except for nearly occluded (>95% stenosis) vessels. These very severe stenoses can occur as the thrombus in the simulations approaches occlusion and the lumen diameter reduces to the grid size.

The initial stenosis geometry is based on an experimental geometry as (38)

$$\frac{r}{R}=1-\frac{d}{2\left(100\%\right)}\left[1-\cos \left(\pi \left(\frac{x}{x_0}+1\right)\right)\right],$$ (9)

where r is the radius at a given axial coordinate, R is the nominal radius, d is the stenosis severity in percent stenosis by diameter, x is the axial distance from the stenosis apex, and x₀ is half of the stenosis length. The stenosis was predefined as thrombus computational cells to create the shape of the wall.

The length of the stenosis, x₀, is set at 3R. We assumed rigid walls, steady flow, axisymmetry, and no vessel curvature other than the presence of the stenosis. Platelet, RBC, and fluid velocity profiles are predefined at their equilibrium distributions at the entrance of the vessel, as described further in the Supporting Material. We apply a diffusivity coefficient of 3 × 10⁻⁵ m²/s in the first three diameters of the computational domain to ensure that concentrations profiles are developed upstream of the stenosis.

Leveque model

The model describing platelet motion can be simplified for blood flow in an axisymmetric straight tube, sometimes referred to as a local Leveque solution. An analytical equation for platelet deposition was proposed in Turitto and Baumgartner (42), and is expanded upon in the Supporting Material for our model,

$$J_{\text{platelet}}=\frac{{\overline{c}}_{\text{platelet}}}{\frac{1}{k_t}+\frac{1.86}{{\left(\frac{\dot{\gamma }{D}_{\text{platelet}}^2}{x}\right)}^{1/3}}},$$ (10)

where ${\overline{c}}_{\text{platelet}}$ is the average platelet volume fraction. The axial dimension, x, is set at 3R for thrombus growth evaluation at the stenosis apex (Eq. 9). This analytical expression is attractive as it greatly simplifies the amount of computation required to generate a result, but assumes parabolic velocity profiles throughout the flow domain. Equation 10 does not account for the nonuniform RBC and platelet concentration profiles.

Measured thrombus progression rates

Experimental thrombus progression was previously determined for a large range of shear rates that varied across a stenosis during growth (100–100,000 s⁻¹) (38). The experimental conditions were replicated as a computational case to determine contributions of transport and platelet kinetics to thrombus growth rates relative to the local shear rate. The nominal radius of the vessel was 0.75 mm with a constant flow rate of 0.25 mL/min applied at the inlet.

Coronary artery flow through a stenosis

A clinically relevant case of a diseased coronary artery was created to compute thrombus shape and occlusion times under pathophysiological conditions. Fractional flow reserve from reactive hyperemia was included, based on Gould et al. (43),

$$\overline{Q}=\{\begin{array}{cc}{Q}_0& d<74\%\\ Q_0\left(0.0015d^2-0.3d+15\right)& d>74\%\end{array},$$ (11)

where Q₀ is the average flow rate in the absence of a stenosis. Stenoses (Table 1) defined by Eq. 9 were placed in a 3 mm-diameter tube to provide conditions that simulate plaque in a coronary artery. As the Reynolds number in coronary arteries is ∼220, we assume laminar flow throughout the simulation (45). The computational mesh prevented complete closure of the stenosis for the growing boundary, thus the simulations were stopped at a 95% diameter stenosis.

Results

Concentration distribution and hemodynamics

A stenosis alters local hemodynamics. At low Re, flow follows the curvature of the stenosis, as depicted by streamlines (top) in Fig. 2 A i. Fluid accelerates along the stenosis until the apex, after which it decelerates, shown by velocity vectors (bottom). Correspondingly, RBCs localize to the center of the vessel (top), whereas platelets marginate to the wall of the vessel (bottom) as a result of the RBC motion, as shown in Fig. 2 A ii. Specifically, the near-wall platelet volume fraction upstream of the stenosis is 0.013, lowering to 0.005 at 1.5 radii upstream of the apex (converging region), as plotted in Fig. 2 A iii. The apex had a maximum volume fraction of 0.002. Because mass is conserved and the average velocity is high at the apex, the area-weighted average platelet concentration falls below the inlet average platelet concentration, but the mass-weighted average remains constant across the axis of the computations. The stenosis is sufficient to alter the platelet concentration profile for downstream portions of the vessel.

Figure 2.

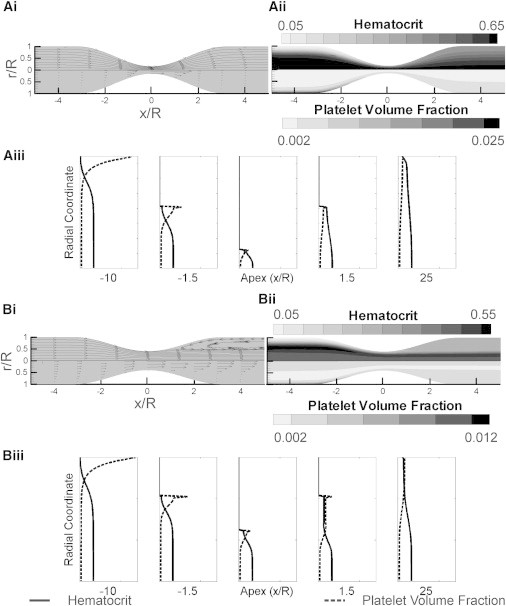
(A) Flow computed from an 84% stenosis by diameter with a Re inlet of 1 to match conditions of an in vitro experiment. (i) Streamlines (top) and velocity vectors (bottom) illustrate steady laminar flow. (ii) RBC (top) and platelet (bottom) volume fraction radial profiles vary slightly along the axis of the vessel. Downstream of the stenosis, the RBCs and platelets disperse more evenly across the vessel, minimizing platelet margination. (iii) Plots of the radial concentration profiles at different axial locations. Margination is clear upstream of the stenosis, but the near-wall platelets are reduced near the apex of the stenosis. Concentration profiles remain disturbed downstream of the stenosis apex. (B) Coronary flow conditions computed from a 60% stenosis by diameter with a Re inlet based on Eq. 11. (i) A recirculation region occurs downstream of the stenosis, as illustrated by streamlines (top) and velocity vectors (bottom). Fluid velocities near the central axis remain high downstream of the stenosis. (ii) Hematocrit (top) and platelet (bottom) concentration contours. The recirculation region has a more uniformly distributed platelet volume fraction over a wider radial distance. Conversely, RBCs congregate in the center stream downstream of the apex with few in the recirculation region. (iii) Radial volume fractions of platelets and RBCs 2 mm downstream of the stenosis apex have a similar profile to the apex, due to the relative rate of the flow compared to the diffusion rate.

Alternatively, we compute these patterns for coronary artery flow conditions; Fig. 2 B, i–iii, for Re = 230. Because there is a downstream separation region, RBCs remain concentrated at the central jet. RBCs and platelets are evenly distributed in the recirculation region. The near-wall platelet count is higher in coronary flow than low Re flow in the far 25 radii downstream from the larger shear-rate-dependent enhanced diffusivity.

Platelet flux for shear rate <6000 s⁻¹

Platelet transport is modeled for four distinct conditions:

• 1.Platelets move by thermal motion in the flow without RBC interaction, similar to platelet-rich plasma;
• 2.Platelets move by enhanced diffusivity (ED) from a uniform RBC distribution;
• 3.Platelets move by ED with margination; and
• 4.Platelets move by the Leveque equation with no kinetic limitation.

Conditions 1–3 are used to determine contributions from margination and ED to platelet transport. Condition 4 is used to evaluate the use of a simpler model. These cases are presented in Fig. 3 A and are compared with fitted experimental data (FED). Kinetic platelet binding rates were set at k_t = 10⁻³ m/s as an arbitrarily high value. Note that greater kinetic rates did not alter the growth rates:

• 1.Thrombus growth rates from platelet transport by thermal motion only (Eq. 3: k = 0) yields a value of ∼10⁻³ μm³/μm² min. Thermal diffusivity alone cannot account for the much higher observed experimental thrombus growth rate.
• 2.Enhanced diffusivity was investigated for a uniform RBC profile. Platelet flux based on ED alone exceeded experimental values with a large root-mean square error (RMSE = 13). Thus, ED is sufficient to supply enough platelets to the surface. Note that the modeled platelet flux from ED alone was consistently below the experimental flux for shear rates below 3000 s⁻¹, but exceeded experimental flux values for higher shear rates. For this condition, no margination/drift was included, resulting in a large number of RBCs near the wall and high ED at the wall.
• 3.ED with the platelet margination from RBC skewing was included in the third condition. Platelet flux correlates with the experimental results very well for shear rates below 6000 s⁻¹ (r = 0.97, p < 0.0001, RMSE = 2.8).
• 4.The Leveque model, depicted in Eq. 10, was used with ED (Eq. 3: ϕ = 0.45) to determine platelet flux. In this model, the flux is linearly proportional to the shear rate as can be seen when ED (Eq. 3) is inserted into Eq. 10. The flux was consistently below the experimental flux for shear rates below 3000 s⁻¹.

Figure 3.

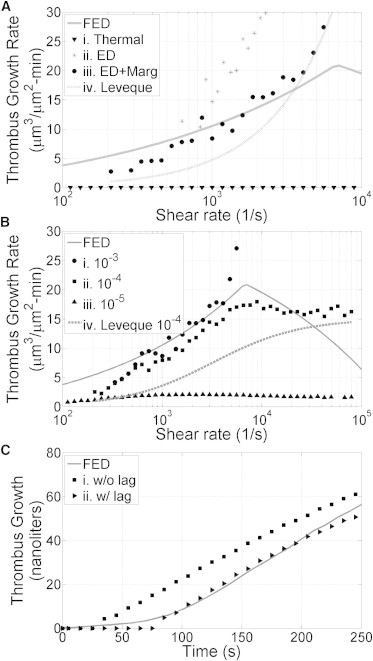
Plots consist of an average accumulation of platelets in the model over a 4-min time span. The experimental curve corresponds to the equation: $J_{\left(<6790s^{-1}\right)}=1.7{\dot{\gamma }}^{0.30}-3.0,J_{\left(>6790s^{-1}\right)}=34-1.1{\dot{\gamma }}^{0.28}\mu {\text{m}}^3/\mu {\text{m}}^2-\min$. (A) Platelet flux to the wall versus shear rates for different model transport conditions compared to experimental thrombus growth rates for an 84% stenosis with a flow rate of 0.25 mL/min and a kinetic binding rate of 10⁻³ m/s, which effectively acts as infinite sink for shear rates <6000 s⁻¹. (i) Platelet flux from thermal motion. (ii) Platelet flux from enhanced diffusivity (ED) only. (iii) Platelet flux with ED and RBC skewing. (iv) Platelet flux from the Leveque approximation. (B) Modeled thrombus growth rates relative to shear under the conditions of panel A, but with different kinetic binding rates: (i) k_t = 10⁻³ m/s, (ii) k_t = 10⁻⁴ m/s, and (iii) k_t = 10⁻⁵ m/s. (iv) The Leveque model is also plotted with a kinetic binding rate, k_t = 10⁻⁴ m/s, for comparison. (C) Modeled thrombus volume versus time for two conditions compared to an average of experimental thrombus growth with a flow rate based of 0.25ml/min and an initial 84% stenosis. (i) k_t = 10⁻⁴ m/s. (ii) k_t = 10⁻⁴ m/s in addition to a lag time for platelet activation under shear as described by Eq. 12. Note that the lag time is added based on the average lag time as a function of shear rate given in Bark et al. (38).

Transport summary

Thermal motion without enhanced diffusivity is not sufficient to obtain platelet fluxes seen in experiments. The best correlation between experimental rates and the computational rates exists when ED and margination are both included in the model. Because platelet transport and experimental thrombus growth rates are on the same order of magnitude for shear rates below 6000 s⁻¹, shear-dependent thrombosis in this range is most likely caused by hemodynamic transport rather than bonding kinetics.

Kinetic limitations for shear rate >7000 s⁻¹

Platelet flux with the assumed function for ED given in Eq. 3 increases without bound as shear rate increases. Thus, platelet flux exceeds the experimental growth rates for all conditions with ED above a shear rate of 7000 s⁻¹. At these high shear rates, platelet binding kinetics may be the dominant factor limiting thrombus growth rates. We thus evaluated kinetic binding rates by varying k_t given in Eq. 8 over three orders of magnitude to find a value that would best match the experimental data of thrombus flux.

For k_t = 10⁻³ m/s and k_t = 10⁻⁴ m/s, thrombus growth rates increase relative to shear at similar rates at low shear rates (below 7000 s⁻¹), as illustrated in Fig. 3 B. Above 7000 s⁻¹, k_t = 10⁻⁴ m/s yields a growth rate that becomes bounded at 20 μm³/μm² min similar to the experiments. A lower kinetic binding rate (k_t = 10⁻⁵ m/s) results in modeled thrombus growth rates that are an order of magnitude smaller than experiments. Thus, a kinetic binding rate of k_t = 10⁻⁴ m/s results in predicted thrombus growth rates that are the most similar to experimental thrombus growth rates (RMSE = 3.6). The Leveque model combined with k_t = 10⁻⁴ m/s predicts smaller thrombus growth rates relative to the numerical model (∼75% at 7000 s⁻¹), but the Leveque model also does not account for margination. The curve could be increased by the same factor, by assuming a higher concentration of near-wall platelets, increasing the C_j,inf term in Eq. 10. Thus, the variations in model parameters indicate that thrombus growth rates appear to be rate-limited by whole blood platelet transport up to shear rates of 6000 s⁻¹, transitioning to binding kinetics above shear rates of 7000 s⁻¹.

Volume growth of thrombus

A transport model including kinetics (ED + margination + k_t = 10⁻⁴ m/s) can be used to predict thrombus volume growth over time in a stenotic artery based on the local hemodynamics. This predicted growth versus time is shown in Fig. 3 C, but does not quite match the experimental observations. In the experiments, there is a consistent lag time of >60 s before volume growth is significant, which is likely due to the time required for shear-dependent activation of platelets adhered to the wall (38). We have added this lag time as a shear-dependent factor based on an experimental fit, mathematically described by

$$t_{\text{lag}\text{time}}=280{\dot{\gamma }}^{-0.2}\text{s}\text{.}$$ (12)

The resultant model of thrombus volume growth including the lag time is depicted in Fig. 3 C and shows good concordance with the experiment. We term this model the full transport model (FTM), which includes ED, margination, kinetics, and activation. The FTM model creates the thrombus that is primarily formed near the stenosis apex, similar to the experiments.

Occlusion time for the full transport model

The model can be further used to predict the location and shape of a thrombus in a stenosis over time. We use the FTM to predict thrombus growth and occlusion times in a human coronary artery. Thrombus is allowed to computationally grow under time-averaged (steady) coronary artery conditions with flow and transport variables updated during the growth that depend on the initial stenosis severity.

Simulations of thrombus growth were performed for a 40, 60, and 80% (diameter) stenosis until the vessel was effectively occluded. Occlusion times relative to initial platelet deposition decrease with respect to stenosis severity (Fig. 4 A).The moderate and severe stenoses can proceed to occlusion in a time-frame consistent with clinical observations of thrombosis in coronary arteries. Additional computations would be required to explore how occlusion times change for other stenosis shapes and other conditions.

Figure 4.

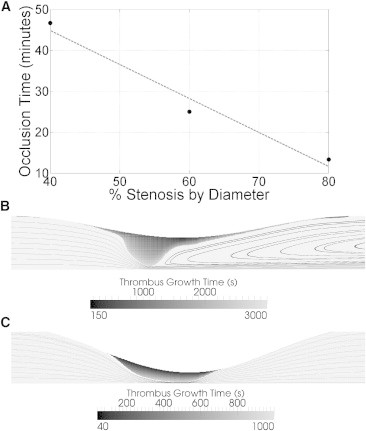
Occlusion time for a given stenosis under average flow conditions of a coronary artery, with the full model. (A) The occlusion time decreases as the stenosis severity increases. (Dashed line) Guide to the eye. (B) Moderate stenosis (40%) creates a focal thrombus at the throat with a large separation zone downstream of the thrombus after 47 min. (C) Severe stenosis (80%) creates a thrombus with a broader base in the throat after 13 min. No separation zone was present in this stenosis, either initially or near occlusion.

Fig. 4, B and C, illustrates the shape of the thrombus near the stenosis apex at a time just before occlusion for two different initial stenoses. Some differences are evident. For an initial stenosis that is moderate (40% by diameter), there is a maximum initial shear of 7530 s⁻¹, with lower shear rates away from the stenosis apex. As thrombus grows, shear rates along the thrombus rise to a wall shear rate that can reach 215,000 s⁻¹, spanning the transition from transport to binding limited growth. The resultant thrombus from these conditions is quite focal just upstream of the apex, and produces a large recirculation zone behind the thrombus (Fig. 4 B).

If the initial stenosis is severe (80%), the initial shear rate is 174,000 s⁻¹ at the apex. The thrombus extends more uniformly in the axial direction with no flow separation as a result in flow rate reductions from fractional flow reserve due to the severity of the stenosis (Fig. 4 C). Thus, very high shear rate thrombus formation does not appear to be strongly affected by the presence of flow separation. Growth at very high shear rates is limited primarily by the kinetic binding rate and less by the local transport hemodynamics resulting in more uniform growth for shear rate locations >7000 s⁻¹. In both cases, the dominant volume of thrombus in stenoses is clearly focused in the throat where shear is highest. Little growth is seen distal to the stenosis apex for either stenosis severities, where recirculation presides and enhanced diffusivity is relatively low.

Discussion

Platelet transport and platelet binding kinetics were investigated in this study to determine their relative contribution to rapid thrombus growth. Rapid platelet accumulation is found to be rate-limited by platelet transport for shear rates below 6000 s⁻¹. These results are in agreement with Turitto and Baumgartner (42), who studied shear rates below 1000 s⁻¹. Regardless, transport-limited growth is often neglected during treatment of at-risk patients for thrombosis and also in medical device development. Locally lowering platelet arrival rates near at-risk substrates has the potential as an alternative antithrombotic therapy relative to antiplatelet drugs that would allow normal hemostasis in the body, while reducing thrombus risk. Antiplatelet drugs that lower the kinetic binding rate of platelets would be expected to have more efficacy at shear rates >7000 s⁻¹, where we found thrombus growth rates to be limited by binding as opposed to transport, as illustrated in Fig. 5.

Figure 5.

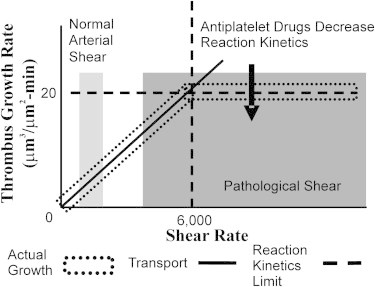
Depiction of the general relationship between thrombus growth that is limited by transport versus growth limited by kinetic binding over a range of pathologic shear rates. (Dark shaded box) Normal human mean arterial shear rates between 50 s⁻¹ in the ascending aorta to 500 s⁻¹ in the coronary arteries. (Light shaded box) Pathological arterial shear rates in stenoses >40%. Drugs that reduce the kinetic binding rate (e.g., competitive inhibitors) will lower the line of kinetic rate-limited binding, but may not affect transport-limited binding.

There may be lower risk for complete thrombus occlusion when the time to occlusion increases (6). Specifically, stenoses with predicted occlusion times that take longer than an hour may never occlude based on the low probability of occlusion for the same stenoses in experimental studies, whereas predicted occlusion within 30 min has a higher probability of fully occluding in experimental studies (5). Our model predicts that axisymmetric idealized severe stenoses (>60% by diameter) have a high probability of occluding (occlusion time <25 min), whereas stenoses that are <40% by diameter have a lower probability for occlusion. Furthermore, thrombi that form for a 40% stenosis have a narrow geometric shape due to the initial transport-limited growth. A narrow thrombus base, relative to a larger base, may be more prone to embolization, due to the higher overall internal stress that exists in the thrombus structure. Our predicted occlusion times using the FTM also match well with experimental occlusion times from Wootton et al. (6), who reported occlusion times for 70 and 50% stenoses that were 15 min and 27 min, respectively. The computational model for slightly more severe stenoses resulted in similar occlusion times: 80% stenosis occluded in 13 min, whereas a 60% stenosis occluded in 25 min.

There remains controversy in the field about whether platelets near a vessel wall experience ED or thermal diffusivity, because this region is a plasma-skimming layer that is relatively void of RBCs. Species transport predictions of thrombosis in the absence of enhanced diffusivity yields platelet flux rates that are lower than experimental growth rates by orders of magnitude, resulting in occlusion that occurs over a month as opposed to minutes seen in experiments (39). Recent work from direct numerical simulations of RBCs show that the plasma skimming layer is very small (44). Correspondingly, this study shows that RBC-dependent ED near the wall can drive the high thrombus growth rates found in experiments. These results indicate that experiments using platelet-rich plasma instead of whole blood would result in very poor platelet transport to a surface, because it would lack RBC-based ED.

The plasma-skimming layer is distinct from platelet margination, which extends from the vessel wall by ∼10% of the vessel diameter in our model. Platelet concentrations profiles in our model of margination consisting of a skewed RBC profile and a RBC-dependent field potential match well with experiments performed in large vessels of 3 mm in diameter, as shown in the Supporting Material (26,45). We neglect possible shear dependence on margination in the model because ED near the stenosis apex is orders of magnitude lower than advection, due the high Péclet number (Pe = LU/D ∼ 10⁵, derived in the Supporting Material).

We found that a kinetic binding rate constant of ∼10⁻⁴ m/s yielded the lowest RMSE. The higher value of 10⁻³ is sufficiently high that it represents an infinite sink of shear rates at <6000 s⁻¹. However, embolism and imperfect platelet-surface interactions may lead to lower net binding rates. This value compares favorably with the 10⁻⁴ m/s value from Jordan et al. (46), but slightly exceeds the value of 5 × 10⁻⁵ m/s found from Wootton et al. (6) and Sorenson et al. (47) for initial platelet deposition. Goodman et al. (48) found a kinetic rate constant of 3.5 × 10⁻³ m/s for activated platelets and a value of 2.5 × 10⁻⁶ m/s for platelets that have not activated. Initial platelet deposition would likely occur by nonactivated circulating platelets that do not have sufficient time to activate before attaching to the stenosis (6,49).

Our kinetic parameter was fit to data containing millions of platelets depositing on thrombus, thus may represent an average rate for a mixture of activated and nonactivated platelets. Furthermore, the experimental trend of decreasing thrombus growth rates at very high shear rates above 10,000 s⁻¹ suggests that the kinetic binding rate for platelets may not be a constant for all shear rates, which may explain why a large range of constants exist in the literature. For example, von Willebrand Factor (VWF) is critical for platelet binding at high shear, but its presence and conformation may not be constant. Recent work by Wellings and Ku (50) indicates that the kinetic binding rates of platelet-platelet interactions through VWF may be dominated by the shear-dependent transport or release of VWF. The von Willebrand Factor also elongates at shear rates near 5000 s⁻¹, which may further contribute to the binding kinetics at high shear rates (51,52). Furthermore, shear-dependent platelet shape change, activation, and drag forces play a role in platelet-binding kinetics. Platelet activation agonists release rates are poorly understood and likely depend on shear, calcium signaling, surface substrates, and the presence of other agonists. Binding kinetics at these high shear rates may be highly complex and models would be highly speculative. Increasing the complexity, the thrombus may break off and embolize with such high shear stresses (37). Unfortunately, little quantitative experimental data are available regarding this mechanism. As a limitation, we did not include shear-dependent binding kinetics or embolization as parameters in our model.

An additional possibility for reducing growth rates is that platelet transport may be limited at very high shear rates. Enhanced diffusivity determined by Zydney and Colton (24) was based on a curve that was fit to data of shear rates that only reached 5000 s⁻¹. Here, we have extrapolated the function for greater shear rates. It is possible that the transport of platelets and RBCs do not continue to increase with shear beyond this point.

This study has several other mechanical limitations. Thrombus occlusion predictions neglect some hemodynamic factors that are considered to have a secondary effect on transport, such as pulsatility, rigid walls, and vessel curvature (49,53,54). Furthermore, the model has limitations as thrombus nears occlusion due to possible vessel collapse and low mesh resolution. Compliant stenoses may potentially collapse from low Bernoulli pressures near the stenosis apex (55,56). The computational mesh of the lumen became large as thrombus grew to occlusion, which limited the study to a 95% stenosis. For >95% stenosis, Fahreus-Lindquist effects may begin to influence transport, and non-Newtonian viscous effects may become more prominent.

Conclusions

Thrombus growth rates during rapid platelet accumulation are found to be transport rate-limited for shear rates <6000 s⁻¹, based on an in silico model of platelet flux with enhanced diffusivity that was validated with experimental measurements of thrombus growth in a stenotic tube. The experimental thrombus growth for all shear rates was best captured by inclusion of enhanced diffusivity, margination, binding kinetics, and an activation lag time. The model can be used to predict occlusion times for new hemodynamic situations such as a patient-specific diseased coronary artery.